On the biomechanics and mechanobiology of growing skin

Abstract

Skin displays an impressive functional plasticity, which allows it to adapt gradually to environmental changes. Tissue expansion takes advantage of this adaptation, and induces a controlled in situ skin growth for defect correction in plastic and reconstructive surgery. Stretches beyond the skin’s physiological limit invoke several mechanotransduction pathways, which increase mitotic activity and collagen synthesis, ultimately resulting in a net gain in skin surface area. However, the interplay between mechanics and biology during tissue expansion remains unquantified. Here we present a continuum model for skin growth that summarizes the underlying mechanotransduction pathways collectively in a single phenomenological variable, the strain-driven area growth. We illustrate the governing equations for growing biological membranes, and demonstrate their computational solution within a nonlinear finite element setting. In displacement-controlled equi-biaxial extension tests, the model accurately predicts the experimentally observed histological, mechanical, and structural features of growing skin, both qualitatively and quantitatively. Acute and chronic elastic uniaxial stretches are 25% and 10%, compared to 36% and 10% reported in the literature. Acute and chronic thickness changes are −28% and −12%, compared to −22% and −7% reported in the literature. Chronic fractional weight gain is 3.3, compared to 2.7 for wet weight and 3.3 for dry weight reported in the literature. In two clinical cases of skin expansion in pediatric forehead reconstruction, the model captures the clinically observed mechanical and structural responses, both acutely and chronically. Our results demonstrate that the field theories of continuum mechanics can reliably predict the mechanical manipulation of thin biological membranes by controlling their mechanotransduction pathways through mechanical overstretch. We anticipate that the proposed skin growth model can be generalized to arbitrary biological membranes, and that it can serve as a valuable tool to virtually manipulate living tissues, simply by means of changes in the mechanical environment.

1. Motivation

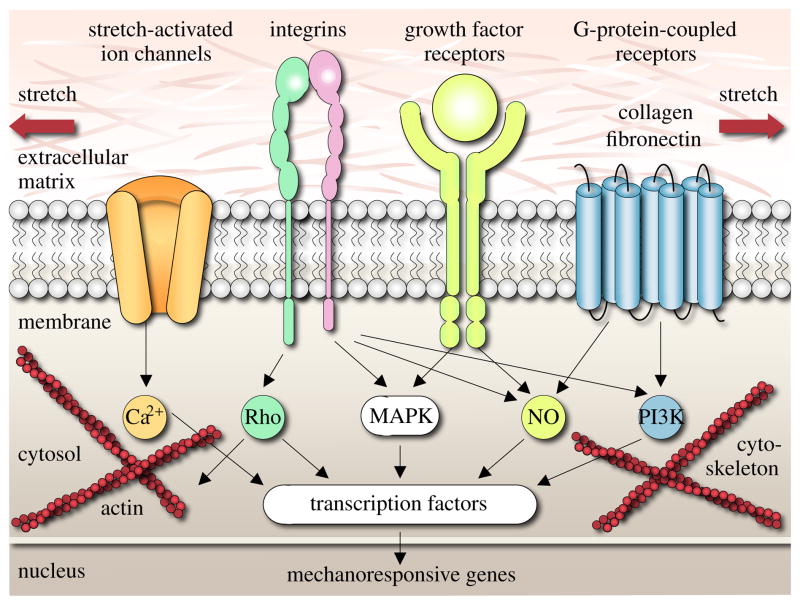
Human skin is a remarkable organ that can be stretched to manyfold its original size, while remaining phenotypically similar to its initial state, without any reported malignant transformation [12, 17]. To enable this incredible expansion, skin is a highly specialized mechanoresponsive interface, characterized through a network of interrelated cascades involving extracellular, membrane, cytosolic, cytoskeletal, and nuclear mechanisms [56]. When skin is stretched beyond its physiological limit, these mechanisms act in concert to restore the homeostatic equilibrium state. In this regulatory process, transmembrane mechanosensors in the form of stretch-activated ion channels, integrins, growth factor receptors, and G-protein-coupled receptors play a key role in translating extracellular events into intracellular signals [31, 69], see Figure 1.

Figure 1.

Mechanotransduction of growing skin. Transmembrane mechanosensors in the form of stretch-activated ion channels, integrins, growth factor receptors, and G-protein-coupled receptors translate extracellular signals into intracellular events, which activate a cascade of interconnected signaling pathways. Biomechanical and biochemical signals converge in the activation of transcription factors, activating gene expression. Mechanotransduction triggers increased mitotic activity and increased collagen synthesis, resulting in an increase in skin surface area to restore the homeostatic equilibrium state [31, 69].

Stretch-activated ion channels open in response to elevated membrane strains, allowing positively charged calcium ions (Ca²⁺) and other cations to enter the cell. Changes in the intracellular calcium concentration are known to regulate intracellular signaling and cytoskeletal remodeling [56]. Integrins are receptors that mediate attachment between a cell and the extracellular matrix [57]. They play a central role in force transmission across the cell membrane, triggering targets such as nitric oxide (NO) signaling, mitogen-associated protein kinases (MAPK), Rho GTPases, and phosphoinositol-3-kinase (PI3K). Growth factor receptors bind to growth factors outside the cell, thereby turning on several receptor mediated pathways inside the cell, such as nitric oxide (NO) signaling and mitogen-associated protein kinases (MAPK) [31]. Mitogen-associated protein kinase signaling pathways convey information to effectors, coordinate incoming information from other signaling cascades, amplify signals, and initiate a variety of response patterns. G protein-coupled receptors are seven-transmembrane proteins, which can potentially be activated by mechanical stretch outside the cell to initiate mechanotransduction pathways inside the cell through second messengers such as nitric oxide (NO) signaling and phosphoinositol-3-kinase (PI3K). Last, intracellular strain can induce conformational changes in the cytoskeleton itself. These changes may affect the binding affinities to specific molecules and thereby activate additional signaling pathways [39].

In summary, mechanical activation initiates multiple signaling pathways, which can have a substantial overlap and crosstalk. However, since mechanically-induced signaling pathways may be shared with classical receptor-mediated pathways, they are typically difficult to study in isolation. It is clear, however, that all these signaling pathways converge to activate transcription factors, which stimulate gene expression and other nuclear events [69]. Overall, the underlying principle is that stretch invokes a cascade of events that trigger increased mitotic activity and increased collagen synthesis, which ultimately result in increased skin surface area to restore the homeostatic equilibrium state [62].

Taking advantage of mechanotransduction is a powerful approach to endogenously engineer new skin. Since it was first introduced in the mid 1950s [47], the controlled mechanical manipulation of skin has opened a whole new frontier in reconstructive surgery. Today tissue expansion is widely used to repair birth defects [6], correct burn injuries [5], and reconstruct breasts after tumor removal [49]. It is the ideal strategy to grow skin that matches the color, texture, hair bearance, and thickness of the surrounding healthy skin, while minimizing scars and risk of rejection [51].

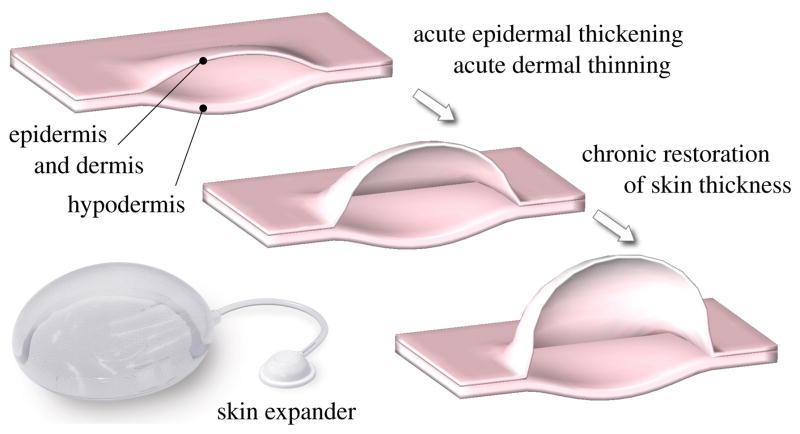
Tissue expansion is an iterative procedure of controlled overstretch, progressive skin growth, and gradual restoration of the homeostatic equilibrium state, repeated in several weekly intervals [25]. To grow skin in a desired location, the surgeon dissects a subcutaneous pocket between the dermis and the hypodermis [27], in which he places the expander. The expander is successively filled with saline solution by a remote injection port, see Figure 2. By visual inspection of skin color, capillary refill, and palpation of the expanded skin, the surgeon heuristically determines the amount of filling [51]. Once enough new skin is produced, typically after a period of multiple weeks, the device is removed, and the new skin is used to repair the adjacent defect zone. Although tissue expansion is a common surgical procedure today, there are no scientific guidelines for optimal device selection. Accordlingly, the appropriate choice of expander shape, expander size, expander location, filling volume, and filling timing remains almost exclusively based on the surgeon’s experience and personal preference [41].

Figure 2.

Biomechanics of growing skin. At biological equilibrium, the skin is in a homeostatic state of resting tension. To grow skin for defect repair, a tissue expander is placed in a subcutaneous pocket underneath the epidermis and the dermis, above the hypodermis. When the expander is inflated, the skin is stretched, associated with an acute dermal thinning attributed to the Poisson effect. Stretches beyond a critical level trigger a series of signaling pathways leading to the creation of new skin. Skin restores its homeostatic state, associated with the chronic restoration of the original thickness. Upon expander removal, elastic deformations retract and inelastic deformations remain.

The first quantitative model for growing skin was proposed only a few years ago, and has unfortunately not received a lot of attention to date [58]. Motivated by this first study on axisymmetric skin growth, conceptually similar to an axisymmetric model for growing cell walls [22], we have recently established a prototype model for growing biological membranes to predict skin growth in a general three-dimensional setting [13]. The model is based on the continuum framework of finite growth [52], originally developed for the isotropic volumetric growth of biological solids [2, 18, 42]. Its key kinematic feature is the multiplicative decomposition of the deformation gradient into a reversible elastic part and an irreversible growth part [19, 43], a concept that was adopted from finite plasticity [40]. Over the past decade, continuum growth theories have been rapidly developed and intensely refined to characterize isotropic [15, 24, 37], transversely isotropic [50, 59], orthotropic [21, 60], and generally anisotropic [3, 46] growth phenomena, both compressibly [44] and incompressibly [30, 53]. Recent trends focus on the computational modeling of finite growth [4, 28], typically by introducing the growth tensor as an internal variable within a nonlinear finite element framework [20, 34], a strategy that we also adopt here. To predict the biomechanics and mechanobiology of growing skin and their impact on stress, strain, and area gain, we adopt a transversely isotropic growth model [13, 14], in which all cellular and molecular mechanisms are collectively summarized in a single phenomenological internal variable, the in-plane area growth. Here, in contrast to our previous model formulated in the material frame of reference [70], we introduce a spatial formulation, which lends itself to a computationally elegant and highly efficient algorithm. To simulate heterogeneous growth phenomena on anatomically realistic geometries, we integrate the growth model into a multi-purpose nonlinear finite element program [63]. We illustrate its features by means of the simple model problem of equi-biaxial extension and through two clinical cases of skin expansion in pediatric forehead reconstruction.

2. Methods

2.1. Continuum model of growing skin

To accurately represent the finite deformations during skin expansion, we adopt the kinematics of finite growth, and introduce the deformation map ϕ, which, at any given time t, maps the material placement X of a physical particle onto its spatial placement x = ϕ (X, t). We then introduce the multiplicative decomposition of the deformation gradient [52],

$$\mathit{F}={\mathbf{\nabla }}_{\mathit{X}}\mathit{\varphi }={\mathit{F}}^{\text{e}}·{\mathit{F}}^{\text{g}}$$ (1)

into a reversible elastic part F^e and an irreversible growth part F^g, in agreement with experimental findings [66]. Here, ∇{∘} = ∂_x{∘}|_t denotes the gradient of a field {∘} (X, t) with respect to the material placement X at fixed time t. Its Jacobian defines the overall change in tissue volume,

$$J=det(\mathit{F})=J^{\text{e}}{J}^{\text{g}}$$ (2)

which we can equivalently decompose into a reversibly elastic volume change J^e = det (F^e) and an irreversibly grown volume change J^g = det (F^g). Skin is a composite material consisting of a 0.1–1.0 mm thick, waterproof, protective outer layer, the epidermis, and a 1.0–4.0 mm thick, load bearing inner layer, the dermis [56], which we idealize jointly as a single layer. We characterize its area stretch through Nanson’s formula

$$\vartheta =\left|\right|\text{cof}(\mathit{F})·{\mathit{n}}_0\left|\right|={\vartheta }^{\text{e}}{\vartheta }^{\text{g}}$$ (3)

in terms of the skin plane normal n₀ in the undeformed reference configuration, where cof(∘) = det (∘) (∘)^−t denotes the cofactor of a second order tensor (∘). The area stretch obeys the multiplicative decomposition into a reversibly elastic area stretch ϑ^e and an irreversibly grown area stretch ϑ^g = ||cof(F^g) · n₀||. To model stretch-induced skin growth, we collectively summarize the effects of mechanotransduction in a single scalar-valued variable ϑ^g, which characterizes the evolution of the in-plane area growth, while the response in the thickness direction n₀ is assumed to be purely elastic [12]. Accordingly, we can express the growth tensor F^g in the following simple format.

$${\mathit{F}}^{\text{g}}=\sqrt{{\vartheta }^{\text{g}}}\mathit{I}+[1-\sqrt{{\vartheta }^{\text{g}}}]{\mathit{n}}_0\otimes {\mathit{n}}_0$$ (4)

Since the material is not assumed to grow in the thickness direction n₀ [51, 64], its area growth is identical to its volume growth, i.e., ϑ^g = det(F^g) = J^g. Using the simple rank-one update structure of F^g, we can apply the Sherman-Morrison formula to invert the growth tensor explicitly,

$${\mathit{F}}^{\text{g}-1}=\frac{1}{\sqrt{{\vartheta }^{\text{g}}}}\mathit{I}+\left[1-\frac{1}{\sqrt{{\vartheta }^{\text{g}}}}\right]{\mathit{n}}_0\otimes {\mathit{n}}_0$$ (5)

and obtain an explicit representation of the elastic tensor F^e,

$${\mathit{F}}^{\text{e}}=\frac{1}{\sqrt{{\vartheta }^{\text{g}}}}\mathit{F}+\left[1-\frac{1}{\sqrt{{\vartheta }^{\text{g}}}}\right]\mathit{n}\otimes {\mathit{n}}_0$$ (6)

in terms of the spatial normal n = F · n₀. From the push forward of the contravariant material and intermediate metric tensors G⁻¹ and G^g−1, we obtain the left Cauchy Green tensor b = F · G⁻¹ · F^t and its counterpart b^e in the deformed, current configuration.

$${\mathit{b}}^{\text{e}}={\mathit{F}}^{\text{e}}·{\mathit{G}}^{g-1}·{\mathit{F}}^{\text{et}}=\frac{1}{{\vartheta }^{\text{g}}}\mathit{b}+\left[1-\frac{1}{{\vartheta }^{\text{g}}}\right]\mathit{n}\otimes \mathit{n}$$ (7)

To focus on the impact of growth, we assume skin to behave isotropically elastic within the in vivo loading range of interest. Accordingly, we introduce the following Helmholtz free energy

$$\psi =\frac{1}{2}\lambda {ln}^2(J^{\text{e}})+\frac{1}{2}\mu [\mathit{g}:{\mathit{b}}^{\text{e}}-3-2ln(J^{\text{e}})]$$ (8)

to evaluate the standard dissipation inequality, which defines the Kirchhoff stress τ as thermodynamically conjugate to covariant spatial metric g.

$$\mathit{\tau }=2\frac{\partial \psi }{\partial \mathit{g}}=[\lambda ln(J^{\text{e}})-\mu ]{\mathit{g}}^{-1}+\mu {\mathit{b}}^{\text{e}}$$ (9)

This implies that the newly created skin will have the same microstructure, density, and stiffness, as the original, native tissue [12, 13]. We model skin growth as a strain-driven process [27], and introduce the following evolution equation for the area growth,

$${\stackrel{.}{\vartheta }}^{\text{g}}=k^{\text{g}}({\vartheta }^{\text{g}}){\phi }^{\text{g}}({\vartheta }^{\text{e}})$$ (10)

in which k^g(ϑ^g) is a weighting function and φ^g(ϑ^e) is a growth criterion similar to a yield function in the theory of plasticity. For the weighting function, we adopt a well-established functional form [42], which we rephrase here in a strain-driven format [20, 21], to control unbounded growth.

$$k^{\text{g}}=\frac{1}{\tau }{\left[\frac{{\vartheta }^{max}-{\vartheta }^{\text{g}}}{{\vartheta }^{max}-1}\right]}^{\gamma }$$ (11)

The adaptation speed τ and the shape parameter for the adaptation curve γ control the speed of adaptation, whereas the maximum area growth ϑ^max defines the biological equilibrium state [28, 42]. For the growth criterion, we assume that growth is driven by the elastic area stretch ϑ^e,

$${\phi }^{\text{g}}=\langle {\vartheta }^{\text{e}}-{\vartheta }^{\text{crit}}\rangle =\langle \vartheta /{\vartheta }^{\text{g}}-{\vartheta }^{\text{crit}}\rangle$$ (12)

and that it is activated only if the elastic area stretch exceeds a critical physiological limit ϑ^crit, where 〈 ∘ 〉 denote the Macaulay brackets.

2.2. Computational model of growing skin

To solve the nonlinear finite element equations of stretch-induced skin growth, we implement the growth model in a custom-designed version of the multipurpose nonlinear finite element program FEAP [63]. To characterize the growth process at each instant in time, we introduce the area growth ϑ^g as an internal variable, and solve the biological equilibrium equation (10) locally at the integration point level. At each discrete time step t, we determine the current area growth ϑ^g for a given current deformation state F and a given area growth ${\vartheta }_{\text{n}}^{\text{g}}$ from the previous time step t_n. Accordingly, we introduce the following finite difference approximation for the material time derivative of the area growth,

$${\stackrel{.}{\vartheta }}^{\text{g}}=[{\vartheta }^{\text{g}}-{\vartheta }_{\text{n}}^{\text{g}}]/\mathrm{\Delta }t$$ (13)

where Δt = t − t_n denotes the current time increment. In the spirit of implicit time stepping schemes, we now reformulate the evolution equation (10) with the help of equation (13), introducing the discrete residual R^ϑ in terms of the unknown area growth ϑ^g.

$${\text{R}}^{\vartheta }={\vartheta }^{\text{g}}-{\vartheta }_{\text{n}}^{\text{g}}-k^{\text{g}}{\phi }^{\text{g}}\mathrm{\Delta }t\doteq 0$$ (14)

We solve this nonlinear equation using a local Newton iteration. Within each iteration step, we calculate the linearization of the residual R^ϑ with respect to the area growth ϑ^g,

$${\text{K}}^{\vartheta }=\frac{\partial {\text{R}}^{\vartheta }}{\partial {\vartheta }^{\text{g}}}=1-\left[\frac{\partial k^{\text{g}}}{\partial {\vartheta }^{\text{g}}}{\phi }^{\text{g}}+k^{\text{g}}\frac{\partial {\phi }^{\text{g}}}{\partial {\vartheta }^{\text{g}}}\right]\mathrm{\Delta }t$$ (15)

in terms of the linearizations of the weighting function ∂k^g/∂ϑ^g = −γk^g/[ϑ^max − ϑ^g] and the growth criterion ∂φ^g/∂ϑ^g = −ϑ/ϑ^g2 introduced in equations (11) and (12). We update the unknown area growth iteratively,

$${\vartheta }^{\text{g}}\leftarrow {\varphi }^{\text{g}}-{\text{R}}^{\vartheta }/{\text{K}}^{\vartheta }$$ (16)

until we achieve convergence, i.e., until the absolute value of the local growth update Δϑ^g = −R^ϑ/K^ϑ is below a user-defined threshold value. Once we have iteratively determined the current area growth ϑ^g, we can successively determine the growth tensor F^g from equation (4), the elastic tensor F^e = F · F^{g − 1} from equation (6), the Kirchhoff stress τ from equation (9), and, finally, the fourth order tensor e of the Eulerian constitutive moduli.

$$\mathbf{e}=2\frac{d\mathit{\tau }}{\text{d}\mathit{g}}={\mathbf{e}}^{\text{e}}+{\mathbf{e}}^{\text{g}}={2\frac{\partial \mathit{\tau }}{\partial \mathit{g}}|}_{F^{\text{g}}}+{\frac{\partial \mathit{\tau }}{\partial {\vartheta }^{\text{g}}}\otimes 2\frac{\partial {\vartheta }^{\text{g}}}{\partial \mathit{g}}|}_F$$ (17)

The first term, the partial derivative of the Kirchhoff stress τ with respect to the covariant spatial metric g, defines elastic constitutive moduli e^e = 2 ∂τ/∂g,

$$2\frac{\partial \mathit{\tau }}{\partial \mathit{g}}=\lambda {\mathit{g}}^{-1}\otimes {\mathit{g}}^{-1}+[\mu -\lambda ln(J^{\text{e}})][{\mathit{g}}^{-1}\overline{\otimes }{\mathit{g}}^{-1}+{\mathit{g}}^{-1}\underset{\_}{\otimes }{\mathit{g}}^{-1}]$$ (18)

where we have used the common abbreviations, {•⊗̄∘}_{i jkl} = {•}_ik {∘}_jl and {•⊗̱∘}_{i jkl} = {•}_il {∘}_jk, for the non-standard fourth order products. The second term

$$\frac{\partial \mathit{\tau }}{\partial {\vartheta }^{\text{g}}}=-\frac{1}{{\vartheta }^{\text{g}2}}\left[\lambda {\vartheta }^{\text{g}}{\mathit{g}}^{-1}+\mu [\mathit{b}-\mathit{n}\otimes \mathit{n}]\right]$$ (19)

depends directly on the constitutive formulation for the Kirchhoff stress τ in equation (9) and indirectly on the particular format of the growth tensor F^g in equation (4). The third term

$$2\frac{\partial {\vartheta }^{\text{g}}}{\partial \mathit{g}}=\frac{1}{\tau }\frac{1}{{\vartheta }^{\text{g}}}{\left[\frac{{\vartheta }^{max}-{\vartheta }^{\text{g}}}{{\vartheta }^{max}-1}\right]}^{\gamma }\frac{1}{{\text{K}}^{\text{g}}}\mathrm{\Delta }t\left[\vartheta {\mathit{g}}^{-1}-\frac{J^2}{\vartheta }[{\mathit{F}}^{-\text{t}}·{\mathit{n}}_0]\otimes [{\mathit{F}}^{-\text{t}}·{\mathit{n}}_0]\right]$$ (20)

consists of the algorithmic linearization of the time discrete evolution equation for the area growth ∂ϑ^g/∂ϑ in equation (16) and of the linearization of the area stretch 2 ∂ϑ/∂g in equation (3). The local stress of equation (9) and the local consistent tangent of equation (17) enter the global righthand side vector and the global iteration matrix of the global Newton iteration. Upon its convergence, we store the corresponding area growth ϑ^g locally at the integration point level.

3. Results

We illustrate the features of the proposed growth model for the simple model problem of displacement driven equi-biaxial extension and for the clinical case of tissue expansion in pediatric forehead reconstruction. For the elastic model, we assume Lamé constants of λ = 0.7141 MPa and μ = 0.1785 MPa, which would correspond to a Young’s modulus of E = 0.5 MPa and Poisson’s ratio of ν = 0.4 in the linear regime [1, 54]. For the growth model, we assume that growth takes place above the critical threshold of ϑ^crit = 1.21, corresponding to uniaxial stretches of 10% [12]. We restrict the maximum area growth to ϑ^max = 4.0, and assume an adaptation speed of τ = 1/12 and growth exponents of γ = 2.0 and γ = 12.0 in examples 3.1 and 3.2. Sensitivity analyses demonstrate that the parameters τ and γ influence the adaptation time and the shape of the adaptation curve, but not the final state of biological equilibrium [28, 70].

3.1. Model problem - Skin growth in equi-biaxial extension

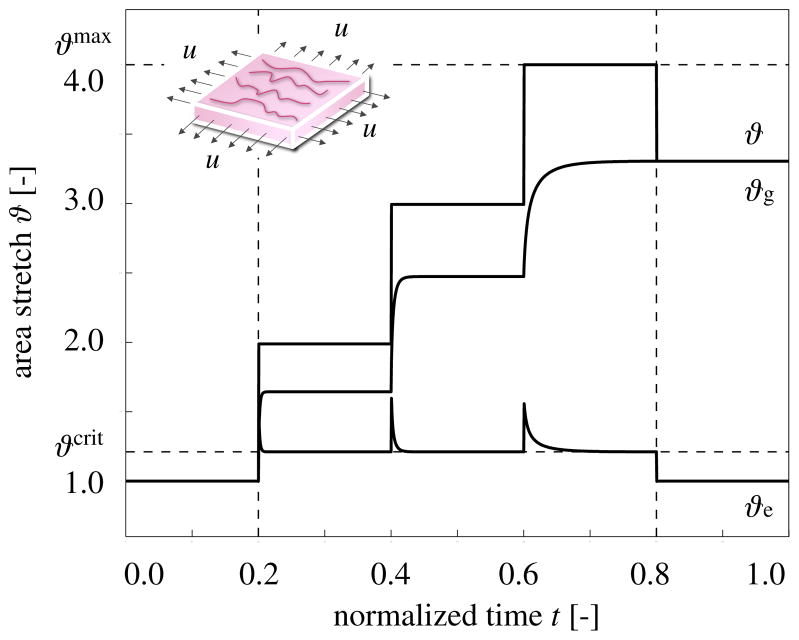
We illustrate the conceptual features of our growth model by exploring the simple model problem of displacement-driven skin expansion of a square 1.0 × 1.0 × 0.2 sheet. In an equi-biaxial setting, we increase the prescribed displacements such that the in-plane area stretch is increased from ϑ = 1.0 to 2.0, 3.0, and 4.0, indicated through the vertical dashed lines in Figure 3. This implies that the skin sheet is gradually stretched to a final size of 2.0 × 2.0, i.e., to four times its original size. After applying the deformation, we allow the tissue to adapt, and recover its homeostatic equilibrium state. After three load increments, we remove the applied stretch and allow the tissue to relax.

Figure 3.

Temporal evolution of total area stretch ϑ, reversible elastic area stretch ϑ^e, and irreversible growth area stretch ϑ^g for displacement driven skin expansion. Displacements are increased and then held constant in three intervals between the vertical dashed lines, and then relaxed. Displacement control induces relaxation indicated through the gradual decrease in elastic stretch ϑ^e and stress, while the growth stretch ϑ^g increases at a constant total stretch ϑ. Horizontal dashed lines represent the elastic stretch limit beyond which skin growth is activated ϑ^crit, and the maximum area growth ϑ^max.

Figure 3 illustrates the resulting temporal evolution of the total area stretch ϑ, the reversible elastic area stretch ϑ^e, and the irreversible area growth ϑ^g. The horizontal dashed lines represent the elastic stretch limit ϑ^crit beyond which skin growth is activated, and the maximum area growth ϑ^max. The curves confirm, that, at all times, the multiplicative decomposition of the deformation gradient F = F^e · F^g introduced in equation (1) carries over to the multiplicative decomposition of the total area stretch ϑ = ϑ^e ϑ^g of equation (3). Convergence towards the homeostatic state manifests itself through a gradual increase of growth ϑ^g at a constant total stretch ϑ, while the elastic stretch ϑ^e, and, accordingly the stresses, decrease. Upon removal of the applied displacements, the elastic stretch instantaneously returns to its baseline value of one, ϑ^e = 1. Since the growth process is assumed to be irreversible, the growth stretch remains constant, ϑ^g = const. The total stretch instantaneously adapts the value of the growth stretch, ϑ = ϑ^g.

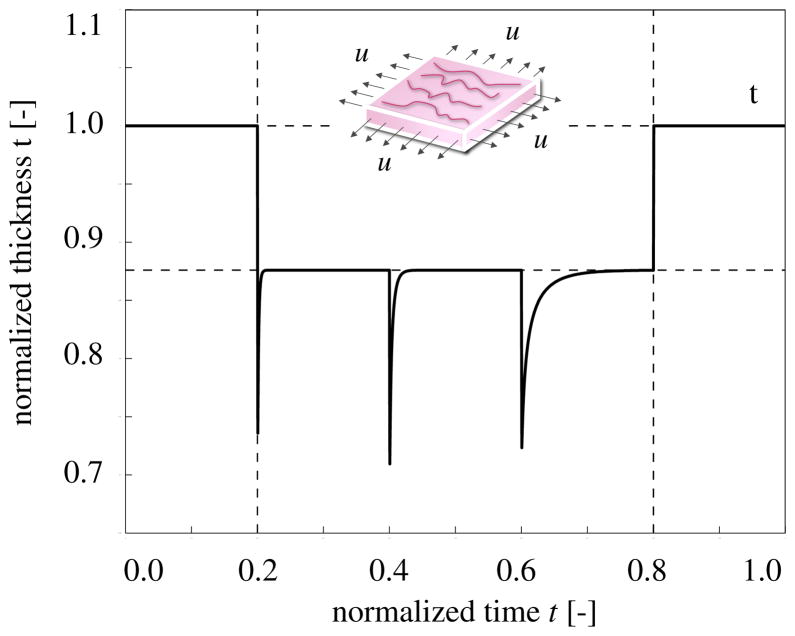
Figure 4 shows the temporal evolution of the skin thickness. Upon loading, the thickness decreases acutely from 1.0 to 0.72, but then returns chronically to its loaded baseline value of 0.88. This value, indicated through the lower horizontal line, is slightly smaller than the original thickness because of the Poisson effect. Upon removal of the applied displacements, the skin thickness immediately returns to its original value of t = 1.0, indicated through the upper horizontal line. Since the model assumes no growth in thickness direction, t^g = 1.0, all thickness changes are fully reversible, t^e = t.

Figure 4.

Temporal evolution of skin thickness t for displacement driven skin expansion. Displacements are increased and then held constant in three intervals between the vertical dashed lines, and then relaxed. Upon stretching, the skin thickness decreases acutely to 0.72, but then returns chronically to the homeostatic equilibrium thickness of 0.88 indicated through the lower horizontal line. This value is smaller than the original thickness because of the Poisson effect. Upon displacement relaxation, however, the skin thickness immediately returns to its original value of 1.0, indicated through the upper horizontal line.

3.2. Clinical problem - Skin growth in pediatric forehead reconstruction

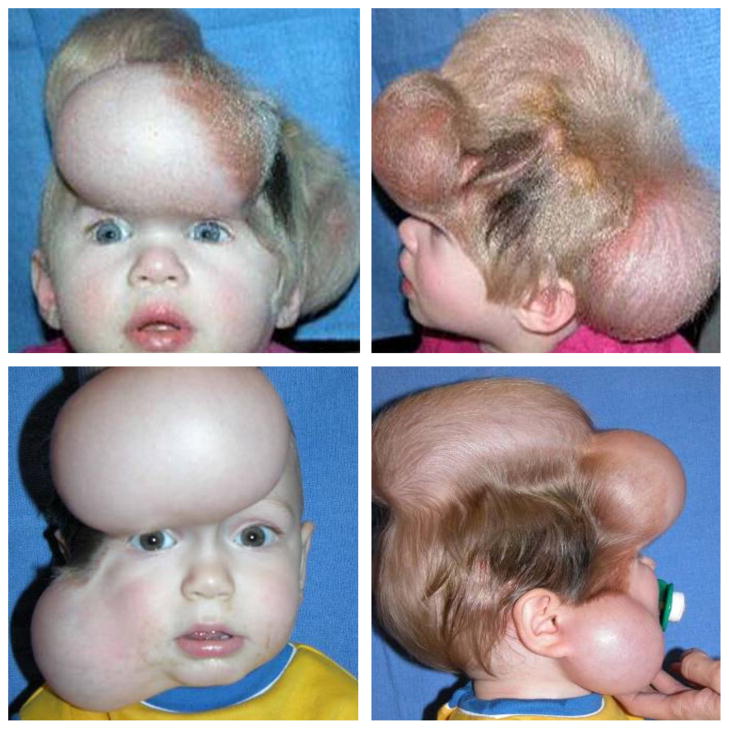
To illustrate the full potential of our model, we simulate skin expansion in pediatric forehead reconstruction for two clinical cases, a one-year old girl in case study I [26], and a one-year old boy in case study II [27], both born with giant congenital nevi affecting almost half of their foreheads, see Figure 5. Because giant congenital nevi place the child at an increased risk of skin cancer, the nevus is typically removed in the early childhood [25]. To reconstruct the defect, preserve function, and maintain aesthetic appearance, both children underwent conrolled tissue expansion [41]. To simulate the process of tissue expansion in an anatomically exact geometry, we create a finite element mesh from three-dimensional computer tomography images of a child of similar age following the procedure outlined in [70]. We identify the skin region by its distinct grey scale value in the computer tomography scans to create a triangular surface mesh, which we further smoothen semi-manually. From the smoothened surface mesh, we create a volume mesh of the skin layer, discretized with 61,228 nodes, 183,684 degrees of freedom, and 30,889 tri-linear brick elements. Last, we assign each element a skin plane normal n₀, corresponding to the normal of the initial surface mesh.

Figure 5.

Skin expansion in pediatric forehead reconstruction. The patients, a one-year old girl, case study I shown in the top row [26], and a one-year old boy, case study II shown in the bottom row [27], both presented with a giant congenital nevus. Three forehead, scalp, and cheek expanders were implanted simultaneously for in situ skin growth. After enough skin is grown, the nevus is removed and the new skin is pulled over the would to close it.

Case study I: Simultaneous forehead, anterior and posterior scalp expansion

The first case study mimics the case of a one-year old girl, whose nevus covered her left posterior forehead [26]. To grow extra skin to cover the defect area, she underwent simultaneous tissue expansion in the forehead and in the anterior and posterior scalp as shown in Figure 5, top row. To model her case, we virtually implant three expanders. First, we implant an expander in the posterior scalp, discretized with 4,726 nodes, 14,178 degrees of freedom, and 2,270 tri-linear brick elements, covering an initial area of 53.1 cm². Second, we implant two closely connected expanders in the forehead and in the scalp, discretized together with 7,954 nodes, 23,862 degrees of freedom, and 3,820 tri-linear brick elements, covering an initial area of 96.3 cm². To simulate tissue expansion, we fix all nodes and release only the expander degrees of freedom, which we then pressurize from underneath. We assume that the adjacent dermis and hypodermis remain closely connected [58].

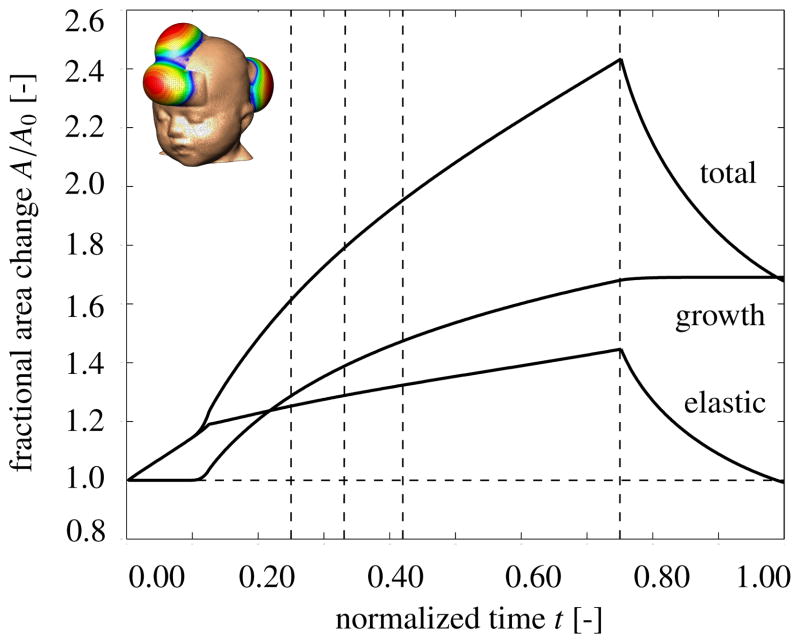
Figure 6 displays the temporal evolution of the normalized total area, elastic area, and growth area upon gradual expander inflation, constant pressure, and gradual expander removal. Once the elastic area stretch reaches the critical threshold of ϑ^crit = 1.21, slightly before the total pressure is applied, at t = 0.125, the tissue starts to grow. As the expander pressure is held constant, growth increases gradually causing the total area to increase. Then, at t = 0.75, the pressure is decreased to remove the expander. The elastic area retracts gradually, while the grown area remains constant. The vertical dashed lines correspond to the discrete time points, t = 0.24, t = 0.33, t = 0.42 and t = 0.75, displayed in Figure 7.

Figure 6.

Skin expansion in pediatric forehead reconstruction. Case study I: Simultaneous forehead, anterior and posterior scalp expansion. Temporal evolution of normalized total area, elastic area, and growth area upon gradual expander inflation, 0.0 < t ≤ 0.125, constant pressure 0.125 < t ≤ 0.75, and deflation 0.75 < t ≤ 1.0. The expanded area increases from 149.4 cm² to 251.2 cm², corresponding to a final fractional area gain of 1.68. Vertical dashed lines correspond to the time points displayed in Figure 7.

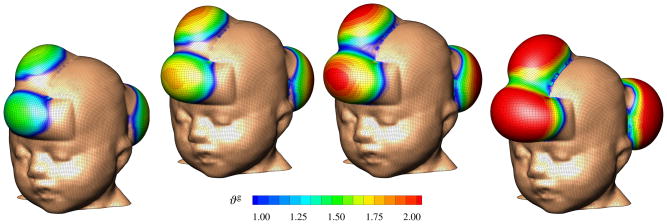
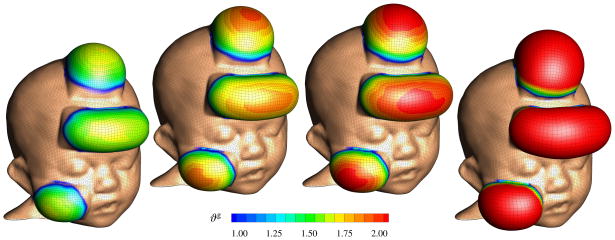
Figure 7.

Skin expansion in pediatric forehead reconstruction. Case study I: Simultaneous forehead, anterior and posterior scalp expansion. Spatio-temporal evolution of area growth displayed at t = 0.24, t = 0.33, t = 0.42 and t = 0.75. The initial area of 149.4 cm² increases gradually as the grown skin area increases to 190.2 cm², 207.4 cm², 220.4 cm², and finally 251.2 cm², from left to right.

Figure 7 illustrates the spatio-temporal evolution of the area growth ϑ^g. Growth is first initiated at the center of the expanders, where the elastic stretch is largest. As growth spreads throughout the entire expanded areas, the initial area of 149.4 cm² increases gradually as the grown skin area increases to 190.2 cm², 207.4 cm², 220.4 cm², and finally 251.2 cm², displayed from left to right. In detail, we observe that the final area in the posterior scalp region is 91.5 cm², corresponding to a fractional area gain of 1.73. In the combined forehead and anterior scalp regions, the final area is 159.6 cm², corresponding to a slightly lower fractional area gain of 1.66. Area growth displays regional variations within 1.0 ≤ ϑ^g ≤ 2.0, i.e., in some regions, the skin has doubled its initial area. Area growth is largest in the center regions and smallest in the peripheries.

Case study II: Simultaneous forehead, scalp, and cheek expansion

The second example mimics the case of a one-year old boy whose nevus covered his right anterior forehead [27]. We simulate his simultaneous tissue expansion with expanders in the forehead, scalp, and cheek as shown in Figure 5, bottom row. First, we virtually implant an expander in the scalp, discretized with 4,356 nodes, 13,068 degrees of freedom, and 2,088 trilinear brick elements, covering an initial area of 50.5 cm². Second, we implant an expander in the cheek, discretized with 2,542 nodes, 7,626 degrees of freedom, and 1,200 tri-linear brick elements, covering an initial area of 29.3 cm². Third, we implant an expander in the forehead, discretized with 3,782 nodes, 11,346 degrees of freedom, and 1,800 tri-linear brick elements, covering an initial area of 48.8 cm². Again, we fix all nodes and release only the expander degrees of freedom, which we then pressurize from underneath, assuming that the adjacent skin remains unaffected.

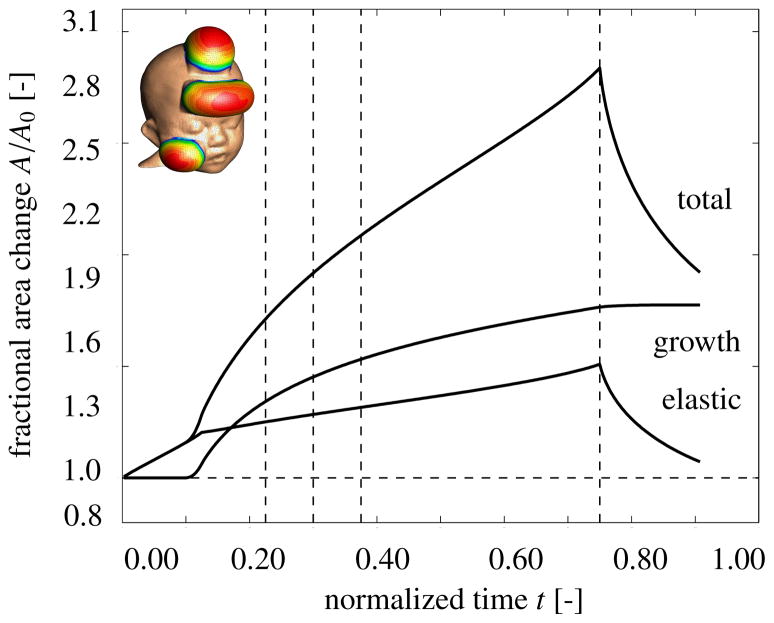
Figure 8 displays the temporal evolution of the normalized total area, elastic area, and growth area upon gradual expander inflation, constant pressure, and gradual expander removal. Similar to Figure 6, the tissue begins to grow once the elastic area stretch reaches the critical threshold of ϑ^crit = 1.21. Slightly after, at t = 0.125, the total pressure is held constant. Similar to the first case study, the skin grows gradually in all three expanded regions. When the pressure is gradually decreased at t = 0.75, the elastic area retracts, while the grown area remains constant. The vertical dashed lines correspond to the discrete time points, t = 0.24, t = 0.33, t = 0.42 and t = 0.75, displayed in Figure 9.

Figure 8.

Skin expansion in pediatric forehead reconstruction. Case study II: Simultaneous forehead, scalp, and cheek expansion. Temporal evolution of normalized total area, elastic area, and growth area upon gradual expander in-flation, 0.0 < t ≤ 0.125, constant pressure 0.125 < t ≤ 0.75, and deflation 0.75 < t ≤ 1.0. The expanded area increases from 128.7 cm² to 227.1 cm², corresponding to a final fractional area gain of 1.77. Vertical dashed lines correspond to the time points displayed in Figure 9.

Figure 9.

Skin expansion in pediatric forehead reconstruction. Case study II: Simultaneous forehead, scalp, and cheek expansion. Spatio-temporal evolution of area growth displayed at t = 0.24, t = 0.33, t = 0.42 and t = 0.75. The initial area of 128.7 cm² increases gradually as the grown skin area increases to 176.0 cm², 191.3 cm², 202.1 cm², and finally 227.1 cm², from left to right.

Figure 9 illustrates the spatio-temporal evolution of the area growth ϑ^g. Since area stretches are largest at the center of the expander, growth is first initiated in this region, spreading gradually throughout the entire expanded areas. During the growth process, the initial area of 128.7 cm² increases to 176.0 cm², 191.3 cm², 202.1 cm², and finally 227.1 cm², displayed from left to right. In detail, we observe that the new area in the scalp is 87.9 cm² with a fractional area gain of 1.74, in the cheek it is 50.6 cm² with a fractional area gain of 1.72, and in the forehead it is 88.6 cm² with the largest fractional area gain of 1.82. The area grows varies locally within the range of 1.0 ≤ ϑ^g ≤ 2.0 with largest values in the center regions, where skin typically more than doubles its initial area.

4. Discussion

Motivated by the mechanotransduction pathways outlined in Section 1, we have introduced a continuum model for growing skin in response to chronic mechanical overstretch. From a kinematic point of view, the model is based on the multiplicative decomposition of the deformation gradient into an elastic part and a growth part [52]. From a constitutive point of view, it introduces four material parameters with a clear physiological interpretation [42, 70], the critical physiological stretch limit ϑ^crit, the maximum area growth ϑ^max, the adaptation speed τ, and the shape of the adaptation curve γ. From a computational point of view, the model is embedded in a standard nonlinear finite element framework, in which the area growth ϑ^g is introduced locally as an internal variable on the integration point level [28, 37]. From an algorithmic point of view, the biological equilibrium problem for this internal variable is solved using a local Newton iteration embedded in a global Newton iteration to solve the mechanical equilibrium problem [20, 50]. Overall, our growth model is unconditionally stable, robust, efficient, conceptually modular, and easily portable. In contrast to the only other skin growth model by other authors, which is based on a rotationally symmetric formulation [58], our model is conceptually generic, and can handle arbitrary skin geometries. In contrast to our own first prototype of the model, which is based on a material formulation [13, 70], the new realization based on a spatial formulation is computationally elegant and efficient, reducing simulation times by approximately factor five.

In Section 3.1, we have demonstrated the conceptual characteristics of our growth model by means of a simple model problem of successive equi-biaxial extension. Upon displacement control, the model predicts the following features: (i) an acute increase in the elastic area stretch ϑ^e, (ii) an acute decrease in thickness t, (iii) a chronic increase in area growth ϑ^g, (iv) a chronic restoration of the homeostatic elastic area stretch ϑ^e → ϑ^crit, and (v) a chronic restoration of the homeostatic equilibrium thickness t. Upon displacement relaxation, the model predicts the following features: (vi) an acute retraction of the elastic area stretch back to its baseline value of ϑ^e = 1.0 and (vii) an acute arrest of further growth with ϑ = ϑ^g = const, see Figures 3 and 4.

Our in silico predictions are in excellent agreement with the in vivo findings reported in the literature. More than three decades ago, the first experimental studies confirmed a net gain in skin area upon tissue expansion [8, 9]. Unexpectedly, this area gain was found to take place upon conservation of cellular morphology, preservation of phenotype, and maintenance of functionality, without an inflammatory response, and without evidence of malignant degeneration [12]. This suggested that the increase in tissue surface area is a result of new tissue being regenerated, instead of being recruited from neighboring regions [17]. It supports our fundamental model assumption that skin is capable to chronically increase its area, represented through equation (3), upon mechanical overstretch, incorporated through equation (12), see Figure 3.

In what follows, we will compare the response of our model to skin growth experiments in the literature [9, 10, 12, 64, 66, 68]. Unfortunately, almost all existing data are based on in vivo tissue expansion studies. For the lack of experimental data, we assume that the in vivo strain state of a pressurized thin membrane is close to our in silico state of equi-biaxial extension. Alternatively, we could simulate the true state of tissue expansion using finite element models [13, 14]. However, since this would introduce additional discretization and modeling errors, we will assume a homogeneous strain state here, and focus on comparing the constitutive, material point response.

4.1. Discussion of acute elastic response

Acutely, tissue expansion has been associated with slight epidermal thickening and significant dermal thinning [9], resulting in an overall thinning and a reduced tensile strength [10]. Mechanically, a study in rodents reported an acute increase in uniaxial stretch of approximately 36% [12]. This is in nice agreement with our model, which predicts an acute elastic area stretch of 1.52, 1.60, and 1.56, corresponding to an average increase in uniaxial stretch of 25%, see Figure 3. Structurally, the same study identified an initial acute decrease in skin thickness from 407 ± 3 μm to 317 ± 4 μm corresponding to an acute thickness reduction of 22% [12]. Again, this is in good quantitative agreement with our model, which predicts an acute average normalized thickness of 0.74, 0.71, and 0.72 corresponding to an acute average thickness decrease of 28%, see Figure 4. Since these acute thickness changes can be attributed primarily to the Poisson effect, they can be utilized to calibrate the elastic material parameters, in particular Poisson’s ratio.

4.2. Discussion of chronic growth response

Chronically, tissue expansion is associated with the gradual restoration of baseline histology, baseline mechanics, and baseline structure [10]. Histologically, a comparison of piglet tissue in expanded and non-expanded regions demonstrated a chronic restoration of the number of epidermal cell layers and a chronic restoration of the epidermal thickness [64]. In addition, immunocytochemistry confirmed that the expanded tissue maintains its phenotypical characteristics and native program of cellular differentiation [68]. Mechanically, in a multiple time-point study in rodents, an acutely increased uniaxial stretch of 36% was reduced chronically to approximately 10% 32 days post expansion [12]. This is in excellent agreement with our model, which predicts an acutely increased uniaxial stretch of 25% and a chronic reduction to 10%, see Figure 3. A uniaxial stretch of 10% would corresponds to an area stretch of ϑ^crit = 1.21. In our model, the model parameter ϑ^crit takes the interpretation of the physiological threshold value, to which the elastic area stretch tends to return during adaptive skin growth, see equation (12). Structurally, after an initial acute thickness decrease of 22%, the same study reports a chronic restoration of the homeostatic equilibrium thickness from initially 425 ± 4 μm to 398 ± 3 μm, corresponding to a chronic thickness reduction of 7% [12]. This agrees well with our model, which predicts a normalized homeostatic equilibrium thickness of 0.88, corresponding to a chronic thickness reduction 12%, see Figure 4. The chronic rodent study also reported that the overall weight of the tissue sample almost tripled, with a fractional weight gain of approximately 2.7 for wet weight and 3.3 for dry weight [12]. In our model, the fractional weight gain is directly proportional to the fractional area gain of ϑ^g = 3.3 which agrees nicely with these experimental findings, see Figure 3. Finally, the study found a conservation of the mechanical properties, for example, a constant breaking strength acutely right after expansion and chronically long term [12]. These findings support our model assumption that ultimately, the newly created skin will have the same microstructure, density, and stiffness, as the original, native tissue [13, 14].

4.3. Discussion of elastic retraction

Acutely, upon expander removal, an instantaneous retraction of the elastic deformation significantly reduces the overall skin area. In controlled in vivo experiments in pigs, the ratio between the reversible elastic deformation to irreversible growth was almost 2:1 [66]. Since our model assumes that the overall deformation gradient can be multiplicatively decomposed into an elastic and growth part, represented through equation (1), it is perfectly capable of reproducing the effect of elastic retraction upon expander removal, see Figures 3, 6, and 8.

4.4. Discussion of growth heterogeneity

Figures 7 and 9 clearly indicate the heterogeneity of the growth process with larger values in the center region and smaller values in the periphery. This is in agreement with in vivo studies, which report a fractional area gain of 3.14, i.e., 50% above average, in the center region, and 2.06, i.e., 25% below average, in the periphery [12]. The authors hypothesized that larger strains in the center region would trigger larger growth. This is in agreement with our model in equation (10), where the evolution of area growth is directly correlated to the amount of overstretch through the growth criterion defined in equation (12).

4.5. Limitations

Although we have presented both qualitative and quantitative comparisons of the proposed model with acute and chronic tissue expansion experiments from the literature, several limitations remain. First and foremost, the most challenging aspect would be to tie the growth law in equation (4) more closely to the underlying mechanobiology described in detail in the introduction section. Comparative gene expression assays and immunohistochemistry of grown versus ungrown tissue samples could help to identify the mechanisms that trigger skin growth on the molecular and cellular level. Similar approaches have been proposed for amelogenesis [16] and tumorigenesis [7, 48] in the past and could also be adopted here. Ideally, this would help to specify our evolution equation for the growth tensor (4) in terms of discrete mechanotransduction cascades through selected extracellular and intracellular events. To this end, we are currently designing a test setup to stretch and grow explanted tissue samples ex vivo. Since most existing data sets on skin growth are based on in vivo measurements of inflated membranes, an ex vivo setting will allow us to create well-defined geometries and boundary conditions such as the equi-biaxial extension test suggested here.

Second, since our goal was to focus primarily on the kinematic characterization of the growth process, the constitutive modeling of the elastic baseline properties of skin has played a minor role. However, the proposed model is inherently modular and the incorporation of more sophisticated constitutive models [67] is relatively straightforward. A typical candidate is a multiple-constituent anisotropic skin model with in-plane anisotropy introduced through a pronounced stiffness along Langer’s lines [35, 36], which we have successfully combined with the proposed growth model in the past [14]. In addition, the growth process itself could be modeled as anisotropic [21], e.g., attributed to a pronounced growth along specific microstructural directions. Similarly, through the deposition of large bundles of compacted immature collagen [10, 33], the underlying collagen network could reorient itself, e.g., to align with the maximum principal strains [29, 38]. Here, we model growth as a strain driven process. This implies that the elastic material parameters, or, accordingly, the corresponding stresses, play a less important role than in stress-driven growth, e.g., in hypertension [37, 50]. In other words, when using the same model with different Lame constants or different constitutive models, we would require different expander pressures to obtain the same deformation pattern, but the growth process itself would still be affected by kinematical quantities only. Along the same lines, we have assumed that the effects of resting tension and residual stress are negligible. Both play a critical role when studying instabilities and buckling [23, 65]. In a previous study, we have explored these phenomena in more detail [13]. Within the context of finite deformations, resting tension and residual stress could be incorporated through another second order tensor, which would mimic the mapping to a pre-strained or residually stressed configuration [46, 61].

Third, for the sake of simplicity, we have modeled skin as homogeneous across the thickness, neglecting its individual layers and their potential interaction. We are currently refining our model utilizing shell kinematics with a higher resolution across the thickness direction. This will facilitate to model the individual skin layers [56], which we believe to be a major source of heterogeneities and residual stresses in real tissue expansion cases [45]. Alternatively, to explore the biomechanical interaction between the growing dermis and the underlying hypodermis during tissue expansion, we could even model growing skin through its own boundary energy [32].

Fourth, at this stage, the chronic response of our model is not yet calibrated in time. We have assumed that chronic growth takes place within a normalized time interval from zero to one. In reality, growth periods range from the order of days in rodents [12] to weeks in pigs [66] and humans [27]. However, with the appropriate experimental data, the duration of the adaptation process can be calibrated easily through the adaptation speed τ [70].

Fifth, we have modeled the tissue expander only implicitly through controlling the expander pressure. In real tissue expansion, the external control parameter is the expander volume [41]. This implies that our simulation displays creep under constant loading, while clinical tissue expansion might rather display relaxation under constant deformation [14]. Moreover, we have assumed that the expander is connected tightly to the expanded tissue, neglecting effects of interface sliding and shear [58]. However, this seems to be a reasonable first assumption, since most current expanders have well-designed textures to promote mild tissue in-growth, primarily to prevent expander migration [11].

Last, while our computational model seems well suited to provide qualitative guidelines and trends, in its present state, it is not recommended for quantitative statements. We will need to perform acute and chronic in vitro and in vivo experiments to truly identify the underling mechanisms which have, up until now, only been represented phenomenologically. Nevertheless, we believe that using the equations of nonlinear continuum mechanics to characterize skin growth represents a significant advancement over the current gold standard to predict tissue growth exclusively in terms of areas, volumes, and empiric correction factors [55, 66].

5. Conclusion

We have presented a continuum model for growing biological membranes in which the underlying mechanobiology is collectively summarized in a single pheonomenological internal variable, the in-plane area growth. The model can reliably predict the characteristic histological, mechanical, and structural features of controlled overstretch-induced skin growth, both acutely and chronically. We anticipate that the proposed skin growth model can be generalized to arbitrary biological membranes, and that it can serve as a valuable tool to virtually manipulate membrane area simply by means of changes in the mechanical environment.