Abstract
Direct measurement of neural currents by means of MRI (ncMRI) can potentially open a high temporal resolution (10-100 ms) window applicable for monitoring dynamics of neurnal activity without loss of the high spatial resolution afforded by MRI. Previously we have shown that the alternating balanced steady states (ABSS) imaging affords high sensitivity to weak periodic currents owing to its amplification of periodic spin phase perturbations. This technique, however, requires precise synchronization of such perturbations to the RF pulses. Herein we extend ABSS imaging to multiple balanced alternating steady states (MASS) for estimation of neural current waveforms. Simulations and phantom experiments show that the off-resonance profile of the MASS signal carries information about the frequency content of driving waveforms. In addition, the method is less sensitive than ABSS to precise waveform timing relative to RF pulses. Thus MASS is potentially applicable to MR imaging of the waveforms of periodic neuronal activity.
Keywords: balanced SSFP, multiple alternating steady states, neural current MRI, MR-encephalography
Introduction
To date the prevalent method for MRI of brain function (Blood Oxygenation Level Dependent contrast, or BOLD) relies on variations in deoxyhemoglobin concentration in cerebral parenchyma that reflect underlying neuronal activity indirectly through neurovascular coupling, which depends on many physiological parameters. The BOLD signal evolves over several seconds, while the most relevant temporal scale for neuronal activity ranges from 10-100ms. It has been suggested that it may be possible to detect neural currents directly by means of MRI (ncMRI) since minute magnetic fields generated by electrical neuronal activity can perturb proton spin phase (1-4). Indeed, in situ (in voxels acquired using MRI) estimates of the peak magnetic field strength adjacent to neural current dipoles yields ΔB = 0.1 -1 nT (2,5,6). Similar estimates were obtained in calculations based on realistic neuron morphology (7). Such estimates are well within the sensitivity of contemporary MR scanners (4). While some recent results raise question about the feasibility of neural current detection by means of ncMRI (8), other studies have reported promising results (9-11).
While previous ncMRI studies focused on detection of neural currents by means of MRI, herein we address a complementary question of measurement of neuronal activity waveforms. Temporal waveforms evoked by repeated presentations of experimental conditions (e.g. event-related potentials -- ERPs) are essential for research employing electrical (EEG) and magnetic (MEG) measurements of brain activity, thus measurement of event-related neural current waveforms by means of ncMRI is critical for bridging the gap between EEG/MEG and ncMRI.
We have previously shown (4) that alternating balanced steady state (ABSS) MRI affords contrast-to-noise ratio (CNR) for periodic spin phase-perturbing currents (i.e. currents perpendicular to Bz) that is superior to that of traditional GRE and SE fMRI (4). Herein we discuss application of balanced SSFP to estimation of current temporal waveforms by means of multiple alternating steady states (MASS) MRI, which is a generalization of the two-state ABSS (4) to multiple states. Our results indicate that multiple alternating states evoked during MASS imaging encode the frequency (and phase) content of the driving spin phase-perturbing waveforms and can be used for estimation of these waveforms. We conclude that MASS imaging is potentially applicable for estimation of waveforms of rapid neuronal activity (at temporal resolution of ~10-100 ms), and may offer a bridge between fMRI and EEG/MEG.
Theory
Multiple Alternating Steady State (MASS) Imaging
Herein we extend two-state ABSS MR imaging (4) to multiple states (MASS) for measuring spin phase-perturbing forces, such as neural currents. A previously suggested possibility for the existence of multiple states in balanced SSFP (12) has been tested using multiple TR values for fat suppression (13).
We use spin phase-perturbing periodic signals to generate multiple alternating balanced steady states by synchronizing a train of N RF pulses to a repeated waveform of that signal: N dynamic steady states result from different exposure of transverse magnetization at each of N TRs to a spin phase-perturbing factor, as determined by the time course of the waveform (figure 1).
Figure 1.
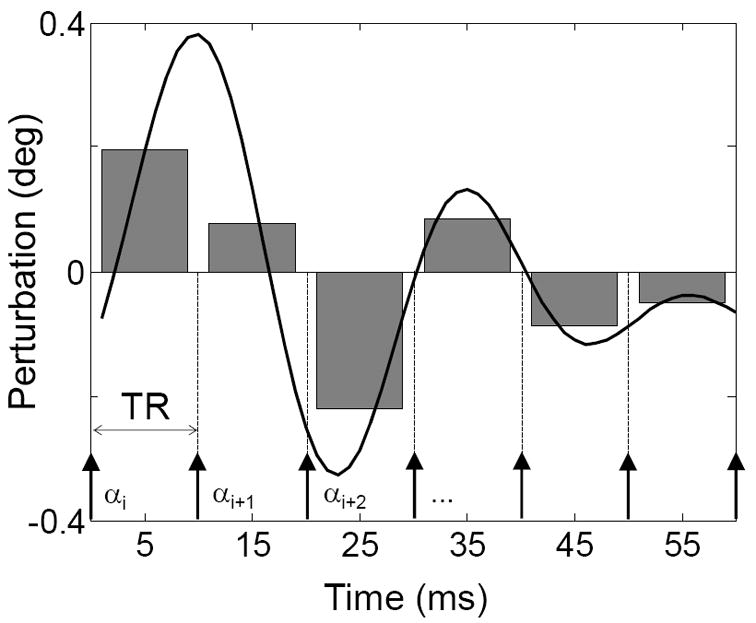
The conceptual basis of the MASS method. The continuous line represents the time course of the spin phase perturbation (in deg) induced by a ΔBz–perturbing function F, such as neuronal current induced spin phase perturbation. Arrows below represent RF pulses. The waveform of duration TW=N·TR ≤T2 is repeated periodically so that magnetization evolves into a dynamic steady state (i.e. multiple alternating states). The grey bars represent the mean perturbation value between successive excitation (RF) pulses. In this example there are N=6 distinct mean values proportional to the integral of ΔBz(i) over an interval τ=[nTR,(n+1)TR]. RF pulses of α deg flip angle are phase cycled using a 180 deg step.
The continuous line in figure 1 represents the time course of a repeated neuronal response-related function Fn (e.g. induced by neural currents) which can be thought of as a dynamically changing off-resonance. The arrows indicate timing of the RF pulses. As long as the waveform duration TW = N·TR < T2, the signal reaches N cyclically alternating dynamic steady states with N equal to the number of TR intervals falling within a period of the waveform. The degree of spin phase perturbation δφj is proportional to the integral of function Fn over the repetition time (TR):
| [1] |
This results in a binned waveform representation (shaded area in figure 1). Below we develop means to measure such binned waveforms, which are applicable for measuring ultra-weak perturbations associated with neural current-induced magnetic fields.
The MASS magnetization for a spin isochromat can be calculated by extending the propagation approach (4, 14). Using matrix notation, the T1 and T2 relaxation can be represented by multiplying the magnetization vector M = [M x M y M z]T by C(t) = exp(−t / T), where (T = diag(T2, T2, T1), and adding a vector D(t) = (I − C (t))[0 0 M0]T. Here I is the 3×3 identity matrix and diag is a diagonal matrix. Spin precession by an angle ϕ is represented by a rotation matrix Rz (ϕ) about the z axis; likewise the RF excitation effect corresponding to flipping magnetization around the x axis by an angle α (with a fixed RF phase) is given by the rotation matrix Rx (α). For the simplified case of an RF pulse of infinitesimal duration, the MASS magnetization vector for N steady states SSi at time TE as a function of off-resonance frequency Δf is given as:
| [2] |
with
| [3] |
and
| [4] |
where
| [5] |
and k = mod(i + j − 2, N) +1 is the state indexing function; φi = 2πΔfτi + aiδφi is the angle accrued over the interval τi given the static off-resonance Δf and the dynamic phase perturbation δφi incurred during the i-th steady state. The flip angle αk alternation implements phase cycling with 180 deg step (i.e. alternates between + α and − α). Time intervals τi are defined as follows:
| [6] |
and ai = τi / TR. Note that propagation of solution for MASS magnetization requires N+1 time intervals between two identical magnetization time points for the no-phase-cycling case and 2N+1 time steps (over 2Tw) in case of 180 deg phase cycling. Products in eq. [2] run backwards from j=N+1 to 2 due to non-commutativity of matrix multiplication (see also Vasanawala et al., 1999).
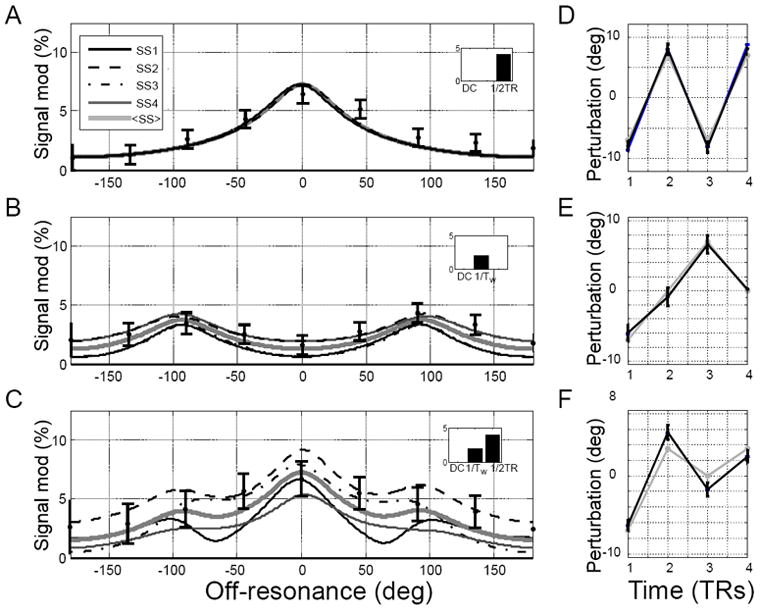
The magnitude and phase off-resonance steady-state profiles for the 4-state MASS transverse magnetization in Figure 2A are calculated using eq. [2]. The relatively high spin phase perturbation of ~5 deg is used in order to stress off-resonance profile differences of the four steady states. Figure 2B plots signal modulation off-resonance profiles induced by the repeated perturbation waveforms. The top panel shows the difference between SSi and SS0 magnitudes in percent of non-perturbed steady state SS0: 100%·(|SSi|−|SS0|)/|SS0| (difference of magnitudes) and the bottom panel shows the magnitude of complex difference between SSi and SS0 : 100%·|SSi − SS0|/|SS0|. Please note that the off-resonance profile for SS0 is equal to the complex mean over all SSi. which can be verified via Bloch equation simulations.
Figure 2.

MASS off-resonance profiles. A: Magnitude (left) and phase (right) of transverse magnetization as a function of static off-resonance for four steady states (SSi, i=[1,4]). The steady states are induced by the waveform δφj ≈ [0,5,−2.5,−1.25] deg (A,B). The gray continuous line in A plots no-modulation state SS0, other states are as in legend. The corresponding signal modulation off-resonance profiles during the 4 states (difference between SSi and the SS0 in % of SS0) are plotted in B: the top panel plots relative “difference of magnitudes” and the bottom panel plots relative “magnitude of difference” (see text for definitions). Simulation parameters are as in experiment (see below): T1/T2 = 800/60ms, TR/TE=20/2.6 ms, flip angle 30 deg.
Methods
MRI images of a current phantom were acquired using a 3T GE Discovery scanner MR750 (GE Healthcare, Waukesha, WI) at the UCSD Center for fMRI and a GE receive/transmit quadrature knee coil. A 2D balanced SSFP sequence with a 1-shot (TE/TR=3.8/32 ms) and 2-shot (TE/TR=2.6/20 ms) spiral-out acquisition (±125 kHz) with FA=30deg, FOV=18cm, 64x64 matrix (inplane resolution 2.8125×2.8125 mm) and 4mm slice thickness was used to acquire a single axial slice through the plane containing the wire inside a current phantom. For the 2-shot acquisition each of the two k-space segments was repeated N=4 times (corresponding to the number of steady states), and image reconstruction was performed using complementary k-space trajectories separated by 4 shots. The RF pulse shape was a simple sinc pulse (bandwidth = 5KHz), and the spiral trajectory was an Archimedean spiral that meets the minimum Fourier sampling criteria (15). A total of 1200 four-state MASS images were acquired resulting in scan durations of 38.4 s and 48 s for 1 and 2-shot scans respectively. The phase of the RF pulse was cycled using a 180 deg step. In order to explore the sensitivity of the bSSFP signal to static off-resonance, a static linear gradient (0.5 G/m) along the X axis was applied, which resulted in a characteristic periodic vertical banding artifact. The mean difference images were calculated by subtracting mean images of each steady state from the average of the steady state images and averaging 200 difference images (nreps=800, initial 400 images discarded to eliminate transient effects).
We used an electric current phantom as a model system for evaluating MASS sensitivity to neural current contrast. A spherical current phantom 100mm in diameter filled with agar was used. The phantom recipe used NiCl2 and an agar mixture such that T1 and T2 were roughly comparable to those of grey matter; NaCl was added to increase the conductivity to mimic the RF load of a head (16). An insulated copper wire (~0.6mm in diameter) was placed in the middle of the phantom along the X direction (left-right) and perpendicular to the B0 vector of the 3T scanner. Cables delivering current to the phantom were arranged parallel to the B0 vector so that only the magnetic field created by current flowing in the perpendicular wire contributed to B0. A ~2.3 kΩ resistor was connected in series to the phantom wire and the current at the peak waveform value was adjusted to either ~0.5 or ~1 mA. The current magnitude was controlled with synchronization precision of 20 μs via an analog output port of a National Instruments I/O card that received trigger TTL pulses from the scanner with every RF pulse. The card was programmed using LabView (National Instruments, Austin, TX) to generate a desired periodic temporal waveform and noise synchronized to scanner RF pulses.
We addressed the effects of the frequency content of driving periodic current waveforms on the MASS signal off-resonance profile by employing waveforms alternating (i) at the rate of (2TR)-1 and resulting in a repeated spin phase perturbation sequence δφ ≈ [−5,5,−5,5] deg, (ii) at the rate (4TR)-1 = Tw -1 and resulting in the sequence δφ ≈ [−5,0,5,0] deg, and (iii) the mean of the aforementioned waveforms resulting in the sequence δφ ≈ [−5,2.5,0,2.5] deg. A 5 deg perturbation over a TR period was produced by a 1 mA current modulation that at a distance of ~22-24mm results in ΔB=9-10 nT and a maximum MASS signal modulation of 7-8%.
In phantom experiments the relatively long TR values (20 and 32 ms) do not result in substantial banding artifacts other than those induced intentionally by applying a static gradient, but thermal drift is substantial over longer scan times. The drift was minimized by using short scans and center frequency resetting before each scan. In addition, we applied a field map correction method to reduce the effect of off-resonance on image blurring (17). We performed a point spread function (PSF) analysis to calculate effective degree of blurring due to T2 and T2* decay and k-space trajectory errors. PSF estimation is essential when evaluating the degree of off-resonance profile blurring. The k-space trajectories were measured by a gradient calibration technique (18). T2 and T2* values were measured on the phantom with SE and GRE sequences, respectively. The measured T2 value was ~60 ms and T2* was ~40 ms. The measured trajectories, T2, and T2* decay caused blurring with FWHM of 1.31 voxel. We conclude, thus, that the PSF does not contribute substantially to estimation errors of the off-resonance profiles from applied linear gradients.
Current waveforms from MASS data were estimated using Bayesian analysis (e.g.(19,20) implemented in Matlab (MathWorks, Inc., Natick, MA): a posterior probability density function (pdf) of waveform values and voxel static off-resonances were estimated using Markov Chain Monte Carlo (MCMC) slice-sampling method, which only requires definition of a pdf up to a scaling constant (21). Specifically, a posterior distribution was defined as follows:
| [7] |
with C as a normalization constant assuring that integral of eq. [7] equals to 1, and the likelihood of data d proportional to a Gaussian pdf:
| [8] |
Here F (Θ,P) = {MSSi / MSS0} is a vector of magnetization (or signal) values for each state i=1..4, normalized to non-perturbed steady state magnetization MSS0 (or signal), calculated from the “forward model”, i.e. from MSSi defined in eq. [2-6]; dj is a vector of measured complex values ranging over m (one or more) voxels j used for waveform estimation and rd =60 is a precision parameter set to an empirically estimated value that enforces a small estimation error (intuitively, in case of independent identically distributed errors, this term sets a soft constraint on the standard deviation of the error to < 2*m*N/rd); Θj = [δφi, Δfj] is a vector of current waveform and voxel-wise static off-resonance parameters; P-vector absorbs all other parameters in eq. [2-6], including relaxation constants and scanning parameters. The prior on current waveform values (in terms of degrees of spin phase perturbation) as well as voxel-wise static off-resonance values is defined as a product of Laplace pdfs and hence enforces small values (sparsity constraint):
| [9] |
where i ranges over waveform values, j ranges over voxels used for waveform estimation. The waveform estimation precision rϕ=0.1 is set empirically to penalize absolute values larger than 1/rϕ=10 deg, and the off-resonance estimation precision rf=1 penalizes off-resonance estimates that are larger than 1 Hz. For simplicity, waveform and static off-resonance estimation was performed using measured MASS image values at 4 adjacent voxels (at the distance of 24 mm from the wire). These values thus formed a vector of 16 complex measurements that were used to estimate 4 waveform and 4 voxel-wise static off-resonance values.
Results
Multiple Steady States Induced in a Current Phantom
In order to test the induction of multiple steady states by a periodic waveform of a spin phase-perturbing factor we imaged a current phantom using a bSSFP pulse sequence with RF pulses synchronized with a neuromorphic 4-bin (N=4) current waveform. Figure 3A shows images and intensity profiles obtained using the MASS sequence entrained by the waveform δφ = [0,2,−1,−0.5] deg. The experimental profiles follow closely those predicted by the theory.
Figure 3.
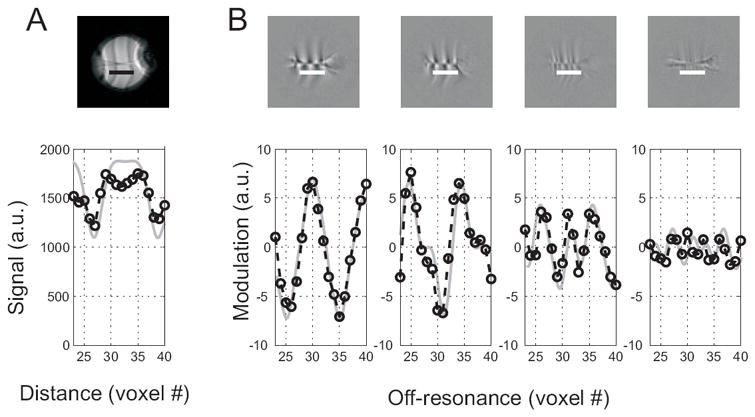
Multiple steady state profiles induced by a periodic current waveform δφj ∝ [0,2,−1,−0.5]. Top row shows an average (n=200) phantom MASS image (A) and modulation patterns corresponding to the four steady states images at the locations indicated by the bars below the centrally placed copper wire (B). The vertical stripes are banding artifacts introduced by a linear X gradient that was applied in order to generate linearly-varying off-resonance. The horizontal line in the middle of the images is the location of the wire. The bar below the central line indicates the site for the profiles depicted in the bottom row. Bottom row: measured (circles and broken interpolating lies) and theoretical (gray continuous) off-resonance profiles. The gray lines corresponding theoretical profiles were calculated using equation [1], low-pass filtered to match the point spread function of the experimental data and scaled to match the measured image and modulation intensity.
Dependence of the MASS signal on the waveform frequency content
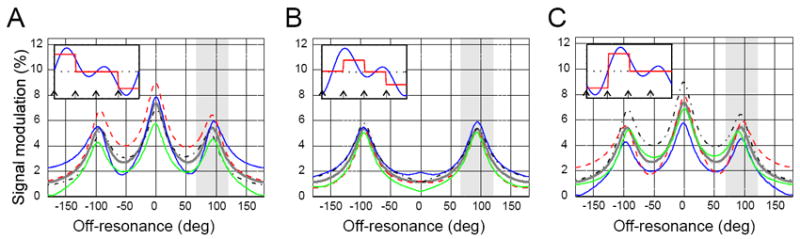
The number of peaks in the modulation profiles depends on the number of steady states and the spin phase-perturbing waveform. Figure 4 illustrates this behavior for the case of N=4 steady states. Simulation and pulse sequence parameters are as in figure 2 except TR/TE=30/3.8 ms. The waveform alternating at Nyquist limit, i.e. rate of (2TR)-1 modulates the MASS signal at the on-resonance (peak in figure 4A). Lower waveform frequencies induce additional side modulation peaks (figure 4B) so that waveforms with rich frequency content induce multiple modulation peaks at off-resonance values determined by the total number of states (figure 4C). The N MASS signal (complex) values at each such peak carry information about the modulating waveform, however, estimation at side peaks are more robust in respect to variations in the lag between the waveform and RF pulses (see below).
Figure 4.
Simulated and experimental steady state modulation profiles as a function of the frequency content of the driving waveform and estimated waveforms. A,B: the magnitude of complex difference modulation profiles induced by waveforms containing only one frequency. Insets represent DFT of the driving waveforms. A: Modulation profiles induced by a waveform alternating at the rate 1/2TR with perturbations δφj ≈ [−5,5,−5,5] deg; B: modulation profiles induced by a waveform alternating at the rate 1/4TR=1/Tw with δφj ≈ [−5,0,5,0] deg; C: modulation profiles induced by a waveform equal to the mean of the top two waveforms δφj ≈ [−5,2.5,0,2.5] deg and thus containing 2 frequencies. The gray thick lines are the mean across simulated states, and the filled circles with error bars represent the measured mean and standard deviation of MASS responses from the phantom experiment. D-E: waveforms estimated from 4 consecutive voxels ~23mm from wire. Black lines are estimated wavefrom values and error bars represent standard deviation of the posterior distributions; gray lines represent the nominal waveforms.
The MCMC estimates of the spin phase-perturbing waveform values are close to the actual waveforms for the single frequency case (figure 4D,E) and deviate slightly from the nominal waveform for the multi-frequency case, possibly due to poor spatial resolution that results in loss of information at some static off-resonance values (figure 4F).
Insensitivity of MASS to waveform lag relative to RF pulses
The MASS method inherits from ABSS the property of spin-phase perturbation amplification (4), while affording lesser sensitivity to the lag between the evoked periodic neuronal response and RF pulses.
As evident from figure 5, shifting the waveform relative to RF pulses by less than one TR affects the MASS response only for the highest waveform modulation frequency (2TR)-1, and shifting by a multiple of TR merely cyclically shifts the steady states. This property makes MASS a robust technique for detection of neural currents in cases when the response latency is not known or is widely dispersed in different areas, as is the case across different cortical areas. Since neuronal responses can exhibit very high temporal precision (2-10 ms)(22,23), repeated evoked responses can be used for extended averaging of MASS signal. In addition, this technique can be adopted for detection of neuronal responses that are accompanied by evoked neuronal oscillations of local field potentials (e.g. at gamma or beta frequencies).
Figure 5.
Simulated steady state modulation profiles as a function of the lag between the RF pulses and the periodic waveform. The alternating steady states are labeled as in Figure 2. Insets show the waveform used in simulation at three values of the lag relative to the first RF pulse (at time =0). The boxcar approximation of the waveform shows the effective sampling of the waveform by the MASS sequence. A: lag = 0, B: lag = π /4, C: lag = π/2. Note that the increase in lag affects the central peak that is most sensitive to the Nyquist (maximum) frequency of the waveform, but the side peaks are not affected much. Gray-shaded area is the off-resonance region insensitive to the lag, and can be used for MASS imaging by selecting phase cycling step of ~90 deg.
Discussion
We propose a method for imaging periodic dynamic spin phase perturbations of low amplitude that can be applicable for imaging evoked event-related neuronal activation waveforms by means of ncMRI at a short temporal scale (10-100ms).
The MASS imaging method produces complex measurements for each of N steady states, thus resulting in 2N-dimensional (N real and N imaginary components) vectors at each voxel. A natural approach to detect MASS modulations is a 2N-dimensional generalization of the t-test: Hotelling’s T2 test (24). Since the values of steady states are not independent, it may be advantageous to preprocess such data by means of SVD dimensionality reduction. The MASS modulation-inducing neuronal activity waveforms can then be further analyzed for the voxels showing significant modulation by means of e.g. Bayesian inversion that employs MCMC estimation of a posterior distribution.
Limitations and extensions of the MASS imaging
While the MASS-based fMRI possesses the potential for high temporal resolution, the requirement for Tw<T2 sets the lower limit for the waveform repetition frequency at about 10Hz. However, EEG/MEG ERP studies show that cognitive ERPs often extend over time intervals beyond 100ms (up to 500ms and more). Thus MASS method would be most suitable for sensory-motor studies and cognitive studies employing brain steady state stimulation methodology (25) that addresses cognitive effects on responses to stimuli presented at high rates (~10-20Hz).
While static B0 inhomogeneities are not a big concern in phantom experiments, the relatively long TR values (20 and 32 ms) may result in substantial banding in the brain, thus further reduction of TR by employing more interleaves may be necessary. Banding artifacts can be further minimized by employing multiple acquisitions at several off-resonance offsets or at different phase cycling steps and using thresholded images as masks to reject voxels around banding artifacts (26,27). Constraining imaging to regions of interest can further mitigate this problem: Our preliminary data from human visual cortex show that banding artifacts can be minimized by applying localized higher order shimming, which reduces inhomogeneities down to 15-25 Hz. Finally, the scanner (thermal) drift can be minimized by means of the compensation technique proposed by Lee et al. (28).
Herein we have not addressed the impact of the physiological noise that can be substantial, especially in the case of 3D acquisition. Carefully selected noise compensation methods such as prospective respiration compensation (28) and 3D navigators will have to be considered when addressing these noise sources.
Acknowledgments
Supported by a NIH/NIBIB grant to G.T.B. (R21 EB008187-02).
References
- 1.Bodurka J, Jesmanowicz A, Hyde JS, Xu H, Estkowski L, Li SJ. Current-induced magnetic resonance phase imaging. J Magn Reson. 1999;137(1):265–271. doi: 10.1006/jmre.1998.1680. [DOI] [PubMed] [Google Scholar]
- 2.Bodurka J, Bandettini PA. Toward direct mapping of neuronal activity: MRI detection of ultraweak, transient magnetic field changes. Magn Reson Med. 2002;47(6):1052–1058. doi: 10.1002/mrm.10159. [DOI] [PubMed] [Google Scholar]
- 3.Bianciardi M, Di Russo F, Aprile T, Maraviglia B, Hagberg GE. Combination of BOLD-fMRI and VEP recordings for spin-echo MRI detection of primary magnetic effects caused by neuronal currents. Magnetic Resonance Imaging. 2004;22(10):1429–1440. doi: 10.1016/j.mri.2004.10.009. [DOI] [PubMed] [Google Scholar]
- 4.Buracas GT, Liu TT, Buxton RB, Frank LR, Wong EC. Imaging periodic currents using alternating balanced steady-state free precession. Magn Reson Med. 2008;59(1):140–148. doi: 10.1002/mrm.21457. [DOI] [PubMed] [Google Scholar]
- 5.Konn D, Gowland P, Bowtell R. MRI detection of weak magnetic fields due to an extended current dipole in a conducting sphere: A model for direct detection of neuronal currents in the brain. Magnetic Resonance in Medicine. 2003;50(1):40–49. doi: 10.1002/mrm.10494. [DOI] [PubMed] [Google Scholar]
- 6.Hagberg GE, Bianciardi M, Maraviglia B. Challenges for detection of neuronal currents by MRI. Magnetic Resonance Imaging. 2006;24(4):483–493. doi: 10.1016/j.mri.2005.12.027. [DOI] [PubMed] [Google Scholar]
- 7.Cassara AM, Hagberg GE, Bianciardi M, Migliore M, Maraviglia B. Realistic simulations of neuronal activity: A contribution to the debate on direct detection of neuronal currents by MRI. Neuroimage. 2008;39(1):87–106. doi: 10.1016/j.neuroimage.2007.08.048. [DOI] [PubMed] [Google Scholar]
- 8.Chu R, de Zwart JA, van Gelderen P, Fukunaga M, Kellman P, Holroyd T, Duyn JH. Hunting for neuronal currents: absence of rapid MRI signal changes during visual-evoked response. Neuroimage. 2004;23(3):1059–1067. doi: 10.1016/j.neuroimage.2004.07.003. [DOI] [PubMed] [Google Scholar]
- 9.Petridou N, Plenz D, Silva AC, Loew M, Bodurka J, Bandettini PA. Direct magnetic resonance detection of neuronal electrical activity. Proc Natl Acad Sci U S A. 2006;103(43):16015–16020. doi: 10.1073/pnas.0603219103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Xue Y, Chen X, Grabowski T, Xiong J. Direct MRI mapping of neuronal activity evoked by electrical stimulation of the median nerve at the right wrist. Magn Reson Med. 2009;61(5):1073–1082. doi: 10.1002/mrm.21857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chow LS, Dagens A, Fu Y, Cook GG, Paley MN. Comparison of BOLD and direct-MR neuronal detection (DND) in the human visual cortex at 3T. Magn Reson Med. 2008;60(5):1147–1154. doi: 10.1002/mrm.21753. [DOI] [PubMed] [Google Scholar]
- 12.Vasanawala SS, Pauly JM, Nishimura DG. Fluctuating equilibrium MRI. Magn Reson Med. 1999;42(5):876–883. doi: 10.1002/(sici)1522-2594(199911)42:5<876::aid-mrm6>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- 13.Cukur T, Nishimura DG. Multiple repetition time balanced steady-state free precession imaging. Magn Reson Med. 2009;62(1):193–204. doi: 10.1002/mrm.21990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hargreaves BA, Vasanawala SS, Pauly JM, Nishimura DG. Characterization and reduction of the transient response in steady-state MR imaging. Magn Reson Med. 2001;46(1):149–158. doi: 10.1002/mrm.1170. [DOI] [PubMed] [Google Scholar]
- 15.Glover GH. Simple analytic spiral K-space algorithm. Magn Reson Med. 1999;42(2):412–415. doi: 10.1002/(sici)1522-2594(199908)42:2<412::aid-mrm25>3.0.co;2-u. [DOI] [PubMed] [Google Scholar]
- 16.Schneiders NJ. Solutions of two paramagnetic ions for use in nuclear magnetic resonance phantoms. Med Phys. 1988;15(1):12–16. doi: 10.1118/1.596155. [DOI] [PubMed] [Google Scholar]
- 17.Noll DC, Meyer CH, Pauly JM, Nishimura DG, Macovski A. A homogeneity correction method for magnetic resonance imaging with time-varying gradients. IEEE Trans Med Imaging. 1991;10(4):629–637. doi: 10.1109/42.108599. [DOI] [PubMed] [Google Scholar]
- 18.Duyn JH, Yang Y, Frank JA, van der Veen JW. Simple correction method for k-space trajectory deviations in MRI. J Magn Reson. 1998;132(1):150–153. doi: 10.1006/jmre.1998.1396. [DOI] [PubMed] [Google Scholar]
- 19.Friston KJ. Bayesian estimation of dynamical systems: an application to fMRI. Neuroimage. 2002;16(2):513–530. doi: 10.1006/nimg.2001.1044. [DOI] [PubMed] [Google Scholar]
- 20.Woolrich MW, Jbabdi S, Patenaude B, Chappell M, Makni S, Behrens T, Beckmann C, Jenkinson M, Smith SM. Bayesian analysis of neuroimaging data in FSL. Neuroimage. 2009;45(1 Suppl):S173–186. doi: 10.1016/j.neuroimage.2008.10.055. [DOI] [PubMed] [Google Scholar]
- 21.Candy JV. In: Bayesian Signal Processing Classical, Modern and Particle Filtering Methods. H S, editor. Hoboken, NJ: Willey; 2009. [Google Scholar]
- 22.Buracas GT, Zador AM, Deweese MR, Albright TD. Efficient discrimination of temporal patterns by motion-sensitive neurons in primate visual cortex. Neuron. 1998;20(5):959–969. doi: 10.1016/s0896-6273(00)80477-8. [DOI] [PubMed] [Google Scholar]
- 23.Buracas GT, Albright TD. Gauging sensory representations in the brain. Trends Neurosci. 1999;22(7):303–309. doi: 10.1016/s0166-2236(98)01376-9. [DOI] [PubMed] [Google Scholar]
- 24.Lee J, Shahram M, Schwartzman A, Pauly JM. Complex data analysis in high-resolution SSFP fMRI. Magn Reson Med. 2007;57(5):905–917. doi: 10.1002/mrm.21195. [DOI] [PubMed] [Google Scholar]
- 25.Muller MM, Picton TW, Valdes-Sosa P, Riera J, Teder-Salejarvi WA, Hillyard SA. Effects of spatial selective attention on the steady-state visual evoked potential in the 20-28 Hz range. Brain Res Cogn Brain Res. 1998;6(4):249–261. doi: 10.1016/s0926-6410(97)00036-0. [DOI] [PubMed] [Google Scholar]
- 26.Miller KL, Hargreaves BA, Lee J, Ress D, deCharms RC, Pauly JM. Functional brain imaging with BOSS FMRI. Conf Proc IEEE Eng Med Biol Soc. 2004;7:5234–5237. doi: 10.1109/IEMBS.2004.1404463. [DOI] [PubMed] [Google Scholar]
- 27.Bangerter NK, Hargreaves BA, Vasanawala SS, Pauly JM, Gold GE, Nishimura DG. Analysis of multiple-acquisition SSFP. Magn Reson Med. 2004;51(5):1038–1047. doi: 10.1002/mrm.20052. [DOI] [PubMed] [Google Scholar]
- 28.Lee J, Santos JM, Conolly SM, Miller KL, Hargreaves BA, Pauly JM. Respiration-induced B0 field fluctuation compensation in balanced SSFP: real-time approach for transition-band SSFP fMRI. Magn Reson Med. 2006;55(5):1197–1201. doi: 10.1002/mrm.20879. [DOI] [PubMed] [Google Scholar]


