Mental visualization of objects from cross-sectional images

Abstract

We extended the classic anorthoscopic viewing procedure to test a model of visualization of 3D structures from 2D cross-sections. Four experiments were conducted to examine key processes described in the model, localizing cross-sections within a common frame of reference and spatiotemporal integration of cross sections into a hierarchical object representation. Participants used a hand-held device to reveal a hidden object as a sequence of cross-sectional images. The process of localization was manipulated by contrasting two displays, in-situ vs. ex-situ, which differed in whether cross sections were presented at their source locations or displaced to a remote screen. The process of integration was manipulated by varying the structural complexity of target objects and their components. Experiments 1 and 2 demonstrated visualization of 2D and 3D line-segment objects and verified predictions about display and complexity effects. In Experiments 3 and 4, the visualized forms were familiar letters and numbers. Errors and orientation effects showed that displacing cross-sectional images to a remote display (ex-situ viewing) impeded the ability to determine spatial relationships among pattern components, a failure of integration at the object level.

1. Introduction

While visual object recognition may seem effortless, it is actually a highly constructive process, involving a stream of processing that begins with the retinal image, advances through a sequence of computational stages, and culminates in a match to representations in memory (Biederman, 1987; Marr, 1982; Tarr & Bülthoff, 1998). The necessity for construction is particularly apparent in the situation where information constituting an object is progressively unveiled from spatially distributed exposures. For example, viewing large objects may require integration across saccades, each with its own retinal projection (Irwin, 1992; Melcher & Moronne, 2003; Rayner, 1978), or people may rotate an object to view it from multiple perspectives (Harmon, Humphrey & Goodale, 1999). Under such conditions the ability to integrate information over time and space is critical to the formation of object representations. Here we study spatiotemporal integration in a particular form: Observers use a sequence of 2D cross sections, taken from a virtual object in 3D space, to obtain a representation of its 3D structure. We wish not only to demonstrate the capability for 3D construction from cross-sections, but also to further understand the underlying processes that make it possible.

1.1 Construction of object representations: a spatiotemporal process

Despite substantial progress in understanding visual object recognition, the underlying processing still remains a matter of debate. The various theories that have been formulated can be broadly categorized into two approaches, view-based vs. structure-based, according to their views on mental object representation (for review, see Riesenhuber & Poggio, 2000 and Tarr & Vuong, 2002). While the two approaches are quite different, and in many aspects mutually contradictory, they share a fundamental idea: The recognition of an object relies on object representations derived from retinal stimulation. In the context of structure-based approaches, for example, Marr’s (1982) computational framework describes how object representation progresses from the retinal image to a “primal sketch” and finally to an object-centered 3D model, whereas Biederman’s Recognition-By-Components theory (1987) proposes an intermediate volumetric representation called a “geon.” In contrast, view-based approaches advocate that retinal images lead to a collection of stored 2D views (Bülthoff, Edelman, & Tarr, 1995; Lawson, Humphreys, & Watson, 1994; Tarr & Bülthoff, 1998), which are compared to incoming targets subject to transformations such as interpolation and mental rotation (Lawson, 1999; Willems & Wagemans, 2001).

The debate over the representations used in object processing should not obscure an important source of information, namely, the spatiotemporal relationships across patterns of visual stimulation as an object is perceived. In the real world, motion of a viewer or an object is arguably more common than static, passive viewing. As a result, the visual system has access to a sequence of images that exhibit temporal and spatial correlations, which it takes advantage of for object perception and recognition. Previous research has shown that such spatiotemporal information can aid in interpreting biological motion (Johansson, 1973), categorizing familiar objects (Lawson, Humphreys, & Watson, 1994), identifying faces (Wallis & Bülthoff, 2001), and recognizing novel objects (Stone 1998, 1999). For example, participants in Stone’s studies (1998, 1999) saw videos of amoeba-like objects that rotated in one direction in the learning phase but in the reversed direction in the subsequent recognition phase. The rotation-reversal produced a significant reduction in recognition performance, suggesting that spatiotemporal information had been incorporated in object representations. Naming familiar objects is also found to be easier when participants viewed structured sequences compared to random sequences of object views (for review see Lawson, 1999).

Although such studies clearly implicate a role for spatiotemporal information in object recognition, few studies have addressed how object representations can be constructed through spatiotemporal integration, particularly in the domain of 3D structures. A difficulty in constructing tasks to study 3D integration per se is how to preclude alternative strategies. For example, the observed effects of structured sequences in recognizing familiar objects might be related to the learning of association between image features and pre-existing object representations, rather than a spatiotemporal process of building an object representation. In order to avoid such confounds, the present research asked people to visualize objects on the basis of their cross-sectional images. In geometry, a cross section is a 2D sample taken from a 3D object by slicing the object with a plane. Cross-sections are thus ideal for studying spatiotemporal integration in a pure form: They have the important properties that they reveal only a small portion of the 3D object, exclude volume information and, often, preclude perceptual exposure of critical features that might, by themselves, support responses. Moreover, being defined in object-centered space, the internal structures shown in cross-sectional images are perspective independent. The motivation for the current research is not only to demonstrate the capability for 3D construction from cross-sections and its role in object recognition, but also to further understand the underlying processes that make it possible. This work can be considered as a 3D analogue of anorthoscopic perception, which we next briefly review.

1.2 Anorthoscopic perception through aperture viewing

A classic technique used to study the integration of spatiotemporally distributed visual exposures is anorthoscopic viewing (Zöllner, 1862), in which a large figure is exposed by passing a small aperture over it, or the figure passes behind a stationary aperture. Over many variations in this paradigm, there is broad agreement that such piecemeal exposures can lead to the perception of the whole figure that transcends the limited aperture available at any one point in time, albeit subject to distortion or noise (Fendrich, Rieger, & Heinze, 2005; Hochberg, 1968; Kosslyn, 1980; Palmer, Kellman, & Shipley, 2006; Parks, 1965; Rock, 1981). Three-dimensional objects that translate or rotate behind an aperture (Day, 1989; Fujita, 1990) can also be recognized anorthoscopically.

Although the mechanisms underlying anorthoscopic perception are still not fully understood, it is commonly accepted that the necessary processes include segmentation of portions of the underlying figure as garnered through occluding aperture, storage of piecemeal information acquired over time, localizing the pieces within a common spatial framework, and finally, assembling the pieces into an integrated form. Of particular interest in this study are the last two processes, namely, localizing the piecemeal views and integrating across views according to their spatial relationships. Together these processes constitute a form of visualization (McGee, 1979).

Two general hypotheses have been suggested to explain how 2D anorthoscopic perception might be accomplished. The “retinal painting” hypothesis, first formulated by Helmholtz (1867), asserts that when an extended scene is viewed through a moving aperture, a representation is constructed by projecting the successive views onto adjacent retinal loci, thereby resulting in an integrated percept. Contravening this hypothesis, however, there is evidence that an anorthoscopic percept can occur when the possibility of retinal painting has been eliminated (Fendrich, Rieger & Heinze, 2005). Moreover, research has shown that even early integration processes, operating at the level of saccades, make use of a spatiotopic frame of reference (Melcher & Moronne, 2003).

An alternative, the post-retinal storage hypothesis, suggests that the information available through the aperture is stored in a working memory and then combined into a whole figure (Girus, Gellman, & Hochberg, 1980; Hochberg, 1968; Parks, 1965; Rock, 1981). This theory requires a mechanism for localizing each visible aperture, by mapping it into a common spatial frame of reference. In the condition where a target object moves behind a stationary aperture, the required spatial description could be derived from “time-of-arrival” and perceived motion (Parks, 1965; Öğmen, 2007). When the aperture moves relative to a stationary object, the spatial locations of successive visual inputs are signalled by cues from the local frame of reference. If the viewer controls the motion aperture, additional cues arise from motor efferent commands and feedback from the kinesthetic system (Loomis, Klatzky, & Lederman, 1991). After the views have been localized, the representation of the whole figure can then potentially be constructed by piecing them together.

1.3 Cross-sectional images: Aperture viewing of 3D objects

Extending the aperture-viewing paradigm into 3D by use of cross-sectional images has immediate application in medical imaging, where computed tomography (CT) or magnetic resonance imaging (MRI), for example, reveal anatomical structures as a sequence of parallel slices. Previous research has shown that reconstruction of 3D objects from 2D images is difficult (National Academies Press, 2006) and strongly depends on the observer’s spatial and imagery abilities (Hegarty, Keehner, Cohen, Montello, & Lippa, 2007; Lanca, 1998). Figure 1 illustrates the experimental task used here: a 3D object is viewed by moving a planar aperture through it. Participants are asked to scan a hidden target with a hand-held device, exposing it as a successive sequence of cross-sectional slices, or images, and by this means to mentally visualize the target. Note that no single image is sufficient to visualize the object as a whole, necessitating the combination of images over space and time.

Figure 1.

Illustration of the experimental task. Participants were asked to explore a hidden pattern (digit “4” constructed from round rods in this example) with a hand-held device, exposing it as a sequence of cross sectional images, and by this means to visualize the target. Alphabetic labels were assigned to the pattern segments and their cross-sections for illustration purposes.

Each cross-sectional image viewed by the participant is a 2D slice through a 3D structure at a specific location. What is required is to establish a correspondence between the 2D images and their origins in 3D space. As was discussed above, two critical processes that potentially limit performance are localizing the viewed slices by mapping into a common spatial frame of reference, and integrating across the resulting set of 2D images. Limitations in either process will affect performance. With respect to the first process, we make no specific assumptions here about the operative frame of reference (e.g., whether it is egocentric or allocentric). However, we do propose that a frame of reference is required in order to spatially relate the slice representations, and that to reduce processing load, a frame of minimum dimensionality adequate for the given task is used. The common frame of reference effectively acts as a “glue”, by which means data from different slices can be spatially registered relative to one another and combined. This constitutes the second process, integration. According to the “post-retinal storage” hypothesis described previously, the assembling of distributed cross-sectional views into objects requires storage and computation in a spatial working memory. It is reasonable to suggest that performance would be impeded by capacity limitations in this memory or associated computational processes, particularly for constructing complex structures.

1.4 Localization by in-situ vs. ex-situ viewing

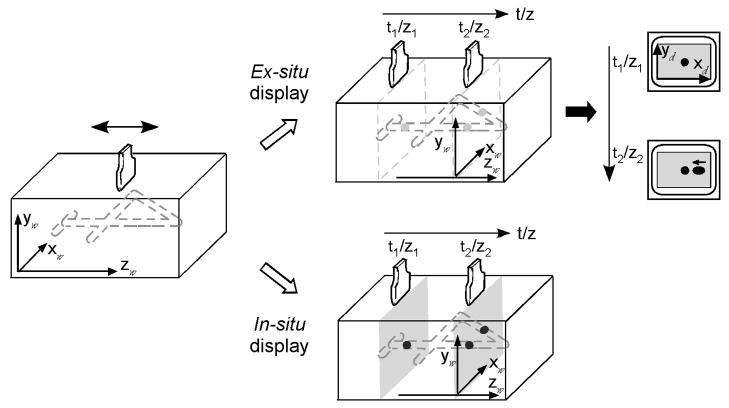
The present study included a manipulation explicitly designed to vary the difficulty of the localization process just described and hence to also impact the process of integration. Two displays were used, in-situ and ex-situ, which differ in whether or not the slices extracted from an object are depicted at their spatial origins. The difference is shown in Figure 2: A digit lying parallel to the ground plane is viewed as a sequence of cross-sections, each of which is created by a planar viewing aperture orthogonal to the ground plane. In the case of in-situ viewing, the aperture is actually a movable visual display that appears in space at precisely the corresponding location of the cross-section in the virtual digit. With ex-situ viewing, the aperture extracts the cross-section of the digit at its current location, but the resulting visual image is displayed on a fixed, remote monitor. The result is to displace the visual data from their spatial source. The two types of displays have direct consequences for the ease of mapping the displayed images to their source locations.

Figure 2.

In-situ vs. ex-situ display of cross-sectional images. In the ex-situ viewing condition (top), the cross-sectional image was displaced to on a remote monitor. With in-situ viewing (bottom), the cross-section was seen at its source location in the space of exploration. The subscripts “w” and “d” denote world and display coordinates, respectively.

In related research, we have documented that an in-situ display supports accurate localization of hidden targets in 3D space (Klatzky, Wu, Shelton, & Stetten, 2008; Wu, Klatzky, Shelton & Stetten, 2005). In contrast, an ex-situ condition, where the depth of a target was determined by a numerical scale on a remote image, led to under-estimation of depth. We also tested whether in-situ and ex-situ viewing conditions were sufficient for people to determine the orientation of a tilted virtual rod (Wu, Klatzky, & Stetten, 2010). Subjects actively moved a viewing device along the upper surface of a box, at each position exposing the cross section of a rod within the box. As the device moved, vertical slant of the rod relative to the surface of the box (pitch) caused its cross section to translate up or down over successive images. Horizontal slant relative to the motion direction of the device (yaw) caused the cross section to translate horizontally. In both cases, the change in the display relative to the movement of the device signaled the slant angle. While both in-situ and ex-situ display modes led to accurate performance in judging a single slant angle, either pitch or yaw, only in-situ viewing allowed participants to visualize a rod slanted simultaneously in both directions.

1.5 Computational processes in integrating 2D cross-sections into 3D objects

We next examine specific computational processes that might be used to construct object representations from 2D cross-sectional slices. We propose that since cross-sectional images carry little volume information and largely preclude perceptual access to critical object features, 3D representations for the object itself and its parts must be computed by integrating 2D cross-sectional slices within a common frame of reference. An analysis of the requisite computational processes is next presented in detail.

First consider the kind of information offered when a planar aperture passes through a stimulus composed of straight-line tubular segments, such as the digit “4” shown in Figures 1 and 2. The result is a sequence of planar images, each a cross-section through the object acquired at a particular location in space. Each image contains regions of distinct luminance, which correspond to cuts through the segments of the stimulus. In our task, the process that limits performance is not the extraction of these regions, which are easily segmented and directly perceived. As was described above, the limiting processes are to assign the regions to locations in a frame of reference, and to integrate them. In this section we concentrate on the process of integration, which can be described at two levels: regions from multiple images are combined into segments, and segments are combined into an object.

At the first level of integration, segments are constructed from the regions visible in individual cross-sectional images. The simplest case is where each segment corresponds to a straight line in the source stimulus. If a cross-section contains a whole segment (i.e., the segment lies parallel to the imaging plane, like the crossbar of the 4 in Figure 1), it can be extracted from a single image. Otherwise, constructing a segment involves detecting endpoints and integrating the intervening cross-sections into a line lying at a particular position and orientation within a frame of reference. In support of the efficacy of this process, previous experiments indicated that the spatial disposition of a straight-line segment could be derived with reasonable accuracy from the displacement of its cross section over successive images (Wu et al., 2010). The process becomes more complex, however, when there are multiple line segments. One complexity is introduced when a continuous line is crossed by another (e.g., the vertical segment in a + symbol is crossed by the horizontal segment). This creates ambiguity at the crossover point as to whether the initially tracked segment has ended; moreover, the region of luminance corresponding to the intersection point must be assigned to both segments. Another issue is what triggers the onset of construction of a new segment, particularly if deviations from straight lines are allowed. The rule of good continuation or “relatability” (Kellman & Shipley, 1991) for perception of static visual displays can be applied here; that is, lines differing in direction are judged as a continuous segment if they connect across a bend of low curvature but as discrete otherwise. A violation of the relatability criterion (as occurs in K traced vertically) would then introduce a new segment.

Given that multiple segments are constructed, a second level of integration is needed to combine them into higher-order structures and ultimately into the object as a whole. Therefore, higher-order pattern analyses may play a role in constructing object representations. For example, recognition of symmetry may reduce memory load, as the reflected part of an object can be coded as such rather than constructed independently. Closed forms reduce the count of vertices and may also introduce top-down expectations about the orientations of segments. Spatial compactness may reduce memory load in terms of the size of the spatial frame to be considered, but could also introduce confusion errors among proximal segments.

On the basis of the above analysis, a number of factors can be identified that could impact on the difficulty of integration. (a) Demands on memory should increase with the complexity of the stimulus, in terms of the total number of segments to be constructed. (b) The orientation of segments relative to the direction of exploration should have an effect. Specifically, segments oblique to the direction of aperture movement, which produce cross sections that vary in spatial location across temporally separated image planes, will be more difficult to process than either those that lie perpendicular to the movement direction and therefore fall entirely within a single cross-section, or segments oriented parallel to the movement direction, cross sections of which remain in the same spatial location over successive images. (c) At the pattern level, the complexity increases with the number of dimensions over which the object spatially varies (2D vs. 3D). (d) Higher-order pattern processes, like detecting symmetry or closed forms, may support construction.

1.6 Goals of the present research

Given the extensive literature on 2D anorthoscopic perception, it is of intrinsic interest to ask simply how well people can perform a 3D analogue, where objects are constructed from a temporal sequence of cross-sectional images, each corresponding to a 2D slice plane. In addition to assessing this basic ability, we tested the theoretical proposals above regarding this process. We included manipulations that were intended to affect processes of localization and integration.

To test our assumption that 3D visualization from cross sections requires a localization process, by which the 2D slices are mapped into a common spatial frame of reference, we contrasted viewing conditions that should facilitate vs. impede this process. The essential manipulation was whether or not the cross sections extracted from an object were displayed at their spatial origins. As described above, with the in-situ display mode, each 2D image was shown to the observer at the same location as the object cross-section it depicts. With the ex-situ mode, the images corresponded to cross sections of an object at a particular location and orientation, but they were viewed on a displaced screen. Like the moving-aperture paradigm of 2D anorthoscopic perception, in-situ viewing co-locates the underlying object features, the currently visible subset of the object, and the aperture (i.e., the planar slice) within a unified spatial framework. In contrast, with ex-situ viewing, the object and the aperture reside in a common 3D space that is distinct from the viewed 2D image.

To test our assumptions that 3D visualization requires a two-level integration process --constructing individual segments from regions within the cross sections, and constructing a representation of the whole multi-segment object -- we manipulated variables intended to influence the processing load at each level. This was done by varying the design of the stimuli and the task to be performed. In Experiments 1 and 2, the stimuli were made of line segments, in conjunction with a task in which visualization was followed by same/different matching. The stimuli in Experiment 1 comprised co-planar segments (i.e., varied only in 2D), whereas those in Experiment 2 were fully 3D. Assuming the integration process proposed above, we constructed stimuli and/or decompositions that were intended to introduce different levels of processing load. These two initial studies established manipulations that affect performance and provide baseline data for efficacy of this process by normal young adults. Experiment 3 used familiar letters with curved as well as straight-line segments, and the task was identification. This allowed us to examine the nature of errors and from them, to infer the basis for integration failures. Finally, Experiment 4 examined the specific effects of in-situ vs. ex-situ viewing on the ability to determine spatial relationships among segments, which is made possible by the process of localization within a common frame of reference.

2. Experiment 1: Constructing planar 3D objects from cross-sectional images

The first experiment investigated how well people could mentally reconstruct a planar object from its cross sections and tested theoretical proposals described above. The participant’s task was to expose a hidden target object as a sequence of cross-sectional images by moving a virtual scanner (described below) along its vertical axis, visualize it from the images, and subsequently compare it with a test object. The stimuli were multi-segment planar objects similar to those described in Palmer (1977). In-situ and ex-situ displays were compared to test whether viewing of cross-sectional images within full 3D space would facilitate visualization, by supporting the mapping of cross sections to a common frame of reference. In addition, the complexity of the objects was systematically manipulated so as to load the integration processes described in the introduction. The accuracy and speed of judgments were measured to evaluate the impact of these manipulations.

2.1 Method

2.1.1 Participants

Twenty graduate and undergraduate students (ten males and ten females with an average age of 20.1±3.5 years) who were naïve to the purposes of this study participated in the experiment. All had normal or corrected-to-normal vision and stereo acuity better than 40” of arc. They all provided informed consent before the experiments.

2.1.2 Design& Experimental stimuli

The independent variables were display mode (in-situ vs. ex-situ) and segment complexity (3 levels, as described below). Display mode was implemented as a between-subject variable, to avoid possible carryover effects attributable to learning, and segment complexity was a within-subject variable.

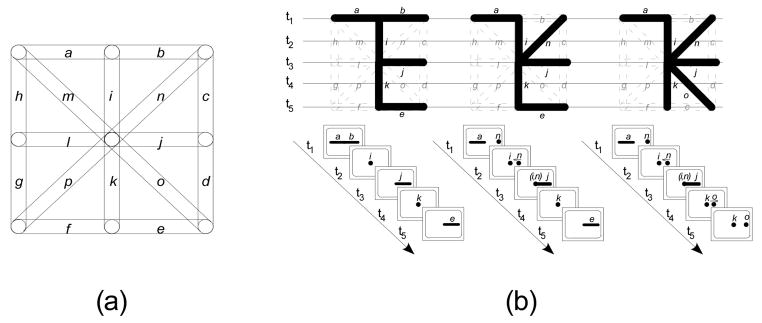
The stimulus patterns were connected co-planar line segments within a bounding envelope of 8.0 × 8.0 cm. Each pattern was constructed by choosing six components from a set of 16 alternatives (see Figure 3 for illustration). Aligned and continuous components merge to form a single unit, to be called a segment of the pattern. The number of segments thus can be smaller than six and vary across patterns (e.g., the 0-, 1-, or 2-diagonal patterns shown in Figure 3 consist of 4, 5, and 5 segments, respectively). For purposes of exploration, the resulting pattern was rendered on a plane parallel to the ground plane, to be called the pattern plane. Extension of the pattern into a third dimension orthogonal to the pattern plane was introduced by rendering each line as a solid rod with a diameter of 0.8 cm. The pattern was explored with a mock transducer. When placed crosswise to the pattern at some point along its vertical axis, the transducer exposed a slice plane perpendicular to the pattern plane, portraying the cross section of the pattern at that point. Bounded regions in a single slice plane will be called elements, corresponding to individual segments at that scanning location. Moving the transducer along the vertical axis of the pattern while maintaining the slice orientation perpendicular to the vertical axis eventually exposed all segments of the pattern as a continuous series of elements, corresponding to its cross sections. Segments having different orientations in the pattern plane exhibited different sequences of elements: A horizontal segment, when intersected by the slice plane, was shown as an element in the shape of a bar; a vertical segment was displayed as a circular element that persisted in successive slice planes until its end was reached, and a segment oblique to the scanning direction was represented as an elliptical element that moved transversely across successive slices. Segments were also differentiated by the locations of their cross sections within the slice plane. By combining the orientation and location information, the viewer could attempt to visualize the segments and ultimately the whole pattern.

Figure 3.

(a) Pattern components. In Experiment 1 Stimulus patterns were constructed by choosing a subset of six components from a total of 16 co-planar alternatives (alphabetically labeled “a–p” for purposes of illustration, adopted after Palmer, 1977). (b) From left to right, examples of 0-, 1-, or 2-diagonal stimulus patterns (top) used in Experiment 1 and their appearance under cross-sectional sampling at five locations (bottom).

A total of 24 patterns was constructed for experimental trials and another six for practice only. The stimulus patterns were categorized into three groups, corresponding to different levels of segment complexity, as manipulated by the number of oblique segments in the pattern (zero, one or two) relative to the number of horizontals and verticals. Our intention with this manipulation was motivated by the theoretical analysis introduced earlier, which identifies sources of temporal and spatial load on the process of integration: Because an oblique segment is exposed over multiple slices, whereas a horizontal segment is exposed within a single cross section, replacing horizontals with obliques increases the number of slices over which the segment is visualized. Because the cross sections of an oblique segment move transversely across successive slices, whereas the vertical segments remain in a constant location on the slice plane, replacing a vertical with an oblique causes the elements of the segment to be spatially dispersed across slices, although the total number of slices needed to expose the segment is unchanged. Altogether, as a pattern contains more oblique segments, there is an increase in the number of spatially and temporally distinct elements in cross-sectional images and thus an increase in processing load.

Outside of the factorial design, we also considered the effects of complexity at the pattern level (cf. individual segment complexity). The patterns were constructed so as to avoid variations in obvious pattern-level properties, such as symmetry or meaningfulness. However, the considerable variability across pattern structure inevitably introduced the possibility of systematic effects on performance due to pattern variation. One variable that was identified is the overall extension of the pattern in space, which we term sprawl; it will be discussed in the analysis below.

Each stimulus was tested only once to preclude repetition effects, constituting a total of 24 experimental trials. These trials were blocked into two blocks of 12 each, randomized within each block. The testing order of blocks was counterbalanced across subjects.

2.1.3 Experimental setup

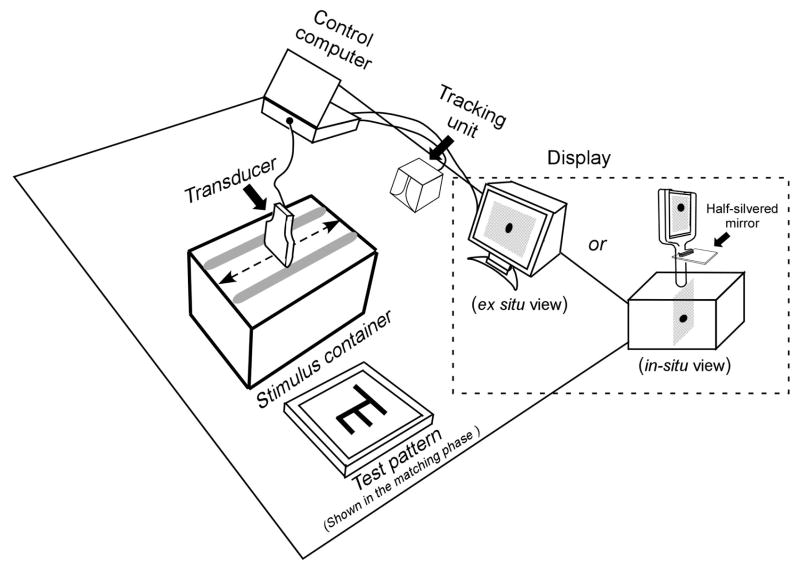
The experimental setup was mounted on a table, as shown in Figure 4. It consisted of a stimulus container, a mock transducer, a display unit for presenting cross-sectional image, an LCD for displaying the matching target, a tracking system and a computer for control and data acquisition.

Figure 4.

Schematic of the experimental setup. Participants used a transducer to scan a target that was hidden inside the stimulus container, exposing it as a sequence of cross-sectional images. Two types of display (in-situ vs. ex-situ) were tested.

The stimulus container was a box of 31(L) × 17(W) × 22 (H) cm. Inside it, a target pattern was virtually created by software as a 3D computer model that was registered relative to the container. Transducer movement was restricted to the vertical axis of the pattern, and transducer orientation was restricted to perpendicular to that axis, by a pair of wood rails longitudinally mounted on the top of the container and running along its length, spaced horizontally to match the transducer width. Next to the stimulus container was placed a 15 inch (38 cm) LCD for presenting the test pattern for the same/different judgment.

The mock transducer was made of wood so as not to interfere with the tracking sensor (miniBIRD 500) embedded inside it to continuously trace its location and orientation. The tracker data were used to determine the relative position of the transducer with respect to the target, and hence control the cross-sectional view to be displayed. The view consisted of an 12.0 cm × 8.0 cm area with a background of random dots (mean luminance: 4.1 cd/m² and 12.5 cd/m² in the in-situ and ex-situ conditions, respectively) representing the cross-section of the box, superimposed on which was the target’s cross-section at that transducer location (luminance: 94.1 cd/m² and 163.1 cd/m², respectively, in the in-situ and ex-situ conditions). A Dell laptop was used to generate and display the cross-sectional images at an updating rate of 51.7 fps.

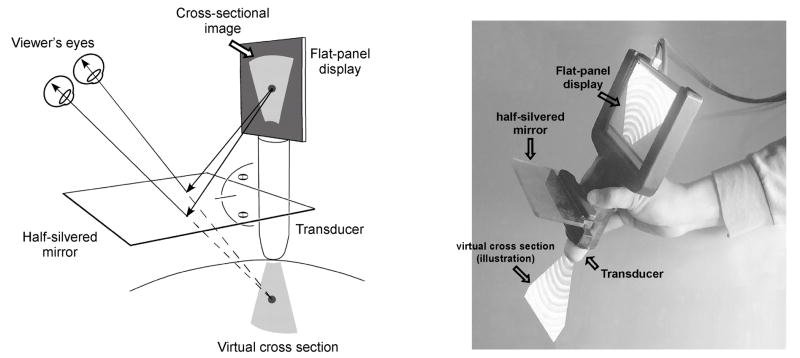
Two displays were used in this study to present subjects the target’s cross-section: (1) an augmented-reality (AR) device (Stetten, 2003; Stetten & Chib, 2001) that creates an in-situ view of the target’s cross-section, and (2) a conventional 15 inch (38 cm) CRT display in the ex-situ viewing condition. The in-situ AR display (see Figure 5) consists of a 5.2 inch (13.2 cm) flat panel screen and a half-silvered mirror that are rigidly mounted to the mock transducer. The half-silvered mirror is placed halfway between the tip of the transducer and the bottom of the screen. As a result of this configuration, when looking into the mirror, the reflection of the screen image is seen as if emitting from the tip of the transducer. Moreover, because of the semi-reflective characteristics of the mirror, the reflection is merged into the viewer’s sight of the container, creating an illusion of a planar slice floating inside the box. The AR display and the rendering of the virtual target were calibrated so that the cross-section of the target was seen exactly at its virtual location. The viewer’s depth perception with this in-situ display has available full binocular cues, including convergence of the eyes and disparity between the left and right retinal images, and has been found to produce depth localization comparable to direct vision (Wu et al., 2005).

Figure 5.

Schematic and photograph of the in-situ display. Through the half-silvered mirror, the cross-sectional image is projected as if it “shines out” from the transducer and illuminates the internal structures (Adapted from Wu, Klatzky, Shelton, & Stetten, 2005, with permission, © 2005 IEEE).

In the ex-situ viewing condition, the cross sectional image was scaled 1:1 with the in-situ target, so that the visual stimulus was matched in size across the two conditions. The distinction was the location of the image: In the ex-situ condition, the image was shown on the center of a 15 inch (38 cm) CRT monitor located approximately 90 cm away from the stimulus container (i.e., the target’s true location). Full visual cues are available to viewers in this viewing condition, but by definition of the ex-situ display, these cues place the perceived location of all cross sectional images on the CRT screen, rather than their spatial origins. The CRT was oriented so that its screen was parallel to the frontal plane of the stimulus container. In addition, along the bottom and right sides of the cross-sectional image, two centimeter rulers were provided to enable accurate measurement of locations inside the image.

2.1.4 Procedure

The subjects were assigned alternately to use the in-situ or ex-situ display. At the beginning of the experiment, they were given an explanation of the task. Graphical animations were used to explain how cross-sectional views of an object were generated. Specifically, examples were given to illustrate the cross-sectional appearance of lines of different orientations (i.e., horizontal, vertical, or oblique). Detailed explanations were provided about how the imaged part of a line could be located in space with reference to the transducer position and orientation. Participants next received six practice trials, in order to familiarize them with the procedure and displays. No feedback regarding accuracy was given during these practice trials and the subsequent experimental sessions.

Each trial had two phases. In the first (scanning) phase, the participant explored a target pattern inside the container by scanning the transducer over it. He or she was instructed to hold the transducer in an upright position and gradually scan the whole length of the container to find the target. The cross section of the target was shown on the CRT in the ex-situ condition, or at the location being scanned in the in-situ condition. The target was usually scanned multiple times by the participant. Once he or she had interpreted the pattern, the participant would hold the transducer and press any key on a keypad to move on to the second (matching) phase. A test pattern then appeared on the matching display (i.e., LCD in Figure 4) and the participant was required to compare it with the remembered target and judged as quickly as possible if two patterns were same or different by pressing one of two keys. In this experiment the test patterns were derived from the target patterns by horizontally or vertically displacing one horizontal segment while maintaining other segments, diagonal or vertical, unchanged. Accuracy of the subject’s judgment and two response times (RTs) were measured: The scanning RT was measured from the first appearance of the target in the cross-sectional views to the onset of the first key press, the matching RT from the presence of the test pattern to the onset of the second key press for a Yes/No judgment. Between the scanning and matching phase, a checkerboard mask was presented for 3 sec. The typical duration of a trial was less than 1 min, and the whole experiment took less than one hour.

2.2 Results and Discussion

For each of the three response measures, 2 × 3 ANOVAs were conducted with display as the between-subject factor and pattern complexity as the within-subject factor. We consider the effects of each independent variable in turn.

2.2.1 Effect of in-situ vs. ex-situ viewing

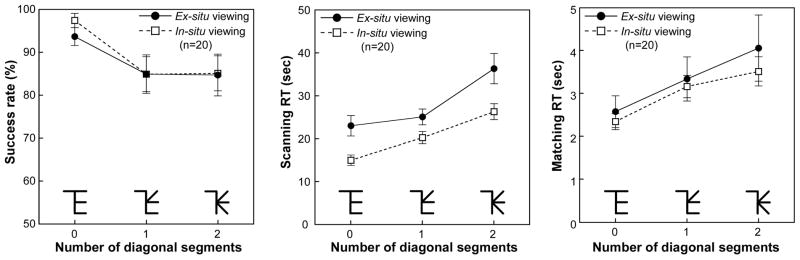
As shown in Figure 6, in-situ viewing allowed subjects to visualize the hidden target from cross-sectional images much faster than using the ex-situ display. Compared to the ex-situ condition, the mean scanning RT across all subjects and stimulus patterns was 26.9% shorter (28.2 sec vs. 20.6 sec, F(1,18)=7.13, p= 0.02) in the in-situ condition, while the overall accuracy was comparable in the two conditions (89.6% vs. 89.4%). This provides support for the hypothesis that spatial grounding of cross-sectional images and source object facilitates mental visualization.

Figure 6.

The results of Experiment 1. The mean accuracy, scanning RTs, and matching RTs in two viewing conditions were plotted as functions of the number of oblique segments in the pattern. Error bars represent the standard error of the mean.

In contrast, the display had little effect on the accuracy rate (F(1,18)=0.20, p=0.66) or matching RT (i.e., the amount of time that the subjects took to compare the visualized target to a test pattern, F(1,18)=0.330, p=0.57). This suggests that the product of visualization, although achieved more slowly by users of the ex-situ display, was comparable across displays.

2.2.2 Effect of segment complexity

Recall that our segment-complexity manipulation was instantiated by varying the number of oblique segments in the stimulus, with the intention of thereby introducing variation in processing load. Replacing a vertical with an oblique increases the load on spatial integration because it spatially disperses the segment elements, and replacing a horizontal with an oblique disperses its elements across both space and time. Performance was strongly affected by segment complexity, as manipulated by the number of oblique segments in comparison to horizontal and vertical segments: Average accuracy was 95.7% when judging 0-oblique patterns but only 85.0% for 2-oblique patterns. The ANOVA revealed a significant main effect of complexity (F(2,36)=4.99, p=0.01) and no interaction with display (F(2,36)=0.16, p=0.86).

In addition, response times increased with the number of oblique segments. The ANOVAs found significant main effects for stimulus configuration for scanning RT (F(2,36)=80.44, p<0.001) and for matching RT F(2,36)=11.60, p<0.001. The interaction between display mode and stimulus complexity was significant (F(2,36)=3.46, p=0.04) for the scanning RT, reflecting a slightly reduced display effect for the moderate-complexity stimuli, but not for the matching RT (F(2,36)=0.26, p=0.77).

2.2.3 Effect of pattern variables on visualization

In addition to the segment complexity that was manipulated in the factorial design, variables that affect complexity at the pattern level would also be expected to impact on visualization, by their impact on the integration process. Here, we identified one such variable, which captured the compactness of the pattern, or conversely, its sprawl. Sprawl was quantified as the longest path between terminal points of the pattern, in terms of number of segments traversed. For example, the letter F has one path of three segments (the path from the upper-horizontal segment to the lower-horizontal segment) and two of two segments (the paths consisting of the vertical segment and one horizontal segment). This measure captures the idea that the longer a concatenation of segments in the pattern, the heavier the computational and memory loads needed to assemble it. To avoid contamination of this variable by the manipulation of the number of diagonals, the scanning RTs and the sprawl measures were transformed to z-scores within each level of segment complexity in the factorial design. A significant positive correlation was found between z-score sprawl and z-score scanning RT (r = 0.68, p<0.001 and r=0.77, p<0.001 respectively, for the ex-situ and in-situ conditions). Thus sprawl, a pattern-level variable, is a strong predictor of visualization difficulty, independent of the complexity of lower-level processes.

3. Experiment 2: Constructing 3D patterns from cross-sectional images

This experiment paralleled the first but addressed subjects’ ability to perceive objects in full 3D from cross-sectional images.

3.1 Method

3.1.1 Participants

Twenty graduate and undergraduate students (twelve males and eight females with an average age of 23.6±4.0 years) were tested. They were naïve to the purposes of this study. All had normal or corrected-to-normal vision and normal stereoscopic vision.

3.1.2 Design & Experimental stimuli

The design was parallel to that of Experiment 1, with the important addition of the spatial dimensionality (2D planar vs. full 3D) of stimulus patterns as a within-subject variable. Accordingly, the complexity of the stimulus patterns varied in terms of number of oblique segments and also dimensionality.

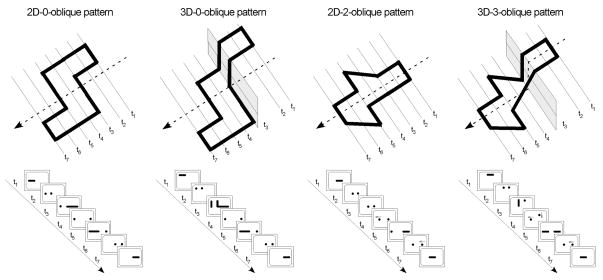
The stimuli in this experiment were closed wireframes made of lines that were oriented parallel, perpendicular or oblique to the cross-sectional plane. The 2D stimuli were formed by a series of coplanar line segments and the number of oblique segments in each pattern was 0 or 2. The 3D patterns were then developed from 2D counterparts by vertically displacing the top and bottom half of the 2D pattern by 6.0 cm (see Figure 7 for illustration), corresponding to elements at different heights in cross-sectional images. The two halves were then connected by adding vertical or oblique segments; hence 3D patterns had more segments than their 2D counterparts. Four groups of stimuli resulted: 2D-0-oblique patterns, 2D-2-oblique patterns, 3D-0-oblique patterns, and 3D-3-oblique patterns.

Figure 7.

Stimulus objects used in Experiment 2. Examples of 2D-0-oblique patterns, 2D-2-oblique patterns, 3D-0-oblique patterns, and 3D-3-oblique patterns and their appearance under cross-sectional sampling at seven locations.

Six patterns of each type were constructed. Each was tested only once across 24 experimental trials in random order for each device condition. In addition, a total of 24 matching patterns were derived from the corresponding targets: 2D matching patterns were derived by horizontally or vertically displacing one horizontal segment, and 3D matching patterns were created similarly, except that more horizontal and vertical segments were displaced in order to maintain closure.

3.1.3 Experimental setup & procedure

The experimental setup was identical to that of Experiment 1. The 3D test pattern was presented on the matching LCD by a 3D model that rotated through 90° (from −45° to +45° at a rotation speed of 30 °/s). According to Bingham & Lind (2008), such a continuous change in viewing perspective is sufficient for accurate perception of 3D shape. The experimental procedure was as in Experiment 1. The accuracy and the response times for scanning and matching were measured.

3.2 Results and Discussion

3.2.1 Effect of in-situ vs. ex-situ viewing

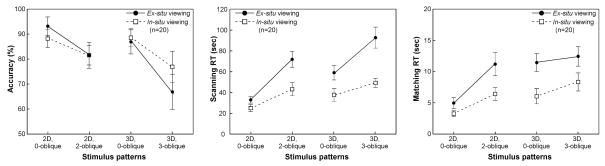
As in the previous experiment, the effects of different displays were observed in response time: The subjects performed the task with similar accuracy using the two displays (F(1,18)=0.11, p=0.75), but displayed faster RT with the in-situ display than the ex-situ display in both scanning (F(1,18)=8.52, p=0.01) and matching (F(1,18)=4.51, p=0.05) phases, as shown in Figure 8.

Figure 8.

The results of Experiment 2. The mean accuracy, scanning RTs, and matching RTs in two viewing conditions were plotted as functions of stimulus group. Error bars represent the standard error of the mean.

3.2.2 Effect of segment complexity and dimensionality

A two-way ANOVA applied to the accuracy data found significant main effects for both spatial dimensionality (F(1,18)=8.17, p=0.01) and number of oblique segments (F(1,18)=17.68, p<0.001). Main effects of these factors were also found to be significant in the scanning and matching RTs (Scanning RTs: F(1,18)=59.56, p<0.001 and F(1,18)= 28.03, p<0.001 for main effects of oblique segments and spatial dimensionality, respectively; Matching RTs: F(1,18)=31.89, p<0.001 and F(1,18)= 28.08, p<0.001, correspondingly). No significant interaction between the two factors was observed in the accuracy (F(1,18)=1.35, p=0.26), scanning RT (F(1,18)=2.14, p=0.16) or matching RT (F(1,18)=4.02, p=0.06) data.

In addition, display mode interacted with both complexity measures: segment complexity, (F(1,18)=8.87, p=0.01) and dimensionality (F(1,18)=4.84, p=0.04). Both types of complexity affected scanning duration more when subjects used the ex-situ rather than the in-situ display.

3.2.3 Effect of pattern complexity on visualization

As in the previous experiment, correlation analyses were conducted on scanning duration to determine the effects of pattern-level complexity variables. Similarly to Experiment 1, we devised a higher-level measure of sprawl to describe pattern compactness. Since the stimuli used here were closed patterns, the 2D patterns were characterized as a core area that could be constructed from the horizontal segments, plus deviations from the core that constituted sprawl. The horizontal segments require no process of integration across slices, because they appear as a whole within a single cross section. The core was identified as the largest sub-area in the pattern bounded by two successive horizontal segments in the pattern plane (see Figure 7), and sprawl was the percentage of total area lying outside the core. As was done previously, to avoid contamination of sprawl by the manipulation of the number of diagonals, the z-score of sprawl and the z-score of the scanning RTs were computed within each 2D pattern subgroup as defined by segment complexity. The correlation between the sprawl and scanning-RT z scores was significant (r = 0.70, p=0.01 and r = 0.67, p=0.02 respectively, for the ex-situ and in-situ conditions).

This measure of sprawl could not be extended from a 2D pattern to its 3D equivalent, because those 2D patterns that had a large core tended to be converted to 3D by elevating a section of the core area. However, the importance of sprawl can be seen with the 3D patterns by considering whether or not the core was interrupted to create the third dimension. The correlation between scanning z-scores and a binary variable indicating whether or not the core was disrupted to create the 3D pattern was 0.71, p < 0.01, indicating that interrupting the core strongly contributed to 3D pattern difficulty.

4. Experiment 3: Letter recognition from cross-sectional images

The purpose of Experiment 3 was to extend the visualization paradigm to familiar forms, for which top-down processing could be invoked. The stimuli were numerical or alphabetical letters, and the participants’ task was to identify the letters from their cross-sections by using an in-situ or ex-situ display. The accuracy and speed of naming responses were measured. To the extent that top-down processing can compensate for the greater difficulty in visualizing forms from the ex-situ display, no difference between the displays would be expected. We predicted, however, that the display effect would be maintained even for familiar forms.

4.1 Method

4.1.1 Participants

Twenty-four graduate or undergraduate students (thirteen males and eleven females with an average age of 20.3±3.0 years) participated in the experiment. All were native English speakers and naïve to the purposes of the study. They had normal or corrected-to-normal vision and stereo acuity better than 40” of arc. They all provided informed consent before the experiments.

4.1.2 Design & Experimental stimuli

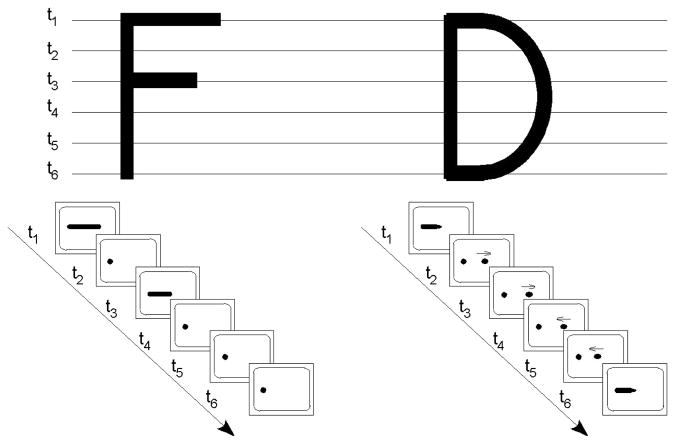
As in the previous experiments, the independent variable was display mode (in-situ vs. ex-situ), which was manipulated within subjects. The stimuli were 24 English letters (A,B,C,D,E,e,F,f,G,g,H,h,J,K,L,N,P,Q,R,r,S,X,y,Z) and 4 numbers (2,3,4,5). The letters and numbers were digitalized and represented as wireframe models, the components of which were straight or curved solid rods with a diameter of 0.8 cm (For illustration, please see Figure 9). All were scaled to a size that allowed them to be displayed in an area of 8.0 × 8.0 cm.

Figure 9.

Examples of the stimulus letters used in Experiment 3.

The experiment was run in two blocks, one for each device, separated by a break. The testing order of display mode was balanced across participants. Each block consisted of one practice trial, followed by 14 experimental trials. The choice of stimuli was randomized within each block with no repeats. Initial practice used a different set of characters (I,T,O,V,7,8).

4.1.3 Experimental setup

The experimental setup was same as described in the previous experiments, except for the addition of a voice-activated switch for measuring the latency of naming responses.

4.1.4 Procedure

As in the previous experiments, all participants first received a detailed explanation of how cross-sectional views of an object were generated and how a given image could be located in space with reference to the transducer position and orientation. Examples were given to illustrate the cross-sectional appearance of straight lines (horizontal, vertical, or oblique) and curves (open or closed). Next, participants received six practice trials, three with each display, in order to familiarize them with the procedure and displays. Feedback was provided during these practice trials but not in the subsequent experimental sessions.

The participant was explicitly informed that the target was a digit or an English letter in upper or lower case, and the task was to identify it from its cross-sections as accurately and quickly as possible. On each trial, the target was presented in a random location inside the container. The participant was instructed to hold the transducer in an upright position and scan the whole length of the container to find the target. He or she could see the cross section of the target on the CRT in the ex-situ condition, or at the location being scanned in the in-situ condition. The target was usually scanned multiple times. As soon as the participant recognized the target, he or she was to report it. Response times, measured from the first appearance of the target in the cross-sectional views to the onset of the naming response, were recorded using a voice-activated switch linked to the control computer. The experimenter recorded the subject’s judgment, and then pressed a key to move onto the next trial. During the inter-trial interval a checkerboard mask was presented on the screen for 3 sec. The typical duration of a trial was less than 1 min, and each experimental block took less than 25 min. There was a 5-min break between the two successive experimental blocks.

4.2 Results and Discussion

4.2.1 Effect of in-situ vs. ex-situ viewing

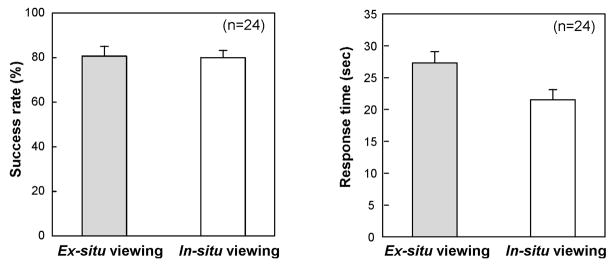
As shown in Figure 10(a), the subjects performed the task with similar accuracy in the two display conditions (paired t-test: t(23)=0.61, p=0.27). Their success rate averaged 82.4% and 80.4% with the in-situ and ex-situ displays, respectively. There were, however, differences in the pattern of errors, as described below. As in previous experiments, the superiority of the in-situ display was shown in the speed of identification: Subjects recognized the patterns faster (21.5 sec vs. 28.4 sec, paired t-test: t(23)=4.08, p<0.001) from cross-sections when using the in-situ rather than the ex-situ display.

Figure 10.

The mean accuracy and RTs observed in Experiment 3. Error bars represent the standard error of the mean.

4.2.2 Effect of pattern on visualization

As in the previous experiments, the number of non-horizontal segments, presumably requiring integration at the segment level, was used to quantify the mental load at the level of segment integration. (There was no measure of sprawl for these patterns.) Correlation analyses revealed a significant positive relationship between the number of integrated segments and mean scanning RTs (r = 0.64, p<0.001 and r=0.53, p=0.003, respectively, for the ex-situ and in-situ conditions).

4.2.3 Error Analysis

The errors were classified into three groups, paralleling the distinction between segments and patterns in Experiments 1 and 2, and adding the top-down influence possible with these familiar letter stimuli. Segment errors are identified when the confusion is clearly attributable to the misperception of segments; for example, straightening the top of a 2 so that it is called a Z. Pattern errors are identified when the individual segments correspond between target and response, but the spatial relationship between segments is confused (e.g. 3 misidentified as S), or the pattern as a whole is mis-oriented (e.g. confusing C with U) relative to the exploration space. Top-down errors take the form of adding segments that create a plausible meaningful pattern, for example, adding a lower line to an F to make it an E, or omitting segments that default to a simpler form that is still a letter, as in E to F. Over 90% of the subjects’ error responses could be unambiguously categorized into one of these three types, by two scorers.

Segment errors were the least frequent (5 mistakes made by 4 subjects with the in-situ display and 5 errors by 5 subjects when using the ex-situ display), indicating that subjects had little problem constructing segments from cross-sectional views.

Pattern-level errors, in which segments or whole letters were mis-oriented spatially, constituted 30.3±1.6% of errors with ex-situ viewing (20 mistakes by 10 subjects) and only 9.5±0.8% (5 mistakes by 4 subjects) when using the in-situ display. This was the only category of error in which display had a significant effect (chi-square χ²= 9.00, p=0.003).

The third type of error, attributable to top-down influence, was most common and varied little across viewing conditions (19 omissions and 18 additions made by 10 subjects with the in-situ display, and 20 omissions and 17 additions by 13 subjects with the ex-situ display).

The effect of display on pattern-level errors, in which segments or characters were mis-oriented, together with the lack of a display effect in the other two categories, helps to pinpoint the component of visualization that is undermined by ex-situ viewing. It appears that the ex-situ display is sufficient to visualize individual segments and to invoke top-down hypotheses. Where the device particularly fails is conveying the spatial relationships among component segments. Because all slices of the underlying target are presented at a common plane in space, the device requires additional spatial processing to localize them in a 3D frame of reference. Presumably, it is the load on the localization process that slowed construction of targets when the ex-situ display was used, relative to in-situ viewing.

Experiment 4 was intended to provide further converging evidence for this interpretation. It used a mental rotation task to examine the effects of the display specifically on the ability to determine spatial relationships among segments.

5. Experiment 4: Identification of disoriented letters

The task in this experiment specifically required judgments of the spatial relationship between target segments. The participants explored a hidden letter and, from the ensuing cross-sectional views, judged whether it was normal or mirror-reversed. The accuracy and speed of naming responses were measured. To isolate spatial relationship judgments as the basis of the task, subjects were explicitly told the identity of the target letter. Despite this elimination of the identification component of the task, we expected to again find an advantage for the in-situ display.

5.1 Method

5.1.1 Participants

A group of twenty undergraduate students (eleven males and nine females with an average age of 19.7±2.7 years) was tested. All were naïve to the purposes of the study, and none participated in the previous experiments.

5.1.2 Experimental setup & procedure

The experimental setup was as described in the previous experiments. The independent variables were display mode (in-situ vs. ex-situ) and letter orientation (0°, 90°, 180°, or 270°). The stimuli were four letters (F, y, J, or R) and their mirror counterparts rotated in four orientations, constituting a set of 32 trials for each display.

The experimental procedure was as in the previous experiment, except that the subject was explicitly informed which letter would be present by a recorded voice, played at the beginning of each trial. The task was to judge from cross-sectional views whether that letter was normal or mirror-imaged as accurately and quickly as possible. The subject made a response by pressing one of two buttons. The experiment was run in four blocks separated by 5-min breaks, two for each display device. Each block consisted of four practice trials, followed by 16 experimental trials. The testing order of these blocks and display mode was counterbalanced across subjects.

5.2 Results and Discussion

The results were pooled across the stimulus letters and erroneous responses were excluded from the analyses. Two-way ANOVAs were applied to the accuracy and RT data with factors of orientation and display mode. The accuracy ANOVA showed, as expected, a significant main effect for display mode (F(1,19)=4.69, p=0.04). The overall accuracy was 78.1% with the in-situ mode and 75.0% with the ex-situ. The RT ANOVA also showed a significant advantage (faster RT) for the in-situ display mode (F(1,19)=10.22, p=0.01). This advantage occurred despite the fact that the identification component of the task was eliminated, thus supporting the hypothesis that ex-situ viewing is particularly disadvantaged with respect to localizing and spatially relating the elements of the pattern.

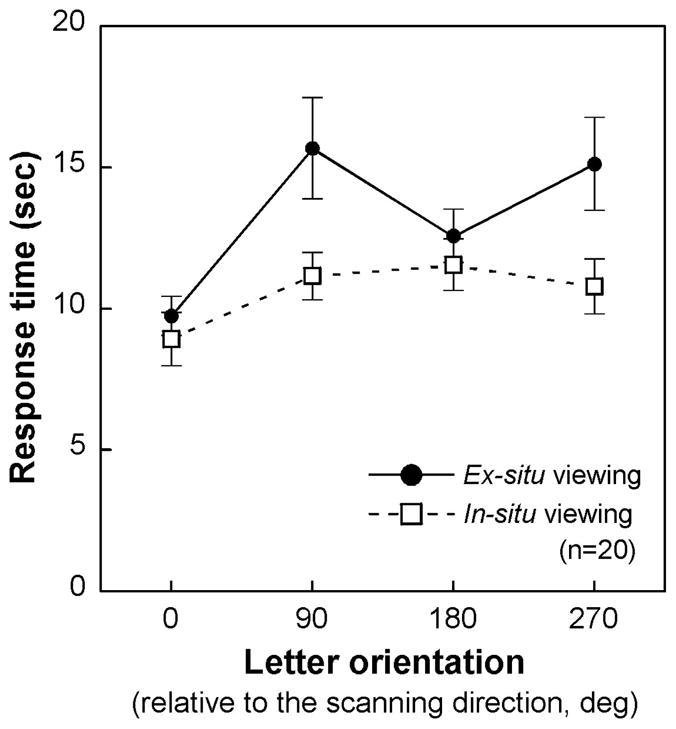
There were also main effects of orientation (for accuracy, F(3,57)=2.89, p=0.04; for RT, F(3,57)=11.25, p<0.001). Accuracy was lower for stimuli at 90° and 270° (71.9% and 71.5%, respectively) relative to upright (81.3%) or inverted (81.6%), and orientation did not significantly modulate the display effect (F(3,57)=0.62, p=0.61). For RT, the display effect was modulated by orientation, as seen in a significant interaction, (F(3,57)=6.70, p<0.001). This is shown in Figure 11, where the device effect on RT can be seen to be greatest for the stimuli that produced slowest responses. This indicates that the most difficult stimuli become so because of the difficulty of spatially relating their components.

Figure 11.

The mean RT observed in Experiment 4 as a function of stimulus orientation. Error bars represent the standard error of the mean.

6. General Discussion

In the present study, we extended the anorthoscopic viewing procedure into 3D and used it to investigate the mental visualization of objects from cross-sections. We propose that two key components of this visualization problem are (a) to localize cross-sectional images within a common frame of reference and (b) to integrate the cross-sections into a coherent object representation. The importance of the first of these processes was shown by the superiority of the in-situ mode, where the cross-sectional images were projected into their source locations, over the ex-situ mode, where the cross-sections were displaced to a remote monitor. The results specifically implicated the disadvantage for ex-situ viewing with respect to localizing the cross sections, so that the image from one could be spatially related to another. This spatial information is critical to the second process, integration. The nature of integration was elucidated by effects of complexity manipulations that pointed to integrative processing at two levels, building individual segments and combining them into a representation of the whole pattern. We next consider further the theoretical implications of these results.

6.1 Effects of viewing mode on visualization

The experiments reported here clearly showed an advantage of the in-situ display over the ex-situ display in the task of visualizing an object from cross-sections. Given our multi-level framework for the process, which separates spatial localization from integration, we can ask whether the display impacts one of these levels or both. Consider first the impact of the display on localization. As was described in the introduction, this process essentially corresponds to restoring the third dimension of the stimulus which is lost in the production of cross-sectional images. As shown in Figures 2 and 5, the in-situ display presents a cross-section at its source location, showing it as a slice residing in space. Full visual depth cues are available to accurately perceive the 3D location of the slice and the object structure depicted within it. In contrast, the ex-situ display is adequate to portray the 2D cross-sectional content but, by virtue of displacing the image from its source location, is inadequate to represent the lost third dimension. Additional processes, if feasible, are then needed to localize the image content in 3D space. Given our paradigm, in which active exploration is used to find the slice location, this involves combining information across different sensory modalities and different sensorimotor frames of reference. This clearly adds cognitive load to what is, in the in-situ context, a direct perceptual process. We have shown that the cost of this load can be considerable, leading to underestimation errors in localizing and directing actions to hidden targets in 3D space, and difficulty in learning image-guided actions (Klatzky et al., 2008; Wu et al., 2005, 2008).

The impact of the display mode on spatially localizing images inevitably cascades to the higher-order process of integration. The nature of this impact depends on whether the viewer can succeed in assigning the cross-sections to a common frame of reference under conditions of the ex-situ display. It is possible that the additional load of a displaced image does not prevent localization, but merely increases inaccuracy and uncertainty. The additional time and error observed with this display would then be a consequence of loss of precision in the coordinates of the cross sections. It is also possible, however, that localization in a common frame of reference fails.

Other research supports the idea that mis-orientation errors result from failure to process within an appropriate frame of reference. In our previous study where the ex situ display was used to determine the pose of a rod in 3D space (Wu et al., 2010), a common error was to report an approximately correct magnitude, but in the wrong direction (e.g., report upward pitch as downward). We attributed this to participants’ failure to construct the required 3D frame, and their consequent reliance on the local 2D frame of the screen. Similarly, reversal errors have been attributed to competing frames of reference when people recognize patterns drawn on the skin. For example, letters are often perceived as being mirror-reversed when drawn on the outstretched palm, which may be represented from an internal or external perspective (Parsons & Shimojo, 1987; see also Oldfield & Phillips, 1983; Parsons, 1987).

It seems likely, then, that the core problem under ex situ viewing lies in a failure to represent the relationships among features by localizing them within the requisite 3D frame. The errors observed in the present Experiment 3 and 4 strongly suggest that by virtue of failures in localization, integration itself failed, particularly at the higher level. Observers were able to identify individual segments but in many cases proved unable to relate them spatially, resulting in errors in the pattern configuration.

6.2 Visualization processes with 3D objects

The effects of the display mode shed light on fundamental computations used to achieve object representation. As was noted in the Introduction, view-based theories suggest that a 3D object can be mentally represented by a collection of 2D views (Bülthoff, Edelman, & Tarr, 1995; Lawson, Humphreys, & Watson, 1994). Accordingly, it might be argued that in the current task, a hidden target might be represented as a sequence of cross sectional views, and recognition then achieved by mentally generating and comparing the test object’s cross sections to the stored views. For example, the letter “F” can be represented as the following characteristic cross sections: two long horizontal bars, one longer and one shorter, interleaved with the views of a single dot. If the current task was solved by this approach, we would expect no effect of the display mode, because each object was depicted by the same 2D views using the two displays. Our experimental results clearly do not support this prediction. Instead, viewers proved capable of interpreting cross-sectional images as highly complex 3D structures. As was noted previously, this act is appropriately called visualization, because it requires complex manipulation of spatial data extracted over time.

Visualization, we propose, combines processes of localization and integration. Our data implicate a role for visual-spatial memory in localization, in the form of a frame of reference that maintains pattern components for a period during which integration can occur. What can be said about the process of integration itself? In our view, this component of visualization recapitulates essential processes of visual perception itself, in that it creates hierarchical structures from input data over a series of computational processes (Palmer & Rock, 1994). As representations derived from component cross-sections are indexed and stored in the visual-spatial memory, integration is the mechanism by which they are related to one another. The computational processes involved in integration must follow rules like those described in the introduction, whereby contiguous elements at one level (e.g., cross sections of a tube) are identified as units at a higher level (e.g., the tube itself), with the ideal of culminating at the level of the pattern as a whole. The resulting hierarchical structure can be passed on for further processing or parsed as needed for other tasks. This proposed sequence of processing is imposed by the computational demands of the task. To the extent that these demands are echoed in visual perception and object cognition, the computational functions would be similar (e.g., object representations by constituent parts and the spatial relation among the parts; Biederman, 1987).

However, the computational mechanism for visualization, which demands post-perceptual working memory for its implementation, transcends the visual system. It is likely to involve higher-level amodal mechanisms (Shimojo, Sasaki, Parsons, & Torii, 1989; Loomis et al., 1991). In this regard, we note that similar integrative processes are demanded in haptic spatial and object perception where information is sequentially sampled. Loomis et al. (1991) compared the recognition of line drawings of common objects by touch or aperture viewing. The results showed that when the size of the visual aperture was truncated to that of the finger pad, the subjects performed with similar accuracy and speed in visual and haptic conditions. It is reasonable to speculate that the limitation in performance is not imposed by different sensory processes, but the result of common, modality-independent processes involved in information integration.

The memory and computational demands of integration are clearly signaled in the present experiments in multiple ways. Not surprisingly, manipulations that extended the spatiotemporal distribution of segments impacted negatively on processing time and/or accuracy. The present studies offer, in addition, novel measurements of complexity at the pattern level, which we have termed sprawl. While sprawl is defined in terms of the topological structure of the pattern, it also captures an aspect of the workload in computation. Though measured in different ways across pattern families, sprawl is essentially a measure of pattern compactness, or rather, itsinverse. The processing consequences of this type of variable cannot be fully determined from the present studies. Greater sprawl may correspond to increased working-memory load or violation of Gestalt principles such as good continuation. We will further examine this topic in future work to advance our knowledge on integrative mechanisms in image-based visualization.

It is important to acknowledge limitations in extending the present research to visualization of 3D objects in general. An obvious limitation is the use of a specialized form of object presentation quite different from the everyday contingencies leading to spatiotemporal integration. Whereas it is common for an object to be exposed piecemeal as it is reoriented in the hand or the viewer moves around it, it is uncommon outside of medical contexts for an object to be exposed as a series of slices by movements of the hand. The foregoing analysis suggests, nonetheless, that cross-sectional visualization incorporates processes relevant to spatiotemporal integration in other 3D contexts, just as anorthoscopic presentation has been used as a model for integration across 2D displays. Moreover, as was noted previously, an advantage of exposing cross-sections is to minimize feature-based strategies and allow integration to be examined directly.

Another limitation of the present research is the restricted domain of objects tested. In principle, any object can be exposed as a series of cross sections. However, the present studies indicate that successful visualization will be optimized when slice views support the extraction of segments. Models of object representation at least open the possibility of direct extension to common objects, by assuming this stimulus domain is composed of regular volumetric primitives that could be viewed in cross section along a major axis. Presumably an advantage would fall to objects with volumetric components that are not highly complex and that lie in sequence or intersect at right angles. Further work is necessary to determine the limitations of spatiotemporal integration of common objects across cross-sectional views.

6.3 Implications for cross-sectional visualization technology

On the applied side, the findings from this study have practical implications, given that cross sectional images are widely used to present 3D data, particularly in medicine. Our experimental results show that the mental visualization of 3D structures is facilitated when the cross sectional images are presented in situ at the source locations. The in situ display thus has substantial potential, we believe, to provide doctors an effective means of exploring 3D data like CT or MRI images in the diagnosis of disease. For example, in the diagnosis of pulmonary embolism (i.e., a blockage of an artery in the lung), in situ visualization has been found to effectively help radiologists browse the CT scans of pulmonary vasculature and trace branches of the blood vessels to identify embolus (Shukla, Wang, Galeotti, Wu, et al. 2009). In the ultrasound-guided surgery, the in situ AR device used in this research has demonstrated superiority in visualizing tissue in clinical tests (Wang, Amesur, Shukla, & Bayless, et al., 2009).

A fundamental limitation of cross-sectional visualization is that the user relies on his or her cognitive capacity to understand 3D information from cross-sectional images. Extensive training is needed to meet the challenges in such mental visualization tasks. One example in medical education is the teaching of sectional anatomy. Students’ failure to understand the correspondence between 2D and 3D representations has been considered a principal impediment to mastering anatomy (LeClair, 2003). As we have shown here, the depiction of images that have different underlying 3D descriptions in a constant frame of reference, as with ex-situ visualization, is one cause of such difficulty. Displays that map coordinates of the depicted object to locations in extrinsic 3D space, as with in-situ viewing, can be used to restore the spatial relationship between the image and its source, thus reducing workload in the visualization process.

Highlights.

• 3D aperture-viewing paradigm to study the visualizing of object from cross-sections

• Two key processes identified: localization and integration of cross-sections

• Ex-situ (cf. in-situ) viewing impedes the localization of cross-sectional images

• The process of integration influenced by display mode and target complexity

• Findings have practical implications particularly in medicine