Detecting Gustatory–Olfactory Flavor Mixtures: Models of Probability Summation

Abstract

Odorants and flavorants typically contain many components. It is generally easier to detect multicomponent stimuli than to detect a single component, through either neural integration or probability summation (PS) (or both). PS assumes that the sensory effects of 2 (or more) stimulus components (e.g., gustatory and olfactory components of a flavorant) are detected in statistically independent channels, that each channel makes a separate decision whether a component is detected, and that the behavioral response depends solely on the separate decisions. Models of PS traditionally assume high thresholds for detecting each component, noise being irrelevant. The core assumptions may be adapted, however, to signal-detection theory, where noise limits detection. The present article derives predictions of high-threshold and signal-detection models of independent-decision PS in detecting gustatory–olfactory flavorants, comparing predictions in yes/no and 2-alternative forced-choice tasks using blocked and intermixed stimulus designs. The models also extend to measures of response times to suprathreshold flavorants. Predictions derived from high-threshold and signal-detection models differ markedly. Available empirical evidence on gustatory–olfactory flavor detection suggests that neither the high-threshold nor the signal-detection versions of PS can readily account for the results, which likely reflect neural integration in the flavor system.

Introduction

In the chemical senses, as in other sensory systems, the ability to detect a weak stimulus—taste, odor, and flavor—often improves when the number of stimulus components increases. Several formulations have been offered to account for the improvement in chemosensory detection, including summation of the effective concentrations of the stimulus components (e.g., Stevens 1997; Cometto-Muñiz et al. 2003; Wise et al. 2007) and summation of the sensory responses to the components (e.g., Marks et al. 2007; Wise et al. 2007). It may be tempting to assess improvements in performance against benchmarks defined by, say, the best detected or most quickly detected individual component. But such benchmarks fail to take account of what has been called “statistical summation” (Fidell 1970) or “probability summation (PS)” (Loveless et al. 1970; Graham and Nachmias 1971; Delwiche and Heffelfinger 2005): The improvement in performance that can occur by chance when a stimulus contains 2 or more components that are detected independently. To use a familiar analogy: detecting a stimulus that has 2 components is like flipping a coin twice instead of once. If the probability of detecting each component is 0.5, like the probability of flipping a single head, then the probability of detecting at least 1 of the 2 components in the mixture would be 0.75, like the probability of turning up at least 1 head in 2 flips.

Traditional models of PS are sometimes called “separate-decision” or “independent-decision models” (e.g., Green and Swets 1966; Fidell 1970; Loveless et al. 1970; Mulligan and Shaw 1980). These models assume that the processing of each stimulus component is independent of the processing of other components and that the neural outputs do not combine. Following common terminology, a subsystem capable of detecting a given stimulus component is termed a “channel.” Instead of assuming that stimulus inputs or sensory outputs combine, PS assumes that a separate decision is made in each channel whether a stimulus is detected, a positive response being made if at least one of the separate decisions is “yes.” Overall detection performance increases as the number of components increases when each additional component provides another opportunity (in an additional channel) to detect the stimulus.

In this article, we describe and evaluate several models of PS that might apply to chemosensory detection, especially the detection of compound (gustatory–olfactory) flavorants presented to the mouth. For example, Ashkenazi and Marks (2004) and Marks et al. (2007) measured sensitivity to vanillin (olfactory) and sucrose (gustatory), separately and combined, and found greater sensitivity to the combinations. Delwiche and Heffelfinger (2005) measured thresholds to pineapple (olfactory) and, in different experiments, aspartame/acesulfame or MSG (gustatory), separately and combined, also found greater sensitivity to the combinations, and raised the possibility that PS might account for the results. We consider these findings later, after we derive appropriate predictions from models of PS.

Goals

The present article has 4 main goals: 1) One is to compare the predictions of separate-decision models of PS derived within 2 broad theoretical frameworks about detection and discrimination: a traditional PS framework of “high-threshold theory,” which assumes little or no sensory noise, and a framework of “signal-detection theory (SDT),” which assumes substantial noise. 2) A second goal is to derive predictions of both high-threshold and signal-detection models of PS in 2 popular detection tasks: yes/no and 2-alternative forced choice (2AFC). 3) The third goal is to derive and compare predictions in 2 experimental designs: in blocked designs, where each possible flavorant, for example, gustatory (G), olfactory (O), and gustatory–olfactory mixture (M), is presented in a separate block of trials, and in interleaved designs, where trials containing single and compound flavorants are interleaved within the same block. 4) The fourth goal is to assess PS models not only when subjects try to detect weak (threshold-level) stimuli, where signal-detection models seem more appropriate than high-threshold models but also when subjects try to respond as quickly as possible to flavorants presented at suprathreshold concentrations, where high-threshold models are more plausible. Note that even though we couch the predictions in terms of the detection of gustatory–olfactory flavor mixtures, the framework of PS is a broad one, as it may also apply to the detection of gustatory mixtures, olfactory mixtures, or indeed multisensory stimuli in any modality—as long as the stochastically independent sensory channels produce separate decisions about the detection of each component.

High-threshold versus signal-detection frameworks

In seeking to account for sensory detection, models of PS traditionally assume a high-threshold process, in which sensory responses are triggered only by stimulus events, intrinsic sensory noise being absent or negligible. When subjects do make false-positive responses (i.e., respond yes when the stimulus is absent), the responses are interpreted not as the result of noise in the perceptual system but as randomly occurring guesses. Evidence is substantial, however, that in detecting weak stimuli, false positives typically do reflect noise in the system, noise that is confused with effects of external stimuli (Green and Swets 1966). Noise is a critical factor limiting detection in virtually all sensory systems—including the chemical senses (e.g., Linker et al. 1964; Semb 1968; O'Mahony 1972; Irwin et al. 1992). Consequently, a central aim of the present article is to develop and compare high-threshold and signal-detection models of PS as they could apply to the detection of gustatory–olfactory flavor mixtures.

Assumptions of the PS models

To repeat, the present models of PS are formulated to describe the detection of flavorants comprising a G component or/and an O component. The models rest on 3 main assumptions: First, each component is detected by a separate subsystem or channel, meaning that activity in the 2 channels is “stochastically independent and uncorrelated”: If noise is present, it is uncorrelated across channels. Moment-to-moment or trial-by-trial variations in the levels of sensory activity produced by the components are uncorrelated. And the probability on any trial of detecting one component is unaffected by the presence of the other component or whether the other component is detected when it is present. Second, on each trial (yes/no task) or in each observation interval of a trial (temporal 2AFC), a separate decision is made in each channel as to whether or in which interval a stimulus (signal) is present. And third, in yes/no tasks, the subject responds yes if the decision is positive in either channel or both. In 2AFC tasks, the subject chooses the interval in which one channel or both detects the stimulus; if neither channel detects the stimulus, the subject guesses.

For convenience of exposition, our models also make 3 auxiliary assumptions: first, that people fully monitor the gustatory channel, the olfactory channel, or both when the psychophysical task requires or encourages it; second, that guessing mechanisms are unbiased in forced-choice tasks; and third, that, in yes/no tasks, subjects maintain constant response criteria across, for example, different blocks of trials. For details regarding the auxiliary assumptions, see Appendix A.

Blocked versus interleaved designs

Within the framework of SDT, models of PS can make markedly different and often surprising predictions depending on whether the flavorants, G, O, and M, are presented in blocked or in interleaved designs (analogous predictions also derive from signal-detection models that assume neural integration of the components; see Marks et al. 2007). In blocked designs, subjects can attend to just the G channel when all stimuli within a block are gustatory and to just the O channel when all stimuli are olfactory. In blocks containing mixtures, however, the subjects must attend to both channels. Because each channel has its own intrinsic noise, overall noise will be greater when subjects attend to both channels rather than only one. In blocked designs, therefore, noise will be greater in blocks with mixtures than in blocks with single-component flavorants, and so, correspondingly, the rate of false-positive responses will be greater. This is not so in intermixed designs, where there is always noise in both channels and where, therefore, the rate of false positives is the same for all flavorants. Ceteris paribus, false-positive rates for mixtures will be the same in interleaved and blocked designs, whereas false-positive rates for single-component flavorants will be greater in interleaved designs. As a consequence, signal-detection models predict different magnitudes of PS when trials are interleaved and blocked.

High-threshold models of PS

Yes/no tasks

No correction for guessing

PS has traditionally been used within the framework of high-threshold models of detection (e.g., Green and Swets 1966; Brown and Hopkins 1967), which assume that noise in each sensory channel is negligible and may be ignored. Consequently, when a stimulus is presented to a given channel, the channel either detects the signal or does not. In yes/no paradigms, the subject is instructed to respond “yes” on trials that the stimulus is detected and “no” on trials that it is not. Subjects may give a small number of false-positive responses on nonstimulus trials, but false positives are treated as random guesses, amenable to correction. Within high-threshold theory, absolute threshold has typically been defined as the level of the stimulus that produces a probability of detection = 0.5.

Consider the detection of gustatory and olfactory flavorants, where p_G and p_O are the high-threshold probabilities that the gustatory channel detects G and the olfactory channel detects O, respectively, when each component is presented alone. PS states that M, a mixture of G and O, essentially provides the subject with 2 independent opportunities to detect the stimulus, so M will be detected with probability, p_M, as given by the equation:

(1)

Equation (1) also appears in Table 1, which summarizes all of the main predictions of the various PS models. If G and O are both presented at their threshold concentrations (p_G = p_O = 0.5), then PS predicts that p_M will equal 0.75.

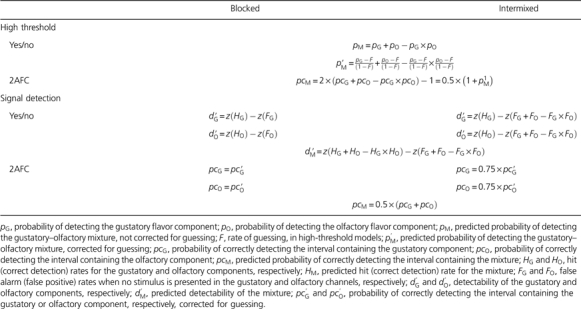
Table 1.

Equations describing the predictions of PS for detection of gustatory–olfactory flavorants (independent decisions), applied to 1) high-threshold and signal-detection models of detection, 2) 2 psychophysical tasks (yes/no; 2AFC), and 3) 2 experimental designs (single flavorants and mixtures presented in separate blocks of trials; single flavorants and mixtures intermixed within a single block of trials)

Thresholds predicted by PS

Because the probability of detecting a flavorant generally increases as its concentration increases, threshold concentrations of the G and O components (concentrations producing detection probability = 0.5) are smaller in mixtures than they are when either G or O is presented alone. In this respect, thresholds for flavor mixtures may suggest some kind of sensory “addition.” But PS alone does not does not specify how far threshold will decline as the number of components increases. The decline in threshold depends on both the number of stimulus components and the slopes of the psychometric functions relating probability of detection to stimulus concentration: the steeper the slope of either component, the greater the change in detection with a given change in concentration, and hence, the smaller the effect of adding a second component, as measured in units of concentration.

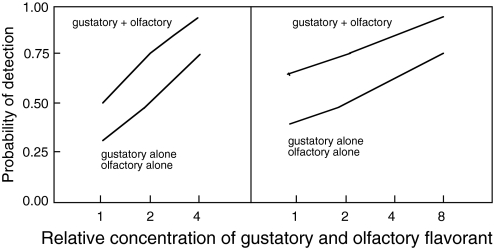
Figure 1 gives 2 sets of examples, each showing theoretical psychometric functions for G and O flavorants (assumed for simplicity to be identical) and for their mixture M. In both sets, the psychometric function for M follows the prediction of the high-threshold model of PS. In the set on the left, PS predicts that the function for the mixture will be separated horizontally from the function for the single components by a factor of 2 in concentration: The threshold of M equals 1 unit on the concentration scale (1 unit of G combined with 1 unit of O) compared with 2 units for G or O alone. In other words, these theoretical functions are consistent with “simple addition of effective stimulus concentration” (as reported by Stevens 1997 for gustatory mixtures and by Cometto-Muñiz et al. 2003 for weak odor mixtures). The appearance of stimulus addition in Figure 1, however, is wholly a consequence of PS.

Figure 1.

Theoretical psychometric functions for single flavorants (gustatory, olfactory) presented alone (lower curve in each pair) and together as a mixture (upper curve in each pair). Detection of the mixture is calculated from a model of PS that assumes high thresholds (negligible noise). The slopes of the functions are shallower in the pair on the right than the pair on the left, thereby producing a greater difference between the thresholds for single components and their mixture (horizontal separation).

In the set on the right, both psychophysical functions are considerably flatter in slope. As a result, PS now predicts that the psychometric function for M will be displaced horizontally from the function for G and O by a factor exceeding 4. That is, the threshold for each component in M is less than 1/4 the threshold for G or O presented alone. This outcome by itself might suggest some kind of “superaddition,” but here it simply reflects the outcome of PS when G and O have relatively flat psychometric functions. As a general rule, given a high-threshold model of PS, the summation ratio (the ratio of threshold concentration of each component presented alone to threshold concentration in the mixture) varies inversely with the slopes of the psychometric functions.

Correction for guessing

The simple PS model expressed in equation (1) assumes that subjects never produce false-positive responses by guessing. It is straightforward to extend the model to incorporate false-positive guesses, F, which can be estimated from the proportion of yes responses on trials containing just water (see Appendix B). Knowing F makes it possible to calculate ${p\prime }_{\text{M}}$, the “true” probability of correctly detecting the mixture when adjusted for guesses:

(2)

where p_G > F and p_O > F (see Macmillan and Creelman 2005).

2AFC tasks

Predictions of the model

The PS model can also apply to results obtained with forced-choice methods, for instance, the commonly used 2AFC, where a flavorant, single or mixture, is presented on each trial in either the first or the second interval, water in the other, and the subject must decide which interval contained the flavorant. According to high-threshold theory, noise per se never leads to detection, so nothing is detected in the interval that contains only water. Defining pc_G, pc_O, and pc_M as the proportions of correct responses given to the gustatory and olfactory components and to their mixture, respectively, the high-threshold model of PS predicts that

(3)

For details, see Appendix C.

In a yes/no task, the proportion of detections (assuming no guesses) increases from 0 (undetected) to 1.0 (always detected). In 2AFC, however, the corresponding proportion of correct responses increases from 0.5 to 1.0. A threshold defined by p = 0.5 in yes/no detection is therefore equivalent to threshold defined by pc = 0.75 in 2AFC. With individual components at threshold (p = 0.5 in yes/no; pc = 0.75 in 2AFC), the high-threshold model predicts detection probability of the mixture to be 0.75 in yes/no and 0.875 in 2AFC.

A graphic illustration

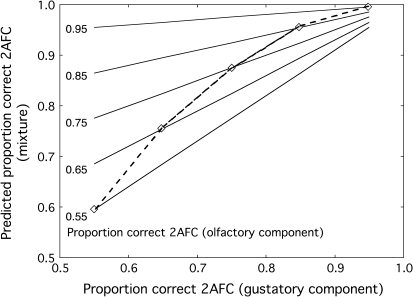
Figure 2 illustrates the predictions made by the high-threshold model of PS for performance in 2AFC. Each curve predicts how the probability of correctly detecting the mixture, pc_M, increases with increasing detectability of the gustatory component, pc_G, 0.5 < pc_G < 1, given a fixed probability of correctly detecting the olfactory component, pc_O, 0.5 < pc_O < 1. Following equation (3), for a given level of pc_O, pc_M increases linearly with pc_G and, for a given level of pc_G, pc_M increases linearly with pc_O. The circles, connected by dashed lines, show how the predicted value of pc_M varies when the 2 components are equally detectable: pc_G = pc_O.

Figure 2.

Predicted proportion correct detection of flavor mixtures (pc_M) in 2AFC, plotted as a function of the detectability of the gustatory component (pc_G = 0.55–0.95) for each of 5 levels of detectability of the olfactory component (pc_O = 0.55–0.95). The dashed line connects points at which pc_G = pc_O. The predictions derive from a high-threshold model of PS.

Signal-detection models

High-threshold theory has a notable weakness: It fails to recognize the role of noise in limiting sensory detection. In yes/no tasks, plots of the proportion of correct detections against the proportion of false-positive responses (receiver-operating characteristics or ROCs) are typically curvilinear, contrary to the straight lines predicted by high-threshold theories that treat false positives as guesses but consistent with the concave functions predicted by SDT (Swets et al. 1961; Green and Swets 1966; Macmillan and Creelman 2005; for ROCs in taste, see the plot by Irwin et al. 1992 of the data of Linker et al. 1964).

In SDT models of PS, increasing the number of stimulus components, and hence, the number of detection channels, increases the number of opportunities to correctly respond to a signal but also increases the number of opportunities to incorrectly respond to noise. Again, it is useful to assess the predictions of PS in 2 psychophysical tasks, yes/no and forced choice. Within a framework of SDT, moreover, the predictions of PS can differ markedly with different experimental designs, in particular, when single-component flavorants and mixtures are presented in separate blocks of trials or interleaved within the same block.

Although several investigators in vision have developed variants of PS that incorporate sensory noise (e.g., Graham 1989; Eckstein et al. 1996; Shimozaki et al. 2002), these models abandon the traditional framework of a separate decision in each channel. A notable example is the model of visual detection proposed by Tyler and Chen (2000). That model is predicated on the existence of very large numbers, perhaps thousands, of cortical detectors responsible for detecting visual stimuli. Tyler and Chen's model is not, however, one of separate decisions but of “maximization.” The model assumes that, across both intervals of a 2AFC, the detection apparatus scans all of the channels for the maximal level of activity (which could be produced by noise alone or by signal + noise) and then chooses the interval in which activity is greatest (the model also assumes that all channels are equally sensitive and have identical Gaussian noise). Although maximization models typically assume that channels are independent, Tyler and Chen do not assume a separate decision in each channel—clearly implausible given the putative existence of perhaps thousands of them. By way of contrast, the present models follow the traditional separate-decision principle of PS. Our models assume that, given gustatory and olfactory flavorants, the flavor system makes separate decisions in just 2 channels and then uses the decisions to make a single behavioral response.

Yes/no tasks

Blocked conditions

In yes/no tasks, each trial either contains a flavorant or does not, and, according to SDT, the subject responds yes when the level of internal activity surpasses criterion, whether this activity is produced by signal + noise or by noise alone. When the level of activity falls below criterion, the subject responds no. In blocked conditions, when trials contain a single flavorant, the subject can ignore the O channel when detecting G or ignore the G channel when detecting O. Performance with single flavorants then may be characterized by H_G and F_G, the hit and false-positive rates in the G channel, and by H_O and F_O, the corresponding rates in the O channel. Using a simple version of SDT in which noise and signal + noise have equal variance, the detectability of each flavorant presented alone, $d_{\text{G}}^{\prime }$ and $d_{\text{O}}^{\prime }$, equals the difference between the corresponding z-transformed hit and false-positive rates:

(4a)

(4b)

In blocks of trials containing mixtures, however, the subjects must monitor both channels, responding yes whenever activity in either channel surpasses that channel's criterion. In the equal-variance SDT version of PS with criterion constant across blocks of trials, the detectability of the mixtures is given by

(5)

For details, see Appendix D-1.

A graphic illustration

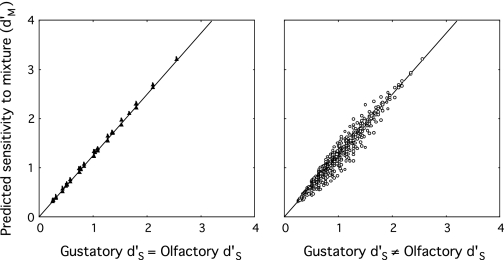
Unfortunately, equations (4) and (5) do not allow a simple way to characterize how sensitivity (d′) to the mixtures depends on sensitivity to the components across all of the possible combinations of hit and false-positive rates in G and O. To examine the relation between $d_{\text{M}}^{\prime }$ and $d_{\text{S}}^{\prime }$ (defined as the average d′ for the single components, $d_{\text{G}}^{\prime }$ and $d_{\text{O}}^{\prime }$), we used equations (4) and (5) to calculate values of $d_{\text{G}}^{\prime }$, $d_{\text{O}}^{\prime }$, and $d_{\text{M}}^{\prime }$ over possible hit rates and false-positive rates between 0.1 and 0.9 in steps of 0.1, under the constraint that, for each combination of H and F and for both G and O, H > F. Using these calculated values, Figure 3 plots $d_{\text{M}}^{\prime }$ against $d_{\text{S}}^{\prime }$, the average of $d_{\text{G}}^{\prime }$ and $d_{\text{O}}^{\prime }$. The left panel shows results for the subset of hit and false-positive rates where both H(G) = H(O) and F(G) = F(O); the right panel shows results where H(G) ≠ H(O) and/or F(G) ≠ F(O).

Figure 3.

Predicted sensitivity (d′_M) to flavor mixtures, plotted as a function of the average sensitivity (d′_S) to each component, gustatory and olfactory. The left panel shows the predictions when the hit rates and false-positive rates for the 2 components are equal. The right panel shows the prediction when the hit rates and/or false-positive rates for the 2 components are unequal. The predictions derive from a signal-detection model of PS, applied to yes/no tasks in which each single-component flavor and the flavor mixture are presented in different blocks of trials.

When H(G) = H(O) and F(G) = F(O), the relation between $d_{\text{M}}^{\prime }$ and $d_{\text{S}}^{\prime }$ is a simple and precise one: $d_{\text{M}}^{\prime }$ is directly proportional to $d_{\text{S}}^{\prime }$ and all of the predicted values fall close to the linear function (r² = 0.999). The slope of the function is 1.25, meaning that $d_{\text{M}}^{\prime }$ is 25% greater than $d_{\text{S}}^{\prime }$. An increase in sensitivity of 25% slightly exceeds the increase of about 19% derived from the maximization model of Tyler and Chen (2000) applied to a system with 2 channels. As the right panel of Figure 3 indicates, the same linear function also broadly characterizes the results when H and/or F differ in G and in O. In some instances, however, the variations around the linear function are substantial, the implications therefore consequential.

Consider the following example: a subject responds yes to a gustatory flavorant with p = 0.5 (H_G = 0.5) and to water with p = 0.05 (F_G = 0.05), giving a value of $d_{\text{G}}^{\prime }$ = 1.64. Furthermore, assume corresponding values for the olfactory flavorant of H_O = 0.5 and F_O = 0.2, giving $d_{\text{O}}^{\prime }$ = 0.84. If the criteria in the G and O channels remain the same in trials containing mixtures, then PS predicts H_M = 0.75 and F_M = 0.24, giving $d_{\text{M}}^{\prime }$ = 1.38. In this example, sensitivity to the mixture is actually smaller than sensitivity to the gustatory flavorant alone: With a signal-detection model of PS, the predicted sensitivity to a mixture can vary widely with changes in the locations of the decision criteria in the 2 channels—even when values of d′ do not change. Given certain locations of response criteria, the addition of a second flavorant could have a greater effect on false positives than on hits, the net result being a reduction rather than an increase in overall sensitivity. It is plausible, however, that subjects would avoid setting their response criteria this way but would adjust the locations of the criteria to avoid such an outcome.

Interleaved conditions

In interleaved conditions, the PS model assumes that subjects fully monitor both the G and the O channels on trials containing single flavorants as well as trials containing mixtures. Thus, with interleaved trials, the same false-positive rate (F_G + F_O − F_G * F_O) limits the detectability of single components and mixtures alike. Sensitivity to mixtures is once again given by

(6)

Equation (6) is identical to equation (5), characterizing $d_{\text{M}}^{\prime }$ in blocked conditions, where H_G = H_G/M, H_O = H_O/M, F_G = F_G/M, and F_O = F_O/M. Sensitivity to single flavorants, however, is now given by

(7a)

(7b)

Comparing equations (7a) and (7b) to (4a) and (4b) makes it clear why the SDT framework predicts greater PS when stimuli are interleaved rather than blocked: not because sensitivity to the mixture is better when stimuli are interleaved, but because sensitivity to the single flavorants is poorer. When trials containing single flavorants and mixtures are interleaved within the same block, all flavorants share a common pooled false-positive rate. Consequently, as long as $d_{\text{G}}^{\prime }$ > 0 and $d_{\text{O}}^{\prime }$ > 0, then $d_{\text{M}}^{\prime }$ > $d_{\text{G}}^{\prime }$ and $d_{\text{M}}^{\prime }$ > $d_{\text{O}}^{\prime }$; that is, sensitivity to the mixtures is always greater than sensitivity to each of the components.

Note that the signal-detection models predict different outcomes when single-component trials and mixture trials are blocked versus interleaved because the models assume that people can attend selectively to the gustatory and olfactory flavorants. If the flavor system were to operate as a unitary attentional channel, attention always being directed fully to both gustatory and olfactory flavorants, then the model would predict equivalent performance in both blocked and interleaved designs. In both, the model would predict the performance derived here for the interleaved condition.

2AFC tasks

In 2AFC, the probability of responding correctly varies from 0.5 (chance) to 1.0 (perfect performance). Once again, it is necessary to treat the blocked and interleaved conditions separately because the signal-detection version of PS makes substantially different predictions in these 2 conditions.

Blocked conditions

When trials are blocked, subjects need monitor only the G or O channel in blocks containing only the gustatory or olfactory flavorant, respectively. Consequently, the overt response probabilities of correctly choosing the intervals containing G and O presented alone, pc_G and pc_O, are equal to the underlying probabilities, pc_G′, and pc_O′, that the intervals containing G and O are chosen correctly within the G and O channels, respectively,

(8a)

(8b)

With mixtures, M, subjects obviously must monitor both channels, so pc_M is given by

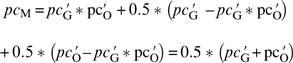(9)

See Appendix D-2. Combining equation (9) with equations (8a) and (8b) gives

(10)

This is a remarkable outcome: Given a signal-detection framework, a 2AFC method, and conditions in which the gustatory flavorants, olfactory flavorants, and mixtures are presented in separate blocks of trials, an independent-decision process of PS predicts averaging. If the individually presented gustatory and olfactory components G and O are equally detectable, pc = pc_G = pc_O, then PS predicts that detection of the mixture M will be the same as the detection of each component alone—that is, the PS model predicts no improvement at all in forced-choice performance. If the components are unequally detectable, PS predicts the detection of the mixture to fall between the detection of the component measures.

Finally, it is important to keep in mind that this prediction follows from the assumption that people can attend separately to gustatory and olfactory flavorants. If not, if attention to both gustatory and olfactory components were always mandatory, then the PS model predicts that performance would be the same when trials are blocked and when they are interleaved.

Interleaved conditions

Within a framework of SDT, a separate-decision model of PS does predict improvement in the detection of mixtures compared with detection of separate components in 2AFC—when trials containing single flavorants and mixtures are interleaved within the same block. Improvement in the detection of mixtures does not occur because the probability of correctly choosing the intervals with the mixtures improves with interleaving—forced-choice detection of mixtures again being described by equation (9)—but because the probabilities of correctly choosing the intervals containing G alone and O alone, pc_G and pc_O, are smaller when trials are interleaved (see Appendix D-3):

(11a)

(11b)

In other words, given PS, interleaving individual gustatory and olfactory flavorants within the same block of trials instead of presenting them in separate blocks results in a 25% reduction in the proportion of correct 2AFC responses (eqs. 11a and 11b vs. eqs. 8a and 8b)—essentially, the result of adding false-positive responses in the unstimulated channel.

When each flavor component is undetectable, performance in both blocked and interleaved conditions is chance, pc_S = 0.5. When performance in the blocked condition increases to pc_S = 0.75, the level used traditionally to define threshold, pc_S in the interleaved condition is predicted to equal 0.625.

What is the empirical evidence?

To the best of our knowledge, only 3 studies have measured sensitivity to threshold-level gustatory and olfactory flavorants and their mixtures in ways that permit analysis in terms of PS. Delwiche and Heffelfinger (2005) measured detection sensitivity to 2 gustatory flavorants, MSG and aspartame/acesulfame potassium mixture, an olfactory flavorant (pineapple), and the 2 possible gustatory–olfactory mixtures, MSG-pineapple and aspartame/acesulfame-pineapple. By combining pineapple with both the sweet aspartame/acesulfame and the savory MSG, the authors could ask whether the detection of flavor mixtures differs when the components were more or less “harmonious.” Sensitivity was measured by presenting, on each trial, either a flavorant or water and by obtaining graded measures of the subject's certainty that the trial contained the one or the other. The authors then transformed these measures into values equivalent to proportion correct in 2AFC. Results were similar for both mixtures, suggesting that “harmony” (or perhaps prior familiarity) had little effect. Because the individual flavorants were presented at several concentrations, Delwiche and Heffelfinger also sought to analyze the results from the perspective of PS, concluding that, in general, their model of PS did not provide a satisfactory account of their results. Unfortunately, this conclusion is not tenable, given that the authors analyzed the data using equation (1), which applies to yes/no tasks rather than equation (3), which applies to forced choice. Relative to the prediction of equation (3), equation (1) substantially overestimates the predicted values. In principle, signal-detection as well as high-threshold models of PS could be tested against the original data, given that Delwiche and Heffelfinger measured hits and false alarms, from which they derived the measures of proportion correct in forced choice.

Marks et al. (2007) used a 2AFC method to measure the detection of sucrose (gustatory), vanillin (olfactory), and sucrose–vanillin flavor mixtures. In the main experiment, 8 subjects detected 9 mixtures produced by combining each of 3 possible concentrations of sucrose with each of 3 possible concentrations of vanillin; trials containing the 9 mixtures were interleaved within each test session and each subject was tested in multiple sessions. The 3 concentrations of each flavorant were selected on the basis of preliminary tests to produce proportions of correct detections of approximately 0.65, 0.75, and 0.85. Sensitivity to the 3 concentrations of the single flavorants was then measured in an auxiliary experiment, sessions of which were interpolated between sessions of the main experiment.

Although Marks et al. (2007) did not analyze their results in terms of PS, it is possible to compare their data to the predictions of both the high-threshold and the signal-detection models. See Figure 4. According to equation (3), which characterizes the high-threshold model, the proportion of correct responses to the mixtures, pc_M, should equal 2 * (pc_G + pc_O − pc_G * pc_O) − 1. Values of pc_G and pc_O were jointly estimated by an iterative method that minimized the sum of squared deviations between predicted and observed values. From equation (3), pc_M should be linearly related to the underlying value of pc_G given a fixed value of pc_O, and, furthermore, the linear functions for different values of pc_O should tend to converge, given how the slopes of the linear functions vary with pc_O. As the left panel of Figure 4 indicates, the predicted values provide a reasonable description of the results, in that the data do conform to a set of converging functions. Recall that the signal-detection model, equation (10), predicts averaging of the component probabilities pc_G and pc_O, hence, parallel functions, as shown by the straight lines in the right panel of Figure 4.

Figure 4.

Average proportions of correct detections of 9 flavor mixtures (sucrose and vanillin), pc_M, compared with the predictions of 2 models of PS: high threshold (left panel) and signal detection (right panel). The straight lines represent best fits based on the 2 models, each of which requires estimating the proportions of correct detections of the individual flavorants, pc_G (sucrose) and pc_O (vanillin). These estimates differ in the 2 models. In each panel, the measures of pc_M are plotted as a function of the estimated value of pc_G, separately for each estimated value of pc_O. Data are from Marks et al. (2007).

Statistical reanalysis of data of Marks et al. (2007) (3 × 3 repeated-measures ANOVA) reveals a significant interaction between gustatory concentration and olfactory concentration, F_2,14 = 3.35, P < 0.025. This interaction signifies a departure from parallelism, inconsistent with the prediction of the signal-detection model, although compatible with the prediction of the high-threshold model. Furthermore, the high-threshold model provides a better overall fit to the data, as quantified by the sum of squared deviations between predicted and observed values: 0.00242 for the high-threshold model versus 0.00433 for the signal-detection model.

It is also possible to compare the predictions of the 2 models of PS with regard to the measures of sensitivity to the pure gustatory and olfactory flavorants, obtained in the auxiliary experiment on the same 8 subjects. Because the high-threshold model predicts “summation” of pc_G and pc_O, whereas the signal-detection model predicts averaging, fitting the high-threshold model to the data produces smaller estimates of pc_G and pc_O than does fitting the signal-detection model. The measured values of pc_G and pc_O as well as the values estimated from the 2 models all appear in Figure 4. It is clear that the high-threshold model of PS underestimates all 3 values of pc_G for pure sucrose and all 3 values of pc_O for pure vanillin, whereas the signal-detection model overestimates all 6 values. Note, however, that detection of pure sucrose and detection of pure vanillin were measured in separate blocks of trials, a condition that, according to the signal-detection model, can lead, through selective attention, to higher values of pc_G and pc_O; results of a second auxiliary experiment by Marks et al. (2007), conducted on 4 of the 8 subjects of the main and first auxiliary experiments, supported this prediction. The results of the second auxiliary experiment gave lower values of pc_G and pc_O when the single flavorants were intermixed rather than blocked.

Taken together, the results of Marks et al. (2007) fail to support either the high-threshold model or the signal-detection model of PS. The results of the main experiments, on the 9 flavor mixtures, are consistent with predictions of the high-threshold model but contravene the predictions of the signal-detection model. Results obtained on single gustatory and olfactory flavorants, however, are inconsistent with values estimated by the high-threshold model, though compatible with those of the signal-detection model. In sum, the empirical results suggest the need for a different model, perhaps a signal-detection model that assumes neural integration.

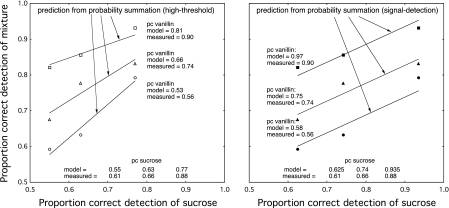
This conclusion needs be tempered by results reported by Ashkenazi and Marks (2004). Although that study did not address flavor summation per se, results pertinent to PS were obtained in preliminary experiments of the study, which used a 2AFC method to measure the following: the detectability of 6 concentrations of sucrose, preselected to produce values of pc_G ranging from 0.55 to 0.95 in steps of 0.08; the detectability of 6 concentrations of vanillin, preselected to produce values of pc_O identical to the values of pc_G; and the detectability of the 6 mixtures of sucrose + vanillin created by combining concentrations of sucrose and vanillin having the same values of pc.

Two findings of Ashkenazi and Marks (2004) are pertinent here. First, the results shown in Figure 1 of their article compared the detection of pure sucrose and pure vanillin in blocked and in intermixed conditions and showed essentially no difference between conditions—unlike the results of Marks et al. (2007), which showed better performance when those same flavorants were blocked, in accord with the predictions of the selective-attention signal-detection model. This finding of Ashkenazi and Marks is more compatible with the high-threshold model than the signal-detection model—although it is conceivable that, for reasons unknown, the subjects in Ashkenazi and Marks's study simply failed to capitalize on the opportunity to attend selectively in the blocked condition.

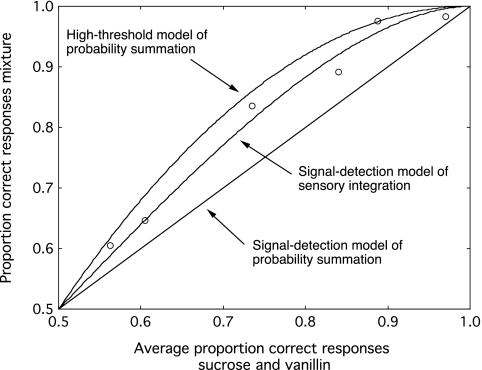
Also pertinent to PS are measures obtained by Ashkenazi and Marks (2004) of detection (proportion correct) of the single gustatory and olfactory flavorants, pc_G and pc_O, relative to the proportion correct detection of their mixtures, pc_M. The circles in Figure 5 plot the values of pc_M as a function of the average value of pc_G and pc_O. The solid line in the figure shows the prediction derived from the high-threshold PS model, assuming no bias in guessing. To make this prediction, we used equations (C2a) and (C2b) to estimate the values of p_G^′ and p_O^′ from pc_G and pc_O, then entered the values of p_G^′ and p_O^′ into equation (3) in order to calculate predicted values of pc_M. The high-threshold PS model overestimates the observed values of pc_M, the fit of the predictions to the data being only modest. By way of comparison, the line with small dashes shows the prediction of the signal-detection model of PS—equation (10), which states that pc_M should equal the average of pc_G and pc_O. Clearly, the signal-detection model of PS fails to account for the fact that detection of the flavor mixtures exceeds the detection of the individual components presented alone. In general, neither the high-threshold nor the signal-detection model provides a very good fit. A better fit comes from a signal-detection model of “sensory integration,” that is, a model that assumes that the sensory (neural) effects of the 2 components are independent but combine linearly. Green and Swets (1966) showed that this model predicts root-mean-square summation:

(12)

The large-dashed line in Figure 5 shows the prediction based on equation (12), a prediction that describes the results reasonably well.

Figure 5.

Probability of correct detection of sucrose–vanillin mixtures (pc_M), plotted against the average probability of correct detection of sucrose alone (pc_G) and vanillin alone (pc_O) in 2AFC. Data are from Ashkenazi and Marks (2004). The solid and small-dashed lines show the predictions of the high-threshold and signal-detection models of PS, respectively. For comparison, the large-dashed line shows the prediction of a signal-detection model of neural integration (Green and Swets 1966), which predicts that the detectability of the mixture, quantified by d′, will equal the square root of the sum of the squared values of d′ of the components.

Simple response times

The PS model readily applies also to tasks that measure simple response times (RTs) to single flavorants and mixtures. Tasks of this sort are often called “detection,” as subjects are commonly instructed to respond as soon as they “detect” the stimulus. But it is important to keep in mind that the stimuli used in tasks of “speeded detection” are typically presented at suprathreshold levels, well above the region of probabilistic detection, so subjects would have no difficult detecting the stimuli in a threshold detection task without time constraint. When stimulus concentrations are sufficiently great, therefore, it may be plausible to adopt the assumption of high-threshold theory that internal noise is inconsequential.

Veldhuizen et al. (2010) recently reported the results of a series of experiments in which subjects were instructed to respond as quickly as possible by pressing a key to any of 3 possible flavorants—sucrose (G), citral (O), and sucrose + citral (M)—but withhold responding to water. Responses to M were faster than responses to the either G or O alone (responses to G were typically faster than responses to O, despite preliminary tests aimed at equating RTs to the single flavorants). The main question was whether PS could explain the results. If performance exceeds the prediction of PS, then the increase in speed of response to the mixture would presumably reflect some kind of neural integration of the G and O signals. Half a century ago, Raab (1962) showed how models of PS could apply to RTs, under the assumption that a response is initiated as soon as activity in any channel surpasses its criterion—what has been called a “race model.” Three decades later, Miller (1982, 1991) applied a similar model of PS to RT measurements in vision and hearing, without, however, assuming stochastic independence. Given that the distributions of RTs to, say, G and O overlap, then, following Miller's general analytic approach, it is possible to construct cumulative distributions of RTs to G and O in order to predict the cumulative distribution of RTs to M, under the assumption of stochastic independence.

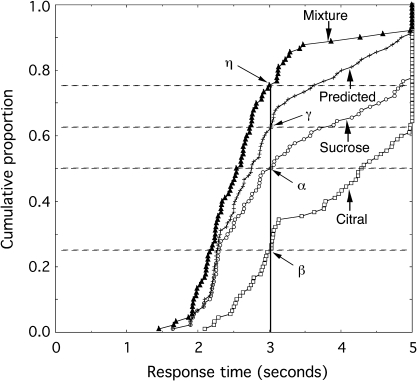
Figure 6 gives an example, using data from one of the subjects of Veldhuizen et al. (2010). In this example, the cumulative distribution for G (sucrose) passes through 0.5 at 3020 ms, which means the probability of responding to G within 3020 ms is 0.5, marked as point α. Moving to the distribution for O (citral), the probability of responding within the same 3020 ms is 0.25, marked as point β. Using the high-threshold model, PS predicts that the mixture should produce a distribution of RTs that, at 3020 ms, would have a cumulative probability of 0.5 + 0.25 − 0.5 * 0.25 = 0.625, marked as point γ. The observed probability on the observed M (mixture) distribution (point η) is about 0.76, inconsistent with the prediction of the PS model but consistent with some kind of neural integration. More generally, given any value of RT, such that $p_{{\text{G}}_{\text{RT}}}$ and $p_{{\text{O}}_{\text{RT}}}$ are the proportions of responses to the gustatory and olfactory stimuli, respectively, that are ≤RT, if the distributions of RTs to G and to O are stochastically independent, and if subjects respond as soon as a response is triggered in either the G or O channel (PS), then, by analogy to equation (1), the proportion of responses to the mixture, $p_{{\text{M}}_{\text{RT}}}$, that is ≤RT will be given by

(13)

Veldhuizen et al. (2010) used the analytic procedure described above to produce, for each subject, a distribution of predicted RTs for the mixture that the authors could compare with the empirical distribution. The results, exemplified in Figure 6, showed that the RTs to the mixture were smaller—response speed was greater—than the values predicted by the high-threshold model of PS. Moreover, Veldhuizen et al. compared results obtained with a blocked as well as an interleaved design, with implications for selective attention (see Appendix E).

Figure 6.

An example of cumulative distributions of simple RTs to individual flavorants and their mixture. Also shown is the cumulative distribution predicted by a high-threshold model of PS. The subject's task was to press a key as quickly as possible in response to any flavorant—sucrose, citral, or their mixture—but not to water. Shown are the data of one subject, taken from Veldhuizen et al. (2010).

Veldhuizen et al. (2010) also presented water as a stimulus, to which the subjects sometimes responded, thereby also producing a distribution of false-positive RTs. Analyzing the data under the assumption that a process of random guessing was superimposed on the process of high-threshold detection, the proportion of false positives at a given RT, F_RT, provides an estimate of the guess rate at time RT. Using these assumptions, Veldhuizen et al. (2010) could take into account the false-positive responses to G, O, and M, following the derivations described in Appendix B. If ${p\prime }_{{\text{G}}_{\text{RT}}}$ and ${p\prime }_{{\text{O}}_{\text{RT}}}$ are the “true” cumulative proportions of detection responses to flavorants G and O, respectively, in time RT, then the true cumulative proportion of detection responses to the mixture, ${p\prime }_{{\text{M}}_{\text{RT}}}$, is given by

(14)

Equation (14) is the RT equivalent to equation (2), which gives the prediction of the high-threshold model of PS in traditional yes/no detection tasks, corrected for false-positive responses. The data of Veldhuizen et al. showed that response speed to M exceeded the predictions of the high-threshold model of PS when false positives were taken into account (eq. 14) as well as when false positives were ignored (eq. 13).

Both equations (13) and (14) give predictions derived from high-threshold theory. It is also possible to analyze results of speeded-detection tasks within a framework of SDT—althoughVeldhuizen et al. (2010) did not do this. Even though a high-threshold model is plausible with the suprathreshold flavorants used by Veldhuizen et al., it is conceivable that the false-positive responses resulted not from guesses, as high-threshold theory assumes, but from sensory noise, some of this noise coming from the gustatory channel and some from the olfactory channel, as SDT would postulate (see Appendix F). Unfortunately, false-positive responses tend to be infrequent in experiments that measure RT, as in the study by Veldhuizen et al. (2010) and small numbers of false-positives preclude testing the signal-detection model. To test signal-detection models of PS, it is useful to encourage relatively high levels of false-positive responding, for instance, by instructing or training subjects to respond very rapidly, with short response deadlines.

Conclusions

Models that assume PS—improvement in detection based on separate decisions made to signals presented in 2 or more stochastically independent channels—have often been applied outside the chemical senses, especially in vision. Nevertheless, PS may plausibly apply in the chemical senses, for example, to account for the detection of flavorants containing gustatory and olfactory components. Nearly half a century ago, Green and Swets (1966) pointed out that the principle of separate decisions, which underlies PS, does not require a high-threshold mechanism for detection but could also apply to decisions made within a signal-detection framework.

In this article, we focus on the detection of gustatory–olfactory flavorants, developing and comparing predictions that derive from models of separate-decision PS formulated within both high-threshold and signal-detection frameworks. The predictions differ markedly within the 2 frameworks, the high-threshold framework generally predicting greater improvement in detection.

The predictions deriving from PS depend not only on the theoretical framework of detection but also on the psychophysical task, yes/no detection, or 2AFC and on the experimental design, single-component flavorants and mixtures presented in separate blocks of trials or interleaved within a single block. In high-threshold theory, PS predicts substantial improvement in detecting mixtures regardless of the task or the experimental design. But in SDT, the predictions deriving from PS are complex: PS generally predicts improvement in detection with interleaved designs using both yes/no and 2AFC tasks and can predict improvement with blocked designs using yes/no tasks; but PS predicts no improvement with blocked designs using 2AFC tasks.

Our final point speaks to the generality of PS. Although this article focuses on the potential application of PS to the detection of gustatory–olfactory flavorants, models of PS may apply in principle to many domains of multicomponent detection—for instance, to flavor stimuli with somatosensory as well as gustatory and olfactory components. Furthermore, PS could also apply to unisensory mixtures of gustatory, olfactory, or chemesthetic stimuli in the chemical senses—and, indeed, beyond the chemical senses, to multicomponent stimuli presented within or between any of the senses. Although the available evidence pertinent to summation of gustatory and olfactory flavorants in tasks of threshold detection (Ashkenazi and Marks 2004; Marks et al. 2007) and speeded response (Veldhuizen et al. 2010), reviewed above, appear inconsistent with both high-threshold and signal-detection based models of PS, sensory responses to multicomponent stimuli may nevertheless be usefully evaluated in these terms, and the models described here provide a useful quantitative framework.

Recommendations

Toward the pragmatic goal just mentioned, we make 3 recommendations regarding the design of experiments to study the detection of multicomponent stimuli:

First, we recommend measuring psychometric functions rather than (just) stimulus thresholds. Psychometric functions not only make it possible to calculate thresholds (Figure 1 and discussion thereof) but also make it possible to test models of PS, which require response probabilities or proportions of correct responses. Measuring psychometric functions, however, commonly requires considerable time and effort, a consideration that leads to the next recommendation.

Second, given the evidence that SDT provides better accounts of detection than does high-threshold theory, for practical reasons, we recommend using forced-choice methods over yes/no methods. To apply signal-detection models to yes/no data and calculate reliable values of d′, it is necessary to obtain relatively large proportions of false-positive responses as well as correct detections. Forced-choice methods are often more efficient in this regard.

Finally, careful consideration needs be given as to whether to present each single component and multicomponent stimulus in its own block of trials or to interleave all stimuli within the same block. Blocked designs encourage selective attention to individual channels in blocks containing single-component stimuli and, in signal-detection models, selective attention can thereby reduce noise and increase detectability of these stimuli, thereby leading to smaller predicted PS. Under ideal circumstances, running experiments under both blocked and interleaved conditions makes it possible to assess the role of selective attention. In their study of speeded detection of suprathreshold flavorants, Veldhuizen et al. (2010) did just this, comparing distributions of RTs to single-component flavorants and mixtures obtained in both blocked and intermixed conditions. The distributions in the 2 conditions were virtually identical over short RTs, but diverged at long RTs, consistent with the inference that selective attention takes time. The implication is that, in flavor perception at least, subjects may be able to capitalize on selective attention in traditional unspeeded tasks of sensory detection. Ideally, therefore, experimental designs would compare results obtained with stimuli blocked and interleaved. But this, of course, is easy for us to say.

Funding

This work was supported by the National Institute on Deafness and Other Communication Disorders at the National Institutes of Health [grant numbers R01 DC006688 and R01 DC009021].

Appendix A. Auxiliary assumptions of the models

In addition to the primary assumptions, the models make 3 auxiliary assumptions. First, the models assume that people fully monitor the G channel, the O channel, or both, whenever the psychophysical task requires or encourages it. That is, the models ignore the possibility that subjects may attend only partially to one channel or another (share attention) or that subjects may switch attention between channels, either during a trial or between trials. Furthermore, the models assume that when subjects receive a single flavorant, G or O, in a given block of trials, the subjects attend to only the channel that detects that flavorant. Implicit in this assumption is the hypothesis that people can attend selectively to either G or O. An alternative assumption—that when flavorants are introduced into the mouth, the flavor system by necessity attends to both the gustatory and olfactory components—is treated briefly in Appendix E.

When a block of trials contains G and O flavorants on different trials, or contains mixtures, the models assume that subjects always attend fully to both channels. To be sure, the assumption of full attention may be optimistic (e.g., Ashkenazi and Marks 2004), but it usefully serves to set upper bounds on predicted performance. Moreover, to incorporate parameters of partial or shared attention would greatly complicate and lengthen the presentation. For discussions of models of PS that treat variations in selective attention, see Mulligan and Shaw (1980) and Treisman (1998).

A second auxiliary assumption is that guessing mechanisms are unbiased in forced-choice tasks. For example, in 2AFC, the subject must decide whether the flavor stimulus was presented in the first or the second observation interval. If no flavorant is detected in either interval, the subject must guess, and our models assume that the subject will choose the first or the second interval with equal probability. Note that in separate-decision models, guessing may occur at either or both of 2 different stages in information processing: early on, within either the gustatory or the olfactory channel, or later, when the separate decisions are combined into a final response. Thus, if either the G or the O channel fails to detect a signal in either interval, that channel must guess. And, under conditions in which both channels are monitored, if the separate decisions disagree—if one channel chooses the first interval and the other the second interval—then the models assume that the final response represents an unbiased guess. Note that the models are easily adapted to incorporate biased guessing; but to simplify the exposition, we ignore any possible bias in guessing.

The third auxiliary assumption has to do with the locations of response criteria. The models based in SDT assume that, in yes/no tasks, subjects maintain constant response criteria across experimental conditions, for example, across different blocks of trials. Again, this is a matter of convenience of exposition as the models can be readily modified to accommodate shifts in criteria.

Appendix B. High-threshold model: yes/no task corrected for false-positive responses

In the high-threshold model of PS, false-positive yes responses are treated as random guesses. If an experiment includes trials containing just water, then the proportion of false-positive responses to water provides a measure of the guessing rate, F. The overall observed probability of yes responses to a flavorant therefore reflects the sum of true detections, p′, plus guesses made on the remaining trials, F * (1 − p′). Measures of F can therefore be used to correct the observed proportions of detection responses to G and O in order to calculate putative measures of true detection, $p_{\text{G}}^{\prime }$ and $p_{\text{O}}^{\prime }$, according to the equations:

(B1a)

(B1b)

where p_G > F and p_O > F. Equations (B1a) and (B1b) give the usual “correction for guessing” (Macmillan and Creelman 2005). Combining equations (B1a) and (B1b) with equation (1) makes it possible to calculate the true detection of the mixture, ${p\prime }_{\text{M}}$:

(B2)

The predicted overall probability of responding yes to mixture M when false positives are taken into account, p_M−F, equals the sum of the true probability of detection plus the probability of false-positive responses (guesses) on trials on which no stimulus is detected:

(B3)

From equations (1), (B2), and (B3), it follows that

(B4)

Given that 0 < F < 1, the predicted probability of responding yes to the mixture when false positives are taken into consideration, p_M−F, is smaller than the predicted probability of responding yes to the mixture when false positives are ignored, p_M. This is to say that the high-threshold model predicts less PS if false positives are taken into account than if false positives are ignored.

Equations (B1)–(B4) assume a uniform rate of false-positive responding, that is, a constant value of F. To test the predictions of a high-threshold model when correcting for F, therefore, it may be helpful to interleave G, O, M, and blank (water) trials within a block so as to ensure a uniform value of F. Alternatively, if G, O, and M are presented in separate blocks, then each block should also include blank (water) trials in order to calculate the value of F associated with each flavor stimulus.

Appendix C. High-threshold model: 2AFC task

First, consider a 2AFC experiment in which the stimulus is a single flavorant, G or O. The subject will detect it with probability ${p\prime }_{\text{G}}$ or ${p\prime }_{\text{O}}$ and will therefore choose the correct interval on the corresponding fraction of trials. On those trials in which they fail to detect the flavorant, equal to (1 − ${p\prime }_{\text{G}}$) or (1 − ${p\prime }_{\text{O}}$), subjects must guess and, assuming no bias in guessing, will choose the correct interval half the time. Consequently, the overall probability of responding correctly on 2AFC trials containing G or O, pc_G or pc_O, is given by

(C1a)

(C1b)

Using the high-threshold model, we may therefore calculate the probabilities of true detection, ${p\prime }_{\text{G}}$ and ${p\prime }_{\text{O}}$, from the observed proportions of correct responses, pc_G and pc_O, by the equations:

(C2a)

(C2b)

If a single flavorant is presented at its threshold concentration, ${p\prime }_{\text{G}}$ or ${p\prime }_{\text{O}}$ = 0.5, and if there is no bias in guessing, then the observed proportion of correct responses will be 0.75, the traditional level of performance taken to define detection threshold in 2AFC tasks.

Equations (C2a) and (C2b) provide formulas to correct forced-choice proportions for guessing, that is, to convert empirical psychometric functions in 2AFC, where the probability of correct response increases from 0.5 to 1.0, into theoretical psychometric functions in which the probability of detection increases from 0.0 to 1.0 (Macmillan and Creelman 2005; for related examples in chemosensation, see Wise et al. 2007; Cometto-Muñiz and Abraham 2009).

Equations (C1) and (C2) describe performance in 2AFC tasks when flavorants are detected by a high-threshold mechanism. Given a high-threshold detection process, it does not matter whether trials containing single flavorants are blocked or interleaved with trials containing mixtures, as long as the guessing parameter F can be established in each condition.

Next, consider what high-threshold PS predicts on trials containing mixtures. Following the derivations used for the components, the probability of correctly choosing the interval containing the mixture, pc_M, equals the sum of the probability of detecting a flavorant on proportion p_M′ of the trials plus the probability of guessing correctly on the remaining trials, where the stimulus is not detected: 0.5 * (1 − ${p\prime }_{\text{M}}$). Thus, pc_M = ${p\prime }_{\text{M}}$ + 0.5 * (1 − ${p\prime }_{\text{M}}$) = 0.5 * (1 + ${p\prime }_{\text{M}}$). With mixtures, flavorants are presented to both the gustatory and the olfactory channels, where ${p\prime }_{\text{G}}$ and ${p\prime }_{\text{O}}$ are the statistically independent probabilities of detecting G and O, respectively. From equation (1), ${p\prime }_{\text{M}}={p\prime }_{\text{G}}+{p\prime }_{\text{O}}-{p\prime }_{\text{G}}*{p\prime }_{\text{O}}$. Thus, the PS model predicts that the probability of choosing the correct interval in 2AFC is given by

(C3)

This analysis is mathematically equivalent to one given by Green and Swets (1966). Rewriting the right side of equation (C3) in terms of proportions of correct detections of the components in 2AFC,

(C4)

Appendix D. Signal-detection models

D-1. Yes/no tasks in blocked conditions

Analysis of both hits and false positives is straightforward: With the mixture, M, channel G detects flavorant G with probability H_G/M and channel O detects flavorant O with probability H_O/M. Therefore, the probability that at least one channel will respond yes, H_M, equals H_G/M + H_O/M − H_G/M * H_O/M. (The values of H_G/M and H_O/M will equal the values of H_G and H_O when the response criterion is constant across the G, O, and M blocks.) Similarly for false positives: In blocks of trials containing mixtures, channels G and O have independent false-positive rates of F_G/M and F_O/M, respectively. By equation (1), the overall rate of false-positive responding, F_M will equal F_G/M + F_O/M − F_G/M * F_O/M.

D-2. 2AFC tasks in blocked conditions

With mixtures, M, subjects monitor both channels, so we need to consider the 4 possible pairs of decisions that may arise in the 2 channels: 1) both the G and the O channels choose correctly; 2) G chooses correctly but O does not; 3) G does not choose correctly but O does; and 4) both G and O choose incorrectly. Because the probabilities pc_G′ and pc_O′ are independent, both channels will make the correct decision (outcome 1) with probability pc_G′ * pc_O′. On those trials in which the G channel makes the correct decision but the O channel does not (outcome 2), with probability pc_G′ * (1 − pc_O′) = pc_G′ − pc_G′ * pc_O′, the 2 decisions conflict and the subjects must guess. Guessing in turn leads the subjects to choose correctly with probability equal to 0.5 * (pc_G′ − pc_G^′ * pc_O′). Analogously, when the O channel decides correctly but the G channel does not (outcome 3), the subjects again must guess, choosing correctly with probability equal to 0.5 * (pc_O′ − pc_G′ * pc_O′). Incorrect decisions in both channels (outcome 4) never lead to correct choices. Consequently, the overall probability of correct responses to M, pc_M, is given by

(D1)

D-3. 2AFC tasks in interleaved conditions

Forced-choice detection of single-component flavorants is lower when trials are interleaved rather than blocked. Consider the detection of the flavorant G alone. With probability pc_G′, the G channel chooses the correct interval. But when trials are interleaved, the subject also monitors the O channel, which receives no flavor stimulus and must guess. Therefore, on only half of the trials on which the G channel chooses correctly will the O channel also choose correctly, 0.5 * pc_G′. On the other half of the trials in which G chooses correctly, the O channel chooses incorrectly, creating a conflict and forcing the subject to guess the interval—and choosing correctly on half of the conflicting trials, 0.5 * 0.5 * pc_G′ = 0.25 * pc_G′. Both channels choose correctly, therefore, on a total of (100−25)% = 75% of the trials on which the G channel detects the correct interval. A similar logic applies to the correct responses to the flavorant O presented alone. Consequently, the overall proportions of correct responses to G alone and O alone are given, respectively, by

(D2a)

(D2b)

Appendix E. Selective attention to gustatory and olfactory channels

Veldhuizen et al. (2010) obtained RTs to single flavorants and mixtures in both blocked and interleaved stimulus conditions. Although Veldhuizen et al. were able to test only high-threshold models of PS, for which the present models predict identical degrees of summation under both conditions, Veldhuizen et al. nevertheless compared the RTs measured in the 2 conditions. In general, RTs to single flavorants were equivalent in blocked and interleaved conditions over about the first 2 s but diverged as RTs grew longer. This outcome suggests that over short durations, attention in the flavor system may be unitary (nonselective), but that as time progresses, attention can become selective. By implication, attention could be selective in typical tasks of threshold detection, where stimulus durations are relatively long (several seconds) and subjects give their responses without time constraint.

The results of Veldhuizen et al. (2010) suggest that, for the first 2 s or so after a flavorant enters the mouth, the stimulus may be fully attended, regardless of its modality, whether gustatory or olfactory. That is, during the first few seconds of processing, full attention may be mandatory, perhaps because attentional mechanisms in flavor perception give privilege to spatial location. Over time, however, attention to single-component flavorants may become selective—analogous to the view of Lockhead (1972) that perceptual processing begins as holistic but becomes increasingly analytic over time. Consequently, and consistent with the findings of Marks et al. (2007), the detection of long-duration flavorants should differ, as the present models predict, when single stimuli and mixtures are blocked and when they are interleaved.

Appendix F. Role of sensory noise in measures of RTs

Several accounts of simple RT assume an underlying process in which, on each trial, the subject's perceptual system cumulates information about the presence of a stimulus (e.g., Grice 1968; Murray 1970). The cumulated information increases over time, and the subject is assumed to respond once the level of cumulated information reaches a criterion. Information fluctuates from moment to moment, so the time needed to reach criterion varies from trial to trial, producing a distribution of RTs (which also include time for deciding and initiating the response). Increasing stimulus concentration reduces average RT because greater concentrations produce greater rates of cumulation of information. Within this framework, it is possible that, in the absence of an external stimulus, intrinsic sensory noise cumulates and, when sufficiently great, may trigger a response, just as noise may exceed criterion and produce a positive response in yes/no tasks of sensory detection.

In the signal-detection model of PS, we would again expect different results when trials containing G, O, and M flavorants are blocked and when they are intermixed. When the single G and O flavorants are presented in separate blocks, false-positive rates should be smaller than they are when flavorants are intermixed. False-positive rates for mixtures, however, should be the same in blocked and intermixed trials—assuming, of course, that criterion remains constant.