Abstract
Genetic imprinting, by which the expression of a gene depends on the parental origin of its alleles, may be subjected to reprogramming through each generation. Currently, such reprogramming is limited to qualitative description only, lacking more precise quantitative estimation for its extent, pattern and mechanism. Here, we present a computational framework for analyzing the magnitude of genetic imprinting and its transgenerational inheritance mode. This quantitative model is based on the breeding scheme of reciprocal backcrosses between reciprocal F1 hybrids and original inbred parents, in which the transmission of genetic imprinting across generations can be tracked. We define a series of quantitative genetic parameters that describe the extent and transmission mode of genetic imprinting and further estimate and test these parameters within a genetic mapping framework using a new powerful computational algorithm. The model and algorithm described will enable geneticists to identify and map imprinted quantitative trait loci and dictate a comprehensive atlas of developmental and epigenetic mechanisms related to genetic imprinting. We illustrate the new discovery of the role of genetic imprinting in regulating hyperoxic acute lung injury survival time using a mouse reciprocal backcross design.
INTRODUCTION
Genomic imprinting is a genetic phenomenon by which certain genes are expressed or repressed depending on which parent the gene was inherited [1–3]. These so-called imprinted genes violate the classical Mendelian inheritance, which are either expressed only from the allele inherited from the mother, such as H19 or CDKN1C [4, 5], or from the allele inherited from the father, such as IGF-2 [6]. From a quantitative genetic perspective, genomic imprinting may provide the organisms that possess it with evolutionary merits by contributing additional genetic variation and conferring a fitness benefit in changing environments [7, 8]. Nowadays, different forms of genomic imprinting have been detected in a variety of species and thought to play an important role in regulating crucial aspects of embryonic growth and development as well as pathogenesis [2, 9]. Recent bioinformatic analyses suggest that the number of imprinted genes may be higher than we thought previously but this remains to be demonstrated experimentally [3, 10].
As a ubiquitous phenomenon, some properties of the imprinting mechanism have been already established; these include the modification of DNA and chromosomes in the form of DNA methylation and possibly heritable chromatin structures [1]. Recently, a body of molecular evidence shows that epigenetic information experiences widespread erasure and reprogramming across generations [11, 12], leading to the transgenerational change of genetic imprinting. Despite an increasing interest in this area, many important issues remain to be resolved, which include the nature of the primary imprints that are inherited from the parental gametes, the genes that control the imprinting process [1], and the pattern of genetic imprinting that is transmitted into and shapes the epigenome of an individual’s progeny [11].
A strategy based on genetic mapping has been shown to be powerful for mapping imprinted quantitative trait loci (iQTL) that control complex traits [13–16]. Compared with the studies of molecular regulation related to epigenegtic variation, the advantage of genetic mapping lies in its quantification of the phenotypic effects of imprinted genes by identifying their number, genome-wide distribution and inheritance mode. Several new iQTLs have been identified for the mediation of body growth in mice [17], endosperm development in maize [18] and canine hip dysplasia [19]. More recently, Wang et al. [20] proposed an innovative reciprocal F2 design for studying the effects of imprinting loci and their interactions with other genetic effects (including the additive, dominant and epistatic). A computational model was derived for characterizing how genetic imprinting effects transmit from generation to generation through these previously unknown genetic interactions. Their model not only confirms the existence of iQTLs for hyperoxic acute lung injury (HALI) survival time in mice [24], but also provides new insights into the genetic control mechanisms of this trait.
In this article, we present a reciprocal backcross design in which the pattern of genetic imprinting can be estimated and mapped. Different from Wang et al.’s F2 design [20] focusing on the test of interactions between genetic imprinting and other genetic components, the new design quantifies the pattern of how genetic imprinting that forms in a parental generation affects the performance of a complex trait in next generations. The new design will also have power to study how genetic imprinting affects the epigenomes of parents and their progeny. In so doing, a series of quantitative genetic parameters that describe the extent and transmission mode of genetic imprinting are defined. A powerful computational algorithm is derived to estimate and test these parameters within the framework of genetic mapping. By analyzing a mouse data set with eight reciprocal backcrosses [25], the new approach identified the same iQTL for HALI survival time, as detected by Wang et al.’ F2 design [20], but illustrated the new discovery of the role of genetic imprinting in this trait through transgenerational transmission. We have performed simulation studies to investigate the statistical properties of the approach, validating its use in dictating a comprehensive atlas of developmental and epigenetic mechanisms related to genetic imprinting.
MODEL
Design
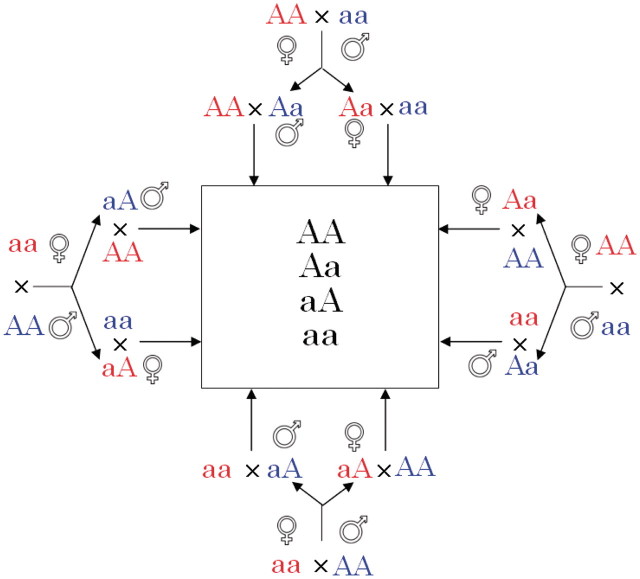
Consider two contrasting inbred lines, each of which can serve as a maternal and paternal parent. Two F1 families are produced from reciprocal crosses. Because of the assumption of parent-of-origin effects, the two families would be different in phenotypic traits. Progeny of different sexes from each F1 family are reciprocally backcrossed with each original parental line, leading to eight possible backcross families. Using a quantitative trait locus (QTL) with two alleles  and
and  , we illustrate such a backcross breeding scheme involving the original parents, reciprocal F1 families and reciprocal backcross families (Figure 1).
, we illustrate such a backcross breeding scheme involving the original parents, reciprocal F1 families and reciprocal backcross families (Figure 1).
Figure 1:
A breeding scheme generating eight reciprocal backcrosses, initiated with two inbred lines AA and aa. The two inbred lines that serve as female and male parents are crossed to generate two reciprocal F families. From each of these two families, two progeny, one being a female and the other being a male, are selected to cross with original parents, leading to eight different backcross families (with four genotype configurations AA, Aa, aA and aa listed in the box).
families. From each of these two families, two progeny, one being a female and the other being a male, are selected to cross with original parents, leading to eight different backcross families (with four genotype configurations AA, Aa, aA and aa listed in the box).
In each backcross population, the same panel of molecular markers is genotyped and also the same trait of interest is phenotyped. An integrative linkage map that covers the genome can be constructed by a linkage analysis with these markers in all these backcross families. The construction of such a map is used to identify imprinted quantitative trait loci (iQTLs) that control the trait. Next, we describe a new model which has power to study how the effect of an iQTL is transmitted from the parental generation to next generation.
Quantitative genetic parameters
Two inbred lines with genotypes 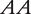 and
and 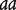 at a QTL, respectively, produce two reciprocal F1 families,
at a QTL, respectively, produce two reciprocal F1 families, 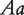 and
and 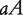 , where the first allele is inherited from the maternal parent and the second allele inherited from the paternal parent. Different from traditional Mendelian genetics, we will consider
, where the first allele is inherited from the maternal parent and the second allele inherited from the paternal parent. Different from traditional Mendelian genetics, we will consider 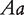 and
and 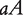 as two different genotypes. By reciprocally backcrossing with the original inbred lines, eight backcrosses will be produced. Figure 1 shows a visual representation of this breeding strategy. Each backcross has two segregating genotypes, which together have 16 genotypes if different parent-of-origins of alleles are considered (Table 1).
as two different genotypes. By reciprocally backcrossing with the original inbred lines, eight backcrosses will be produced. Figure 1 shows a visual representation of this breeding strategy. Each backcross has two segregating genotypes, which together have 16 genotypes if different parent-of-origins of alleles are considered (Table 1).
Table 1:
Genetic components of 16 genotypes derived from two-way reciprocal backcrosses, initiated with two inbred lines AA and aa
| Backcross |
Genetic components |
||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No. | Mating | Genotype | Value | µ | a | d | i | i1 | i2 | i3 | i4 | i5 | i6 | i7 | i8 | I1 | I2 | I3 | I4 |
| 1 | AA × Aa | AA | µ11 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| Aa | µ12 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | ||
| 2 | aa × Aa | aA | µ21 | 1 | 0 | 1 | −1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| Aa | µ22 | 1 | −1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | ||
| 3 | AA × aA | Aa | µ31 | 1 | 0 | 1 | 1 | 0 | 0 | −1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| AA | µ32 | 1 | 1 | 0 | 0 | −1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | ||
| 4 | aa × aA | aa | µ41 | 1 | −1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −1 | 0 | 0 | 0 | 0 | 1 |
| aA | µ42 | 1 | 0 | 1 | −1 | 0 | 0 | 0 | 0 | −1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | ||
| 5 | Aa × AA | AA | µ51 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | −1 | 0 | 0 | 0 |
| aA | µ52 | 1 | 0 | 1 | −1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | −1 | 0 | ||
| 6 | Aa × aa | Aa | µ61 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | −1 | 0 | 0 |
| aa | µ62 | 1 | −1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | −1 | ||
| 7 | aA × AA | aA | µ71 | 1 | 0 | 1 | −1 | 0 | 0 | 0 | 0 | 0 | −1 | 0 | 0 | 0 | 0 | −1 | 0 |
| AA | µ72 | 1 | 1 | 0 | 0 | 0 | −1 | 0 | 0 | 0 | 0 | 0 | 0 | −1 | 0 | 0 | 0 | ||
| 8 | aa × aH | aa | µ81 | 1 | −1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −1 | 0 | 0 | 0 | −1 |
| Aa | µ82 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | −1 | 0 | 0 | 0 | 0 | 0 | −1 | 0 | 0 | ||
Let μkj denote the genotypic value of a parent-of-origin-specific genotype, where k = 1, … , 8 is the backcross identity and j = 1, 2 is the QTL genotype within each backcross. Table 1 lists different genetic components of any μkj. Below, we explain the genetic meaning of each component.
All 16 backcross genotypes are sorted into four groups AA, Aa, aA and aa. Without considering the influence of genetic imprinting produced in the F1 family, these four groups should contain the additive (a), dominant (d) and imprinting effects (i, due to the difference between Aa and aA). If the parental imprinting is considered, we will need to define additional parameters to describe μkj. Let us first consider genotype AA. There are four types of backcrosses which produce AA, which are shown as follows:
 |
(1) |
where a is the additive effect which is positive for genotype AA; i1 is the genetic imprinting effect, produced in reciprocal F1 crosses of two inbred lines, is transmitted to genotype AA through the paternal parent of the backcross; i2 is the genetic imprinting effect, produced in reciprocal F crosses of two inbred lines, is transmitted to genotype AA through the maternal parent of the backcross; and I1 is the genetic imprinting effect due to the difference of the imprinted F
crosses of two inbred lines, is transmitted to genotype AA through the maternal parent of the backcross; and I1 is the genetic imprinting effect due to the difference of the imprinted F progeny as the maternal and paternal parents of the backcross, which is transmitted to genotype AA.
progeny as the maternal and paternal parents of the backcross, which is transmitted to genotype AA.
Similarly, the genotypic value of genotype Aa can be partitioned into the following components:
 |
(2) |
where d is the dominant effect due to the allelic interaction between A and a; i is the genetic imprinting effect which is positive for genotype Aa; i3 is the genetic imprinting effect, produced in reciprocal F1 crosses of two inbred lines, is transmitted to genotype Aa through the paternal parent of the backcross; i4 is the genetic imprinting effect, produced in reciprocal F1 crosses of two inbred lines, is transmitted to genotype Aa through the maternal parent of the backcross; and I2 is the genetic imprinting effect due to the difference of the imprinted F1 progeny as the maternal and paternal parents of the backcross, which is transmitted to genotype Aa.
The genotypic value of genotype aA can be partitioned into the following components:
 |
(3) |
where d is the dominant effect due to the allelic interaction between A and a; i is the genetic imprinting effect which is negative for genotype aA; i5 is the genetic imprinting effect, produced in reciprocal F1 crosses of two inbred lines, is transmitted to genotype aA through the paternal parent of the backcross; i6 is the genetic imprinting effect, produced in reciprocal F1 crosses of two inbred lines, is transmitted to genotype aA through the maternal parent of the backcross; and I3 is the genetic imprinting effect due to the difference of the imprinted F1 progeny as the maternal and paternal parents of the backcross, which is transmitted to genotype aA.
The genotypic value of genotype aa can be partitioned into the following components:
 |
(4) |
where a is the additive which is negative for genotype aa; i7 is the genetic imprinting effect, produced in reciprocal F1 crosses of two inbred lines, is transmitted to genotype aa through the paternal parent of the backcross; i8 is the genetic imprinting effect, produced in reciprocal F1 crosses of two inbred lines, is transmitted to genotype aa through the maternal parent of the backcross; and I4 is the genetic imprinting effect due to the difference of the imprinted F1 progeny as the maternal and paternal parents of the backcross, which is transmitted to genotype aa.
Estimation
The genetic effect parameters for iQTLs described above can be estimated using a genetic mapping model. The Expectation-Maximization (EM) algorithm was implemented to estimate these parameters. Furthermore, each of these effects can be tested individually or jointly, depending on the purpose of the mapping study. Note that the signs of the estimates of each parameter will explain the direction of expression of the alleles inherited from two original inbred lines.
Consider the same pair of markers, typed for the eight backcrosses, between which a QTL is assumed to be located. For any progeny i within a backcross k, we derive the conditional probability of a QTL genotype j, (expressed as 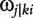 ), conditional upon the genotype for the two markers which this subject carries [21].
), conditional upon the genotype for the two markers which this subject carries [21].
The joint likelihood of phenotypic values 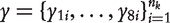 by combing these eight backcrosses is written as
by combing these eight backcrosses is written as
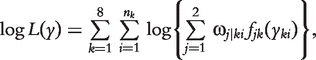 |
(5) |
where nk is the size of backcross k and fjk (yki) is the normal distribution of the trait with mean μjk and variance σ2k.
The EM algorithm is implemented to estimate the genotypic means and variances for each backcross. In the E step, the posterior probabilities of QTL genotype j carried by progeny i within backcross k is calculated using
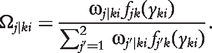 |
(6) |
In the E step, genotypic values and variances are calculated by the following log-likelihood equations:
| (7) |
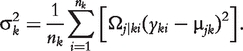 |
(8) |
Both the E and M steps are iterated until the estimates converge to a stable value. The stable estimates are the maximum likelihood estimate (MLE) of the parameters.
The MLEs of various genetic components can be estimated by solving a group of regular equations in Table 1. They are expressed as
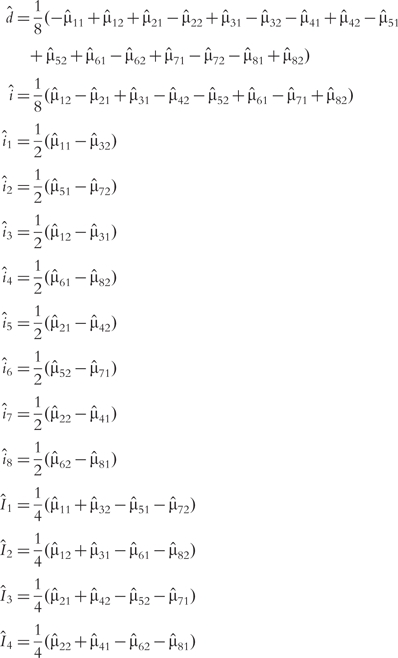 |
Hypothesis testing
The existence of a QTL can be tested by formulating the hypotheses
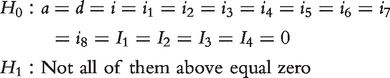 |
(9) |
The log-likelihood ratio test statistic is calculated under the H0 and H1. The critical threshold for claiming the existence of a significant QTL is determined from permutation tests [22]. To overcome heavy computational burden of permutation tests, Chang et al. [23] proposed a score statistic to determine the critical threshold. Each genetic component contributes to genotypic values of backcross genotypes. Their individual contributions can be tested by formulating the null hypothesis of letting them equal zero, separately.
It is interesting to test how different backcross genotypes are affected by imprinting effects that are produced in the previous generation. For example, the genotype AA contains imprinting effects i1, i2 and I1. The influences of these imprinting effects on genotypic value of AA can be tested by formulating the null hypothesis,
| (10) |
Similarly, the influences of imprinting effects on genotypic values of other genotypes Aa, aA and aa can be tested using
| (11) |
| (12) |
| (13) |
Except for the overall test (9) of the existence of a QTL in which the QTL position in the H0 is not identifiable, all the hypotheses have an H0 nested within an H1 so that the log-likelihood ratios for these hypotheses can be thought of as being asymptotically distributed with the degree of freedom equal to the difference in the numbers of parameters between the H0 and H1.
RESULTS
iQTL detection
Prows et al. [25] detected a pronounced difference in HALI survival time between two reciprocal F1 families derived from inbred lines C57BL/6J and 129X1/SvJ, suggesting a significant imprinting effect formed during the F1 cross. Two contrasting mouse strains in survival time due to HALI, sensitive C57BL/6J (B) (i.e. die early) and resistant 129X1/SvJ (S), are reciprocally crossed to generate two types of F1 families, (BS and SB). Then, using the strategy shown in Figure 1, eight reciprocal backcrosses were generated. A total of 935 backcross mice was composed of 154 for B(BS), 105 for B(SB), 97 for (BS)B, 100 (SB)B, 122 for S(BS), 94 for S(SB), 106 for (BS)S and 157 for (SB)S. All 935 backcross mice were typed for 78 polymorphic microsatellite markers. An integrated linkage map for the eight backcrosses was constructed using these markers distributed at 20–25 cM intervals across the 19 autosomes. The phenotype used for QTL mapping, HALI survival time, was log transformed, since the transformed data better display a normal distribution. For a description of breeding schemes, DNA analysis, map construction and phenotypic measurement see [25].
By analyzing the data of reciprocal mouse backcrosses, three significant QTLs were identified for this trait located near marker Mit303 on chromosome 1, between markers Mit17 and Mit145 on chromosome 4, and between markers Mit251 and Mit5 on chromosome 15 (Supplementary Figure S1). The three QTLs were confirmed in F2 reciprocal crosses by Prows et al. [25] who named these QTLs Shali1, Shali2, and Shali3, respectively. Using a traditional interval mapping approach for analyzing current reciprocal backcross data, the third QTL was detected in the backcrosses inbred with 129X1/SvJ and the F1 parent, but not detected in the backcrosses inbred with C57BL/6J and the F1 parent. Shali3 (chromosome 15) was also identified by our model that incorporates the imprinting inheritance of a QTL.
The model allows the dissection of the phenotypic value for each detected QTL into different genotypic components; results are tabulated in Table 2. Hypothesis tests for each of these components were performed to determine their significance. At QTL  , we did not see significant additive (a) and dominant effects (d) expressed in the backcross, but a significant imprinting effect (i,P = 4.44 × 10−5) was identified. This imprinting effect is due to the stronger expression of the allele inherited from the C57BL/6J line over the allele from the 129X1/SvJ line. The imprinted effect formed during the F1 cross will be transmitted into backcross genotypes in a different manner. This type of imprinting effect can be transmitted into genotypes AA and aa through the paternal F1 parent (i1, P = 1.80 × 10−7; i7, P = 8.34 × 10−8) but not through the maternal F1 parent (i2, P = 0.80; i8, P = 0.026). The use of the imprinted F1 as a maternal or paternal parent for the backcross does not provide a significant effect on HALI survival time for these two genotypes (I1, P = 0.817; I4, P = 0.017). A different pattern was observed for the influences of the imprinting F
, we did not see significant additive (a) and dominant effects (d) expressed in the backcross, but a significant imprinting effect (i,P = 4.44 × 10−5) was identified. This imprinting effect is due to the stronger expression of the allele inherited from the C57BL/6J line over the allele from the 129X1/SvJ line. The imprinted effect formed during the F1 cross will be transmitted into backcross genotypes in a different manner. This type of imprinting effect can be transmitted into genotypes AA and aa through the paternal F1 parent (i1, P = 1.80 × 10−7; i7, P = 8.34 × 10−8) but not through the maternal F1 parent (i2, P = 0.80; i8, P = 0.026). The use of the imprinted F1 as a maternal or paternal parent for the backcross does not provide a significant effect on HALI survival time for these two genotypes (I1, P = 0.817; I4, P = 0.017). A different pattern was observed for the influences of the imprinting F effect on backcross genotypes Aa and aA (Table 2).
effect on backcross genotypes Aa and aA (Table 2).
Table 2:
MLEs of genetic effect parameters for three iQTLs located on different chromosomes
| Parameters | Shali1 | Shali2 | Shali3 |
|---|---|---|---|
| Chromosome | 1 | 4 | 15 |
| Marker | Mit303 | Mit17-Mit145 | Mit251-Mit5 |
| a | −0.4019 (0.8091) | −6.1861 (0.0001) | −2.9845 (0.0492) |
| d | −2.4975 (0.2502) | −3.7639 (0.0590) | 5.6168 (0.0207) |
| i | 6.4736 (4.44 x 10−5) | 1.1276 (0.5573) | −0.2091 (0.7302) |
| i1 | 17.1527 (1.80 x 10−7) | 7.8175 (0.0144) | 10.8010 (0.0015) |
| i2 | −3.8091 (0.1762) | −2.0088 (0.4678) | −7.6901 (0.0080) |
| I1 | 1.0406 (0.8172) | 3.0030 (0.1697) | 5.5933 (0.0132) |
| i3 | 11.0660 (0.0006) | 20.7042 (3.57 x 10−10) | 16.8675 (2.13 x 10−7) |
| i4 | 14.8744 (2.74 x 10−5) | 8.4647 (0.0076) | 16.7952 (2.50 x 10−7) |
| I2 | −5.7034 (0.0201) | 2.9111 (0.3290) | −1.4955 (0.5090) |
| i5 | 2.7380 (0.3225) | 13.8441 (8.15 x 10−7) | 14.3514 (8.05 x 10−7) |
| i6 | −3.7382 (0.1525) | −6.0602 (0.0244) | 0.8139 (0.7729) |
| I3 | 5.2299 (0.0058) | 3.5995 (0.0891) | 4.9523 (0.0239) |
| i7 | 15.8341 (8.34 x 10−8) | 6.2880 (0.0350) | 4.2877 (0.1437) |
| i8 | 6.9503 (0.0263) | 13.4987 (0.0001) | 5.6526 (0.1170) |
| I4 | 5.4985 (0.0174) | −2.2938 (0.3763) | −3.9439 (0.0892) |
The significance level for each parameter is given in the parentheses.
At QTL 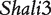 , a significant dominant effect was found, but no additive and imprinting effects were significant (Table 2). At QTL Shali3, the additive effect is more significant than the dominant effect, but there is no imprinting effect. Despite, no significant imprinting effect detected for these two QTLs, the imprinting effects expressed in the F1 cross can be transmitted to their different backcross genotypes through various patterns of transmission. For example, through both maternal and paternal F1 parents, this imprinting effect is expressed in backcross genotype Aa; yet in genotype aa no imprinting effect was transmitted. It appears that the transmission of the F1 imprinting effect through the maternal parent was important for backcross genotypes AA and aA. Specific patterns of transmission can be identified for different genotypes at the QTL on chromosome 15.
, a significant dominant effect was found, but no additive and imprinting effects were significant (Table 2). At QTL Shali3, the additive effect is more significant than the dominant effect, but there is no imprinting effect. Despite, no significant imprinting effect detected for these two QTLs, the imprinting effects expressed in the F1 cross can be transmitted to their different backcross genotypes through various patterns of transmission. For example, through both maternal and paternal F1 parents, this imprinting effect is expressed in backcross genotype Aa; yet in genotype aa no imprinting effect was transmitted. It appears that the transmission of the F1 imprinting effect through the maternal parent was important for backcross genotypes AA and aA. Specific patterns of transmission can be identified for different genotypes at the QTL on chromosome 15.
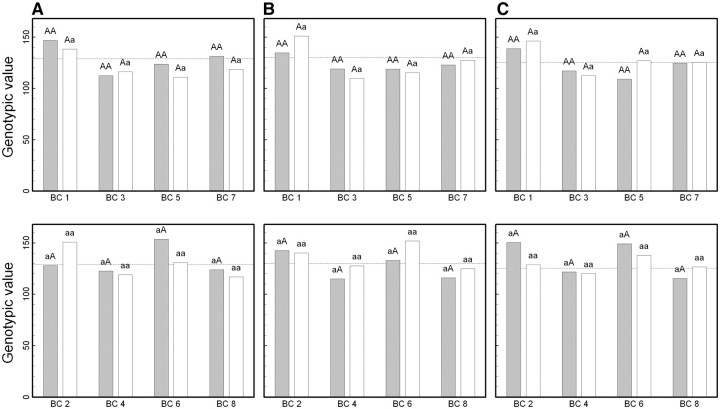
Figure 2 demonstrates the differences of the same backcross genotype at QTL 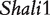 when it was generated through different breeding schemes. If there was no imprinting effect, the same genotype should have no difference among these schemes. For example, genotype AA was supposed to have a genotypic value μ + a, but owing to the occurrence of i1, i2 and I1, it was significantly different among different breeding schemes (Figure 2A). The cumulative effect of these three parameters was tested using hypothesis (10), which was found to be significant (P < 10−4). There were different genotypic values for backcross genotype Aa under different breeding schemes because the contributions of i3, i4 and I2 are significant (Figure 2A). Similarly, we observed different genotypic values for both backcross genotypes aA (Figure 2A) and aa (Figure 2A) because their underlying components contribute significantly to the overall genotypic values. At QTL
when it was generated through different breeding schemes. If there was no imprinting effect, the same genotype should have no difference among these schemes. For example, genotype AA was supposed to have a genotypic value μ + a, but owing to the occurrence of i1, i2 and I1, it was significantly different among different breeding schemes (Figure 2A). The cumulative effect of these three parameters was tested using hypothesis (10), which was found to be significant (P < 10−4). There were different genotypic values for backcross genotype Aa under different breeding schemes because the contributions of i3, i4 and I2 are significant (Figure 2A). Similarly, we observed different genotypic values for both backcross genotypes aA (Figure 2A) and aa (Figure 2A) because their underlying components contribute significantly to the overall genotypic values. At QTL 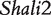 (Figure 2B) and QTL Shali3 (Figure 2C), the value of each genotype was found to differ, depending on the breeding scheme from which it is derived.
(Figure 2B) and QTL Shali3 (Figure 2C), the value of each genotype was found to differ, depending on the breeding scheme from which it is derived.
Figure 2:

Component dissection of the genotypic value, per the model given in Table 1, for HALI survival time at a particular QTL genotype, AA, Aa, aA and aa, derived from eight reciprocal backcrosses for QTL 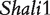 near markers Mit303 on chromosome 1 (A), QTL
near markers Mit303 on chromosome 1 (A), QTL 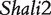 between markers Mit17 and Mit145 on chromosome 4 (B), and QTL Shali3 between markers Mit251 and Mit5 on chromosome 15 (C). The values for each of 15 components, a, d, i1, i2, i3, i4, i5, i6, i7, I8 and I4, shown in circles, are expressed by the height of component-labeled bars.
between markers Mit17 and Mit145 on chromosome 4 (B), and QTL Shali3 between markers Mit251 and Mit5 on chromosome 15 (C). The values for each of 15 components, a, d, i1, i2, i3, i4, i5, i6, i7, I8 and I4, shown in circles, are expressed by the height of component-labeled bars.
Within the same backcross, there are two different genotypes at each QTL. A traditional approach can only detect the difference of the two QTL genotypes due to an additive or dominant effect. However, our model can discern these differences by examining the occurrence of imprinting effects and their transmission patterns. For example, within backcross B(BS), two genotypes BB and BS are different purely due to the additive and dominant effects according to classic genetics, but their difference also includes imprinting effects formed in the F1 cross and expressed in each of these two genotypes, i.e. i1, i3, I1 and I2. Figure 3 illustrates these genotypic differences for each backcross.
Figure 3:
Genotypic values for HALI survival time at a particular QTL genotype, AA, Aa, aA and aa, derived from eight reciprocal backcrosses for QTL 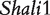 near markers Mit303 on chromosome 1 (A), QTL
near markers Mit303 on chromosome 1 (A), QTL 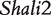 between markers Mit17 and Mit145 on chromosome 4 (B), and QTL Shali3 between markers Mit251 and Mit5 on chromosome 15 (C). The dot horizontal line is denoted as the overall mean μ.
between markers Mit17 and Mit145 on chromosome 4 (B), and QTL Shali3 between markers Mit251 and Mit5 on chromosome 15 (C). The dot horizontal line is denoted as the overall mean μ.
Simulation
By mimicking the reciprocal backcross scheme used in the above mouse example, we performed simulation studies to examine the statistical behavior of the new model. We simulated a new set of phenotypic data using the genetic effects estimated from QTL 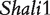 and residual errors scaled for a particular heritability level. Different sample sizes (100 and 400 for each backcross) and heritabilities (0.1 and 0.4) are assumed. Table 3 lists the results of the MLEs of different parameters and their standard errors. In general, all genetic parameters can be reasonably estimated when a sample size is 100 and heritability is 0.1. The excellent precision of the estimation of the imprinting effect derived from the difference of maternal and paternal F1 parent can be obtained by increasing the sample size for each backcross to 400. Of course, increased heritability by minimizing the noise of phenotypic measurement can always enhance our estimation even with a modest sample size (i.e. 100).
and residual errors scaled for a particular heritability level. Different sample sizes (100 and 400 for each backcross) and heritabilities (0.1 and 0.4) are assumed. Table 3 lists the results of the MLEs of different parameters and their standard errors. In general, all genetic parameters can be reasonably estimated when a sample size is 100 and heritability is 0.1. The excellent precision of the estimation of the imprinting effect derived from the difference of maternal and paternal F1 parent can be obtained by increasing the sample size for each backcross to 400. Of course, increased heritability by minimizing the noise of phenotypic measurement can always enhance our estimation even with a modest sample size (i.e. 100).
Table 3:
The mean MLEs of genetic effect parameters from simulated reciprocal backcrosses with different sample sizes (n) and heritabilities (H2)
| (n, H2) |
|||||
|---|---|---|---|---|---|
| Parameters | True values | (100, 0.1) | (100, 0.4) | (400, 0.1) | (400, 0.4) |
| a | −0.01 | −0.010 ± 0.016 | −0.010 ± 0.008 | −0.010 ± 0.006 | −0.010 ± 0.003 |
| d | −0.02 | −0.020 ± 0.023 | −0.020 ± 0.012 | −0.020 ± 0.009 | −0.020 ± 0.005 |
| i | 0.05 | 0.049 ± 0.016 | 0.050 ± 0.008 | 0.050 ± 0.006 | 0.050 ± 0.003 |
| i1 | 0.15 | 0.150 ± 0.032 | 0.150 ± 0.016 | 0.150 ± 0.013 | 0.150 ± 0.006 |
| i2 | −0.03 | −0.030 ± 0.033 | −0.030 ± 0.016 | −0.030 ± 0.013 | −0.030 ± 0.007 |
| I1 | 0.01 | 0.011 ± 0.022 | 0.010 ± 0.011 | 0.010 ± 0.009 | 0.010 ± 0.005 |
| i3 | 0.1 | 0.099 ± 0.032 | 0.100 ± 0.016 | 0.100 ± 0.013 | 0.100 ± 0.007 |
| i4 | 0.1 | 0.100 ± 0.032 | 0.100 ± 0.016 | 0.100 ± 0.013 | 0.100 ± 0.006 |
| I2 | −0.05 | −0.050 ± 0.023 | −0.050 ± 0.011 | −0.050 ± 0.009 | −0.050 ± 0.005 |
| i5 | 0.02 | 0.019 ± 0.032 | 0.020 ± 0.016 | 0.020 ± 0.013 | 0.020 ± 0.006 |
| i6 | −0.03 | −0.030 ± 0.032 | −0.030 ± 0.016 | −0.030 ± 0.013 | −0.030 ± 0.007 |
| I3 | 0.05 | 0.050 ± 0.023 | 0.050 ± 0.011 | 0.050 ± 0.009 | 0.050 ± 0.005 |
| i7 | 0.1 | 0.101 ± 0.033 | 0.101 ± 0.016 | 0.100 ± 0.013 | 0.100 ± 0.006 |
| i8 | 0.06 | 0.061 ± 0.032 | 0.059 ± 0.016 | 0.060 ± 0.013 | 0.060 ± 0.007 |
| I4 | 0.04 | 0.039 ± 0.023 | 0.040 ± 0.011 | 0.040 ± 0.009 | 0.040 ± 0.005 |
Standard errors were calculated from 200 simulation replicates.
Given the estimated effect values for QTL 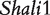 , we ran an additional simulation to assess the power of our model by assuming different heritabilities and sample sizes (Table 4). Our model has good power to detect most of these genetic effects. For some small values, larger sample sizes and/or heritabilities are required. In any case, we found that our model has an acceptable false positive rates, usually with 0.04–0.06 (Table 4). Thus, there is a small possibility for our model to detect a significant genetic effect although it does not occur. This simulation provides a general guidance for designing any new cross experiment in terms of sample size determination in a hope to obtain convincing results.
, we ran an additional simulation to assess the power of our model by assuming different heritabilities and sample sizes (Table 4). Our model has good power to detect most of these genetic effects. For some small values, larger sample sizes and/or heritabilities are required. In any case, we found that our model has an acceptable false positive rates, usually with 0.04–0.06 (Table 4). Thus, there is a small possibility for our model to detect a significant genetic effect although it does not occur. This simulation provides a general guidance for designing any new cross experiment in terms of sample size determination in a hope to obtain convincing results.
Table 4:
Power and false positive rates (FPR) of the model to estimate each genetic effect parameter from simulated reciprocal backcrosses with different sample sizes (n) and heritabilities (H2)
| Power |
FDR |
|||||||
|---|---|---|---|---|---|---|---|---|
| Hypothesis | (100, 0.1) | (100, 0.4) | (400, 0.1) | (400, 0.4) | (100, 0.1) | (100, 0.4) | (400, 0.1) | (400, 0.4) |
| i = 0 | 88 | 100 | 100 | 100 | 5.40 | 6.00 | 4.60 | 5.00 |
| i1 = 0 | 99 | 100 | 100 | 100 | 5.25 | 4.55 | 5.10 | 5.60 |
| i2 = 0 | 18 | 48 | 65 | 100 | 5.55 | 4.40 | 4.95 | 5.15 |
| i3 = 0 | 88 | 100 | 100 | 100 | 5.75 | 5.80 | 4.90 | 4.65 |
| i4 = 0 | 88 | 100 | 100 | 100 | 6.10 | 4.95 | 4.95 | 5.55 |
| i5 = 0 | 9 | 26 | 33 | 87 | 5.65 | 5.05 | 5.35 | 6.15 |
| i6 = 0 | 16 | 49 | 63 | 100 | 5.95 | 5.35 | 5.95 | 5.5 |
| i7 = 0 | 88 | 100 | 100 | 100 | 4.85 | 4.75 | 5.55 | 4.55 |
| i8 = 0 | 48 | 95 | 99 | 100 | 5.05 | 4.95 | 4.75 | 5.45 |
| I1 = 0 | 8 | 15 | 20 | 60 | 5.50 | 5.75 | 5.65 | 4.75 |
| I2 = 0 | 61 | 99 | 100 | 100 | 4.50 | 5.00 | 5.45 | 3.80 |
| I3 = 0 | 60 | 100 | 100 | 100 | 6.10 | 5.30 | 5.95 | 5.25 |
| I4 = 0 | 42 | 95 | 99 | 100 | 5.60 | 5.10 | 5.35 | 5.75 |
DISCUSSION
As an epigenetic form of gene regulation, genomic imprinting influences the expression of marked or imprinted genes during gametogenesis and embryonic development in a parent-of-origin-specific manner. Imprinting functions through methylation and histone modifications, which are established in the germline and maintained throughout all somatic cells of an organism. Recent emerging evidence suggests that genetic imprinting may not be transferred between generations through epigenetic remodeling and reprogramming, in order to ensure the totipotency of the zygote and prevent perpetuation of abnormal epigenetic states [11, 26–29]. To address whether transgenerational epigenetic reprogramming occurs, Wang et al. [20] proposed a new mapping model for mapping imprinted quantitative trait loci (iQTLs) showing the transgenerational inheritance of imprinting effects using a reciprocal F2 design. By analyzing a published data set of mice [24], this model identified several iQTLs for survival time due to HALI. The main result obtained was that, while most of genetic imprinting effects established in the previous generation might be erased, some were still transmitted to the next generations through their interactions with other genetic effects.
The model proposed for a reciprocal backcross design in this article builds upon Wang et al.’s work to make two key contributions. First, it provides successful inferences about parent-of-origin effects at iQTLs for HALI survival time from an extensive data analysis of mouse reciprocal backcrosses [25]. The new model confirms the QTLs (i.e. 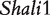 and
and 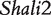 ) discovered by traditional mapping approaches, validating the genetic usefulness of our model. Second, we here put forward a series of new genetic parameters that define the transgenerational inheritance of iQTLs, greatly facilitating our understanding of the genetic mechanisms of imprinting effects. By linking these definitions with a mapping study, the new model allows the genome-wide scan and discovery of iQTLs, their number, the type and magnitude of their effects, their genetic interactions and genotype–environment interactions. Although many iQTLs have been identified for different traits in plants, animals and humans [3, 10, 17–19], this model will, for the first time, make it possible to study the interplay between iQTLs and transgenerational epigenetic inheritance. The newly defined parameters for genomic imprinting for HALI survival time will help understand the genetic control mechanisms of this trait in terms of the underlying inheritance, transmission and interactions.
) discovered by traditional mapping approaches, validating the genetic usefulness of our model. Second, we here put forward a series of new genetic parameters that define the transgenerational inheritance of iQTLs, greatly facilitating our understanding of the genetic mechanisms of imprinting effects. By linking these definitions with a mapping study, the new model allows the genome-wide scan and discovery of iQTLs, their number, the type and magnitude of their effects, their genetic interactions and genotype–environment interactions. Although many iQTLs have been identified for different traits in plants, animals and humans [3, 10, 17–19], this model will, for the first time, make it possible to study the interplay between iQTLs and transgenerational epigenetic inheritance. The newly defined parameters for genomic imprinting for HALI survival time will help understand the genetic control mechanisms of this trait in terms of the underlying inheritance, transmission and interactions.
Acute lung injury and adult respiratory distress syndrome, associated with 38.5% mortality or nearly 75 000 deaths/year in the United States [30], are fatal to any population, especially older people. The genetic control of survival time due to this disease has been studied using the animal model system—mouse. Prows et al. [24] detected the two major QTLs (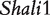 and
and 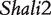 ) for HALI survival time in a reciprocal F2 population derived from sensitive C57BL/6J and resistant 129X1/SvJ inbred mouse strains, and these two QTLs were confirmed by a subsequent mapping study using the reciprocal backcross design produced by the same inbred lines [25]. All these QTLs were further confirmed by Wang et al.’s imprinting model [20] and the model presented here. The new imprinting models provide an explanation about the genetic underpinnings for imprinting inheritance at these QTLs. For example, any identical genotype should be expressed equally under the same condition, but in our study it was found to have different values due to the impact of transgenerational imprinting effects (Figure 2). In Wang et al. [20] and here, we used HALI survival time as an example to assess the usefulness of these models. It can be anticipated that the models can be used to study any other quantitative traits. In other species like maize, similar cross schemes are made [18], thus the models will find its immediate application in general genetic studies.
) for HALI survival time in a reciprocal F2 population derived from sensitive C57BL/6J and resistant 129X1/SvJ inbred mouse strains, and these two QTLs were confirmed by a subsequent mapping study using the reciprocal backcross design produced by the same inbred lines [25]. All these QTLs were further confirmed by Wang et al.’s imprinting model [20] and the model presented here. The new imprinting models provide an explanation about the genetic underpinnings for imprinting inheritance at these QTLs. For example, any identical genotype should be expressed equally under the same condition, but in our study it was found to have different values due to the impact of transgenerational imprinting effects (Figure 2). In Wang et al. [20] and here, we used HALI survival time as an example to assess the usefulness of these models. It can be anticipated that the models can be used to study any other quantitative traits. In other species like maize, similar cross schemes are made [18], thus the models will find its immediate application in general genetic studies.
Maternal effects may confound the estimation of genomic imprinting. By incorporating Cui’s model [31] into our four-way reciprocal crosses, it is possible to estimate and eliminate the confounding maternal effect from estimated imprinting effects. In addition, several mechanisms have evolved to erase the epigenetic marks, including germline and somatic reprogramming of DNA methylation and chromatin proteins. However, our previous [20] and current studies using different designs on the same data set found that at some iQTLs the epigenetic marks are not cleared across generations. Other examples of this include genomic imprinting in mammals, mating type switching in yeast and paramutation in plants [11]. The resistance of these imprinted loci to reprogramming may be regarded as part of normal development, but they should not be independent of environmental triggers. Our models can be used to address fundamental issues of what is the extent of resistance to transgenerational epigenetic reprogramming and whether or not epigenetic marks established in response to environmental cues are also resistant [11]. Further, when the processes of DNA methylation and chromatin proteins are integrated, our model will enable geneticists to predict which type of epigenetic marks will be erased and which will not be erased.
SUPPLEMENTARY DATA
Supplementary data are available online at http://bib.oxfordjournals.org/.
Key Points.
Genetic imprinting is an important mechanism for genetic control of complex traits
Genetic imprinting may be subject to reprogramming through generations.
We describe a computational model for identifying imprinting QTLs (iQTLs) and testing whether the genetic effect of iQTLs transmit from one generation to next.
The model has been validated by analyzing a real data set for mouse genetic mapping and through computer simulation.
The model provides an important tool for studying the imprinting genetic control of complex traits.
FUNDING
Joint grant DMS/NIGMS-0540745; the Changjiang Scholars Award; ‘One-thousand Person Plan’ Award at Beijing Forestry University.
Supplementary Material
Biographies
Chenguang Wang obtained his PhD in Statistics at the University of Florida in 2010. He is a biostatistician in the Office of Surveillance and Biometrics, Center for Devices and Radiological Health, Food and Drug Administration. His interest is in developing statistical models for genetic studies.
Zhong Wang obtained his PhD in Engineering Mechanics at Dalian University of Technology in 2000. He found and managed a software company in Japan from 2000 to 2008. He is a post-doctoral researcher in the Center for Statistical Genetics at the Pennsylvania State University. He writes computer software for statistical genetic models.
Daniel R. Prows obtained his PhD in Pharmaceutical Sciences at the University of Cincinnati in 1995. He is Associate Professor of Genetics at the University of Cincinnati College of Medicine. His interest is the genetic mapping of complex traits in mice. His research program has identified several important QTLs for hyperoxic acute lung injury survival time using backcross and F2 populations.
Rongling Wu obtained his PhD in Quantitative Genetics at the University of Washington in 1995. He is Professor of Statistics and Genetics and the Director of the Center for Statistical Genetics at the Pennsylvania State University. Dr Wu is also Changjiang Scholars Professor of Genetics and the Director of the Center for Computational Biology at Beijing Forestry University. His interest is to unravel the genetic roots for the outcome of a biological trait by dissecting the trait into its biochemical and developmental pathways. He uses multi-disciplinary tools, integrating genetics, molecular biology, statistics, mathematics, computer sciences and engineering, to solve genetic problems.
References
- 1.Reik W. The Wellcome Prize Lecture. Genetic imprinting: the battle of the sexes rages on. Exp Physiol. 1996;81:161–72. doi: 10.1113/expphysiol.1996.sp003922. [DOI] [PubMed] [Google Scholar]
- 2.Reik W, Dean W, Walter J. Epigenetic reprogramming in mammalian development. Science. 2001;293:1089–93. doi: 10.1126/science.1063443. [DOI] [PubMed] [Google Scholar]
- 3.Luedi PP, Dietrich FS, Weidman JR, et al. Computational and experimental identification of novel human imprinted genes. Genome Res. 2007;17:1723–30. doi: 10.1101/gr.6584707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Leibovitch MP, Nguyen VC, Gross MS, et al. The human ASM (adult skeletal muscle) gene: expression and chromosomal assignment to 11p15. Biochem Biophys Res Commun. 1991;180:1241–50. doi: 10.1016/s0006-291x(05)81329-4. [DOI] [PubMed] [Google Scholar]
- 5.Matsuoka S, Edwards MC, Bai C, et al. p57KIP2, a structurally distinct member of the p21CIP1 Cdk inhibitor family, is a candidate tumor suppressor gene. Genes Dev. 1995;9:650–62. doi: 10.1101/gad.9.6.650. [DOI] [PubMed] [Google Scholar]
- 6.O’Dell SD, Day IN. Insulin-like growth factor II (IGF-II) Intl J Biochem Cell Biol. 1998;30:767–71. doi: 10.1016/s1357-2725(98)00048-x. [DOI] [PubMed] [Google Scholar]
- 7.Moore T, Haig D. Genomic imprinting in mammalian development: a parental tug-of-war. Trends Genet. 1991;7:45–49. doi: 10.1016/0168-9525(91)90230-N. [DOI] [PubMed] [Google Scholar]
- 8.Wilkins JF, Haig D. What good is genomic imprinting: the function of parent-specific gene expression. Nat Rev Genet. 2003;4:359–68. doi: 10.1038/nrg1062. [DOI] [PubMed] [Google Scholar]
- 9.Wilkinson LS, Davies W, Isles AR. Genomic imprinting effects on brain development and function. Nat Rev Neurosci. 2007;4:1–19. doi: 10.1038/nrn2235. [DOI] [PubMed] [Google Scholar]
- 10.Luedi PP, Hartemink AJ, Jirtle RL. Genome-wide prediction of imprinted murine genes. Genome Res. 2005;15:875–84. doi: 10.1101/gr.3303505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Youngson NA, Whitelaw E. Transgenerational epigenetic effects. Annu Rev Genomics Hum Genet. 2008;9:233–57. doi: 10.1146/annurev.genom.9.081307.164445. [DOI] [PubMed] [Google Scholar]
- 12.Whitelaw NC, Whitelaw E. Transgenerational epigenetic inheritance in health and disease. Curr Opin Genet Dev. 2008;18:273–9. doi: 10.1016/j.gde.2008.07.001. [DOI] [PubMed] [Google Scholar]
- 13.de Koning DJ, Bovenhuis H, van Arendonk JA. On the detection of imprinted quantitative trait loci in experimental crosses of outbred species. Genetics. 2002;161:931–8. doi: 10.1093/genetics/161.2.931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cui YH, Lu Q, Cheverud J, et al. Model for mapping imprinted quantitative trait loci in an inbred F2 design. Genomics. 2006;87:54351. doi: 10.1016/j.ygeno.2005.11.021. [DOI] [PubMed] [Google Scholar]
- 15.Cui YH, Cheverud JM, Wu RL. A statistical model for dissecting genomic imprinting through genetic mapping. Genetica. 2007;130:227–39. doi: 10.1007/s10709-006-9101-x. [DOI] [PubMed] [Google Scholar]
- 16.Sandor C, Georges M. On the detection of imprinted quantitative trait loci in line crosses: effect of linkage disequilibrium. Genetics. 2008;180:1167–75. doi: 10.1534/genetics.108.092551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Cheverud JM, Hager R, Roseman C, et al. Genomic imprinting effects on adult body composition in mice. Proc Natl Acad Sci. 2008;105:4253–8. doi: 10.1073/pnas.0706562105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Li YC, Coelho CM, Liu T, et al. A statistical strategy to estimate maternal-zygotic interactions and parent-of-origin effects of QTLs for seed development. PLoS One. 2007;3:e3131. doi: 10.1371/journal.pone.0003131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Liu T, Todhunter RJ, Wu S, et al. A random model for mapping imprinted quantitative trait loci in a structured pedigree: an implication for mapping canine hip dysplasia. Genomics. 2007;90:276–84. doi: 10.1016/j.ygeno.2007.04.004. [DOI] [PubMed] [Google Scholar]
- 20.Wang CG, Wang Z, Luo JT, et al. A model for transgenerational imprinting variation in complex traits. PLoS One. 2010;5(7):e11396. doi: 10.1371/journal.pone.0011396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wu RL, Ma CX, Casella G. New York: Springer-Verlag; 2007. Statistical Genetics of Quantitative Traits: Linkage, Maps, and QTL. [Google Scholar]
- 22.Churchill GA, Doerge RW. Empirical threshold values for quantitative trait mapping. Genetics. 1994;138:963–71. doi: 10.1093/genetics/138.3.963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chang MR, Wu RL, Wu S, Casella G. Score statistics of quantitative trait locus mapping. Stat Appl Genet Mol Biol. 2009;8(1) doi: 10.2202/1544-6115.1386. Article 16. [DOI] [PubMed] [Google Scholar]
- 24.Prows DR, Hafertepen AP, Winterberg AV, et al. A genetic mouse model to investigate hyperoxic acute lung injury survival. Physiol Genomics. 2007;30:262–70. doi: 10.1152/physiolgenomics.00232.2006. [DOI] [PubMed] [Google Scholar]
- 25.Prows DR, Winterberg AV, Gibbons WJ, Jr, et al. Reciprocal backcross mice confirm major loci linked to hyperoxic acute lung injury survival time. Physiol Genomics. 2009;38:158–68. doi: 10.1152/physiolgenomics.90392.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Cooney CA, Dave AA, Wolff GL. Maternal methyl supplements in mice affect epigenetic variation and DNA methylation of offspring. J Nutr. 2002;132:2393–400. doi: 10.1093/jn/132.8.2393S. [DOI] [PubMed] [Google Scholar]
- 27.Drake AJ, Walker BR, Seckl JR. Intergenerational consequences of fetal programming by in utero exposure to glucocorticoids in rats. Am J Physiol Regul Integr Comp Physiol. 2005;288:R34–8. doi: 10.1152/ajpregu.00106.2004. [DOI] [PubMed] [Google Scholar]
- 28.Waterland RA, Jirtle RL. Transposable elements: targets for early nutritional effects on epigenetic gene regulation. Mol Cell Biol. 2003;23:5293–300. doi: 10.1128/MCB.23.15.5293-5300.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Crews D, Gore AC, Hsu TS, et al. Transgenerational epigenetic imprints on mate preference. Proc Natl Acad Sci USA. 2007;104:5942–6. doi: 10.1073/pnas.0610410104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Rubenfeld GD, Caldwell E, Peabody E, et al. Incidence and outcomes of acute lung injury. N Engl J Med. 2005;353:1685–93. doi: 10.1056/NEJMoa050333. [DOI] [PubMed] [Google Scholar]
- 31.Cui Y. A statistical framework for genome-wide scanning and testing imprinted quantitative trait loci. J Theor Biol. 2007;244:115–126. doi: 10.1016/j.jtbi.2006.07.009. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.