Choosing orientation: influence of cargo geometry and ActA polarization on actin comet tails

ETOC: We reconstitute actin-based motility using ellipsoidal particles mimicking the rod shape of Listeria monocytogenes and systematically analyze bead motile behaviors. By combining features of elastic propulsion and tethered-ratchet actin-polymerization models, we can explain our observations with a comprehensive new biophysical model.

Abstract

Networks of polymerizing actin filaments can propel intracellular pathogens and drive movement of artificial particles in reconstituted systems. While biochemical mechanisms activating actin network assembly have been well characterized, it remains unclear how particle geometry and large-scale force balance affect emergent properties of movement. We reconstituted actin-based motility using ellipsoidal beads resembling the geometry of Listeria monocytogenes. Beads coated uniformly with the L. monocytogenes ActA protein migrated equally well in either of two distinct orientations, with their long axes parallel or perpendicular to the direction of motion, while intermediate orientations were unstable. When beads were coated with a fluid lipid bilayer rendering ActA laterally mobile, beads predominantly migrated with their long axes parallel to the direction of motion, mimicking the orientation of motile L. monocytogenes. Generating an accurate biophysical model to account for our observations required the combination of elastic-propulsion and tethered-ratchet actin-polymerization theories. Our results indicate that the characteristic orientation of L. monocytogenes must be due to polarized ActA rather than intrinsic actin network forces. Furthermore, viscoelastic stresses, forces, and torques produced by individual actin filaments and lateral movement of molecular complexes must all be incorporated to correctly predict large-scale behavior in the actin-based movement of nonspherical particles.

INTRODUCTION

A large number of infectious microorganisms make a living as intracellular parasites that replicate within the cytoplasm of infected host cells. Some pathogens, including multiple unrelated bacteria and viruses, can employ actin polymerization–based mechanisms to propel themselves within and between host cells by exploiting molecular components from the host cytoplasmic environment and assembling a structure commonly referred to as an actin “comet tail” (Bernardini et al., 1989; Tilney and Portnoy, 1989; Cudmore et al., 1995; Gouin et al., 2005). An actin comet tail is formed from a large number of actin filaments cross-linked in a dendritic meshwork through the activity of the host cell's Arp2/3 protein complex, which nucleates actin filaments and organizes them into a dendritic network (Welch et al., 1997; Mullins et al., 1998; Cameron et al., 2001). Pathogenic bacteria, such as Listeria monocytogenes and Shigella flexneri, recruit and activate the Arp2/3 complex and initiate local actin polymerization within the host-cell cytoplasm by expressing their surface-bound virulence proteins, ActA and IcsA/VirG, respectively (Kocks et al., 1995; Gouin et al., 1999). Initially, actin from the host cell polymerizes on the surface of these bacteria as relatively symmetrical “clouds” of filaments that eventually become reorganized into polarized tails that propel these bacteria through the cytoplasm and allow them to spread from cell to cell (Tilney and Portnoy, 1989).

Both ActA and IcsA are expressed on the bacterial surface in an asymmetric manner, with protein density at one pole much higher than at the other; this surface polarity is correlated with the invariable formation of an actin comet tail on the pole that has a higher density of these virulence factors (Goldberg et al., 1993; Kocks et al., 1993; Smith et al., 1995; Rafelski and Theriot, 2006). The polar localization of these two proteins may be responsible for the orientation of bacteria during migration in infected cells: most bacteria migrate parallel to their long axes, and only rarely do the bacteria move sideways (Tilney and Portnoy, 1989; Goldberg and Theriot, 1995; Lauer et al., 2001; Soo and Theriot, 2005a). Alternatively, the observed orientation of moving bacteria in host cells may be due to a geometrical or mechanical preference for movement of a rod-shaped particle parallel to its long axis through a viscous environment.

The development of reconstituted motility systems, in which bacteria or artificial cargoes can be propelled by actin comet tails when placed in cytoplasmic extracts or a mixture of purified proteins, has allowed the examination of biochemical and biophysical parameters governing actin polymerization–based motility (Cameron et al., 1999; Loisel et al., 1999; Bernheim-Groswasser et al., 2002; Giardini et al., 2003; Upadhyaya et al., 2003; Schwartz et al., 2004; Soo and Theriot, 2005a). Furthermore, several biophysical models have been established to describe the forces generated by actin polymerization in the comet tail of bacteria (Peskin et al., 1993; Mogilner and Oster, 1996, 2003; Gerbal et al., 2000a; Dickinson and Purich, 2002; Dickinson et al., 2004). The tethered, elastic, Brownian ratchet model and clamped-filament model provide microscopic descriptions of the forces generated by actin polymerization at the surface of the cargo. In the tethered, elastic-ratchet model, the ends of actin filaments attach to the cargo transiently and thus resist the propulsion of the cargo; these filaments then detach and are able to generate a propulsive force (Mogilner and Oster, 1996, 2003). The clamped-filament model proposes instead that the ends of all actin filaments are attached to the cargo via end-tracking motor proteins that repeatedly step to remain bound to the ends of filaments as these elongate and move the cargo forward (Dickinson and Purich, 2002; Dickinson et al., 2004). A significant limitation of these microscopic models as originally formulated is that they consider only the force and speed generated by actin growth against a load but ignore cargo shape and trajectory curvature. In contrast, the elastic-propulsion model operates on a larger scale than these two microscopic models and thus considers the overall geometry of the cargo (Gerbal et al., 2000a). This model describes a pattern of strain accumulation in the actin comet tail, which is treated as a cross-linked gel, given that the comet tail has been shown to behave as an elastic gel experimentally (Gerbal et al., 2000b), and predicts forces that are directed inward, orthogonal to the long axis of the bacterium, creating stresses that are relieved at the back of the bacterium as it moves forward (Gerbal et al., 2000a). Consistent with this model, deformable cargoes, such as phospholipid vesicles and oil droplets, are distorted into teardrop shapes by actin comet tails, suggesting the existence of significant stresses orthogonal to the direction of motion (Giardini et al., 2003; Upadhyaya et al., 2003; Boukellal et al., 2004). Within the framework of this elastic-propulsion model, which includes specific assumptions, the geometry of the moving cargo should have a significant effect on force production by actin polymerization, and the actin-based motility of rod-shaped bacteria would be most stable parallel to the long axis simply by virtue of the elongated shape of the bacteria (Gerbal et al., 2000a). A recent version of this mesoscopic model represents the viscoelastic actin network as series of particles subject to viscous drag and coupled by springs that break when stretched beyond a threshold (Dayel et al., 2009). When this model was simulated under circumstances in which actin-filament depolymerization does not occur—so that stress in the actin gel can be relieved only by network breakage—it gave rise to predictions of movement in an orientation perpendicular to the long axis only (Dayel et al., 2009). Unfortunately, most experimental studies on propulsion of artificial particles by comet tails have used spherical polystyrene beads, so the effects of shape and orientation could not be addressed (Cameron et al., 1999, 2004; Bernheim-Groswasser et al., 2002). However, there is a small amount of tantalizing experimental evidence showing that asymmetric cargoes exhibiting both flat and curved surfaces can form comet tails on any surface, regardless of the local surface curvature (Schwartz et al., 2004).

To investigate the contribution of cargo geometry to the typical orientation of rod-shaped bacteria being propelled by actin comet tails, we reconstituted actin polymerization–based motility using ellipsoidal beads uniformly coated with the L. monocytogenes ActA protein, which mimicked the overall shape of bacterial rods, while eliminating any possible influence of polarized protein expression. We also examined how ActA mobility and polarization affected motility, and how the placement of the actin comet tail on the surface of ellipsoidal beads changed with variations in motile behaviors. We found that, separately, the elastic or tethered-ratchet models of propulsion by actin comet tails are insufficient to predict the observed behaviors. We propose a combined elastic-ratchet model that takes particle geometry into account and connects quantitative measurements of ellipsoidal bead motility at the mesoscopic scale to biophysical activities of actin filaments at the molecular scale.

RESULTS

Ellipsoidal beads predominantly migrate oriented either parallel or perpendicular to their long axes

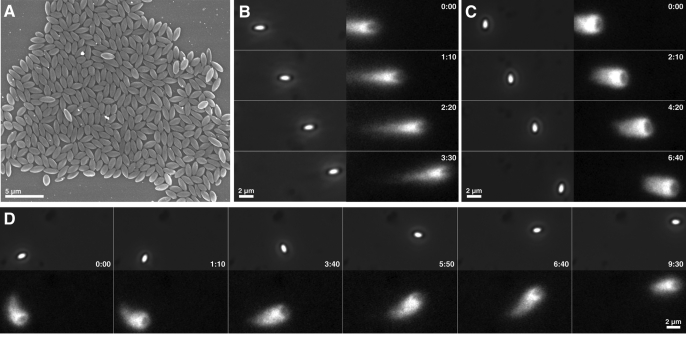
For these studies, polystyrene ellipsoidal beads were manufactured to approximate the size and geometrical shape of wild-type, rod-shaped L. monocytogenes. These ellipsoidal beads, which exhibited a consistent size (on average 1.8 μm long [SD = 0.3] × 0.8 μm wide [SD = 0.2]; n = 30) and an aspect ratio of ∼2 (Figure 1A), were uniformly coated with a functional soluble form of the L. monocytogenes ActA protein and assayed for actin-based motility (Cameron et al., 1999). Within 2–4 h after addition to cytoplasmic extracts from Xenopus laevis eggs, more than 80% of these ActA-coated ellipsoidal beads formed actin comet tails and exhibited robust steady-state motility resembling the movement of L. monocytogenes (Figure 1, B–D). Beads appeared to move primarily in either of two distinct orientations: parallel or perpendicular to the long axis of the bead (Figure 1, B–D). To describe the relative orientation of an ellipsoidal bead, we will hereinafter refer to beads as being in the “parallel” or “perpendicular” orientation, when the bead's long axis is either parallel or perpendicular, respectively, to the direction of movement and to the major axis of the actin comet tail. The minor population of beads with intermediate orientations will be referred to as being in the “diagonal” orientation.

FIGURE 1:

ActA-coated ellipsoidal beads display a preference for two distinct orientations when migrating in cytoplasmic extracts. (A) Scanning electron micrograph of the ellipsoidal polystyrene beads used in this study shows their consistent sizes (on average 1.8 μm × 0.8 μm) and an aspect ratio of ∼2. Scale bar: 5 μm. (B and C) Beads uniformly coated with ActA and placed in X. laevis egg extracts containing fluorescent actin form comet tails and persistently migrate with the long axis of each bead typically oriented either parallel (B) or perpendicular (C) to the direction of motion. Phase-contrast (left column) and actin fluorescence (right column) image pairs are shown. (D) Migrating ellipsoidal beads occasionally and spontaneously switched orientations (in this case, from perpendicular to parallel) or migrated in curved paths. Corresponding phase-contrast (top row) and actin fluorescence (bottom row) images are shown. Scale bar: 2 μm. Time: min:s.

Interestingly, migrating ellipsoidal beads would occasionally and spontaneously switch from one orientation to the other. Figure 1D illustrates a bead switching from the perpendicular to the parallel orientation. While most ellipsoidal beads moved in fairly straight trajectories, a few generated slightly curved trajectories, but were seldom observed to change direction dramatically or move in regularly curved trajectories typical of L. monocytogenes, such as sinusoidal, winding “S” or figure-eight curves (Soo and Theriot, 2005b; Shenoy et al., 2007).

Spontaneous motility initiation occurs parallel to the long axis of ellipsoidal beads

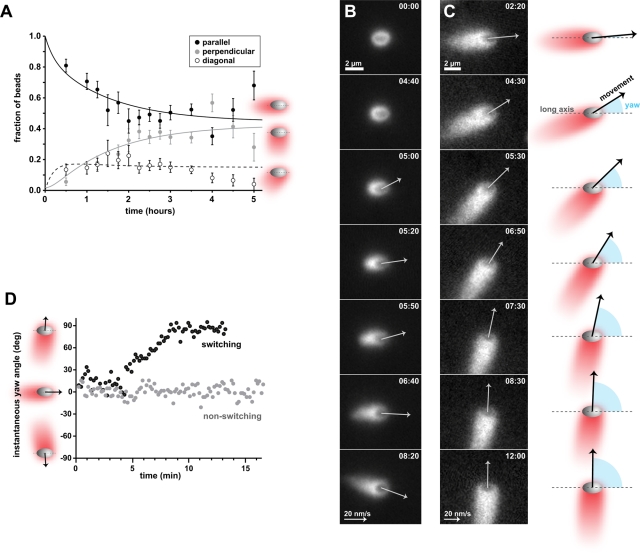
It was surprising that ellipsoidal beads appeared to move equally well in both the parallel and perpendicular orientation at steady state. To understand how this distribution of bead orientations was established over time, we compared the frequency of bead orientations relative to their actin comet tails using several hundred still images collected over a 5-h time course. Within 30 min of ellipsoidal beads being added to cytoplasmic extracts containing fluorescent actin, ∼10% of the beads counted had developed actin tails, while the rest were stationary and remained associated with actin clouds. The majority of beads started out forming comet tails parallel to the long axis, while beads with tails perpendicular to the long axis were rare at early time points (Figure 2A). By 2 h, most of the beads (78%) were associated with comet tails, and there was an approximately equal fraction of beads in the parallel (Figure 2A, black circles) and perpendicular (Figure 2A, gray circles) orientations. The percentage of beads in the diagonal orientation also peaked by 2 h (22%) and gradually decreased during the rest of the time course (Figure 2A, open circles).

FIGURE 2:

Ellipsoidal bead orientation becomes bistable as beads reach steady-state motility. (A) The orientation of ellipsoidal beads was monitored during a time course of 5 h after addition of beads to cytoplasmic extracts. Bead orientation reaches a steady state after ∼2 h. Static images were collected, and each bead was classified as having an actin comet tail that extended in an orientation parallel, perpendicular, or diagonal to the long axis of the bead. These comet tail positions relative to bead orientation are schematized on the right. The majority of beads start out moving with comet tails oriented parallel to the long axis (black circles). After 2–4 h, the fraction of beads with tails parallel to the long axis of the bead decreased and that of beads with tails perpendicular to the long axis increased (gray circles), reaching similar levels. Error bars represent SE of the multinomial distribution. Curves represent one possible fit to a differential equation model for reversible conversion between the parallel and perpendicular orientations, with the diagonal orientation (open circles) as an intermediate. (B) Beads spontaneously break symmetry and start moving parallel to the long axis. A representative bead is shown. Spontaneous symmetry breaking occurs in the absence of collisions or interaction with other beads. An ellipsoidal bead is shown in the bead frame of reference: images were computationally translated and rotated so that the bead remained stationary with its long axis positioned horizontally, while the bead's surroundings moved around in each frame of the time-lapse sequences. Arrows depict the direction of movement and the speed of the bead (length of arrow is proportional to speed). Speeds corresponding to Brownian motion and <10 nm/s were omitted. Reference arrow: 20 nm/s. Scale bar: 2 μm. Time: min:s. See also Video S1. (C) Beads can also spontaneously change orientation during migration. This bead switches from moving in the parallel orientation to moving in the perpendicular orientation. The schematics on the right depict the orientation and direction of movement of the bead in each frame. The yaw angle (cyan) is defined as the angle between the long axis of a bead and the vector describing the movement of the bead. The bead is shown in the bead frame of reference as in (B). See also Video S2. (D) The yaw angle is used to quantitatively follow the orientation of migrating beads in time. Yaw angles close to 0° correspond to beads migrating parallel to the long axis, whereas yaw angles close to −90° or 90° correspond to beads migrating perpendicular to the long axis. The yaw angle of a nonswitching bead that migrated parallel to the long axis (gray circles) moderately fluctuated around 0°. The yaw angles of the bead in (C) (black circles) start close to 0° and gradually increase to ∼90°, corresponding to the switch in orientation observed in (C).

To test the hypothesis that the initial direction of ellipsoidal bead movement was predominantly parallel to the long axis of beads, we examined time-lapse sequences of individual beads undergoing motility initiation or “symmetry-breaking” events. Ellipsoidal beads assembled a thin and nearly symmetrical actin cloud before breaking symmetry, forming a comet tail, and moving directionally (Figure 2B and Supplemental Video S1). All beads observed to spontaneously break symmetry in the absence of obstructions (n = 15/15) started migrating in the parallel orientation. Most of these beads continued moving in the parallel orientation during the first 10 min after symmetry breaking, while a few engaged in at least one orientation switch within that time frame (Table 1). Some beads were observed to initiate movement while in contact with other beads or immediately after a collision with a moving bead. In this scenario, a few beads were able to break symmetry in the perpendicular orientation (Table 1). These data suggest that, during initial comet tail assembly and movement, which predominantly occurred between ∼0.5–1.5 h after addition of ellipsoidal beads to cytoplasmic extracts, beads exhibited a strong preference for tail formation and movement parallel to the long axis of the bead, with a low probability of switching orientation within a few minutes of initiating movement. After the initial period of movement (>1.5 h), beads engaged in additional orientation switching until the steady-state distributions of beads moving in the parallel and perpendicular orientation were approximately equal.

TABLE 1:

Summary of orientation during motility initiation and switching for uncoated beads.

	Motility initiation
	Start migrating parallel	1 switch	2 switches	Start migrating perpendicular	1 switch	2 switches	Parallel-to-perpendicular switching events	Perpendicular-to-parallel switching events
Spontaneous (n = 15 beads)	15	5	1	0	0	0	6	1
Collision-induced (n = 20 beads)	17	0	0	3	0	0	0	0
Total (n = 35 beads)	32	5	1	3	0	0	6	1
	Steady-state motility
	Beads	1 switch	2 switches			Events	Parallel to perpendicular	Perpendicular to parallel
Spontaneous	64	55	9			73	42	31
Collision-induced	35	30	5			40	22	18
Total	99	85	14			113	64	49

Ellipsoidal beads occasionally switch orientation during steady-state motility

After examining the likelihood of orientation switching immediately after motility initiation, we decided to determine how often orientation switching occurred during steady-state motility. Steady-state motility consisted of robust bead movement leading to an approximately equal number of beads in the parallel and perpendicular orientation (2–4 h after adding beads to cytoplasmic extracts). In a large-scale sample of time-lapse sequences in which the steady-state movement of 605 ellipsoidal beads was analyzed, we counted 64 beads that spontaneously switched orientation at least once in the absence of any observable external stimuli. Nine of these beads engaged in a second orientation switch back to their original orientation (Table 1). These observations showed that spontaneous orientation switching was a rare event after beads achieved their stable orientations at steady-state motility. We observed that 58% of the switching events represented spontaneous switches from the parallel to the perpendicular orientation and 42% reflected switching events from the perpendicular to the parallel orientation (Table 1), which is not a significant difference. See Figure 1C for a representative example of perpendicular-to-parallel orientation switching and Figure 2C and Video S2 for an example of parallel-to-perpendicular orientation switching. Collisions and interactions with neighboring beads triggered the orientation switch of an additional 35 beads (Table 1). When these collision-induced bead orientation switches were taken into account, the total bead orientation switching frequencies changed slightly to 57% for parallel-to-perpendicular and 43% for perpendicular-to-parallel switching (Table 1).

To generate a quantitative measure of the orientation of migrating ellipsoids as they switched orientation over time, we calculated the angle between the long axis of each bead and the vector describing the bead's movement. This angle, which we refer to as “yaw angle” (see Materials and Methods and Figure 2C) conveyed information about the bead's orientation: small yaw angles close to 0° correspond to beads migrating in the parallel orientation, whereas angles close to −90° or 90° correspond to beads migrating perpendicularly. Yaw angles allowed us to monitor bead orientation over time, revealing moderate fluctuations in bead orientation in short timescales and also large changes in bead orientation during switching (Figure 2D). Switching events were not instantaneous, but usually took place over a period of several minutes, during which time the beads appeared transiently positioned in the diagonal orientation.

Our data suggest that, although the majority of ellipsoidal beads undergo stable motility at steady state, beads are inherently capable of switching orientations at a low frequency. The combination of spontaneous and collision-induced orientation switching observed in our system drives the population from a mostly parallel orientation immediately after symmetry breaking to a balanced distribution in both parallel and perpendicular orientations at steady state. The similar frequency of steady-state beads moving in the parallel and perpendicular orientations, and the approximately equal likelihood of switching in either direction, suggests the two major orientations are energetically and mechanically nearly equivalent, while diagonal orientations are disfavored.

Ellipsoidal beads with laterally mobile ActA typically migrate oriented parallel to their long axes

In the experiments described in the preceding three sections, ActA protein was immobilized on the bead surface (i.e., the attachment points could not move), and the protein was uniformly distributed. Previously, we had found that spherical beads covered with a fluid lipid bilayer prior to ActA coating could also support comet tail formation, but with the interesting modification that ActA protein became polarized to the rear of the bead (Giardini et al., 2003), presumably as the subset of attached filaments pulled the laterally mobile ActA to the rear. A similar colocalization has also been observed between the comet tail and different actin-polymerization activators (based on neuronal Wiskott–Aldrich Syndrome protein) on oil droplets and unilamellar vesicles (Trichet et al., 2007; Delatour et al., 2008). We therefore expected that lipid coating of ellipsoidal beads should change both the lateral mobility of the attachment points and the overall polarity of the ActA protein. Since ActA has been shown to be polarized on the surface of L. monocytogenes (Kocks et al., 1993; Rafelski and Theriot, 2006), and the bacteria (unlike uniformly coated ellipsoidal beads) show a marked preference for movement in the parallel orientation, we expected that lipid coating would have a measurable effect on ellipsoidal bead movement.

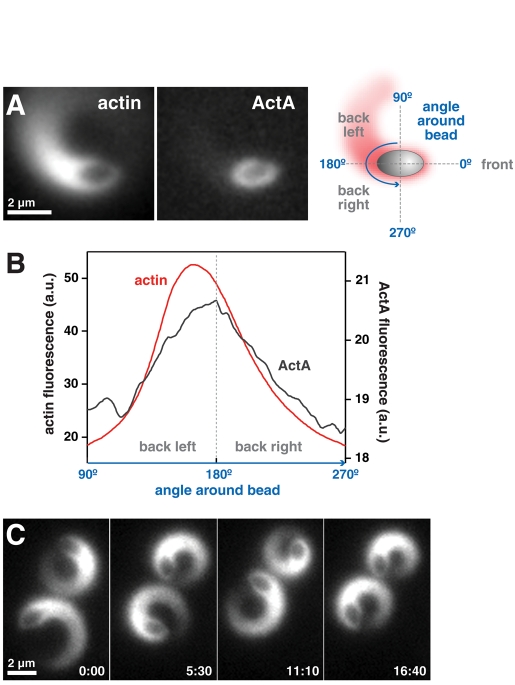
To determine how ActA localization and mobility affected ellipsoid motility, we permitted lateral mobility of ActA on a fluid surface by coating ellipsoidal beads with unilamellar vesicles containing a lipid bound to purified ActA. These beads will be referred to as “lipid-coated” beads, while beads coated with ActA without lipid will be referred to as “uncoated.” When the distribution of fluorescent ActA and actin was measured along the surface of a migrating lipid-coated bead, ActA was observed in a polar distribution that colocalized with the actin comet tail (Figure 3, A and B). When we examined their time-lapse sequences, we found that, unlike uncoated ellipsoidal beads, these lipid-coated beads moved with a robust preference for the parallel orientation (Figure 3A). Lipid-coated beads were also observed to be capable of a novel and striking motility phenotype in which they moved in tight persistent circles (Figure 3C and Video S3), a phenotype not previously reported for artificial particles, but occasionally seen for live bacteria (Lauer et al., 2001; Auerbuch et al., 2003; Soo and Theriot, 2005a; Shenoy et al., 2007). After examining the motion of 165 lipid-coated ellipsoidal beads, we found that 17% of the beads moved in persistent, tight circles, whereas <2% of uncoated beads were able to move in circular trajectories, and these few examples showed less angular persistence than the lipid-coated beads. Other types of complex trajectories, such as S-shaped paths, were also occasionally observed for these beads. Our observations showed that the surface mobility of ActA allowed for its polarization, which correlated with the tendency of ellipsoidal beads to move in the parallel orientation and engage in circling behaviors.

FIGURE 3:

Mobile ActA clusters with the actin comet tail and can generate persistently circling ellipsoidal beads. (A) The time-averaged projections of image sequences (actin and ActA) of a curving lipid-coated bead that migrates in the parallel orientation are shown. The average actin and ActA fluorescence on the surface of the bead were measured as depicted in the schematic on the right. Scale bar: 2 μm. (B) The average ActA and actin fluorescence intensities of the bead in (A) are plotted. The angle around the back surface of the bead is plotted on the x-axis (left side of the bead: 90°; back of the bead: 180°; right side of the bead: 270°). The distributions of both ActA and actin are asymmetrical, with increased localization on the left of the bead corresponding to the inside of the curve. The motility of this bead is characterized by an average angular velocity of 3.43°/s, average yaw angle of 9.67°, and average speed of 11.7 nm/s. (C) Ellipsoidal beads with lipid-coated surfaces and mobile ActA were often observed to migrate in tight persistent circles. This behavioral phenotype was extremely uncommon for uncoated beads. Scale bar: 2 μm. Time: min:s.

Quantitative analysis confirms the lack of orientation bias observed in uncoated beads and bias for the parallel orientation in lipid-coated beads

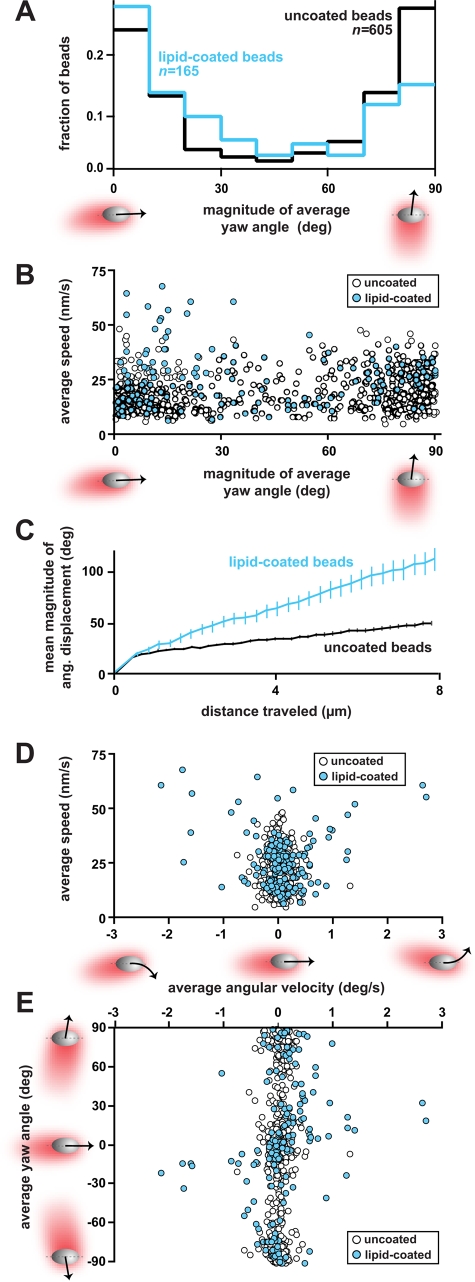
To quantify the overall orientation of each bead in the population, we averaged the instantaneous yaw angles obtained from each frame of the sequence containing each bead's trajectory. Overall, the distribution of the magnitude of the time-averaged yaw angles for a large population of uncoated beads (n = 605) was U-shaped (Figure 4A), confirming our qualitative impression of bead orientation. This distribution of average orientations at steady state is consistent with the frequencies of comet tail orientations found after 2 h of adding beads to cytoplasmic extracts during a time course (see Figure 2A). For further analysis, the magnitude of the average yaw angle was used to classify each bead based on orientation. Beads maintaining an average yaw angle of 0°–30° were classified as moving in the parallel orientation, and those maintaining an average yaw angle of 60°–90° were classified as moving in the perpendicular orientation. Based on this classification, 42% of uncoated beads migrated in the parallel orientation, while 47% migrated in the perpendicular orientation (Table 2 and Figure 4A). Moreover, the average yaw angle over the entire population of uncoated beads was close to 45°, reflecting the approximately equal number of beads migrating in each of the two preferred orientations—parallel or perpendicular (Table 2).

FIGURE 4:

Lipid-coated beads with mobile ActA exhibit significant changes in orientation, speed, and angular velocity. (A) The distribution of magnitudes of the average yaw angles of uncoated beads (black line) revealed that the majority of uncoated beads moved in either the parallel orientation (average yaw angle: 0°–30°) or perpendicular orientation (average yaw angle: 60°–90°). These two orientations were approximately equally prevalent in the population of uncoated beads. Lipid-coated beads (cyan line) showed a strong preference to move in the parallel orientation, as opposed to the perpendicular orientation. (B) The speed of beads depended slightly on bead orientation. A modest correlation (Spearman's r = 0.15, p < 0.05) between the average speed and average yaw angle was observed for uncoated beads (open circles). Lipid-coated beads (cyan circles) migrated significantly faster (by Wilcoxon rank-sum test, p < 0.001; mean of average speed = 25.9 nm/s; SD = 12.5; n = 165) compared with uncoated beads (mean of average speed = 19.9 nm/s; SD = 8.7; n = 605). (C) Lipid-coated beads had increased angular displacements compared with uncoated beads. The mean of the magnitudes of the angular displacement is plotted as a function of distance traveled for each population. Error bars = SEM. (D) On average, most ellipsoidal beads had small average angular velocities during migration. A subpopulation of lipid-coated beads (n = 17) exhibited large average angular velocities greater than 0.8°/s in magnitude. This subpopulation generally corresponded to beads migrating in tight persistent circles and fast speeds. (E) Curving beads with increased angular velocities generally had small yaw angles and were thus oriented close to the parallel orientation. The average yaw angle of each bead is plotted as a function of the average angular velocity.

TABLE 2:

Summary of average speed, angular velocity, and yaw angle for uncoated, lipid-coated beads and subpopulations based on motile behavior.

	Uncoated beads
	Mean of average speed (nm/s)	SD	Mean magnitude of average angular velocity (deg/s)	SD	Mean magnitude of average yaw angle (deg)	SD
Spheres (n = 184)	22.0	7.7	N/A	N/A	N/A	N/A
Ellipsoids (n = 605)	19.9	8.7	0.10	0.11	46.9	34.0
Parallel (n = 255)	18.2	8.1	0.10	0.13	9.9	7.5
Perpendicular (n = 287)	21.2	8.8	0.10	0.10	80.1	7.5
Lipid-coated beads
Ellipsoids (n = 165)	25.9	12.5	0.33	0.46	38.0	31.1
Parallel (n = 85)	26.5	14.8	0.35	0.52	11.1	8.3
Perpendicular (n = 52)	26.1	6.7	0.20	0.19	78.2	8.4
Fast subpopulation ≥50 nm/s (n = 10)	59.2	5.1	1.37	0.97	14.3	8.9
Circling subpopulation ≥0.8°/s (n = 17)	42.8	16.2	1.46	0.58	26.4	18.4

In the population of lipid-coated beads (n = 165), the percentage of beads generally migrating in the perpendicular orientation was significantly reduced, such that only 31% of the beads migrated in the perpendicular orientation, while 51% remained in the parallel orientation (Table 2 and Figure 4A). For both uncoated and lipid-coated beads, movement in the diagonal orientation was infrequent, and few beads in the population migrated in this manner when averaged over time (Table 2 and Figure 4A). This smaller group included beads that switched orientation and beads that had slightly curved trajectories.

ActA mobility allows ellipsoidal beads to attain unusually fast speeds and greater trajectory curvature

Our observations thus far allowed us to determine that the nature of the attachment of actin filaments on the surface of beads—that is, mobile or immobile attachment—had significant effects on bead orientation. To determine whether this change in filament attachment affected the motile behavior of ellipsoidal beads, we quantitatively measured and compared the speed and trajectory curvature of uncoated and lipid-coated beads. When we examined speed, we found that, on average, lipid-coated beads migrated significantly faster (by Wilcoxon rank-sum test, p < 0.001) compared with uncoated beads (Figure 4B and Table 2). On closer inspection, it was clear that a subpopulation of lipid-coated beads was contributing to the large average speed of the entire population. This subpopulation (n = 10) had particularly fast speeds and average yaw angles smaller than 33° in magnitude, demonstrating that the fastest lipid-coated beads migrated primarily in the parallel orientation (Figure 4B and Table 2).

In addition, lipid-coated ellipsoidal beads displayed greater average trajectory curvature compared with uncoated beads (Figure 4, C and D, and Table 2). Closer examination revealed that a subpopulation of lipid-coated beads (n = 17), which generally corresponded to the circling individuals readily discerned by eye (see Figure 3C), had remarkably large angular velocities compared with the rest of the population, with magnitudes greater than 0.8°/s (Table 2). As mentioned above, we found only a single bead migrating in this manner in the uncoated population. These circling, lipid-coated beads had a tendency to curve without any obvious preference in turning direction (clockwise vs. counterclockwise trajectory; Figure 4, D and E).

Overall our results demonstrate that ActA polarization due to lateral mobility on a fluid surface has profound effects on motility, such as enhanced speed and increased trajectory curvature. As we show in our simulations (see next section), the experimentally observed differences between lipid-coated and uncoated beads, that is, preference for the parallel orientation and increased circling, are directly predicted properties that emerge from the simple alteration of the actin-attachment sites on the particle surface from being fixed (for uncoated beads) to being laterally mobile (with lipid coating).

Mechanics of a viscoelastic actin network combined with branching of pushing and tethered filaments at the actin–bead interface explain ellipsoidal bead behaviors

Three striking and unexpected features of our observations must be consistent with an accurate biophysical description of actin-based movement. First, movement of ellipsoidal beads is approximately equally stable in either parallel or perpendicular orientations, whereas movement for lipid-coated beads with mobile ActA is more stable in the parallel orientation. Second, movement at intermediate yaw angles is unstable, although orientation switching does occur as a relatively rare event. Third, spontaneous symmetry breaking occurs in the parallel orientation exclusively.

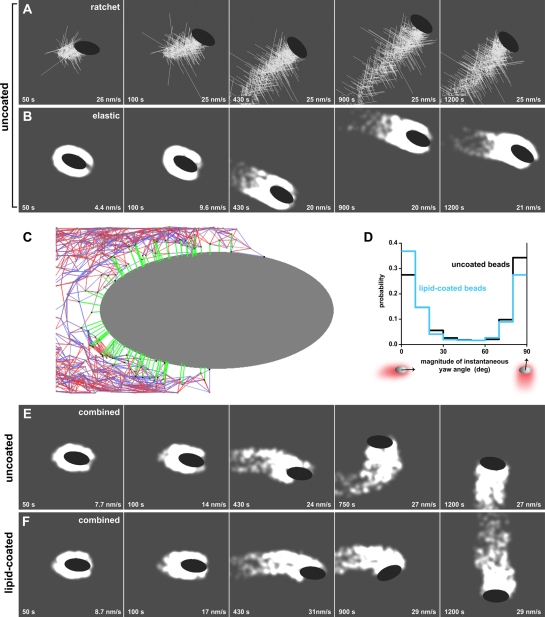
We considered a number of existing theories of actin-based force generation to determine whether any could explain these findings. We found that models of force generation by filament end-tracking proteins (Dickinson and Purich, 2002; Dickinson et al., 2004), by pushing filaments as tethered ratchets (Mogilner and Oster, 1996, 2003; Dickinson and Purich, 2002; Dickinson et al., 2004), or by an elastic gel in the simplest form of the elastic-propulsion model (Gerbal et al., 2000a) cannot independently explain our experimental results. First, when filaments in the comet tail were modeled as tethered ratchets growing from a completely rigid tail with branching dynamics, we found that the motile beads stabilized in the perpendicular orientation only (Figure 5A and Video S4). Similar results were obtained when filaments in the comet tail were modeled as ratchets with uniform nucleation along the surface instead of branching dynamics (Video S5). On the other hand, when we used the simple continuous model of a growing elastic actin tail, the beads broke symmetry and moved stably in the parallel orientation only (Figure 5B and Video S6). Using this elastic model, we also simulated a bead that broke symmetry in the perpendicular orientation—a situation that did not occur spontaneously in our experiments—by placing the initial cloud asymmetrically on the side of the bead (Video S7). After initiating movement in the perpendicular orientation, the bead rapidly turned to the parallel orientation without switching back, showing that when beads migrate using only elastic propulsion, the parallel orientation is preferred at steady state regardless of bead orientation during symmetry breaking.

FIGURE 5:

A combined viscoelastic-ratchet model of actin polymerization recapitulates the migration of ellipsoidal beads. (A) Snapshots show a simulated ellipsoidal bead being propelled by actin filaments acting as ratchets with autocatalytic branching dynamics. The bead initiates motility in the parallel orientation and rapidly switches to migrating in the perpendicular orientation, where it remains during the length of the simulation. See also Video S4. (B) Simulations of a bead propelled only by a viscoelastic actin tail, without explicit filament ratchets, show that the bead exclusively migrates in the parallel orientation. The tail is illustrated by a continuous actin density so that the shading is proportional to the local number of actin network nodes. A lighter shade corresponds to higher density. See also Video S6. (C) Schematic of the combined viscoelastic-ratchet model depicts a migrating bead (gray) that is pushed by an actin network (red, blue, and green). The actin network is represented by a deformable node-and-spring network, at which growing filaments (green) are anchored. Network springs can be stretched (blue) or compressed (red). The springs break when a certain stretch-force threshold is exceeded. The nodes and springs also disassemble with a constant rate. The barbed end of each newly created filament grows against the bead surface exerting a pushing force, while the pointed end remains anchored at the network. All forces and torques generated by filament pushing and spring deformations are balanced. (D) The combined viscoelastic-ratchet model predicts a U-shaped distribution of instantaneous yaw-angle magnitudes for both uncoated (black line) and lipid-coated (cyan line) beads. The distribution for the lipid-coated beads is slightly skewed toward greater parallel orientation probability. (E) Simulations of an uncoated migrating bead using the combined viscoelastic-ratchet model show that the bead breaks symmetry in the parallel orientation and eventually switches to migrate in the perpendicular orientation (at ∼700 s). Note that the time for the fourth frame of this sequence does not correspond to the other panels. See also Video S8. (F) Simulations of a lipid-coated migrating bead using the combined viscoelastic-ratchet model with the same initial condition as in (E) show that the bead breaks symmetry in the parallel orientation and eventually switches to migrate in the perpendicular orientation (at ∼900 s). See also Video S9. Time: s. Speed: nm/s.

These individual models of actin-based propulsion were incapable of recapitulating ellipsoidal bead migration as observed experimentally. However, we can satisfactorily explain most features of our data with a combination of the tethered-ratchet polymerization theory (Mogilner and Oster, 2003) and the elastic-propulsion model (Gerbal et al., 2000a; our mathematical model in the Supplemental Material). According to both theories, transient attachments of actin filaments from the comet tail to the surface of a moving particle cause an effective drag on the particle, in our case, an ellipsoidal bead. This drag is overcome by a pushing force generated by elastic recoil of bent filaments growing against the surface (Mogilner and Oster, 2003), macroscopic elastic stress of the growing actin network (Bernheim-Groswasser et al., 2005), or more likely, a combination of both mechanisms. Based on our two-dimensional computational mesoscopic model of actin propulsion, which combines elastic-propulsion and actin-filament branching mechanics, the actin meshwork of the comet tail is represented as a node-and-spring viscoelastic network (Figure 5C), similar to a model recently reported (Dayel et al., 2009). The network springs are linear and exert elastic forces. When these springs are stretched beyond a threshold, they break and introduce viscoelastic instead of just elastic actin-tail behavior. Viscoelastic forces are included explicitly in the balance of forces on the surface of the bead, the ellipsoidal geometry of which is also incorporated in the model. In addition to this actin network, individual actin filaments are represented as semirigid rods growing from nodes at the actin tail–bead interface. These filaments impinge on the bead surface and exert active pushing forces resisted by filaments transiently attaching to the surface. Together, these pushing and tethering forces effectively generate reactive viscoelastic stresses in the actin network.

In our simulations, addition of individual dynamic filaments to the interface of the elastic actin gel and the ellipsoidal bead was crucial in allowing the motile bead to become bistable, moving persistently both in parallel and perpendicular orientations, as shown by both simulations and analytical estimates (Figure 5, D and E, Video S8, and our mathematical model in the Supplemental Material). With a specific choice of model parameters, our simulations generated in silico bead movements that mimic the observed in vitro bead behaviors. Specifically, simulated beads initiated motility in the parallel orientation (Figure 5E and Video S8), in agreement with the data (see Figure 2B and Table 2). These particular results differ from a recent report, which showed perpendicular symmetry breaking both in vitro and in silico (Dayel et al., 2009), probably due to differences in the experimental conditions, which are discussed further in our mathematical model (Supplemental Material). Furthermore, our simulations predicted that the diagonal orientation of ellipsoidal beads is unstable, because the average torque, produced by hundreds of pushing and pulling filaments and elastic stresses, goes out of balance, and this balance is restored only when a bead approaches the parallel or perpendicular orientation. This combined viscoelastic-ratchet model also recapitulates the process of switching between parallel and perpendicular orientation in the range of once per tens of minutes, consistent with the overall orientation bistability observed and in semiquantitative agreement with the experimental data (switching rate 1 in ∼170 min; see our mathematical model in the Supplemental Material for additional discussion). When we simulated the behavior of migrating ellipsoidal beads and calculated yaw angles, we found that the combined model generated a U-shaped distribution of instantaneous yaw angles, suggestive of the bistability in bead orientation observed in the system (Figure 5D).

Using the combined model and our observations of the effects of ActA lateral surface mobility on ellipsoidal bead behavior, we simulated the movement of lipid-coated beads under identical conditions to determine whether this model could also account for the changed behavior resulting from this experimental perturbation. The sole changes to the model were to allow the attachment points (ActA) to be pulled backward by actin filaments when attached and to relieve the tethering forces parallel to the bead surface (see our mathematical model in the Supplemental Material). Simulations showed that beads with laterally mobile ActA broke symmetry and migrated stably in the parallel orientation but were also able to switch orientation (Figure 5F and Video S9). However, these beads stayed in the parallel orientation for a longer time before switching orientation (Figure 5F and Video S9, switches at ∼900 s), as compared with uncoated beads (Figure 5E and Video S8, switches at ∼700 s). Yaw-angle estimates obtained from simulations of lipid-coated bead movement also generated a U-shaped distribution of instantaneous yaw angles, predicting migration in both the parallel and perpendicular orientations, but with the parallel orientation slightly predominating (Figure 5D). The foregoing simulations were all performed in two dimensions; in the more realistic three-dimensional case, computer simulations of the deforming viscoelastic actin tail become forbiddingly long. Therefore, in three dimensions we simulated a formally rigid actin tail with effective point-like elastic forces, which capture macroscopic elastic effects. Qualitatively, the three-dimensional approximation of the combined viscoelastic-ratchet model gave results similar to those of the two-dimensional model, although the three-dimensional model shows an even greater bias for migration in the parallel orientation by lipid-coated beads, providing an even better fit to the experimental data (see Figure 4A and our mathematical model in the Supplemental Material).

The combined viscoelastic-ratchet model can qualitatively explain the emergence of circling in lipid-coated ellipsoidal beads. On moving lipid-coated beads, surface molecular complexes (ActA) attached to actin filaments are dragged rearward with respect to the bead, as suggested by our experimental observations (see Figure 3A and Giardini et al., 2003). The distribution of pulling forces generated by the tail is therefore expected to be biased toward the rear. The distribution of ActA is, however, more or less symmetric with respect to the long axis of the bead (Figure 3B), so that the pulling forces, having the same symmetry, create no torque. In contrast, the distribution of pushing forces, which is expected to follow the actin distribution, can be biased toward one side, for example, toward the left side of the bead, as shown in Figure 3B. These skewed pushing forces are locally normal to the bead surface and create a significant torque due to the ellipsoidal bead geometry (in which surface normals are not directed toward the bead's center). This torque is in a direction that would cause the lipid-coated bead shown in Figure 3B to rotate counterclockwise, as was observed. We further discuss this effect in our mathematical model (Supplemental Material).

Bead orientation influences speed

Elastic biophysical models predict that shape and local curvature of the bead surface should have an effect on actin polymerization–based force generation that would in turn affect the speed of cargoes (Gerbal et al., 2000a; Noireaux et al., 2000; Bernheim-Groswasser et al., 2005). In the development of the combined viscoelastic-ratchet model, we primarily considered bead orientation, and therefore wondered whether speed could be used as an independent measurement to test the accuracy of the model predictions. To elucidate whether the speed or mode of force generation by the comet tail might be related to the orientation of beads, we measured the speed of uncoated beads as a function of their yaw angles. As a control, we determined the movement of uncoated spherical beads of comparable size (1-μm diameter) and found they moved at speeds similar to those for ellipsoids (Table 2), but ellipsoids had a distinctly slower subpopulation that contributed to their slightly lower average speed (Supplemental Figure S1). Like uncoated ellipsoidal beads, uncoated spherical beads moved in very straight trajectories. For ellipsoidal beads, there was a weak correlation (Spearman's r = 0.15, p < 0.05) between the average speed and yaw angle over the population, such that beads migrating in the perpendicular orientation were on average slightly faster than beads in the parallel orientation (Table 2) with a statistically significant difference (by Wilcoxon rank-sum test, p < 0.001).

When we used the combined viscoelastic-ratchet model to determine the expected speed of beads in each orientation, we found that the speed of beads migrating in the perpendicular orientation was ∼24% higher than that of beads in the parallel orientation (see our mathematical model in the Supplemental Material), in good agreement with our experimental data, which shows a 16% increase (Table 2). Notably, Figure 4E and Video S8 demonstrate the increased speed predicted when the simulated ellipsoid approaches or completely switches to the perpendicular orientation. The explanation stems from the force balance: the pulling force is proportional to speed, while the pushing force is a decreasing function of speed (Mogilner, 2006). For beads migrating in the perpendicular orientation, a larger component of the total pushing force propels the bead, whereas in the parallel orientation, only a small component of the pushing force propels the bead, because a significant fraction of the pushing forces squeeze the bead and do not contribute to the forward movement (see our mathematical model in the Supplemental Material).

Actin comet tail redistribution on the bead surface precedes changes in bead orientation

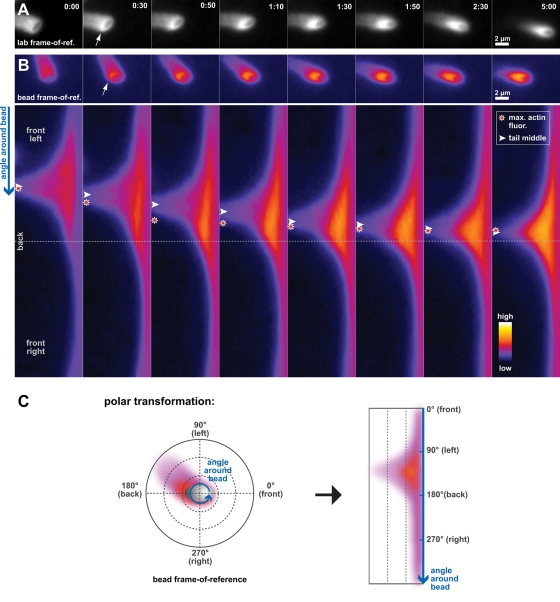
An underlying assumption of our theoretical framework has been that net bead movement behavior is caused by the balance of forces and torque exerted by the actin network at the bead surface. The excellent agreement between the steady-state movement data and our combined viscoelastic model suggests that torque generated by changes in the arrangement of the actin comet tail on the surface of moving beads should correlate with changes in their orientation. To test this hypothesis, we directly examined actin distributions on the surfaces of individual beads during events in which beads switched orientation or changed direction in their trajectories. We asked how the orientation switch was related, over time, to the distribution of actin around the bead. As mentioned earlier, spontaneous orientation switching was a rare event for beads migrating at steady state (see Table 1), but these events did reveal noticeable rearrangements of actin in the comet tail on the surface of lipid-coated beads (Figure 6 and Video S10). Similar actin distribution rearrangements were also observed in uncoated beads, but they were less pronounced (unpublished data). As illustrated in Figure 6, a lipid-coated bead's gradual switch from the perpendicular to the parallel orientation was accompanied by a marked increase in actin in the region of the bead that was to become the new back. The increase in actin density at the new back of the bead was followed by the repositioning of the comet tail such that it became roughly centered at the new back.

FIGURE 6:

Actin redistribution in the comet tail precedes changes in ellipsoidal bead orientation. (A) Fluorescent actin levels were observed to increase at the pole of a lipid-coated bead that became the new back (arrow at 0:30) prior to the bead fully switching from the perpendicular to the parallel orientation. Images are shown in the lab frame of reference. Time: min:s. (B) Time-lapse frames in the bead frame of reference (top), which correspond to the frames shown in panel (A), were used to generate polar-transformation images (bottom). The angular position around the bead is represented as vertical position in the transformed images. Arrowheads indicate the approximate position of the middle of the comet tail. Stars indicate the location of the maximum actin fluorescence measured on the bead surface. Before switching orientation (time = 0:00), the middle of the bead's actin comet tail effectively coincides with the position of the maximum actin fluorescence (overlapping arrowhead and star). While switching orientation, actin accumulates near the prospective back of the bead (see stars; times = 0:30–1:30) before the entire tail shifts position and follows the direction of the initial actin redistribution. Eventually, the bead completely switches to the parallel orientation, as the middle of the comet tail and the maximum actin fluorescence go back to spatially coincide (times = 1:50–5:00). Images were pseudocolored in ImageJ (Fire lookup table). Scale bar: 2 μm. Time: min:s. See also Video S10. (C) The schematic illustrates the overall approach used in the polar transformation of images. Images in the bead frame of reference are processed so that the angle around the centroid of the bead becomes the y-axis (blue arrow) of polar-transformed images.

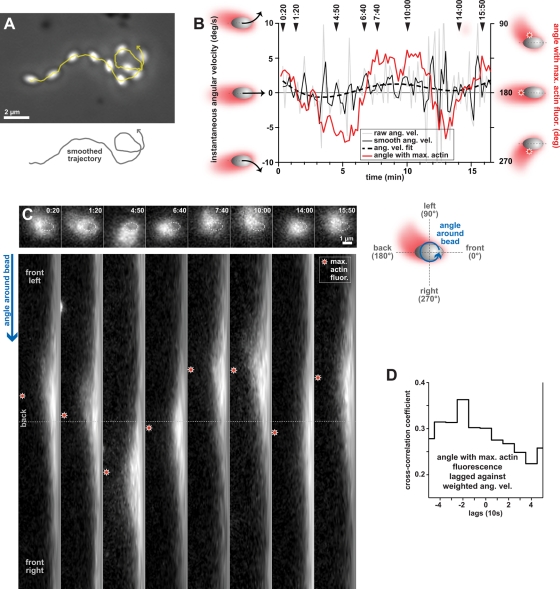
Since we observed that changes in bead orientation were preceded by actin comet tail rearrangements, we wondered whether these changes in actin distribution could also be involved in changes in motile behavior. To determine this, we analyzed the movement of an uncoated bead that changed direction multiple times during its trajectory. The particular bead shown in Figure 7 started off migrating for ∼2 min in a counterclockwise trajectory, changed to migrating clockwise for ∼3 min, and ended by describing a counterclockwise loop. As the angular velocity of the bead alternated from positive to negative and back to positive, the position with the highest level of actin on the bead's surface also alternated and correlated with changes in bead direction (Figure 7B). During these changes in direction, increased actin density was found on the surface of the bead corresponding to the inside of the curve, and the actin tail appeared to slide about the back of the bead from one side to the other (Figure 7, B and C, and Video S11). Interestingly, the time-lagged cross-correlation of the smoothed version of angular velocity with the position of the maximum actin intensity showed that changes in the direction of a bead's trajectory preceded (by ∼20 s) rearrangements in the placement of the actin comet tail on the bead's surface (Figure 7D). In addition, the speed of this bead appeared to vary contemporaneously with angular velocity (unpublished data). Thus changes in bead speed appeared to also precede rearrangements of actin in the comet tail. Additional cross-correlation analysis revealed that rearrangements of actin in the comet tail near the surface of this bead preceded (by at least 10 s) changes in orientation as measured by its yaw angle (unpublished data), similar to what was observed for the bead in Figure 6. To summarize, our data shows that while changes in bead orientation are downstream effects of changes in comet tail distribution on the bead surface, bead movement (speed and angular velocity) may be a causal predecessor of changes in actin distribution during bead migration. We propose that perturbations to bead movement, in combination with subsequent rearrangements of the comet tail on the surface of the bead, generate the torque necessary to ultimately change the orientation of the bead during migration. In our mathematical model (Supplemental Material), we discuss how the temporal sequence of changes in motion, bead orientation, and actin density can be understood from the modeling point of view.

FIGURE 7:

The actin comet tail alternates position from side to side as an ellipsoidal bead changes direction in its trajectory. (A) Phase-contrast images from multiple frames of a time-lapse sequence are composited to show the location of an uncoated bead that changes direction along its trajectory. The raw trajectory is shown in yellow and the arrowhead indicates that the bead moved from left to right. A smoothed version of the track is shown below the image to clarify the direction of the final loop. Scale bar: 2 μm. (B) The instantaneous angular velocity (left y-axis) and angular position of the maximum actin fluorescence on the bead surface (right y-axis) correlate with each other as the bead changes direction. The raw instantaneous angular velocity of the bead (gray line) was smoothed using a weighted average (black solid line) and fit using a polynomial function (dashed black line). The left y-axis of the graph was truncated at −10°/s and 10°/s so that five values greater than 10°/s in magnitude are not shown. The angular position of the maximum actin fluorescence on the bead surface (right y-axis, red line) is used to follow the location of the comet tail. The time points indicated at the top of the graph correspond to the images in (C). (C) The actin comet tail slides about the back of the bead from one side to the other as the bead changes direction. Time-lapse images in the bead frame of reference (top) generated the polar-transformation images (bottom). The location of the bead is depicted by the outline (top, dashed white ellipses). The angle around the bead is represented vertically in the transformed images. Stars indicate the location of the maximum actin fluorescence measured on the bead surface. Images shown correspond to time points indicated in the graph in (B). The schematic on the right illustrates the polar transformation. Scale bar: 1 μm. Time: min:s. See also Video S11. (D) The time-lagged cross-correlation of the angular position of the maximum actin fluorescence on the bead and the weighted angular velocity shows a peak at a time lag of −2 (or −20 s). Changes in the direction of bead trajectory turning (angular velocity) preceded the repositioning of the comet tail on the bead's surface by ∼20 s.

DISCUSSION

Based on the original elastic model of bacterial actin-based propulsion, actin gel growth should generate significant squeezing forces on curved surfaces, such as the back of a bacterium, propelling the bacterium forward (Gerbal et al., 2000a). Such squeezing forces have been demonstrated on deformable lipid vesicles and oil droplets, which become compressed to a teardrop shape (Giardini et al., 2003; Upadhyaya et al., 2003; Boukellal et al., 2004). According to the elastic-propulsion model, both rod-shaped bacteria and ellipsoidal beads are predicted to move most stably in the direction parallel to their long axes, because most of the squeezing occurs at the sides, generating a torque that aligns the long axis of the particle with that of the actin tail. In contrast, the tethered-ratchet model with specific parameters and assumptions (see our mathematical model in the Supplemental Material), predicts that ellipsoidal beads should move in the perpendicular orientation, because the bead in a skewed orientation experiences a net force pushing the bead forward not only parallel to the long axis of the comet tail, but also perpendicular to it. The direction of this perpendicular push is such that the bead's lagging pole rotates away from the long axis of the tail. This rotation causes the lagging pole to effectively lose actin filaments, while the leading pole gets exposed to nascent filaments. As a result, the actin network spreads down the long side of the bead surface, keeping the bead in the perpendicular orientation. Instead of the scenarios predicted by the elastic-propulsion and tethered-ratchet models, we found experimentally that ellipsoidal beads had no preference for either orientation during steady-state motility. The combination of actin network elasticity and filament ratcheting with branching dynamics into a mesoscopic model was necessary to explain our experimental results. Our combined model predicts that beads that migrate in the parallel orientation experience a torque generated by elastic actin squeezing, which dominates and aligns the bead with the actin tail's long axis. When beads migrate in the perpendicular orientation, squeezing is weaker, and the geometric and kinetic effects of the branching actin filaments in the network dominate. Strikingly, the elastic squeezing effect and actin-filament pushing and spreading combine in such a way that the overall stability of movement is very similar for the two orientations, and the population of beads distributes itself almost evenly between them. Preliminary simulations showed that the qualitative result of the model—the bistability of bead orientation—is robust when the model's parameters are varied, but the predicted fraction of beads in each orientation is a function of the parameter values. Our combined model could be applicable to other important protrusive phenomena as discussed in our mathematical model (Supplemental Material).

Because the actin-based motility of actual bacteria is almost exclusively parallel to their long axis, it is likely that the polar distribution of bacterial proteins that initiate motility is more important than their shape for determining their orientation during migration. In fact, Escherichia coli bacteria expressing the S. flexneri IcsA/VirG proteins exhibited a much shallower gradient of protein polarization than wild-type S. flexneri (Robbins et al., 2001) and occasionally migrated perpendicular to their long axes (Goldberg and Theriot, 1995) in a manner similar to our ellipsoidal beads uniformly coated with ActA. For normal L. monocytogenes, polarization of ActA is a direct consequence of the pattern of cell wall growth (Rafelski and Theriot, 2006), enforcing persistent unidirectional movement parallel to the bacterial long axis.

Although L. monocytogenes is similar in shape to the ellipsoidal beads used in this study, it is important to note that differences in the localization of the ActA protein in these two systems have significant impact on biophysical motile parameters. L. monocytogenes expresses ActA in a polarized manner, while the surfaces of ellipsoidal beads were coated uniformly with ActA. When we bound ActA protein to a fluid lipid layer coating the surface of ellipsoidal beads and thus allowed ActA to freely move, ActA became polar and colocalized with the actin comet tail, as observed previously for spherical beads (Giardini et al., 2003). This lateral mobility and consequent polar ActA distribution allowed ellipsoidal beads to recapitulate the predominant orientation and curved trajectories, such as tight circles, commonly observed in wild-type, migrating L. monocytogenes. Thus the polarization of ActA in L. monocytogenes is probably crucial not only for its characteristic orientation but also for the complex motile behaviors in which it engages.

Since ActA is the only bacterial factor necessary for the actin-based motility of artificial particles, this protein likely represents the site of actin-filament attachment to the surface of beads, either directly by binding or indirectly through interactions with cytoplasmic proteins, such as Enabled/vasodilator-stimulated phosphoprotein (Ena/VASP) family members or the Arp2/3 complex, which are proteins known to bind directly to actin filaments (Pistor et al., 1995; Gertler et al., 1996; Mullins et al., 1997; Huttelmaier et al., 1999; Zalevsky et al., 2001). When mobile ActA becomes clustered on the back of lipid-coated ellipsoidal beads, the distribution of pulling filaments attached to ActA—and thus attached to the bead—could become significantly biased, creating a rearward force applied at the back of the bead that generates torque, rotating beads toward the parallel orientation. The computational simulations revealed that behavioral features of lipid-coated beads compared with uncoated beads—preference for the parallel orientation and increased circling—can arise from the simple introduction of lateral mobility of attachment points on the particle surface without any other changes in model parameters.

Specific mutations in the ActA protein or in binding partners that alter their biochemical activities and interactions have been shown to cause changes in large-scale behavior strongly reminiscent of several of our observations. For example, mutation of Ena/VASP-binding domains in ActA or deletion of the F-actin–binding domain in Ena/VASP can cause L. monocytogenes to move in small tight circles (Auerbuch et al., 2003) similar to the extreme curved patterns of lipid-coated ellipsoids (see Figure 3). Even more strikingly, a cluster of charged-to-alanine mutations in a region of ActA with unknown function generates a bacterial strain that can “skid” and move sideways (perpendicular to the long axis) in host cells (Lauer et al., 2001). These behavioral changes are not due to changes in the degree of polarization of the ActA protein on the bacterial surface, as protein polarization in the mutant is indistinguishable from that of the wild-type (Rafelski, 2005). Instead, the large-scale behavioral changes arising from these mutations are likely to be due to modest changes in affinity, binding kinetics, or biochemical activity for surface-associated proteins. Because we are able to phenocopy these biochemical alterations with purely physical changes in protein distribution or lateral mobility in ellipsoidal beads, these comparisons open a window for exploring the connections between protein–protein interactions at the molecular scale and large-scale cooperative emergent behaviors of whole motile systems.

The propulsion of cargo, such as bacteria, vesicles, and artificial beads, by polymerizing networks of actin filaments represents an attractive and widely used model system for actin-based motility amenable to both biochemical and biophysical dissection. In this study, we characterized several unexpected large-scale changes in movement caused by simple physical alterations of the underlying cargo: deformation of spherical beads into ellipsoidal shapes and enhancement of lateral mobility for attachment points of actin filaments to the cargo. These physical changes phenocopy several previously described mutant behaviors of motile bacteria. By incorporating realistic geometries and combining existing biophysical models of actin force generation, we are able to explain most quantitative features of our data, further confirming the broad explanatory power of this hybrid physical model. These findings illustrate some of the ways that large-scale complex changes in behavior can emerge cooperatively from alterations in molecular functions.

MATERIALS AND METHODS

Preparation of ellipsoidal beads

Ellipsoidal beads were prepared as previously described (Lu et al., 2001). Briefly, 1-μm carboxylated polystyrene microspheres (Polysciences, Warrington, PA) were placed in a viscoelastic matrix (6% polyvinyl alcohol), heated to ∼200°C in a box oven, and stretched uniaxially. The film containing the beads was cooled and dissolved using an isopropanol/water mixture to recover the beads before functionalizing their surfaces with carboxylate. Electron microscopy revealed that the beads used in this study had average dimensions of 1.8 μm × 0.8 μm (length, SD = 0.3; width, SD = 0.2; n = 30), with an average aspect ratio of 2.2.

For coating beads with a lipid bilayer, a 50:1 ratio of carboxylated ellipsoidal beads were mixed with unilamellar vesicles (lipid composition consisted of a 46:50:2:2 M ratio of phosphatidylcholine:cholesterol:fluorescein-phosphatidylethanolamine:Ni-nitrolotriacetic acid chelating lipid) and prepared as previously described (Hope et al., 1985; Linseisen et al., 1997; Giardini et al., 2003). All phospholipids were obtained from Avanti Polar Lipids (Alabaster, AL). His-tagged ActA was purified as previously described (Welch et al., 1998; Cameron et al., 1999) and adsorbed on the surface of uncoated or lipid-coated beads at saturating amounts (Giardini et al., 2003). For direct visualization of ActA, cysteine-modified ActA (Upadhyaya et al., 2003) was labeled with fluorescein-5-maleimide (Invitrogen, Carlsbad, CA) using the manufacturer's protocol. Briefly, 10 μM ActA-cysteine was incubated with 0.2 mM fluorescein-5-maleimide for 1 h at room temperature in phosphate buffered saline (137 mM NaCl, 2.7 mM KCl, 8.03 mM Na₂HPO₄, 1.47 mM KH₂PO₄). The fluorescein-ActA was then purified by dialysis and gel filtration.

Bead motility assays

Motility assays in this study were adapted from previous work (Cameron et al., 1999). Slides were prepared by adding ActA-coated or ActA-lipid-coated beads to X. laevis egg cytoplasmic extract, which was diluted to 40% of the original protein concentration (using Xenopus extract buffer; Murray, 1991) and supplemented with trace amounts of tetramethylrhodamine iodoacetamide–labeled monomeric actin and an ATP-regenerating mix (Murray, 1991). The slide chamber depth was restricted using 2-μm silica spherical beads. Bead motility was visualized on a Zeiss Axioplan microscope (Jena, Germany) equipped with phase-contrast and epifluorescence optics and a CCD camera (MicroMax 512 BFT; Princeton Instruments, Trenton, NJ). Phase-contrast and fluorescence images were acquired every 10 s for 100 frames for most time-lapse sequences using MetaMorph software (Molecular Devices, Sunnyvale, CA). All time-lapse sequences taken during steady-state bead motility were acquired between 2 and 4 h after preparing the slide. For the uncoated and lipid-coated ellipsoidal bead populations, a total of 113 and 50 time-lapse sequences were analyzed, respectively. These sequences generated a total number of 605 (50,426 data points) and 165 (12,651 data points) bead trajectories at steady state for uncoated and lipid-coated ellipsoids, respectively. Stationary beads with actin clouds and beads undergoing Brownian motion or symmetry breaking were excluded from our analysis of steady-state movement, as were any track segments during which beads underwent collisions.

Bead movement and fluorescence analysis

Bead positions and orientations were computed from phase-contrast images and assembled into tracks essentially as previously described (Soo and Theriot, 2005b). Trajectories with fewer than 40 data points and track segments during which beads physically interacted with neighboring beads were excluded from the data set, as were cloud-associated beads undergoing Brownian motion. Image sequences in transformed coordinates (bead frame of reference and polar) with linear interpolation were generated using custom plug-ins to ImageJ (http://rsb.info.nih.gov/ij).

For ellipsoidal beads, yaw was defined as the angle between the average orientation of the long axis of a bead in two consecutive time-lapse frames and the vector describing the bead's movement between those frames (for a simplified diagram, see Figure 2C). Yaw angles were constrained to range between −90° and 90°. Instantaneous speed values were calculated by dividing the straight-line displacement of the centroids of tracked beads by the time elapsed (10 s) between consecutive frames of a time-lapse sequence. The mean of the time-averaged instantaneous speed of each bead (mean of average speed) was usually reported for each population. Instantaneous angular velocities were calculated by dividing the angle between consecutive vectors describing the bead's trajectory by the elapsed time (10 s). The mean of the magnitudes of the time-averaged instantaneous angular velocities of beads (mean magnitude of average angular velocity) was reported for each population (Table 2).

For the time course of tail formation, slides were prepared at time zero and images were collected at each of the designated times over a 5-h period. For each time point, 50 phase-contrast and fluorescence images were acquired across each slide using a 10 × 5 grid. The numbers of beads with comet tails generally parallel, perpendicular, or diagonal to the long axis were counted. Each data point consisted of between 38 and 576 counted beads.

The maximum actin fluorescence on the comet tail was calculated by using polar-transformed images obtained from images in the bead frame of reference and centered on the bead. The fluorescence intensity was averaged in each of 512 regions of 1 pixel × 20 pixels (corresponding to 0.7° × ∼2 μm) along the angle coordinate. The position of the region with the largest average fluorescence value was then reported in degrees and reflected an angle around the bead. Time-lagged cross-correlations were performed using the TSTOOL interface in Matlab software (MathWorks, Natick, MA). Smoothing of the instantaneous angular velocity values was generated in GraphPad Prism software (La Jolla, CA) using a weighted average of five nearest neighbors based on the method of Savitsky and Golay (1964) using a cubic equation. The angular velocity fit-in was generated using a seventh-order polynomial function.

Mathematical modeling of ellipsoidal bead migration

We simulated stochastic coupled dynamics of two populations of actin filaments (attached and detached) at the surface of ellipsoidal beads, calculated the forces and torques exerted by the filaments on the beads, and computed the beads' movements according to the zero total force and torque requirements as described in our mathematical model (Supplemental Material). Simulations were performed on a desktop computer; the code, written in C, is available upon request.

Abbreviation used:

Ena/VASP

Enabled/vasodilator-stimulated phosphoprotein