Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Aug 15.
Published in final edited form as: Neuroimage. 2011 Oct 20;62(2):706–712. doi: 10.1016/j.neuroimage.2011.10.039

Spiral Imaging in fMRI

Gary H Glover 1
PMCID: PMC3279621  NIHMSID: NIHMS333712  PMID: 22036995

Abstract

T2*-weighted Blood Oxygen Level Dependent (BOLD) functional magnetic resonance imaging (fMRI) requires efficient acquisition methods in order to fully sample the brain in a several second time period. The most widely used approach is Echo Planar Imaging (EPI), which utilizes a Cartesian trajectory to cover k-space. This trajectory is subject to ghosts from off-resonance and gradient imperfections and is intrinsically sensitive to cardiac-induced pulsatile motion from substantial first- and higher order moments of the gradient waveform near the k-space origin. In addition, only the readout direction gradient contributes significant energy to the trajectory. By contrast, the Spiral method samples k-space with an Archimedean or similar trajectory that begins at the k-space center and spirals to the edge (Spiral-out), or its reverse, ending at the origin (Spiral-in). Spiral methods have reduced sensitivity to motion, shorter readout times, improved signal recovery in most frontal and parietal brain regions, and exhibit blurring artifacts instead of ghosts or geometric distortion. Methods combining Spiral-in and Spiral-out trajectories have further advantages in terms of diminished susceptibility-induced signal dropout and increased BOLD signal. In measurements of temporal signal to noise ratio measured in 8 subjects, Spiral-in/out exhibited significant increases over EPI in voxel volumes recovered in frontal and whole brain regions (18% and 10%, respectively).

Keywords: functional magnetic resonance imaging, fMRI, Spiral

Introduction

Blood Oxygen Level Dependent (BOLD) functional magnetic resonance imaging (fMRI) (Bandettini et al., 1992; Kwong et al., 1992; Mansfield, 1977; Ogawa et al., 1990) typically uses T2*-weighted imaging to detect changes in deoxyhemoglobin concentration consequent to altered neural metabolism. Because absolute MR image intensities have no intrinsic meaning, relative differences in signal levels (contrast) are utilized to infer neural differences in brain state. In effect, a timeseries signal of interest is always compared to another timeseries, which is either a model-based regressor in the case of task-evoked experiments or signals from another brain region in the case of functional connectivity. Motion of the brain can create apparent time-varying contrast differences that, because the BOLD contrast is small, can be interpreted as true activation. It is therefore important that each time frame be acquired with the shortest possible duration, consistent with tradeoffs between desired signal to noise ratio (SNR), brain coverage, and spatial and temporal resolution. This argues for the use of single- or few-shot acquisition methods, such as Echo Planar Imaging (EPI) (Mansfield, 1977) or Spiral (Noll et al., 1995).

Unfortunately, such rapid acquisitions are affected by localized off-resonance conditions that result from susceptibility induced field gradients (SFGs), which cause geometric image distortion, ghosting and signal dropout, especially in brain regions adjoining air interfaces (Cho and Ro, 1992). These effects are exacerbated by long readout trajectories, and thus another requirement for fMRI acquisitions is to gather the data for each image as quickly as possible. A typical 3.4mm × 3.4 mm pixel resolution EPI acquisition will have a readout duration of ~30 ms, which is a significant fraction of T2* at 3T.

In the following, we begin with a discussion of EPI, followed by Spiral methods with a comparison to EPI, concluding with a historical perspective on Spiral applications to fMRI.

EPI

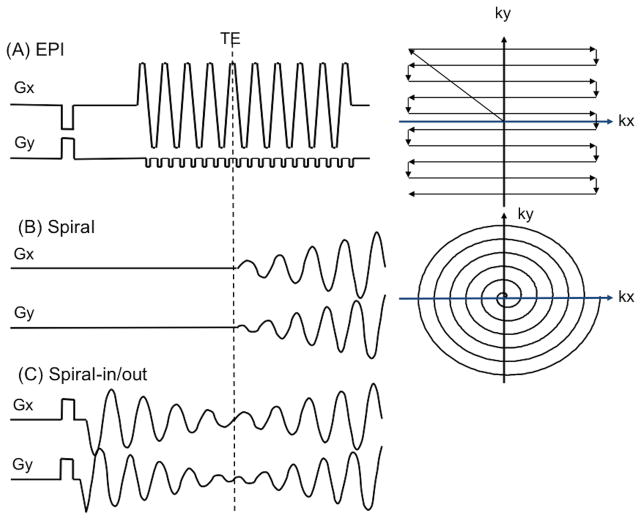
The typical fMRI acquisition uses EPI, with k-space trajectory and pulse sequence shown in Fig. 1(A). This trajectory covers a Cartesian k-space with lines whose direction alternates as ky (phase encoding direction) advances from top to bottom as shown. Because of the need to turn the corner at the end of every kx (frequency encoding or readout direction) line and the fact that much of the line is acquired during ramping of the Gx gradient, the speed in k-space, d|k|/dt − γ|G(t)|, is not constant (γ = gyromagnetic ratio for protons, |G| is the magnitude of the complex gradient waveform Gx + i Gy). Furthermore, the energy contributed by the Gy gradient is negligible compared to that of the Gx gradient, so that only one gradient axis (Gx) is active in the traversal of k-space. Both effects increase the duration of the readout acquisition. Note also that rate of k-space traversal is highly asymmetric, i.e., d|kx|/dt ≫ d|ky|/dt. Typically, each kx line is acquired in ~0.5 ms, so the kx bandwidth is ~2000 Hz/pixel, while the equivalent bandwidth in the ky direction is ~30 Hz/pixel. In practice, therefore, geometric distortions and ghosting due to off-resonance occur primarily in the phase encoding direction. Nyquist ghosting (Jezzard and Clare, 1999) occurs because imperfections in the gradients cause asymmetry in the center of the kx readout, and since the direction alternates every other line, the result is a perturbation manifested at a distance of half the field of view (FOV).

Figure 1.

Figure 1

Open in a new tab

K-space trajectory and pulse sequence diagrams for (A) EPI, (B) Spiral, (C) Spiral-in/out.

Spiral

The Spiral k-space trajectory and pulse sequence is shown in Fig. 1(B). First described by Ahn (Ahn et al., 1986), the trajectory starts at the origin and spirals to the edge of k-space, typically using an Archimedean design,

k(t)=kx(t)+iky(t)=Nintθ(t)Deiθ(t)G(t)=Gx(t)+iGy(t)=1γdkdt, (1)

where Nint is the number of interleaves, D is the FOV, and θ is a function of time t that describes the azimuthal trajectory sweep. The design of θ is governed by constraints of the gradient system determined by slew rate limit S0 imposed by either hardware or biophysical considerations of peripheral nerve stimulation, or the gradient amplitude limit, Gmax:

|dGdt|≤S0∣G∣≤Gmax. (2)

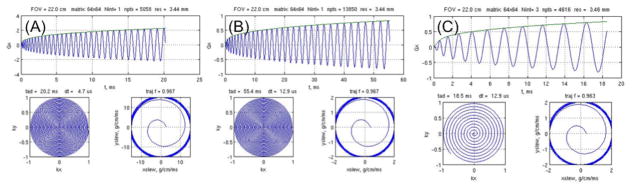
Equations 1 – 2 result in a differential equation that can be solved for θ by iterative means (King et al., 1995; Meyer et al., 1992) or by various approximations (Duyn and Yang, 1997; Glover, 1999). Generally the trajectory is slew rate limited near k = 0, where it begins with zero gradient amplitude (top condition in Eq. 2). As the amplitude of |G| increases during the readout, it may reach Gmax, at which the solution switches to one in which the slew rate S0 can no longer be maintained (second condition in Eq. 2). This rarely happens in fMRI acquisitions, however. In the early days of fMRI before so-called “EPI gradients” were commonly available, the limited amplitude and slew-rate capabilities required multi-shot spirals to maintain a modest readout trajectory, as shown in Fig. 2.

Figure 2.

Figure 2

Open in a new tab

Spiral design with (A) 3.43 × 3.43 mm resolution is 20.2 ms long and remains slew-rate limited for gradient hardware with Gmax = 50 mT/m, S0 = 150 mT/m/s. (B) With early (non-EPI) gradient hardware available ca. 1993 (10 mT/m, 20 mT/m/s), the single-shot readout trajectory was prohibitively long (55.4 ms) and a three-shot trajectory was required for fMRI experiments (C).

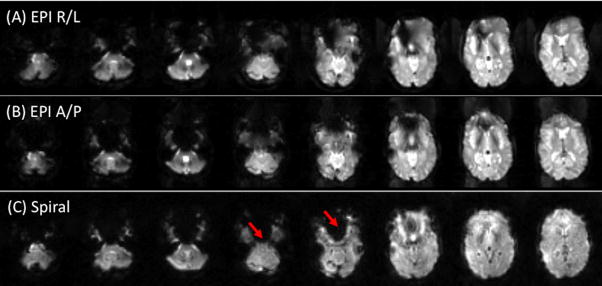
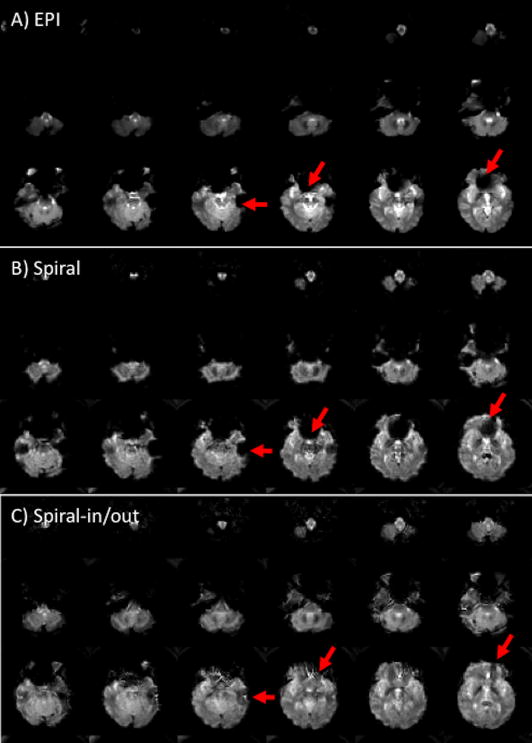
Comparison of the two pulse sequences in Fig. 1 shows qualitatively that the Spiral sequence has a shorter readout duration than that of EPI, which is directly attributable to 1) Spiral’s use of both Gx and Gy gradient axes to drive the trajectory, as opposed to just Gx for EPI, and 2) not acquiring the k-space corners. The shorter readout reduces off-resonance-induced geometric distortion (in EPI) and blurring (in Spiral) as well as SFG-initiated signal dropout (Glover and Lai, 1998) (Yang et al., 1998). Figure 3 shows T2*-weighted images for EPI and Spiral acquisitions. The asymmetry of the EPI trajectory’s speed of traversal is amply demonstrated by the different geometric distortions seen when swapping phase and frequency encoding directions. Since Spiral has a symmetric trajectory, there is no fast and slow direction, and SFGs cause blurring rather than voxel displacement. Because the Spiral readout duration is shorter, the blurring is arguably less intrusive than EPI’s distortion, and the signal loss in most frontal regions is also less than with EPI except in a few slices as shown.

Figure 3.

Figure 3

Open in a new tab

EPI images with phase encoding direction R/L (A) or A/P (B). Susceptibility-induced field gradients (SFGs) cause geometric distortion along the phase encoding direction. With Spiral (C), SFGs instead cause blurring. Note that there is increased signal in most slices with Spiral, but loss in several slices (arrows).

A second difference between EPI and Spiral is the intrinsic sensitivity to motion from vascularly-driven brain pulsatility is different. If spins at position x(t) move during the readout, additional phase δφ is accumulated proportional to moments Mn of the gradients and the spins’ velocity v, acceleration a, and higher order terms (Bernstein et al., 2004):

δφ=γ∫G(t)x(t)dt=γ(vM1+aM2+⋯)Mn=1n∫G(t)tN(t)dt. (3)

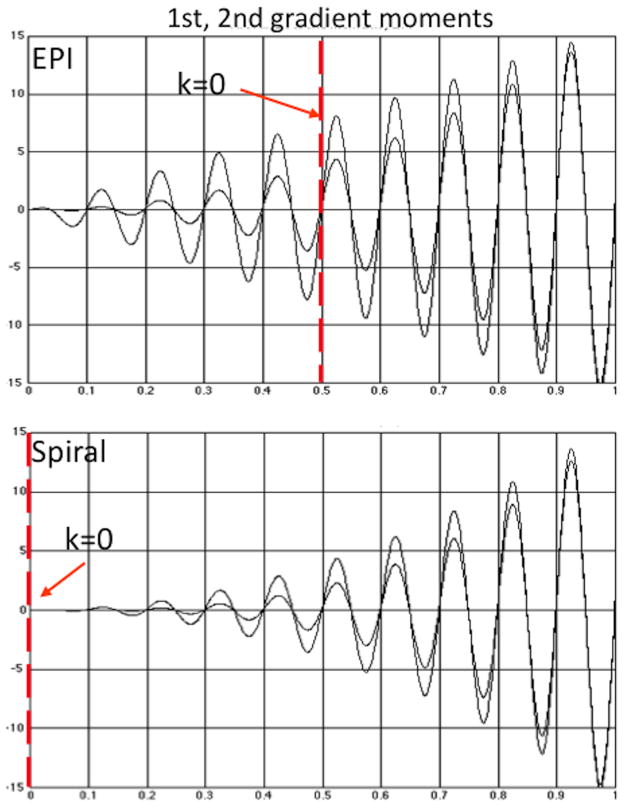
This phase error causes variable artifacts in the images depending on the timing of the readout with respect to the brain motion, which thereby gives rise to additional noise in the time series. Figure 4 shows plots of moments for both sequences, which appear very similar. However, the origin of k-space (i.e., the echo time TE) occurs half-way through the EPI readout, and while all moments are zero at exactly k = 0, they grow rapidly at a slight distance from the origin. For Spiral all moments remain low for a relatively large radius around the origin (at the beginning of the readout), which leads to reduced motion sensitivity. This was demonstrated by Yang, et al. (Yang et al., 1998), where the improvement in activation with Spiral compared with EPI was attributed to the reduced time-series noise exhibited with Spiral.

Figure 4.

Figure 4

Open in a new tab

Plots of gradient moments show similarity between EPI and Spiral; however the origin of k-space in EPI (the TE) occurs half-way through the readout, where the moments are large at a slight distance from k = 0. For Spiral the moments remain low for a relatively large radius around the origin, which leads to reduced sensitivity to motion.

In general, SFG-induced signal dropout in frontal and parietal regions is worsened at 3T compared with 1.5T, and it is not clear whether there is an advantage to using the higher field when studying cognition in these regions. Therefore, visual perception, visuospatial working memory, and affect-processing tasks were utilized to quantify BOLD signal at 1.5T and 3T using a Spiral acquisition method (Krasnow et al., 2003). The findings demonstrated significant advantages in prefrontal and other association cortices for 3T over 1.5T.

Spiral-in/out

While the Spiral method has been found to have some advantages for fMRI as described above, it was recognized that there remained significant signal loss in frontal and parietal brain regions from SFGs. It was speculated that a spiral-in trajectory ending at TE would create an image with superior signal recovery and BOLD sensitivity in regions with foreshortened T2* (Bornert et al., 2000), and that this trajectory could be followed immediately by a conventional spiral-out trajectory to create a second image, at no cost in the scan time/slice (see Fig 1(C). This was found to be the case (Glover and Lai, 1998), with example images shown in Fig. 5. As may be seen, the signal recovery in frontal and temporal regions is superior to that with EPI (and Spiral in some slices), because the Spiral-in information fills in regions with shortened T2*. Various approaches for adaptively combining the spiral-in and spiral-out images were examined (Glover and Thomason, 2004), and the most practical method was found to be voxelwise linear addition with weighting determined by the average signal intensity for the two image time-series. In a comparison between Spiral-in/out and Spiral using tasks eliciting activation in ventral medial prefrontal cortex, amygdala and dorsolateral prefrontal cortex, the Spiral-in/out method was found to be superior in both amplitude and number of voxels exhibiting significant BOLD contrast (Preston et al., 2004). In principle, if the noise in the -in and –out images is uncorrelated, the tSNR in uniform brain should be √2 × greater for Spiral-in/out compared with spiral-out only, since there are two images contributing equally to the combined image. However, the tSNR advantage was found to be only ~1.3x, which was attributed to noise correlation from the physiological processes of respiration and vascularity (Glover and Law, 2001). Nevertheless, this is a substantial advantage that derives from longer total readout time, without the artifact penalty that would occur if the two images were in effect combined coherently (i.e. in reconstruction as one image).

Figure 5.

Figure 5

Open in a new tab

T2*-weighted Spiral-in/out images (C) compared with EPI (A) and Spiral (B) (TE = 30 ms, 3.43×3.43×4mm, 3T). Inclusion of the Spiral-in information substantially reduces signal degradation from SFGs compared to both EPI and Spiral (arrows).

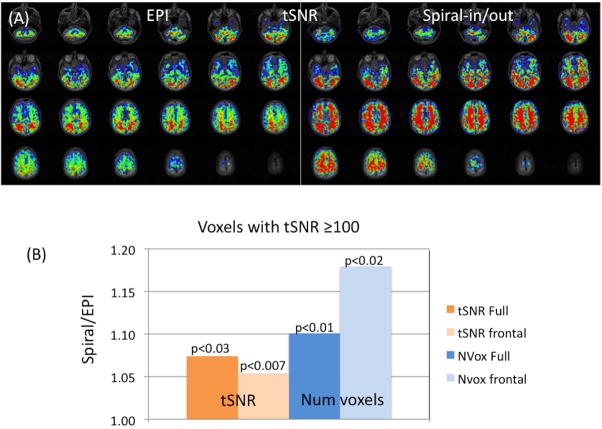
A direct comparison of the BOLD performance for Spiral-in/out and EPI has not been previously reported, although Spiral-out has been found to be superior to EPI (Yang et al., 1998), and Spiral-in/out has been demonstrated to be superior to Spiral-out (Preston et al., 2004). Here, we report measurements of tSNR (which mirrors the BOLD sensitivity (Glover and Lai, 1998)) for the two methods, with results for 8 subjects shown in Fig. 6. For the full-brain measurements, the Spiral-in/out method demonstrated significantly greater average tSNR (1.07x, p<0.030, paired t-test) and more voxels above tSNR threshold of 100 (1.10x, p<0.011). In frontal regions, Spiral-in/out voxels above threshold had significantly higher tSNR (1.05x, p < 0.011), and were significantly greater in number (1.18x, p < 0.023). These results suggest a sensitivity advantage of the Spiral-in/out method over EPI in both uniform brain and particularly in frontal regions affected by SFG-induced signal dropout.

Figure 6.

Figure 6

Open in a new tab

(A) Maps of tSNR comparing EPI (left) and Spiral-in/out (right) for one subject (scale: 82 ≤ tSNR ≤ 227). Scan parameters: 3T, TE = 30 ms, TR = 2s, 3.43×3.43×4mm, 24 slices/no gap,100 time frames. (B) Summary of average measurements (8 subjects) showing ratios of tSNR and voxel volumes for Spiral-in/out and EPI at a threshold of tSNR ≥ 100; average whole-brain tSNR was 155 for EPI and 166 for Spiral-in/out. Additional measurements were made for a region containing only11 slices covering frontal/anterior brain regions that demonstrate typical signal dropout (denoted “frontal”). All comparisons showed significant advantages for Spiral-in/out (paired t-test 1-tailed) (note 18% increased number of voxels in frontal regions).

Variable density Spiral

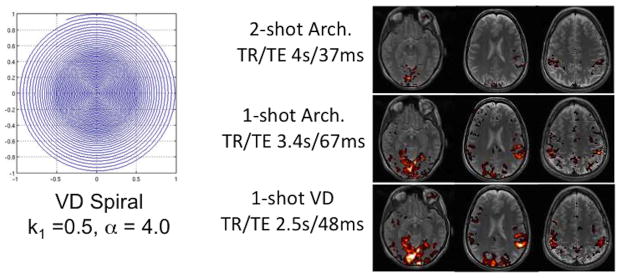
With typical fMRI resolution (e.g. 64×64 matrix) the single-shot Spiral or EPI readout duration is about 20 – 30 ms, which is short enough to provide acceptable levels of off-resonance effects for most applications. However, increasing interest in higher resolution fMRI requires much longer readouts to cover the greater area of k-space. For 128×128 matrix and other parameters held constant, the single-shot Spiral trajectory will be nearly 60 ms long (and the EPI readout even longer), which will lead to substantial distortion. One solution is the use of parallel imaging, which can reduce the readout duration at an expense in SNR ((Law et al., 2008; Pruessmann et al., 2001; Weiger et al., 2002), Another approach is to use multiple-shot or interleaved imaging, in which >1 TR is required to cover all of k-space (Glover and Lai, 1998). With Spiral, the duration of a 2-shot acquisition will be ~29 ms, but the tSNR will be reduced because the total data acquisition time integrated over the scan is reduced by about half. A third approach is to take advantage of judicious undersampling of the high spatial frequencies by using a non-Archimedean spiral trajectory (Kim et al., 2003; Tsai and Nishimura, 2000). By linearly increasing the spacing between spiral turns beginning at a radius k1 from the origin and ending with a spacing of α × the nominal spacing for full sampling density at the edge, the readout duration can be significantly reduced without significantly impairing the impulse response function (Chang and Glover, 2010). Results demonstrated that acceptable artifact levels can be attained with single-shot variable-density Spiral designs applied to high resolution fMRI, with improved tSNR and BOLD contrast as shown in Fig. 7 for designs with 128×128 matrix. Thus, the use of such methods is a viable alternative for fMRI applications using smaller voxels than is typical.

Figure 7.

Figure 7

Open in a new tab

(Left) Representative variable density (VD) Spiral k-space design for 1.72×1.72 mm pixel size, and (Right) single-subject results comparing single- and 2-shot Archimedean (Arch.) designs with single-shot VD design. The TE and TR (/volume) were set to minimums allowed by each acquisition for the same total scan time. In each case the TE was dictated by the readout time + the slice selection radio frequency and gradient pulses because a Spiral-in/out design was employed (Chang and Glover, 2010).

Historical perspective

In June, 1992 the Richard M. Lucas Center for Imaging was dedicated at Stanford with keynote address by Nobel Laureate Richard J. Ernst, and fMRI studies were begun in the fall with colleagues from the Psychology Dept. Initial experiments utilized Spoiled Grass acquisitions with 1 or 2 slices and a net TR per volume of 6.4s or 12.8s, respectively. The 1.5T magnet had “conventional” gradients with 10 mT/m, 20 mT/m/s characteristics, and it was not possible to perform single-shot MRI such as EPI. Various alternative GRE pulse sequences were therefore developed (Glover et al., 1993; Glover and Lee, 1993), but none were fully satisfactory because of the slow data collection rates that could be obtained with Cartesian trajectories. However, EE grad student Craig Meyer had been experimenting with multi-shot spiral methods for cardiac MRI (Meyer et al., 1992). The spiral trajectory was efficient enough (and the gradient fidelity precise enough) that even with low speed gradients only a few “shots” were adequate to obtain excellent coronary artery images. The effectiveness of spiral methods in this temporally-demanding application inspired postdoc Adrian Lee to further develop and apply multishot spiral methods for fMRI (as in Fig. 1(C)), and he demonstrated activation movies for observing venous outflow (Lee and Glover, 1995). Stanford EE graduate Doug Noll brought the spiral technique with him to Michigan and was active in Spiral’s further development for fMRI (Noll et al., 1995). Thus, it was because of lack of high speed gradients that spiral methods were employed at Stanford from nearly the first to enable fMRI experiments. When “EPI gradients” were finally installed in 1995, we continued to utilize spiral methods because of the advantages that it apparently offered.

An obvious question is, “If Spiral is so meritorious, why haven’t the venders incorporated it into their products?” The answer is that the trajectory is highly demanding of the gradient subsystem, because two axes are simultaneously driving the readout at the slew-rate limit. Not only does the duty cycle need to be high, but the trajectory precision needed was initially difficult to achieve and corrections were required with some scanners (Ding et al., 1997). In addition, early receivers had limited acquisition bandwidth and buffer length for data storage. Moreover, the reconstruction required interpolation of the raw data (Jackson et al., 1991), which resulted in extra processing time, in an era when computers were not as powerful as Moore’s Law demonstrates today. These limitations caused artifacts or modest performance that discouraged widespread development. By now venders have developed Spiral methods as either products or works-in-progress, but their availability and full deployment remains limited.

Discussion

The development of fMRI acquisition methods has centered on the use of two rapid methods, EPI and Spiral. The later technique was developed initially at Stanford in response to hardware limitations that precluded the use of EPI; these limitations were mitigated by Spiral because the trajectory is efficient, has diminished sensitivity to motion and can acquire full brain imaging volumes with several-second TRs in multi-shot interleaving. Over the years since the early experiments, more powerful and higher field strength systems have become available, and the burgeoning use of fMRI in cognitive and clinical neuroscience has continued to drive the development of advanced fMRI methods using Spiral trajectories (Bammer et al., 2005; Guo and Song, 2003; Sha et al., 2003; Truong and Song, 2008). Other fMRI developments using spiral readouts include 3D (Hu and Glover, 2007, 2009; Lai and Glover, 1998; Yang et al., 1996; Yang et al., 1999), Hadamard sub-slice encoding (Glover and Chang, 2011), diffusion (Liu et al., 2004; Liu et al., 2005; Song et al., 2004), and perfusion (Hsu and Glover, 2006).

Implementation of Spiral methods, however, is more complex than EPI. High gradient fidelity or k-space corrections are needed to avoid artifacts. Moreover, interpolation in k-space is needed during reconstruction. Furthermore, while parallel imaging has been demonstrated using Spiral trajectories, it is clearly more compute intensive than Cartesian methods.

In some frontal brain regions, EPI provides greater signal recovery than Spiral (Figs. 3,5). That is because EPI’s trajectory samples the transverse magnetization before TE as well as after, thereby increasing the signal from short-T2* components. The acquisition of the Spiral-in image performs an analogous process in Spiral-in/out techniques, although adaptive combination allows an optimization of the sampling in each voxel. In addition, the Spiral-in/out method has an SNR advantage over EPI in magnetically uniform brain regions because of its overall longer acquisition time.

In summary, Spiral-in/out methods have advantages in terms of signal recovery in regions compromised by SFGs as well as in providing greater SNR in uniform regions, which translates to improved BOLD contrast. Variable density trajectories allow substantial undersampling without significant artifacts, allowing higher resolution acquisitions. The inherently circular sampling results in blurring rather than geometric distortion, and because the trajectory is shorter, the blurring tends to be less intrusive. However, these methods engender greater challenges in their implementation, especially in image reconstruction and demand on the gradient system. Nevertheless, these engineering challenges have been largely mitigated, and Spiral techniques provide a good choice for many fMRI applications.

Acknowledgments

The author gratefully acknowledges his many students and colleagues who, over nearly 20 years, have made substantial contributions to the methodology of fMRI. Funding support for this manuscript and new results was supplied from NIH grant P41-RR009784.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Ahn C, Kim J, Cho Z. High speed spiral scan echo planar NMR imaging. IEEE Trans Med Imaging MI-5. 1986:2–7. doi: 10.1109/TMI.1986.4307732. [DOI] [PubMed] [Google Scholar]
  2. Bammer R, Skare S, Newbould R, Liu C, Thijs V, Ropele S, Clayton DB, Krueger G, Moseley ME, Glover GH. Foundations of advanced magnetic resonance imaging. NeuroRx. 2005;2:167–196. doi: 10.1602/neurorx.2.2.167. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bandettini PA, Wong EC, Hinks RS, Tikofsky RS, Hyde JS. Time course EPI of human brain function during task activation. Magn Reson Med. 1992;25:390–397. doi: 10.1002/mrm.1910250220. [DOI] [PubMed] [Google Scholar]
  4. Bernstein MA, King KF, Zhou XJ. Handbook of MRI Pulse sequences. Elsevier Press; New York: 2004. [Google Scholar]
  5. Bornert P, Aldefeld B, Eggers H. Reversed spiral MR imaging. Magn Reson Med. 2000;44:479–484. doi: 10.1002/1522-2594(200009)44:3<479::aid-mrm20>3.0.co;2-2. [DOI] [PubMed] [Google Scholar]
  6. Chang C, Glover GH. Variable-density spiral-in/out functional magnetic resonance imaging. Magn Reson Med. 2010;65:1287–1296. doi: 10.1002/mrm.22722. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Cho ZH, Ro YM. Reduction of susceptibility artifact in gradient-echo imaging. Magn Reson Med. 1992;23:193–200. doi: 10.1002/mrm.1910230120. [DOI] [PubMed] [Google Scholar]
  8. Ding X, Tkach J, Ruggieri P, Perl J, Masaryk T. Improvement of spiral MRI with the measured k-space trajectory. J Magn Reson Imaging. 1997;7:938–940. doi: 10.1002/jmri.1880070525. [DOI] [PubMed] [Google Scholar]
  9. Duyn JH, Yang Y. Fast spiral magnetic resonance imaging with trapezoidal gradients. Journal of Magnetic Resonance. 1997;128:130–134. doi: 10.1006/jmre.1997.1237. [DOI] [PubMed] [Google Scholar]
  10. Glover G, Chang C. Hadamard-encoded sub-slice fMRI for reduced signal dropout. Magn Reson Imaging. 2011 doi: 10.1016/j.mri.2011.07.019. (in press) [DOI] [PubMed] [Google Scholar]
  11. Glover G, Lee A, Gabrieli J, Illes J, Newsome W, Rumelhart D, Shadlen M, Wandell B. Efficient skip-echo Hadamard sequence for brain activcation studies. JMRI; Society of Magnetic Resonance Imaging Annual 1993 Meeting; San Francisco. 1993. p. S37. [Google Scholar]
  12. Glover GH. Simple analytic spiral K-space algorithm. Magn Reson Med. 1999;42:412–415. doi: 10.1002/(sici)1522-2594(199908)42:2<412::aid-mrm25>3.0.co;2-u. [DOI] [PubMed] [Google Scholar]
  13. Glover GH, Lai S. Self-navigated spiral fMRI: interleaved versus single-shot. Magnetic Resonance in Medicine. 1998;39:361–368. doi: 10.1002/mrm.1910390305. [DOI] [PubMed] [Google Scholar]
  14. Glover GH, Law CS. Spiral-in/out BOLD fMRI for increased SNR and reduced susceptibility artifacts. Magn Reson Med. 2001;46:515–522. doi: 10.1002/mrm.1222. [DOI] [PubMed] [Google Scholar]
  15. Glover GH, Lee AT. Motion artifacts in fMRI: comparison of 2DFT with PR and spiral scan methods. Proc. 12th Annual Meeting, Society of Magnetic Resonance in Medcine; New York. 1993. p. 197. [DOI] [PubMed] [Google Scholar]
  16. Glover GH, Thomason ME. Improved combination of spiral-in/out images for BOLD fMRI. Magn Reson Med. 2004;51:863–868. doi: 10.1002/mrm.20016. [DOI] [PubMed] [Google Scholar]
  17. Guo H, Song AW. Single-shot spiral image acquisition with embedded z-shimming for susceptibility signal recovery. J Magn Reson Imaging. 2003;18:389–395. doi: 10.1002/jmri.10355. [DOI] [PubMed] [Google Scholar]
  18. Hsu JJ, Glover GH. Rapid MRI method for mapping the longitudinal relaxation time. J Magn Reson. 2006;181:98–106. doi: 10.1016/j.jmr.2006.03.014. [DOI] [PubMed] [Google Scholar]
  19. Hu Y, Glover GH. Three-dimensional spiral technique for high-resolution functional MRI. Magn Reson Med. 2007;58:947–951. doi: 10.1002/mrm.21328. [DOI] [PubMed] [Google Scholar]
  20. Hu Y, Glover GH. Increasing spatial coverage for high-resolution functional MRI. Magn Reson Med. 2009;61:716–722. doi: 10.1002/mrm.21898. [DOI] [PubMed] [Google Scholar]
  21. Jackson JI, Meyer CH, Nishimura DG, Macovski A. Selection of a convolution function for Fourier inversion using gridding. IEEE Trans Med Imaging. 1991;10:473–478. doi: 10.1109/42.97598. [DOI] [PubMed] [Google Scholar]
  22. Jezzard P, Clare S. Sources of distortion in functional MRI data. Human Brain Mapping. 1999;8:80–85. doi: 10.1002/(SICI)1097-0193(1999)8:2/3&#x0003c;80::AID-HBM2&#x0003e;3.0.CO;2-C. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Kim DH, Adalsteinsson E, Spielman DM. Simple analytic variable density spiral design. Magn Reson Med. 2003;50:214–219. doi: 10.1002/mrm.10493. [DOI] [PubMed] [Google Scholar]
  24. King KF, Foo TK, Crawford CR. Optimized gradient waveforms for spiral scanning. Magn Reson Med. 1995;34:156–160. doi: 10.1002/mrm.1910340205. [DOI] [PubMed] [Google Scholar]
  25. Krasnow B, Tamm L, Greicius MD, Yang TT, Glover GH, Reiss AL, Menon V. Comparison of fMRI activation at 3 and 1.5 T during perceptual, cognitive, and affective processing. Neuroimage. 2003;18:813–826. doi: 10.1016/s1053-8119(03)00002-8. [DOI] [PubMed] [Google Scholar]
  26. Kwong KK, Belliveau JW, Chesler DA, Goldberg IE, Weisskoff RM, Poncelet BP, Kennedy DN, Hoppel BE, Cohen MS, Turner R. Dynamic magnetic resonance imaging of human brain activity during primary sensory stimulation. Proc Natl Acad Sci U S A. 1992;89:5675–5679. doi: 10.1073/pnas.89.12.5675. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Lai S, Glover G. Three-Dimensional Spiral fMRI technique: a comparison with 2D spiral acquisition. Magn Reson Med. 1998;39:68–78. doi: 10.1002/mrm.1910390112. [DOI] [PubMed] [Google Scholar]
  28. Law CS, Liu C, Glover GH. Sliding-window sensitivity encoding (SENSE) calibration for reducing noise in functional MRI (fMRI) Magn Reson Med. 2008;60:1090–1103. doi: 10.1002/mrm.21701. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Lee AT, Glover GH. Discrimination of large venous vessels in time-course spiral Blood Oxygen Dependent Magnetic resonance functional neuroimaging. Magn Reson Med. 1995;33:745–754. doi: 10.1002/mrm.1910330602. [DOI] [PubMed] [Google Scholar]
  30. Liu C, Bammer R, Kim DH, Moseley ME. Self-navigated interleaved spiral (SNAILS): application to high-resolution diffusion tensor imaging. Magn Reson Med. 2004;52:1388–1396. doi: 10.1002/mrm.20288. [DOI] [PubMed] [Google Scholar]
  31. Liu CRB, Moseley ME. High resolution multi-shot SENSE DTI using self-navigated interleaved spirals (SNAILS). 13th annual meeting of ISMRM; Miami. 2005. p. 10. [Google Scholar]
  32. Mansfield P. Multi-planar image formation using NMR spin echoes. J Phys Chem C. 1977;10:L55–L58. [Google Scholar]
  33. Meyer CH, Hu BS, Nishimura DG, Macovski A. Fast spiral coronary artery imaging. Magn Reson Med. 1992;28:202–213. doi: 10.1002/mrm.1910280204. [DOI] [PubMed] [Google Scholar]
  34. Noll D, Cohen J, Meyer C, Schneider W. Spiral k-space MR imaging of cortical activation. JMRI. 1995;5(1):49–57. doi: 10.1002/jmri.1880050112. [DOI] [PubMed] [Google Scholar]
  35. Ogawa S, Lee TM, Kay AR, Tank DW. Brain magnetic resonance imaging with contrast dependent on blood oxygenation. Proc Natl Acad Sci U S A. 1990;87:9868–9872. doi: 10.1073/pnas.87.24.9868. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Preston AR, Thomason ME, Ochsner KN, Cooper JC, Glover GH. Comparison of spiral-in/out and spiral-out BOLD fMRI at 1.5 and 3 T. Neuroimage. 2004;21:291–301. doi: 10.1016/j.neuroimage.2003.09.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Pruessmann KP, Weiger M, Bornert P, Boesiger P. Advances in sensitivity encoding with arbitrary k-space trajectories. Magn Reson Med. 2001;46:638–651. doi: 10.1002/mrm.1241. [DOI] [PubMed] [Google Scholar]
  38. Sha L, Guo H, Song AW. An improved gridding method for spiral MRI using nonuniform fast Fourier transform. J Magn Reson. 2003;162:250–258. doi: 10.1016/s1090-7807(03)00107-1. [DOI] [PubMed] [Google Scholar]
  39. Song A, Emberger K, Michelich C, McCarthy G. FMRI signal source analysis using diffusion-weighted spiral-in acquisition. Conf Proc IEEE Eng Med Biol Soc. 2004;6:4417–4420. doi: 10.1109/IEMBS.2004.1404228. [DOI] [PubMed] [Google Scholar]
  40. Truong TK, Song AW. Single-shot dual-z-shimmed sensitivity-encoded spiral-in/out imaging for functional MRI with reduced susceptibility artifacts. Magn Reson Med. 2008;59:221–227. doi: 10.1002/mrm.21473. [DOI] [PubMed] [Google Scholar]
  41. Tsai CM, Nishimura DG. Reduced aliasing artifacts using variable-density k-space sampling trajectories. Magn Reson Med. 2000;43:452–458. doi: 10.1002/(sici)1522-2594(200003)43:3<452::aid-mrm18>3.0.co;2-b. [DOI] [PubMed] [Google Scholar]
  42. Weiger M, Pruessmann KP, Osterbauer R, Bornert P, Boesiger P, Jezzard P. Sensitivity-encoded single-shot spiral imaging for reduced susceptibility artifacts in BOLD fMRI. Magn Reson Med. 2002;48:860–866. doi: 10.1002/mrm.10286. [DOI] [PubMed] [Google Scholar]
  43. Yang Y, Glover GH, van Gelderen P, Mattay VS, Santha AK, Sexton RH, Ramsey NF, Moonen CT, Weinberger DR, Frank JA, Duyn JH. Fast 3D functional magnetic resonance imaging at 1.5 T with spiral acquisition. Magn Reson Med. 1996;36:620–626. doi: 10.1002/mrm.1910360418. [DOI] [PubMed] [Google Scholar]
  44. Yang Y, Glover GH, van Gelderen P, Patel AC, Mattay VS, Frank JA, Duyn JH. A comparison of fast MR scan techniques for cerebral activation studies at 1.5 Tesla. Magnetic Resonance in Medicine. 1998;39:61–67. doi: 10.1002/mrm.1910390111. [DOI] [PubMed] [Google Scholar]
  45. Yang Y, Wen H, Mattay VS, Balaban RS, Frank JA, Duyn JH. Comparison of 3D BOLD functional MRI with spiral acquisition at 1.5 and 4.0 T. Neuroimage. 1999;9:446–451. doi: 10.1006/nimg.1998.0422. [DOI] [PubMed] [Google Scholar]

RESOURCES