Active linking in evolutionary games

Abstract

In the traditional approach to evolutionary game theory, the individuals of a population meet each other at random, and they have no control over the frequency or duration of interactions. Here we remove these simplifying assumptions. We introduce a new model, where individuals differ in the rate at which they seek new interactions. Once a link between two individuals has formed, the productivity of this link is evaluated. Links can be broken off at different rates. In a limiting case, the linking dynamics introduces a simple transformation of the payoff matrix. We outline conditions for evolutionary stability. As a specific example, we study the interaction between cooperators and defectors. We find a simple relationship that characterizes those linking dynamics which allow natural selection to favor cooperation over defection.

1 Introduction

Game theoretic ideas were first introduced to biology by Hamilton (1964) and Trivers (1971), but the field of evolutionary game theory was founded by Maynard Smith and Price (1973) and Maynard Smith (1982). The mathematical foundation of evolutionary game dynamics is the replicator equation (Taylor and Jonker, 1978; Hofbauer et al., 1979; Zeeman, 1980), which is a system of ordinary differential equations describing how the relative abundances (frequencies) of strategies change over time as a consequence of frequency dependent selection. The payoff from the game is interpreted as biological fitness. Individuals reproduce proportional to their fitness. The expected payoff of an individual is a linear function of the frequencies of all strategies; the coefficients of this function are the entries of the payoff matrix. For detailed reviews of the replicator equation and other approaches to evolutionary game dynamics, see Fudenberg and Tirole (1991), Weibull (1995), Samuelson (1997), Cressman (2003), Hofbauer and Sigmund (1998, 2003), Gintis (2000) and Nowak and Sigmund (2004).

A typical assumption of evolutionary game dynamics is that individuals meet each other at random either in infinitely large, well-mixed populations (which is the standard approach), in finite populations (Nowak et al., 2004; Imhof and Nowak, 2006; Taylor et al., 2004; Fudenberg et al., 2006; Traulsen et al., 2006a,b), in spatially extended systems (Nowak and May, 1992; Nakamaru et al., 1998; Killingback and Doebeli, 1996; van Baalen and Rand, 1998; Irwin and Taylor, 2001; Hauert and Doebeli, 2004; Ifti et al., 2004; Nakamaru and Iwasa, 2005; Jansen and van Baalen, 2006) or on graphs (Lieberman et al., 2005; Santos and Pacheco, 2005; Santos et al., 2005, 2006a,b; Ohtsuki et al., 2006). Taylor and Nowak (2006) analyze a scenario where the interaction rate does depend on the strategies. In all these cases, however, individuals cannot influence how often they will interact and how long particular interactions will last. On the other hand, other studies have explored the possibility of individuals meeting assortatively, by means of selective partner choice (Eshel and Cavalli-Sforza, 1982; Noë and Hammerstein, 1994; Skyrms and Pemantle, 2000; Bala and Goyal, 2001; Ebel and Bornholdt, 2002; Eguiluz et al., 2005; Biely et al., 2005) or by means of volunteering participation (Peck and Feld-man, 1986; Hauert et al., 2002; Szabó and Hauert, 2002; Hauert and Szabó, 2003; Aktipis, 2004).

Let us therefore consider a simple model where the members of a population seek new interactions at different rates. Moreover, established interactions last for different amounts of time. The basic idea is that interactions which benefit both partners are more durable than interactions where one partner is exploited by the other. Also the optimum rate at which new interaction partners are being sought may differ for the different strategies of an evolutionary game.

In Section 2, we introduce the basic model, together with numerical examples. In Section 3 we analyze the evolutionary dynamics adopting, as a particular example, the favorite game in town: the competition between cooperators and defectors. Section 4 offers conclusions. Different limits associated with variable selection pressures and population sizes are discussed in the appendix.

2 The basic model of linking dynamics

Consider a game between two strategies, A and B. The total population size is constant and given by N. There are N_A individuals who use strategy A and N_B individuals who use strategy B. We have N = N_A + N_B.

An interaction between two players occurs if there is link between these players. Links are formed at certain rates and have specific life-times. Denote by X(t) the number of AA links at time t. Similarly, Y (t) and Z(t) denote the number of AB and BB links at time t. The maximum possible number of AA, AB and BB links is respectively given by

$$\begin{array}{l}{X}_m=N_A(N_A-1)/2\\ Y_m=N_A{N}_B\\ Z_m=N_B(N_B-1)/2\end{array}$$

Suppose A and B players have a propensity to form new links denoted by α_A and α_B, such that AA links are formed at a rate ${\alpha }_A^2$, AB links are formed at a rate α_Aα_B and BB links are formed at a rate ${\alpha }_B^2$. The death rates of AA, AB and BB links are given by β_AA, β_AB and β_BB, respectively. Thus, the average life-times of links are given by τ_AA = 1/β_AA, τ_AB = 1/β_AB and τ_BB = 1/β_BB.

Linking dynamics can be described by a system of three ordinary differential equations for the number of links

$$\begin{array}{l}\stackrel{.}{X}={\alpha }_A^2(X_m-X)-{\beta }_{AA}X\\ \stackrel{.}{Y}={\alpha }_A{\alpha }_B(Y_m-Y)-{\beta }_{AB}Y\\ \stackrel{.}{Z}={\alpha }_B^2(Z_m-Z)-{\beta }_{BB}Z\end{array}$$

In the steady state, the number of links of the three different types is given by

$$\begin{array}{l}{X}^{\ast }=X_m\frac{{\alpha }_A^2}{{\alpha }_A^2+{\beta }_{AA}}\\ Y^{\ast }=Y_m\frac{{\alpha }_A{\alpha }_B}{{\alpha }_A{\alpha }_B+{\beta }_{AB}}\\ Z^{\ast }=Z_m\frac{{\alpha }_B^2}{{\alpha }_A^2+{\beta }_{BB}}\end{array}$$

The fractions of active links in the steady state are given by

$$\begin{array}{l}{\phi }_{AA}=\frac{{\alpha }_A^2}{{\alpha }_A^2+{\beta }_{AA}}\\ {\phi }_{AB}=\frac{{\alpha }_A{\alpha }_B}{{\alpha }_A{\alpha }_B+{\beta }_{AB}}\\ {\phi }_{BB}=\frac{{\alpha }_B^2}{{\alpha }_B^2+{\beta }_{BB}}\end{array}$$

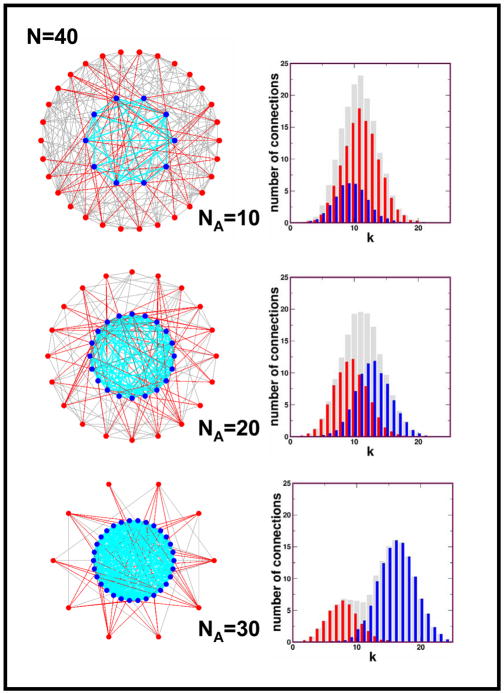
Examples of population structures attained under steady-state dynamics for three different combinations of (N_A, N_B) are shown in figure 1.

Figure 1.

Left panels Results of active linking dynamics for a population size of N = 40 individuals. A-players are located in the “inner-circle”, and are represented by blue circles. Links between A-players are drawn with solid cyan lines. B-players are represented by red-circles on the outer rim, and BB-links are drawn with solid grey lines. AB-links are drawn with solid red lines. Three different steady state scenarios are shown, corresponding to different number of N_A players: N_A = 10 (top), N_A = 20 (middle), and N_A = 30 (bottom). The resulting plots provide a snapshot of a configuration after each graph has attained a steady state condition. We started from complete graphs, links being created and destroyed at rates determined by the following parameter choice: α_D = 0.4, β_CC = 0.2, β_CD = 0.8 and β_DD = 0.3, which lead to α_C ≈ 0.56 by solving Eq. (9). The fractions of active links become φ_CC ≈ 0.61, φ_CD ≈ 0.22 and φ_DD ≈ 0.35, respectively. Right panels: Degree distributions associated with steady state configurations reached via active linking dynamics. Results shown correspond to an average over 1000 steady-state configurations for each value of N_A. The red-spikes show the degree-distribution associated with B-players only, the blue-spikes show the degree-distribution associated with A-players only, whereas the grey-spikes show the sum of the blue and red distributions. As N_A increases, the average connectivity associated with A-players increases, as expected, the relative proportion of AA and AB links being dictated by the parameter choice. For the parameters quoted, and for a prisoner’s dilemma game with b = 2 and c = 1 (cf. Eq. (6)), the rescaled payoff matrix reads a′ = 0.60, b′ = −0.22, c′ = 0.44, d′ = 0. In other words, active linking dynamics changes the game from a prisoner’s dilemma into a coordination game which favours cooperation whenever N_A/N > 58%.

Let us now consider a game between A and B given by the payoff matrix

$$\left(\begin{array}{ccc}& A& B\\ A& a& b\\ B& c& d\end{array}\right)$$

where we assume that entries are positive. At the steady state of the linking dynamics, the average fitness of A and B individuals is respectively given by

$$f_A=f_0+a{\phi }_{AA}(N_A-1)+b{\phi }_{AB}{N}_B$$ (1)

and

$$f_B=f_0+c{\phi }_{AB}{N}_A+d{\phi }_{BB}(N_B-1).$$ (2)

Here f₀ denotes the baseline fitness that is independent of the game under consideration. Eqs. (1) and (2) suggest that the linking dynamics introduces a simple transformation of the payoff matrix. We can study standard evolutionary game dynamics using the modified payoff matrix

$$\left(\begin{array}{ccc}& A& B\\ A& a{\phi }_{AA}& b{\phi }_{AB}\\ B& c{\phi }_{AB}& d{\phi }_{BB}\end{array}\right)=\left(\begin{array}{ccc}& A& B\\ A& a^{\prime }& b^{\prime }\\ B& c^{\prime }& d^{\prime }\end{array}\right)$$ (3)

3 Evolutionary dynamics

Let us now study how the frequencies of strategies A and B change under evolutionary dynamics. We assume that the linking dynamics occurs on a fast time scale (τ_a). On a slower time scale (τ_e), evolutionary updating occurs. Reproduction can be genetic or cultural. When τ_a ≪ τ_e, the steady state of the linking dynamics determines the average payoff and fitness of individuals. Moreover, since we are dealing with a finite population size, we may consider different update processes, such as a frequency dependent Moran process (Nowak et al., 2004; Taylor et al., 2004) or a frequency dependent Wright-Fisher process (Imhof and Nowak, 2006) (see also the appendix). In the first case, at each time step, an individual is chosen for reproduction proportional to fitness; the offspring replaces a randomly chosen neighbor. In the second case, each individual produces a number of offspring proportional to fitness; the next generation is sampled from this pool of offspring. In both cases, the total population size is constant and given by N. We can calculate the fixation probabilities of strategies A and B. Let ρ_A denote the probability that a single A player introduced into a population of B players will generate a lineage that takes over the entire population. For neutral selection, a = b = c = d, we have ρ_A = ρ_B = 1/N. In the limit of weak selection (large baseline fitness, f₀) we find that ρ_A > 1/N if

$$a^{\prime }+2b^{\prime }>c^{\prime }+2d^{\prime }.$$ (4)

This condition is known as the 1/3-rule (Nowak et al., 2004; Imhof and Nowak, 2006); if the fitness of A is greater than the fitness of B at a frequency of x_A = 1/3 then the fixation probability of A is greater than 1/N. This relationship also holds for modified stochastic processes that use pairwise comparison rules for updating (see Traulsen et al. (2006a) and appendix) and for games on graphs (Ohtsuki and Nowak, 2006a,b).

Let us introduce the quantity

$$\chi =a^{\prime }+2b^{\prime }-c^{\prime }-2d^{\prime }=a{\phi }_{AA}+(2b-c){\phi }_{AB}-2d{\phi }_{BB}.$$ (5)

If χ > 0 then condition (4) is fulfilled and a single mutant is advantageous, that is, ρ_A > 1/N for weak selection. In terms of the α and β parameters describing the birth and death rates of links, we obtain

$$\chi =a\frac{{\alpha }_A^2}{{\alpha }_A^2+{\beta }_{AA}}+(2b-c)\frac{{\alpha }_A{\alpha }_B}{{\alpha }_A{\alpha }_B+{\beta }_{AB}}-2d\frac{{\alpha }_B^2}{{\alpha }_B^2+{\beta }_{BB}}.$$

For non-negative payoff values we observe that χ is always a decreasing function of β_AA and an increasing function of β_BB. For maximizing the evolutionary success of strategy A it is best that AA links are long-lived and BB links are short-lived. If 2b > c then χ is a decreasing function of β_AB, which means long-lived AB links favor A. If 2b < c then short-lived AB links favor A. It is possible to find payoff values, where χ exhibits an intermediate extremum (maximum or minimum) as function of α_A or α_B. This leads to the interesting situation where the chances of A are maximized at intermediate rates of forming new links (see below).

For large, well-mixed populations (see appendix), the relative ordering of the payoff-matrix elements is important in determining the dynamical behaviour of the system. Whenever c > a > d > b the system evolves into the absorbing state characterized by 100 % B-players. For c > a > b > d the system exhibits an interior stable fixed-point at a fraction of A-players given by N_A/N ≈ (b − d)/(b + c − a −s d), whereas this point becomes an unstable fixed point whenever a > c > b > d. The rescaling of the payoff matrix induced by active linking dynamics may lead to a radically different dynamical evolution of the system, since it acts to change the ranking of the elements in the payoff matrix, and hence the effective nature of the game under study.

3.1 Evolution of cooperation

As a specific example, we want to investigate the interaction between cooperators and defectors (Axelrod and Hamilton, 1981; Nowak and Sigmund, 1992, 1993; Doebeli et al., 2004). A cooperator, C, pays a cost c for every link, and the partner of this link receives a benefit b. Defectors, D, pay no cost and distribute no benefits. We assume b > c otherwise cooperation has no net benefit. Therefore, the payoff matrix becomes

$$\left(\begin{array}{ccc}& A& B\\ A& a& b\\ B& c& d\end{array}\right)\to \left(\begin{array}{ccc}& C& D\\ C& b-c& -c\\ D& b& 0\end{array}\right)$$ (6)

Cooperators and defectors seek to establish links at rates α_C and α_D, respectively. The death rates of links are given by β_CC, β_CD and β_DD. From Eq. (5) we have

$$\chi =(b-c){\phi }_{CC}-(b+2c){\phi }_{CD}.$$

If χ > 0 then the fixation probability of a cooperator, ρ_C, is greater than 1/N. The condition χ > 0 can be written as

$$\frac{b}{c}>1+3\frac{{\phi }_{CD}}{{\phi }_{CC}-{\phi }_{CD}}.$$ (7)

If the frequency of CC links exceeds the frequency of CD links, cooperators can be favored given that the benefit to cost ratio fulfills inequality (7). We can also introduce a parameter, s > 0, which quantifies how much more frequent CC links are compared to CD links. Let

$${\phi }_{CC}={\phi }_{CD}(1+s).$$

We obtain the simple relationship

$$\frac{b}{c}>1+\frac{3}{s}.$$

In terms of the birth and death rates of links, the crucial condition becomes

$$\frac{b}{c}>1+3\frac{{\alpha }_D({\alpha }_C^2+{\beta }_{CC})}{{\alpha }_C{\beta }_{CD}-{\alpha }_D{\beta }_{CC}}.$$ (8)

The critical benefit-to-cost ratio is a decreasing function of β_CD and an increasing function of α_D and β_CC. Obviously, the evolution of cooperation is easier if CC links are long-lived while CD links are short-lived. Furthermore, if defectors are slow to form new links, then cooperators have better chances. More interestingly, the critical benefit-to-cost ratio assumes a minimum value for an intermediate value of α_C. Thus, there is an optimum rate at which cooperators should try to establish new links. This optimum is given by

$${\widehat{\alpha }}_C={\alpha }_D\frac{{\beta }_{CC}}{{\beta }_{CD}}(1+\sqrt{1+\frac{{\beta }_{CD}^2}{{\alpha }_D^2{\beta }_{CC}}}).$$ (9)

We note that inequality (8) also implies that the fixation probability of defectors, ρ_D, is less than 1/N and that a single defector in a large population of cooperators has a lower fitness than the resident cooperators. Thus, inequality (8) is the crucial condition for ‘active linking’ to facilitate the natural selection of cooperation. For the parameters used in connection with figure 1 (note that α_C was obtained from Eq. (9)), and for a prisoner’s dilemma game in which b = 2 and c = 1, the primed payoff matrix leads to a coordination game favouring cooperation whenever N_A > 58% (cf. Fig. 1). Hence, fast active linking dynamics paves the way for cooperation to thrive.

Up to now, we have assumed that the parameters α and β remain constant throughout evolution.

Here, we discuss the case that also these parameters are under selection. If different cooperators have different values of α_C and β_CC, those that have the longest interactions with other cooperators will be most successful and selection decreases β_CC. On the other hand, successful cooperators end their interaction with defectors fast, leading to selection for high values of β_CD. Among the defectors, selection will favor those that have small values of β_CD and a high propensity to form new links, i.e., high α_D.

A further possibility including such a selection mechanism is to introduce a payoff dependent active linking dynamics. For instance, we may associate the propensity to form new links, as well as the lifetime of different types of links with the productivity of those links assessed in terms of entries in the payoff-matrix. Here, we explore the case in which cooperators and defectors share the same propensity to form new links α_C = α_D = α, whereas the lifetimes of different types of links are directly related to the average profit expected from that link.

Assuming that

$$\begin{array}{l}{\tau }_{AA}=\kappa a\\ {\tau }_{AB}=\frac{\kappa }{2}(b+c)\\ {\tau }_{BB}=\kappa d\end{array}$$

then we may write, for the prisoner’s dilemma, τ_CC = 2τ_CD and τ_DD = 0, as a result of the entries in the payoff matrix. Eq. (8) now reads

$$\frac{b}{c}<1+3{\alpha }^2{\tau }_{CD}.$$

Clearly, the larger the lifetime of the non-assortative CD-links, the more difficult it gets for cooperators to thrive under active linking dynamics.

Note finally, that whenever φ_AA = φ_AB = φ_BB, then the rescaling of the payoff matrix amounts to multiply all terms by a positive constant. Such a rescaling of the payoff matrix will not change the nature of dilemma at stake, but it might lead to a different intensity of selection, depending on the update mechanism.

4 Conclusions

By equipping individuals with the capacity to control the nature and duration of their interactions with others, we introduce a linking dynamics which, in the limit when it takes place faster than evolutionary dynamics, leads to simple transformation of the payoff matrix. The rescaling may effectively lead to an evolutionary dynamics involving a different type of game, now played in a finite, well-mixed population. This equivalence allows one to utilize many of the methods recently developed for finite, well-mixed populations, employing them in this a-priori more complicated setting. In particular, one can write down the conditions which ultimately allow natural selection to favor cooperation over defection.

5 Appendix

5.1 The Pairwise comparison rule, τ_a ≪ τ_e

Assuming τ_a ≪ τ_e, links will have time to readjust before a new strategy update takes place. We shall adopt here the paiwrise comparison rule, which has been recently shown to provide a unifying framework to discuss strategy dynamics at all levels of selection, from weak selection to imitation dynamics (Traulsen et al., 2006a). According to this rule, two individuals from the population, A and B are randomly chosen for update. The strategy of A will replace that of B with a probability given by

$$p=\frac{1}{1+e^{-\beta (\pi (A)-\pi (B))}}$$

whereas the reverse will happen with probability 1 − p. We can calculate the fixa-tion probabilities of strategies A and B. Let ρ_A(k) denote the probability that k A players introduced into a population of B players will generate a lineage that takes over the entire population. For the pairwise comparison rule we find (Traulsen et al., 2006a)

$${\rho }_A(k)=\frac{\text{erf}[{\xi }_k]-\text{erf}[{\xi }_0]}{\text{erf}[{\xi }_N]-\text{erf}[{\xi }_0]}$$ (10)

where $\text{erf}(x)=\frac{2}{\sqrt{\pi }}{\int }_0^{x}dy{e}^{-y^2}$ is the error function, ${\xi }_k=\sqrt{\frac{\beta }{u}}(ku+v)$, 2u = a′ − b′ − c′ + d′ and 2v = −a′ + b′ N − c′ N + c′, which simplifies to

$${\rho }_A(k)=\frac{e^{-2\beta vk}-1}{e^{-2\beta vN}-1}.$$

whenever u = 0. The quantity β, which in physics corresponds to an inverse temperature, here controls the intensity of selection, namely, β → ∞ leads to cultural update via imitation dynamics, whereas in the limit β ≪ 1 one recovers the weak selection limit of the frequency dependent Moran process (Nowak et al., 2004) discussed below.

5.2 Large population size, τ_a ≪ τ_e

Given that the number of A players in the population is k, one instance of the pairwise comparison process introduced above leads to either the maintenance of the total fraction k/N on the population, its increase to (k + 1)/N or its decrease to (k − 1)/N. The transition probabilities can be written as (Traulsen et al., 2006a)

$$T^{\pm }(k)=\frac{k}{N}\frac{N-k}{N}\frac{1}{1+e^{\mp \beta ({\pi }_A(k)-{\pi }_B(k))}}$$

When the population size N is large, this process can be approximated by a Langevin equation for the fraction x = k/N of A players in the population (Traulsen et al., 2005)

$$\stackrel{.}{x}=a(x)+b(x)\zeta$$ (11)

with a drift term a(x) = T⁺(k)−T⁻ (k), a diffusion term $b(x)=\sqrt{(T^{+}(k)+T^{-}(k))/N}$ and where ζ is uncorrelated Gaussian noise with unit variance. Since, for the pairwise comparison rule, and for large N,

$$a(x)=x(1-x)tanh\left(\frac{\beta }{2}[{\pi }_A(x)-{\pi }_B(x)]\right)$$

and

$$b(x)=\sqrt{\frac{x(1-x)}{N}}$$

we obtain the following differential equation describing the evolution of the fraction of A players under active linking dynamics at all levels of selection intensity

$$\stackrel{.}{x}=x(1-x)tanh\left(\frac{\beta }{2}[{\pi }_A(x)-{\pi }_B(x)]\right)+\sqrt{\frac{x(1-x)}{N}}\zeta$$

5.3 Infinite population size and weak selection, τ_a ≪ τ_e

When N → ∞ the second term in Eq. (11) vanishes as $1/\sqrt{N}$. On the other hand, for weak selection (β ≪ 1) tanh(x) = x + O(x³) and we encounter again the replicator dynamics of infinite, well-mixed populations

$$\stackrel{.}{x}=\frac{\beta }{2}x(1-x)({\pi }_A(x)-{\pi }_B(x))$$

except for a rescaling of time which, intuitively, scales with the intensity of selection β. Notice, however, that now the payoffs are to be evaluated with the rescaled payoff matrix resulting from the active-linking dynamics introduced here.

5.4 The limit τ_a ≫ τ_e

Whenever τ_a ≫ τ_e the active-linking plays no role, and strategy evolution will proceed on a static graph. In other words, the graph topology at the start of the evolutionary process, together with the initial number of A players will ultimately dictate the most likely fate of evolution. Assuming we start from a well-mixed population of size N (complete graph), in which we have k A players at start, Eq. (10) provides us with the exact expression for the fixation probability of strategy A. Notice, however, that unlike the previous limit, now the coefficients are to be computed making use of the original (unprimed) payoff matrix elements.

In the limit of weak selection, we recover again the 1/3 rule for the original (unprimed) payoff matrix. Whenever the starting graph is not complete, there is little we can say for arbitratry intensity of selection. However, for weak selection and large population sizes, the following limit applies.

5.5 Infinite population size and weak selection τ_a ≫ τ_e

In the limit of infinite population and weak selection, describable by a graph in which, on average, every vertex has K links, the strategy dynamics will again converge to a replicator like equation with an additional term reflecting the local structure of the population (Ohtsuki and Nowak, 2006b)

$$\stackrel{.}{x}=x({\pi }_A(x)+g_A-\langle \pi \rangle )$$

where, as usual, π_A(x) = ax + b(1 − x), π_B(x) = cx + d(1 − x) and 〈π〉 = xπ_A(x) + (1 − x)π_B(x). The local competition terms g_i are given by g_i = Σ_j x_jb_ij (i, j = A, B), where the matrix b_ij reads (for the pairwise comparison rule)

$$\left(\begin{array}{ccc}& A& B\\ A& 0& \eta \\ B& -\eta & 0\end{array}\right)$$

with η = (a + b − c − d)/(K − 2) (Ohtsuki and Nowak, 2006b). In other words, under weak selection strategy evolution will depend on the graph topology: For large, well mixed populations the conventional replicator dynamics is expected to apply, whereas for graphs with an average number of links per vertex K, a modified replicator dynamics will dictate strategy evolution.