Global Structure of a Three-Way Junction in a Phi29 Packaging RNA Dimer Determined Using Site-Directed Spin Labeling

Abstract

The condensation of bacteriophage phi29 genomic DNA into its preformed procapsid requires the DNA packaging motor, which is the strongest known biological motor. The packaging motor is an intricate ring-shaped protein/ RNA complex, and its function requires an RNA component called packaging RNA (pRNA). Current structural information on pRNA is limited, which hinders studies of motor function. Here, we used site-directed spin labeling to map the conformation of a pRNA three-way junction that bridges binding sites for the motor ATPase and the procapsid. The studies were carried out on a pRNA dimer, which is the simplest ring-shaped pRNA complex and serves as a functional intermediate during motor assembly. Using a nucleotide-independent labeling scheme, stable nitroxide radicals were attached to eight specific pRNA sites without perturbing RNA folding and dimer formation, and a total of 17 internitroxide distances spanning the three-way junction were measured using Double Electron–Electron Resonance spectroscopy. The measured distances, together with steric chemical constraints, were used to select 3662 viable three-way junction models from a pool of 65 billion. The results reveal a similar conformation among the viable models, with two of the helices (H_T and H_L) adopting an acute bend. This is in contrast to a recently reported pRNA tetramer crystal structure, in which H_T and H_L stack onto each other linearly. The studies establish a new method for mapping global structures of complex RNA molecules, and provide information on pRNA conformation that aids investigations of phi29 packaging motor and developments of pRNA-based nanomedicine and nanomaterial.

INTRODUCTION

RNA participates in all cellular processes associated with the maintenance and expression of genetic information, and knowledge of molecular basis of RNA function is essential for understanding basic biology.¹ A key in understanding RNA function is information on its three-dimensional conformations, which can be highly complex as demonstrated by the rapidly growing number of high-resolution structures of RNA and RNA/protein complex.^2,3 To advance our ability to derive RNA structural information under physiological conditions, here we present work on mapping the global structure of an RNA junction using the method of site-directed spin labeling (SDSL).⁴ In SDSL, chemically stable nitroxide radicals (i.e., the spin labels) are covalently attached at specific sites of a macromolecule. The behavior of the nitroxide is monitored using electron paramagnetic resonance (EPR) spectroscopy, from which local information on the macromolecule is obtained. SDSL can be applied to study structure and dynamics of large biomolecular complexes under physiological conditions, and has been demonstrated to provide unique information on proteins^5–7 and nucleic acids.^8–10 One of the EPR observables used in SDSL studies is the distance between a pair of nitroxides, which can be obtained by measuring electron spin dipolar coupling using either continuous-wave (cw-) EPR or more recently, pulsed EPR techniques.^8,11 In particular, pulsed Double Electron–Electron Resonance (DEER or PELDOR)^12–14 has been developed and successfully applied to measure distance between 20 and 80 Å in biological systems.¹⁵ In protein studies, many examples have been reported in which the DEER measured distances enable monitoring of conformational change^16–22 and direct assessment of protein structure.^23–30 In addition, DEER measured distances have been used to monitor RNA conformational changes upon ligand binding.^31–33

Here, we report the use of multiple DEER distances for de novo mapping of the global structure (i.e., the overall shape) of a three-way junction (3-wj) in a noncoding RNA, the packaging RNA³⁴ (pRNA, also known as prohead RNA) in the DNA packaging motor of bacteriophage phi29. Phi29 packaging motor utilizes chemical energy derived from hydrolyzing host ATP to condense its linear double-stranded DNA genome into a preformed capsid.^35,36 It is reported to be the strongest bio-molecular motor, capable of generating forces that are 2- to 8-fold higher than myosin and RNA polymerase.³⁷ Interestingly, the phi29 packaging motor is a protein/RNA complex, with the RNA component (pRNA) being essential for in vivo and in vitro motor function.³⁴ Studies have shown that pRNA forms an oligomeric ring within the motor, with pRNA monomers interacting with each other through intermolecular base-pairing between two loop regions (i.e., the R- and L-loop, Figure 1A) in an Mg²⁺ dependent fashion.^35,36,38 The exact composition of the pRNA ring has been a subject of debate,^38–43 although it is clear that motor functions are preserved with pRNA mutants in which the R- and L-loops maintain intermolecular base-pairing.^38,39 As pRNA significantly stimulates motor ATPase (i.e., gp16) activity,^44,45 information on pRNA structure and function is an integral part of understanding the mechanism of the phi29 motor. Furthermore, pRNA-based constructs, such as dimers, trimers, and their variants, have been used in developing novel artificial nanostructures for material and therapeutic applications.⁴⁶ Understanding of pRNA conformations will be highly beneficial for these efforts.

Figure 1.

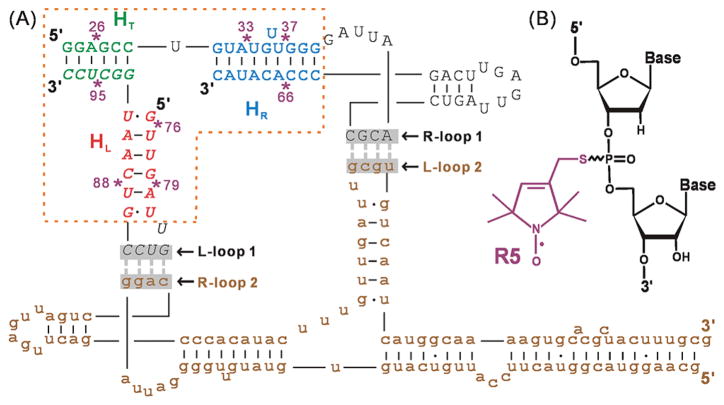
(A) Dimer construct used for SDSL mapping of pRNA 3-wj global structure (see also Supporting Information Figure S1). Upper-case letters show the two respective RNA strands constituting br_B/a′, and brown lower-case letters show the unlabeled full-length monomer A/b′. The 3-wj is indicated by the dotted box, with the H_T (green), H_R (blue), and H_L (red) helices marked. Spin labeling sites are indicated by “*” and numbered according to the corresponding full-length pRNA sites. The two sets of interacting R- and L-loops are marked and shadowed. (B) The R5 spin label. Note that following previously validated distance measurement protocols,^51,70,71 all data reported here were acquired without separating the R_p and S_p phosphorothioate diastereomers present at each attachment site.

Currently available information on the conformation of pRNA includes a model of a dimer that was initially constructed using chemical probing and photo-cross-linking data⁴⁷ and then further refined using inter-pRNA distances measured by single-molecule fluorescence resonance energy transfer;⁴⁸ an NMR structure of a hairpin subdomain within a pRNA monomer;⁴⁹ and a 3.5 Å crystal structure of a pRNA tetramer.⁴³ However, many questions remain unresolved. For example, the dimer model⁴⁸ and the tetramer crystal structure⁴³ show differences in the conformation of the junction defined by three pRNA helices designated as H_T, H_R, and H_L (Figure 1A, Supporting Information Figure S1). This junction bridges binding sites for the motor ATPase (binding to the extended H_T) and the procapsid (binding to H_R/H_L),^35,36 and its conformation is of great interest in elucidating the motor mechanism. However, in the dimer studies, there is no reported distance measurement spanning this 3-wj within the monomeric unit;⁴⁸ consequently, this junction conformation within a pRNA dimer remains to be determined.

In this work, using a nucleotide-independent nitroxide labeling scheme^50,51 and DEER spectroscopy, 17 distances spanning the 3-wj were measured in a previously reported functional pRNA dimer. Modeling based on steric and distance constraints was carried out to reveal the spatial arrangement of the RNA helices, which defines the 3-wj global structure. The results reveal an alternative 3-wj fold in pRNA dimer as compared to that reported in the pRNA tetramer crystal structure,⁴³ thus demonstrating versatility in pRNA conformation. These studies establish a new method for mapping global structures of complex RNA molecules, and provide information that may advance our understanding of phi29 packaging motor function as well as facilitate pRNA-based nanomedicine and nanomaterial developments.

MATERIALS AND METHODS

Synthesis of RNAs

The two pRNA constructs used in this work are designated as A/b′ and br_B/a′ (Figure 1A and Supporting Information Figure S1). The 118-nucleotide (nt) A/b′ was generated by in vitro run-off transcription using a linearized double-stranded DNA template that contains a T7 RNA polymerase promoter followed by the RNA sequence,⁵² with the 5′ terminus of the DNA antisense strand mutated to 5′-GCGC-3′ to allow linearization of the plasmid using the Hinp1I restriction endonuclease (cleaving 5′…G/CGC…3′, New England Biolabs, Inc.). The transcribed RNA was purified by denaturing polyacrylamide gel electrophoresis (PAGE), then quantified and stored as previously described.⁵²

The br_B/a′ construct contains two noncovalently linked RNA strands designated as a′_23 and B_49 (Supporting Information Figure S1C), with nucleotides numbered according to the corresponding 118-nt RNA. The 23-nt a′_23 RNA was generated by solid-phase chemical synthesis. The 49-nt B_49 RNA was generated by in vitro transcription using single-stranded DNA templates⁵² or by solid-phase chemical synthesis. All chemically synthesized oligonucleotides were purchased from Integrated DNA Technologies, Inc. (Coralville, IA).

Spin Labeling of RNAs

One or two nitroxide spin labels, 1-oxyl-2,2,5,5-tetramethylpyrroline (R5), were attached to either a′_23 or B_49 using the phosphorothioate labeling scheme.^50,51 Specifically, phosphorothioate modifications were introduced at specific sites within a′_23 or B_49 during solid-phase chemical synthesis. A R5 precursor, 1-oxyl-2,2,5,5-tetramethyl-Δ3-methane-sulfonyloxy-methylpyrroline (Toronto Research Chemicals, North York, Canada) was activated and then immediately reacted with the crude oligonucleotides.⁵¹ Each labeling site was designated by the corresponding nucleotide number. Labeled a′_23 was purified using HPLC.⁵¹ Labeled B_49 was purified by denaturing PAGE, eluted in water, and recovered by ethanol precipitation. Temperature during gel purification and elution was controlled at 4 °C to minimize label detachment from RNA. RNA concentrations were quantified by UV absorbance at 260 nm using extinction coefficients of 227 000 and 488 000 M⁻¹ cm⁻¹ for a′_23 and B_49, respectively. The degree of nitroxide labeling was determined using a spin-counting procedure,⁵³ and was found to be ~100% for all samples used in pulsed EPR measurements. Labeled RNAs were resuspended in deionized water for immediate use, or stored at −80 °C.

Biochemical Characterization of Spin Labeled pRNA Dimers

The dissociation constant (K_d) between³²P labeled A/b′ RNA (*A/b′) and a partner RNA (unmodified br_B/a′, or br_B/a′ with spin label(s) attached) was measured in 50 mM Tris-HCl (pH 7.6) and 3 mM MgCl₂. The ratio of a′_23 and B_49 was kept at 1:1. In each measurement, proper amount of individual RNA strands (e.g., *A/b′, a′_23, and B_49 for forming a dimer of A/b′||br_B/a′) were mixed, heated at 95 °C for 1 min, then cooled down at room temperature for 2 min. Proper amount of Tris-HCl (pH 7.6) and MgCl₂ were then added to achieve the desired buffer concentrations, and the mixture was incubated at 17 °C for 1 h. Monomer and dimer were resolved using a native gel, which was run at ~17 °C with 50 mM Tris-HCl (pH 7.6) and 3 mM MgCl₂ present in the electrophoresis solution. Gels were then dried and quantified using a Personal Molecular Imager (Bio-Rad, Inc.). K_d values were obtained by fitting the dependence of the fraction of dimer (α) versus partner RNA concentrations ([partner RNA]) to the following equation using the program Kaleidagraph (Synergy, PA):

$$\alpha =\frac{[\text{partner}\text{RNA}]}{[\text{partner}\text{RNA}]+K_{\text{d}}}$$ (1)

Preparation of Spin Labeled pRNA Dimers for EPR Measurements

Spin labeled dimers of A/b′||br_B/a′ were assembled using A/b′, a′_23, and B_49, with R5 attached at specific sites within br_B/a′. The ratio of A/b′, a′_23, and B_49 was kept at 1.2:1:1. For each EPR sample, A/b′, a′_23, and B_49 were mixed together and lyophilized. The sample was resuspended in a glycerol solution, incubated at 95 °C for 1 min, and then cooled down at room temperature for 2 min. Proper amount of Tris-HCl (pH 7.6) and MgCl₂ was added, and each sample was then incubated at 17 °C for 1 h before transferred to an EPR capillary (see below). The final EPR sample contained 50 mM Tris-HCl (pH 7.6), 3 mM MgCl₂, 60 μM R5 labeled br_B/a′, 72 μM A/b′, and 50% (v/v) glycerol. Control experiments indicated that this assembling procedure affords the best balance between the desired pRNA dimer and the undesired monomer and higher oligomers (see Results and Supporting Information Figure S2). Assembling monomeric br_B/a′ from a′_23 and B_49 prior to dimer formation has no effect on measured dimer K_d and inter-R5 distances.

EPR Spectroscopy

DEER spectroscopy was carried out to measure inter-R5 distances. The 20-μL samples were placed in a round quartz capillary (2.0 mm i.d., 2.4 mm o.d., Vitrocom, Inc., Mountain Lakes, NJ) sealed at one end, and were flash-frozen in liquid nitrogen. Measurements were carried out at 80 K on a Bruker ELEXSYS E580 X-band spectrometer with an ER4118-MS3-EN resonator. A dead-time free four-pulse scheme¹⁴ was used, with the pump pulse frequency set at the center of the nitroxide spectrum and the observer frequency being approximately 70 MHz higher. The observer π pulse was 32 ns. The pump π pulse was optimized using a nutation experiment⁵⁴ and was usually set at 24 or 28 ns. The video bandwidth was fixed at 200 MHz. The shot repetition time was set at 714 μs based on a measured T₁ of approximately 560 μs.⁵⁵ Accumulation time in each measurement ranged from 3 to 16 h with 1024 shots per point. Interspin distance distributions were computed from the resulting dipolar evolution data using Defit 3.7.^21,55,56 In the analyses, background in the dipolar evolution data was corrected by fitting an exponential decay corresponding to a homogeneous 3-dimentional distribution of electron spin to the last half of the data. The analyses yielded two key parameters that describe the interspin distance distribution: the most probable distance (r₀) and the width of the distribution (characterized by the half-width at the half-maximum, w_r). On the basis of repeated measurements, errors in measured r₀ were less than 7% of the reported values.

Continuous-wave EPR spectroscopy was carried out on a X-band Bruker EMX spectrometer as previously reported.⁵³

Constructing RNA Modules for 3-wj Global Structure Modeling

To model the pRNA 3-wj, RNA helices corresponding to the respective sequences of H_T, H_R, and H_L (Figure 1A) were built using standard A-form geometry.^57,58 Note that the U₃₅ bulge in the H_R helix was modeled using a homologous U-bulge structure in the 16S rRNA.⁵⁹ This bulge is known to be dispensable,^43,60,61 and its inclusion in the H_R module minimally affects the overall helix geometry and the subsequent interhelical distance calculations. For each helix, the previously developed NASNOX program^51,62 was used to obtain the ensemble of sterically allowed R5 conformers at each nucleotide. The average coordinates of the R5 nitrogen atoms for each ensemble were computed and recorded as a pseudo atom (designated as “NOX”) associated with the corresponding nucleotide in the pdb file. In addition, the helical axis was generated using the program CURVES⁶³ and recorded within the pdb file. In subsequent transformations of each helix, all associated NOX pseudo atoms and the helical axes were subjected to the same operations as that of the other atoms. Distances between pairs of NOX pseudo atoms were used to represent the expected inter-R5 distances between the corresponding nucleotides in a given model (see below).

Grid Search for Modeling of 3-wj Global Structure

Models of 3-wj were generated using the NOX-modified helices, with H_T fixed while H_R and H_L independently translated and rotated as rigid bodies. A translation operation was implemented by adding an offset (Δx, Δy, Δz) to the coordinate of each atom within the respective helix. Each rotation corresponded to transformations about a set of Euler angles (α,β,γ) defined with respect to the same external reference frame, and was achieved via matrix multiplication operations. In-house programs written in MATLAB were generated to systematically vary the 12 parameters corresponding to the independent transformation of H_R and H_L, as well as to assess each resulting model.

The grid search starts from a hand-built initial model that does not conform to the DEER measured distances but satisfies the following two sets of constraints. The first are steric constraints, which specify that the distance between any two atoms must be greater than the sum of the corresponding radii (i.e., no overlapping atoms). The second are connection constraints (affecting how far apart the helices are positioned), which are chosen based on the number of nucleotides spanning between two helices in the wild-type pRNA: H_T and H_L are separated by zero nucleotide, and thus, the distance from residue 91 O3′ to residue 92 C5′ was set as 0–4.5 Å (3 covalent bonds); H_T and H_R are separated by one nucleotide (U₂₉), thus, the distance from residue 28 O3′ to residue 30 C5′ was set at 0–10 Å; and H_R and H_L are separated by three nucleotides (U₇₂U₇₃U₇₄), thus, the distance from residue 71 O3′ to residue 75 C5′ was set at 0–20 Å. From the initial model, rotation parameters were individually varied from 0° to 360° with a step-size of 30°, and translation parameters were varied from −15 Å to 15 Å with a step-size of 5 Å. The resulting models that satisfy both steric and connection constraints were recorded and designated as the “sterically-allowed” ensemble.

The sterically allowable ensemble was then assessed according to the DEER measured distances. For each model, an RMSD_deer parameter was computed, which is defined as the root-mean-square-deviation (RMSD_deer) between DEER measured inter-R5 distances (r^deer) and corresponding inter-NOX distances (r^model) (eq 2):

$${\text{RMSD}}_{\text{deer}}^j=\sqrt{\frac{1}{N}\sum _i{(r^{\text{deer}}-r^{\text{model}-j})}_i^2}$$ (2)

For a given model, the RMSD_deer values differ by less than 0.1 Å when r^model was computed using the NOX pseudo atoms (see above) or calculated from the entire R5 ensembles obtained using NASNOX, with the latter being much more demanding on computation resources. Therefore, RMSD_deer calculated using NOX pseudo atoms was used throughout this work. Models with RMSD_deer ≤ 5 Å were deemed to satisfy the DEER constraints, and were designated as viable models. Upon identifying the ensemble of viable models, the model with the lowest RMSD_deer value was again used as the starting model to carry out a fine search, in which each rotation parameter was varied from the existing value in a ±15° range with a step-size of 5°, and each translation parameter was varied from the existing value in a ±1 Å range with a step-size of 1 Å. The model with the lowest RMSD_deer value from the fine search was selected as the best-fit model.

To assess the impact of the widths of DEER measured distance distributions (w_r) on the outcome of 3-wj modeling, the sterically allowed ensemble described above was ranked according to a modified RMSD metric (RMSD_mod) defined as:

$${\text{RMSD}}_{\text{mod}}^j=\sqrt{\frac{1}{N}\sum _i{\left(\frac{r^{\text{deer}}-r^{\text{model}-j}}{w_{\text{r}}}\right)}_i^2}$$ (3)

Random Docking Search for Modeling the 3-wj Global Structure

With H_T, H_R, and H_L modules described above, models of 3-wj were obtained using a conformational description similar to that presented in a previous work⁶⁴ and a conformational sampling method based on Metropolis Monte Carlo algorithm. The models were assessed using steric, connection, and DEER constraints as described above.

Characterization of Structural Models

Heavy atom root-mean-square-deviations between structural models were calculated using the program VMD.⁶⁵ For each model, interhelical angles between H_T/H_L, H_T/H_R, and H_R/H_L were computed from the dot products of corresponding helical axes.

RESULTS

Biochemical Characterization of Spin-Labeled pRNAs

Our studies were carried out on a pRNA dimer, which has been proposed to serve as an intermediate during pRNA assembly.⁶⁶ A pRNA dimer also represents the simplest ring-shaped pRNA complex, as it contains two sets of intermolecular R/L loop pairing that constrain the pRNA procapsid binding domain in a closed ring topology⁶⁷ (Figure 1A). Two pseudo-symmetric pRNA monomers were used, where the R- and L-loops are designed to minimize homo-oligomer formations (e.g., self-dimer, trimer, etc.) and favor heterodimer assembly.^52,66 To facilitate spin labeling, one monomer was substituted by a truncated 2-piece construct (designated as br_B/a′),⁵² in which the H_T helix noncovalently staples the R- and L-loop subdomains together (Figure 1A). This two-piece construct is fully functional in forming pRNA/pRNA complexes⁵² and in supporting DNA packaging.⁶⁸ All results reported here were obtained in the context of this pRNA dimer.

A phosphorothioate scheme^50,51 was used to efficiently attach nitroxide spin labels (designated as R5, Figure 1B) at eight br_B/a′ sites (Figure 1A) that are not involved in pRNA inter-domain interactions.⁶⁹ The use of R5 for measuring nanometer distances in DNA and RNA has been experimentally validated,^70,71 and a program (NASNOX) has been established for fast and accurate interpretation of measured inter-R5 distances based on the parent nucleic acid structure.^51,62 These prior studies set a solid foundation for mapping the pRNA 3-wj global structure.

For each R5-labeled br_B/a′, the standard state free energy of dimer formation (ΔG⁰) differs by <1.0 kcal/mol from that of the unmodified construct (Table 1, Supporting Information Figure S3). As ΔG° depends on proper pRNA folding to enable simultaneous formation of the two sets of R/L loop interaction,⁵² the small ΔG° changes indicate R5 labeling does not significantly disrupt pRNA folding.

Table 1.

Standard State Free Energy of Dimer Formation between the 118-nt A/b′ pRNA and br_B/a′^a

label positionb		Kd (nM)c	ΔG°17 °C (kcal/mol)d	ΔΔG°17 °C (kcal/mol)e
None		175 ± 63	−8.96 ± 0.26	-
Single labeled	(26; --)	273 ± 99	−8.71 ± 0.26	0.25
	(33; --)	219 ± 94	−8.83 ± 0.32	0.13
	(37; --)	196 ± 32	−8.90 ± 0.10	0.06
	(66; --)	198 ± 27	−8.89 ± 0.08	0.07
	(76; --)	249 ± 109	−8.76 ± 0.33	0.20
	(79; --)	203 ± 101	−8.88 ± 0.40	0.08
	(88; --)	601 ± 326	−8.25 ± 0.45	0.71
	(95; --)	252 ± 119	−8.75 ± 0.37	0.21
Double labeled	(26; 37)	493 ± 121	−8.36 ± 0.16	0.60
	(26; 76)	616 ± 158	−8.24 ± 0.17	0.73
	(26; 79)	657 ± 160	−8.20 ± 0.16	0.76
	(26; 88)	929 ± 200	−8.00 ± 0.14	0.96
	(33; 76)	449 ± 73	−8.42 ± 0.10	0.52
	(33; 79)	522 ± 16	−8.33 ± 0.02	0.63
	(33; 95)	411 ± 143	−8.47 ± 0.25	0.49
	(37; 76)	497 ± 131	−8.36 ± 0.18	0.60
	(37; 79)	320 ± 5	−8.61 ± 0.01	0.35
	(37; 88)	617 ± 158	−8.24 ± 0.17	0.72
	(37; 95)	313 ± 121	−8.63 ± 0.28	0.33
	(66; 76)	235 ± 56	−8.79 ± 0.16	0.17
	(66; 79)	319 ± 59	−8.61 ± 0.12	0.35
	(66; 95)	297 ± 33	−8.66 ± 0.07	0.30
	(76; 95)	228 ± 1	−8.81 ± 0.00	0.15
	(79; 95)	284 ± 52	−8.68 ± 0.12	0.28
	(88; 95)	402 ± 79	−8.48 ± 0.13	0.48

^aMeasurements were carried out at 17 °C in 50 mM Tris-HCl, pH 7.6, 3 mM MgCl₂ as described in Materials and Methods.

^bDesignated by the sequence number(s) of the R5 attachment site(s).

^cErrors obtained from multiple measurements.

^dErrors calculated from propagating errors of K_d measurement.

^eΔΔG° = ΔG°(spin labeled br_B/a′) − ΔG°(unmodified br_B/a′).

Interhelical Distances Measured Using Pulsed EPR Spectroscopy

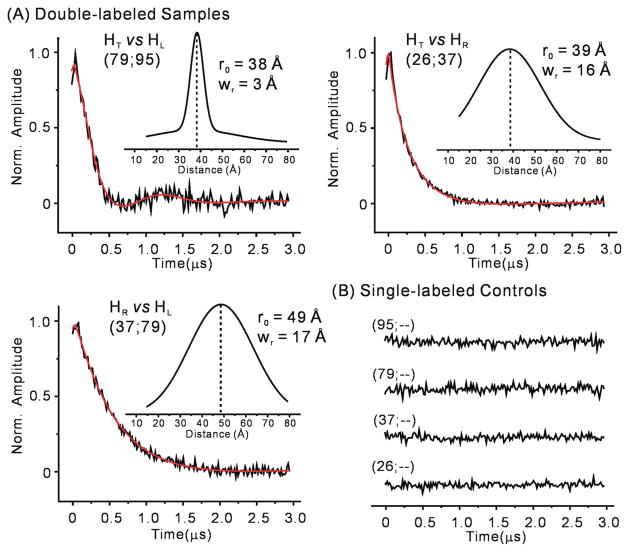
Upon confirming assembly of R5-labeled dimers under EPR conditions using native gels (Supporting Information Figure S2) and DEER (Supporting Information Figure S4), 17 sets of inter-R5 distances spanning the 3-wj were measured (Table 2). In each case, the normalized background-corrected dipolar evolution trace for the double-labeled sample showed a clear decay, while the corresponding single-labeled samples revealed flat traces without oscillation or decay pattern (Figure 2 and Supporting Information Figures S5 and S6). This ensures that distances measured using the double-labeled samples are not biased by RNA aggregation. The dipolar evolution traces were analyzed using the Defit program, in which one or more Gaussian functions are used to extract interspin distance distribution profiles.⁵⁶ The analyses provide two key parameters to describe the resulting interspin distance distribution: the most probable distance (r₀) and the width of distance distribution (w_r) (see Materials and Methods). The measurements yielded r₀ values ranging from 28 to 49 Å, with w_r being 3–18 Å (Table 2, Figure 2, Supporting Information Figure S6 and Table S1). In most DEER measurements, an evolution time of 3 μs was used, which is sufficient for obtaining reliable r₀ values up to 50 Å even in situations where a broad distance distribution results in a decaying DEER trace without clear oscillations.⁷² Consistent with previous reports,^70,71 repeated measurements indicated that errors in measured r₀ are <7% of the reported values. The r₀ values were subsequently used as one of the main constraints in modeling (see below).

Table 2.

Interhelical Distances

data seta		inter-R5 distance (Å)
		DEER measuredb	EPR-based modelc	crystal structured
HT vs HL	(76; 95)	28	26.4	27.6
	(79; 95)	38	37.5	38.0
	(88; 95)	34	30.3	29.7
	(26; 76)	28e	30.7	23.7
	(26; 79)	35e	31.6	30.1
	(26; 88)	37	37.2	10.7
HT vs HR	(26; 37)	39	38.6	44.8
	(33; 95)	32e	30.4	40.8
	(37; 95)	40	43.4	45.5
	(66; 95)	30e	25.9	22.8
HR vs HL	(33; 76)	39	41.0	23.5
	(33; 79)	44	43.0	38.1
	(37; 76)	48	50.8	36.4
	(37; 79)	49	47.4	52.6
	(37; 88)	40	39.3	50.2
	(66; 76)	35	38.8	18.8
	(66; 79)	41	39.1	35.6
RMSDdeer		-	2.43	10.2

^aEach designated by corresponding labeling site numbers.

^bMost probable distances listed. Estimated errors are less than 7% based on repeated measurements.

^cInter-NOX distances (see Materials and Methods) in the best-fit model shown in Figure 3A.

^dNASNOX predicted average inter-R5 distances obtained from the pRNA tetramer crystal structure.⁴³

^eMajor population listed.

Figure 2.

(A) Examples of DEER measured inter-R5 distances between pRNA helices. Each data set is designated by the labeling site numbers (see Figure 1A). Normalized and background-corrected experimental dipolar evolution data (black lines) were fit (red lines) using the Defit program. Insets show computed distance distribution profiles, with the most probable distance (r₀) and the width of the distribution (w_r) indicated. (B) Dipolar evolution data of corresponding single-labeled pRNA samples. Additional data sets are shown in Supporting Information Figures S5 and S6.

Statistical analysis built into the Defit program indicated that 13 of the 17 data sets can be adequately fit with one population of interspin distances, while the remaining 4 data sets each contains one additional population (Table 2, Supporting Information Figure S6). In these four data sets, the r₀ of the longer-distance population varies substantially depending on the range of dipolar evolution data used for fitting the decay background. In addition, these r₀ values fall between 47 and 60 Å, which are at the upper limit of the accurately measurable distances with the use of the corresponding dipolar evolution time (2 to 3 μs as limited by the sample phase memory time).⁷² These observations suggest that the longer-distance populations are likely artifacts. They were excluded from further investigation.

The width of distance distribution (w_r) provides a measure of disordering in the interspin distances. The origin of disorder lies in variations in: (i) positioning of nitroxide pyrroline rings with respect to the RNA helices; and (ii) RNA conformations, including the relative spatial arrangement between RNA helices. In pRNA distance measurements, 14 of the 17 data sets give w_r exceeding 5 Å (Supporting Information Table S1). These large w_r values reflect distance distributions that are broader than those previously reported on DNA and RNA duplexes.^70,71 They suggest disordering in the spatial arrangement between RNA helices in the 3-wj. Interestingly, interhelical distances between H_T and H_R, and between H_L and H_R, overall show larger w_r than those between H_T and H_L (Supporting Information Table S1). This may indicate that positioning of H_R is variable.

The DEER data obtained on pRNA samples were also analyzed with the DeerAnalysis program developed by Jeschke and co-workers,⁷³ which uses a model free Tikhonov regularization method to extract interspin distance distributions. Data sets with oscillating echo evolution traces (and therefore narrow distance distributions, e.g., (79; 95)) show consistent distance distribution profiles when analyzed using either Defit or DeerAnalysis (Supporting Information Figure S7). For those data sets without oscillations, such as (33; 76), the optimized regularization parameter used in Tikhonov fits is undetermined, and consequently, the shape of distance distribution profiles cannot be adequately determined (Supporting Information Figure S8). This hampers further efforts on dissecting subpopulations in distance distribution profiles using a previously reported procedure.²² None the less, Defit and DeerAnalysis render similar average distances (i.e., r₀) and comparable distribution widths when the entire distance distribution profiles are considered (Supporting Information Figure S8). As Defit has been successfully applied in studies where disordering in protein structures results in DEER traces without oscillations,^21,56 it was used in this work to describe inter-R5 distance distribution profiles.

Modeling the Three-Way Junction Global Structure Using DEER Measured Distances

Using a set of in-house programs, a grid search approach was employed to evaluate over 65 billion unique models where the spatial arrangement was varied between three A-form helices corresponding to H_T, H_R, and H_L (see Materials and Methods). The search yielded ~480 000 sterically allowed models that conform to steric and chemical bonding constraints. An RMSD_deer metric was then computed, which corresponds to the root-mean-square-deviation of inter-R5 distances between DEER-measured values (i.e., the r₀ values) and those derived on each model. With a DEER constraint of RMSD_deer ≤ 5 Å, which slightly exceeds errors of the measured r₀ (≤7% of measured values, see above), 3662 viable models were found to satisfy the DEER constraints, which is <0.8% of the sterically allowed population. Expanding the range of translation parameters from ±15 to ±20 Å resulted in no significant increase of viable models, indicating sufficient coverage of the parameter space.

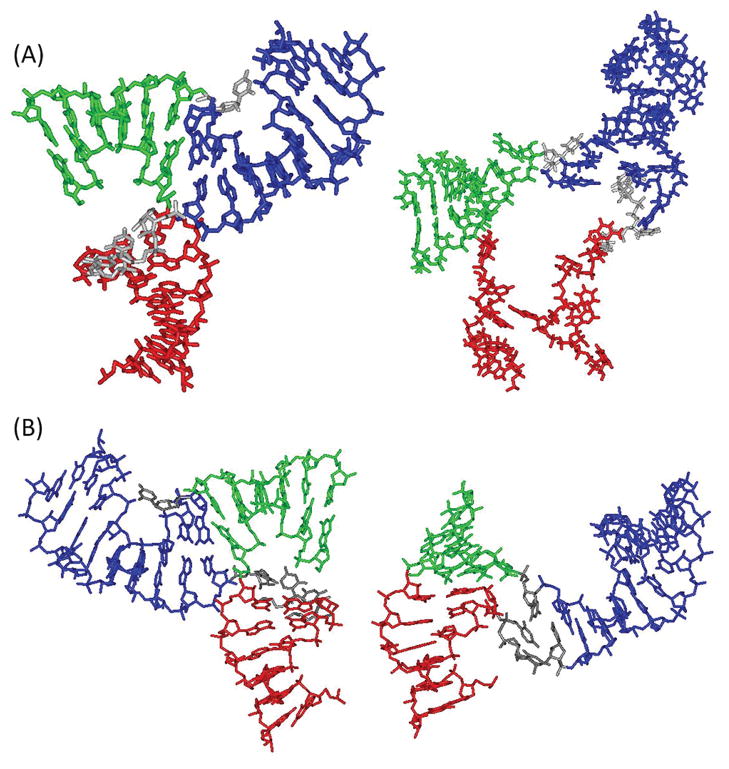
The grid search yielded a best-fit model with an RMSD_deer of 2.43 Å (Figure 3A, Table 2). It shows a T-shaped 3-wj, with an acute bent between H_T and H_L (interhelical angel θ_T,L = 93°) and an approximately linear arrangement between H_R and H_L (θ_R,L = 142°) (Figure 3A). Further analyses revealed that, when compared to the best-fit model, the ensemble of 3662 viable models shows a heavy atom root-mean-square-deviation distribution of 5.0 ± 1.4 Å (Supporting Information Figure S9). Distribution of each interhelical angle shows predominately one population, with angles between H_T/H_L, H_T/H_R, and H_L/H_R being 99° ± 19°, 57° ± 19°, and 147° ± 15°, respectively (Figure 3B). Overall, EPR data reveal that, in pRNA dimer, the 3-wj adopts one family of conformation with an acute kink between H_T and H_L.

Figure 3.

Models of the pRNA 3-wj derived based on DEER distances measured in pRNA dimer. (A) Best-fit model obtained from grid search using the RMSD_deer criterion. H_T, H_L, and H_R are shown in green, red, and blue, respectively. Angles between the respective helical axes are shown in the inset. To demonstrate that the best-fit model does satisfy the connection constraint, connections between H_T/H_R (U₂₉), H_R/H_L (U₇₂U₇₃U₇₄), and H_T/H_L (no nucleotide present) were manually built-in using conformations observed in the pRNA tetramer crystal structure⁴³ (pdb no. 3R4F) with slight adjustment of backbone torsion angles. (B) Interhelical angle distributions from the 3662 viable models obtained using the RMSD_deer criterion. (C) Best-fit model obtained from grid search using the Rmsd_mod criterion. The interhelical angles between H_T/H_L, H_T/H_R, and H_R/H_L are 90°, 46°, and 134°, respectively. (D) Best-fit model obtained from random docking search.

To assess the impact of the widths of distance distribution (w_r) on the outcome of 3-wj modeling, the sterically allowed ensemble identified in the grid search was ranked according to a modified RMSD metric (RMSD_mod, see Materials and Methods). The top-ranked model obtained using the RMSD_mod criterion shows minimal difference from the best-fit model identified by the RMSD_deer criterion (compare panels A and C in Figure 3), with the root-mean-square-deviation between corresponding heavy atoms being 1.7 Å. Furthermore, an allowable ensemble was constructed by selecting 3662 lowest RMSD_mod models, which matches the number of models satisfying the RMSD_deer ≤ 5 Å criterion. This ensemble also shows one population of RNA conformation, and interhelical angles between H_T/H_L, H_T/H_R, and H_L/H_R are 77° ± 16°, 59° ± 26°, and 120° ± 26°, respectively. Importantly, no allowable model has θ_T,L < 45°, which suggests H_T and H_L are kinked rather than linearly stacked. All these characteristics match those observed in the RMSD_deer ≤5 Å ensemble. We note that there are alternative means to incorporate w_r into the search criterion. In addition, for DEER traces that show decay without oscillation due to intrinsic flexibility of pRNA, our ability to measure w_r accurately is limited. Nonetheless, RMSD_mod analyses suggest that the uncertainty arisen from the measured distance distribution width is unlikely to alter the conclusion that the EPR-based 3-wj models adopt a kinked configuration between H_T and H_L.

Models of 3-wj were also obtained using a random docking search (Figure 3D), which uses a fundamentally different algorithm as compared to the grid search (see Materials and Methods). From this search, the model that fits best to the DEER measured distance has an RMSD_deer of 2.86 Å. The structural differences between the best models from grid search and random docking search are minimal, with heavy atom root-mean-square-deviation being approximately 2.4 Å between these two models (compare panels A and D in Figure 3).

We note that in the pRNA dimer construct used in this study, U₇₂U₇₃U₇₄ is present in the full length A/b′ monomer, but absent in br_B/a′ (Figure 1A). Considering the symmetry of the pRNA dimer, enforcing the connection constraint from residue 71 O3′ to residue 75 C5′ (i.e., accounting for U₇₂U₇₃U₇₄) is justified. Furthermore, the distance between residue 71 O3′ and residue 75 C5′ is 16.5 Å in the EPR-based model (Figure 3A), which is very similar to the value measured in the crystal structure (16.7 Å).⁴³ As controls, modeling without enforcing the connection constraint from residue 71 O3′ to residue 75 C5′ was carried out. Such a search yielded the same top-ranked model and a similar interhelical angle distribution pattern as compared to the search with the constraint, although the resulting viable model ensemble is larger as expected.

Assessing Previously Reported Three-Way Junction Conformations Using DEER Measured Distances

The DEER measured distances allow direct assessments of two pRNA 3-wj conformations that were reported during the course of this SDSL work. The Guo group has reported a model of pRNA dimer, which was obtained based on biochemical data and distances measured using single-molecule fluorescence resonance energy transfer (smFRET).^47,48 In this FRET-based model, the pRNA 3-wj shows a kinked H_T/H_L conformation, which is characteristically similar to the EPR-based model described above (Figure 4A). However, in the FRET study, there is no reported FRET measurement spanning the pRNA 3-wj,⁴⁸ and clear differences are present between the FRET-model and the EPR-model (Figure 4A).

Figure 4.

Comparison of 3-wj models obtained from different studies. In each panel, the H_T, H_L, and H_R helices are shown in green, red, and blue, respectively. (A) Comparison between the EPR-derived model (left) and the FRET-based model⁴⁸ (right). Inter-R5 distances were not predicted for the FRET model, which shows largely irregular helical conformations around the 3-wj. Nevertheless, both models show a kinked conformation between H_T and H_L, and a more linear conformation between H_L and H_R. (B) Comparison between the EPR-derived model (left) and that observed in the tetramer crystal structure⁴³ (right). The two models were aligned according to H_L. The EPR model shows a kinked conformation between H_T and H_L, while the crystal structure shows a linearly stacked H_T and H_L.

Very recently, a 3.5 Å resolution crystal structure of a pRNA tetramer was reported (PDB no. 3R4F).⁴³ When R5 was modeled at the corresponding sites of this tetramer crystal structure, the resulting inter-R5 distances deviate from the DEER measured distances with an RMSD_deer of 10.2 Å, with five of the data sets showing deviation >10 Å (Table 2, bolded). Particularly, for data set (26; 88), which measures distance between H_T and H_L, r₀ predicted using the tetramer crystal structure differs from the DEER measured value by 26 Å (10.7 vs 37 Å, Table 2), which significantly exceeds the measured distance distribution half-width (w_r = 17 Å, Supporting Information Table S1). Modeling using the crystal structure also shows that at these two sites, R5 can be adequately accommodated simultaneously without distorting the RNA. Furthermore, cw-EPR spectra of all double-labeled samples, including that of (26; 88), show no line-broadening compared to single-labeled controls (Supporting Information Figure S10). This indicates that inter-R5 distance at (26; 88) is >20 Å,^74–76 which is not compatible with the 10.7 Å value predicted based on the tetramer crystal structure. Overall, even though many of the DEER measured distances reported here show broad distributions, the significant deviations between the measured r₀ and those predicted based on the crystal structure suggest that the majority of the 3-wj conformation in the pRNA dimer in solution deviates from the conformation reported in the tetramer crystal structure.

Examination of the crystal structure⁴³ reveals that H_T, H_L, and H_R each adopts an A-form conformation as assumed in our model search. However, in the crystal structure, H_T and H_L are stacked nearly linearly, while H_R and H_L adopt a relatively kinked conformation (θ_T,L = 15°, θ_T,R = 78°, and θ_L,R = 93°) (Figure 4B). This is characteristically different from the kinked H_T/H_L conformation in the EPR-derived model. As discussed above, the kinked H_T/H_L conformation persists in all EPR-based models, including those obtained using the RMSD_mod criterion that takes into account the widths of measured distance distributions. The analyses therefore support the conclusion that the 3-wj conformations are different between the pRNA tetramer crystal structure and the pRNA dimer in solution state.

DISCUSSION

Global Conformation of the pRNA Three-Way Junction

EPR measured distances have been widely used to assess the viability of existing models or to distinguish competing models.^6,7,21,77 Results reported here show that the 3-wj conformation in the pRNA tetramer crystal structure does not conform to the DEER measured interhelical distances in the dimer in solution state (see Results). Consequently, the EPR-based 3-wj model displays clear differences in the relative orientations between H_T, H_L, and H_R as compared to the tetramer crystal structure (Figure 4B). Furthermore, the EPR-derived model shows similar characteristics to the model constructed based on biochemical and smFRET data (Figure 4A). Together the results suggest that the 3-wj conformation in the dimer in solution is different from that in the tetramer crystal structure. We do note that, in addition to variations in salt and buffer conditions, EPR and crystallography studies used different monomeric pRNA constructs, although both contructs represent a truncated pRNA resembling the procapsid binding domain and have been shown to be functional.^43,52,68 For example, in the EPR study, the U₇₂U₇₃U₇₄ linker was deleted in one of the pRNA monomer (Figure 1A). This may affect relative positioning of H_R with respect to H_L and H_T, and indeed, there are indications that positioning of H_R is more variable than that of H_L and H_T (see Results). However, deleting U₇₂U₇₃U₇₄ should have a much less drastic effect on the relative spatial arrangement between H_T and H_L, which shows the biggest deviation between the crystal structure and the EPR-based model (Figure 4B).

In a pRNA oligomer, H_R and H_L are constrained by the intermolecular R/L loop base-pairing and ultimately interact to form the ring-shaped pRNA/pRNA interface (Figure 1A).^38,39,66 Between pRNA dimer and tetramer, changes in relative H_R/H_L configurations are likely needed to accommodate the increased ring size. Interestingly, results presented here indicate that relative positioning of H_T with respect to H_L and H_R is different between the dimer and the tetramer. If one considers that H_R and H_L define the pRNA ring, this will imply that the relative positioning of H_T with respect to the pRNA ring changes in different pRNA oligomeric states. Note that the (extended) H_T contains the binding site for the phi29 motor ATPase (i.e., gp16), while H_L and H_R form the pRNA ring that binds to the procapsid.^35,36 Global structural changes in 3-wj, which alter the relative spatial arrangement between H_T, H_R and H_L, will change the spatial relationship between the motor ATPase and the procapsid. This is consistent with a recent proposal that pRNA serves as a communicator to bridge different parts of the motor during packaging.⁴³ In addition, the linearly stacked H_T/H_L conformation observed in the tetramer crystal structure has been used directly to model pRNA pentamer and hexamer.⁴³ The variability of junction conformation between the dimer and the tetramer reported here suggests more complexity in modeling pRNA oligomers.

Information on the pRNA 3-wj also impacts efforts on developing pRNA-based artificial nanostructures for material and therapeutic applications.⁴⁶ For example, taking advantage of the R/L loop interactions, pRNA variants have been engineered to assemble oligomeric RNA arrays and superstructures.⁷⁸ The 3-wj strongly influences the shape of the monomeric pRNA unit and, therefore, impacts the morphology of the arrays and superstructures. As such, information obtained here on 3-wj conformation, as well as how it may change in different oligomeric states, should aid the rational design of these superstructures. In addition, pRNA 3-wj has been used as a scaffold for assembling therapeutic modules such as interfering RNA, ribozyme, and small molecule agents (e.g., folate), and the resulting multifunctional nanoparticles seem to be able to function in vivo.⁷⁹ As the 3-wj controls the related positioning of the therapeutic modules, information on its conformation reported here should benefit these developments.

Modeling RNA Global Structure Using Multiple DEER Measured Distances

While there are now a growing number of reports on SDSL mapping of protein conformations,^23–30 SDSL mapping of nucleic acids conformation is limited.^31–33 In this study, we demonstrated a general strategy to map the global structure of nucleic acids. Multiple distances in the nanometer range were measured using an advanced pulsed EPR methodology (i.e., DEER) and a nucleotide independent nitroxide label (i.e., R5) that can be efficiently attached to multiple RNA sites. In parallel, a de novo pool of RNA models were constructed, which allows explicit computation of internitroxide distances in each model. The DEER measured distances were then used as constraints to select viable RNA conformations. When all 17 sets of distances were applied, less than 0.8% of sterically allowed models were deemed viable, clearly demonstrating the power of DEER measured long-range distances on mapping RNA global structure.

However, there remain a number of unanswered questions. For example, how does the amount of DEER distances affect modeling? As a first step in addressing this question, searches were carried out using only 12 of the 17 DEER distances while omitting data sets (26; 76), (26; 79), (26; 88), (26; 37), and (37; 88) (see Table 2). This yielded 26 390 viable models with RMSD_deer < 5 Å, which is approximately 7 times larger than that obtained with all 17 distances. Key characteristics between these two pools of model are very similar: the top-ranked models deviate with a heavy atom root-mean-square-deviation of 3.5 Å; and the average interhelical angles are almost identical (Supporting Information Figure S11). This further strengthens the confidence on the 3-wj conformation reported above (Figure 3). The pool obtained using 12 DEER distances does show broader interhelical angle distributions (Supporting Information Figure S11) and, more interestingly, includes a small fraction of models (3.6%) with θ_T,L < 45°, which is approaching a more linear H_T/H_L configuration. Therefore, the additional 5 distances, including data set (26; 88) that shows a large deviation between the DEER measurement and that predicted from the tetramer crystal structure, do push the models further away from the linearly stacked H_T/H_L configuration. We note that a prior study in protein indicates both the amount of distance constraints and the location of the labeling sites are important for optimal structural determination.⁸⁰ Further studies are needed in order to achieve rational selection of optimal labeling sites for mapping RNA global structure.

SDSL uses a small nitroxide probe that is less intrusive as compared to most fluorophores, and avoids a number of issues faced by crystallography (e.g., crystalline sample preparation, interference from lattice packing) and NMR (e.g., limitation on molecule size). The nanometer distances measured by SDSL/EPR provide a unique set of long-range constraints. While work reported here demonstrates de novo mapping of RNA global structure, combining SDSL/EPR with other experimental and computational approaches should be particularly powerful in mapping tertiary structure of complex nucleic acid and protein/nucleic acid systems.