Wetting-Induced Budding of Vesicles in Contact with Several Aqueous Phases

Abstract

Osmotic deflation of vesicles enclosing two liquid phases can lead to bulging of one of the phases from the vesicle body. This budding process is preceded by a complete to partial wetting transition of one of the liquid phases on the membrane and depends on the membrane tensions and the tension of the interface between the enclosed liquid phases. These tensions dominate in different morphology regimes, the crossover of which initiates the budding process. In addition, the degree of budding can be controlled by aspiration via micropipets. We also demonstrate that the budding direction can be reversed if there are two external phases in contact with the vesicle.

1. Introduction

Budding processes of biological membranes are essential for cell functioning. They are involved, for example, in vesicular trafficking, which requires the selective loading of cargo molecules into the vesicles, or in endo- and exocytosis, where the membrane invaginates inward or outward. In giant vesicles, model membrane systems with cell-size dimensions,¹ budding may be induced by a number of possible mechanisms. For example, a slight area difference between the two monolayer leaflets of the membrane or a change in the vesicle area-to-volume ratio may lead to budding.^2,3 In homogeneous membranes, budding is driven by the minimization of the bending energy.^4,5 In multicomponent membranes containing phase separated domains, budding is governed by the interplay of bending rigidity and line tension of these domains.⁶⁻⁹

In the aforementioned studies, the membrane properties play a crucial role, whereas the enclosed homogeneous fluid is an inert “spectator” phase. However, when two (or more) liquid phases are in contact with the membrane, their interactions with the bilayer become relevant for the vesicle morphology. Recently, such novel soft matter systems were realized¹⁰⁻¹³ and phase separation inside vesicles was reported to lead to protein partitioning in one of the liquid phases.^10,11 Budding has also been observed, but the underlying mechanism remains to be elucidated.

To shed light on this problem, we use giant unilamellar vesicles loaded with homogeneous aqueous solutions of water-soluble polymers. Osmotic deflation of the vesicle induces phase separation in the interior solution and, at the same time, creates excess membrane area. Depending on membrane properties such as the membrane tension and spontaneous curvature, the area created during deflation may be stored in membrane nanotubes¹³ and/or may lead to vesicle budding as shown in this paper. The budding direction can be reversed if the phase separation occurs in the vesicle exterior. A systematic study of the budding process reveals that it requires the wetting of the membrane by both liquid phases. This wetting-induced budding provides a possible mechanism for the selective loading of cargo molecules into transport vesicles in cells.

2. Experimental Section

To prepare vesicles encapsulating two phases we used a homogeneous aqueous solution composed of 4.05 wt % poly(ethylene glycol) (PEG, 8 kg/mol) and 2.22 wt % dextran (400–500 kg/mol); see the Supporting Information. The membrane consists of 95.9 mol % dioleoylphosphatidylcholine, 4.0 mol % G_M1 Ganglioside and 0.1 mol % fluorescent lipid marker; see the Supporting Information. After formation, the vesicles are diluted in an isotonic solution containing 4.41 wt % PEG and 1.45 wt % dextran. The osmolarity of the external medium is then increased by adding a hypertonic solution of 3.92 wt % PEG, 2.14 wt % dextran, and 3.27 wt % sucrose. This composition in the exterior solution implies that its density is between those of the PEG-rich and dextran-rich phases, but smaller than the overall density of the solution inside the vesicles. These conditions ensure that the vesicles sediment to the chamber bottom and that the symmetry axis of the budded vesicles is vertically oriented; see Figure 1a–f. In this way, the vesicles can be observed from the side using a horizontally aligned microscope. The vesicle axial symmetry allows for quantitative analysis of their shapes in contrast to the systems explored previously.^10,11

Figure 1.

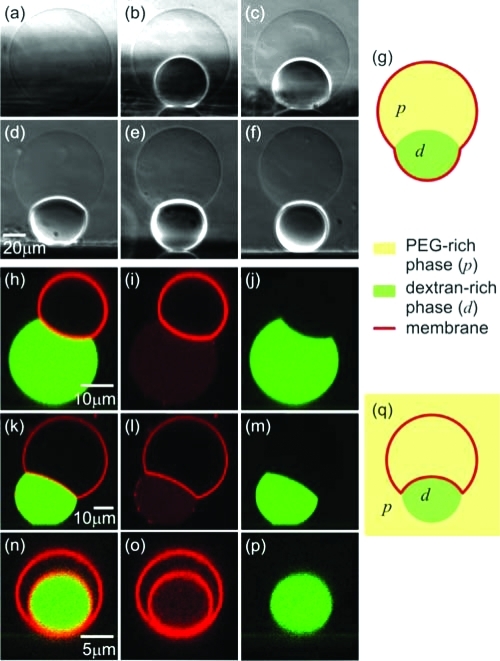
Outward (a–g) and inward (h–q) budding of vesicles in contact with several aqueous solutions. (a–f) Side-view phase contrast images and (g) a cartoon of a vesicle sitting on a glass substrate and subjected to osmotic deflation. Initially, the vesicle contains a homogeneous polymer solution (a). After phase separation (b), the heavier and denser dextran-rich phase is located at the vesicle bottom. Further deflation causes the dextran-rich phase to wet the membrane (c), and then to bud out (d–f). The osmolarity ratio r from (a) to (f) is 1.0, 1.14, 1.32, 1.46, 1.65, and 1.76, respectively. The system was left to equilibrate for at least 2 h after each consecutive deflation step. (h–p) xz-confocal scans and (q) a cartoon of vesicles in contact with fluorescently labeled droplets of dextran-rich phase (green). The membrane is also fluorescently labeled (red). The confocal images in the rows (h–j), (k–m), and (n–p) show the mixed fluorescence signal, and the red and green channels separately. Inspection of (i,l) shows that the interface between the dextran-rich droplets and the PEG-rich background contains essentially no lipid.

In order to induce the phase separation outside the vesicles as in Figure 1h–q, we prepared a polymer solution composed of 6.87 wt % PEG and 2.86 wt % dextran. A small fraction of dextran (1.25 wt % of the total dextran) was labeled with fluorescein isothiocyanate. The polymer solution was left at room temperature (23 °C) for 2.5 days after which complete phase separation was achieved. Then, the two phases were separated. Vesicles with G_M1-doped membranes were prepared in the PEG-rich phase at room temperature using electroformation. Approximately 2 μL dextran-rich phase was mixed with 200 μL vesicle solution in the microscopy chamber (occasionally a mixture of 100 μL PEG-rich phase and 100 μL vesicle solution was used). The chamber was shaken gently in order to break the dextran-rich phase into tiny droplets, and to increase the possibility for contact between the vesicles and the dextran-rich droplets. The vesicles with dextran-rich droplets were imaged after 2 h or on the next day.

For the micropipet aspiration experiments, performed only on vesicles encapsulating two phases, the vesicles are predeflated with the hypertonic solution, increasing the external osmolarity by 32%, and then, left to equilibrate for one day. Aspiration is realized by means of a glass capillary, approximately 20 μm in diameter, connected to a home-built hydrostatic pressure system. After each consecutive pressure change, the vesicle is left to equilibrate for about 3 min.

The interfacial tension of the phase separated polymer solution is independently measured in bulk using spinning drop tensiometer; see the Supporting Information. All experiments are performed at room temperature.

3. Results

Budding

Figure 1a–g shows side-view images and a cartoon of a vesicle at different degrees of deflation described by the osmolarity ratio r, which we define to be the ratio r_ex/r_in,0 between the deflation-dependent osmolarity r_ex within the exterior compartment and the initial osmolarity r_in,0 within the interior compartment. Initially, the vesicle interior is homogeneous; see Figure 1a. The phase separation within the vesicle is induced via osmotic deflation by adding the hypertonic solution to the external medium. The resulting osmotic unbalance forces water out of the vesicle. Since the polymers cannot permeate the membrane, their concentration in the vesicle increases. Once it is above the binodal (see Figure S1 in the Supporting Information), the enclosed solution separates into PEG-rich and dextran-rich phases; see Figure 1b. The dextran-rich droplet is always located at the bottom of the vesicle because of its higher density compared to the PEG-rich phase. When the vesicle is further deflated with r > 1.3, the dextran-rich phase starts to wet the membrane; see Figure 1c. The change in the morphology of the dextran-rich droplet indicates a wetting transition from complete wetting of the PEG-rich phase in Figure 1b to partial wetting in Figure 1c as previously described in ref (12).

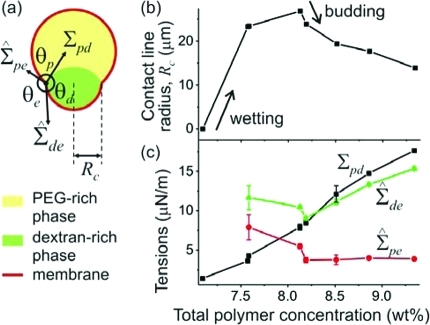
After the dextran droplet starts wetting the membrane, the radius R_c of the three-phase contact line, where the external medium (e), the PEG-rich phase (p) and the dextran-rich phase (d) are in close proximity, increases at first; see Figures 1c and 2a,b. At the same time, the interfacial tension Σ_pd between the liquid phases pulls on the membrane along this contact line and leads to budding and a decrease in R_c at higher polymer concentrations; see Figure 2b. The budding process from the spherical vesicle shape in Figure 1c to the pair of two spherical caps in Figure 1d should be regarded as a strongly concentration-dependent but smooth crossover rather than as a sharp transition. This crossover behavior is most clearly seen in the behavior of the contact line radius R_c; see Figure 2b. As the osmolarity is increased further, the dextran-rich phase protrudes further out; see Figure 1e,f. Finally, the dextran-rich phase may form a completely spherical bud whereby the area of the pd interface is close to zero.

Figure 2.

(a) Schematic illustration of the contact angles and the tensions at the three-phase contact line (⊙) with radius R_c. (b) Evolution of the radius R_c with increasing polymer concentration. When the dextran-rich phase starts wetting the membrane, R_c first increases, but then decreases during the budding process. (c) Evolution of the three tensions with increasing polymer concentrations. The weight ratio of dextran and PEG is 0.55. The error bars of Σ̂_pe and Σ̂_de indicate the error introduced by image fitting. The 1st, 3rd, 5th, and 6th points from these data sets for the membrane tensions correspond to the images (c–f) in Figure 1.

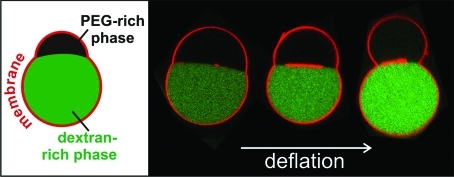
The excess membrane area governs the shape of the budded vesicle. Thus, vesicles with different initial area adopt diverse shapes upon deflation; see the Supporting Information. Wetting-induced budding can also occur toward the vesicle interior; see Figure 1h–q, when the exterior solution undergoes phase separation. The observations in these samples show analogous vesicle morphologies. For low excess membrane area, the dextran-rich droplets wet the membrane but deform the vesicle only slightly; see Figure 1h–j, while strongly deflated vesicles may engulf the dextran-rich droplets completely; see Figure 1n–p.

Force Balance at the Three-Phase Contact Line

After the wetting transition, the surface of the dextran-rich droplet exhibits a “kink” at the three-phase contact line; see Figure 1c–h,j,k,m,q. This contact line divides the vesicle membrane into pe and de segments. Because of the compositional difference of the p and d phases, these two membrane segments experience two distinct tensions, Σ̂_pe and Σ̂_de; see Figure 2a.

By fitting the vesicle and the drop contours in the microscopy images with circular arcs, we obtain the three contact angles θ_e, θ_p, and θ_d with θ_e + θ_p + θ_d = 2π; see Figure 2a. For outward budding, these contact angles are related to the membrane tensions Σ̂_pe and Σ̂_de and the interfacial tension Σ_pd, via

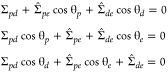1

The case of inward budding is described in the Supporting Information. These equations are analogous to Neumann’s triangle for capillary surfaces.¹⁴ From the analysis of the vesicle images, we can calculate the total polymer concentration within the vesicle at every osmolarity ratio r, assuming that the volume change corresponds to the loss of water. The interfacial tension Σ_pd in eqs 1 is measured independently for bulk polymer solutions; see the Supporting Information. Knowing Σ_pd, we can compute the tensions Σ̂_pe and Σ̂_de from eqs 1; see Figure 2c. The interfacial tension Σ_pd increases with the total polymer concentration because the composition difference between the coexisting phases is enhanced. Interestingly, the tensions Σ̂_pe and Σ̂_de behave significantly differently from Σ_pd. Their nonmonotonic dependence on the polymer concentration arises from two competing effects of the deflation process. First, the total vesicle volume is decreased, which in the absence of any other constraint, would act to reduce the membrane tensions Σ̂_pe and Σ̂_de. However, deflation also increases the interfacial tension Σ_pd; see Figure 2c, which may be balanced in two ways following (eqs 1): (i) by a reduction of the area of the pd interface, which as a consequence leads to a reduction in the contact angle θ_e, or (ii) by an increase in the membrane tensions Σ̂_pe and/or Σ̂_de. Inspection of Figure 2c shows that Σ̂_pe and Σ̂_de first decrease at low polymer concentrations, which implies that the increased interfacial tension Σ_pd can be balanced by a reduction of the contact angle θ_e alone. However, as the polymer concentration is further increased, the tension Σ̂_de passes through a minimum and starts to increase whereas the tension Σ̂_pe stays essentially constant. Thus, in this second concentration range, the increase in the interfacial tension Σ_pd is primarily balanced by an increase in the tension Σ̂_de. Indeed, we will argue further below that the pe membrane segment cannot pull “against” the pd interface. The two concentration ranges in which either the membrane tensions or the interfacial tension dominate correspond to two different vesicle morphologies as observed optically: sphere or a pair of spherical caps; see Figure 1. The crossover between these two morphologies marks the budding process.

Vesicle Micropipet Aspiration

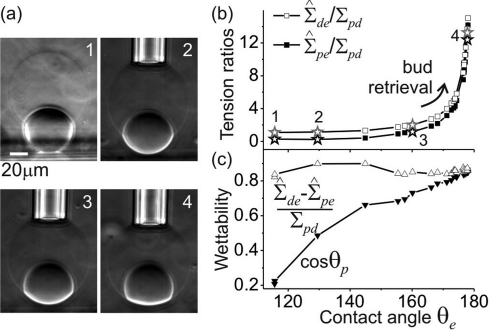
For a fixed composition of the polymer phases, the interfacial tension Σ_pd is constant. However, the membrane tensions Σ̂_pe and Σ̂_de can be externally manipulated. Using a micropipet, we apply suction pressure to a deflated dumbbell-like vesicle; see Figure 3a. The pressure produces mild membrane tensions in the range 4–383 μN/m; see the Supporting Information, which do not lead to membrane stretching.¹⁵ The angle θ_e, which characterizes the degree of budding, increases with the applied suction pressure, i.e., the bud is retrieved and the budding process is reversed. Simultaneously, the excess area of the vesicle part outside of the pipet is reduced, a reduction that could also be achieved by vesicle inflation, i.e., by the reverse of the process shown in Figure 1.

Figure 3.

(a) Side-view phase contrast images of a vesicle under different suction pressures. The small dense droplet at the vesicle bottom is the dextran-rich phase. The bright cylindrical part in the second image is the glass micropipet. (b) The tension ratios as a function of the contact angle θ_e describing the degree of budding. The stars in the data correspond to the images in (a) as indicated by the numbers. (c) Wettabilities, as defined in the text, as a function of the contact angle θ_e. The upper set of data confirms eq 4.

The tension Σ̂_pe is imposed by the micropipet; see the Supporting Information, and the tension Σ̂_de can be calculated from the measured contact angles via eqs 1. The two tensions normalized by the interfacial tension Σ_pd are shown in Figure 3b as a function of the angle θ_e. For small θ_e or high degree of budding, the tensions Σ̂_pe and Σ̂_de change only weakly. In the regime of large θ_e or low degree of budding, these tensions increase significantly. The crossover between these two regimes indicates the budding (or bud retrieval) process, which is continuous.

The sharp increase in Σ̂_pe and Σ̂_de at high aspiration pressures or large θ_e can be understood by considering the force balance at the three-phase contact line as in (1), which imply Σ̂_pe/sin θ_d = Σ̂_de/sin θ_p = Σ_pd/sin θ_e. As the contact angle θ_e approaches π, small changes in θ_e lead to significant changes in Σ̂_pe and Σ̂_de. For the regime of lower aspiration pressures (smaller θ_e), where the changes in the tensions Σ̂_pe and Σ̂_de are insignificant; see Figure 3b, the vesicle shape is governed primarily by the minimization of the interfacial area A_pd; see the sequence of images 3 to 1 in Figure 3a and Figure S4 in the Supporting Information.

In these experiments, the compositions of the two phases and the membrane do not change. Thus, the wettability of one of the phases, for example the PEG-rich phase, on the membrane should be constant. If we consider a planar membrane, i.e., θ_e = π, this wettability will be characterized by cos θ_p. To examine the limit of a planar membrane, we plot cos θ_p as a function of the angle θ_e in Figure 3c. The planar membrane limit is described by the angle θ_p* ≡ θ_p (θ_e ≈ π). Linear extrapolation of the data in the range 155° < θ_e < 178° leads to cos θ_p* ≅ 0.87 or an angle of 30°. For such a planar surface, the wettability is defined as (Σ̂_de – Σ̂_pe)/Σ_pd. Following eqs 1, one obtains

2

We will now consider the limit of a planar membrane in which the contact angle θ_e approaches π. We expand the right-hand side of eq 2 with respect to (π – θ_e), see the Supporting Information, which leads to

3

where O(π – θ_e) indicates terms of order π – θ_e.

Furthermore, from the experimental data we find that (Σ̂_de – Σ̂_pe)/Σ_pd is approximately constant over the whole θ_e range with an average value of 0.86 ± 0.02; see Figure 3c, which implies the relation

4

This observation can be understood if one considers the membrane shape on different length scales. When viewed with optical resolution as in Figures 1 and 3, the membrane shape exhibits a kink that defines the contact angle θ_e. However, this kink cannot persist to small scales since the membrane has a finite bending rigidity and a sharp kink would imply an infinite bending energy. Therefore, the membrane should be smoothly curved on small scales and its contact with the pd interface should be characterized by an intrinsic contact angle θ_in, which represents the angle between the pd interface and the plane tangent to the membrane along the contact line.¹⁶ The relations 2 and 4 then imply that the angle θ_p* is identical with the intrinsic contact angle θ_in as introduced in ref (16). It represents the actual contact angle between the membrane and the pd interface at the nanometer scale. For the polymer composition as studied in the aspiration experiments, we obtain cos θ_p* ≅ 0.87 from linear extrapolation of cos θ_p as in Figure 3c and cos θ_p* = 0.86 ± 0.02 from relation 4. Thus, both estimates lead to θ_in = θ_p* ≅ 0.53 or 30° providing us with two methods to determine the intrinsic contact angle.

Since θ_in is smaller than 90°, the pe membrane segment and the pd interface pull roughly in the same direction. An increase in the interfacial tension arising, e.g., from an increase in the polymer concentrations, must then be primarily balanced by an increase in the mechanical tension Σ̂_de of the de membrane segment, which agrees with the data in Figure 2c for high polymer concentrations.

4. Discussion

Above, the budding process was analyzed using the force balance relations in eqs 1, which can be directly applied to the images as obtained by optical microscopy. As explained in ref (16), these force balance relations are valid in the tension-dominated regime, i.e., on length scales that exceed the characteristic scale Σ_pd/κ ≅ 100 nm, where κ is the bending rigidity of the membrane. On smaller scales, one obtains more complex force and torque balance equations, which also depend on the bending rigidity κ.¹⁶ However, the bending rigidity does not affect the intrinsic contact angle. Indeed, as shown here, we are able to deduce the existence of this contact angle from the coarse-grained force balance eqs 1 alone by considering the limit of a planar membrane, for which the effective contact angle θ_e approaches the limiting value θ_e = π; see the line of arguments after eq 2.

Wetting-induced budding requires contact of the membrane with both phases, whereby the budding direction depends on whether the two phases are inside or outside the vesicle; see Figure 1. If the membrane is wetted completely by one of them, wetting-induced budding cannot occur. Instead, the excess area created during deflation is stored in nanotubes stabilized by the membrane spontaneous curvature.¹³ Therefore, the wetting transition as in Figure 1b,c precedes the budding process.

More generally, the degree of budding and tubular formation results from the competition between the spontaneous curvature of the membrane and the wetting properties of the aqueous phases on the membrane. Spontaneous curvature favors tube formation. Since this process consumes excess membrane area, it also acts to suppress budding. Budding, on the other hand, is favored when neither one of the aqueous phases dominantly wets the membrane (i.e., partial wetting). Since the membrane must be wetted by both aqueous phases during the budding process, it cannot occur if the system exhibits complete wetting.

After the wetting transition, one has Σ_pd = (Σ̂_de – Σ̂_pe)/cos θ_in > Σ̂_de – Σ̂_pe corresponding to partial wetting with intrinsic contact angle θ_in. The energy cost of increasing the contact area between the membrane and the dextran-rich phase is smaller than the energy gain of decreasing the pd interfacial area. With deflation, the tensions Σ̂_pe and Σ̂_pe decrease and budding occurs spontaneously provided excess membrane area is available. Upon further deflation, the tension Σ̂_pe, which is dominated by the membrane spontaneous curvature¹³ saturates; see Figure 2c. This behavior reflects the fact that at high polymer concentration the fraction of dextran in the PEG-rich phase becomes negligible; see the Supporting Information.

Wetting-induced budding is not limited to equilibrated vesicles. It can also occur during the phase separation process if the transient tensions satisfy Σ_pd > Σ̂_de – Σ̂_pe and there is excess membrane area. More than one bud can form in a metastable state, as observed in our own experiments and in ref (11).

5. Conclusions

Vesicles in contact with two phases in the interior or exterior can undergo budding, provided the membrane is partially wetted by both phases and excess area is available. If one of the phases does not wet the membrane, it will exist as a small droplet inside or outside the vesicle. The budding process is governed by the interplay between the membrane tensions Σ̂_pe and Σ̂_de and the interfacial tension Σ_pd. We demonstrated that for a fixed composition of the liquid phases the budding process can be reversed by applying tension to the membrane.

The process of wetting-induced budding provides a possible mechanism for the selective vesicular transport in cells. Molecular crowding widely exists in the interior of cells and can lead to microcompartmentation. The membrane prefers to enclose macromolecular solutions, to which it has higher affinity, thus loading the appropriate molecules in transport vesicles. Wetting of a membrane by a liquid droplet creates a contact line, which may enhance endocytotic or exocytotic processes. Wetting-induced budding of vesicles in cells could be used to locally regulate and compartmentalize cellular processes such as protein synthesis, to restrict chemical reactions to particular segments of the membrane surface or parts of the cell, or to terminate such reactions by dewetting or bud retraction. Wetting-induced budding may also provide simple physical mechanism for vesicle shedding,¹⁷ involved in membrane traffic and molecule transfer among neighboring cells or to the cell exterior.

Supporting Information Available

Materials; giant vesicle preparation using electroformation; phase diagram of the polymer aqueous solution; batch measurements on deflated vesicles; force balance and intrinsic contact angle for inward budding; interfacial tension measurements; vesicle aspiration with micropipets; derivation of eq 3 in the main text; calculated vesicle shapes; saturation of the tension Σ̂_pe at high osmolarity ratios. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Author Present Address

^† Department of Biological Sciences and Program in Molecular and Computational Biology, University of Southern California, Los Angeles, California 90089.

Author Present Address

^‡ University Chemical Laboratories, University of Cambridge, Lensfield Road, Cambridge CB2 1EW, United Kingdom.