Abstract
In order to apply Sr/Ca and 44Ca/40Ca fractionation during calcium carbonate (CaCO3) formation as a proxy to reconstruct paleo-environments, it is essential to evaluate the impact of various environmental factors. In this study, a CO2 diffusion technique was used to crystallize inorganic calcite from aqueous solutions at different ionic strength/salinity by the addition of NaCl at 25 °C. Results show that the discrimination of Sr2+ versus Ca2+ during calcite formation is mainly controlled by precipitation rate (R in μmol/m2/h) and is weakly influenced by ionic strength/salinity. In analogy to Sr incorporation, 44Ca/40Ca fractionation during precipitation of calcite is weakly influenced by ionic strength/salinity too. At 25 °C the calcium isotope fractionation between calcite and aqueous calcium ions (Δ44/40Cacalcite-aq = δ44/40Cacalcite − δ44/40Caaq) correlates inversely to log R values for all experiments. In addition, an inverse relationship between Δ44/40Cacalcite-aq and log DSr, which is independent of temperature, precipitation rate, and aqueous (Sr/Ca)aq ratio, is not affected by ionic strength/salinity either. Considering the log DSr and Δ44/40Cacalcite-aq relationship, Sr/Ca and δ44/40Cacalcite values of precipitated calcite can be used as an excellent multi-proxy approach to reconstruct environmental conditions (e.g., temperature, precipitation rate) of calcite growth and diagenetic alteration.
1. Introduction
Trace and minor metal ratios (e.g., Sr/Ca and Mg/Ca) and stable isotope ratios (e.g., 18O/16O and 44Ca/40Ca) in biogenic CaCO3 have been widely used to estimate past sea surface temperatures (SST; e.g., Rostek et al., 1993; Elderfield and Ganssen, 2000; Gussone et al., 2004; Barker et al., 2005; Corrège, 2006). In addition, it is commonly accepted that the oxygen isotope ratio (18O/16O) in biogenic calcium carbonates is a function of salinity of the solution from which calcium carbonates were grown. Thus, combined with other chemical or isotopic indicators, 18O/16O ratios in biogenic calcium carbonates can also be used as a proxy for past sea surface salinity (SSS; e.g., Eisma et al., 1976; Rostek et al., 1993; Gussone et al., 2004; Sampei et al., 2005; Corrège, 2006).
Until now, only a few studies have examined the effect of salinity on 44Ca/40Ca ratios in biogenic calcium carbonates. The calcium isotopic composition of Thoracosphaera heimii (dinoflagellate) cysts was found to have no significant correlation with salinity (Gussone et al., 2010), whereas that of the planktic foraminifer, Globigerinoides ruber, was observed to have a negative linear correlation presumably due to a growth rate effect (Kısakürek et al., 2011).
The magnitude of salinity influence on Sr/Ca or Mg/Ca ratios in biogenic calcium carbonates remains disputed. Some studies (e.g., Eisma et al., 1976; Rosales et al., 2004) suggest a negligible salinity effect on Sr/Ca and/or Mg/Ca ratios in molluscs, whereas others (e.g., Klein et al., 1996; Nürnberg et al., 1996; Lea et al., 1999; Ferguson et al., 2008; Kısakürek et al., 2008, 2011; Dissard et al., 2010) postulate either a noticeable or a strong salinity effect on Sr/Ca and/or Mg/Ca ratios in mollusks and foraminifera. Additional studies (e.g., Dueñas-Bohórquez et al., 2009) indicate that salinity only influences Mg/Ca ratios but not Sr/Ca ratios in cultured planktonic foraminifera. The high Mg/Ca ratios of planktic foraminifera in high salinity environments were observed to be associated with early diagenetic effects through the precipitation of high-Mg-calcite overgrowths rather than physiological uptake (Hoogakker et al., 2009). However, foraminifera from the Atlantic coretop samples of Arbuszewski et al. (2010) have no diagenetic coatings but still show a clear salinity effect on Mg/Ca ratios. Thus, Arbuszewski et al. (2010) concluded that diagenetic overgrowth mechanism suggested by Hoogakker et al. (2009) for the high Mg/Ca ratios of foraminifera at high salinity was not applicable to their samples taken from open Atlantic Ocean.
Metabolic mechanisms may overprint mineralogical salinity effects on trace element incorporation in biogenic carbonates. However, even in inorganic precipitation experiments, the extent to which salinity influences Sr/Ca ratios of calcium carbonate crystals is also still under debate. Some studies (e.g., Holland et al., 1963, 1964; Katz et al., 1972; Gaetani and Cohen, 2006) indicate that Sr/Ca ratios in inorganic calcium carbonates are insensitive to variations in salinity. Holland et al. (1963, 1964) reported that, at temperatures between 90 and 100 °C, the Sr/Ca ratio in aragonite was essentially constant when NaCl concentrations varied from 36.2 to 3640 mM, and the Sr/Ca ratio in calcite was essentially independent of NaCl concentrations up to 1400 mM. In contrast, the experimental results of Pingitore and Eastman (1986) imply a significant decrease of Sr/Ca ratios in calcite with increasing salinity. They reported that Sr distribution coefficients (i.e., their partition coefficient k Sr) ranged from 0.10 to 0.19 without NaCl in the growth solutions of calcite but from 0.04 to 0.06 with 480 mM NaCl in the growth solutions. Thus, the presence of dissolved NaCl significantly lowered the Sr/Ca ratio in calcite. Pingitore and Eastman (1986) proposed a multiple site model and argued that the depression of Sr partitioning in the presence of NaCl might be due to competition between Na+ and Sr2+ for non-lattice sites. Although values for respective precipitation rates are not given in Pingitore and Eastman (1986) as in most of the other studies, their experiments indicated that fast precipitation resulted in more Sr partitioning into calcite. The multiple site model was again proposed by Pingitore and Eastman (1986) as a possible cause of rate effect on Sr partitioning. They suggested that non-lattice sites probably were related to site defects with preferential incorporation of larger cations (such as Sr2+) than Ca2+. Fast precipitation results in more crystal defects and thus a larger partition coefficient k Sr.
It is not a trivial task to constrain the impact of ionic strength on Sr/Ca and 44Ca/40Ca fractionation during inorganic calcium carbonate formation. If no ionic strength effect is identified on Sr/Ca and 44Ca/40Ca ratios, both may be used as potential proxies for past SST and to isolate temperature and salinity effects on 18O/16O ratio in inorganic calcium carbonates. If a salinity effect does exist, Sr/Ca and 44Ca/40Ca ratios can be calibrated by salinity, and may be used to trace past SSS. However, in any of the tasks above special attention has to be given to precipitation rate, as a strong rate impact on Sr incorporation and calcium isotope fractionation during inorganic calcite precipitation is known from previous studies (e.g., Lorens, 1981; Tesoriero and Pankow, 1996; Lemarchand et al., 2004; Tang et al., 2008a,b).
In our previous studies (Tang et al., 2008a,b), the effect of temperature and precipitation rate on Sr/Ca and 44Ca/40Ca fractionation was investigated and the possibility to use Sr/Ca and 44Ca/40Ca fractionation as a multi-proxy to decipher calcite precipitation conditions was discussed. In this study, inorganic calcite was precipitated from aqueous solutions at different ionic strength/salinity by the addition of NaCl. Our purpose was to investigate the impact of salinity/ionic strength on Sr/Ca and 44Ca/40Ca fractionation during the precipitation of inorganic calcite at well-known physicochemical conditions and precipitation rates.
2. Methods
All experiments were conducted at room temperature (25 ± 0.5 °C) in a temperature-controlled laboratory or a water bath. The chemicals used in our experiments, CaCl2·2H2O, SrCl2·6H2O, NaCl, NaOH, NaHCO3, and NH4Cl (Merck), were reagent grade. Deionized water (18.2 MΩ cm, ELGA PURELAB Maxima) was used to prepare aqueous solutions. Values of pH were measured by a pH combination electrode (SCHOTT Blue Line 28 pH Pt 1000), calibrated at 25 °C with NIST certified buffer solutions (pH 4.01, 7.00, and 10.00). Calcite was grown from 10 mM CaCl2 + 5 mM NH4Cl + 0.1 mM SrCl2 background solution. Although two experiments (Experiments #12 and #13 in Table 1 ) were conducted without Sr addition, about 0.7 μM of Sr in the growth solution was still observed by ICP-OES analyses due to the Sr content of the reagent grade CaCl2·2H2O used in our experiments. In order to investigate the effect of salinity/ionic strength on Sr/Ca and 44Ca/40Ca fractionation in calcite, precipitation experiments were conducted with (1) background solution; (2) background solution + 257 mM NaCl; and (3) background solution + 797 mM NaCl.
Table 1.
Experimental data for Sr/Ca and 44Ca/40Ca fractionation during inorganic calcite formation from solutions with different salinities/ionic strengths at room temperature (25 ± 0.5 °C).
| No. | pH | I (mM) | Salinity (‰) | [NH4Cl] (mM) | [NaCl] (mM) | [Ca]o (mM) | [Sr]o (μM) | Sr in calcite (mg/kg CaCO3) | SIcalcite | log Ra (μmol/m2/h) | log DSrb | Δ44/40Cacalcite-aq (‰) ± 2SEMc (n) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 9.6 | 96.1 | 1477 | 1.21 | 4.2 | −0.79 | −1.50 ± 0.19 (6) | |||||
| 2 | 9.6 | 94.6 | 1131 | 1.11 | 3.6 | −0.91 | −1.17 ± 0.10 (2) | |||||
| 3 | 9.8 | 96.7 | 976 | 1.11 | 3.1 | −0.97 | −1.04 ± 0.10 (4) | |||||
| 4 | 9.7 | 95.1 | 830 | 0.94 | 3.0 | −1.03 | −0.80 ± 0.10 (4) | |||||
| 5 | 10.0 | 96.5 | 600 | 0.66 | 2.3 | −1.18 | −0.62 ± 0.16 (6) | |||||
| 6 | 9.9 | 96.1 | 932 | 0.89 | 3.3 | −0.97 | −1.03 ± 0.12 (4) | |||||
| 7 | 35 | 1.8 | 0 | 9.9 | 93.1 | 525 | 0.65 | 2.4 | −1.21 | −0.51 ± 0.10 (2) | ||
| 8 | 9.7 | 92.1 | 673 | 0.69 | 2.4 | −1.12 | −0.67 ± 0.10 (2) | |||||
| 9 | 9.9 | 94.3 | 1503 | 1.21 | 4.2 | −0.76 | −1.37 ± 0.15 (7) | |||||
| 10 | 10.0 | 94.9 | 1387 | 1.12 | 3.9 | −0.79 | −1.47 ± 0.17 (6) | |||||
| 11 | 10.3 | 96.5 | 1355 | 1.23 | 4.0 | −0.81 | −1.41 ± 0.10 (2) | |||||
| 12 | 9.8 | 0.78 | 9.37 | 1.07 | 3.8 | −0.90 | −0.93 ± 0.10 (6) | |||||
| 13 | 8.3 | 5 | 9.9 | 0.67 | 4.20 | 0.78 | 2.4 | −1.17 | −0.73 ± 0.23 (8) | |||
| 14 | 9.9 | 99.2 | 1168 | 0.99 | 3.0 | −0.91 | −1.16 ± 0.20 (7) | |||||
| 15 | 9.3 | 93.3 | 1099 | 0.96 | 2.8 | −0.97 | −0.99 ± 0.01 (2) | |||||
| 16 | 9.2 | 93.3 | 1210 | 0.86 | 2.7 | −0.96 | −0.83 ± 0.08 (3) | |||||
| 17 | 292 | 16.8 | 257 | 9.0 | 90.2 | 959 | 1.17 | 3.4 | −1.03 | −0.68 ± 0.20 (5) | ||
| 18 | 8.2 | 82.0 | 838 | 1.13 | 3.2 | −1.08 | −0.66 ± 0.12 (5) | |||||
| 19 | 9.2 | 93.1 | 1200 | 1.07 | 3.2 | −0.93 | −1.02 ± 0.10 (3) | |||||
| 20 | 9.7 | 98.9 | 532 | 0.88 | 2.2 | −1.26 | −0.71 ± 0.11 (4) | |||||
| 21 | 8.7 | 90.7 | 532 | 0.84 | 1.9 | −1.25 | −0.38 ± 0.05 (3) | |||||
| 22 | 9.3 | 87.2 | 921 | 1.05 | 3.6 | −0.99 | −1.12 ± 0.12 (4) | |||||
| 23 | 9.1 | 83.0 | 598 | 0.63 | 3.6 | −1.11 | −0.91 ± 0.05 (2) | |||||
| 24 | 832 | 49 | 799 | 9.5 | 92.0 | 703 | 0.80 | 3.7 | −1.07 | −0.71 ± 0.06 (2) | ||
| 25 | 9.2 | 91.0 | 762 | 1.22 | 3.7 | −1.07 | −0.83 ± 0.05 (2) | |||||
| 26 | 9.6 | 89.0 | 806 | 0.83 | 3.8 | −1.01 | −0.79 ± 0.22 (4) | |||||
pH: pH of growth solution; I: ionic strength; [Ca]o: initial Ca concentration; [Sr]o: initial Sr concentration; SIcalcite: critical saturation index with respect to calcite; R: precipitation rate of calcite; DSr: distribution coefficient for Sr in calcite; Δ44/40Cacalcite-aq = δ44/40Cacalcite − δ44/40Caaq. Experiments #1–13 are from Tang et al. (2008b). n is the number of repeat measurements.
Error of measured precipitation rate is log R ± 0.12, estimated from three duplicate experiments (see Tang et al., 2008a).
Error of measured Sr distribution coefficient is log DSr ± 0.03, estimated from three duplicate experiments (see Tang et al., 2008a).
SEM is the standard error of the mean.
A CO2-diffusion technique was used to spontaneously precipitate inorganic calcite from the experimental solutions. Experimental setup has been described in detail in our previous study (Tang et al., 2008a). Briefly, a polyethylene (PE) bottle containing 0.5 L of 0.83 M NaHCO3 solution was soaked in a vessel containing 5 L of the growth solution (background solution with NaCl as described above). According to Dietzel et al. (2004), PE membrane allows CO2 diffusion from the NaHCO3 solution to the growth solution, but prevents any cation diffusion from the growth solution to the NaHCO3 solution and vice versa. Thus, calcite precipitation only occurs in the growth solution. The pH of the growth solution is kept constant at 8.30 by automatic pH-stat titration with an accuracy of ±0.03 (Schott TitroLine alpha plus). To assure a homogeneous solution for calcite growth, the growth solution was stirred at 200 rpm using a floating stir bar (NALGENE® Labware, DS6630-4000). The precipitation rate of calcite was controlled by adjusting the flux of CO2 by changing the pH of the NaHCO3 solution and/or the thickness of PE membrane.
Formation of calcite as a single CaCO3 polymorph was verified using X-ray diffraction (XRD, goniometer type Philips PW 1130/1370), Infrared Spectroscopy (FTIR, Perkin Elmer 1600), Micro Raman Spectroscopy (LABRAM HR-800UV), and imaging by scanning electron microscopy (SEM, ZEISS Ultra 55). Typical FT-IR spectra and FT-Raman spectra of calcite grown from our CO2-diffusion technique were presented in Tang et al. (2008a). All calcite precipitates of our experiments exhibit typical rhombohedral habit (Fig. 1 ). Precipitation rates (R) were calculated from the amount of calcite precipitated, growth time, and specific surface area. Specific surface area was estimated from particle size distribution of the final solid phase with a centrifugal particle size analyzer (SHIMADZU SA-CP2). Typical cumulative particle size distribution curves and the data about specific surface area of calcite as a function of growth time were also presented in Tang et al. (2008a). The reader is referred to Tang et al. (2008a) for more details about the procedure to estimate precipitation rate.
Fig. 1.
Representative scanning electron micrographs (SEM) of calcite grown from solutions with different ionic strengths: (a) I = 35 mM (No. 1 in Table 1); (b) I = 292 mM (No. 18); and (c) I = 832 mM (No. 26).
During each experiment, the chemical evolution of the growth solution was monitored by ICP-OES (Perkin Elmer Optima 4300DV) measurement of small volumes (5 ml) of the growth solution, sampled at specific time intervals. Because calcite crystals grown from our experiments are tiny (particle size less than 50 μm), an aliquot (about 10 mg) of well-mixed solid calcite crystals was sufficient for determining the cation composition of precipitated calcite. Thus, in our studies, about 10 mg of solid calcite crystals from each experiment was dissolved into 20 ml of 2% bidistilled HNO3 solution and the digestion solution was analyzed by ICP-OES.
In this study, the Sr/Ca fractionation between calcite and solution is expressed as a Sr distribution coefficient according to the equation
| (1) |
where ([Sr]/[Ca])calcite is the molar Sr/Ca ratio of precipitated calcite and ([Sr]/[Ca])aq is the molar Sr/Ca ratio of the growth solution. Apparent D Sr value for each experiment was estimated from the composition of initial and final growth solution and cation content of precipitated calcite. On average, Ca and Sr concentrations decreased by 10% and 2%, respectively, during the experiments. The overall evolution of the Sr distribution of the bulk calcite can be described by the expression (Usdowski, 1975)
| (2) |
where ([Sr]/[Ca])bulk calcite is the Sr/Ca molar ratio in the bulk calcite, ([Sr]/[Ca])aq,o is the initial Sr/Ca molar ratio in the aqueous solution before calcite precipitation, and ([Ca]/[Ca]o)aq is the molar concentration ratio of aqueous Ca to the initial aqueous Ca (Tang et al., 2008a for more details about the estimation of D Sr values).
Calcium isotope ratios of calcites and CaCl2·2H2O used for the growth solutions were measured with a Thermo Fisher Triton TI (Thermal Ionization Mass Spectrometer, TIMS) closely following the procedure described in Heuser et al. (2002). About 2 mg of calcite taken from well-mixed samples or 2 mg of CaCl2·2H2O were dissolved in 2.2 N ultrapure HCl, evaporated and re-dissolved with a Ca concentration of 160 ng/μl. The solutions were mixed with a 43Ca/48Ca double spike and evaporated to dryness. About 300 ng of the sample-spike mixture were loaded with 1.5 μl of 2.2 N HCl and 1 μl of TaCl5 activator solution on a zone-refined Re filament for TIMS measurements. More details about the Ca isotope measurements were given in Tang et al. (2008b).
Following the suggestion of Eisenhauer et al. (2004), the 44Ca/40Ca ratios are reported as δ44/40Ca (‰) values relative to the NIST standard SRM915a, where δ44/40Ca = [(44Ca/40Ca)sample/(44Ca/40Ca)SRM915a − 1] × 1000. Calcium isotope fractionation between calcite and solution is expressed as Δ44/40Cacalcite-aq = δ44/40Cacalcite − δ44/40Caaq, where δ44/40Cacalcite and δ44/40Caaq are the Ca isotope composition of calcite and the growth solution, respectively. The δ44/40Ca of CaCl2·2H2O was determined as 1.10 ± 0.04 ‰ (±2 standard errors of the mean, n = 9) in the first set of experiments (#1–22, Table 1) and 0.98 ± 0.08 ‰ (n = 5) in experiments #23–26. The external reproducibility of δ44/40Ca, based on repeated measurements of NIST SRM915a, was ±0.10‰ (standard deviation, n = 52). IAPSO seawater standards measured during sample analyses showed a δ44/40Ca of 1.84 ± 0.08‰ (±2 standard errors of the mean, n = 13). Total Ca blanks for the isotope analyses were less than 1%.
3. Results
Calculated ionic strengths/salinities, estimated precipitation rates, and measured D Sr and Δ44/40Cacalcite-aq values for each experiment are given in Table 1.
3.1. DSr values measured at different ionic strengths/salinities
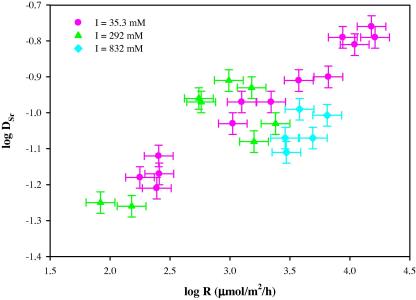
D Sr values measured at different ionic strengths are plotted in Fig. 2 as a function of precipitation rate (R). As shown in Fig. 2, Sr incorporation into calcite is highly influenced by precipitation rate. D Sr values generally increase with increasing precipitation rates. By contrast, an increase of ionic strength from 35 to 832 mM (salinity from ∼2‰ to 49‰) only leads to some variations in D Sr values. It is not very clear that D Sr values will decrease with increasing ionic strengths, mainly due to the scattered data points obtained at an ionic strength of 292 mM (see Fig. 2).
Fig. 2.
log DSr versus log R for inorganic calcite grown from solutions with different ionic strengths. DSr is the Sr distribution coefficient of calcite. R is the precipitation rate of calcite (T = 25 °C; pH 8.3).
To identify the contribution of precipitation rate (R) and ionic strength (I) to variation in D Sr values, linear regression analyses were carried out using the statistic software R (version 2.7.1). Table 2 presents linear regression results in detail. According to linear regression analyses, the relationship between log D Sr and log R at three ionic strengths investigated in this study can be described as follows,
| (3) |
Eq. (3) is very similar to the rate equation of D Sr at 25 °C and ionic strength = 35 mM reported in our previous study (Tang et al., 2008a). But r 2 value for Eq. (3) is 0.667, whereas r 2 value for the rate equation of D Sr at 25 °C and ionic strength = 35 mM is 0.97 (Tang et al., 2008a). This indicates that variation in ionic strength weakens the relationship between log D Sr and log R at 25 °C. The contribution of both precipitation rate (R) and ionic strength (I) to variation in D Sr values can be described as follows,
| (4) |
Eq. (4) indicates that increase of ionic strength statistically decreases D Sr values.
Table 2.
The output of coefficients and the associated summary for: (a) a simple linear regression between log DSr and log R; and (b) a multiple linear regression between log DSr and log R + ionic strength (I).
| Coefficients | Standard error | t stat | p-value | Lower 95% | Upper 95% | |
|---|---|---|---|---|---|---|
| (a) | ||||||
| Intercept | −1.571 | 0.083 | −19.026 | 5.55e−16 | −1.741 | −1.400 |
| log R | 0.176 | 0.025 | 6.934 | 3.60e−7 | 0.123 | 0.228 |
| Summary | The regression equation: log DSr = (−1.571 ± 0.171) + (0.176 ± 0.053) · log R Residual standard error: 0.08288 on 24 degrees of freedom r2: 0.667, adjusted r2: 0.653 F-statistic: 48.08 on 1 and 24 DF, p-value: 3.6e−7 |
|||||
| (b) | ||||||
| Intercept | −1.566 | 0.066 | −23.832 | <2e−16 | −1.702 | −1.430 |
| log R | 0.186 | 0.020 | 9.223 | 3.44e−9 | 0.146 | 0.231 |
| I | −0.170 | 0.044 | −3.859 | 7.97e−4 | −0.261 | −0.079 |
| Summary | The regression equation: log DSr = (−1.566 ± 0.136) + (0.186 ± 0.043) · log R − (0.170 ± 0.091) · I Residual standard error: 0.06596 on 23 degrees of freedom r2: 0.798, adjusted r2: 0.780 F-statistic: 45.4 on 2 and 23 DF, p-value: 1.033e−8 |
|||||
In Table 2, “p-value” for each variable (i.e., log R or I) is the possibility that the coefficient (slope) of each variable = 0, in other words, the possibility that there is no relationship between log D Sr and log R or I. The “p-value” for the regression equation is the possibility that all coefficients (slopes) are 0, in other words, the possibility that this regression equation is caused by the noisy data. In the test of significance, typical values for the significance level are 0.1, 0.05, and 0.01. In this study, we choose 0.01 as the significance level. If “p-value” is less than or equal to 0.01, the influence of precipitation rate (R) or ionic strength (I) to D Sr values is considered to be statistically significant. As shown in Table 2, “p-values” for the slope of log R = 0 are far less than 0.01 in both single and multiple linear regressions. Therefore, precipitation rate (R) surely influences observed D Sr values. The “p-value” for the slope of ionic strength (I) = 0 in a multiple linear regression is 7.97e−4, less than 0.01. Thus, it is valid to say that ionic strength (I) also influences observed D Sr values.
Although “p-values” indicate that both precipitation rate (R) and ionic strength (I) will influence Sr partitioning, r 2 (the square of the correlation) values in Table 2 tell us that Sr partitioning is mainly controlled by precipitation rate (R). As shown in Table 2, “r 2” for a simple linear regression between log D Sr and log R is 0.667, which means that 66.7% of variation in log D Sr values is caused by log R. Value of “r 2” for a multiple linear regression between log D Sr and log R + ionic strength (I) is 0.798, which means that the additional effect of ionic strength (I) only accounts for 13.1% (i.e., 0.798–0.667) of variation in log D Sr values.
Previous studies (e.g., Zhang and Dawe, 1998; Zuddas and Mucci, 1998) indicate that an increase of ionic strength might increase precipitation rate. To evaluate the possible effect of ionic strength on precipitation rate in our experiments, an ideal way is to conduct the experiments at the same conditions except for ionic strength and to determine precipitation rates at different ionic strengths. Unfortunately, we did not conduct such a series of experiments. However, statistical analyses might provide useful information to test the correlation between precipitation rate and ionic strength in our experiments. In multiple linear regressions, if there is a correlation between two variables, one of them should be eliminated from the regression model. When a variable was eliminated from the regression model, calculated AIC (Akaike’s Information Criterion) value for the model will change. The model with the smallest AIC value is the suitable model. Therefore, calculated AIC values for different linear regression models can provide useful information about any possible correlation between two variables. If an increase in ionic strength leads to an increase in precipitation rate (i.e., there is a correlation between ionic strength and precipitation rate), the elimination of log R or ionic strength (I) from multiple linear regressions would result in a smaller AIC value. Our calculations using the statistic software R (version 2.7.1) show that AIC = −100.33 when log R was eliminated from the linear regression model, AIC = −127.58 when ionic strength (I) was eliminated from the linear regression model, and AIC = −138.56 when both log R and I were included in the linear regression model. Calculated AIC values indicate that elimination of log R or ionic strength (I) did not result in a smaller AIC value and the suitable regression model should include both precipitation rate and ionic strength. This means that there is no significant correlation between precipitation rate and ionic strength.
In summary, our linear regression analyses indicate that ionic strength indeed influences Sr partitioning, supported by “p-values” for the slope of ionic strength (I) = 0 in a multiple linear regression and calculated AIC values. However, calculated “r 2” values indicate that ionic strength influences Sr partitioning in a minor degree and Sr partitioning is mainly controlled by precipitation rate. Calculated AIC values also indicate that precipitation rates are not significantly affected by ionic strength in our inorganic calcite formation experiments.
3.2. Δ44/40Cacalcite-aq values measured at different ionic strengths/salinities
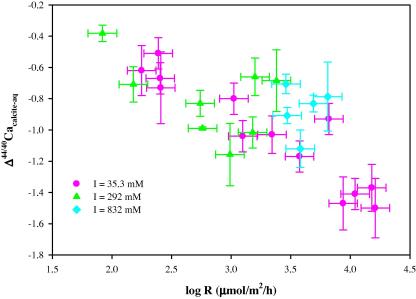
When Δ44/40Cacalcite-aq values measured at different ionic strengths are plotted as a function of precipitation rate (Fig. 3 ), it is obvious that precipitation rate is the primary factor that controls Ca isotope fractionation between precipitated calcite and the growth solution. In general, a fast precipitation will result in a larger absolute Δ44/40Cacalcite-aq value. The presence of NaCl in the growth solution leads to some variations in Δ44/40Cacalcite-aq values. But Fig. 3 shows that Δ44/40Cacalcite-aq values are less sensitive to changes in ionic strengths than to changes in precipitation rates.
Fig. 3.
Δ44/40Cacalcite-aq versus log R for inorganic calcite grown from solutions with different ionic strengths. Δ44/40Cacalcite-aq = δ44/40Cacalcite − δ44/40Caaq, where δ44/40Cacalcite is 44Ca/40Ca ratio measured in calcite relative to the SRM915a standard and δ44/40Caaq is 44Ca/40Ca ratio measured in the growth solution relative to the SRM915a standard. R is the precipitation rate of calcite (T = 25 °C; pH 8.3).
Linear regression analyses were also carried out using the statistic software R (version 2.7.1) to evaluate the contribution of precipitation rate (R) and ionic strength (I) to variation in Δ44/40Cacalcite-aq values. Table 3 presents linear regression results in detail. Linear regression results show that the relationship between Δ44/40Cacalcite-aq and log R at three ionic strengths investigated in this study can be described as follows,
| (5) |
Eq. (5) is slightly different to the rate equation of Δ44/40Cacalcite-aq at 25 °C and ionic strength = 35 mM reported in our previous study (Tang et al., 2008b). This indicates that variation in ionic strength influences the relationship between Δ44/40Cacalcite-aq and log R at 25 °C in some degree. The contribution of both precipitation rate (R) and ionic strength (I) to variation in Δ44/40Cacalcite-aq values can be described as follows,
| (6) |
Eq. (6) indicates that increase of ionic strength statistically increases Δ44/40Cacalcite-aq values.
Table 3.
The output of coefficients and the associated summary for: (a) a simple linear regression between Δ44/40Cacalcite-aq and log R; and (b) a multiple linear regression between Δ44/40Cacalcite-aq and log R + ionic strength (I).
| Coefficients | Standard error | t stat | p-value | Lower 95% | Upper 95% | |
|---|---|---|---|---|---|---|
| (a) | ||||||
| Intercept | 0.166 | 0.197 | 0.841 | 0.409 | −0.242 | 0.573 |
| log R | −0.341 | 0.061 | −5.632 | 8.48e−6 | −0.466 | −0.216 |
| Summary | The regression equation is Δ44/40Cacalcite-aq = (0.166 ± 0.408) − (0.341 ± 0.125) · log R Residual standard error: 0.1982 on 24 degrees of freedom r2: 0.569, adjusted r2: 0.551 F-statistic: 31.72 on 1 and 24 DF, p-value: 8.481e−6 |
|||||
| (b) | ||||||
| Intercept | 0.157 | 0.174 | 0.903 | 0.376 | −0.203 | 0.517 |
| log R | −0.366 | 0.054 | −6.772 | 6.6e−7 | −0.478 | −0.254 |
| I | 0.329 | 0.117 | 2.825 | 9.6e−3 | 0.088 | 0.570 |
| Summary | The regression equation Δ44/40Cacalcite-aq = (0.157 ± 0.360) − (0.366 ± 0.112) · log R + (0.329 ± 0.241) · I Residual standard error: 0.1744 on 23 degrees of freedom r2: 0.680, adjusted r2: 0.652 F-statistic: 24.46 on 2 and 23 DF, p-value: 2.023e−6 |
|||||
In Table 3, “p-value” and “r 2” have the same definition as those in Table 2. As shown in Table 3, “p-values” for the slope of log R = 0 are far less than 0.01 in both single and multiple linear regressions. Therefore, precipitation rate (R) apparently influences observed Δ44/40Cacalcite-aq values. The “p-value” for the slope of ionic strength (I) = 0 in a multiple linear regression is 9.6e−3, slightly less than 0.01. Thus, it is valid to say that ionic strength (I) also influences observed Δ44/40Cacalcite-aq values.
However, r 2 values in Table 3 indicate that Ca isotope fractionation is mainly controlled by precipitation rate (R). As shown in Table 3, “r 2” for a simple linear regression between Δ44/40Cacalcite-aq and log R is 0.569, which means that 56.9% of variation in Δ44/40Cacalcite-aq values are caused by log R. Value of “r 2” for a multiple linear regression between Δ44/40Cacalcite-aq and log R + ionic strength (I) is 0.680, which means that the additional effect of ionic strength (I) only accounts for 11.1% (i.e., 0.680–0.569) of variation in Δ44/40Cacalcite-aq values.
Once again, calculated AIC values for linear regressions between Δ44/40Cacalcite-aq and log R + ionic strength (I) indicate that, in our calcite precipitation experiments, precipitation rate of calcite was not effectively influenced by ionic strength. As discussed above, if there is a correlation between ionic strength and precipitation rate, the elimination of log R or ionic strength (I) from multiple linear regressions would result in a smaller AIC value. Our calculations using the statistic software R (version 2.7.1) show that, in linear regressions between Δ44/40Cacalcite-aq and log R + ionic strength (I), AIC = −61.48 when log R was eliminated from the linear regression model, AIC = −82.24 when ionic strength (I) was eliminated from the linear regression model, and AIC = −87.99 when both log R and I were included in the linear regression model. Calculated AIC values show that elimination of log R or ionic strength (I) did not result in a smaller AIC value and the suitable regression model should include both precipitation rate and ionic strength.
In summary, linear regression analyses indicate that ionic strength plays a similar role in Ca isotope fractionation as it does in Sr partitioning. That is, ionic strength indeed influences Ca isotope fractionation, supported by “p-values” for the slope of ionic strength (I) = 0 in a multiple linear regression (see Table 3) and calculated AIC values. However, calculated “r 2” values (see Table 3) indicate that ionic strength influences Ca isotope fractionation in a minor degree and Ca isotope fractionation is mainly controlled by precipitation rate.
3.3. Relationship between DSr and Δ44/40Cacalcite-aq at different ionic strengths/salinities
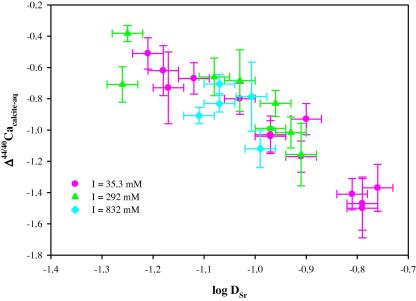
In our previous study (Tang et al., 2008b), we noticed a strong relationship between D Sr and Δ44/40Cacalcite-aq and this relationship was observed to be independent of temperature, precipitation rate, and Sr/Ca ratio in the growth solution. Our new experimental data further verify this relationship and document that the strong relationship between D Sr and Δ44/40Cacalcite-aq is also independent of ionic strength from about 35 up to 832 mM (Fig. 4 ).
Fig. 4.
Correlation between Δ44/40Cacalcite-aq and log DSr [Δ44/40Cacalcite-aq = (−1.90 ± 0.23) · log DSr − 2.85 ± 0.22, R2 = 0.90, p < 10−15, n = 31] observed in our experiments conducted at ionic strength ranging from 35 to 832 mM (salinity from ∼2‰ to 49‰).
4. Discussion
4.1. Salinity/Ionic strength effect on Sr2+/Ca2+ in calcite
In our experiments, calcite spontaneously grew from solution. Under such conditions, the increase of ionic strength from about 35 to 832 mM has no significant influence on D Sr values at constant apparent precipitation rates (see Fig. 2). Statistical analysis (see above) reveals that observed variation in D Sr values is largely driven by precipitation rate in accordance with our earlier results (Tang et al., 2008a). Ionic strength effects are minor and only contribute to 13.1% of the explained variation in D Sr values. Because, in the multiple linear regression, the “p-value” for the slope of ionic strength = 0 is less than 0.01, a correlation between ionic strength and D Sr values does exist, although the contribution of ionic strength to variation in D Sr values is minor. In accordance with this result, previous studies (e.g., Holland et al., 1963, 1964; Gaetani and Cohen, 2006) reported an insignificant ionic strength effect on D Sr values (also called partition coefficient, k Sr, within some studies) in unseeded experiments, where inorganic calcium carbonate was spontaneously precipitated. However, a strong ionic strength effect on Sr distribution coefficient of calcite was observed in experiments of Pingitore and Eastman (1986), where seeds were used to induce calcite precipitation. In their experiments, elevated ionic strength depressed Sr incorporation into calcite (causing low D Sr values). Besides ionic strength effect, Pingitore and Eastman (1986) also reported a strong effect of aqueous Sr concentration on D Sr values. In contrast, in experiments where inorganic calcium carbonates were spontaneously precipitated (Holland et al., 1963, 1964; Gaetani and Cohen, 2006; Tang et al., 2008a), D Sr values were independent of Sr concentrations in the growth solution. Thus, different experimental conditions might result in distinct Sr incorporation behavior into calcite.
Pingitore and Eastman (1986) used a multiple site model to interpret the effects of aqueous Sr concentration and ionic strength and on their k Sr values (given as D Sr in the following text). More specifically, Pingitore and Eastman (1986) argued that two types of sites are involved in Sr incorporation during calcite formation: (1) normal lattice sites and (2) non-lattice sites (wherein site defects favor Sr versus Ca incorporation). The abundance of non-lattice sites is less than that of normal lattice sites. As a result, non-lattice contribution to D Sr is significant at low aqueous Sr concentrations and becomes less important with increasing aqueous Sr concentrations. Thus, measured D Sr values depend inversely on aqueous Sr concentrations in their experiments. Using the multiple site model, Pingitore and Eastman (1986) interpreted that the decrease in D Sr values with increasing ionic strength was owing to competition between Sr2+ and Na+ ions for non-lattice sites. If both normal lattice sites and non-lattice sites were involved in Sr incorporation and Na competes for limited non-lattice sites with Sr, higher Na concentration at high ionic strength will lower Sr incorporation at constant R. Thus, the multiple site model of Pingitore and Eastman (1986) might be reasonable to describe Sr incorporation into calcite under their experimental conditions where seeds were used to induce calcite precipitation.
But from the view of kinetics of calcite growth, strong negative ionic strength effect on D Sr values observed by Pingitore and Eastman (1986) is perplexing. Previous studies on the influence of high ionic strength on inorganic calcite precipitation using a seed-induced technique (e.g., Zhang and Dawe, 1998; Zuddas and Mucci, 1998) suggest that the precipitation rate of calcite will increase with increasing ionic strength. It is well documented that Sr incorporation into calcite is a precipitation rate-controlled process and fast precipitation leads to a larger D Sr value (Fig. 2; Lorens, 1981; Tesoriero and Pankow, 1996; Tang et al., 2008a). Thus, during seed-induced precipitations, D Sr values are expected to be positively correlated with ionic strength, because an increase in ionic strength will result in an increase in precipitation rate and thus an increase in D Sr values. Indeed, several culture experiments (i.e., Lea et al., 1999; Kısakürek et al., 2008; Dissard et al., 2010) reported that Sr/Ca ratio in foraminiferal calcite increases with increasing salinity. Because all these culture experiments suggest that the Sr/Ca ratios in foraminiferal calcite are primarily controlled by the growth rate, the positive relationship between salinity and Sr/Ca ratios observed in these culture experiments was unanimously interpreted by the corresponding authors as a result of a kinetic effect, i.e., salinity indirectly influences the Sr/Ca ratios most likely through its impact on the growth rate of foraminiferal calcite. In a word, a strong negative correlation between ionic strength and Sr partitioning observed in Pingitore and Eastman’s (1986) seed-induced calcite precipitations is inconsistent with a weakly positive correlation between ionic strength and Sr partitioning reported in most of previous studies and is difficult to understand in view of kinetics of calcite growth.
In current studies as well as previous experiments where inorganic calcium carbonates were spontaneously precipitated (Holland et al., 1963, 1964; Gaetani and Cohen, 2006; Tang et al., 2008a), D Sr values were independent of Sr concentrations in the growth solution and weakly influenced by ionic strength. This is inconsistent with the significant non-lattice contribution to D Sr at low aqueous Sr concentrations and the competition for non-lattice sites between Na+ and Sr2+ at high ionic strengths suggested by the multiple site model. Thus, the multiple site model is not applicable to spontaneous calcite precipitation. Moreover, linear regression analyses (see Sections 3.1 and 3.2) indicate that, in our spontaneous calcite precipitations, ionic strength is not correlated with precipitation rate, at least not at a statistic significance level. This is inconsistent with a positive correlation between ionic strength and precipitation rate observed in seed-induced calcite precipitation (e.g., Zhang and Dawe, 1998; Zuddas and Mucci, 1998). Therefore, we argue that main controls on calcite growth are different between seed-induced precipitation and spontaneous precipitation. Calcite growth rates are not only controlled by the degree of supersaturation but also affected by aqueous Ca2+/CO3 2− ratio (Nehrke et al., 2007), ionic strength (Zhang and Dawe, 1998; Zuddas and Mucci, 1998), and pH (Ruiz-Agudo et al., 2011). The degree of supersaturation is relatively lower during seed-induced precipitation than during spontaneous precipitation. As a result, the solution composition such as aqueous Ca2+/CO3 2− ratio, ionic strength, and pH might play a larger role in calcite growth during seed-induced precipitation, whereas, the degree of supersaturation might play a more important role in calcite growth during spontaneous precipitation. In addition, during seed-induced precipitation, Sr partitioning may occur at the surface of seeds and the multi sites may already exist for the competition between Na+ and Sr2+. But during spontaneous precipitation, there are no existing surface sites and Sr partitioning might be mainly controlled by the first nucleus of crystal at critical supersaturation. Therefore, during spontaneous precipitation such as our inorganic calcite formation, Sr partitioning is mainly controlled by precipitation rate and ionic strength only plays a minor role in Sr partitioning.
According to our previous studies (Tang et al., 2008a), Sr partitioning in calcite under our experimental conditions can be successfully interpreted by the surface enrichment model (SEMO), i.e., the degree of disequilibrium Sr partitioning in calcite depends on the competition between the entrapment of the composition of Sr-enriched surface layer by crystal growth and the ion diffusion in the newly formed crystal lattice. Fast precipitation will favor the entrapment of the composition of Sr-enriched surface layer and increase the distance for ion diffusion in the newly formed crystal lattice. As a result, Sr partitioning is sensitive to precipitation rate. However, ionic strength does not effectively influence calcite growth in our experiments suggested by linear regression analyses (see Section 3.1) and cannot influence ion diffusion as temperature does. Therefore, a weak impact of ionic strength on Sr partitioning is expected by the surface entrapment model.
4.2. Salinity/Ionic strength effect on 44Ca/40Ca ratios in calcite
An increase of ionic strength from 35 to 832 mM (salinity from ∼2‰ to 49‰) does not significantly change the Δ44/40Cacalcite-aq values in our experiments at a given precipitation rate (see Table 1). Instead, Δ44/40Cacalcite-aq values of calcite precipitated at different ionic strengths generally follow the same trend in the plot of Δ44/40Cacalcite-aq versus log R (see Fig. 3). Statistical analysis (see above) indicates that ionic strength effects only account for 11.1% of the explained variation in Δ44/40Cacalcite-aq values. However, in the multiple linear regression between Δ44/40Cacalcite-aq and log R + ionic strength (I), the p value for the slope of ionic strength = 0 is close to 0.01 but less than 0.05. Thus, it is still valid to say that ionic strength indeed influences Δ44/40Cacalcite-aq values during inorganic calcite formation. Our results suggest that precipitation rate is the primary factor that controls Ca isotope fractionation during inorganic calcite formation at 25 °C. To our knowledge, few studies have been carried out to investigate systematically ionic strength effect on Ca isotopes in calcium carbonates. Lemarchand et al. (2004) precipitated inorganic calcite spontaneously from two types of growth solutions with ionic strength of 450 and 850 mM, respectively (salinity of 22.7‰ and 37.8‰, respectively). In their Δ44/40Ca versus log R plot no difference between the two solutions was obtained (see Fig. 7 in Lemarchand et al., 2004). In accordance, culture experiments with the dinoflagellate species T. heimii by Gussone et al. (2010) indicate that there is no significant correlation between the analyzed 44Ca/40Ca ratio in CaCO3 and salinity. On the other hand, culturing experiments on planktic foraminifera, G. ruber and Globigerinella siphonifera, by Kısakürek et al. (2011) demonstrated systematic variations in δ44/40Ca with salinity. Although the total variation in the studied species was on the same order as the external reproducibility, the salinity response of calcium isotope ratios was consistent with a kinetic effect. Therefore, studies on inorganic calcite and coccolithophores suggest that 44Ca/40Ca ratios in calcite are weakly influenced by ionic strength, whereas in low Mg foraminifera, ionic strength appears to have a noticeable effect on calcium isotope fractionation through kinetics of calcite growth.
According to our previous studies (Tang et al., 2008b), Ca isotope fractionation during inorganic calcite formation under our experimental conditions can also be successfully interpreted by the surface enrichment model (SEMO). Based on SEMO model calculations (see Tang et al., 2008b for the calculations in detail), precipitation rate effect on Ca isotope fractionation is due to the effective entrapment of 44Ca-depleted surface layer by crystal growth before ion diffusion re-equilibrates any abnormal composition in the newly-formed crystal lattice. Although ionic strength does not effectively influence calcite growth in our experiments suggested by linear regression analyses (see Section 3.2) and cannot influence ion diffusion as temperature does, ionic strength might influence the composition of the surface layer as we discussed in Tang et al. (2008b). Therefore, a weak impact of ionic strength on Ca isotope fractionation is expected by the surface entrapment model.
4.3. Sr/Ca and 44Ca/40Ca ratios in calcite as environmental proxies
In our previous studies (Tang et al., 2008a,b), we discussed the potential use of Sr/Ca and 44Ca/40Ca ratios in calcite as environmental proxies based on our experiments. Our previous experiments demonstrated that both Sr/Ca and 44Ca/40Ca ratios in calcite are sensitive to precipitation rate and temperature. Neither precipitation rate nor temperature dominantly controlled Sr/Ca and 44Ca/40Ca ratios. Thus, we argued that Sr/Ca and 44Ca/40Ca ratios could be used as an indicator of precipitation rate or temperature if one of these two factors was well-known. However, at that time, because all of our experiments were conducted at low ionic strength/salinity, we pointed out that the application of Sr/Ca and 44Ca/40Ca ratios as environmental proxies was only valid in terrestrial water systems and might be limited in marine environments. Our new experimental data presented in this study provide strong evidence that both Sr/Ca and 44Ca/40Ca ratios in calcite are weakly influenced by ionic strength/salinity. Thus, Sr/Ca and 44Ca/40Ca ratios can also be used individually as an environmental proxy or be combined as a multi-proxy application in paleoceanographic studies. As both Sr/Ca and 44Ca/40Ca ratios are sensitive to temperature (see Tang et al., 2008a,b) but weakly influenced by ionic strength (see Figs. 2 and 3), Sr/Ca and 44Ca/40Ca ratios in marine calcites not only provide information about SST, but also are helpful to isolate salinity effects from temperature effects in stable oxygen isotope signals.
The strong relationship between log D Sr and Δ44/40Cacalcite-aq, independent of environmental factors (e.g., temperature, aqueous Sr/Ca ratio, precipitation rate, salinity/ionic strength; Fig. 4; see also Tang et al., 2008b), reflects the same mechanism (i.e., the surface entrapment by crystal growth) controlling both Sr incorporation and Ca isotope fractionation during inorganic calcite formation (Tang et al., 2008b). This strong relationship between log D Sr and Δ44/40Cacalcite-aq can be found in both biogenic and inorganic calcite (see Fig. 7 of Tang et al., 2008b) and thus can be used to recalculate Sr/Ca or Ca isotopic composition in calcite if reasonable assumptions of the aqueous Sr/Ca ratio or Ca isotopic composition can be made. For this purpose, knowledge on environmental parameters during calcite formation like temperature, precipitation rate, and ionic strength is not required (see Fig. 4). Moreover, any deviation from the log D Sr/Δ44/40Cacalcite-aq relationship can be used to decipher the diagenetic CaCO3 alteration.
5. Conclusion
Our experiments indicate that Sr/Ca and 44Ca/40Ca ratios in calcite are primarily controlled by precipitation rate at 25 °C. The rate-dependence of Sr/Ca and 44Ca/40Ca ratios in calcite is slightly influenced by variations in ionic strength investigated in our experiments. Thus, ionic strength has a weak impact on Sr/Ca and 44Ca/40Ca ratios in calcite. The positive linear relationship between salinity and Sr/Ca ratio observed in biogenic calcite can be reasonably explained by more rapid kinetics of calcite growth caused by the increase of salinity.
A strong correlation between the Sr distribution coefficient and 44Ca/40Ca isotope fractionation of calcite is not affected by changes in ionic strength, which verifies that the surface entrapment mechanism may control both Sr incorporation and Ca isotope fractionation during calcite formation as pointed out in our previous study (Tang et al., 2008b). Our experiments show a weak impact of ionic strength on both Sr/Ca and 44Ca/40Ca ratios in calcite. Thus, if the rates of calcite growth can be approximated, Sr/Ca and 44Ca/40Ca ratios in marine calcium carbonates may be used as proxies for SST, but also to discriminate between temperature and salinity effects on oxygen isotope ratios in marine calcium carbonates. The strong correlation between Sr partitioning and Ca isotope fractionation in calcite can be used to reveal the solid composition of calcite, i.e., 44Ca/40Ca ratio in calcite can be estimated from Sr/Ca ratio and vice versa, if reasonable assumptions of the aqueous Sr/Ca ratio or Ca isotopic composition can be made. What is more, the estimation of 44Ca/40Ca ratio or Sr/Ca ratio can be made even when environmental parameters during calcite formation such as temperature, precipitation rate, and ionic strength are unknown.
Acknowledgments
The present study was funded by the European Scientific Foundation (ESF) project CASIOPEIA (DFG, Ei272/20-1/-2) and financially supported by the Austrian Science Fund (FWF I34-B06). We wish to thank the associate editor, Robert H. Byrne, the reviewer, M.S. Fantle, and an anonymous reviewer for their constructive comments and suggestions, which greatly improved this manuscript.
Associate editor: Robert H. Byrne
References
- Arbuszewski J., deMenocal P., Kaplan A., Farmer E.C. On the fidelity of shell-derived δ18Oseawater estimates. Earth Planet. Sci. Lett. 2010;300:185–196. [Google Scholar]
- Barker S., Cacho I., Benway H., Tachikawa K. Planktonic foraminiferal Mg/Ca as a proxy for past oceanic temperatures: a methodological overview and data compilation for the last glacial maximum. Q. Sci. Rev. 2005;24:821–834. [Google Scholar]
- Corrège T. Sea surface temperature and salinity reconstruction from coral geochemical tracers. Paleogeogr. Paleoclimatol. Paleoecol. 2006;232:408–428. [Google Scholar]
- Dietzel M., Gussone N., Eisenhauer A. Co-precipitation of Sr2+ and Ba2+ with aragonite by membrane diffusion of CO2 between 10 and 50 °C . Chem. Geol. 2004;203:139–151. [Google Scholar]
- Dissard D., Nehrke G., Reichart G.J., Bijma J. The impact of salinity on the Mg/Ca and Sr/Ca ratio in the benthic foraminifera Ammonia tepida: results from culture experiments. Geochim. Cosmochim. Acta. 2010;74:928–940. [Google Scholar]
- Dueñas-Bohórquez A., da Rocha R.E., Kuroyanagi A., Bijma J., Reichart G.-J. Effect of salinity and seawater calcite saturation state on Mg and Sr incorporation in cultured planktonic foraminifera. Mar. Micropaleontol. 2009;73:178–189. [Google Scholar]
- Eisenhauer A., Nägler T., Stille P., Kramers J., Gussone N., Bock B., Fietzke J., Hippler D., Schmitt A.-D. Proposal for an international agreement on Ca notation as result of the discussions from the workshops on stable isotope measurements in Davos (Goldschmidt 2002) and Nice (EGS-AGU-EUG 2003) Geostand. Geoanal. Res. 2004;28:149–151. [Google Scholar]
- Eisma D., Mook W.G., Das H.A. Shell characteristics, isotopic composition and trace-element contents of some euryhaline molluscs as indicators of salinity. Paleogeogr. Paleoclimatol. Paleoecol. 1976;19:39–62. [Google Scholar]
- Elderfield H., Ganssen G. Past temperature and δ18O of surface ocean waters inferred from foraminiferal Mg/Ca ratios. Nature. 2000;405:442–445. doi: 10.1038/35013033. [DOI] [PubMed] [Google Scholar]
- Ferguson J.E., Henderson G.M., Kucera M., Rickaby R.E.M. Systematic change of foraminiferal Mg/Ca ratios across a strong salinity gradient. Earth Planet. Sci. Lett. 2008;265:153–166. [Google Scholar]
- Gaetani G.A., Cohen A.L. Element partitioning during precipitation of aragonite from seawater: a framework for understanding paleoproxies. Geochim. Cosmochim. Acta. 2006;70:4617–4634. [Google Scholar]
- Gussone N., Eisenhauer A., Tiedemann R., Haug G.H., Heuser A., Bock B., Nägler Th.F., Müller A. Reconstruction of Caribbean Sea surface temperature and salinity fluctuations in response to the Pliocene closure of the Central American Gateway and radiative forcing, using δ44/40Ca, δ18O, and Mg/Ca ratios. Earth Planet. Sci. Lett. 2004;227:201–214. [Google Scholar]
- Gussone N., Zonneveld K., Kuhnert H. Minor element and Ca isotope composition of calcareous dinoflagellate cysts of cultured Thoracosphaera heimii. Earth Planet. Sci. Lett. 2010;289:180–188. [Google Scholar]
- Heuser A., Eisenhauer A., Gussone N., Bock B., Hansen B.T., Nägler T.F. Measurement of calcium isotopes (δ44Ca) using a multicollector TIMS technique. Int. J. Mass Spectrom. 2002;220:387–399. [Google Scholar]
- Hoogakker B.A.A., Klinkhammer G.P., Elderfield H., Rohling E.J., Hayward C. Mg/Ca paleothermometry in high salinity environments. Earth Planet. Sci. Lett. 2009;284:583–589. [Google Scholar]
- Holland H.D., Borcsik M., Munoz J., Oxburgh U.M. The coprecipitation of Sr+2 with aragonite and of Ca+2 with strontianite between 90 and l00 °C . Geochim. Cosmochim. Acta. 1963;27:957–977. [Google Scholar]
- Holland H.D., Holland H.J., Munoz J.L. The coprecipitation of cations with CaCO3: II. The coprecipitation of Sr+2 with calcite between 90 and 100 °C . Geochim. Cosmochim. Acta. 1964;28:1287–1301. [Google Scholar]
- Katz A., Sass E., Starinsry A., Holland H.D. Strontium behavior in the aragonite–calcite transformation: an experimental study at 40–98 °C . Geochim. Cosmochim. Acta. 1972;36:481–496. [Google Scholar]
- Kısakürek B., Eisenhauer A., Böhm F., Garbe-Schönberg D., Erez J. Controls on shell Mg/Ca and Sr/Ca in cultured planktonic foraminiferan, Globigerinoides ruber (white) Earth Planet. Sci. Lett. 2008;273:260–269. [Google Scholar]
- Kısakürek B., Eisenhauer A., Böhm F., Hathorne E.C., Erez J. Controls on calcium isotope fractionation in cultured planktic foraminifera, Globigerinoides ruber and Globigerinella siphonifera. Geochim. Cosmochim. Acta. 2011;75:427–443. [Google Scholar]
- Klein R.T., Lohmann K.C., Thayer W. Sr/Ca and 13C/12C ratios in skeletal calcite of Mytilus trossulus: covariation with metabolic rate, salinity, and carbon isotopic composition of seawater. Geochim. Cosmochim. Acta. 1996;60:4027–4221. [Google Scholar]
- Lea D.W., Mashiotta T.A., Spero H.J. Controls on magnesium and strontium uptake in planktonic foraminifera determined by live culturing. Geochim. Cosmochim. Acta. 1999;63:2369–2379. [Google Scholar]
- Lemarchand D., Wasserburg G.J., Papanastassiou D.A. Rate-controlled calcium isotope fractionation in synthetic calcite. Geochim. Cosmochim. Acta. 2004;68:4665–4678. [Google Scholar]
- Lorens R.B. Sr, Cd, Mn and Co distribution coefficients in calcite as a function of calcite precipitation rate. Geochim. Cosmochim. Acta. 1981;45:553–561. [Google Scholar]
- Nehrke G., Reichart G.J., Van Cappellen P., Meile C., Bijma J. Dependence of calcite growth rate and Sr partitioning on solution stoichiometry: non-Kossel crystal growth. Geochim. Cosmochim. Acta. 2007;71:2240–2249. [Google Scholar]
- Nürnberg D., Bijma J., Hemleben C. Assessing the reliability of magnesium in foraminiferal calcite as a proxy for water mass temperatures. Geochim. Cosmochim. Acta. 1996;60:803–814. [Google Scholar]
- Pingitore N.E., Jr., Eastman M.P. The coprecipitation of Sr2+ with calcite at 25 °C and 1 atm . Geochim. Cosmochim. Acta. 1986;50:2195–2203. [Google Scholar]
- Rosales I., Robles S., Quesada S. Elemental and oxygen isotope composition of early Jurassic belemnites: salinity vs. temperature signals. J. Sed. Res. 2004;74:342–354. [Google Scholar]
- Rostek F., Ruhland G., Bassinot F.C., Müller P.J., Labeyrle L.D., Lancelot Y., Bard E. Reconstructing sea surface temperature and salinity using δ18O and alkenone records. Nature. 1993;364:319–321. [Google Scholar]
- Ruiz-Agudo E., Putnis C.V., Rodriguez-Navarro C., Putnis A. Effect of pH on calcite growth at constant ratio and supersaturation . Geochim. Cosmochim. Acta. 2011;75:284–296. [Google Scholar]
- Sampei Y., Matsumoto E., Dettman D.L., Tokuoka T., Abe O. Paleosalinity in a brackish lake during the Holocene based on stable oxygen and carbon isotopes of shell carbonate in Nakaumi Lagoon, southwest Japan. Paleogeogr. Paleoclimatol. Paleoecol. 2005;224:352–366. [Google Scholar]
- Tang J., Köhler S.J., Dietzel M. Sr2+/Ca2+ and 44Ca/40Ca fractionation during inorganic calcite formation: I. Sr incorporation. Geochim. Cosmochim. Acta. 2008;72:3718–3732. doi: 10.1016/j.gca.2011.10.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang J., Dietzel M., Böhm F., Köhler S.J., Eisenhauer A. Sr2+/Ca2+ and 44Ca/40Ca fractionation during inorganic calcite formation: II. Ca isotopes. Geochim. Cosmochim. Acta. 2008;72:3733–3745. doi: 10.1016/j.gca.2011.10.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tesoriero A.J., Pankow J.F. Solid solution partitioning of Sr2+, Ba2+, and Cd2+ to calcite. Geochim. Cosmochim. Acta. 1996;60:1053–1063. [Google Scholar]
- Usdowski H.E. Springer-Verlag; Berlin, Heidelberg: 1975. Fraktionierung der Spurenelemente bei der Kristallisation. p. 104. [Google Scholar]
- Zhang Y.P., Dawe R. The kinetics of calcite precipitation from a high salinity water. Appl. Geochem. 1998;13:177–184. [Google Scholar]
- Zuddas P., Mucci A. Kinetics of calcite precipitation from seawater: II. The influence of the ionic strength. Geochim. Cosmochim. Acta. 1998;62:757–766. [Google Scholar]