Empirical Performance of Cross-Validation With Oracle Methods in a Genomics Context

Abstract

When employing model selection methods with oracle properties such as the smoothly clipped absolute deviation (SCAD) and the Adaptive Lasso, it is typical to estimate the smoothing parameter by m-fold cross-validation, for example, m = 10. In problems where the true regression function is sparse and the signals large, such cross-validation typically works well. However, in regression modeling of genomic studies involving Single Nucleotide Polymorphisms (SNP), the true regression functions, while thought to be sparse, do not have large signals. We demonstrate empirically that in such problems, the number of selected variables using SCAD and the Adaptive Lasso, with 10-fold cross-validation, is a random variable that has considerable and surprising variation. Similar remarks apply to non-oracle methods such as the Lasso. Our study strongly questions the suitability of performing only a single run of m-fold cross-validation with any oracle method, and not just the SCAD and Adaptive Lasso.

1. INTRODUCTION

1.1 Model Selection via Penalization

Traditional model selection procedures such as forward, backward, and stepwise regression is practical when the number of parameters is small; however, it can be cumbersome with high dimensional parameter vectors. In contrast, penalization methods are more efficient in high-dimensional contexts such as the genomics context in this article.

In the typical regression problem, estimation of the parameters involves the minimization of the objective function, which can be represented by the sum of the squared residuals, namely

$${\left|\right|Y-X\mathit{\beta }\left|\right|}^2,$$ (1)

where || · || is the Euclidian norm, Y is a vector of responses, X is a matrix with column rank p, the number of predictors, and β is a parameter vector. In this problem the objective function imposes no condition on the size of the parameter vector, β; however, one can impose such a condition to reduce the size of certain coefficients and completely zero out others, thereby performing model selection via constrained optimization. Tibshirani (1996) proposed adding such constraints to (1) and called it the “least absolute shrinkage and selection operator,” or Lasso. In his article, Tibshirani proposed the minimization of the objective function (1) but subject to the condition that ${\sum }_{j=1}^p\mid {\beta }_j\mid \le \lambda$, where λ ≥ 0. This constrained minimization problem is equivalent to solving the unconstrained Lagrangian which is

$${\left|\right|Y-X\mathit{\beta }\left|\right|}^2+\lambda \sum _{j=1}^p\mid {\beta }_j\mid .$$ (2)

In (2) the parameter λ is called the penalty because depending on its size we can reduce or completely zero out the magnitude of some of the regression coefficients β_j. If we replace λ|β_j| in (2) with a generic function p_λ(| β_j|), which we will refer to as the penalty function, then expression (2) becomes the penalized form of the least squares problem. If we let the penalty function p_λ(| β_j|) = λ|β_j|, then we are back to the Lasso; however, other specifications of this penalty function have improved the performance of the penalized least squares problem. Indeed, one can select a penalty function so that, as the sample size increases and the parameters remain fixed, estimates of the regression parameters eventually match the estimates that would have been obtained had we known which variables were conditionally independent of the outcome. This is called the oracle property. There are now many such oracle procedures, but here we focus on two of them, the smoothly clipped absolute deviation (SCAD) method of Fan and Li (2001) and the Adaptive Lasso of Zou (2006). Both possess the oracle property and their respective penalty functions improve estimation by reducing bias in the parameter estimation, increase sparsity by zeroing out coefficients of small size, which in turn reduces complexity, and are continuous. The last requirement is necessary for stability in model selection (Fan and Li 2001). SCAD uses a spline function with knots at λ and aλ as its penalty function and its derivative is given by

$$p_{\lambda }^{\prime }({\beta }_j)=\lambda \left\{I({\beta }_j\le \lambda )+\frac{{(a\lambda -{\beta }_j)}_{+}}{(a-1)\lambda }I({\beta }_j>\lambda )\right\}.$$ (3)

Typically, the constant a = 3.7 is used in practice (Fan and Li 2001). The Adaptive Lasso uses as its penalty function

$$p_{\lambda }(\mid {\beta }_j\mid )=\lambda \frac{\mid {\beta }_j\mid }{\mid {\beta }_{j,\text{OLS}}\mid },$$ (4)

where β_j,OLS is the ordinary least squares estimate of β_j.

In common among these penalization methods is the necessity of determining the value of the penalty, λ, that minimizes the appropriate objective function. It is customary to use cross-validation to determine the value of such a parameter. Specifically, m-fold cross-validation partitions the available observations into a prespecified, fixed, number of sets, m, each with a roughly equal number of observations and determines the prediction error in each set by using the observations in the m − 1 other sets to fit the model. If we are interested in determining the value of λ that gives the smallest prediction error, we would specify a set of values for λ to determine the prediction error using cross-validation for each value and select the λ with the smallest prediction error.

However, we have found that one application of cross-validation to select λ, and therefore the model parameters associated with that λ, can be quite variable, even when used with oracle methods such as SCAD and Adaptive Lasso. We present empirical evidence of the performance of cross-validation when used to select the penalty of the two oracle methods introduced. In what follows we present our application of penalization in a genomics context, and rather than linear regression such as in (1), we will focus on logistic regression.

1.2 Penalization in the Context of SNP Data

Consider a logistic regression model of the form

$$\text{pr}(Y=1\mid X)=H({\beta }_0+X^{\text{T}}\mathcal{B}),$$ (5)

where H(·) is the logistic regression function and X is a vector, possibly of high dimension. Interest often focuses of course on selecting those components of X whose corresponding regression parameters are nonzero. For subject i, X_i = (x_i1, …, x_ip)^T and 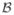= (β₁, …, β_p)^T.

The Adaptive Lasso (Zou 2006) and SCAD are two methods that have the property of an “oracle” method (Fan and Li 2001), that is, as the sample size n → ∞, it selects with probability one the correct regression model and the nonzero estimates are asymptotically normal with the same covariance matrix as if the nonzero coefficients were known a priori. Both the SCAD and Adaptive Lasso maximize a penalized log-likelihood

$$\sum _{i=1}^n\left[Y_{i}log\{H({\beta }_0+X_i^{\text{T}}\mathcal{B})\}+(1-Y_i)\times log\{1-H({\beta }_0+X_i^{\text{T}}\mathcal{B})\}\right]-\sum _{j=1}^p{p}_{\lambda }(\mid {\beta }_j\mid ),$$ (6)

where the appropriate penalty function for each method is given in (3) and (4).

These methods involve a smoothing parameter that has to be estimated from the data, such as λ in (6), and this is often achieved by a variant of cross-validation. Often, m-fold cross-validation is used, where m = 10 is a standard choice; see, for example, James et al. (2009) for a recent example. In this case, given the data, the estimated value of λ, λ̂, is a random variable depending on the random partitioning of the data in the m-fold cross-validation algorithm. It then follows that the number of nonzero coefficients selected by maximizing (6) using λ̂, N(λ̂), is also a random variable.

In problems where the sample size is large, and the signals sparse but large, N(λ̂) tends to have small variability. However, in logistic regression association studies involving Single Nucleotide Polymorphisms (SNP), the true regression functions, while thought to be sparse, do not have large odds ratios. They are instead unlikely to be larger than 1.5, corresponding to a regression parameter of log(1.5) = 0.4. When signals are sparse but small the question we address is as follows: should 10-fold cross-validation in implementing oracle methods such as the SCAD and the Adaptive Lasso be recommended?

We investigate this issue empirically. In Section 2.1 we apply the SCAD and Adaptive Lasso to a case-control study with 23 SNP. We find that the number of nonzero estimated coefficients, N(λ̂), is highly variable from one cross-validation to another, and implausibly too large. In Section 2.2, we perform a simulation study linked to the case-control example, with similar results. We also use the BIC method of selecting the penalty parameter outlined by Wang et al. (2007) for the SCAD method.

Our conclusion, summarized in Section 3, is that performing only a single run of 10-fold cross-validation with oracle methods such as SCAD and the Adaptive Lasso can be a dangerous statistical practice. As we see in the analysis of the case-control data, when small signals are expected it is far better to run cross-validation multiple times to get a better picture of what really is going on in the data. This opens up the question of how to do model selection and parameter estimation in sparse data with modest signals.

2. EMPIRICAL WORK

2.1 Analysis of Prostate Cancer Data

The data used here are from an ongoing population-based case-control study of prostate cancer that will be analyzed scientifically in another forum. The study has 23 SNP in the 8q24 chromosomal region and a total sample size of n = 7667, with approximately half cases and controls. In single variable logistic regressions, all of the SNP were statistically significant and most had p-values much smaller than the nominal level. The aim of the study is to estimate how many independent effects were in the dataset. The SNP were not independent of one another. They occur in blocks of size (5, 1, 1, 3, 7, 2, 1, 1, 1, 1), with high correlations within blocks, typically over 0.6 and as high as 0.9, see Table 1 for more details.

Table 1.

Correlation structure of the SNP data among the controls. The block sizes are in parentheses, and the entries are the average absolute value of the correlation. Here “NA” indicates a block of size 1.

Block	1	2	3	4	5	6	7	8	9	10
Block 1 (5)	0.79	0.76	0.25	0.04	0.06	0.04	0.02	0.03	0.05	0.03
Block 2 (1)	0.76	NA	0.22	0.08	0.09	0.08	0.06	0.02	0.09	0.00
Block 3 (1)	0.25	0.22	NA	0.07	0.06	0.08	0.07	0.07	0.06	0.09
Block 4 (3)	0.04	0.08	0.07	0.75	0.53	0.55	0.58	0.35	0.63	0.35
Block 5 (7)	0.06	0.09	0.06	0.53	0.58	0.58	0.58	0.44	0.63	0.41
Block 6 (2)	0.04	0.08	0.08	0.55	0.58	0.94	0.74	0.18	0.82	0.27
Block 7 (1)	0.02	0.06	0.07	0.58	0.58	0.74	NA	0.26	0.89	0.23
Block 8 (1)	0.03	0.02	0.07	0.35	0.44	0.18	0.26	NA	0.29	0.87
Block 9 (1)	0.05	0.09	0.06	0.63	0.63	0.82	0.89	0.29	NA	0.25
Block 10 (1)	0.03	0.00	0.09	0.35	0.41	0.27	0.23	0.87	0.25	NA

Table 2 displays the number of variables selected by the Lasso, Adaptive Lasso, SCAD and Full SCAD for 1000 different crossvalidation runs. The SCAD here represents the minimization of the SCAD objective function using the one-step local linear approximation method of Zou and Li (2008) and full SCAD is the original algorithm of Fan and Li (2001). The number of nonzero estimated coefficients N(λ̂) is both extremely variable and surprisingly large, for example, regardless of what method is used 8 or more SNP are selected over 50% of the time. We have computed the percentage of times each variable was selected over the 1000 runs of the Adaptive Lasso. For example, variable 23 was selected in every cross-validation run, while variable 22 was selected in over 90% of the runs but less than 100%. If one insists that a variable appears at least 90% of the time, the data suggest 5 independent effects. In contrast, if we use BIC to select the penalty parameter, λ, SCAD and Full SCAD only select 1 independent effect.

Table 2.

Results of analysis of prostate cancer data after 1, 000 10-fold crossvalidation runs of Lasso, Adaptive Lasso, one step SCAD, and full SCAD. The entries are the number of times there are k nonzero nonintercept parameters. The value of k is shown in the first column.

Distribution of number of parameters selected
Nonintercept variable	Lasso	Adaptive Lasso	SCAD	Full SCAD
1	0	0	11	15
2	0	0	1	53
3	0	1	2	74
4	0	22	28	152
5	0	231	17	39
6	0	73	38	148
7	2	81	0	47
8	0	179	167	0
9	336	146	173	184
10	654	65	0	0
11	2	125	0	0
12	0	64	563	0
13	0	6	0	0
14	0	0	0	0
15	6	7	0	0
16	0	0	0	288
17	0	0	0	0
18	0	0	0	0
19	0	0	0	0
20	0	0	0	0
21	0	0	0	0
22	0	0	0	0
23	0	0	0	0

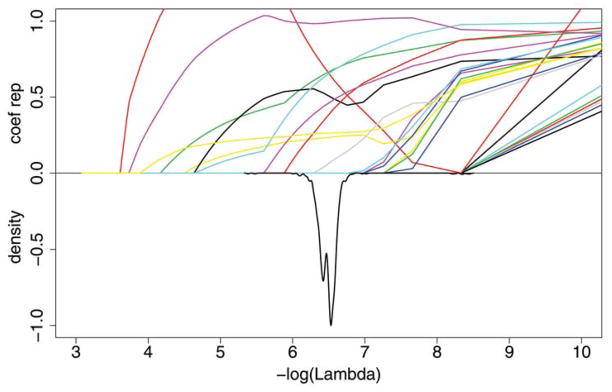
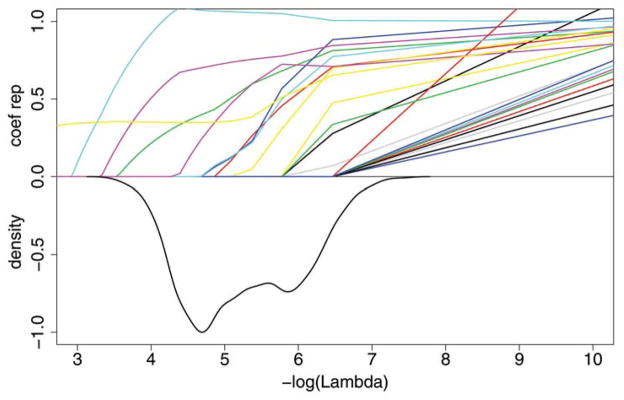
Graphical summaries for the SNP data are given in the top panels of Figure 1 for the Lasso and Figure 2 for the Adaptive Lasso. In both figures, the bottom half of the plot shows a density estimate of the selected values of the smoothing parameter over the 1000 cross-validation runs. The top half of each plot shows the size of the coefficient estimates relative to their ordinary logistic regression estimates as λ is varied. The variability of the estimates of λ and the variability in the number of nonzero estimates is clear from these figures. One striking feature of these figures is that the Adaptive Lasso smoothing parameter estimates are much more variable than those of the Lasso.

Figure 1.

Plot for Lasso for the SNP data. Each colored line on the top half of the graph represents a different coefficient and shows the magnitude of that coefficient, relative to the ordinary logistic regression estimate, when the smoothing parameter λ varies. The smaller lambda, that is, the larger −log(λ), allows more variables to be included in the model. The bottom half of the graph shows the negative of the normalized density function to demonstrate the range of λ that were selected in the 1000 cross-validation runs. The online version of this figure is in color

Figure 2.

Plot for Adaptive Lasso for the SNP data. Each colored line on the top half of the graph represents a different coefficient and shows the magnitude of that coefficient, relative to the ordinary logistic regression estimate, when the smoothing parameter λ varies. The smaller lambda, that is, the larger −log(λ), allows more variables to be included in the model. The bottom half of the graph shows the negative of the normalized density function to demonstrate the range of λ that were selected in the 1000 cross-validation runs. The online version of this figure is in color

2.2 Simulation Study

In our simulation study, we set the sample size n = 10, 000, and selected the covariates by sampling with replacement from the controls in the SNP data. We set the regression parameter 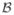= (0, 0, −0.15, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.15, 0.20, 0, 0, 0, 0, 0, 0, 0, 0, 0.40)^T, so that there are four independent effects, with relative risks (1.16, 1.16, 1.22, 1.50), where the relative risk is the exponential of the regression coefficient. These are roughly in accord with the overall estimates of four SNP in the actual data.

With the somewhat greater sample size we expect the SCAD and Adaptive Lasso to have better properties than in the data, but as seen in Table 3, even though there are only 4 independent effects, the Adaptive Lasso with 10-fold cross-validation selects 8 or more variables more than 50% of the time and the one step SCAD selects 14 more than 80% of the time. In general the full SCAD selects a smaller number of variables than all other methods, but still selects at least 10 more than 50% of the time, see Table 3. In addition, if we use BIC to select the penalty λ in SCAD, fewer variables are chosen, however at least 7 are chosen more than 50% of the time, see Table 4, so that BIC is not a panacea.

Table 3.

Results for the simulation in Section 2.2 using the Lasso, Adaptive Lasso, one step SCAD, and full SCAD. The entries are the number of times there are k non-zero non-intercept parameters. The value of k is shown in the first column.

Distribution of number of parameters selected
Nonintercept variable	Lasso	Adaptive Lasso	SCAD	Full SCAD
1	0	0	3	11
2	0	2	0	36
3	1	13	0	61
4	1	22	9	131
5	6	44	23	107
6	17	43	57	93
7	48	58	86	83
8	69	57	92	69
9	81	73	79	70
10	92	74	83	43
11	82	76	131	25
12	79	84	127	26
13	95	79	106	45
14	84	52	107	54
15	67	33	59	55
16	61	30	24	48
17	37	13	9	32
18	48	13	3	7
19	39	13	1	3
20	37	6	1	1
21	24	3	0	0
22	15	1	0	0
23	17	211	0	0

Table 4.

Results of simulation in Section 2.2 using BIC to select the penalty in the one step SCAD and full SCAD. The entries show the number of times there are k nonzero nonintercept parameters out of 1000 simulations. The value of k is shown in the first column.

Distribution of number of parameters selected
Nonintercept variable	SCAD	Full SCAD
1	0	0
2	0	0
3	267	384
4	63	65
5	87	23
6	60	10
7	40	30
8	27	34
9	35	55
10	53	59
11	67	64
12	72	46
13	71	45
14	68	38
15	57	43
16	21	45
17	8	27
18	3	23
19	1	3
20	0	2
21	0	2
22	0	2
23	0	0

2.3 Summary

The data analysis of Section 2.1 and the simulation of Section 2.2 show that 10-fold cross-validation, even with oracle methods such as the Adaptive Lasso and SCAD, will have a quite variable number of nonzero parameters, and it is not readily the case that independent effects can be detected by the parameter estimates alone. However, with 1000 runs of cross-validation, the overall summary measures and graphs suggest that a clearer picture will arise. In practice, of course, it would not be desirable to run 1000 regularized logistic regressions, for speed if nothing else, and this opens up the issue of how to actually analyze such data.

3. DISCUSSION

SCAD and the Adaptive Lasso are consistent model selectors. There has been some theoretical work about their behavior when the effects are sparse but small in the contiguous sense (Hjort and Claeskens 2003; Leeb and Pötscher 2005; Pötscher and Leeb 2007). However, as far as we are aware, there has been no study of the Adaptive Lasso and SCAD in the sparse but small effect case when the smoothing parameter is selected by the common method of m-fold cross-validation. We have restricted our attention to 10-fold cross-validation, but in our examples similar results are found for m = 20 and m = 5.

Our empirical evidence is admittedly limited, but we strongly question the suitability of performing only a single run of 10-fold crossvalidation with any oracle method, and not just SCAD and the Adaptive Lasso.