Uniform color spaces and natural image statistics

Abstract

Many aspects of visual coding have been successfully predicted by starting from the statistics of natural scenes and then asking how the stimulus could be efficiently represented. We started from the representation of color characterized by uniform color spaces, and then asked what type of color environment they implied. These spaces are designed to represent equal perceptual differences in color discrimination or appearance by equal distances in the space. The relative sensitivity to different axes within the space might therefore reflect the gamut of colors in natural scenes. To examine this, we projected perceptually uniform distributions within the Munsell, CIEL*u*v* or CIEL*a*b* spaces into cone-opponent space. All were elongated along a bluish-yellowish axis reflecting covarying signals along the L-M and S-L+M cardinal axes, a pattern typical (though not identical) to many natural environments. In turn, color distributions from environments were more uniform when projected into the CIEL*a*b* perceptual space than when represented in a normalized cone-opponent space. These analyses suggest the bluish-yellowish bias in environmental colors might be an important factor shaping chromatic sensitivity, and also suggest that perceptually uniform color metrics could be derived from natural scene statistics and potentially tailored to specific environments.

Introduction

Uniform color spaces are designed with the aim that equal distances in the space correspond to color differences of equal perceptual magnitude. Color differences do not vary linearly with changes in the stimulus spectrum, and thus it is well known that linear color spaces, for example based on the spectral sensitivities of the cones or cone-opponent channels, are not perceptually uniform. Uniform spaces must therefore apply distortions of the cone excitations in order to compensate for the variations in visual sensitivity and appearance for different stimuli and viewing conditions.

A number of uniform color spaces have been developed and are in wide use^1–4. The structure of these spaces is based on empirical measurements of color discrimination and appearance. For example, the Munsell and Natural Color systems are color order systems and were derived from scaling experiments measuring the suprathreshold appearance differences between samples differing along defined dimensions corresponding to lightness, value, or chroma or to the Hering primaries^{5, 6}. Other spaces such as CIE L*u*v* and L*a*b* were based on transformations of the CIE 1931 tristimulus values so that threshold color differences were equated in different regions of color space^{7, 8}, and are designed to provide a uniform metric for representing color differences. Different perceptual color spaces or order systems thus approximately embody the characteristics of human color vision at threshold and/or suprathreshold levels. But what gives rise to these characteristics?

A powerful approach to understanding visual coding has been to characterize the properties of the visual environment and then ask what these properties predict about visual representations^9–11. Many previous studies have adopted this strategy to specifically examine the visual encoding of color. For example, the distribution of intensity levels or chromaticities in natural scenes is not flat but instead is strongly peaked, so that most points in the scene have lower contrast. The most efficient representation of contrast should give equal importance to all possible levels of the channel’s output, and this predicts the sigmoidal response of the neural contrast response (so that the response changes rapidly at stimulus levels that are common while saturating at levels that are rare)^{12, 13}. The probability distributions of colors in scenes have also been used to infer the number and organization of semantic categories required to represent color^{14, 15} and lightness¹⁶. Similar arguments have been used to predict the relative sensitivity to different color directions based on the relative range of the stimulus distribution along different axes (e.g. so that sensitivity to the cone contrasts signaling chromatic differences is much higher than for luminance differences because the available chromatic contrasts are much more restricted)¹³. Moreover, redundancy reduction has provided a functional account of the transformation of the cone responses into an opponent representation^17–23, while independent components analysis of scene statistics has been used to predict the color and spatial characteristics of cortical cells²⁴. Analyses based on natural scene statistics have also been used to derive the spatiochromatic properties of receptive fields^25–28 and spatial color contrast²⁹, as well as to infer the interdependence of different perceptual attributes defining color³⁰.

From this perspective, uniform color spaces are of potential interest because they should reflect visual representations of color that are matched to properties of the color environment. For example, the relative scaling along different axes should reflect the gamut of color signals along these axes. The spaces might therefore provide clues about the structure of the environment that the visual system is calibrated for. We were specifically interested in what these spaces might suggest about the dominant axis of color variation in the environment. In many natural scenes colors tend to vary primarily along bluish-yellowish axes, which correspond to variations in the longwave-sensitive (L) cones opposed by signals in both the medium- (M) and shortwave-sensitive (S) cones^{22, 31, 32}. If the perceptual scaling of color were matched to this variation, then we might expect these spaces to reveal reduced sensitivity for such axes. To test this, we projected distributions that were perceptually uniform by the metrics of different spaces, into cone-opponent space, and then compared these predicted distributions to the color variations observed in natural images. Conversely, we also started with empirically defined natural color distributions and asked how evenly sampled they became when projected into perceptually uniform color spaces.

Methods

Color spaces

We analyzed three common uniform color spaces: the Munsell color system, CIE 1976 L*u*v* and CIE 1976 L*a*b*. For each we generated a set of colors based on a uniform sampling within a sphere defined by the lightness and chromatic dimensions of the space. For the Munsell space points were sampled in cylindrical coordinates and were based on tabled values of Munsell coordinates. For L*u*v* and L*a*b* we instead sampled in much finer steps along Cartesian coordinates within a sphere. Differences in sampling density between the spaces were thus arbitrary but do not affect the analyses. The sphere was centered on a presumed adapting background corresponding to (0.33, 0.329), and had a radius of 4 in value and chroma (Munsell) or 25 in delta E (for CIE Luv and Lab). Coordinates within each space were converted into the corresponding values in a scaled version of the linear cone-opponent space of MacLeod and Boynton³³ and Derrington, Krauskopf and Lennie³⁴. The latter represents color in terms of contrast (relative to the adapting background color) along the three cardinal axes of early post-receptoral color coding: an achromatic axis (L+M+S) and two chromatic axes defined by the opposing signals in long- and medium-wavelength sensitive cones (L−M), or the opposing signals in the short-wavelength cones vs. the L and M cones [S-(L+M)]³⁵. The relative scaling of the three axes is arbitrary or task-specific. For our analysis we used the scaling from our previous measurements of natural color distributions^{22, 31}, which in turn was chosen to roughly equate sensitivity and adaptation along the different axes²¹. Coordinates in the space are defined by:

$$\begin{array}{l}\text{L}-\text{M}=1953\ast ({\text{r}}_{\text{mb}}-.6568)\\ \text{S}-\text{L}+\text{M}=5533\ast ({\text{b}}_{\text{mb}}-.01825)\end{array}$$

where r_mb and b_mb are the coordinates in the MacLeod-Boynton diagram and (0.6568, 0.01825) the MacLeod-Boynton chromaticity of Illuminant C.

After projection into the cone-opponent space, the set of contrasts were analyzed to estimate the principal components of the distribution as well as the relative variance along the principal axes.

Results

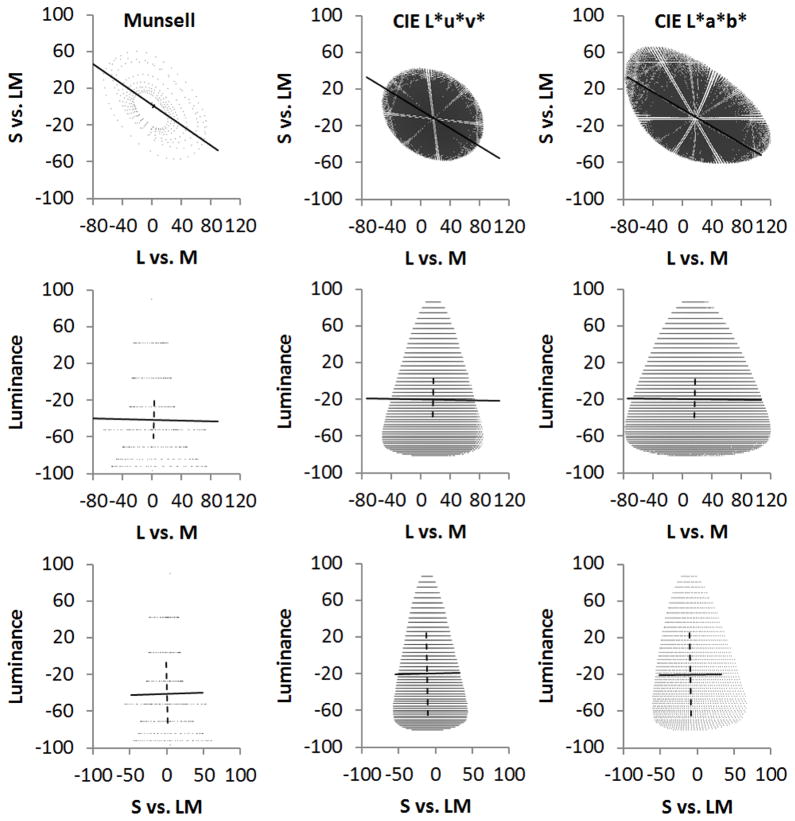
Figure 1 shows the projections into the cone-opponent space of color distributions that are uniform within the Munsell, CIE L*u*v* or CIE L*a*b* spaces. The three columns plot the coordinates along the three different pairs of cardinal axes. To examine the bias in the distributions, we estimated the angles of the three orthogonal principal axes of the contrast variations. These are shown by the solid lines within each distribution. For all 3 spaces, the color distributions become strongly elongated along the second and fourth quadrants of the cone-opponent space. We refer to variations between these quadrants in general as a “bluish-yellowish” variation, since unique blue falls in the second quadrant and unique yellow in the fourth quadrant of our cone opponent space³⁶. For the uniform spaces the principal axis is at −29 deg (Table 1). This is not a pure blue-yellow axis but instead corresponds to a color variation roughly from bluish-green to orange, though again to variations in the L cones opposed by both the S and M cones. Thus all 3 spaces predict a weaker sensitivity to this color direction, insofar as larger differences in cone excitation along this axis are required for the same perceptual difference.

Figure 1.

Spherical distributions in the Munsell (left), CIE L*u*v* (middle) or CIE L*a*b* (right) spaces projected into the cone opponent space. Each row plots the distributions along different pairs of the cardinal axes; top: the S vs. LM isoluminant plane; middle: luminance and LM plane; bottom: luminance vs. S plane. Lines show the axes of the first (solid) or second (dashed) principal components of the distributions in each of the projected planes.

Table 1.

Principal axes and cone-opponent contrasts of spherical distributions in the uniform color spaces.

Color Space	RMS (s.d.)			Primary		Secondary	Primary RMS (s.d.)	Secondary RMS (s.d.)
	L vs. M (Rel. Cont.)	S vs. LM (Rel. Cont.)	Luminance (Rel. Cont.)	Theta (degrees)	Phi (degrees)	Psi (degrees)
CIELAB Sphere	41.95	27.42	38.73	−25	−0.5	89	50.56	47.10
CIELuv Sphere	28.32	20.77	38.73	−26	−0.8	89	39.45	39.56
Munsell Sphere	32.74	25.21	43.96	−29	−1.2	89	58.08	54.93

Consistent with this shallow angle, the variance in color signals along the L−M axis is roughly 1.4 times greater than contrasts along the S-L+M axis. Note that the scaling within the cone-opponent space was based on estimates of the relative sensitivity to the two axes²¹, and thus this relative sensitivity is at least approximately preserved in each of the uniform spaces. That is, the spaces give roughly equal perceptual weight to the independent signals along the cardinal chromatic axes. This is very different from the relative weights in terms of metrics such as cone contrasts, for which the relative sensitivity to signals along the cardinal axes is markedly different^{37, 38}.

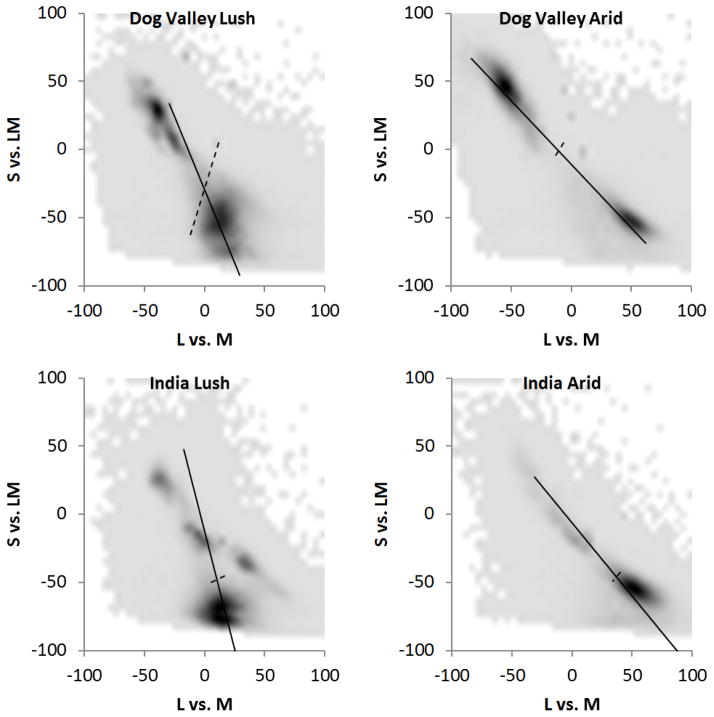
The perceptually uniform distributions share similar characteristics - and important differences - to the distributions of colors in natural environments. For example, Figure 2 plots the distribution of chromaticities (i.e. the S vs. LM plane) within the same cone-opponent space for collections of outdoor scenes sampled by Webster, Mizokami, and Webster³¹. The four distributions were measured for two locations (Western Ghats in India or the Sierra Nevadas in the US), and at two different times of the year (corresponding to “wet” and “dry” seasons). Details of these images and analyses are given in Webster et al³¹. All four of the natural color distributions again have a strong orientation along the negative diagonal of the space, in part reflecting the variation from sky to earth, (though this bias persists in the color distributions restricted to earth)³¹. There is thus a rough qualitative agreement between the color bias in the scenes and the bias predicted by uniform color metrics. However, chromatic contrasts in the natural distributions are more strongly tilted toward the vertical axis, with angles ranging from −45 deg or more. Thus the scenes had a higher relative variance in S-L+M contrasts than predicted by the spaces.

Figure 2.

Natural color distributions measured from two outdoor locations (top: Sierra Nevadas, USA; bottom: Western Ghats, India) and during two seasons (lush and arid)³¹. Plots show the pooled distributions of the chromaticities from individual scenes sampled in each environment. Lines show the axes of the first (solid) or second (dashed) principal components of the distributions in each of the projected planes.

If the “bluish-yellowish” bias in uniform spaces reflected scaling that (albeit roughly) matches the perceptual gamut of color to the range of colors in natural scenes, then the color distributions taken from scenes should become more uniform when projected into the perceptual spaces. To test this, we converted the color distributions for the four environments into CIE L*a*b*, and then compared the shapes of the distributions within the uniform vs. cone-opponent space. To ensure that this analysis was not affected by the arbitrary choice of scaling along the cone-opponent axes, we first converted each of the four raw distributions shown in Figure 2 by weighting the relative contribution of the separate sky and earth color distributions for each environment so that the mean chromaticity was as close as possible to white³⁹. Next, we rescaled the cone-opponent axes so that the RMS contrast along each axis was equated. This allowed the distributions to be as close as possible to spherical in the linear cone-opponent space (since they were now forced to have equal radii along the three cardinal axes). Finally, we measured how uniform the resulting distributions were from the ratio of the variances along the principal and orthogonal axes in the chromatic plane. A ratio of 1 corresponded to an effectively circular distribution, while values greater than 1 corresponded to distributions that were instead elliptical and thus less uniform These ratios are shown in Table 2 and compared to the ratios taken when the same distributions were projected into CIE L*a*b*. For all four environments the chromatic variance along the principal and orthogonal axes is more similar within the uniform color space. That is, the natural color distributions are themselves more uniform when represented by a perceptually uniform color space such as CIE L*a*b*.

Table 2.

Ratio of variance in signals along the principal and orthogonal chromatic axes of the natural distributions from the four environments. Values closer to one represent more circular or unbiased distributions. Cone-opponent ratio gives a measure of the bias when the color distributions are represented in the cone-opponent space after rescaling the space so that the variance along each cardinal axis is equated. L*a*b* ratio gives a measure of the bias when the chromaticities are instead represented by their coordinates in the uniform color space.

Natural Distribution	Cone-Opponent Ratio	CIE L*a*b*
Dog Valley Lush	2.80	2.05
Dog Valley Arid	4.50	3.61
India Lush	1.96	1.46
India Arid	4.23	1.62
Mean	3.37	2.19

Discussion

In this study we started with the premise that uniform color spaces embody the transformations of the cone signals required to efficiently represent the statistics of color distributions in the observer’s environment, and then asked what kind of color environment the spaces implied. The general structure of these spaces shows important parallels with the structure of color in natural scenes. This suggests that at least some of the general characteristics of common uniform color spaces can be qualitatively accounted for by the characteristics of the color environment, and in turn, could point to which environmental characteristics have been important in shaping the perceptual representation.

As we showed, one of these general characteristics is for chromatic sensitivity to be lowest for “bluish-yellowish” color directions, in which signals from the S and M cones covary. This bias is not surprising, because color spaces like CIE L*u*v* and L*a*b* were derived from the McAdam ellipses describing just noticeable color differences^{40, 41}, and Boynton et al.⁴² showed that these ellipses are oriented along a bluish-yellowish axis. Heightened discrimination along the orthogonal, reddish-greenish direction has also been found by Krauskopf and Gegenfurtner⁴³ and Danilova and Mollon⁴⁴. Moreover, this sensitivity bias has been observed in a number of other contexts. For example, achromatic settings show more variation both within and between observers along the blue-yellow dimension^{45, 46}. At suprathreshold, McDermott et al.⁴⁷ found in a visual search task that blue-yellow backgrounds were less effective distractors for reddish or greenish targets than vice versa, while Juricevic, Wilkins and Webster⁴⁸ found that ratings of visual discomfort (potentially related to effective stimulus contrast⁴⁹) were lower for blue-yellow patterns than reddish-greenish patterns defined by the orthogonal axis. Weaker sensitivity to bluish-yellowish contrasts has also been reported in adaptation effects such as the McCollough effect⁵⁰. Finally, a recent study by Goddard et al.⁵¹ found that BOLD responses in different visual cortical areas were weaker for bluish-yellowish patterns than for reddish-greenish patterns matched for the same cardinal axis components. Thus the bias seen in perceptually uniform spaces is consistent with a general sensitivity bias against bluish-yellowish color directions seen in many visual tasks.

However, this bias is nevertheless of interest because it reflects an interaction between the L−M and S-(L+M) cardinal axes that have been thought to be central to the early postreceptoral encoding of chromatic signals^{34, 35}, and thus raises the question of how these axes are matched to color in the environment. Color signals along these axes have been found to vary roughly (though not completely) independently for some natural scenes (of dense vegetation), and this had led to suggestions that the cardinal axes are the optimal opponent transformations for representing natural color signals²⁰. However, as noted this independence is not characteristic of many natural environments. Webster and Mollon²² and Webster et al.³¹ found that the dominant axes varied from close to the S-(L+M) axis for scenes composed primarily of lush vegetation, but tended toward a pure blue-yellow variation for more panoramic and arid scenes. The present results suggest that more bluish-yellowish scenes may have played a more dominant role in shaping chromatic sensitivity. A related and possibly mutual factor is that the blue-yellow axis is also the principal axis of variation in natural daylight^52–54. In either case, our results are consistent with the idea that the greater variance in the natural world along the bluish-yellowish dimension is matched by a weaker relative sensitivity to this dimension in color vision, as reflected in the scaling of uniform color spaces. This is further suggested by our finding that natural color distributions themselves become less biased when represented in perceptually uniform color spaces.

Our results also highlight discrepancies between the stimulus distributions and the perceptual scaling of color. Quantitatively, there was a clear difference between the actual axis of minimum sensitivity implied by the perceptual spaces and the axis of maximum contrast in the color distributions. Specifically, the perceptual minima are along axes that are more orange-cyan than a pure blue-yellow, and fall outside the range of any of the outdoor scenes sampled by Webster et al, which instead varied from axes close to unique blue-yellow to purple-yellowish green axes close to the S axis³¹. This raises the possibility that color sensitivity has been shaped in the short term by environments with different color distributions. In fact, natural scenes may be uncharacteristic of the colors most individuals are exposed to in the more carpentered environments of modern societies. The color distributions of such environments are not well characterized, in part because of the interest in understanding the visual environments that shaped adaptations of the visual system over evolutionary timescales^{20, 22, 24, 31, 55–58}. Thus it remains to be seen whether largely indoor and constructed environments might provide a more accurate prediction of the ontogeny of color sensitivity.

A second clear discrepancy is that these color spaces do not reflect the characteristics of color contrast discrimination. While the CIE spaces were purportedly intended to reflect color differences for an observer adapted to daylight⁵⁹, under this adaptation sensitivity is best near the adapting point and falls with increasing saturation or contrast from white^{13, 43, 60}. In the CIE spaces sensitivity instead decreases monotonically with increasing S cone activity while remaining relatively constant with variations along the L−M axis, a pattern which is more typical of adaptation to the chromaticity that is being judged^{43, 61}. This scaling is consistent with the transformations of cone signals that would be required to adjust to changes in the illuminant to maintain color constancy⁶², but does not capture contrast sensitivity, which does roughly follow the non-uniform distribution of contrasts in scenes^{12, 13}. Uniform spaces that were constructed based on empirical measurements of contrast discrimination or on characteristic contrast distributions might therefore provide a better perceptual metric for some viewing contexts.

Finally, we have discussed uniform color spaces as if they were in fact perceptually uniform. Yet it is well known that they only approximate human judgments, and the fact that there is more than one “uniform” space highlights that there can be important discrepancies between distances within the space and observers’ perceptions of those differences. For instance, the metrics for spaces like CIE L*u*v* and L*a*b* were in part constrained by the desire to provide a relatively simple and general transformation from CIE 1931 chromaticities. Because they were based on threshold discrimination they do not accurately predict large color differences and this has prompted exploration of alternative measures, for example based on reaction times for suprathreshold stimuli^{63, 64}. Because they were based on uniform fields they also fail to predict color differences at high spatial frequencies or in complex images, and this has led to elaborated spaces that include weightings for spatial contrast sensitivity^65–67. Our analyses suggest that another potential measure to exploit for predicting the perceptual impact of large color differences would be of the color statistics of the environment. Such considerations also suggest the possibility of tailoring perceptual color spaces to specific environments or contexts. To the extent that individuals are immersed in particular color worlds, for example because of their culture or vocation, their sensitivity may be adapted to the idiosyncratic color distributions of their environment⁶⁸. The principles we explored could be used to guide the construction of spaces that better capture the experience of color for observers in these contexts, and thus could in theory better predict perceptual judgments and performance for these observers.