Scleral Mechanics: Comparing Whole Globe Inflation and Uniaxial Testing

Abstract

The purpose of this study was to assess fundamental differences between the mechanics of the posterior sclera in paired eyes using uniaxial and whole globe inflation testing, with an emphasis on the relationship between testing conditions and observed tissue behavior. Twenty porcine eyes, consisting of matched pairs from 10 pigs, were used in this study. Within pairs, one eye was tested with 10 cycles of globe pressurization to 150 mmHg (~10x normal IOP) while biaxial strains were tracked via an optical system at the posterior sclera. An excised posterior strip from the second eye was subjected to traditional uniaxial testing in which mechanical hysteresis was recorded from 10 cycles to a peak stress of 0.13 MPa (roughly equivalent to the circumferential wall stress produced by an IOP of 150 mmHg under the thin-walled pressure vessel assumption). For approximately equivalent loads, peak strains were more than twice as high in uniaxial tests than in inflation tests. Different trends in the load-deformation plots were seen between the tests, including an extended “toe” region in the uniaxial test, a generally steeper curve in the inflation tests, and reduced variability in the inflation tests. The unique opportunity of being able to mechanically load a whole globe under near physiologic conditions alongside a standard uniaxially tested specimen reveals the effects of testing artifacts relevant to most uniaxially tested soft tissues. Whole globe inflation offers testing conditions that significantly alter load-deformation behavior relative to uniaxial testing; consequently, laboratory studies of interventions or conditions that alter scleral mechanics may greatly benefit from these findings.

1.1 Introduction

The sclera is a collagenous tissue that comprises the eye’s outer shell. Naturally this tissue functions in a state of biaxial stress.(Mattson et al., 2010) The sclera’s mechanical properties have an important role in defining the course of myopia, glaucoma, and other ocular conditions.(M. J. Girard, Suh, Bottlang, Burgoyne, & Downs, 2009 Nov; McBrien & Gentle, 2003; McBrien, Jobling, & Gentle, 2009; Phillips, Khalaj, & McBrien, 2000; Siegwart & Norton, 1999) Mechanical testing of the sclera is crucial for the evaluation of treatments that stiffen the sclera to treat myopia, an area of growing research interest.(Mattson et al., 2010; Wollensak & Iomdina, 2008a; Wollensak & Iomdina, 2009) In this context, both uniaxial(Iseli, Spoerl, Wiedemann, Krueger, & Seiler, 2008; Schultz, Lotz, Lee, Trinidad, & Stewart, 2008; Wollensak & Spoerl, 2004; Wollensak & Iomdina, 2008b)and multiaxial(Eilaghi et al., 2010; Mattson et al., 2010) testing methods have been utilized in evaluating scleral mechanics. Uniaxial testing of scleral strips is relatively simple to perform but suffers from inherent shortcomings, since the test does not represent physiologic conditions. Gripping techniques can cause stress concentrations and sample slippage, flattening of the sample disturbs the natural curvature of the tissue and introduces tensile and compressive loads, frayed edges can compromise the strength of the tissue, etc.(Greene & McMahon, 1979; Mattson et al., 2010) These testing conditions inevitably lead to uncertainties in the load-deformation relationship as experimentally derived tissue behavior is a function of both inherent tissue properties and testing conditions (i.e. boundary condition effects). This issue is especially relevant since the degree to which observed behavior is directly related to testing conditions is often unknown or unreported. Whole globe inflation tests that more closely approximate physiologic conditions, which we find as technically challenging to perform as uniaxial tests, avoid most issues related to uniaxial tests. An analysis looking into the relationship between apparent differences in mechanical behavior between the two mentioned testing methodologies, with an emphasis on effects of testing conditions, is lacking.

Importantly, these described issues are all in addition to limitations of uniaxial testing that are inherent in the test regardless of how well testing conditions are managed. For instance, uniaxial testing is generally insufficient to fully characterize tissue properties, particularly, anisotropy. Additionally, development of an accurate constitutive model necessitates an understanding of the stress-strain relationship beyond the capabilities of simple uniaxial tension tests. Such limitations, along with previously mentioned testing artifacts are especially significant when translating experimentally derived data into clinically relevant situations, i.e. looking at the effects of crosslinking on tissue stiffness or the effects of trauma incidents on tissue strength.

We have adapted a method for in vitro assessment of biaxial scleral mechanics with the intent of demonstrating differences in mechanical parameters between whole globe inflation tests and traditional uniaxial tests. Due to the natural biaxial state of the sclera, we hypothesized that the whole globe inflation method would yield mechanical information that reflects load-deformation relationships in vivo more accurately than uniaxial testing. Additionally, it was hypothesized that peak stress levels used in traditional uniaxial tests and purported to be analogous to physiologic loading would tend to overestimate strain values. To investigate this possibility, we utilized paired eyes from pigs to compare the mechanical data generated by a method of whole globe inflation testing and traditional uniaxial testing.

1.2 Methods

1.2.1 Tissue Preparation

Ten pairs of freshly excised porcine eyes (Sierra for Medical Science, Whittier, CA; age of pigs 6-8 months) were used in these experiments. Each pair consisted of eyes from a single animal. All eyes were stored in a moist chamber, refrigerated at 4°C, and used for experimentation w ithin 48 hours of enucleation, a storage condition which prior work has shown does not affect tissue integrity. The sagittal and transverse diameters of each eye were measured upon arrival using a digital caliper (CD-8” PS, Mitutoyo Corp., Japan) and the posterior scleral thickness was recorded using an ultrasound pachymeter (Pachette 3, DGH Technology, Inc., Exton, PA) to ensure there was no significant difference in geometry between pairs (average difference in sagittal diameter = 0.3 (standard deviation (SD) = 0.3) mm (p > 0.05), average difference in transverse diameter = 0.3 (0.3) mm (p > 0.05), average difference in thickness = 0.06 (0.04) mm (p > 0.05), n = 10 pairs). Other features determinative to the mechanics of the posterior sclera were assumed to be similar. Selection of eyes within pairs to be used in either the whole globe inflation or uniaxial test was random. Both uniaxial and whole globe inflation testing were performed on a similar target region of the posterior sclera (Figure 1).

Figure 1.

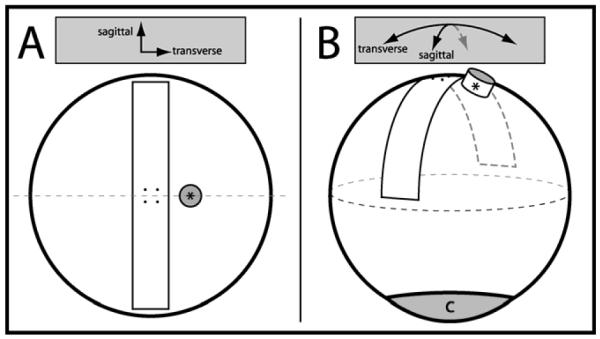
(A) Rendering of the camera view above showing the anatomical position of the excised scleral tensile sample and strain targets. For both uniaxial and whole globe inflation testing, the strain target grid was centered 4 to 5 mm temporal to the edge of the optic nerve head (*), corresponding to the posterior pole of the globe. (B) Isometric rendering of the excised scleral strip location relative to the optic nerve head and cornea (c).

1.2.2 Uniaxial Mechanical Testing

The first eye in each pair was subjected to uniaxial testing using the method that we have described previously,(Schultz et al., 2008) with several changes to the testing conditions (Figure 2A, 2B). In the current study, testing was performed in a mineral oil bath at 37°C (Mineral Oil – Light, Fi sher Scientific, Fair Lawn, NJ), rather than saline at room temperature, in order to avoid swelling that could bias the mechanical properties(Greene & McMahon, 1979). Oil bath temperature was maintained constant using a compact drive pump (Masterflex L/S Compact Drive, Barnant Company, Barrington, IL) and thermostat. The centers of the scleral strips, which measured 9 mm x 40 mm, were blotted dry temporarily and the bottom halves of four beads (1 mm diameter) were coated with a minimal amount of cyanoacrylate in order to adhere a two by two square grid, with side lengths of 4 mm (Figure 1).

Figure 2.

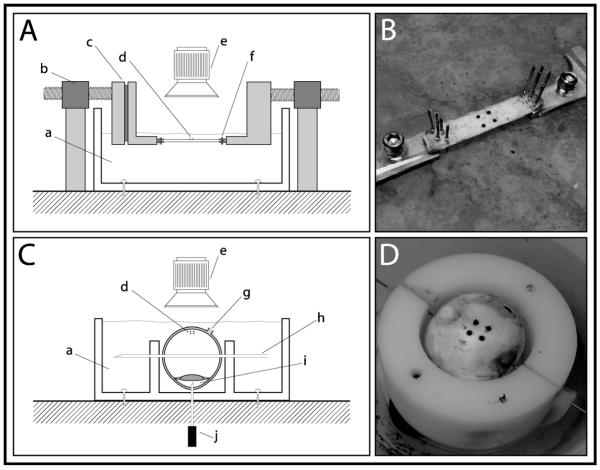
Uniaxial and whole globe inflation system setup. (A) Schematic diagram of uniaxial scleral strip held in place by gripping pins with stress being applied via dual motors on either side of sample and (B) photograph of a scleral tensile sample with local strain markers undergoing uniaxial tension. (C) Whole globe held in place by skewer and inflation needle with pressure being delivered via inflation needle in the anterior chamber; (a) oil bath (b) computer controlled linear actuator (c) clamp with force transducer (d) local strain targets (e) camera (f) gripping pins (g) optic nerve head (h) 22- gauge needle skewer (i) anterior chamber (j) 20-gauge needle to computer controlled pressure reservoir and (D) whole globe with local strain targets undergoing circumferential tension.

Peak inflation pressure was chosen to be ten times physiologic IOP, considering physiologic IOP to be 15 mmHg.(Ruiz-Ederra et al., 2005) A peak of 150 mmHg represents the highest IOP achieved during brief moments of squinting and eye rubbing.(Coleman & Trokel, 1969) To arrive at a rough peak value for uniaxial testing the globe was approximated as a thin-walled spherical pressure vessel; circumferential wall stresses (σ_c) were calculated using the following equation:

$${\sigma }_{\mathrm{c}}=Pr∕2t$$ [Equation 1]

where P (MPa) is the intraocular pressure, r (mm) is globe radius, and t (mm) is globe wall thickness. For each pair of eyes the equivalent peak load was calculated from the eye tested in the inflation test, and was measured during uniaxial testing using a 1.1-lb force transducer (Interface SMT1-1.1, Scottsdale, AZ). The zero-stress state of each specimen was established by initially loading the specimen in slight compression and then applying a slight tensile load of approximately 0.0025 MPa to each scleral sample. This loading state was used as the reference state for the specimen for the remainder of the test. Thin-walled pressure vessel equations are generally accepted when t/r < 1/10, as was the case for the eyes tested in this experiment. Though the eye is not a perfect sphere, other reports have used such an assumption as it provides a good first approximation and solid analytic footing.(Eilaghi et al., 2010; Kling, Remon, Perez-Escudero, Merayo-Lloves, & Marcos, 2010; Ku & Greene, 1981)

1.2.3 Whole Globe Inflation Mechanical Testing

The second eye in each pair was subjected to whole globe inflation testing. After the posterior aspect of the globe was blotted dry, cyanoacrylate was used to adhere the bottom halves of four beads in a two by two square grid similar to the uniaxial case. A 22-gauge needle three inches in length was used to skewer the eye at the equator for stability during testing, and the eye was then placed in a custom inflation testing device adapted from Greene(Greene & McMahon, 1979) (Figure 2C, 2D). Mineral oil at 37°C was used to k eep the eye moist prior to and during testing as above. The inflation device provided variable intraocular pressure through an adjustable fluid column, which was connected to the eye via a 20-gauge needle inserted into the anterior chamber of the globe. The three points of attachment to the globe from the skewering and pressure-applying needles stabilized the eye and prevented it from translating or rotating during experimentation. Aside from these points of attachment the globe was free to expand, and sufficient clearance was provided to prevent the globe holder from interfering with globe expansion. We assumed equivalent pressure throughout the eye, as the pressurizing needle was inserted into the aqueous of the anterior chamber in order to avoid clogging by vitreous. Intraocular pressure was adjusted between 0 and 10 times normal IOP (i.e. circumferential wall stresses ranged from 0 to approximately 0.130 MPa under the thin-walled assumption described above) with pressure being applied at a rate of approximately 0.35 mmHg s⁻¹.

Similar to the uniaxial testing regime, nine preconditioning cycles were imposed on the whole globe, and the tenth cycle was recorded for data analysis. Samples were also tested under quasi-static conditions (dε/dt < 0.001/s) to minimize strain rate dependent behavior. The zero-stress state of each specimen was established by initially loading the specimen under a positive near zero pressure equivalent to the tension applied to the sample in the uniaxial case under the thin-walled pressure vessel assumption (verified by a pneumatonometer, Mentor 30 Classic, Mentor Ophthalmics, Norwell, MA).

During testing, strain targets were tracked every two seconds using a high precision CCTV camera (Panasonic WV-BD400, Matsushita Communication Industrial Co., Ltd., Japan) and custom software (LabView and IMAQ Vision, National Instruments, Austin, TX), as in the uniaxial testing regime. For whole globe inflation testing camera tracking occurred in two dimensions, though the globe inflated in three dimensions. Since arc strain is geometrically identical to chord strain, this had no effect on our analysis.

1.2.4 Data Analysis

The first nine preconditioning cycles in either test allowed for the load-deformation curves to stabilize. Initial testing showed that by the tenth cycle, curves had sufficiently converged (strains at peak loads were within 2% of the previous cycle).

An exponential curve fit, described by Fung, was calculated using the following equation:

$$\sigma \left(\epsilon \right)\text{or}\mathrm{IOP}\left(\epsilon \right)=[\mathrm{A}∕\mathrm{B}]({\mathrm{e}}^{\mathrm{B}\epsilon }-1)$$ [Equation 2]

Where A and B are data fitting coefficients, ε is unitless strain, σ (MPa) is stress, and IOP (mmHg) is pressure.(Fung, 1993; Schultz et al., 2008) A Levenberg-Marquardt method was used in the data fitting algorithm to minimize variation in the curve fit (MATLAB, The Mathworks Inc., Natick, MA). In the uniaxial test, a single load-deformation curve was fit to the axial stresses and strains acting along the direction of the load. For whole globe inflation testing, two load-deformation curves were fit to circumferential stresses and strains acting on two perpendicular directions along the surface of the globe (to account for the biaxial stress state). An IOP-strain relationship was formulated to present the data graphically, though, the thin-walled pressure vessel assumption was used to create a stress-strain relationship for extracting approximate stiffness values.

For both uniaxial and whole globe inflation tests, the tangent modulus (E_T) was calculated to measure scleral stiffness rather than the elastic modulus (E), as stiffness values were not necessarily derived from the linear region of the stress-strain curve. In the uniaxial case, the following expression, a simplified version of Hooke’s law for a state of uniaxial stress, can be derived:

$${\sigma }_{\mathrm{a}}=\mathrm{E}\epsilon$$ [Equation 3]

where σ_a (MPa) represents axial stress. Differentiating axial stress with respect to strain and rearranging terms,

$${\mathrm{E}}_{⊺}=d{\sigma }_{\mathrm{a}}∕d\epsilon$$ [Equation 4]

To account for the more complex loading state of the whole globe inflation tests, a different model was used to calculate stiffness values. Since a pressure vessel acts in a state of biaxial stress, Poisson’s effect was included in the analysis. Using Hooke’s Law, applied to a thin-walled pressure vessel, the following relationship can be derived:

$${\sigma }_{\mathrm{c}}=\mathrm{E}\epsilon ∕(1-\nu )$$ [Equation 5]

where σ_c (MPa) represents circumferential wall stress and ν is Poisson’s ratio. Differentiating circumferential wall stress with respect to strain, assuming a Poisson ratio of 0.5 (i.e. nearly incompressible material), and rearranging terms,

$${\mathrm{E}}_{⊺}=1∕2d{\sigma }_c∕d\epsilon$$ [Equation 6]

Tangent moduli were calculated at 1% strain and at peak load for both uniaxial and whole globe inflation testing.

1.3 Results

Whole globe inflation testing resulted in positive strains for both transverse and sagittal directions, as uniform stress was imparted in all directions on the scleral surface. Positive strains in both directions better represent the true response of tissue to multiaxial stresses that occur in vivo due to IOP. In contrast, uniaxial strip testing had positive sagittal strains that resulted in negative (compressive) transverse strains, as expected.

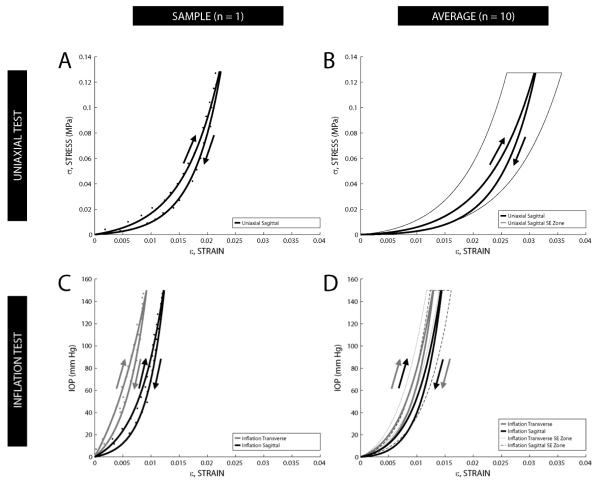
The data for all 10 pairs were analyzed individually and averaged to produce composite sagittal whole globe inflation, transverse whole globe inflation, and sagittal uniaxial curves using Equation 2 (Figure 3). It is important to note that the ordinate is different for the uniaxial and whole globe inflation tests (MPa versus IOP), though applied loads for both tests were approximately equivalent based on the thin-walled pressure vessel assumption. Data from both tests are summarized in Tables 1a and 1b.

Figure 3.

(A) Sample stress-strain hysteresis data from one uniaxial tested eye; arrows indicate loading and unloading of tissue. (B) Uniaxial composite exponential curve fit of stress-strain hysteresis data (n = 10 pairs) for each half-cycle. (C) Sample stress-strain hysteresis data from one whole globe inflation tested eye. (D) Whole globe inflation composite exponential curve fit of IOP-strain hysteresis data (n = 10 pairs) for each half-cycle. Composite curves were generated by averaging the sum of the individual functions for each fit along the strain axis (i.e. 1/n Σε_n(σ or IOP), n=10). A zone encompassing the standard error (SE) of the mean strain values for the loading portion of each of the three hysteresis loops is delineated by a thin dashed or solid line.

Table 1a.

Mechanical Results Summary, Uniaxial Testing

Test	Direction	ε (%)	ET(MPa)
		Peak Strain	Loading		Unloading
			1% Strain	Peak Load	Peak Load	1% Strain
Uniaxial	Sagittal	3.06 (1.54)	2.96 (2.49)	17.24 (7.20)	21.32 (8.00)	2.32 (2.27)

n = 10. Standard deviation in parentheses.

Table 1b.

Mechanical Results Summary, Whole Globe Inflation Testing

Test	Direction	ε (%)	ET(MPa)***
		Peak Strain	Loading		Unloading
			1% Strain	Peak Load	Peak Load	1% Strain
Whole Globe Inflation	Sagittal	1.40 (0.60)	6.29 (4.27)*	14.88 (3.84)	17.18 (3.64)	6.09 (4.77)*
	Transverse	1.24 (0.35)	6.24 (3.12)**	13.29 (4.00)	15.97 (4.01)	6.33 (3.56)**

^*n = 10 (Indicates n = 8,

^**Indicates n = 7 (i.e. for samples that didn’t reach 1% strain)).

^***Indicates values were calculated under thin-walled pressure vessel assumption. Standard deviation in parentheses.

Primary differences seen in the load-deformation behavior of whole globe inflation tests as compared to uniaxial tests include: a shorter “toe” region, a generally steeper load-deformation relationship, and a decrease in tissue variability. Overall, whole globe inflation tests yielded higher stiffness values than uniaxial tests for equivalent strains—approximately 2.1 times greater at 1% strain. At equivalent peak loads uniaxial testing showed a slightly higher stiffness, approximately 1.2-1.3 times greater than whole globe inflation. Also, at peak loads, uniaxial strain values were 2.2-2.5 times greater than those from whole globe inflation tests. There was a statistically significant difference between the whole globe inflation and uniaxial tension tests for the peak strain values (p < 0.005) and the stiffness values at 1% strain (p < 0.05).

1.4 Discussion

Our objective in this study was to compare an adapted version of a previously described method of whole globe inflation mechanical testing with traditional uniaxial strip testing. We found that tracking surface strain markers at the posterior sclera is feasible in porcine eyes and likely applicable to eyes from humans or other species (as porcine scleral rigidity is similar to human scleral rigidity).(Asejczyk-Widlicka & Pierscionek, 2008)

As was expected, significant differences were seen between the results of the uniaxial and whole globe inflation tests. Though not directly comparable, since uniaxial data is in the form of stress-strain and whole globe inflation data is presented as IOP-strain, trends and unique features from either test can still be related, and the thin-walled pressure vessel assumption can aid in rough comparisons. The differences seen are attributed to a relatively high degree of artifactual behavior resultant from testing conditions, primarily from the uniaxial test. Care was taken to ensure that testing condition effects were minimized or at least well defined. For example, a ~4.5 to 1 length to width ratio was used for uniaxially tested strips to minimize Saint-Venant related issues (i.e. non-uniform stress application near the source of the load). Nevertheless, some boundary conditions are inevitably unavoidable and their effects are difficult to control, such as tissue gripping. Waldman found that bovine pericardia tissue properties were significantly affected by gripping technique.(Waldman & Lee, 2002) To better understand the implications of artifacts from the testing conditions in the uniaxial tests, the following table (Table 2) briefly explains the importance of each in terms of their potential effects.

Table 2.

Testing Conditions / Artifacts Summary for Uniaxial Testing

Testing Condition/Issue	Effects
Straightening curved specimen	Unbuckling/loading of fibers, deviation from physiologic geometry of tissue/fibers, creation of points/regions of stress concentration
Cutting sample	Disruption of natural tension and orientation of fibers, creation of points/regions of stress concentration.
Gripping technique	Non-uniform stress distribution (particularly around grips), restriction of lateral contraction, tissue slippage, realignment of fibers (along loading axis)
Saint Venant’s Principle	Disruption in load distribution; non-uniformity in load transfer from grips to tissue
Anisotropy	Increased apparent variability (may be sign of anisotropy—the direction of sample loading affects representation/generalizability of extracted properties)
Zero-stress state*	Increased apparent variability (Load-deformation variability affected by definition and consistency of initial no-load state of tissue, particularly affected is “toe” region, where slight changes in load are associated with large increases in deformation)

^*Indicates that whole globe inflation is also affected.

A closer look at the load-deformation curves helps reveal the practical meaning of differences between the two tests studied. Load-deformation curves are typically broken down into three regions; first, the initial “toe” region where the load-deformation relationship is exponential, next, the linear region, and last, the nonlinear region which ends in tissue rupture. The initial region before the elbow is also called the elastic region (reversible deformation), and this region is of high significance because it represents the physiologic range in which tissues normally operate.(Fung, 1993) Whole globe inflation curves had an obvious elbow in the curve that occurred early in the loading. Alternately, curves from uniaxial testing had gradually rising trajectory, with less of an obvious initial elbow. This difference seems reasonable because in whole globe inflation testing, scleral tissue was being stretched uniformly and becoming stiff relatively quickly; whereas in scleral strips, compression in the perpendicular direction allowed for more distensibility and higher strains in the loading direction. Such a difference has substantial implications for clinical applications. For instance, an investigation using uniaxial tests to look at the dose-response relationship between a collagen crosslinker and scleral stiffness may report findings irrelevant to the physiologic portion of the load-deformation curve. The differences seen in the relative stiffness values at 1% strain and peak load between our two tests add merit to this discussion. While stiffness values were calculated at similar numeric points along the stress-strain curve in both tests, the actual location along the curve in terms of region (exponential, linear, or non-linear) must be considered as well. Without knowing the geometry of a complete curve (i.e. tested to rupture) it is difficult to definitively delineate the regions; however, our data reveals markedly different curve shapes within a localized range. This aids in explaining the differences seen in our scleral stiffness data at 1% strain and peak load between the two tests. The region, and location along a region, from which stiffness values are calculated plays a role in the relative differences seen in stiffness. Clinically, this becomes important when analyzing the effects of treatments that alter the mechanical properties of any soft tissues, such as the sclera.

Recently, investigators studying the mechanics of sclera and other tissues have begun to emphasize the shortcomings of uniaxial strip testing and hence the need for more physiologic multiaxial testing. Bass et al compared biaxial and uniaxial testing of human annulus fibrosus and concluded that uniaxial methods cannot be used to predict multiaxial stress behaviors in vivo.(Bass, Ashford, Segal, & Lotz, 2004) Multiaxial testing in the form of globe inflation specifically for ophthalmic research has also recently shown signs of rapid growth. Elsheikh and Anderson performed a comparative study of corneal strip versus corneal inflation tests and detailed the many inherent deficiencies in uniaxial testing due to the flattening of an originally curved specimen, a concern for uniaxial testing of sclera as well.(Elsheikh & Anderson, 2005) Myers et al have developed methods of evaluating the response to globe inflation for bovine and mouse sclera.(Myers et al., 2010; Myers, Coudrillier, Boyce, & Nguyen, 2010)(Myers et al., 2010; Myers, Coudrillier et al., 2010) Their studies looked at issues such as where displacement was most pronounced in the peripapillary region of globes, and provided information to better characterize the viscoelastic properties of the sclera. Thornton et al performed a study demonstrating the clinical relevance of inflation testing by looking at the effect of IOP on the ONH and surrounding sclera using crosslinking, with results relevant to mitigation of glaucoma.(Thornton, Dupps, Roy, & Krueger, 2009) Bisplinghoff et al have focused on trauma to whole globes with interest in globe rupture pressure, dynamic behavior, developing prediction tools, etc.(Bisplinghoff, McNally, Brozoski, & Duma, 2008; Bisplinghoff, McNally, & Duma, 2009; Bisplinghoff, McNally, Manoogian, & Duma, 2009) The cornea has also been the subject of globe inflation testing—Boyce et al have looked at full-field deformation of bovine cornea to gain better understanding of the tissue’s non-linear behavior as well as deformation behavior across the cornea.(Boyce, Grazier, Jones, & Nguyen, 2008) In using inflation tests rather than traditional uniaxial strip tests, insights gained in the lab are more easily translatable to the clinic, as demonstrated by several of these examples.

This study was able to show simple yet improved whole globe inflation testing incorporating aspects of methods reported previously.(M. J. Girard, Downs, Burgoyne, & Suh, 2008; Ku & Greene, 1981) By mounting the eye with a skewer-type needle at the equator, inserting a pressurizing cannula in the anterior chamber, and placing fiducial markers on the surface of the sclera, we were able to calculate actual localized circumferential strains and correlate IOP with multiaxial scleral deformation. Previously, varying pitfalls in biaxial experiments have limited the strength of comparing uniaxial and biaxial or inflation tests. Eilaghi and co-authors performed planar biaxial testing of human eyes, which introduces many of the same problems as traditional uniaxial testing such as straightening a naturally curved specimen and fraying the collagen fibers from cutting the sample.(Eilaghi et al., 2010) In Ku and Greene’s study, IOP was correlated with only the anterior-posterior diameter of the eye, which is a less accurate method than looking at localized strains (i.e. deformation patterns may not be uniform.(Ku & Greene, 1981) Elsheikh and Anderson performed a comparative study of uniaxial and inflation tests of corneal samples, though whole eyes were not used, creating the potential for errors due to tissue mounting.(Elsheikh & Anderson, 2005)

Our study is distinct in that it compares basic mechanical features of scleral tissue between traditional uniaxial strip testing and whole globe inflation testing using paired eyes and localized strain measurements. We found that the set-up time and experimental time needed to perform whole globe inflation testing was similar to that of uniaxial testing.

Our data revealed some degree of variability within a relatively homogeneous population of eyes. Whole globe inflation testing sometimes identified the sagittal direction as stiffer, whereas other times the transverse direction appeared stiffer. The average of the sagittal to transverse peak strain was close to one (1.16 ± 0.49), showing that on average the stiffness was similar. However, the coefficient of variation was 0.49/1.16 = 42%. Additionally, the average of the sagittal to transverse peak stiffness (at max strain) was also close to one (1.19 ± .34), but with a coefficient of variation of 0.34/1.19 = 28%. This may be a consequence of the fact that fibers are predominantly oriented circumferentially to the ONH in the immediate peripapillary region.(Greene, 1980) Thus, it is not surprising to observe a degree of variation within the ten eye pairs that were tested. Importantly, this data provides information about the anisotropy of scleral tissue that is difficult to obtain from uniaxial tests. It should be noted that preliminary data showed no statistically significant difference in mechanical parameters from paired eyes (n = 5 pairs), when both eyes were tested using the whole globe inflation method (sagittal, transverse peak strains (p = 0.77, 0.78)). These results help assure that variation between uniaxial and whole globe inflation was primarily a response of the testing environment and individual animal differences, not from variation within pairs.

Directly comparing the biaxial scleral data from our study and from prior reports(Eilaghi et al., 2010; M. J. Girard et al., 2008; Ku & Greene, 1981; Mattson et al., 2010) is difficult because of methodological, analytical, and species differences. Compared to Ku and Greene who performed whole globe inflation testing in rabbit eyes, our IOP-strain curves of porcine globes were about twice as stiff as that of the rabbit’s. Girard and co-authors studied porcine eyes but only inflated the posterior half of the sclera, clamped at the equator onto a customized apparatus, and compared to our results found four times more strain in the 5-45 mmHg region.(M. J. Girard et al., 2008) We believe this discrepancy can be attributed to the difference in inflation method. Also, these investigators kept their tissue samples in buffered saline, which can cause swelling and likely affected tissue mechanics.(Greene & McMahon, 1979) Mattson and co-authors used a similar whole globe inflation testing setup to ours, but studied shape restoration and creep behavior of eyes from two- to three-week old and adult rabbits, making comparisons to our porcine stress-strain data challenging (younger eyes generally demonstrate higher elasticity).(Mattson et al., 2010) Eilaghi’s group performed planar biaxial tests of human tissue, and IOP-strain data from our study (though different in species) falls within a similar range to theirs.(Eilaghi et al., 2010)

Similar to this study, Bass and coauthors found uniaxial tests to produce considerably higher strains than biaxial tests in human annulus fibrosis.(Bass et al., 2004) However, in the study by Elsheikh and coauthors looking at the cornea, uniaxial tests had lower strains than inflation tests.(Elsheikh & Anderson, 2005) Differences in the degree of anisotropy may be the cause of such discrepancies, as the mechanical properties of tissues vary based on the orientation of their components (i.e. fibers).(Elsheikh & Anderson, 2005)

Though the whole globe inflation method circumvented many challenges inherent in uniaxial testing, one limitation should be mentioned. The pressurizing needle was inserted into the aqueous of the anterior chamber of the eye because the vitreous in the posterior chamber was viscous enough such that it clogged the cannulating needle. The concern with the tip’s position in the anterior chamber is whether the pressure adequately equalized between the anterior and posterior chamber. Preliminary tests using a tonometer verified consistent pressures throughout the globe. Currently, we are investigating the effects of storage method and length of storage time on tissue properties, again by utilizing paired eyes, to expand on the work reported by Girard and co-authors.(M. Girard, Suh, Hart, Burgoyne, & Downs, 2007) Our preliminary data as well as the work by Girard and co-authors show that storage time (and temperature), within the tested ranges, minimally affect mechanical properties of the sclera.

Due to the testing artifacts inherent in uniaxial tests, a direct comparison of mechanical properties with a near physiologic test such as our whole globe inflation test is challenging, partly because it is difficult to even know how much of a uniaxial test represents tissue properties and how much represents bias from the testing environment. While Waldman found that their suturing and clamping techniques resulted in considerably different mechanical properties of bovine pericardia, they go on to claim that it is likely neither method actually reflects true in situ tissue properties.(Waldman & Lee, 2002) Their claim can be generalized to other related testing conditions, and consequently, it becomes difficult to define a set of standards that should be followed for all research groups looking at scleral mechanics. Our described method presents minimal boundary conditions, near physiologic loading, can be used for any region of the sclera (and potentially the cornea), is relatively simple to perform, and offers more information than uniaxial testing. A comparison between the tests is important in demonstrating differences between methodologies, but even more important is that it brings about an awareness of the underlying mechanisms of such differences.

1.5 Conclusion

In summary, our study demonstrated that the whole globe inflation mechanical testing method is feasible, simple, and repeatable in porcine eyes. We believe that this method, which is more physiologically relevant than uniaxial testing, could be a useful method to understand how the sclera responds to elevation of IOP in vivo, and also help in interpreting uniaxial testing results. This study is timely considering the growing interest in scleral cross-linking as a method to modulate scleral stiffness and as a form of therapy for certain eye diseases. In looking at the differences in mechanical properties found between uniaxial and whole globe inflation testing in this study it is important to note that uniaxial testing may add “quick-and-dirty” insight into relative comparisons of mechanical properties of tissues, but more physiologic testing regimes such as whole globe inflation testing offer considerably more value in providing both relative and absolute tissue parameters, with minimal additional complexity.

Highlights.

• - The study evaluates the biomechanics of porcine sclera in paired eyes using two different testing modalities

• - Traditional uniaxial strip testing is compared to inflation testing of a whole eye

• - The comparison highlights artifacts associated with uniaxial testing of soft tissues

• - Inflation testing yields mechanical data that is more physiologically relevant