Abstract
Circadian rhythms in physiology and behavior are regulated by the SCN. When assessed by expression of clock genes, at least 2 distinct functional cell types are discernible within the SCN: nonrhythmic, light-inducible, retinorecipient cells and rhythmic autonomous oscillator cells that are not directly retinorecipient. To predict the responses of the circadian system, the authors have proposed a model based on these biological properties. In this model, output of rhythmic oscillator cells regulates the activity of the gate cells. The gate cells provide a daily organizing signal that maintains phase coherence among the oscillator cells. In the absence of external stimuli, this arrangement yields a multicomponent system capable of producing a self-sustained consensus rhythm. This follow-up study considers how the system responds when the gate cells are activated by an external stimulus, simulating a response to an entraining (or phase-setting) signal. In this model, the authors find that the system can be entrained to periods within the circadian range, that the free-running system can be phase shifted by timed activation of the gate, and that the phase response curve for activation is similar to that observed when animals are exposed to a light pulse. Finally, exogenous triggering of the gate over a number of days can organize an arrhythmic system, simulating the light-dependent reappearance of rhythmicity in a population of disorganized, independent oscillators. The model demonstrates that a single mechanism (i.e., the output of gate cells) can account for not only free-running and entrained rhythmicity but also other circadian phenomena, including limits of entrainment, a PRC with both delay and advance zones, and the light-dependent reappearance of rhythmicity in an arrhythmic animal.
Keywords: zeitgeber, zeitnehmer, coupling, oscillator, synchronization
The circadian system has evolved to adapt organisms to temporally recurrent events in their environment. While it is known that circadian rhythms can be generated within individual cells by autoregulatory transcription-translation feedback loops (Reppert and Weaver, 2001), recent studies highlight the importance of network properties and functional heterogeneity of the circadian systems. The mammalian circadian clock, located in the SCN, is a heterogeneous structure, composed of numerous functionally distinct cell types (Antle and Silver, 2005; Dardente et al., 2002; Hamada et al., 2001; Karatsoreos et al., 2004; Yan et al., 1999). Notable among these is a population of cells that respond to photic input but that do not exhibit a detectable rhythm in clock gene expression or electrical activity, as well as a separate population of cells that are intrinsically rhythmic but that do not immediately respond to photic input (Antle and Silver, 2005; Hamada et al., 2001; Jobst and Allen, 2002; Karatsoreos et al., 2004). Determining the network organization of the SCN is essential for developing a complete understanding of the mammalian circadian system.
A fundamental question regarding organization of the SCN concerns how a population of independent oscillators produces a coherent output. Electrophysiological evidence demonstrates that SCN neurons oscillate with a wide range of periods (Liu et al., 1997; Nakamura et al., 2001, 2002; Welsh et al., 1995) that must be coordinated to produce a coherent output. One hypothesis suggests that individual oscillators are weakly coupled and oscillate together with the mean period of the population (Liu et al., 1997). Although there is evidence for electrical coupling among some cells in the SCN (Colwell et al., 2003; Long et al., 2005; Michel and Colwell, 2001), examination of clock gene expression by in situ hybridization (Hamada et al., 2004) or by using fluorescent or luminescent reporters for clock gene expression (Quintero et al., 2003; Yamaguchi et al., 2003) indicates that cells in the SCN do not oscillate in synchrony. Rather, they exhibit a specific spatiotemporal pattern of clock gene expression appearing first in the dorsomedial SCN and then spreading ventrally at later phases (Hamada et al., 2004; Yamaguchi et al., 2003). Lack of synchrony among SCN neurons is also observed using multi-electrode plates where some neurons have a circadian rhythm in firing rate that is in antiphase to the dominant SCN firing rate rhythm (Nakamura et al., 2001).
Enright (1980) proposed a model free of coupling that demonstrated that a population of oscillators with different and variable periods could produce a coherent rhythmic output. Essentially, inactive oscillators were phase advanced to a common phase when the summed output of the population reached a predetermined threshold (Enright, 1980). We sought to understand basic clock behavior in a conceptual model that explained how a population of independent oscillators, each of which had a distinct phase and period, could be organized to produce a consensus population output (Antle et al., 2003). Our model neither requires nor excludes coupling among individual rhythmic cells. This two-component model is based on known properties of the SCN in which one component has intrinsically rhythmic “oscillator cells” that are not directly retinorecipient. The other component consists of “gate cells” that are sensitive to photic zeitgebers. These gate cells are also sensitive to the state of the circadian clock and, as such, regulate the clock’s own sensitivity to external signals. Such processes have been termed zeitnehmers (Roenneberg and Merrow, 1998; Roenneberg et al., 1997–1998) and are observed in the circadian systems of a wide range of species. The resetting signal of gate cells pulls the phases of the oscillator cells closer together on a daily basis (Antle et al., 2003), maintaining a coordinated rhythmic output. The properties of gate cells are based on SCN neurons that are induced to express Per mRNA or cFos in response to a light pulse but do not have detectable rhythms in expression of these genes (Hamada et al., 2001; Karatsoreos et al., 2004; Silver et al., 1996). Cells with “gate properties” contain calbindin (CalB) in hamsters and gastrin-releasing peptide (GRP) in mice (Hamada et al., 2001; Karatsoreos et al., 2004). Furthermore, in hamsters, small lesions that ablate the region of CalB–containing cells but spare a large volume of the remaining SCN tissue eliminate overt rhythmicity (Kriegsfeld et al., 2004; LeSauter and Silver, 1999), suggesting that cells in this region are necessary for expression of rhythmicity. Recent evidence from organotypic slice cultures of Per1:luciferase mouse SCN (Yamaguchi et al., 2003) indicate that a signal from the ventral SCN is necessary for maintaining phase relationships among oscillator cells. Phase relationships among rhythmic cells are stable in the slice culture over many days, but when the dorsal third of the SCN is separated from the ventral two thirds, coherent phase relationships among the rhythmic cells are only maintained in the ventral portion. The dorsal cells, although still individually rhythmic, lose their coherent phase relationship and produce an arrhythmic system. Thus, cells in the ventral aspect of the SCN maintain phase coherence among the oscillators. This is consistent with the role and anatomical location proposed for gate cells (Antle et al., 2003).
Implicit in our model, but not directly examined in the initial presentation, was the assumption that the gate cells were triggered not only by the output of the ensemble of oscillators but also by exogenous stimuli. The advantage of this arrangement is that a single mechanism (i.e., the output of gate cells) can account for both free-running rhythmicity and entrainment. The assumption that gate cells could be exogenously triggered was based largely on the physiological evidence that nonrhythmic cells in the ventrolateral SCN receive synaptic input from the eye (Bryant et al., 2000) and exhibit immediate-early gene and clock gene expression following a light pulse (Hamada et al., 2001; Karatsoreos et al., 2004; Rusak et al., 1990; Silver et al., 1996; Yan and Okamura, 2002; Yan et al., 1999).
Given the anatomical and functional heterogeneity of the SCN, an appreciation for the network organization of these separate components is essential for understanding the functioning of the circadian clock. The present simulations are designed to examine how the network model of the circadian clock responds to exogenous stimuli. The following situations are modeled: response of the system to a light pulse, entrainment of the system by daily light pulses, limits of entrainment to various T cycles, and reappearance of rhythmicity following an application of an external zeitgeber in a system initially composed of desynchronized oscillators.
METHODS
The Model
Mathematica 5.2 (Wolfram Research, Inc., Champaign, IL) and an Apple PowerBook G4 were used to create the model and to run all simulations. For display and analysis, some output was loaded into Circadia (Behavioral Cybernetics, Cambridge, MA) and converted into actograms.
How a Single Cell Oscillates
Complex multidimensional oscillator models (Goldbeter, 1995) are mathematically equivalent to parametric van der Pol limit cycles under appropriate translation (Forger and Kronauer, 2002). Based on this, each cell in the present model oscillates using a polar transformation of the van der Pol equations, similar to the approximation of the polar form previously employed (Antle et al., 2003) but revised to the exact polar form. The van der Pol oscillator is described in rectangular coordinates (x,y) by the equations:
which translate to polar coordinates (r, θ) as:
where ε is the stiffness coefficient that sets the weight of the nonlinear component, α sets the frequency of the oscillator, β is a scaling coefficient, and the polar coordinates are defined by the angle θ and the radius r. Using the Forger and Kronauer (2002) system in polar coordinates yields a system where phase (θ) decreases as time increases (i.e., phase goes from 2π through π to 0). While this has no effect on the performance of the model (oscillators moving from 0 through π to 2π would behave the same), this fact is relevant for proper interpretation of the present simulations. In all simulations, ε was set at 0.2, β was set at 1, and α was randomly determined for each oscillator, following a normal distribution that had a defined mean period and variance depending on the simulation. The output of an individual oscillator i at time t was measured using:
The Ensemble
Each simulation was run on an “ensemble” of 200 oscillators, with mean periods of 22, 24, or 26 h with a standard deviation of 1.5. The starting phase for each oscillator was uniformly distributed over 3 h (i.e., between 0 and π/4), with the exception of the “reappearance of rhythmicity” simulations, where initial oscillator phases were uniformly distributed over 24 h. The internal gate was set with a threshold of 0.1 and a hold-off (i.e., time period during which the gate could not be triggered by the oscillator ensemble; see Antle et al., 2003) of 20 h. This hold-off keeps the gate from firing continuously when the system output is above threshold. The ensemble output at time t was considered to be the mean of the individual oscillator outputs.
The Gate
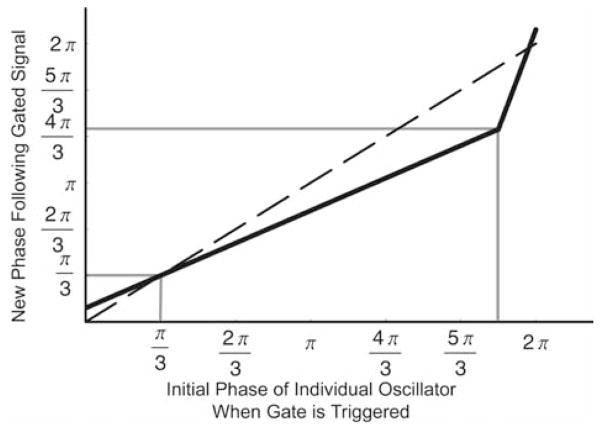
When the gate “fires,” it resets the phases of the oscillators, as previously described (Antle et al., 2003). Briefly, the gate signal delays the phase of fast oscillators and advances the phase of slow oscillators. This has the net effect of reducing the variance of the θ component of the ensemble. The r component of each oscillator is then adjusted to ensure that the mean limit cycle maintains the same location in the phase space. The resetting effect of the gate is defined by 3 parameters: the slope of the resetting function and the points of intersection with the null-resetting function. The resetting function used for the present simulations is a refinement of the function employed in our previous model (Antle et al., 2003). The slope of our function is increased between 11π/6 to 2π to eliminate the asymptotic discontinuity at the 2π to 0 transition. Thus, this new resetting function now intersects the null-resetting function at 2 points (Fig. 1).
Figure 1.
Resetting function that describes how the phase of an individual oscillator is reset by the gate. Phase is indicated over a range from 0 to 2π along both the x and y axes. The dashed line represents the function for no change in phase. The solid black line represents the resetting function employed in all simulations. Solid grey lines show phase of intersect and maximum change. This function was selected as it is similar to our previously validated function (Antle et al., 2003) but includes a more physiological connection between the maximal phase delays and advances near the 2π → 0 transition. The individual oscillators’ phase decreases as time increases. Therefore, later phases are represented at the left of the x-axis and bottom of the y-axis, while earlier phases are represented at the right of the x-axis and top of the y-axis. Thus, portions of the reset function below the null-reset function advance the phase of individual oscillators, while portions above the null-reset function delay them.
The Simulations
Simulations were run using a single gate that could be activated in one of two ways: either endogenously or exogenously. Endogenous activation was triggered once each cycle when the output of the ensemble exceeded a threshold of 0.1, similar to what has previously been employed (Antle et al., 2003). Exogenous activation of the gate was triggered at specific hours to simulate light pulses at various points of the circadian cycle and was not subject to the hold-off. The resetting function for each type of activation was identical.
Phase Response Curve
Exposing a free-running animal to light during the subjective night resets the phase of the circadian clock. The magnitude and direction of the reset is phase dependent and is described by a PRC. We examined the resetting properties of the model by triggering the gate at precise phases. Two resetting functions were employed, the one depicted in Figure 1 and a weaker function with the same null intersect at π/3 and an inflection at 11π/6, but with a slope of 0.8 instead of 0.7 used in the rest of the simulations. A PRC was constructed by running 24 separate simulations on ensembles of 200 oscillators with periods that were normally distributed with a mean of 24 h. The internal resetting signal always used the function presented in Figure 1, with resetting by light pulses (i.e., when the gate was force triggered rather than self-triggered) using either the same resetting functions (Fig. 1) or the weaker function with a slope of 0.8. To probe the system’s responsiveness to exogenous activation at every circadian phase, each of the 24 simulations was run for 800 one-hour time steps and received a single light pulse at one of 24 time points at about the midpoint of the simulations (i.e., at hours 400–423). Unlike the model, biological systems cannot be activated at every circadian phase. This could be modeled by having the gate open at some times and closed at others but requires first that one know at what phases this should occur relative to the system’s output. The present simulations should help identify these phases such that future simulations could include such a parameter. For that reason, the gate was always responsive to exogenous stimulation in the present simulations. The acrophases were identified with a cosine-fitting routine. Regression lines were fit to the acrophases before and after the light pulse. The acrophase for the day following the gate activation was predicted for each regression line, and the time between these 2 predicted acrophases was used to determine the phase shift. This was done using Circadia’s “compare fitted lines” routine based on the methods described by Daan and Pittendrigh (1976).
Entrainment
For the circadian system to be adaptive, organisms must synchronize their endogenous circadian rhythms with the oscillations in their environment through entrainment. Furthermore, if our model can be phase shifted by discrete activation (see previous simulation above), then it should also exhibit entrainment to daily activation. The entrainment simulations were modeled with ensembles of 200 oscillators with periods that were normally distributed with a mean of either 22 or 26 h. The simulations were run for 900 one-hour time steps. Starting with hour 302 and ending with hour 590, the gate was triggered once every 24 h (i.e., at hours 302, 326, 350, 374, 398, 422, 446, 470, 494, 518, 542, 566, and 590) to simulate daily light pulses. These time points were selected to cover the middle third of the simulations, with the first and last thirds left undisturbed for comparison. The results were then imported into Circadia to create actograms.
Organisms can entrain only to light cycles with periods in the circadian range (i.e., between ~21 and 28 h; Moore-Ede et al., 1982). The limits of entrainment for our model were obtained by running simulations on ensembles of 200 oscillators. Each simulation was run for 900 one-hour time steps. A T cycle between 15 and 32 h in length was applied starting with hour 301 and ending prior to hour 600. These time points were selected to cover the middle third of the simulations, with the first and last thirds left undisturbed for comparison. The simulations were run twice, using a resetting function with a slope of either 0.7 or 0.8 between 0 and 11π/6. In each case, the function intersected with the null-resetting function at π/3. Each T cycle simulation was then imported into Circadia, where the simulation’s period during the T cycle could be determined using a cosine spectrum analysis and fast Fourier transform, which yielded identical results for all the simulations. All days during the T cycle were used to calculate the period, unless there were obvious initial transient cycles that established a particular phase angle of entrainment prior to a stable free run (e.g., Fig. 4C, first 3 cycles of imposed T cycle). In these cases, the initial transient cycles were omitted. The period with the greatest power was taken as the dominant period for the system. We concluded that a system was entrained when the period of the ensemble, τ, was equal to the period of the T cycle.
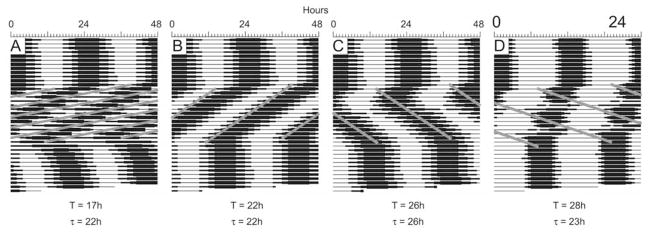
Figure 4.
Representative actograms depicting limits of entrainment. The period of the applied T cycle (the frequency with which the gate was exogenously triggered) is presented, as is the period of the system (τ), as calculated by cosine spectrum analysis. The systems were allowed to free run for about 12 cycles before the T cycle was applied (using the resetting function with a slope of 0.7). The T cycle was applied for about 12 cycles (indicated by the diagonal gray lines on the actograms), after which the system was allowed to free run again.
Reappearance of Rhythmicity
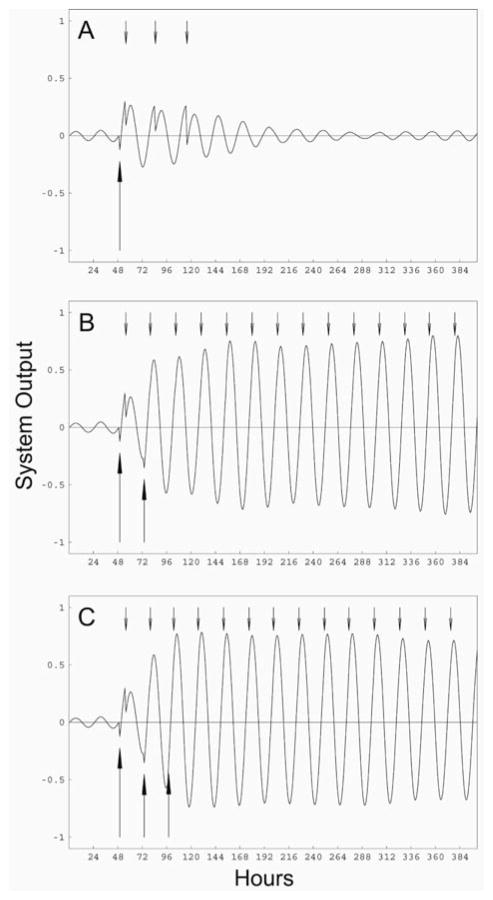
Ground squirrels emerging from hibernation are initially arrhythmic and appear to require exposure to a number of light-dark cycles before full-amplitude rhythmicity is regained (Hut et al., 2002a, 2002b). This state may result from desynchronization of individual SCN neurons (Hut et al., 2002a). The simulations that examined reappearance of rhythmicity were performed with ensembles of 200 oscillators with periods that were normally distributed with a mean of 24 h. The initial phase of the oscillators was uniformly distributed between 0 and 2π (i.e., over 24 h). The internal gate was set with a threshold of 0.25 instead of 0.1 so that the system would not spontaneously self-organize (Antle et al., 2003). All 3 simulations were run for 400 one-hour time steps. The first simulation had a single light pulse in hour 49, the second had light pulses in hours 49 and 73, and the third simulation had light pulses in hours 49, 73, and 97. These time points allowed 2 full “days” to pass undisturbed prior to the application of light pulses to obtain arrhythmic baseline data. In the second and third simulations, the light pulses were separated by 24 h.
RESULTS
Phase Response Curve
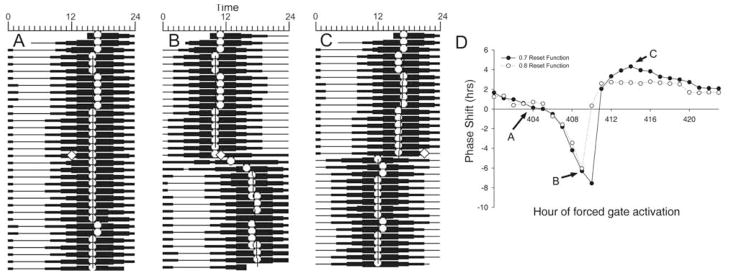
Light pulses were simulated by triggering the gate at particular time points (i.e., 1 of 24 consecutive hours midway through the simulation). The output of the ensemble was adjusted in a phase-dependent manner using the strong reset function presented in Figure 1 (i.e., with a slope of 0.7). Sample actograms depicting no change, a phase delay, and a phase advance to this function are presented in Figure 2A–C. Some phase shifts exhibited prominent reorganization over a number of cycles following the gate activation (e.g., Fig. 2B). Figure 2D presents the PRC constructed from light pulses applied at different times over a 24-h period. When a weaker resetting function was used (i.e., with a slope of 0.8), the maximal advances and delays were decreased, although the overall shape remained largely unchanged (dashed line in Fig. 2D).
Figure 2.
Resetting the ensemble with a single light pulse. (A–C) Actograms derived from the output of the model. Each horizontal line represent one 24-h period, with successive “days” plotted below the previous day. White circles represent the acrophase for each individual cycle. The width of the horizontal line is proportional to the amplitude of the system output. White diamonds represent the phase at which the gate was triggered exogenously, simulating a discrete “light pulse.” Regression lines were fit to the acrophases both before and after the light pulse. (D) A phase response curve constructed from light pulses presented at 1 of 24 consecutive hours. Shifts depicted in panels A to C are indicated by letters and arrows referencing the solid line. Solid line represents shifts to the reset function in Figure 1, while the dashed line represents shifts to a weaker function with a slope of 0.8 instead of 0.7.
Entrainment
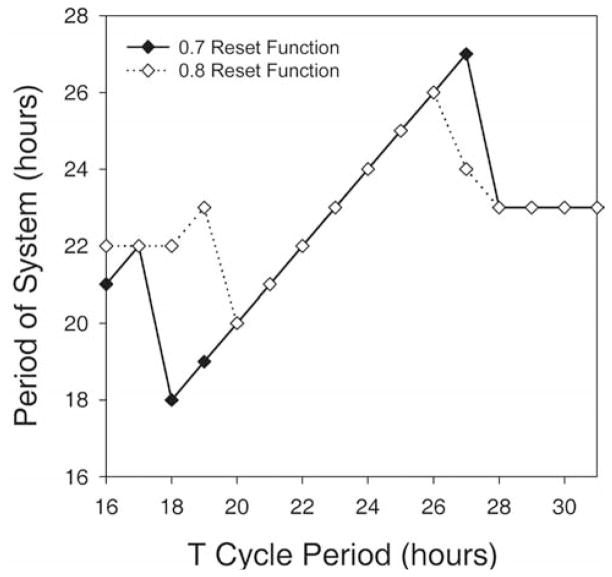
Fast ensembles with a period of 22 h and slow ensembles with a period of 26 h were each entrained by daily applications of light pulses. Figure 3 presents actograms produced from the output of the 2 simulations. When testing the limits of entrainment for systems composed of oscillators that had a mean period of 24 h, we found that entrainment occurred for T cycles in the circadian range. For the reset function with a slope of 0.7 between 0 and 11π/6, entrainment was observed only to T cycles with periods between 18 and 27 h (Fig. 4B,C; solid line in Fig. 5). For the reset function with a slope of 0.8, entrainment was observed only to T cycles with periods between 20 and 26 h (dashed line in Fig. 5). T cycles outside these ranges produced disorganized outputs with dominant periods that differed greatly (i.e., > 4 h) from the applied T cycle (Fig. 4A,D; Fig. 5).
Figure 3.
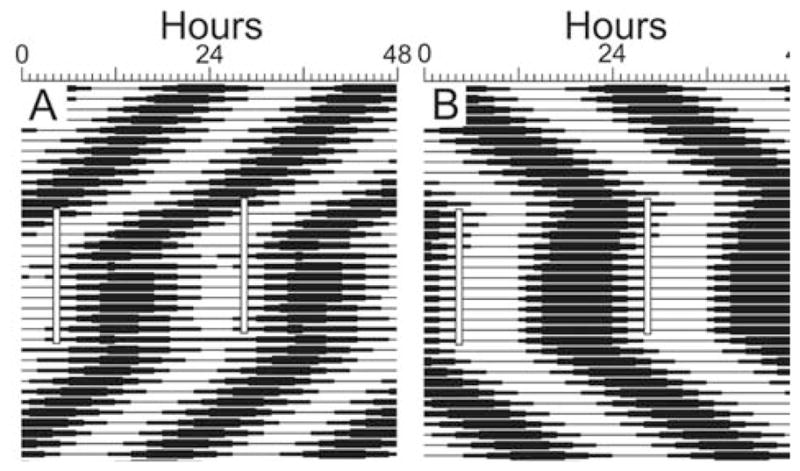
Entrainment of the ensembles by simulated daily light pulses. Double-plotted actograms derived from the output of the model are presented. Ensembles with mean periods of (A) 22 h or (B) 26 h were allowed to oscillate undisturbed for about 12 cycles, after which the gate was triggered exogenously at the same time every 24 h. This persisted for 13 cycles, after which the systems were allowed to free run.
Figure 5.
Relationship between applied T cycle period and the resulting period of the system (τ), as determined by cosine spectrum analysis. The solid line represents the τ produced using the reset function with a slope of 0.7 (Fig. 1), while the dashed line indicates the τ produced using the weaker function with a slope of 0.8.
Reappearance of Rhythmicity
The effect of a zeitgeber on an arrhythmic system composed of desynchronized oscillators was modeled with an ensemble of oscillators that had evenly distributed initial phases. Self-sustaining rhythmicity required 2 or more applications of the zeitgeber (Fig. 6). A single zeitgeber pulse produced transient organization that quickly damped into arrhythmicity. Two light pulses produced sufficient organization to generate self-sustained oscillations, although full-amplitude rhythmicity was not achieved until after about 5 cycles. Three light pulses were far more effective, producing full-amplitude rhythmicity by the first cycle following the final light pulse.
Figure 6.
Simulation of restarting the circadian system following emergence from hibernation. Each simulation was performed with 200 oscillators with periods that were normally distributed with a mean of 24 h and a standard deviation of 1.5 h. The initial phases of the oscillators were uniformly distributed between 0 and 2π. Large upward arrows denote the times that the gate was exogenously triggered, simulating light exposure. Small downward arrows denote the times that the gate was endogenously triggered by the output of the ensemble of oscillators. The gate was exogenously triggered (A) once, (B) twice, or (C) 3 times.
DISCUSSION
The present model demonstrates that nonrhythmic gate cells, which are sensitive to both environmental signals and the consensus output of the oscillator ensemble, can perform 2 distinct functions: they maintain coordinated rhythmic output of the circadian system in the absence of external perturbations (Antle et al., 2003), and they regulate the phase and period of the circadian system when triggered by exogenous signals (present results). These findings demonstrate that free-running rhythmicity, resetting, and entrainment of the circadian system may be produced by a single mechanism: the output of gate cells. Our relatively simple model simulates not only free-running and entrained rhythmicity but also simulates various other circadian phenomena, including limits of entrainment, a PRC with both delay and advance zones, and the light-dependent reappearance of rhythmicity in an arrhythmic animal.
Simulating Circadian Phenomena
The output of the oscillator ensemble can be entrained by triggering the gate at the same time every day, mimicking exposure to a daily scheduled light pulse. The phase angle of entrainment depends on the system’s free-running period. Animals with short circadian periods will entrain to light pulses that fall near their onset of activity, whereas animals with long circadian periods will entrain to light pulses that fall near their activity offset (Pittendrigh and Daan, 1976). In our simulation, fast systems with 22-h periods entrain to daily gate activation just after the nadir of their rhythmic output, while slow systems with 26-h periods entrain to daily gate activation about midway through the falling phase of their output.
Examination of the limits of entrainment reveals that a system composed of oscillators with a mean period of 24 h can be entrained within the circadian range (i.e., 18–27 h). Outside this range, the period of the system no longer matches the imposed period, a finding consistent with biological observations. These limits are consistent with the PRC generated using single forced activation of the gate (i.e., ~7.5-h delay and about ~4-h advance). Moving the slope of our resetting function closer to the null-reset function decreased the amplitude of our PRC and yielded narrower limits of entrainment more in line with those observed in animal models (Moore-Ede et al., 1982).
By triggering the gate at specific time points during the free-running simulation, it was possible to build a PRC. Some phase shifts exhibited prominent reorganization over a number of cycles following the gate activation (e.g., Fig. 2B), suggesting an interaction between the initial effect of the exogenously triggered gate and the later effect of the endogenously activated gate over the next few cycles. The effect of this interaction appears to be that the magnitude of the resulting phase shifts is augmented by the subsequent reorganization of the system over the next few cycles and may be similar to what is occurring in biological systems that exhibit transient cycles prior to establishing a stable free-running rhythm following exposure to a light pulse.
Our PRC matched the general pattern of that observed in biological systems: the delay zone precedes the advance zone and follows phases where stimulation produces little or no effect on phase. Our PRC does differ from those observed in biological systems in that dead zones are typically much longer, with a duration typically similar to the duration of the light portion of the LD cycle. In our simulations, a response close to zero was observed only at 2 time points (hour 404 and 405, Fig. 2D). This difference is not surprising as we set up our current simulations so as to understand what effect the gate would have on the system at every circadian phase, while the circadian system in animals can only be activated by light during the subjective night (Rusak et al., 1990). One aspect of the biology acknowledged by our model, which has yet to be incorporated, is that the gate is open at one time of the day and closed at another and, as such, can only be exogenously activated at certain phases. Recently, entrainment has been modeled with the inclusion of a dead zone, a daily phase during which levels of clock genes cannot be altered by exposure to a zeitgeber (Geier et al., 2005). The present simulations provide the necessary information to properly time an explicit dead zone in future versions of our model. The acrophase of our system’s output corresponds to early subjective night as gate activation at this phase produces phase delays (Fig. 2B). This conclusion is consistent with the phase angle of entrainment for the 22-h system (Fig. 3A), which requires daily delays and entrains to light falling after the nadir but prior to the acrophase. Entrainment of the 26-h system requires daily advances, which occur midway through the falling phase of the system’s output (Fig. 3B). Based on these observations, an explicit dead zone could be placed over the trough of the system’s output in future versions of the model.
In the present model, exogenous and endogenous triggering of the gate resets the oscillators in an identical fashion (i.e., the same resetting function was applied). In biological systems, it is possible that triggering the gate with light may have a different effect on the phase of the oscillators than triggering the gate endogenously with the output of the oscillator ensemble. The strength of a resetting signal could be related to the number of gate cells activated or to the amount of neurotransmitter released by each gate cell and could be represented in this model using a reset function with a different slope, such as those examined both in the present and prior simulations (Antle et al., 2003). Similarly, different light intensities or durations could be simulated with different slopes of the resetting function. Stronger activation by an exogenous signal would produce greater coherence of the system by supplementing or overriding the weaker daily activation from the endogenous signal. This is consistent with the suggestion of using more intense zeitgebers to reverse age-related loss of circadian amplitude (Weinert, 2000). This age-related loss of amplitude may result from gradual loss of synchrony among oscillators. This loss of synchrony may also be observed in mice housed in constant bright light, which exhibit a decrease in the amplitude of their locomotor rhythms before eventually becoming arrhythmic (Ohta et al., 2005). While whole SCN explants from these mice do not exhibit detectable rhythmicity, individual SCN neurons continue to express circadian oscillations, consistent with a weakened or nonfunctional gate that is unable to maintain phase coherence among oscillators in the ensemble.
The final circadian phenomenon considered within our model is the reappearance of rhythmicity following application of an entraining signal, such as is observed in ground squirrels following hibernation and in zebrafish and fruit flies raised in constant darkness (Hut et al., 2002a, 2002b; Kaneko and Cahill, 2005; Power et al., 1995). In our simulations, a single exogenous activation of the gate yields organization of the system that damps over a few cycles (Fig. 6A). This situation is similar to initiating oscillations with a serum shock in fibroblast cultures (Balsalobre et al., 1998). Following the initial organization, the culture exhibits a rapidly dampening oscillation resulting from desynchronization of its individual oscillator cells (Nagoshi et al., 2004; Welsh et al., 2004). Externally triggering the gate on 2 or 3 successive days can bring the oscillations to sufficient amplitude to initiate endogenous triggering of the gate, after which the system is able to maintain oscillations without further external activation (Fig. 6B,C). This matches the experimental observation that arrhythmic ground squirrels emerging from hibernation often require exposure to a number of light-dark cycles before rhythmicity reappears (Hut et al., 2002a, 2002b). These simulations are consistent with the suggestion that posthibernation arrhythmicity results from internal desynchronization of individual SCN neurons (Antle et al., 2003; Hut et al., 2002a, 2002b). Similar findings have been recently reported in 3 other model systems. The first example is mice with a mutation in the Per2 gene. These mice frequently become arrhythmic but regain rhythmicity following a light pulse (Spoelstra et al., 2004) or exposure to constant light (Steinlechner et al., 2002). This could represent an impaired gate or an impaired response to the gate that leads to loss of synchrony among oscillators unless the gate is triggered by a strong external stimulus. The second example is zebrafish, which do not exhibit a circadian rhythm in gene expression unless they have first been exposed to a number of light-dark cycles (Kaneko and Cahill, 2005), possibly resulting from oscillating cells that are desynchronized. Finally, Drosophila raised in constant darkness are behaviorally arrhythmic until they are exposed to a light pulse as adults (Power et al., 1995).
Nature of the Signals
Two peptides described to date have the properties required of gate signals. Vasoactive intestinal polypeptide (VIP) and GRP are both located in the ventrolateral SCN and mimic the effects of light when applied to the SCN (Antle and Silver, 2005). Some VIP cells are directly retinorecipient in rats (Kawamoto et al., 2003). VIP-deficient mice and VIP receptor VPAC2 knockout mice are behaviorally arrhythmic in constant conditions (Colwell et al., 2003; Harmar et al., 2002), even though some SCN neurons retain rhythmicity in mutant mice lacking either VIP or the VPAC2 receptor (Aton et al., 2005; Brown et al., 2005). These observations are consistent with an SCN wherein the individual oscillator cells are desynchronized due to the lack of a daily organizing signal from the gate. GRP is also a good candidate for an entrainment signaling molecule, as it is found in about 50% of CalB cells in hamsters. Recent findings indicate that GRP activates a subset of hamster SCN neurons, lying above the CalB region in the dorsolateral SCN, termed cap cells (Antle et al., 2005) and that GRP receptor mRNA is found in the dorsomedial mouse SCN (Karatsoreos et al., 2006). Furthermore, GRP promotes cellular rhythmicity in the absence of VIP-VPAC2 receptor signaling in mice (Brown et al., 2005), indicating that GRP is able to substitute as a gate signal when the VIP signaling system is defective. It is possible that these 2 neuropeptides can independently serve as the gate signal. Alternatively, these peptides may interact (Albers et al., 1991) to produce the complete gate signal. This possibility is strengthened by the observation that in the rat, only those VIP cells that contain GRP are light responsive (Kawamoto et al., 2003), suggesting that gate cells may contain both of these neurotransmitters.
Target of the Signal
While oscillators exhibit a wide range of periods, some studies suggest that oscillator cells may have a specific spatial arrangement with respect to phase and period. Rhythmic expression of vasopressin occurs first in SCN cells near the third ventricle, spreads ventrally, and then recedes back to this spot (Hamada et al., 2004). A similar pattern and time course is observed with Period gene expression quantified with in situ hybridization (Hamada et al., 2004) or with a luminescent reporter (Yamaguchi et al., 2003). Evidence from an in vitro organotypic SCN slice culture where the coronal SCN slice is bisected horizontally suggests that oscillator cells in the dorsal SCN oscillate with shorter periods than those in the ventral SCN (Noguchi et al., 2004). These findings suggest that the dorsal cells may initiate the rhythmic response among the oscillators, and it is possible that gate cells may directly contact these cells. This would be consistent with recent models suggesting that only a few long-range connections are required to coordinate activity among distant regions (Buzsaki et al., 2004). However, when dorsal SCN cells are separated from the gate cell–containing ventral SCN, they become desynchronized (Yamaguchi et al., 2003), while oscillator cells in the more ventral regions can maintain phase coherence. This suggests that the dorsal SCN cells are not necessary for maintenance of phase coherence; in contrast, the presence of the gate cells does appear necessary. Finally, it is possible that the signal from the gate that organizes the phases of the oscillators may act in a diffusible rather than synaptic manner, as SCN explants are able to initiate and maintain coherent oscillations in cortical glial cultures 0.5 mm away. Determining which oscillator cells receive input from the gate cells will be essential to understanding the network properties of the SCN. Unraveling the circuitry of these regions will allow future refinements of the model to incorporate the spatial organization of individual oscillator cells.
In conclusion, the present findings demonstrate that the network organization of light-inducible gate cells and rhythmic oscillator cells may be fundamental to producing a system with a single coherent rhythmic output. Furthermore, the resetting signal from the gate cells can maintain phase coherence among the oscillator cells in free-running conditions, entrain the system to daily exogenous signals, phase shift a free-running system, and reinitiate oscillations in a system composed of desynchronized oscillators. Potential physiological correlates for some components of the “gate and oscillator” model have been identified. The retinohypothalamic tract likely releases the neurotransmitter glutamate to activate the gate cells during light exposure. CalB, VIP, and GRP cells in the SCN core may serve a role as gate cells. It is clear that there are numerous peptidergic phenotypes in the SCN (Antle and Silver, 2005), and it remains to be determined whether they each have unique functions within the circadian network. Other elements remain to be discovered, such as the SCN targets of the gate cells and how and which feedback signals from the oscillators reach gate cells. In addition, it will be important to examine how nonphotic zeitgebers act on gates and oscillators. Exercise- and arousal-induced phase shifts are thought to be mediated by nonphotic input from the median raphe and intergeniculate leaflet, which innervate distinct regions of the SCN (Morin et al., 2006) that may include both gate and oscillator cells. Other non-photic signals such as food may influence the gate-oscillator system through yet another mechanism. Determining how these zeitgebers act on the gate and oscillator cells to influence overall clock function will be essential to fully understand the network organization of the mammalian circadian system.
Acknowledgments
This work was supported by a fellowship from the Canadian Institutes of Health Research and grants from the Natural Sciences and Engineering Research Council of Canada (MCA) and the National Institutes of Health (37919, RS). We thank Kimberly Hagel for her excellent technical assistance.
References
- Albers HE, Liou SY, Stopa EG, Zoeller RT. Interaction of colocalized neuropeptides: Functional significance in the circadian timing system. J Neurosci. 1991;11:846–851. doi: 10.1523/JNEUROSCI.11-03-00846.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Antle MC, Foley DK, Foley NC, Silver R. Gates and oscillators: A network model of the brain clock. J Biol Rhythms. 2003;18:339–350. doi: 10.1177/0748730403253840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Antle MC, Kriegsfeld LJ, Silver R. Signaling within the master clock of the brain: Localized activation of mitogen-activated protein kinase by gastrin-releasing peptide. J Neurosci. 2005;25:2447–2454. doi: 10.1523/JNEUROSCI.4696-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Antle MC, Silver R. Orchestrating time: Arrangements of the brain circadian clock. Trends Neurosci. 2005;28:145–151. doi: 10.1016/j.tins.2005.01.003. [DOI] [PubMed] [Google Scholar]
- Aton SJ, Colwell CS, Harmar AJ, Waschek J, Herzog ED. Vasoactive intestinal polypeptide mediates circadian rhythmicity and synchrony in mammalian clock neurons. Nat Neurosci. 2005;8:476–483. doi: 10.1038/nn1419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balsalobre A, Damiola F, Schibler U. A serum shock induces circadian gene expression in mammalian tissue culture cells. Cell. 1998;93:929–937. doi: 10.1016/s0092-8674(00)81199-x. [DOI] [PubMed] [Google Scholar]
- Brown TM, Hughes AT, Piggins HD. Gastrin-releasing peptide promotes suprachiasmatic nuclei cellular rhythmicity in the absence of vasoactive intestinal polypeptide-VPAC2 receptor signaling. J Neurosci. 2005;25:11155–11164. doi: 10.1523/JNEUROSCI.3821-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bryant DN, LeSauter J, Silver R, Romero MT. Retinal innervation of calbindin-D28K cells in the hamster suprachiasmatic nucleus: Ultrastructural characterization. J Biol Rhythms. 2000;15:103–111. doi: 10.1177/074873040001500204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsaki G, Geisler C, Henze DA, Wang XJ. Interneuron diversity series: Circuit complexity and axon wiring economy of cortical interneurons. Trends Neurosci. 2004;27:186–193. doi: 10.1016/j.tins.2004.02.007. [DOI] [PubMed] [Google Scholar]
- Colwell CS, Michel S, Itri J, Rodriguez W, Tam J, Lelievre V, Hu Z, Liu X, Waschek JA. Disrupted circadian rhythms in VIP- and PHI-deficient mice. Am J Physiol Regul Integr Comp Physiol. 2003;285:R939–R949. doi: 10.1152/ajpregu.00200.2003. [DOI] [PubMed] [Google Scholar]
- Daan S, Pittendrigh CS. A functional analysis of circadian pacemakers in nocturnal rodents: II. The variability of phase response curves. J Comp Physiol. 1976;106:253–266. [Google Scholar]
- Dardente H, Poirel VJ, Klosen P, Pevet P, Masson-Pevet M. Per and neuropeptide expression in the rat suprachiasmatic nuclei: Compartmentalization and differential cellular induction by light. Brain Res. 2002;958:261–271. doi: 10.1016/s0006-8993(02)03563-1. [DOI] [PubMed] [Google Scholar]
- Enright JT. Temporal precision in circadian systems: A reliable neuronal clock from unreliable components? Science. 1980;209:1542–1545. doi: 10.1126/science.7433976. [DOI] [PubMed] [Google Scholar]
- Forger DB, Kronauer RE. Reconciling mathematical models of biological clocks by averaging on approximate manifolds. SIAM J Appl Math. 2002;62:1281–1298. [Google Scholar]
- Geier F, Becker-Weimann S, Kramer A, Herzel H. Entrainment in a model of the mammalian circadian oscillator. J Biol Rhythms. 2005;20:83–93. doi: 10.1177/0748730404269309. [DOI] [PubMed] [Google Scholar]
- Goldbeter A. A model for circadian oscillations in the Drosophila period protein (PER) Proc R Soc Lond B Biol Sci. 1995;261:319–324. doi: 10.1098/rspb.1995.0153. [DOI] [PubMed] [Google Scholar]
- Hamada T, Antle MC, Silver R. Temporal and spatial expression patterns of canonical clock genes and clock-controlled genes in the suprachiasmatic nucleus. Eur J Neurosci. 2004;19:1741–1748. doi: 10.1111/j.1460-9568.2004.03275.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamada T, LeSauter J, Venuti JM, Silver R. Expression of Period genes: Rhythmic and nonrhythmic compartments of the suprachiasmatic nucleus pacemaker. J Neurosci. 2001;21:7742–7750. doi: 10.1523/JNEUROSCI.21-19-07742.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harmar AJ, Marston HM, Shen S, Spratt C, West KM, Sheward WJ, Morrison CF, Dorin JR, Piggins HD, Reubi JC, et al. The VPAC(2) receptor is essential for circadian function in the mouse suprachiasmatic nuclei. Cell. 2002;109:497–508. doi: 10.1016/s0092-8674(02)00736-5. [DOI] [PubMed] [Google Scholar]
- Hut RA, Barnes BM, Daan S. Body temperature patterns before, during, and after semi-natural hibernation in the European ground squirrel. J Comp Physiol [B] 2002a;172:47–58. doi: 10.1007/s003600100226. [DOI] [PubMed] [Google Scholar]
- Hut RA, Van der Zee EA, Jansen K, Gerkema MP, Daan S. Gradual reappearance of post-hibernation circadian rhythmicity correlates with numbers of vaso-pressin-containing neurons in the suprachiasmatic nuclei of European ground squirrels. J Comp Physiol [B] 2002b;172:59–70. doi: 10.1007/s003600100227. [DOI] [PubMed] [Google Scholar]
- Jobst EE, Allen CN. Calbindin neurons in the hamster suprachiasmatic nucleus do not exhibit a circadian variation in spontaneous firing rate. Eur J Neurosci. 2002;16:2469–2474. doi: 10.1046/j.1460-9568.2002.02309.x. [DOI] [PubMed] [Google Scholar]
- Kaneko M, Cahill GM. Light-dependent development of circadian gene expression in transgenic zebrafish. PLoS Biol. 2005;3:e34. doi: 10.1371/journal.pbio.0030034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karatsoreos IN, Romeo RD, McEwen BS, Silver R. Diurnal regulation of the gastrin-releasing peptide receptor in the mouse circadian clock. Eur J Neurosci. 2006;23:1047–1053. doi: 10.1111/j.1460-9568.2006.04633.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karatsoreos IN, Yan L, LeSauter J, Silver R. Phenotype matters: Identification of light-responsive cells in the mouse suprachiasmatic nucleus. J Neurosci. 2004;24:68–75. doi: 10.1523/JNEUROSCI.1666-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawamoto K, Nagano M, Kanda F, Chihara K, Shigeyoshi Y, Okamura H. Two types of VIP neuronal components in rat suprachiasmatic nucleus. J Neurosci Res. 2003;74:852–857. doi: 10.1002/jnr.10751. [DOI] [PubMed] [Google Scholar]
- Kriegsfeld LJ, LeSauter J, Silver R. Targeted microlesions reveal novel organization of the hamster suprachiasmatic nucleus. J Neurosci. 2004;24:2449–2457. doi: 10.1523/JNEUROSCI.5323-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LeSauter J, Silver R. Localization of a suprachiasmatic nucleus subregion regulating locomotor rhythmicity. J Neurosci. 1999;19:5574–5585. doi: 10.1523/JNEUROSCI.19-13-05574.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu C, Weaver DR, Strogatz SH, Reppert SM. Cellular construction of a circadian clock: Period determination in the suprachiasmatic nuclei. Cell. 1997;91:855–860. doi: 10.1016/s0092-8674(00)80473-0. [DOI] [PubMed] [Google Scholar]
- Long M, Jutras M, Connors B, Burwell R. Electrical synapses coordinate activity in the suprachiasmatic nucleus. Nat Neurosci. 2005;8:61–66. doi: 10.1038/nn1361. [DOI] [PubMed] [Google Scholar]
- Michel S, Colwell CS. Cellular communication and coupling within the suprachiasmatic nucleus. Chronobiol Int. 2001;18:579–600. doi: 10.1081/cbi-100106074. [DOI] [PubMed] [Google Scholar]
- Moore-Ede MC, Sulzman FM, Fuller CA. The Clocks That Time Us: Physiology of the Circadian Timing System. Cambridge, MA: Harvard University Press; 1982. [Google Scholar]
- Morin LP, Shivers KY, Blanchard JH, Muscat L. Complex organization of mouse and rat suprachiasmatic nucleus. Neuroscience. 2006;137:1285–1297. doi: 10.1016/j.neuroscience.2005.10.030. [DOI] [PubMed] [Google Scholar]
- Nagoshi E, Saini C, Bauer C, Laroche T, Naef F, Schibler U. Circadian gene expression in individual fibroblasts: Cell-autonomous and self-sustained oscillators pass time to daughter cells. Cell. 2004;119:693–705. doi: 10.1016/j.cell.2004.11.015. [DOI] [PubMed] [Google Scholar]
- Nakamura W, Honma S, Shirakawa T, Honma K. Regional pacemakers composed of multiple oscillator neurons in the rat suprachiasmatic nucleus. Eur J Neurosci. 2001;14:666–674. doi: 10.1046/j.0953-816x.2001.01684.x. [DOI] [PubMed] [Google Scholar]
- Nakamura W, Honma S, Shirakawa T, Honma K. Clock mutation lengthens the circadian period without damping rhythms in individual SCN neurons. Nat Neurosci. 2002;5:399–400. doi: 10.1038/nn843. [DOI] [PubMed] [Google Scholar]
- Noguchi T, Watanabe K, Ogura A, Yamaoka S. The clock in the dorsal suprachiasmatic nucleus runs faster than that in the ventral. Eur J Neurosci. 2004;20:3199–3202. doi: 10.1111/j.1460-9568.2004.03784.x. [DOI] [PubMed] [Google Scholar]
- Ohta H, Yamazaki S, McMahon DG. Constant light desynchronizes mammalian clock neurons. Nat Neurosci. 2005;8:267–269. doi: 10.1038/nn1395. [DOI] [PubMed] [Google Scholar]
- Pittendrigh CS, Daan S. A functional analysis of circadian pacemakers in nocturnal rodents: IV. Entrainment: Pacemaker as a clock. J Comp Physiol. 1976;106:291–331. [Google Scholar]
- Power J, Ringo J, Dowse H. The role of light in the initiation of circadian activity rhythms of adult Drosophila melanogaster. J Neurogenet. 1995;9:227–238. doi: 10.3109/01677069509084159. [DOI] [PubMed] [Google Scholar]
- Quintero JE, Kuhlman SJ, McMahon DG. The biological clock nucleus: A multiphasic oscillator network regulated by light. J Neurosci. 2003;23:8070–8076. doi: 10.1523/JNEUROSCI.23-22-08070.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reppert SM, Weaver DR. Molecular analysis of mammalian circadian rhythms. Annu Rev Physiol. 2001;63:647–676. doi: 10.1146/annurev.physiol.63.1.647. [DOI] [PubMed] [Google Scholar]
- Roenneberg T, Merrow M. Molecular circadian oscillators: An alternative hypothesis. J Biol Rhythms. 1998;13:167–179. doi: 10.1177/074873098129000011. [DOI] [PubMed] [Google Scholar]
- Roenneberg T, Merrow M, Eisensamer B. Cellular mechanisms of circadian systems. Zoology. 1997–1998;100:273–286. [Google Scholar]
- Rusak B, Robertson HA, Wisden W, Hunt SP. Light pulses that shift rhythms induce gene expression in the suprachiasmatic nucleus. Science. 1990;248:1237–1240. doi: 10.1126/science.2112267. [DOI] [PubMed] [Google Scholar]
- Silver R, Romero MT, Besmer HR, Leak R, Nunez JM, LeSauter J. Calbindin-D28K cells in the hamster SCN express light-induced Fos. Neuroreport. 1996;7:1224–1228. doi: 10.1097/00001756-199604260-00026. [DOI] [PubMed] [Google Scholar]
- Spoelstra K, Albrecht U, van der Horst GTJ, Brauer V, Daan S. Phase responses to light pulses in mice lacking functional per or cry genes. J Biol Rhythms. 2004;19:518–529. doi: 10.1177/0748730404268122. [DOI] [PubMed] [Google Scholar]
- Steinlechner S, Jacobmeier B, Scherbarth F, Dernbach H, Kruse F, Albrecht U. Robust circadian rhythmicity of Per1 and Per2 mutant mice in constant light, and dynamics of Per1 and Per2 gene expression under long and short photoperiods. J Biol Rhythms. 2002;17:202–209. doi: 10.1177/074873040201700303. [DOI] [PubMed] [Google Scholar]
- Weinert D. Age-dependent changes of the circadian system. Chronobiol Int. 2000;17:261–283. doi: 10.1081/cbi-100101048. [DOI] [PubMed] [Google Scholar]
- Welsh DK, Logothetis DE, Meister M, Reppert SM. Individual neurons dissociated from rat suprachiasmatic nucleus express independently phased circadian firing rhythms. Neuron. 1995;14:697–706. doi: 10.1016/0896-6273(95)90214-7. [DOI] [PubMed] [Google Scholar]
- Welsh DK, Yoo SH, Liu AC, Takahashi JS, Kay SA. Bioluminescence imaging of individual fibroblasts reveals persistent, independently phased circadian rhythms of clock gene expression. Curr Biol. 2004;14:2289–2295. doi: 10.1016/j.cub.2004.11.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamaguchi S, Isejima H, Matsuo T, Okura R, Yagita K, Kobayashi M, Okamura H. Synchronization of cellular clocks in the suprachiasmatic nucleus. Science. 2003;302:1408–1412. doi: 10.1126/science.1089287. [DOI] [PubMed] [Google Scholar]
- Yan L, Okamura H. Gradients in the circadian expression of Per1 and Per2 genes in the rat suprachiasmatic nucleus. Eur J Neurosci. 2002;15:1153–1162. doi: 10.1046/j.1460-9568.2002.01955.x. [DOI] [PubMed] [Google Scholar]
- Yan L, Takekida S, Shigeyoshi Y, Okamura H. Per1 and Per2 gene expression in the rat suprachiasmatic nucleus: Circadian profile and the compartment-specific response to light. Neuroscience. 1999;94:141–150. doi: 10.1016/s0306-4522(99)00223-7. [DOI] [PubMed] [Google Scholar]