Abstract
Stable Zn isotopes are fractionated in roots and leaves of plants. Analyses demonstrate that the heavy Zn isotopes are enriched in the root system of plants with respect to shoots and leaves as well as the host soil, but the fractionation mechanisms remain unclear. Here we show that the origin of this isotope fractionation is due to a chemical isotope effect upon complexation by Zn malates and citrates in the aerial parts and by phosphates in the roots. We calculated the Zn isotope effect in aqueous citrates, malates, and phosphates by ab initio methods. For pH<5, the Zn isotopic compositions of the various parts of the plants are expected to be similar to those of groundwater. In the neutral to alkaline region, the calculations correctly predict that 66Zn is enriched over 64Zn in roots, which concentrate phosphates, with respect to leaves, which concentrate malates and citrates, by about one permil. It is proposed that Zn isotope fractionation represents a useful tracer of Zn availability and mobility in soils.
Introduction
Using XAFS microspectroscopy [1], it was found that Zn is dominantly bound to phosphate in the root system of the pseudo-metallophyte Arabidopsis halleri and to malate and citrate in the aerial parts. The importance of this observation was strengthened by the remarkable discovery [2] that 66Zn in the root system of plants grown in a controlled environment is enriched over 64Zn by 0.6 permil (‰) with respect to the aerial parts of the plant, an observation replicated and confirmed on plants collected in their natural habitat [3]–[5]. Because zinc isotopic variability in the natural environment is relatively narrow, with the exception of FeMn-hydroxide deposits, Zn isotope variability in plants is reflected in soils [5], [6]. In addition, it is well established that the absorption and desorption of both Zn and phosphates are strongly responsive to the pH of groundwater, hence the implications for water pollution are particularly important [7]. Zinc isotopes therefore have the potential to be a tracer of soil status and evolution as well as of water quality. Isotope fractionation by hydrated Zn ion, chlorides, sulfides, sulfates, carbonates, and citrates has recently been evaluated by ab initio methods [8], [9]. Here we set out to calculate by the same techniques Zn isotope fractionation for phosphates and malates and extend previous results for citrates. We then discuss the implications for plant physiology and soil status.
Materials and Methods
Theoretical background
Isotopic exchange in chemical reactions can be represented by two half-reactions,
 |
(1) |
or
 |
(2) |
where A and A′ are the heavy and light isotopes of the element A, and X and Y represent ligands. The difference between half-reactions 1 and 2 corresponds to a reaction of isotopic exchange between AX and AY:
 |
(3) |
The isotope separation factor α between AX and AY is defined as
 |
(4) |
where ([A]/[A′])X and ([A]/[A′])Y are the isotopic ratios A/A′ measured in the complexes AX (and A′X) and AY (and A′Y), respectively. The isotope enrichment factor is defined as αm−1. Since α is close to 1, α−1 can be approximated as ln α.
Deviations of isotopic ratios from a reference value in parts per 1000 are conventionally defined as
 |
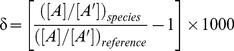(5) |
If AX (and A′X) is the major component in the system, Σ[A]/Σ[A′] is approximated to be ([A]/[A′])X such that an approximation expression δ≈103 ln α is suitable.
The standard theory of chemical isotope fractionation is based on mass-dependent isotopic differences in vibrational energies of isotopologues [10], [11]. The isotope enrichment factor is proportional to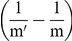 
with m and m′ the masses of two isotopes (prime represents the light isotope).
The isotope enrichment ln α due to intramolecular vibrations can be evaluated from the reduced partition function ratio (RPFR) β = (s/s′)f defined as
 |
(6) |
where the sum extends over all the molecular vibrational level with primed variables referring to the light isotopologue and
 |
(7) |
In this equation, νi stands for vibrational frequencies, s for the symmetry number of the molecule, and ui = hνi/kT. The isotope enrichment factor due to the molecular vibration can be evaluated from the frequencies summed over all the different modes. The partition function ratio (s/s′)f for isotopologues A′X and AX (A′Y and AY, respectively) is noted βX (βY, respectively). In the isotopic exchange reaction 3, isotope fractionation can be estimated from the relation ln α≈ln βY−ln βX. Contribution of other isotope effects, such as the nuclear field shift effect, to ln β is less than 10% for the Zn chloride system [12]. An adequate approximation of fractionation factors between different Zn species may be obtained by the conventional mass-dependent theory. All the calculations were made for the 66Zn/64Zn ratio.
In the present study, the optimized structures of Zn species were first determined for 64Zn. The intramolecular vibrational frequencies νi were calculated for each complex. ln b(ui′) was determined by substituting νi into Eq. (7). Then 64Zn was replaced by 66Zn and the vibrational frequencies were calculated again for the same molecular structures to obtain ln b(ui), from which ln β was then determined.
Computational details
Orbital geometries and vibrational frequencies of aqueous Zn(II) species were computed using density functional theory (DFT) as implemented by the Gaussian09 code [13], [14]. The DFT method employed here is a hybrid density functional consisting of Becke's three-parameter non-local hybrid exchange potential (B3) [15] with Lee-Yang and Parr (LYP) [16] non-local functionals. In a quantum chemical study, the convergence of the reaction energies of Zn(II) species is excellent in 6–311+G(d,p) or higher basis sets [17]. Hence, the 6–311+G(d,p) basis set, which is an all-electron basis set, was chosen for H, C, O, P, and Zn. The geometry optimization and intramolecular vibrational frequency analysis were performed for the hydrated Zn ion, hydrated Zn citrates, hydrated Zn malates, and hydrated Zn phosphates. For hydrated Zn ion, the results were reproduced from our previous studie [9], [12]. Molecules were modeled without any forced symmetry. An “ultrafine” numerical integration grid was used and the SCF convergence criterion was set to 10−9.
Results
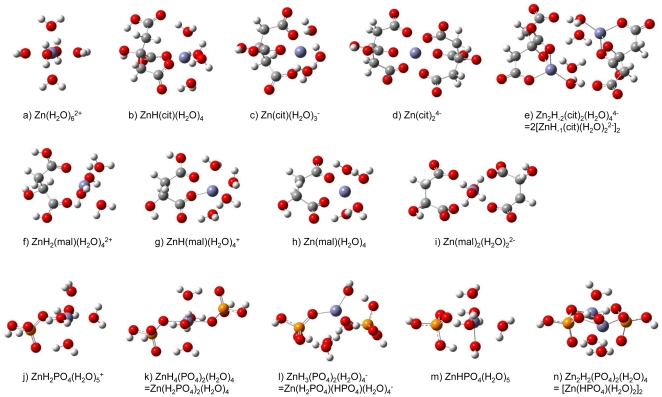
The possible Zn species are shown in Figure 1 and the ln β values obtained are shown in Table 1 . The optimized structure Cartesian coordinates are given in the File S1. The hydrated Zn2+ ion possesses six H2O molecules in its first coordination shell and complexation with large anions such as Cl− decreases the coordination number from six to four (see [12]). In the present study, we therefore assumed that the coordination number of Zn species is six. Coordination with multidentate ligands, however, sometimes decreases the coordination number due to stereochemical restriction.
Figure 1. Molecular structures of hydrated Zn2+ and aqueous Zn citrates, malates, and phosphates.
Structures are drawn by using GaussView5 (Gaussian Inc.) [14]. Symbols are: Zn (iris), P (orange), O (red), C (gray), and H (white).
Table 1. Logarithm of the reduced partition function, ln β (‰), for the isotope pair 66Zn/64Zn.
| Species | Temperature (K) | |||||
| 273 | 298 | 323 | 373 | 473 | 573 | |
| Zn(H2O)6 2+ | 3.854 | 3.263 | 2.797 | 2.119 | 1.334 | 0.915 |
| ZnH(cit)(H2O)4 | 4.033 | 3.419 | 2.934 | 2.227 | 1.406 | 0.967 |
| Zn(cit)(H2O)3 − | 4.154 | 3.523 | 3.024 | 2.297 | 1.452 | 0.999 |
| Zn(cit)(H2O)3 − a) | − | 3.94a) | − | − | − | − |
| Zn(cit)2 4− | 2.889 | 2.437 | 2.083 | 1.572 | 0.986 | 0.675 |
| Zn2H−2(cit)2(H2O)4 4− | 5.330 | 4.523 | 3.884 | 2.953 | 1.867 | 1.284 |
| ZnH2(mal)(H2O)4 2+ | 3.842 | 3.250 | 2.784 | 2.107 | 1.325 | 0.909 |
| ZnH(mal)(H2O)4 + | 3.984 | 3.376 | 2.896 | 2.197 | 1.386 | 0.952 |
| Zn(mal)(H2O)4 | 4.103 | 3.479 | 2.987 | 2.268 | 1.433 | 0.986 |
| Zn(mal)2(H2O)2 2− | 3.274 | 2.771 | 2.376 | 1.801 | 1.135 | 0.780 |
| ZnH2PO4(H2O)5 + | 4.092 | 3.468 | 2.975 | 2.257 | 1.424 | 0.978 |
| ZnH4(PO4)2(H2O)4 | 4.047 | 3.428 | 2.940 | 2.229 | 1.405 | 0.965 |
| ZnH3(PO4)2(H2O)4 − | 5.027 | 4.268 | 3.667 | 2.789 | 1.764 | 1.214 |
| ZnHPO4(H2O)5 | 4.188 | 3.559 | 3.060 | 2.330 | 1.476 | 1.017 |
| Zn2H2(PO4)2(H2O)4 | 5.156 | 4.380 | 3.765 | 2.865 | 1.814 | 1.249 |
Initial input configuration was taken from a model molecule “ZnCit01” of the literature [8]. The LanL2DZ basis set was chosen for Zn and the 6–31G(d) basis set for H, C, and O. ln β = 3.93‰ at 298 K was reported.
Four citrate species, Zn(cit)−, ZnH(cit)0, Zn(cit)2 4−, and Zn2H−2(cit)2 4−, were found in a titration measurement [18]. The molecular structure and ln β for hydrated Zn monocitrate, Zn(cit)(H2O)n −, have been estimated by the ab initio method [8]. Our calculations, which reproduced these results, were expanded to Zn(cit)2 4−, hydrated ZnH(cit), and hydrated Zn2H−2(cit)2 4−. Since citrate ion (cit)3− is a tridentate ligand, Zn(cit)(H2O)3 − and Zn(cit)2(H2O)0 4− were calculated as hydrated Zn(cit)− and Zn(cit)2 4−, respectively. The monoprotonated citrate ion H(cit)2− showed a bidentate character, such that four H2O were arranged in the empty coordination sites of ZnH(cit). The deprotonated citrate ion H−1(cit)4− is a strong anionic ligand. Calculations show that the Zn2+coordination number for the dimeric species Zn2H−2(cit)2 4− must be reduced to four. Zn2H−2(cit)2(H2O)4 4−, in which two H2O bind to Zn2+ and another two bridge the H−1(cit)4− ligands, was optimized.
Several species of Zn malates were found in titration studies [19], [20]. According to these authors, ZnH2(mal)2+, ZnH(mal)+, and Zn(mal)0 emerge as the potential malate species. A higher-order complexation of Zn(mal)2 2− may exist [20]. Malate ion (mal)2− and its protonated species were treated as bidentate ligands, with H2O molecules arranged in the empty coordination sites of Zn malates.
Complexation of Zn in orthophosphate solutions has been studied in a pioneering work using titration method [21]. The results were reexamined and several different species were found [22]. Literature data suggest the existence of five Zn phosphate species, ZnH2PO4 +, ZnH4(PO4)2, ZnH3(PO4)2 −, ZnHPO4, and Zn2H2(PO4)2. Except for strong acidic/basic conditions (pH<3 and pH>11), the hydrogen phosphate ions, H2PO4 − and HPO4 2−, are the major anionic species in orthophosphate solutions. Cadmium ion, Cd2+, a congener ion of Zn2+, in orthophosphate solutions shows a sixfold coordination, in which five coordination sites are occupied by H2O and one by an oxygen atom of the hydrogen phosphate ion [23]. Hence, H2PO4 − and HPO4 2− are treated as monodentate ligands. Since the bonding power of HPO4 2− is stronger than that of H2PO4 −, HPO4 2− attracts H+ from a H2O molecule in ZnHPO4(H2O)5 and the optimized structure resembles that of ZnH2PO4(H2O)4OH. For ZnH4(PO4)2, cis- and trans- configurations of Zn(H2PO4)2(H2O)4 were tested and the trans-configuration was energetically stable. Calculations of ZnH3(PO4)2 − as Zn(H2PO4)(HPO4)(H2O)4 deformed six coordination to smaller values. Dehydrated H2O molecules bridged H2PO4 − and HPO4 2−. Configuration of dimeric species such as Zn2H2(PO4)2 has been suggested in the literature [21] and was applied in this study.
Discussion
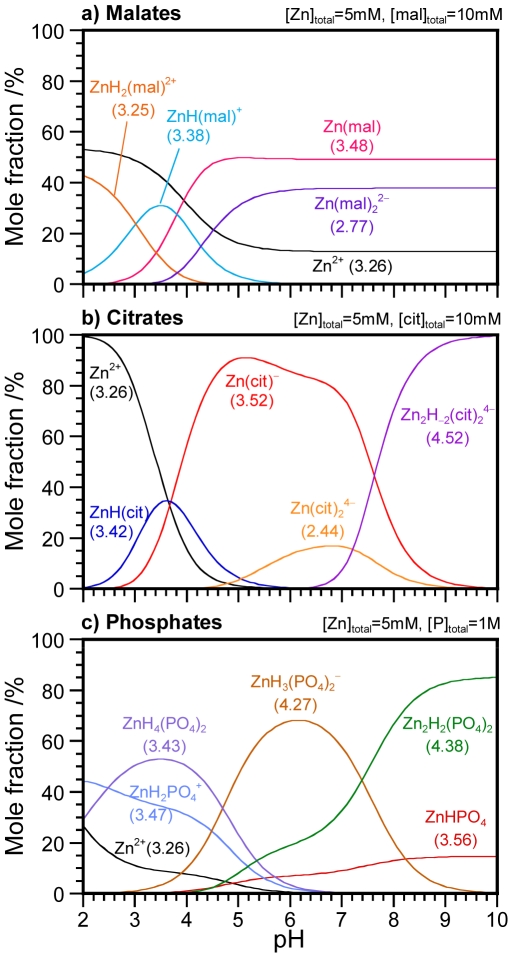
Mole fractions of Zn citrates, malates, and phosphates are shown in Figure 2 as functions of pH. These values were calculated from literature data on formation constants [18], [20]–[22] and acid dissociation constants [18], [20], [21]. As an example, concentrations of Zn and citrate were set to the values in the literature [18], i.e., [Zn]total = 0.005 mol dm−1 (M) and [cit] total = 0.01 M. Similar conditions were chosen for malates. For the phosphate system, we kept [Zn]total at the same level as in the other systems and used a rather high phosphate concentration of [P]total = 1 M. In Figure 2 , the ln β values at 298 K (see Table 1 ) are shown in parentheses. Isotope fractionation δ66Zn (‰) is the difference between the ln β values of the different species. We calculated δ66Zn between Zn2+, Zn citrates, malates, and phosphates ( Figure 3 ). Let us first discuss 66Zn/64Zn fractionation between these species, at acidic, neutral, and basic regions. In the low pH region (pH<5), ln β values of all species are tightly grouped between 3.26 and 3.47‰. In the neutral region, ln β is 4.3–4.4‰ for the major phosphate species and ∼3.5‰ for Zn citrates and malates. The difference is therefore about 0.8–0.9‰. Fractionation with respect to the original solution with positive δ66Zn in phosphates and negative δ66Zn in citrates and malates therefore is expected. In the basic region (pH>8), the major phosphate and citrate species show ln β∼4.4–4.5‰, while Zn malates and Zn2+ show ln β<3.5‰. The difference is about 0.9–1‰. Negative δ66Zn in malates and positive δ66Zn in phosphates and citrates are again expected. Overall, phosphates preferentially concentrate isotopically heavy Zn, whereas Zn2+ and malates concentrate the light Zn isotopes. Isotope fractionation in citrates varies from positive to negative depending on pH but does not seem to alter either the phosphate/malate or the phosphate/Zn2+ systems. Zinc isotope fractionation between phosphate and Zn2+ and between phosphate and malate therefore is of the order of 1‰ at pH>5. The presence of citrates may affect both Zn speciation and δ66Zn, but for pH<8, phosphate isotopically remains the heaviest Zn compound.
Figure 2. Mole fractions of Zn species as functions of pH at 298 K.
Mole fractions of Zn species were calculated by using formation constants and acid dissociation constants reported in the literature [18], [20]–[22]. The ln β values at 298 K are shown in parentheses. a) Mole fractions of Zn species in malate solutions. Total concentrations of Zn and malate are 5 mM and 10 mM, respectively. b) Mole fractions of Zn species in citrate solutions. Total concentrations of Zn and citrate are 5 mM and 10 mM, respectively. c) Mole fractions of Zn species in orthophosphate solutions. Total concentrations of Zn and phosphate are 5 mM and 1 M, respectively.
Figure 3. Isotope fractionation δ66Zn of hydrated Zn2+, and aqueous citrates, malates, and phosphates at 298 K.
Mole fractions of Zn species were calculated by using formation constants and acid dissociation constants reported in the literature [18], [20]–[22]. Isotope fractionation δ66Zn (‰) compared with the bulk solution (averaged δ66Zn in the whole solution, δ66Zn = 0) is shown together as a dotted line. The calculation procedure of δ66Zn is from [9]. a) Malate-phosphate system. Total concentrations of Zn, malate, and phosphate are 5 mM, 10 mM, and 1 M, respectively. b) Citrate-phosphate system. Total concentrations of Zn, citrate, and phosphate are 5 mM, 10 mM, and 1 M, respectively.
Using EXAFS and x-ray microfluorescence, it was pointed out that for a number of Arabidopsis species, Zn is mostly distributed among phosphates, malates and citrates, with phosphates being present notably in the root system [1]. In situ determination of pH by pseudoradiometric methods demonstrated that, cytoplasmic pH is generally stable at around 7.2 [24]. Both spectrometric and isotopic evidence [2], [3], [5] indicate that Zn phosphates must be the species responsible for Zn isotope fractionation between the root system, rich in phosphates and characterized by isotopically heavy Zn, and the aerial parts, rich in malate and characterized by isotopically light Zn. Phosphate may also account for the high δ66Zn of herbaceous plants with respect to nutrient solutions [5]. The presence of phosphate with a preferential uptake of heavy Zn explains why leachable Zn in soils has high δ66Zn [25], whereas residual silicates have low δ66Zn [5], [6].
Nevertheless, pH at the spot of root hair initiation can drop below 4.5 [26], [27]. Low pH are consistent with the finding [4] that the root system of the Zn hyperaccumulator Arabidopsis halleri has much higher δ66Zn than the root system of the nonaccumulator Arabidopsis petraea. A simple explanation of this observation is that the pH is regulated around a neutral value by the root system of Arabidopsis halleri, which promotes phosphate dissociation and Zn complexation. In contrast, in the root system of Arabidopsis petraea, pH drops to values pH<5 Zn, with the consequence that phosphate complexation is minimal and Zn isotope fractionation is greatly reduced.
In general, the fates of Zn and phosphate seem to be strongly connected and Zn isotopes should provide a new perspective on the chemistry of soils and groundwater. Phosphates are adsorbed on iron hydroxide precipitating in seawater [28], estuaries [29], and, at pH<7, soils [30]. Adsorption of Zn-phosphate liberated by the drainage of soils appears to be a straightforward explanation for the high δ66Zn of ferromanganese nodules [31]. Potential applications to the origin of field experiments [7] involving injection of solutions with well-controlled chemistry and pH into a polluted soil show that Zn and P are released coherently when the pH of the solution falls below 5, which is consistent with the release of Zn initially bound in phosphate. Natural Zn leached from plant roots should be isotopically heavy, whereas the composition of a pollutant should reflect Zn from ores and be substantially lighter.
Conclusions
We investigated fractionation of 66Zn and 64Zn between phosphates, malates, and citrates, three Zn compounds abundant in plants, using ab initio techniques for a broad range of pH conditions. We found that, for pH>5, Zn phosphate is 1‰ heavier than Zn2+ and Zn malate and, for pH<8, the heavy character of Zn phosphates is not greatly affected by the presence of citrates. This result accounts for the high δ66Zn found for roots and herbaceous plants with respect to leaves and sprouts.
Supporting Information
Optimized structure Cartesian coordinates of hydrated Zn2+ ion, citrates, malates, and phosphates (see Figure 1).
(DOC)
Acknowledgments
Janne Blichert-Toft kindly edited the manuscript. Discussions with Sylvain Pichat, Zuzana Fekiacova, Anne-Marie Aucour, Marie-Laure Pons, and Frédéric Moynier on Zn isotopes in plants are gratefully acknowledged.
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: The authors have no support or funding to report.
References
- 1.Sarret G, Saumitou-Laprade P, Bert V, Proux O, Hazemann JL, et al. Forms of zinc accumulated in the hyperaccumulator Arabidopsis halleri. Plant Physiology. 2002;130:1815–1826. doi: 10.1104/pp.007799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Weiss DJ, Mason TFD, Zhao FJ, Kirk GJD, Coles BJ, et al. Isotopic discrimination of zinc in higher plants. New Phytologist. 2005;165:703–710. doi: 10.1111/j.1469-8137.2004.01307.x. [DOI] [PubMed] [Google Scholar]
- 3.Moynier F, Pichat S, Pons M, Fike D, Balter V, et al. Isotopic fractionation and transport mechanisms of Zn in plants. Chemical Geology. 2009;267:125–130. [Google Scholar]
- 4.Aucour AM, Pichat S, Macnair MR, Oger P. Fractionation of stable zinc isotopes in the zinc hyperaccumulator Arabidopsis halleri and nonaccumulator Arabidopsis petraea. Environmental Science and Technology. 2011;45:9212–9217. doi: 10.1021/es200874x. [DOI] [PubMed] [Google Scholar]
- 5.Viers J, Oliva P, Nonell A, Gélabert A, Sonke JE, et al. Evidence of Zn isotopic fractionation in a soil-plant system of a pristine tropical watershed (Nsimi, Cameroon). Chemical Geology. 2007;239:124–137. [Google Scholar]
- 6.Peel K, Weiss D, Sigg L. Zinc isotope composition of settling particles as a proxy for biogeochemical processes in lakes: Insights from the eutrophic Lake Greifen, Switzerland. Limnology and Oceanography. 2009;54:1699–1708. [Google Scholar]
- 7.Kent DB, Wilkie JA, Davis JA. Modeling the movement of a pH perturbation and its impact on adsorbed zinc and phosphate in a wastewater-contaminated aquifer. Water Resources Research. 2007;43:W07440. [Google Scholar]
- 8.Black JR, Kavner A, Schauble EA. Calculation of equilibrium stable isotope partition function ratios for aqueous zinc complexes and metallic zinc. Geochimica et Cosmochimica Acta. 2011;75:769–783. [Google Scholar]
- 9.Fujii T, Moynier F, Pons M, Albarède F. The origin of Zn isotope fractionation in sulfides. Geochimica et Cosmochimica Acta. 2011;75:7632–7643. [Google Scholar]
- 10.Urey HC. The thermodynamic properties of isotopic substances. Journal of the Chemical Society. 1947:562–581. doi: 10.1039/jr9470000562. [DOI] [PubMed] [Google Scholar]
- 11.Bigeleisen J, Mayer MG. Calculation of equilibrium constants for isotopic exchange reactions. Journal of Chemical Physics. 1947;15:261–267. [Google Scholar]
- 12.Fujii T, Moynier F, Telouk P, Abe M. Experimental and theoretical investigation of isotope fractionation of zinc between aqua, chloro, and macrocyclic complexes. the Journal of Physical Chemistry A. 2010;114:2543–2552. doi: 10.1021/jp908642f. [DOI] [PubMed] [Google Scholar]
- 13.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, et al. 2009. Gaussian 09, Revision B.01, Gaussian, Inc.: Wallingford CT.
- 14.Dennington R, Keith T, Millam J. 2009. GaussView, Version 5.0.8.: Semichem Inc., Shawnee Mission KS.
- 15.Becke AD. Density-functional thermochemistry. 3. The role of exact exchange. Journal of Chemical Physics. 1993;98:5648–5652. [Google Scholar]
- 16.Lee CT, Yang WT, Parr RG. Development of the colle-salvetti correlation-energy formula into a functional of the electron-density. Physical Review B. 1988;37:785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 17.Rulíšek L, Havlas Z. Ab initio calculations of monosubstituted (CH3OH, CH3SH, NH3) hydrated ions of Zn2+ and Ni2+. the Journal of Physical Chemistry A. 1999;103:1634–1639. [Google Scholar]
- 18.Capone S, Derobertis A, Destefano C, Sammartano S. Formation and stability of zinc(II) and cadmium(II) citrate complexes in aqueous-solution at various temperatures. Talanta. 1986;33:763–767. doi: 10.1016/0039-9140(86)80184-9. [DOI] [PubMed] [Google Scholar]
- 19.Makar GKR, Touche MLD, Williams DR. Thermodynamic considerations in coordination. Part XXIII. Formation constants for complexes of protons, zinc(II), and acid anions and their use in computer evaluation of a better zinc therapeutical. Journal of Chemical Society Dalton Transactions. 1976;11:1016–1019. [Google Scholar]
- 20.Berthon G, Varsamidis A, Blaquiere C. Histamine as a ligand in blood plasma. Part 7. Malate, malonate, maleate and tartrate as adjuvants of zinc to favor histamine tissue diffusion through mixed-ligand coordination. In vitro tests on lymphocyte proliferation. Agents Actions. 1987;22:231–247. doi: 10.1007/BF02009051. [DOI] [PubMed] [Google Scholar]
- 21.Childs CW. A potentiometric study on equilibria in aqueous divalent metal orthophosphate solutions. Inorganic Chemistry. 1970;9:2465–2469. [Google Scholar]
- 22.Iuliano M. Complexation equilibria in zinc(II) orthophosphate solutions. Annali di Chimica. 1994;84:187–209. [Google Scholar]
- 23.Magini M, Licheri G, Piccaluga G, Paschina G. X-ray diffraction of ions in aqueous solutions: Hydration and complex formation. CRC Press: Boca Raton; 1988. [Google Scholar]
- 24.Swanson SJ, Choi WG, Chanoca A, Gilroy S. In vivo imaging of Ca2+, pH, and reactive oxygen species using fluorescent probes in plants. Annual Review of Plant Biology. 2011;62:273–297. doi: 10.1146/annurev-arplant-042110-103832. [DOI] [PubMed] [Google Scholar]
- 25.Arnold T, Schönbächler M, Rehkämper M, Dong S, Zhao FJ, et al. Measurement of zinc stable isotope ratios in biogeochemical matrices by double-spike MC-ICPMS and determination of the isotope ratio pool available for plants from soil. Analytical and Bioanalytical Chemistry. 2008;398:3115–3125. doi: 10.1007/s00216-010-4231-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bibikova TN, Jacob T, Dahse I, Gilroy S. Localized changes in apoplastic and cytoplasmic pH are associated with root hair development in Arabidopsis thaliana. Development. 1998;125:2925–2934. doi: 10.1242/dev.125.15.2925. [DOI] [PubMed] [Google Scholar]
- 27.Fasano JM, Swanson SJ, Blancaflor EB, Dowd PE, Kao TH, et al. Changes in root cap pH are required for the gravity response of the Arabidopsis root. the Plant Cell. 2001;13:907–921. doi: 10.1105/tpc.13.4.907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Berner R. Phosphate removal from sea water by adsorption on volcanogenic ferric oxides. Earth and Planetary Science Letters. 1973;18:77–86. [Google Scholar]
- 29.Upchurch JB, Edzwald JK, Omelia CR. Phosphates in sediments of pamlico estuary. Environmental Science and Technology. 1974;8:56–58. [Google Scholar]
- 30.Stevenson F, Cole M. Cycles of Soil: Carbon, Nitrogen, Phosphorus, Sulfur, and Micronutrients. John Wiley & Sons Inc, New York; 1999. [Google Scholar]
- 31.Maréchal CN, Douchet C, Nicolas E, Albarède F. The abundance of zinc isotopes as a marine biogeochemical tracer. Geochemistry, Geophysics, Geosystems. 2000;1 10.1029/1999GC000029. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Optimized structure Cartesian coordinates of hydrated Zn2+ ion, citrates, malates, and phosphates (see Figure 1).
(DOC)