Abstract
Purpose: Precise 3D modeling of the mitral valve has the potential to improve our understanding of valve morphology, particularly in the setting of mitral regurgitation (MR). Toward this goal, the authors have developed a user-initialized algorithm for reconstructing valve geometry from transesophageal 3D ultrasound (3D US) image data.
Methods: Semi-automated image analysis was performed on transesophageal 3D US images obtained from 14 subjects with MR ranging from trace to severe. Image analysis of the mitral valve at midsystole had two stages: user-initialized segmentation and 3D deformable modeling with continuous medial representation (cm-rep). Semi-automated segmentation began with user-identification of valve location in 2D projection images generated from 3D US data. The mitral leaflets were then automatically segmented in 3D using the level set method. Second, a bileaflet deformable medial model was fitted to the binary valve segmentation by Bayesian optimization. The resulting cm-rep provided a visual reconstruction of the mitral valve, from which localized measurements of valve morphology were automatically derived. The features extracted from the fitted cm-rep included annular area, annular circumference, annular height, intercommissural width, septolateral length, total tenting volume, and percent anterior tenting volume. These measurements were compared to those obtained by expert manual tracing. Regurgitant orifice area (ROA) measurements were compared to qualitative assessments of MR severity. The accuracy of valve shape representation with cm-rep was evaluated in terms of the Dice overlap between the fitted cm-rep and its target segmentation.
Results: The morphological features and anatomic ROA derived from semi-automated image analysis were consistent with manual tracing of 3D US image data and with qualitative assessments of MR severity made on clinical radiology. The fitted cm-reps accurately captured valve shape and demonstrated patient-specific differences in valve morphology among subjects with varying degrees of MR severity. Minimal variation in the Dice overlap and morphological measurements was observed when different cm-rep templates were used to initialize model fitting.
Conclusions: This study demonstrates the use of deformable medial modeling for semi-automated 3D reconstruction of mitral valve geometry using transesophageal 3D US. The proposed algorithm provides a parametric geometrical representation of the mitral leaflets, which can be used to evaluate valve morphology in clinical ultrasound images.
Keywords: image analysis, shape analysis, segmentation, ultrasound, mitral valve
INTRODUCTION
Conventionally, assessment of the mitral valve is achieved by qualitative 2D ultrasound image analysis, which derives structural and dynamic information from cross-sectional views of the valve. Published guidelines for performing a transesophageal 2D ultrasound examination1 describe 20 standard views that must be comprehensively interpreted by an observer to evaluate the complex morphology of the mitral valve, consisting of two leaflets (anterior and posterior) and a fibrous ring (the annulus) surrounding the leaflets. More recent three-dimensional ultrasound (3D US) overcomes the inherent limitations of 2D ultrasound interpretation by enabling real-time 3D visualization of valve geometry. In fact, it was not until the advent of 3D US technology that Levine and colleagues first described the saddle shape of the human mitral valve annulus, which had been previously thought to have the shape of a planar ring.2, 3 Since these early morphological studies, advances in 3D US transesophageal transducer design and signal processing have opened a previously unexplored avenue for quantitative study of mitral valve geometry and mechanics. The current commercial clinical scanners can acquire full-volume, nearly isotropic data sets with submillimeter resolution showing the mitral valve in three dimensions through a midesophageal window, with a matrix-array probe that contains a few thousand individual active elements. Although several commercial software packages allow for manual tracing and user-guided measurement of valve dimensions in these 3D US data sets, manual analysis is time-consuming and labor-intensive and is therefore impractical for routine clinical use. Additionally, a more efficient means of noninvasive 3D valve morphometry would add quantitative patient-specific information on valve structure to the standard qualitative clinical assessments. Such information has potential to improve diagnosis, risk stratification, and periprocedural care of patients with ischemic MR, a condition in which a structurally normal mitral valve is rendered incompetent as a result of myocardial infarction induced remodeling.
To date, many valve morphometry studies have employed manual tracing to reconstruct valve geometry from 3D US image data.2, 4, 5, 6, 7, 8, 9 Alternatively, valve geometry has been invasively assessed in animal models by sonomicrometric array localization10, 11, 12 and biplane radiography with tantalum markers.13, 14, 15 Several studies have explored automated ultrasound image analysis of the mitral valve,16, 17, 18, 19, 20, 21, 22 including tracking of the anterior leaflet in 2D ultrasound images and segmentation and tracking of the mitral annulus with 3D ultrasound. The recent work of Ionasec et al.18 models and quantifies aortic and mitral valve dynamics using a nonrigid landmark motion model. With that technique, the mitral valve is represented by seven anatomic landmarks, which are tracked throughout the cardiac cycle using a trajectory spectrum learning algorithm. The landmark locations and learned boundary detectors guide fitting of a surface representation of the valve in cardiac computed tomography (CT) and real-time 3D US image data. While this method identifies correspondences on the valves of different subjects and on the same valve at multiple time points, it does not provide volumetric segmentations and the valve is represented by only a few points. In another study, Burlina et al.20 demonstrate 3D segmentation of the open mitral valve using a thin tissue detector, dynamic contour method, and manual correction. Those authors develop a mechanical model to infer the closed position of the valve given a static 3D mesh reconstruction of the open valve obtained from segmentation. Schneider et al.19, 21 describe a semi-automated method for locating the mitral annulus and subsequently estimating and refining a search space coordinate system to generate a mesh of the mitral leaflets at diastole. The segmentation algorithms proposed in the latter two works produce surface representations of the open valve from 3D US images. Finally, Shang et al.22 demonstrate volumetric rendering of the mitral valve using an intensity-based level set method, but this segmentation algorithm also captures extraneous structures with similar intensities, such as the left ventricular wall, in addition to the mitral leaflets.
The objective of this paper is to introduce a novel approach to valve delineation and morphometry that produces volumetric reconstructions of the anterior and posterior leaflets at midsystole in transesophageal 3D US images. Midsystole was selected for analysis in this work since it is most relevant in identifying leaflet malcoaptation in patients with MR. While segmentation allows for delineation and visualization of anatomical structures, the extraction of quantitative, clinical information requires additional knowledge of anatomic landmarks and valve shape, which segmentation alone may not always provide. In this paper, we propose an additional step in which a continuous medial representation (cm-rep) of the valve is obtained from the results of image segmentation in order to match anatomic landmarks. While there are several approaches to obtain a medial representation of an anatomic structure, we propose a method first described by Pizer et al.23 and later extended by Yushkevich et al.,24 in which different instances of a structure are fitted with a deformable medial template whose skeletal branching configuration is preserved during deformation. Here, deformable medial modeling is used to represent 3D valve geometry derived from image segmentation in a compact manner suitable for statistical shape analysis. The advantage of deformable medial modeling is that it is able to account for shape variability across a patient population while preserving the topology of the anatomic structure being analyzed. Furthermore, the deformable model establishes correspondences on valves of different subjects, which facilitates the measurement of clinically relevant morphological features.
Volumetric representation with cm-rep is advantageous in valve modeling. Unlike a surface representation of the valve which may be attracted to the image gradient on either the atrial or ventricular leaflet surfaces, cm-rep delineates the atrial and ventricular surfaces separately and prevents intersection of these surfaces by enforcing a positive radial thickness field. This could lead to more accurate assessments of leaflet geometry. Moreover, localized leaflet thickness measurements derived from cm-reps could serve as indicators of myxomatous change, identifiers of secondary chordal attachment, and useful input to biomechanical simulations of the mitral valve.
Section 2 details our approach to valve morphometry using 3D US. Section 2 begins with an overview of 3D US image acquisition and describes the components of the semi-automated image analysis algorithm, including user-initialized image segmentation and deformable modeling with cm-rep. A brief explanation of a well-established manual valve delineation technique used for validation of semi-automated morphometry is also presented. The section concludes with a description of how clinically relevant features of valve morphology are extracted from a medial representation of the valve. Section 3 presents a comparison of manual and semi-automated image analysis, as well as assessments of deformable model fitting accuracy. The section concludes with an example of a clinically significant observation derived from automated 3D US image analysis that is currently unobtainable by standard 2D ultrasound. Section 4 provides a discussion of the study, and the conclusion is presented in Sec. 5.
MATERIALS AND METHODS
Image acquisition
Intra-operative transesophageal 3D US data sets, devoid of significant signal dropouts and stitching artifacts, were obtained from 14 patients with MR ranging from trace to severe. The MR of patients with moderate to severe disease was of ischemic origin. The electrocardiographically gated full-volume images were acquired with the iE33 platform (Philips Medical Systems, Andover, MA) using a 2–7 MHz transesophageal matrix-array transducer over four consecutive cardiac cycles. The frame rate was 17–30 Hz with an imaging depth of 12–16 cm. The images were acquired such that the atrial surface of the mitral leaflets was in a direct line of vision along the axial dimension of the image. The image volumes were exported in Cartesian format (224 × 208 × 208 voxels), with an approximate isotropic resolution of 0.6–0.8 mm. From each 3D US data series, an image volume delineating the mitral valve at midsystole (a single time point in the cardiac cycle) was selected for semi-automated image analysis.
Semi-automated valve morphometry
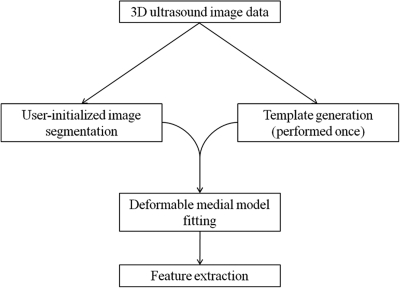
Image analysis involves multiple steps, including user-initialized segmentation, deformable medial modeling, and morphological feature extraction. A schematic of the analysis is presented in Fig. 1, and the details are outlined in Secs. 2B1 - 2B2 and Sec. 2D.
Figure 1.
Schematic of semi-automated image analysis. First, a deformable medial template of the mitral valve is generated from 3D ultrasound image data. This template generation step is performed once. Then, for each subject in the study, a 3D ultrasound image of the mitral valve is segmented using the level set method. The template is then deformed to fit each segmented image. Finally, morphological features are automatically computed from the fitted medial representation of each valve.
User-initialized segmentation
Semi-automated segmentation has two steps: user-initialized region of interest (ROI) extraction, and 3D active contour segmentation based on region competition. In the absence of valve shape priors derived from training data, a simple algorithm for user-initialized ROI extraction establishes boundaries between the anterior and posterior leaflets and between the mitral leaflets and adjacent tissue. Once these boundaries are established, 3D active contour evolution delineates the anterior and posterior leaflets in the 3D US image volume.
User-initialized ROI extraction.
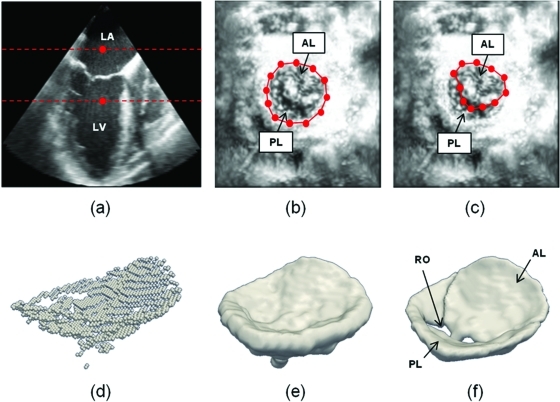
Semi-automated segmentation begins with user identification of the valve in the axial (basal-apical) dimension of the 3D US image volume, denoted by {V0(x,y,z); x = 1 … Nx, y = 1 … Ny, z = 1 … Nz}, where Nx, Ny, and Nz are the number of voxels in the x, y, and z directions of the image volume. In this framework, the axial dimension of the image volume is synonymous with the z-axis and the lateral dimensions are synonymous with the x- and y-axes. The user initializes two points demarcating a region containing the valve in a long-axis cross-section of V0, shown in Fig. 2a. With these user-initialized points, a 2D maximum intensity projection image, Imax(x,y), is constructed from the image volume
| (1) |
The projection is generated along the axial dimension of the 3D image, providing an atrial perspective of the valve. Contrast-limited adaptive histogram equalization25 of Imax(x,y) locally enhances the contrast of the projection image and thereby improves the visibility of the annular rim and leaflet coaptation zone of the mitral valve. In this enhanced projection image, a user marks a series of Na ordered points on the annulus {An; n = 1 … Na}, shown in Fig. 2b. The user then marks a second series of Nal points {ALn; n = 1 … Nal} outlining the anterior leaflet in 2D, shown in Fig. 2c. The user may choose any Na and Nal that adequately delineate the valve in Imax (generally about 15–20 points). Next, two 2D binary mask images, IA and IAL, are automatically created from polygons enclosing An and ALn. A 2D mask image of the posterior leaflet is also obtained by subtraction: IPL = IA – IAL. First, IA is used to create a masked image containing the entire valve in the lateral dimensions of the 3D US image volume
| (2) |
To identify a tighter 3D region of interest enclosing the valve along the axial image dimension, a dilation operation is applied to the set of maximum intensity voxels used to generate the projection image Imax. Let VM,bin denote this set of points
| (3) |
Although, in general, we cannot guarantee that the voxels in VM,bin are continuous in 3D, in practice they trace a voxel-thin surface through the center of the valve [Fig. 2d]. To produce a shaped ROI containing the valve, VM,bin is morphologically dilated with a spherical structuring element of radius 1.5 mm [Fig. 2e]. The volume Vmasked is then point-wise multiplied by the largest connected component of the dilated VM,bin to extract an image region containing the valve in Vmasked
| (4) |
Multiplication of the masked image volume and the dilated binary image of M is a simple means of imposing a thickness prior on image segmentation. It prevents the segmentation from identifying cardiac tissue surrounding the annulus as part of the valve.
Figure 2.
Outline of semi-automated segmentation. (a) The user initializes two points in a long-axis cross-section of the 3D US image volume, identifying an ROI (red) containing the valve along the axial dimension. (b) The user initializes a series of annular points in an enhanced projection image depicting the valve from an atrial perspective. (c) The user shifts posterior annular points into the coaptation zone, forming an outline of the anterior leaflet in the enhanced projection image. (d) A 3D point cloud delineating the valve is automatically generated. (e) The 3D point cloud is morphologically dilated with a spherical structuring element to obtain an ROI containing the valve. (f) A final segmentation of the valve is obtained by thresholding and active contour evolution. (LA = left atrium, LV = left ventricle, AL = anterior leaflet, PL = posterior leaflet, RO = regurgitant orifice).
Segmentation by 3D active contour evolution.
A binary segmentation of the valve in is then obtained by 3D active contour evolution based on region competition, described by Zhu and Yuille.26 In this scheme, an evolving estimate of the valve surface is represented by a closed contour, which, in turn, is represented numerically as the zero level set of a function , which is negative inside the region enclosed by the contour and positive outside of the contour. The function Ф evolves over time t according to the evolution equation
| (5) |
where F is an application-specific signed “speed function.” Note that is a unit vector orthogonal to the level sets of Ф, and hence, F gives the speed of contour propagation in the normal direction. We use a modified version of Zhu and Yuille’s speed function F, presented in Ref. 27, to drive contour evolution
| (6) |
Here, Pobj is the probability that a voxel belongs to the object of interest, Pbg is the probability that the voxel belongs to the background of the image, is the mean curvature of the contour, and α and β are weights. We estimate the probabilities in Eq. 6 by applying a soft threshold to . Since each 3D US data set is obtained with different acquisition parameters, such as gain and dynamic range, an appropriate threshold is interactively determined from the long-axis cross-sectional image in Fig. 2a. Generally, this threshold is an intensity value corresponding to 60 percent of the area of the histogram of Vmasked in Eq. 2. The contour evolution equation [Eq. 5] is then solved using an extreme narrow band implementation of the level set method.28 The image that defines the initial contour is negative inside the binary object of the thresholded and positive outside the object, and the speed image (Pobj − Pbg) that drives contour evolution is positive inside the binary object and negative outside the object. Contour evolution propagates for 100 iterations, and a curvature parameter weight of β = 2.0 is used to eliminate fine jaggedness on the leaflet boundary. Compared to straightforward thresholding, 3D active contour segmentation has the advantage of establishing smooth boundaries in ultrasound images that have noisy image intensity edges, but relatively homogeneous intensity distributions in the valve tissue and surrounding blood pool.
Once a binary image of the entire valve is obtained, two separate binary images of the anterior and posterior leaflets are generated by masking the lateral dimensions of the valve segmentation with IAL and IPL. An example of the final segmentation result is illustrated in Fig. 2f. The entire segmentation algorithm is implemented as a combination of functions implemented in matlab (Mathworks, Natick, MA) and the convert3D toolkit.29
Deformable medial modeling
Once 3D image segmentations of the anterior and posterior leaflets are obtained, our technique models each mitral leaflet using 3D continuous medial representation (cm-rep). Unlike a surface representation that describes an object’s boundary geometry, medial representation is a compact representation of shape that describes the geometry of an object’s medial axis. First introduced by Blum in Ref. 30, an object’s medial axis is defined as the locus of centers and radii of maximal inscribed balls (MIBs) of the object. In three dimensions, a medial axis is a locus of tuples , in which m refers to points on the medial axis formed by the centers of the MIBs and R refers to the radii of the MIBs centered at those points or, equivalently, to the distance between the medial axis and object surface. As described earlier, this representation is particularly useful for assessing an object’s localized thickness (derived from R) and for characterizing how the object locally bends (determined by the curvature of the medial axis).
Given an object’s image segmentation, the medial axis of the object can be derived from its boundary using a number of deterministic geometric skeletonization algorithms.31, 32, 33, 34, 35 However, these deterministic algorithms do not necessarily preserve the branching configuration of the medial axes of similar anatomic structures, which presents a challenge to morphometric analysis. To circumvent this problem, cm-rep utilizes the idea of inverse skeletonization, whereby an object is defined first by its medial axis and the object boundary is constructed analytically from its skeleton. In this framework, the cm-rep of a mitral leaflet is obtained by fitting a deformable medial model, also referred to as a template, to its image segmentation. During template deformation, the branching configuration of the medial axis is preserved, thus facilitating morphometric comparison of mitral valves of different subjects.
Extending the discrete version of medial representation presented by Pizer et al.,23 cm-rep models the medial axis as a combination of continuous parametric medial manifolds () and thickness is parametrically represented as a scalar field () defined over the medial manifolds. Here, m and R can be any user-specified mesh, surface, or function. The object boundary is described as the envelope of the family of MIBs with centers m and radii R located on the medial axis. If the medial manifold is locally parameterized by , the envelope can be expressed as the set of points b that satisfy the following system of equations:
| (7) |
where , the equation of a sphere. The first equation is necessary for b to lie on a sphere centered at m(u), and the second is necessary for b to lie on the envelope.
Solving Eq. 7 for b, we obtain two solutions, and , corresponding to surface patches that lie on the opposite sides of the medial axis at m(u)
| (8) |
where is the unit normal vector to m, and is the Riemannian gradient of R on the manifold m. The local geometry of a point on the medial manifold is illustrated for reference in Fig. 3.
Figure 3.
The local geometry of a point on the medial manifold. The ball represents a medial node m(u1,u2), and the vectors ∂m/∂u1 and ∂m/∂u2 span the tangent plane to m. The vector ∇mR lies in the tangent plane and points in the direction of maximal change of the radial thickness field R on m. The points of tangency between a ball centered at m(u1,u2) with radius R and the boundary of the object are b+ and b−. Unit vectors U+ and U− point from m(u1,u2) toward b+ and b− and are perpendicular to the object boundary at these points.
The above equation provides a parametric form of b if m is the medial axis of b, but for arbitrary {m,R}, applying Eq. 8 can generate a pair of surfaces that do not form the boundary of a 3D object. Thus, it does not guarantee a “valid” boundary, i.e., a surface that encloses a region in . Among the equality and inequality constraints that must be satisfied for valid medial geometry, which are formally described in Ref. 24, the most challenging constraint to satisfy is the one that ensures that the boundary is a closed surface. Namely, the following equality constraint ensures that and collapse to a single point for , implying that the whole boundary collapses to one point along the medial edge
| (9) |
This constraint is a nonlinear function of {m,R}, and it must hold at an infinite number of points along the medial edge curves. In deformable modeling applications, this presents a severely over-constrained optimization problem, since the number of points where the constraint must be satisfied is infinite, while the number of coefficients or control points defining the medial manifold is finite and preferably small. As a solution to this problem, we leverage a technique described in Ref. 36, which models R as a solution of a fourth-order biharmonic partial differential equation (PDE) with linear boundary conditions. The biharmonic PDE is a bijective mapping that transforms points from a vector space, parameterized by {m,ρ,τ}, into the set of all radial fields R defined over m that satisfy Eq. 9. In this framework, the curve forming the boundary of the medial manifold, , is parameterized by the arclength s: , where L is the length of . The parameter τ represents the value of R along the medial edge: , and ρ is a scalar field on m. The PDE is not written in terms of R itself, but in terms of another function, . Given τ > 0 and |dτ/ds| < 1 everywhere on γ, the function φ must satisfy the following:
| (10) |
where denotes the Laplace-Beltrami operator on the manifold m, and v(s) is the outward unit normal vector along γ(s). Provided that the solution φ is non-negative everywhere on m, it can be verified that satisfies the equality constraint [Eq. 9] on the medial edge. Details on the numerical solution of the biharmonic PDE using finite differences can be found in Ref. 36.
In this study, the valve is modeled as two separate leaflets, where each leaflet is a simple object, one whose skeleton consists of a single medial manifold. The combination of the two leaflets’ medial models is referred to as the medial representation of the entire valve. Here, the cm-reps of the two leaflets are parameterized independently, and the leaflets themselves are not required to connect.
Template generation.
A particular instance of the valve is defined by fitting a bileaflet deformable medial template to the leaflets’ binary segmentations. Therefore, a deformable template must be generated prior to fitting the model to a new instance of the valve. Our choice for representation of each medial manifold is a triangulated mesh, as it is a simple representation that can be defined on an arbitrary domain. The medial template for each leaflet is constructed in a manner similar to that used in Ref. 37. With the freedom to define cm-reps over arbitrary domains, the template can be any hand-created model as long as the topological configuration is consistent with that of the anatomic structure. In this study, a data-driven initial model is designed and the cm-rep domain Ω ∈ for each leaflet is defined by flattening the skeleton of the anatomic structure under constraints that minimize local distortion.
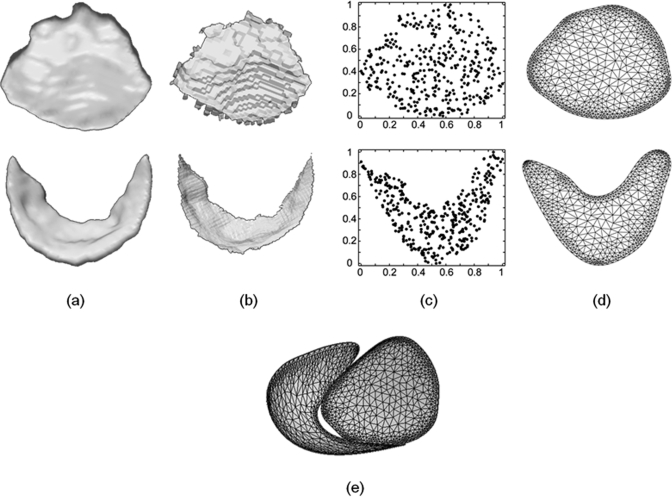
The template generation process is illustrated in Fig. 4. One of 14 3D US data sets is arbitrarily selected for template creation, and binary segmentations of the anterior and posterior leaflets at midsystole are obtained by user-initialized segmentation (Sec. 2B1). For each leaflet, the Voronoi skeleton of the binary image is computed using QHull38 and simple heuristics34 are used to prune away the least salient branches of the skeleton, as shown in Fig. 4b. Specifically, the pruning algorithm deletes faces in the Voronoi diagram for which the ratio of the geodesic distance between the generating points to the Euclidean distance between those points is less than 4. The maximum variance unfolding (MVU) technique39 is then used to determine a two-dimensional embedding of the skeletons’ vertices that minimally distorts the distances between neighboring vertices. The embedding assigns a pair of coordinates to each of the vertices xi in the skeleton [Fig. 4c], and low-degree polynomial surfaces are fitted to the data to obtain a smooth medial manifold. The cm-rep domain Ω is then obtained by rasterizing and morphologically closing the scatter plot of , producing a region homeomorphic to a disc in . An outer contour of this region is obtained by sampling a set of 90 points along the domain boundary, and an inner contour, just within the domain boundary, is generated by creating two samples for each vertex of the outer contour. The purpose of generating an inner contour in addition to the outer contour is to create a mesh with a high density of triangles just within the domain boundary to ensure the stability of finite difference approximations at the medial edges. Finally, a constrained conforming Delaunay triangulation of Ω is computed using the meshing program Triangle.40 The triangulation is performed such that no angle smaller than 32° is obtained. The resulting bileaflet medial template is illustrated in Fig. 4e.
Figure 4.
Schematic of the template generation process. (a) A 3D US image volume is segmented to obtain binary images of the anterior (top) and posterior (bottom) mitral leaflets. (b) The binary images are skeletonized in 3D. (c) A 2D scatter plot of the skeletons’ vertices in u1,u2 space. (d) The constrained conforming Delaunay triangulation of the region containing the skeletons’ vertices. (e) The combined medial manifolds of the anterior and posterior leaflets used for deformable modeling.
Template fitting.
For each of the 14 subjects in the study, the medial model defined by {m,ρ,τ} is deformed to fit the binary leaflet segmentations by Bayesian optimization (Fig. 5). Template fitting has five stages: one alignment stage and four deformation stages. During the first (alignment) stage, Jenkinson’s FLIRT affine registration tool41, 42 is used to obtain a similarity transform that aligns the posterior template with the posterior leaflet segmentation. This transform is applied to both leaflets simultaneously during this initialization stage. Then, during the first three deformation stages, the leaflet medial models are separately deformed to fit the binary leaflet segmentations in a multiresolution fashion. The objective function minimized during deformation incorporates the volumetric overlap error between the medial model and binary segmentation, as well as regularization terms and inequality constraints required by inverse skeletonization, detailed in the Appendix. To correct for any intersection of the leaflet models, the medial models of the two leaflets are combined into a single model during the final deformation stage. The vertices of the two leaflets are assigned different labels, indicating which binary segmentation should be used for overlap computation. During the simultaneous fitting of both leaflets in this stage, a leaflet intersection penalty term (described in Sec. 6 of the Appendix) is used to correct and prevent intersection of the leaflets’ medial models. Figure 6 demonstrates that this final fitting stage corrects for model intersection along the leaflet coaptation.
Figure 5.
A medial representation of the valve is obtained by fitting a valve template to a binary image of the valve produced by segmentation.
Figure 6.
Leaflet overlap at the coaptation line (shown on left) is corrected during the final model fitting stage (shown on right). Magnifications of leaflet overlap and leaflet overlap correction are shown below the valves.
When fitting medial models to binary segmentations, we do not optimize directly over the vertices of the medial mesh, as there are too many parameters to optimize in the early stages of model fitting. For instance, each leaflet representation contains several hundred vertices (498 vertices for the anterior leaflet and 612 vertices for the posterior leaflet), each of which is associated with five components (m,ρ,τ). For increased efficiency, we use spectral decomposition of the medial mesh for a coarse-to-fine fitting strategy. Here, we define an orthogonal basis on the 3D mesh using the eigenfunctions of the Laplace operator, the generalization of the Fourier basis on the plane. These basis functions are a set of k functions that satisfy , where Δ denotes the Laplace operator and λk are eigenvalues of the generalized eigenvector problem. Using an implementation described by Belkin and Niyogi,43 the Laplace operator for a function ψ on the mesh is estimated at vertex i as
where N1(i) denotes the one-ring of i, i.e., the set of vertices adjacent to i by an edge. Thus, the medial model can be deformed smoothly by modifying the coefficients of a small number of basis functions rather than all vertices of the template mesh.36 To achieve a coarse-to-fine model fitting, the number of Laplace basis functions defined on the template is increased from 10, to 40, to 70 during the four deformation stages. The target binary images are smoothed by a Gaussian kernel with standard deviation 0.8 during the first stage, 0.6 during the second stage, and 0.2 during the third and fourth stages. A total of about 1400 total iterations is required for the fitting of each leaflet.
Manual valve delineation
To validate the measurements derived from automated analysis of the 3D US images, the same 14 image volumes selected for automated analysis were manually traced by a trained observer using an Echo-View 5.4 workstation (TomTec Imaging Systems, Munich, Germany). In each of 14 tracings, the observer marked 36 points on the mitral annulus and drew freehand curves across the atrial surface of the leaflets in a series of 2D planes. Each manual tracing required three to five hours for completion and produced a 500–1000 point data set delineating the atrial surface in three dimensions. A detailed description of this manual delineation process can be found in Refs. 9, 44.
Feature extraction
Seven features of valve morphology at midsystole, listed below, were derived from both manual and semi-automated image analysis:
Annular area—the area enclosed by the projection of the annular points onto a least squares plane fitted through the annulus
Annular circumference—sum of distances between consecutive annular points
Annular height—maximum distance between two annular points, where unsigned distance is measured between the annular point and its projection onto a least squares plane fitted through the annulus
Intercommissural width—distance between the anterior and posterior commissures
Septolateral length—distance between midpoints on the anterior and posterior annulus
Total tenting volume—the volume enclosed by thin-plate splines fitted through the leaflets and the annular curve
Percent anterior tenting volume—the tenting volume enclosed by the anterior leaflet divided by the total tenting volume, multiplied by 100
These features underscore clinically significant aspects of valve morphology.5, 8, 46 Annular dimensions indicate the presence of annular dilatation and identify whether an individual’s annulus is predominantly saddle-shaped or planar. Leaflet tenting features are indicative of subvalvular remodeling. In addition to these seven measurements, leaflet thickness (the radial thickness function R mapped to the medial manifold) and regurgitant orifice area (the area enclosed by the projection of the regurgitant orifice onto a least squares plane fitted through the annulus) were computed from the fitted cm-reps.
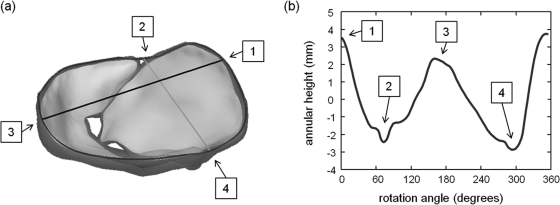
Here, annular geometry is extracted directly from the fitted medial model of the valve (Fig. 7). The annulus is defined by points on the cm-rep boundary mapped to the outer edges of the medial manifolds of the anterior and posterior leaflets. The annular points on the posterior leaflet are labeled on the medial template itself, whereas the annular points on the anterior leaflet are identified geometrically. Specifically, the anterior annular points are defined as points on the anterior leaflet cm-rep boundary mapped to medial manifold edges that are not contained within the convex hull of the posterior leaflet. The anterior and posterior commissures are identified as points on the annular curve where the anterior and posterior leaflets meet, a definition that is consistent with the protocol described by Jassar et al.9 and Vergnat et al.8 An alternative definition of the commissures is described by Carpentier et al.,46 wherein several millimeters of valve tissue separates the free edge of the commissures from the annulus. Sometimes the commissures exist as separate leaflet segments, but more often the area is a subtle structure. Given that commissures and/or commissural leaflets are difficult to define when the valve is closed, the commissural definition of Jassar et al.9 and Vergnat et al.8 is used in this work.
Figure 7.
Automated extraction of annular geometry. (a) The annulus (bold curve) is identified as points on the valve boundary mapped to the outer edges of the leaflets’ medial manifolds. Annular landmarks include: (1) the anterior aortic peak, (2) the anterior commissure, (3) the midpoint on the posterior annulus, and (4) the posterior commissure. The line from (1) to (3) represents the septolateral diameter, and the line from (2) to (4) represents the intercommissural width. (b) Annular height is plotted as a function of rotation angle, where 0° corresponds to the anterior aortic peak of the annulus.
Comparison of manual and semi-automated valve delineation
In addition to comparing the manually and automatically derived features listed in Sec. 2D, each manual tracing of the valve was aligned with the atrial surface of the fitted cm-rep and the distance between the two surfaces was computed. Alignment was performed by determining the best rotation and translation that matched a series of six landmarks identified on both the manual tracing and semi-automated reconstruction. These six landmarks included the anterior and posterior commissures, the anterior and posterior leaflet tips, the anterior aortic peak, and the midpoint of the posterior annulus. Here, rigid alignment was necessary prior to surface comparison since the manual tracings and semi-automated reconstructions did not share a common origin or image orientation; manual tracing was performed in a commercial software package, while semi-automated analysis was performed on images that were converted from their native format into Cartesian coordinates prior to exportation.
Evaluation of valve shape approximation bias
Two commonly raised concerns regarding mesh-to-volume registration are: (1) the ability of the deformable model to approximate the shape of the object, and (2) the shape approximation bias introduced by template design. To address the first concern, the Dice similarity coefficient measuring the overlap between each patient’s valve segmentation and the fitted medial model was computed. To assess the extent of leaflet shape approximation bias introduced by template design, image data from two subjects (different from the subject that was used for template design in Sec. 2B2A) were selected to generate two additional templates by the same method. These two subjects were chosen such that the three templates created in this study represented the three categories of MR severity (trace, mild, and moderate to severe). Using the Bayesian optimization method described in Sec. 2B2B, these two templates were fitted to the binary valve segmentations of all 14 patients, and the clinical measurements described in Sec. 2D were automatically derived from the fitted medial representation of each valve. The average coefficient of variation of each measurement was computed from three template fittings for each patient. In addition, the Dice similarity coefficients of each patient’s binary valve segmentation and the three corresponding fitted models were computed.
ROA sensitivity analysis
To assess the sensitivity of the regurgitant orifice area (ROA) measurements to user initialization, segmentation and model fitting were performed on the same 14 3D US image volumes after applying varying displacements to the user-initialized points described in Sec. 2B1A. For each user-initialized point, a given displacement was added to the points on the manually traced contours in a random direction. The displacement values tested were 0.0, 0.5, 1.0, 1.5, and 2.0 mm. The maximum displacement value of 2.0 mm was chosen based on the following rationale: if two opposing annular points were displaced in opposite directions by 2.0 mm, the annular diameter would change by 4.0 mm, which is more than 10% of the average annular diameter (∼30 mm). Here, it is assumed that interobserver variability in the measurement of annular diameter is within 10%, which has been previously confirmed.9 For each displacement value, the average percent difference in the ROA measurement was computed. Percent difference was defined as the difference between the manual and automated measurement, divided by the average of the two measurements, multiplied by 100.
RESULTS
Accuracy of semi-automated valve morphometry
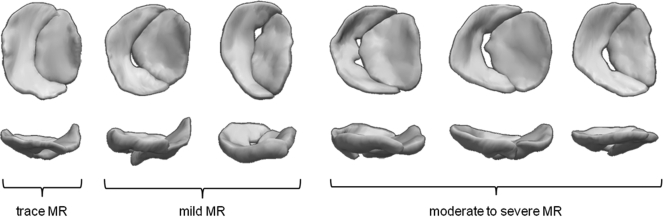
Semi-automated mitral valve reconstructions for six of the patients in the study are shown in Fig. 8. Each valve is shown at midsystole. The three valves on the left are of patients with trace to mild MR who underwent cardiac surgery unrelated to the mitral valve. The three valves on the right are of patients with moderate to severe ischemic MR. These valve reconstructions, generated from image segmentation and model fitting, show patient-specific variations in valve morphology in regard to annular geometry, regurgitant orifice size, and regurgitant orifice location.
Figure 8.
Automated reconstructions of the valves of six patients. All valves are depicted at midsystole. For each valve, an atrial view is shown on top and a side view is shown on the bottom. The anterior leaflet is on the right, the posterist leaflet on the left. Clinical assessments of MR severity, based on Doppler imaging, are indicated.
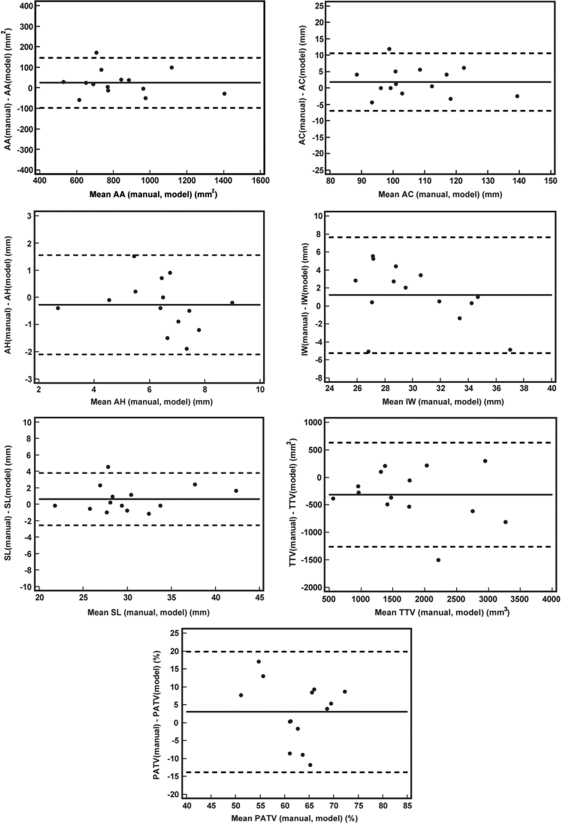
The range of values and differences in the seven clinically relevant measurements derived from automated 3D US analysis and manual delineation of the valve at midsystole are listed in Table Table I.. The mean absolute differences ± standard deviations are shown for each disease category. Bland-Altman plots comparing manual and automated measurements are presented in Fig. 9. The mean biases of the automated model-based approach relative to manual measurement were −22.4 mm2 for annular area, −1.8 mm for annular circumference, 0.3 mm for annular height, −1.2 mm for intercommissural width, −0.6 mm for septolateral length, 318 mm3 for total tenting volume, and −3.0% for percent anterior tenting volume.
Table I.
The range in valve measurements derived from semi-automated analysis, and the average difference ± standard deviation in valve measurements derived from semi-automated and manual 3D US image analysis (shown in italics). The values are shown separately for all subjects, subjects with trace to mild MR, and subjects with moderate to severe MR. (AA = annular area, AC = annular circumference, AH = annular height, IW = intercommissural width, SL = septolateral length, TTV = total tenting volume, PATV = percent anterior tenting volume).
| AA (mm2) | AC (mm) | AH (mm) | IW (mm) | SL (mm) | TTV (mm3) | PATV (%) | |
|---|---|---|---|---|---|---|---|
| All subjects (n = 14) | 517.0–1421.8 | 86.6–140.8 | 2.9–9.1 | 24.4–39.5 | 21.9–41.6 | 762–3678 | 46.3–71.2 |
| 47.1 ± 45.4 | 3.6 ± 3.1 | 0.7 ± 0.6 | 2.8 ± 1.9 | 1.2 ± 1.2 | 432 ± 374 | 7.5 ± 4.8 | |
| Trace to mild MR (n = 8) | 517.0–1002.8 | 86.6–120.0 | 4.6–8.3 | 24.4–34.1 | 21.9–30.4 | 762–3066 | 47.3–68.2 |
| 56.0 ± 52.6 | 3.8 ± 3.8 | 0.8 ± 0.6 | 2.7 ± 1.8 | 1.3 ± 1.4 | 315 ± 193 | 7.0 ± 3.8 | |
| Moderate to severe MR (n = 6) | 770.3–1421.8 | 96.3–140.8 | 2.9–9.1 | 24.6–39.5 | 27.9–41.6 | 1040–3678 | 46.3–71.2 |
| 35.1 ± 34.5 | 3.2 ± 2.3 | 0.7 ± 0.6 | 3.0 ± 2.3 | 1.1 ± 0.8 | 587 ± 511 | 8.1 ± 6.2 | |
| Average percent difference (n=14) | 6.0% | 3.4% | 11.7% | 9.7% | 4.1% | 26.2% | 12.2% |
Figure 9.
Bland-Alman plots showing the difference between manual and automated measurements as a function of the mean measurement for each of 14 patients. (AA = annular area, AC = annular circumference, AH = annular height, IW = intercommissural width, SL = septolateral length, TTV = total tenting volume, PATV = percent anterior tenting volume).
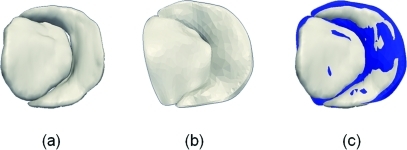
After alignment, the average Euclidean distance between the manual tracing and atrial surface of the fitted cm-rep was roughly 1.3 ± 0.7 mm for both the anterior and posterior leaflets. These differences were comparable to the 3D US image volume resolution (0.6–0.8 mm) and the radial thicknesses of the valves observed in this study (R = 0.2–2 mm). An example of a manual segmentation and fitted cm-rep is presented in Fig. 10.
Figure 10.
Semi-automated and manual reconstructions of a mitral valve. (a) A fitted cm-rep of the valve. (b) Manual tracing of the atrial surface of the valve in the same image data. (b) Manual tracing (blue) overlaid on the fitted cm-rep.
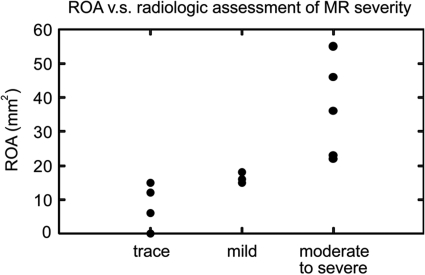
To assess the accuracy of automated ROA measurements, the ROA derived from semi-automated 3D US analysis was compared to a qualitative assessment of MR severity on intra-operative clinical radiology. For each of 14 patients, MR severity was reported as trace or mild, or moderate to severe based on intraoperative Doppler imaging. By semi-automated image analysis, the ROA was 0–18 mm2 in patients with trace or mild MR and 22–55 mm2 in patients with moderate to severe MR. Figure 11 illustrates the consistency between quantitative measurements of the orifice area and qualitative assessment of MR severity made on clinical radiology. By single-factor analysis of variance (ANOVA), there was a statistically significant difference in the ROA measurements of the three categories of MR severity (p = 0.002). The sensitivity of the ROA measurements with respect to user initialization is presented in Table Table II.. For each level of initialization noise, the p-value obtained by single-factor ANOVA indicated a statistically significant difference in the ROA measurements of three categories of MR severity. As initialization noise increased, the percent change in the ROA measurement increased, and statistical significance decreased as initialization noise reached 2.0 mm.
Figure 11.
Automated measurement of the regurgitant orifice area (ROA) is shown as a function of MR severity assessed by intraoperative Doppler imaging.
Table II.
Average percent difference in the regurgitant orifice area (ROA) when noise is applied to the user-initialized points in semi-automated segmentation. The p-values obtained by single-factor ANOVA indicate a statistically significant difference in the ROA measurements of three categories of MR severity (trace, mild, and moderate to severe).
| Initialization noise | |||||
|---|---|---|---|---|---|
| 0.0 mm | 0.5 mm | 1.0 mm | 1.5 mm | 2.0 mm | |
| Percent difference in ROA | — | 3.7 ± 4.5 | 8.5 ± 6.0 | 7.6 ± 7.9 | 10.5 ± 7.5 |
| p-value | 0.002 | 0.019 | 0.008 | 0.001 | 0.044 |
Accuracy of valve shape approximation with cm-rep
The Dice similarity coefficients, measuring the overlap between each binary image segmentation and the fitted cm-rep, are shown in Table Table III.. Note that the Dice coefficient examines the suitability of cm-rep as a representation of valve shape, rather than the accuracy of segmentation. With the initial valve template designed from the image data of a patient with severe MR, the average Dice coefficients were 0.908 and 0.881 for the anterior and posterior leaflets, with all coefficients greater than 0.825. The maximum change in the Dice coefficient measured using three different templates was 0.062. The average coefficients of variation in the morphological measurements derived from the three template fittings were 2.0% for annular area, 2.1% for annular circumference, 12.6% for annular height, 2.7% for intercommissural width, 1.7% for septolateral length, 7.7% for total tenting volume, and 3.4% for percent anterior tenting volume.
Table III.
Dice similarity coefficient measuring overlap between the binary segmentation and fitted medial model using three different templates. The Dice similarities for the anterior and posterior leaflets are separately computed. S1, S3, and S5 refer to the valve templates generated from image data acquired from Subjects 1 (severe MR), 3 (mild MR), and 5 (trace MR), respectively.
| Dice similary coefficient—Anterior leaflet | Dice similarity coefficient—Posterior leaflet | |||||
|---|---|---|---|---|---|---|
| S1 | S3 | S5 | S1 | S3 | S5 | |
| Average | 0.908 | 0.903 | 0.908 | 0.881 | 0.891 | 0.893 |
| Minimum | 0.865 | 0.847 | 0.870 | 0.825 | 0.864 | 0.834 |
| Maximum | 0.941 | 0.929 | 0.928 | 0.906 | 0.915 | 0.918 |
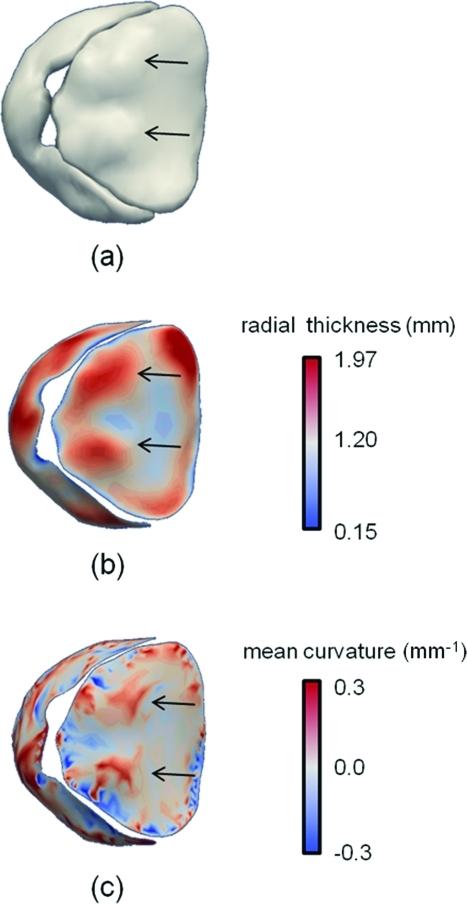
Clinical relevance of automatically derived leaflet thickness and curvature measurements
An interesting advantage of the semi-automated 3D US image analysis technique is that foci of probable secondary anterior chordal tethering can be easily identified on medial representations of the valve. In Fig. 12, a ventricular view of the valve illustrates that these foci manifest as: (a) bulges on the anterior leaflet, (b) local increases in the radial thickness field, and (c) regions of high mean curvature convex toward the left ventricle. One to three such foci were observed on the medial representation of each subject in the study.
Figure 12.
Probable foci of anterior chordal tethering are identified on the ventricular side of the anterior leaflet. These foci, marked by black arrows, are identified as (a) bulges on the valve reconstruction, (b) local areas of thickening on the medial manifold, (c) regions of high mean curvature convex toward the left ventricle.
DISCUSSION
Contributions
This study introduces a novel approach to valve morphometry that provides a comprehensive, automated assessment of 3D valve geometry by ultrasound image analysis. In addition to the measurement of valve dimensions, an appropriate shape representation for the mitral valve should capture at least three clinically significant components of valve geometry: leaflet curvature, a surrogate measure of valvular stress;44 leaflet thickness, an indicator of myoxomatous change and marker of secondary chordal attachment; and annular geometry, information which can help optimize valve repair strategies. In general, features such as thickness and medial curvature can be derived from the Blum skeleton of an object, i.e., a surface or set of surfaces produced by thinning the object uniformly, or evolving the boundary at uniform speed along the inward normal, until the object becomes infinitesimally thin.30, 47, 48 Features derived from skeletons, however, are challenging to use in morphometric analysis because the number and configuration of medial manifolds in the skeleton of the anatomic structure can vary between subjects, even for structures with simple shape. This challenge is magnified in ultrasound image analysis, where the object’s skeleton is deterministically derived from a characteristically noisy boundary representation. To overcome this difficulty, Pizer et al.23 leverage a discrete medial representation (m-rep) approach whereby different instances of a structure are fitted with a deformable template whose skeletal branching configuration is preserved during deformation. To generate continuums of skeleton-derived features with this strategy, Yushkevich et al.24, 36 extend the m-rep approach into the continuous realm, modeling skeletons and boundaries of objects as continuous parametric manifolds. Deformable modeling with cm-rep has the advantage of imposing a shape-based coordinate system on the anatomic structure which supports a continuous, one-to-one, onto mapping of the interiors of fitted models to a common coordinate system. This representation has been effectively used in morphometric studies of a number of anatomic structures, including the ventricular myocardium.49 In the studies of mitral valve morphology, the correspondence between the skeleton and object boundary established by cm-rep parametrization is exploited for annular detection. With cm-rep, the annulus is the curve formed by points on the object boundary that map to the edge of the medial manifold. In sum, cm-rep is an appropriate model for representing mitral valve shape, as it allows for identification of clinically significant components of valve geometry, it establishes points of correspondence between valves of different subjects, and it ensures that leaflet topology is consistent for all subjects in the study.
The segmentation method proposed in this work exploits the contrast in 3D transesophageal images and uses projections of 3D data to eliminate the need for the user to navigate a 3D image volume during initialization. Unlike the semi-automated methods presented in Refs. 16, 18, 20, 21, our algorithm provides volumetric representations of valve geometry. Given average Dice overlaps of ∼0.9, this study demonstrates that a deformable medial model can accurately capture patient-specific valve shape. Moreover, the results of this study demonstrate that user-initialized 3D US image analysis provides a quantitative valve assessment that is consistent with manual delineation. The errors and biases in our measurements are within the range of interobserver variability in manual image analysis presented by Jassar et al.9 and are within the range of error in annular measurements presented by Ionasec et al.,18 who use an automated image analysis technique. While the average percent difference in total tenting volume between manual and semi-automated image analysis is high (26.2%), the average percent difference in the contribution of the anterior leaflet to the total tenting volume is lower (12.2%). This indicates that the relative contributions of each leaflet to total tenting volume are likely more accurate than the absolute tenting volume measurement obtained by semi-automated analysis. Finally, the average distance between manually traced and semi-automatically derived surfaces (1.3 ± 0.7 mm) is comparable to that reported by Schneider et al.21 (0.76 ± 0.65 mm for the open valve) and Ionasec et al.18 (1.54 mm for the valve at multiple time points). This average distance is also consistent with interobserver variability in manual image analysis, with reported mean distances of 2.4 ± 0.8 and 0.6 ± 0.2 mm for the annulus and mitral leaflets, respectively.9
The advantage of semi-automated image analysis over manual valve delineation is a significant reduction in user-interaction time: manual valve delineation requires 3–5 h of expert interaction, whereas automated image analysis requires 1 min of user interaction. Automated image analysis provides localized morphological measurements in three dimensions, which unlike measurements derived from 2D ultrasound, are not influenced by scanning plane selection. The valve reconstructions in Fig. 8 and quantitative ROA measurements in Fig. 11 illustrate that pathologic variations in valve morphology can be identified in patients with different degrees of MR severity, particularly in regard to the location and size of the regurgitant orifice. An added advantage of this study is that the semi-automated algorithm is applied to data acquired with a modality that is nonionizing, portable, widely accessible, and capable of real-time image acquisition. With the ability to noninvasively assess valve morphology in human subjects, this technique has potential to build on the knowledge previously obtained with more invasive tools, like sonomicrometry and biplane radiography, that have been used to study mitral valve disease in animal models.
Challenges
There are several challenges that, if addressed, could enhance the image analysis algorithms presented in this study. For one, segmentation and model fitting do not fully exploit prior information of valve shape, which could potentially enhance the robustness of image analysis by guiding segmentation and template fitting in the presence of image noise. While the proposed segmentation scheme is useful for delineating the valve in the absence of a shape prior, it may be ineffective in data sets with excessive image noise, signal dropouts, or shadowing artifacts. Second, the method assumes that the atrial surface of the leaflets is in direct view along the axial dimension of the image volume. If the mitral valve were imaged at a different angle, the image projection Imax in Eq. 1 would have to be computed along an axis perpendicular to the plane of the valve to ensure the accuracy of ROA measurements. Additionally, manual initialization of the coaptation in a 2D projection image could restrict leaflet overlap in the coaptation zone. As an improvement to this method, a regularization scheme could be imposed on the points detected from the 2D maximum intensity projection image [Fig. 1d] to ensure the accuracy of the 3D mask image used for segmentation. Or, as an alternative to the approach described in this study, the cm-reps of each leaflet could be fitted directly to the 3D US image data, to accomplish segmentation and shape modeling in a common framework. Along these lines, previous studies have explored the use of medial representation for segmentation of anatomic structures.23, 50, 51, 52, 53 The incorporation of leaflet shape and appearance priors in such a framework could aid in identifying features like leaflet overlap and increase the robustness of segmentation in the presence of common ultrasound image artifacts.
In this study, the valve was modeled as two separate leaflets, each with a single medial manifold. An advantage of modeling the leaflets separately is that it circumvents topological challenges of fitting a single medial representation to a valve that may or may not have a regurgitant orifice at systole. A drawback of this technique is that discontinuities at the commissures require that annular geometry be approximated at the commissural zones. This approximation likely explains why the average coefficient of variation for three template fittings was higher for annular height than for the other morphological measurements.
Finally, the raw 3D US image data acquired in this study could not be accessed using commercial software, which required that automated segmentation be accomplished in images that were converted from their native format into Cartesian coordinates prior to exportation. Manual tracings of the atrial surface were completed in a commercial software package in which the image data were uploaded in its native format. In both cases, the image processing steps and conversion utilities used to represent the image data in a Cartesian format were inaccessible. If access to the raw image data were available, both manual and automated segmentation could be implemented in the raw data space to avoid inaccuracies introduced by interpolation and to enhance comparison of the two image analysis techniques.
CONCLUSIONS
This study demonstrates a novel, noninvasive technique for mitral valve morphometry. Semi-automated image analysis of 3D US data significantly reduces user-interaction and yields morphometric features that are consistent with manual image analysis and qualitative MR severity assessments made by Doppler imaging. 3D deformable medial modeling provides a compact, parametric representation of valve shape, which can be exploited for automated evaluation of local variations in leaflet and annular geometry. This work lays the foundation for future statistical studies of time-dependent valve morphology and dynamics.
Table IV.
The terms and weights used in the objective function during each stage of model fitting.
| Term | Description | Fitting phase 1: 10 basis functions, leaflets fitted separately | Fitting phase 2: 40 basis functions, leaflets fitted separately | Fitting phase 3: 70 basis functions, leaflets fitted separately | Fitting phase 4: 70 basis functions, leaflets fitted simultaneously |
|---|---|---|---|---|---|
| Volume overlap | 1 | 1 | 1 | 1 | |
| Boundary Jacobian constraint | 10−2 | 10−2 | 10−2 | 10−2 | |
| Radial thickness constraint | 10−4 | 10−4 | 10−4 | 10−4 | |
| Boundary constraint | 10−1 | 10−1 | 10−1 | 10−1 | |
| Loop tangent constraint | 10−2 | 10−2 | 10−2 | 10−2 | |
| Leaflet intersection constraint | 10−1 | 10−1 | 10−1 | 10−1 | |
| Medial triangle regularizer | 0 | 10 | 30 | 30 | |
| Boundary triangle regularizer | 0 | 10 | 30 | 30 |
ACKNOWLEDGMENTS
This research was supported by the National Institutes of Health T32 EB009384 from the NIBIB, an American Heart Association Great Rivers Affiliate predoctoral fellowship (10PRE3510014), and the National Institutes of Health HL63954 and HL73021 from the NHLBI. P. Yushkevich’s effort in this project was supported by the National Institutes of Health K25 AG027785 and R21 NS061111. A. Jassar was supported by a postdoctoral fellowship from the American Heart Association, and M. Vergnat was supported by a French Federation of Cardiology Research Grant.
Bayesian Objective Function for Deformable Medial Modeling
In this work, we fit deformable medial models to binary segmentations of the mitral leaflets. The objective function minimized during model fitting takes the following form:
where w are the relative weights of terms T. The likelihood term measures how well the model overlaps binary images of the mitral leaflets, the validity terms enforce inequality constraints that are required for valid medial geometry, and the regularity terms regularize the deformable mesh. Table Table III. summarizes these terms and weights.
Note that “valid” medial geometry involves satisfying both equality and inequality constraints, as described in Sec. 2B2. While the equality constraint in Eq. 9 is satisfied in the linear boundary conditions of the biharmonic PDE [Eq. 10], the inequality constraints are incorporated as soft penalty terms in the objective function. The reason for enforcing the inequality constraints in this manner is that conjugate gradient descent is used for optimization. A more elegant scheme for satisfying medial geometry inequality constraints would be a constrained optimization problem, using a software package like IPOPT, where the five validity terms are specified as constraints, and the objective function consists of only likelihood and regularity terms. In this work, however, conjugate gradient descent suffices for optimization.
Below, a brief summary of each penalty term in the objective function is presented, along with a description of how the penalty term is formulated. The validity terms, or soft penalties that enforce medial geometry inequality constraints, are posed as barrier functions such that the penalty rapidly increases as the term gets closer to violating the constraint.
: Volume overlap
Summary
This likelihood term ensures that the deformable model overlaps the binary image of each leaflet.
Formulation of the penalty term
Each leaflet is represented by a mask image , such that M is positive inside the segmentation and negative outside. Let C denote the interior of the medial model, i.e., the region of space enclosed by the medial model boundary. Then the overlap likelihood takes the form
The integral is computed by numerical integration along the spokes of the medial model, where each spoke is a line segment from a node on the medial mesh to the corresponding boundary node or . The image M is sampled along a fixed number of points along each spoke. The volume element is computed by interpolating between the average area of medial triangles adjacent to and the average area of the boundary triangles adjacent to or , and multiplying by the sampling interval along the spoke. When the leaflet medial models are combined and fitted simultaneously, each medial node is assigned a label that indicates which binary image to sample during the overlap computation.
: Boundary Jacobian constraint
Summary
This penalty prevents singularities on the medial model boundary by ensuring that the Jacobian of the medial-boundary mapping [Eq. 8] is positive. It additionally penalizes excessively large values of the Jacobian. Thus, it enforces the following inequality constraints: and , where is the Jacobian of the medial-boundary mapping and M is an arbitrarily large value.
Formulation of the penalty term
The Jacobian is approximated for each triangle on the medial mesh. Let , , be the medial nodes forming a mesh triangle t. The Jacobian for each side of the boundary is estimated as follows:
where s denotes the side of the boundary, i.e., + or –. The penalty for the given triangle is computed using an exponential barrier function that penalizes Jacobian values that are excessively small and excessively large. The total penalty is integrated over all triangles T in the medial mesh
where M = 20, α = 10, β = 1 are the parameters used in this work.
: Radial thickness constraint
Summary
This term ensures that the radial thickness field R remains positive during model fitting, i.e., .
Formulation of the penalty term
The penalty term is posed as
where N is the number of medial nodes and the Ri is the radial thickness value at medial node .
: Boundary constraint
Summary
This term ensures that each medial node that is not at the medial edge satisfies the constraint . This penalty term ensures that derivatives of are well defined on the interior of the medial manifold.
Formulation of the penalty term
This penalty term takes the form of the barrier function:
where NI is the total number of interior medial nodes and α = 6 × 10−5 is the constant used in this study.
: Loop tangent constraint
Summary
This term ensures that at medial edge nodes, where and are the partial derivatives on the medial manifold with respect to a local surface parameterization (u1,u2). This penalty term is needed because the Loop tangent scheme, based on Hoppe et al.,54 can create degenerate (parallel) tangent vectors for edge vertices with valence greater than 4.
Formulation of the penalty term
The penalty takes the form of the following barrier function
where α is the angle between the and vectors at the medial node . The reasoning behind this term is that values of α around 20° are acceptable, but smaller angles may lead to degenerate tangent vectors and are therefore undesirable. In this formulation, the penalty for α = 20° is 1, and the penalty rapidly increases as α approaches 0°.
: Leaflet intersection constraint
Summary
This term prevents overlaps and self-intersections in the medial model by ensuring that no boundary point in the model lies inside one of the balls defined by {m, R} on the medial axis. For every node j,k on the medial mesh, the inequality constraint is posed as and .
Formulation of the penalty term
The penalty term is posed as follows:
where j,k refer to nodes on the medial mesh and α = 10 and β = 0.8 are constants. This penalty function yields a value of 1 when , which indicates that a boundary point bk in the model lies inside another ball defined by {mj, Rj}. The penalty rapidly drops to zero at . The factor α controls the slope of the error function, and the factor β controls the value of at which the penalty term falls to zero.
Medial triangle shape regularizer
Summary
This regularity term controls the quality of the medial mesh by penalizing small angles in mesh triangles.
Formulation of the penalty term
The term is formulated as
where is the angle at vertex k of triangle t and α = 1 × 10−3 is the parameter used in this study.
Boundary triangle shape regularizer
This regularity term controls the quality of the boundary mesh by penalizing small angles in mesh triangles. The term is posed the same as the medial triangle shape regularizer.
References
- Shanewise J. S., Cheung A. T., Aronson S., Stewart W. J., Weiss R. L., Mark J. B., Savage R. M., Sears-Rogan P., Mathew J. P., Quinones M. A., Cahalan M. K., and Savino J. S., “ASE/SCA guidelines for performing a comprehensive intraoperative multiplane transesophageal echocardiography examination: recommendations of the American Society of Echocardiography Council for Intraoperative Echocardiography and the Society of Cardiovascular Anesthesiologists Task Force for Certification in Perioperative Transesophageal Echocardiography,” J. Am. Soc. Echocardiogr. 12(10), 884–900 (1999). 10.1016/S0894-7317(99)70199-9 [DOI] [PubMed] [Google Scholar]
- Levine R. A., Handschumacher M. D., Sanfilippo A. J., Hagege A. A., Harrigan P., Marshall J. E., and Weyman A. E., “Three-dimensional echocardiographic reconstruction of the mitral valve, with implications for the diagnosis of mitral valve prolapse,” Circulation 80(3), 589–598 (1989). 10.1161/01.CIR.80.3.589 [DOI] [PubMed] [Google Scholar]
- Levine R. A., Triulzi M. O., Harrigan P., and Weyman A. E., “The relationship of mitral annular shape to the diagnosis of mitral valve prolapse,” Circulation 75(4), 756–767 (1987). 10.1161/01.CIR.75.4.756 [DOI] [PubMed] [Google Scholar]
- Ryan L. P., Jackson B. M., Enomoto Y., Parish L., Plappert T. J., St John-Sutton M. G., Gorman R. C., and J. H.GormanIII, “Description of regional mitral annular nonplanarity in healthy human subjects: a novel methodology,” J. Thorac. Cardiovasc. Surg. 134(3), 644–648 (2007). 10.1016/j.jtcvs.2007.04.001 [DOI] [PubMed] [Google Scholar]
- Ryan L. P., Jackson B. M., Parish L. M., Sakamoto H., Plappert T. J., St John M.-Sutton, J. H.GormanIII and Gorman R. C., “Mitral valve tenting index for assessment of subvalvular remodeling,” Ann. Thorac. Surg. 84(4), 1243–1249 (2007). 10.1016/j.athoracsur.2007.05.005 [DOI] [PubMed] [Google Scholar]
- Yamaura Y., Watanabe N., Ogasawara Y., Yamamoto K., Kawamoto T., Toyota E., Akasaka T., and Yoshida K., “Geometrical demonstration and three-dimensional quantitative analysis of the mitral valve with real-time three-dimensional echocardiography: Novel anatomical image creation system,” J. Echocardiogr. 2(4), 99–104 (2004). 10.2303/jecho.2.99 [DOI] [Google Scholar]
- Sugeng L., Chandra S., and Lang R. M., “Three-dimensional echocardiography for assessment of mitral valve regurgitation,” Curr. Opin. Cardiol. 24(5), 420–425 (2009). 10.1097/HCO.0b013e32832e1675 [DOI] [PubMed] [Google Scholar]
- Vergnat M., Jassar A. S., Jackson B. M., Ryan L. P., Eperjesi T. J., Pouch A. M., Weiss S. J., Cheung A. T., Acker M. A., J. H.GormanIII and Gorman R. C., “Ischemic mitral regurgitation: a quantitative three-dimensional echocardiographic analysis,” Ann. Thorac. Surg. 91(1), 157–164 (2011). 10.1016/j.athoracsur.2010.09.078 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jassar A. S., Brinster C. J., Vergnat M., Robb J. D., Eperjesi T. J., Pouch A. M., Cheung A. T., Weiss S. J., Acker M. A., J. H.GormanIII, Gorman R. C., and Jackson B. M., “Quantitative mitral valve modeling using real-time three-dimensional echocardiography: technique and repeatability,” Ann. Thorac. Surg. 91(1), 165–171 (2011). 10.1016/j.athoracsur.2010.10.034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- J. H.GormanIII, Gupta K. B., Streicher J. T., Gorman R. C., Jackson B. M., Ratcliffe M. B., Bogen D. K., and L. H.Edmunds, Jr., “Dynamic three-dimensional imaging of the mitral valve and left ventricle by rapid sonomicrometry array localization,” J. Thorac. Cardiovasc. Surg. 112(3), 712–726 (1996). 10.1016/S0022-5223(96)70056-9 [DOI] [PubMed] [Google Scholar]
- J. H.GormanIII, Gorman R. C., Jackson B. M., Hiramatsu Y., Gikakis N., Kelley S. T., Sutton M. G., Plappert T., and L. H.Edmunds, Jr., “Distortions of the mitral valve in acute ischemic mitral regurgitation,” Ann. Thorac. Surg. 64(4), 1026–1031 (1997). 10.1016/S0003-4975(97)00850-3 [DOI] [PubMed] [Google Scholar]
- Sacks M. S., Enomoto Y., Graybill J. R., Merryman W. D., Zeeshan A., Yoganathan A. P., Levy R. J., Gorman R. C., and J. H.GormanIII, “In-vivo dynamic deformation of the mitral valve anterior leaflet,” Ann. Thorac. Surg. 82(4), 1369–1377 (2006). 10.1016/j.athoracsur.2006.03.117 [DOI] [PubMed] [Google Scholar]
- Lai D. T., Timek T. A., Dagum P., Green G. R., Glasson J. R., Daughters G. T., Liang D., N. B.Ingels, Jr., and Miller D. C., “The effects of ring annuloplasty on mitral leaflet geometry during acute left ventricular ischemia,” J. Thorac. Cardiovasc. Surg. 120(5), 966–975 (2000). 10.1067/mtc.2000.110186 [DOI] [PubMed] [Google Scholar]
- Timek T. A., Dagum P., Lai D. T., Liang D., Daughters G. T., Tibayan F., N. B.Ingels, Jr., and Miller D. C., “Tachycardia-induced cardiomyopathy in the ovine heart: mitral annular dynamic three-dimensional geometry,” J. Thorac. Cardiovasc. Surg. 125(2), 315–324 (2003). 10.1067/mtc.2003.80 [DOI] [PubMed] [Google Scholar]
- Goktepe S., Bothe W., Kvitting J. P., Swanson J. C., Ingels N. B., Miller D. C., and Kuhl E., “Anterior mitral leaflet curvature in the beating ovine heart: a case study using videofluoroscopic markers and subdivision surfaces ” Biomech. Model. Mechanobiol. 9(3), 281–293 (2010). 10.1007/s10237-009-0176-z [DOI] [PubMed] [Google Scholar]
- Martin S., Daanen V., Troccaz J., and Chavanon O., “Tracking of the mitral valve leaflet in echocardiography images,” Presented at the 3rd IEEE International Symposium on Biomedical Imaging: Nano to Macro (Arlington, VA (IEEE), 2006).
- Veronesi F., Corsi C., Sugeng L., Mor-Avi V., Caiani E. G., Weinert L., Lamberti C., and Lang R. M., “A study of functional anatomy of aortic-mitral valve coupling using 3D matrix transesophageal echocardiography,” Circ. Cardiovasc. Imaging 2(1), 24–31 (2009). 10.1161/CIRCIMAGING.108.785907 [DOI] [PubMed] [Google Scholar]
- Ionasec R. I., Voigt I., Georgescu B., Wang Y., Houle H., Vega-Higuera F., Navab N., and Comaniciu D., “Patient-specific modeling and quantification of the aortic and mitral valves from 4-D cardiac CT and TEE,” IEEE Trans. Med. Imaging 29(9), 1636–1651 (2010). 10.1109/TMI.2010.2048756 [DOI] [PubMed] [Google Scholar]
- Schneider R. J., Perrin D. P., Vasilyev N. V., Marx G. R., del Nido P. J., and Howe R. D., “Mitral annulus segmentation from 3D ultrasound using graph cuts,” IEEE Trans. Med. Imaging 29(9), 1676–1687 (2010). 10.1109/TMI.2010.2050595 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burlina P., Sprouse C., DeMenthon D., Jorstad A., Juang R., Contijoch F., Abraham T., Yuh D., and McVeigh E., “Patient-specific modeling and analysis of the mitral valve using 3D-TEE,” Lecture Notes in Computer Science (2010), Vol. 6135, pp. 135–146. 10.1007/978-3-642-13711-2_13 [DOI] [Google Scholar]
- Schneider R. J., Burke W. C., Marx G. R., del Nido P. J., and Howe R. D., “Modeling mitral valve leaflets from three-dimensional ultrasound” Lecture Notes in Computer Science (Springer-Verlag, 2011), Vol. 6666, pp. 215–222. [Google Scholar]
- Shang Y., Yang X., Zhu L., Deklerck R., and Nyssen E., “Region competition based active contour for medical object extraction,” Comput. Med. Imaging Graph. 32(2), 109–117 (2008). 10.1016/j.compmedimag.2007.10.004 [DOI] [PubMed] [Google Scholar]
- Pizer S. M., Fletcher P. T., Joshi S., Thall A., Chen J. Z., Fridman Y., Fritsch D. S., Gash A. G., Glotzer J. M., Jiroutek M. R., Lu C., Muller K. E., Tracton G., Yushkevich P., and Chaney E. L., “Deformable m-reps for 3D medical image segmentation,” Int. J. Comput. Vis. 55(2), 85–106 (2003). 10.1023/A:1026313132218 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yushkevich P. A., Zhang H., and Gee J. C., “Continuous medial representation for anatomical structures,” IEEE Trans. Med. Imaging. 25(12), 1547–1564 (2006). 10.1109/TMI.2006.884634 [DOI] [PubMed] [Google Scholar]
- Zuiderveld K., “Contrast limited adaptive histograph equalization,” in Graphic Gems IV (Academic Professional, San Diego, 1994), pp. 474–485. [Google Scholar]
- Zhu S. C. and Yuille A., “Region competition: unifying snakes, region growing, and Bayes/MDL for multiband image segmentation,” IEEE Trans. Pattern Anal. Mach. Intell. 18(9), 884–900 (1996). 10.1109/34.537343 [DOI] [Google Scholar]
- Yushkevich P. A., Piven J., Hazlett H. C., Smith R. G., Ho S., Gee J. C., and Gerig G., “User-guided 3D active contour segmentation of anatomical structures: significantly improved efficiency and reliability,” Neuroimage 31(3), 1116–1128 (2006). 10.1016/j.neuroimage.2006.01.015 [DOI] [PubMed] [Google Scholar]
- Sethian J. A., Level Set Methods and Fast Marching Methods: Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision and Material Science (Cambridge University Press, Cambridge, 1999). [Google Scholar]
- www.itksnap.org/c3d.
- Blum H., “A transformation for extracting new descriptors of shape,” in Models for the Perception of Speech and Visual Form, edited by Wathen-Dunn W. (MIT, Cambridge, 1967), pp. 362–380. [Google Scholar]
- Bouix S., Pruessner J. C., Louis Collins D., and Siddiqi K., “Hippocampal shape analysis using medial surfaces,” Neuroimage 25(4), 1077–1089 (2005). 10.1016/j.neuroimage.2004.12.051 [DOI] [PubMed] [Google Scholar]
- Kimia B., Tannenbaum A., and Zucker S., “Shape, shocks, and deformations I: the components of two-dimensional shape and the reaction-diffusion space,” Int. J. Comput. Vis. 15, 189–224 (1995). 10.1007/BF01451741 [DOI] [Google Scholar]
- Ogniewicz R. L. and Kubler O., “Hierarchic Voronoi skeletons,” Pattern Recogn. 28(3), 343–359 (1995). 10.1016/0031-3203(94)00105-U [DOI] [Google Scholar]
- Naef M., Kubler O., Kikinis R., Shenton M., and Szekely G., “Characterization and recognition of 3D organ shapes in medical image analysis using skeletonization,” IEEE Workshop on Mathematical Methods in Biomedical Image Analysis, 139–150 (1996).
- Siddiqi K., Shokoufandeh A., Dickinson S. J., and Zucker S. W., “Shock graphs and shape matching,” Int. J. Comput. Vis. 35(1), 13–32 (1999). 10.1023/A:1008102926703 [DOI] [Google Scholar]
- Yushkevich P. A., “Continuous medial representation of brain structures using the biharmonic PDE,” Neuroimage 45(1 Suppl), S99–S110 (2009). 10.1016/j.neuroimage.2008.10.051 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yushkevich P. A., Zhang H., Simon T. J., and Gee J. C., “Structure-specific statistical mapping of white matter tracts,” Neuroimage 41(2), 448–461 (2008). 10.1016/j.neuroimage.2008.01.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- www.qhull.org.
- Weinberger K. Q. and Saul L. K., “Unsupervised learning of image manifolds by semidefinite programming,” Int. J. Comput. Vis. 70(1), 77–90 (2006). 10.1007/s11263-005-4939-z [DOI] [Google Scholar]
- Shewchuk J. R., “Delaunay refinement algorithms for triangular mesh generation,” Comput Geom.: Theory Appl. 22, 21–74 (2002). 10.1016/S0925-7721(01)00047-5 [DOI] [Google Scholar]
- Jenkinson M. and Smith S., “A global optimization method for robust affine registration of brain images,” Med. Image Anal. 5(2), 143–156 (2001). 10.1016/S1361-8415(01)00036-6 [DOI] [PubMed] [Google Scholar]
- Jenkinson M., Bannister P., Brady M., and Smith S., “Improved optimization for the robust and accurate linear registration and motion correction of brain images,” Neuroimage 17(2), 825–841 (2002). 10.1006/nimg.2002.1132 [DOI] [PubMed] [Google Scholar]
- Belkin M. and Niyogi P., “Laplacian eigenmaps for dimensionality reduction and data representation,” Neural Comput. 15(6), 1373–1396 (2003). 10.1162/089976603321780317 [DOI] [Google Scholar]
- Ryan L. P., Jackson B. M., Eperjesi T. J., Plappert T. J., St John-Sutton M., Gorman R. C., and J. H.GormanIII, “A methodology for assessing human mitral leaflet curvature using real-time 3-dimensional echocardiography,” J. Thorac. Cardiovasc. Surg. 136 (3), 726–734 (2008). 10.1016/j.jtcvs.2008.02.073 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song J. M., Fukuda S., Kihara T., Shin M. S., Garcia M. J., Thomas J. D. and Shiota T., “Value of mitral valve tenting volume determined by real-time three-dimensional echocardiography in patients with functional mitral regurgitation,” Am. J. Cardiol. 98(8), 1088–1093 (2006). 10.1016/j.amjcard.2006.05.036 [DOI] [PubMed] [Google Scholar]
- Carpentier A., Adams D. H., and Filsoufi F., Carpentier’s Reconstructive Valve Surgery: From Valve Analysis to Valve Reconstruction (Saunders, Maryland Heights, Missouri, 2010). [Google Scholar]
- Damon J., “On the smoothness and geometry of boundaries associated with skeletal structures II: geometry in the Blum case,” Compos. Math. 140(6), 1657–1674 (2004). 10.1007/s11263-005-4946-5 [DOI] [Google Scholar]
- Damon J., “Determining the geometry of boundaries of objects from medial data,” Int. J. Comput. Vis. 63(1), 45–64 (2005). 10.1007/s11263-005-4946-5 [DOI] [Google Scholar]
- Sun H., Avants B. B., Frangi A. F., Sukno F., Geel J. C., and Yushkevich P. A., “Cardiac medial modeling and time-course heart wall thickness analysis,” Med Image Comput Comput Assist Interv Int Conf Med Image Comput Comput Assist Interv 11(Pt 2), 766–773 (2008). 10.1007/978-3-540-85990-1-92 [DOI] [PubMed] [Google Scholar]
- Pizer S. M., Fletcher P. T., Joshi S., Gash A. G., Stough J., Thall A., Tracton G., and Chaney E. L., “A method and software for segmentation of anatomic object ensembles by deformable m-reps,” Med. Phys. 32(5), 1335–1345 (2005). 10.1118/1.1869872 [DOI] [PubMed] [Google Scholar]
- Rao M., Stough J., Chi Y. Y., Muller K., Tracton G., Pizer S.M., and Chaney E. L., “Comparison of human and automatic segmentations of kidneys from CT images,” Int. J. Radiat. Oncol., Biol., Phys. 61(3), 954–960 (2005). 10.1016/j.ijrobp.2004.11.014 [DOI] [PubMed] [Google Scholar]
- Stough J. V., Broadhurst R. E., Pizer S. M., and Chaney E. L., “Regional appearance in deformable model segmentation,” Inf. Process. Med. Imaging 20, 532–543 (2007). 10.1007/978-3-540-73273-0_44 [DOI] [PubMed] [Google Scholar]
- Sun H., Frangi A. F., Wang H., Sukno F. M., Tobon C.-Gomez, and Yushkevich P. A., “Automatic cardiac MRI segmentation using a biventricular deformable medial model,” Med. Image Comput. Comput. Assist. Interv. 13(Pt 1), 468–475 (2010). [DOI] [PubMed] [Google Scholar]
- Hoppe H., De Rose T., Duchamp T., Halstead M., Jin H., McDonald J., Schweitzer J., Stuetzle W., “Piecewise Smooth Surface Reconstruction,” Proceedings of SIGGRAPH 1994 (ACM Press, New York, 1994), pp. 295–302.