Quantitative accuracy of MAP reconstruction for dynamic PET imaging in small animals

Abstract

Purpose: Iterative reconstruction algorithms are becoming more commonly employed in positron emission tomography (PET) imaging; however, the quantitative accuracy of the reconstructed images still requires validation for various levels of contrast and counting statistics.

Methods: The authors present an evaluation of the quantitative accuracy of the 3D maximum a posteriori (3D-MAP) image reconstruction algorithm for dynamic PET imaging with comparisons to two of the most widely used reconstruction algorithms: the 2D filtered-backprojection (2D-FBP) and 2D-ordered subsets expectation maximization (2D-OSEM) on the Siemens microPET scanners. The study was performed for various levels of count density encountered in typical dynamic scanning as well as the imaging of cardiac activity concentration in small animal studies on the Focus 120. Specially designed phantoms were used for evaluation of the spatial resolution, image quality, and quantitative accuracy. A normal mouse was employed to evaluate the accuracy of the blood time activity concentration extracted from left ventricle regions of interest (ROIs) within the images as compared to the actual blood activity concentration measured from arterial blood sampling.

Results: For MAP reconstructions, the spatial resolution and contrast have been found to reach a stable value after 20 iterations independent of the β values (i.e., hyper parameter which controls the weight of the penalty term) and count density within the frame. The spatial resolution obtained with 3D-MAP reaches values of ∼1.0 mm with a β of 0.01 while the 2D-FBP has value of 1.8 mm and 2D-OSEM has a value of 1.6 mm. It has been observed that the lower the hyper parameter β used in MAP, more iterations are needed to reach the stable noise level (i.e., image roughness). The spatial resolution is improved by using a lower β value at the expense of higher image noise. However, with similar noise level the spatial resolution achieved by 3D-MAP was observed to be better than that by 2D-FBP or 2D-OSEM. Using an image quality phantom containing hot spheres, the estimated activity concentration in the largest sphere has the expected concentration relative to the background area for all the MAP images. The obtained recovery coefficients have been also shown to be almost independent of the count density. 2D-FBP and 2D-OSEM do not perform as well, yielding recovery coefficients lower than those observed with 3D-MAP (approximately 33% lower for the smallest sphere). However, a small positive bias was observed in MAP reconstructed images for frames of very low count density. This bias is present in the uniform area for count density of less than 0.05 × 10⁶ counts/ml. For the dynamic mouse study, it was observed that 3D-MAP (even gated at diastole) cannot predict accurately the blood activity concentration due to residual spill-over activity from the myocardium into the left ventricle (approximately 15%). However, 3D-MAP predicts blood activity concentration closer to blood sampling than 2D-FBP.

Conclusions: The authors observed that 3D-MAP produces more accurate activity concentration estimates than 2D-FBP or 2D-OSEM at all practical levels of statistics and contrasts due to improved spatial resolution leading to lesser partial volume effect.

INTRODUCTION

Small animal positron emission tomography (PET) imaging is emerging as a major research tool for the in-vivo imaging of biological functions. The accrued spatial resolution and sensitivity of these cameras allows for the imaging of pharmacokinetics of radio-labeled probes in small laboratory animals as well as quantitative estimates in terms of local tracer concentrations. In other words, PET has the advantage over other noninvasive imaging modalities of offering a very high sensitivity and allowing for quantitative estimates of the radio-activity concentration in living animals. Mice are often the animal model of choice for reasons of cost and availability of a large variety of transgenic animal models. The small size of this animal, however, imposes stringent requirements for this task when accurate quantitative imaging is required. This is especially true for small organs such as the myocardium wall. The traditionally limited spatial resolution of PET leads to partial volume effects which hinder accurate estimation of radio-activity in structure smaller than approximately two to three times the system spatial resolution. In the occurrence, the transverse spatial resolution of the microPET scanner has been reported to be approximately 1.7 mm at 1 cm away from the center of the field of view (FOV),^{1, 2} thereby limiting to objects larger than 3.5 mm for which complete recovery is to be expected. Such resolution indicates that for objects with dimension smaller than 3–5 mm, incomplete estimation of the activity would occur and that careful correction for spill-over and partial volume effects are likely required in the data analysis.

Recent development of image reconstruction algorithms attempts to improve the spatial resolution by an accurate modeling of the system response to the detection of the annihilation photons, the physics of positron decay (photon noncollinearity and positron range) and the statistical nature of nuclear decay by an accurate description in terms of Poisson statistics. The 3D maximum a posteriori (3D-MAP) algorithm³ distributed with the Siemens PreClinical Solution microPET cameras is such an algorithm and implements these corrections (with the exception of the positron range correction). Developed initially for the Siemens ECAT HR +  clinical cameras,⁴ the same algorithm was presented in Refs. ^{3, 5} for applications in the UCLA prototype small animal PET scanner and was later implemented in the Siemens Pre-Clinical suite of small animal PET cameras. Improvement in the system resolution and improved quantitation accuracy was reported⁵ for the small structures evaluated, but the complete recovery of the activity concentration was not achieved. A modified version of this code that includes the positron range correction was employed to study the quantitative uptake in-vivo for various tracers.^{6, 7}

Numerous studies on the quantitative accuracy of iterative image reconstruction algorithms have been reported, in particular on the 2D-OSEM (ordered subset expectation maximization).^{8, 9, 10, 11} Especially, in the case of 2D-OSEM, it has been reported that the convergence is slower in areas of lower counts than that for the high count regions. Moreover, 3D-OSEM has been studied in Ref. 12 for clinical scanners, compared different weighting schemes, and compared to 2D filtered-backprojection (2D-FBP) and 2D-OSEM. It appears that 2D-OSEM does not show apparent image degradation as compared to 3D-OSEM for data with a noise level typical of a whole-body FDG scan. Few, however, have reported on the quantitative performance of iterative algorithms that incorporate modeling in order to achieve improved spatial resolution. The quantitative accuracy of the MAP algorithm and its lesion detection capabilities have been evaluated^{13, 14} in theoretical studies. More recently, the noise and signal properties of iterative reconstructions incorporating the point spread function (PSF) were studied in Refs. ^{15, 16, 17, 18}. The accuracy of 3D-OSEM for the HRRT has been reported in Refs. ^{19, 20} as function of the number of iterations over a range of activity concentration.

In traditional image reconstruction algorithms for dynamic studies, each frame of a dynamic series is reconstructed independently. This approach can lead to nonoptimal reconstructions where the independent image reconstruction of each histogrammed frame of data can be very noisy. Moreover, independent frame reconstruction does not utilize data from any other temporal frames; furthermore, the reconstruction task does not consider the tracer kinetic modeling.^{21, 22, 23} In order to address the issues with the conventional dynamic imaging, a number of four-dimensional (4D) PET and direct parametric image reconstruction approaches have been developed over the years. These image reconstruction strategies in dynamic PET have been recently reviewed,^{21, 24} though the optimal 4D PET reconstruction protocol has yet to be determined for various tracers and applications.

The blood activity concentration is an important parameter for all radiopharmaceutical kinetic modeling analysis and is referred in this case to the blood input function as it serves as one of the input parameters. Several techniques for extraction of this quantity are discussed in Ref. 25. Since the spatial resolution is typically not sufficient to directly extract the blood activity concentration from images, postprocessing techniques are usually employed.^{26, 27, 28, 29} There is therefore a great interest in providing PET images from which the blood activity concentration can be directly obtained, and careful evaluation of novel image reconstruction algorithm aiming at improving resolution and quantitative accuracy is thus warranted.

In this report, we present an experimental evaluation of the performance of the MAP algorithm (provided by Siemens Preclinical Systems) with regard to the quantitative accuracy for various level of count density. A special attention will be given to the imaging of cardiac activity concentration in small animal studies, with interest in dynamic experiments over a wide range of statistics. The objective of this paper is to report on the quantitative accuracy of the 3D-MAP reconstruction algorithm and comparison with two of the most widely used algorithms, 2D-FBP and 2D-OSEM, employed with their respective standard parameters, available on the Siemens microPETs (in the occurrence the microPET-F120 used here).

METHODS

The results presented were acquired on the high-resolution small animal PET scanner, microPET-F120 (Siemens Preclinical Systems, Knoxville, TN). This scanner is made of 4 rings of block detectors composed of an array of 12 × 12 Lutetium oxyortho silicate (LSO) scintillation crystals of 1.6 × 1.6 × 10 mm with optical coupling to a position sensitive photomultiplier tube via a coherent bundle of square optical fibers. The performance evaluation of this scanner was described in Refs. ^{1, 2}. This system presents a FOV of 10.8 cm in the transverse direction and 7.6 cm axially. This camera is capable of spatial resolution (in the transverse direction) of 1.7 mm at 1 cm away from the center of the FOV and a sensitivity of 7% with 2D-FBP reconstructions. Specially designed phantoms were built for evaluation of the spatial resolution, image quality, and quantitative accuracy.

Image reconstruction

Images were reconstructed by 2D-FBP with a ramp filter operated at Nyquist frequency from FORE (Ref. ³⁰) rebinned sinograms. The 2D-OSEM image reconstructions were performed on the same FORE rebinned sinograms with the default values of 4 iterations and 16 subsets. Maximum a posteriori (MAP) is a penalized statistical iterative image reconstruction algorithm that maximizes log-likelihood of the Poisson statistics and uses the Huber potential as the regularization term. The algorithm is described in Ref. 3. The regularization term is used to penalize sharp fluctuations between neighboring voxels and therefore controls image smoothness. The weight of the penalty term is controlled via the hyperparameter β. In other words, the hyperparameter (β) controls the importance of the prior and thus the smoothness in the images. Larger values of β yield smoother images, while lower values decreases the importance of the penalty term and yield a solution closer to the MLEM (maximum likelihood expectation maximization) algorithm.³¹ The system model accounts for the system detector response, detector sensitivity, depth of interaction, normalization, and photon noncollinearity. The image reconstruction algorithms used here are those provided by the manufacturer (RECON V02.4600). MAP reconstruction was performed using the shifted-Poisson model where data were precorrected for random coincidences (default mode). Images were generated from fully 3D sinograms for 20 iterations (unless otherwise indicated) using the standard procedure which consists in first performing 2 iterations of 3D-OSEM (12 subsets) and then 18 iterations of the accelerated version of 3D-MAP (i.e., FASTMAP).³²

Spatial resolution

The quest for better spatial resolution is often accompanied by an increase in image noise. In fact, spatial resolution measurement should always be performed with an estimate of the image variance. To this effect, a phantom was designed to allow measurement of spatial resolution and evaluation of the image noise at the same time. This phantom is composed of two capillary tubes immersed in water. Radioactivity can be separately filled in the capillary tubes and the uniform water area surrounding the tubes. The phantom has cylindrical geometry with overall dimension of 2.5 cm in diameter and 2.5 cm long. One capillary line source is placed at the center while the other one is placed at 8 mm radial offset. The phantom was prepared by a 300:1 ratio of activity concentration between the capillary tube and the uniform area. Due to the small inner diameter of the tube (250 μm), the peak to uniform area ratio in the reconstructed images was only of 10–20 depending on the reconstruction algorithm. Images were reconstructed with a pixel size of 0.2 mm on a matrix of 256 × 256 pixels and 95 planes.

The full width at half the maximum (FWHM) was extracted from a Gaussian function fitted on a profile traced through the capillary line source in the transverse direction. Profiles were fitted on 11 adjacent planes in the transverse direction of the capillary at the center and in the transverse and radial direction for the capillary tube at 8 mm from the center. The estimate of noise in the image (i.e., voxel-noise or image roughness) was extracted from the standard deviation of a 4.2 mm diameter region of interest (ROI) placed in the uniform background region, and the average standard deviation of the 11 planes was calculated.

Quantitative accuracy

Quantitative accuracy was assessed by using a mouse size phantom containing an arrangement of fillable spheres and fillable lung inserts. This phantom is similar in construction to the recently adopted NEMA 2008 small animal image quality phantom.³³ This phantom differs by the fillable rods that were replaced by a hollow cavity where fillable spheres were inserted. The overall internal dimensions of the phantom are 5 cm long and 3 cm in diameter. Two lung inserts with dimensions of 8 mm inner diameter and 15 mm in length were attached to the lid at one end of the cylinder and fillable spheres (spheres were purchased from Data Spectrum, NC) were attached to the other end on short stems. Three fillable spheres were attached to the bottom lid. The sphere volumes were 0.063, 0.125, and 0.5 ml. Two separate experiments were performed. In the first experiment, the phantom was prepared by filling the whole phantom with ¹⁸F-FDG and with a sphere-to-background ratio of 10.11–1. In the second experiment, an initial ratio of 10.76–1 was used, but this time the spheres were filled with ¹¹C solution, and the uniform areas were filled with ¹⁸F solution. For both experiments, the total initial activity of the phantom was kept below 18 MBq (0.500 mCi) to maintain a low system deadtime. The phantom was placed at the center of the FOV with the spheres at approximately 0.5 cm from the center of the FOV in the transverse direction and at the center of the FOV in the axial direction. Data acquisition was performed for 10 min in the first experiment and for 2 h in the second experiment. Attenuation correction was determined from a numerical model of the phantom forward projected to produce an attenuation sinogram file.

In the experiment with ¹⁸F only, the acquired list-mode file was processed to generate a series of dynamic 3D sinograms of multiple frames with various time durations: 20 × 0.5, 20 × 1, 20 × 2, 20 × 5, 20 × 10, 20 × 30, and 10 × 60 s. The objective of the first study is to evaluate the accuracy of the various image reconstruction algorithms with very different levels of statistics and object sizes. The sinograms were then reconstructed with 2D-FBP, 2D-OSEM, and 3D-MAP with normalization, attenuation, and scatter corrections with a zoom of 2 to yield a voxel size of 0.433 × 0.433 × 0.796 mm³/voxel (i.e., 0.433 ×  0.433 mm² in the xy plane with a slice thickness of 0.796 mm in the z direction). The MAP reconstructions were performed with increasing values of β. Data were analyzed by drawing ROIs on the plane passing through the center of the spheres with diameters of 0.216, 0.43, and 0.65 cm corresponding to integer multiples of the voxel width. These diameters of the ROIs correspond to 43%, 69%, and 66% of the actual sphere diameter of volume 0.063, 0.125, and 0.5 ml, respectively. The absolute distances between the edge of the ROI and the edge of the sphere are 0.142, 0.097, and 0.167 cm for the aforementioned spheres, respectively. A larger circular ROI was traced in the uniform section of the phantom to estimate the average background activity from the reconstructed images. The reference background activity concentration was obtained from a high statistics (230 s) frame with this ROI for each reconstruction algorithm. The ratio of activity concentration from the uniform areas and the spheres with respect to the reference background concentration was plotted as a function of the expected count density within each region and the standard deviation of those average values was then calculated for each group of frame of equal duration. The expected regional count density in the spheres is given by

$$\mathit{Count}\mathit{Density}=\#\mathit{Trues}·\frac{\mathit{Concentration}\mathit{Ratio}}{\mathit{Phantom}\mathit{Volume}-\sum \mathit{Sphere}{\mathit{Volume}}_i+\mathit{Concentration}\mathit{Ratio}\times \sum \mathit{Sphere}{\mathit{Volume}}_i}$$ (1)

where the #Trues is the number of true coincidences collected for a given frame duration. The count density represents the number of events originating for a given region of the phantom based on the acquired total number of events. This estimate does not account for the variation in sensitivity across the FOV thus approximate but importantly scales with the number of true coincidences. In addition, the contrast recovery coefficient, defined by Eq. 2, was also calculated as a function of the number of iterations for the MAP reconstructions

$${\mathit{Contrast}}_{\mathit{hot}}=\left(\frac{\frac{C_H}{C_B}-1}{\frac{A_H}{A_B}-1}\right)\times 100\%$$ (2)

where C_B is the mean counts within the background region in the image, C_H is the mean counts within the hot region in the image, A_H is the measured (known) activity for the hot region, and A_B is the measured activity for the background region.

In the second experiment using this same phantom, the activity concentrations in the ¹¹C filled spheres were estimated from the reconstructed images to evaluate dynamically the system response. ROIs were drawn on the spheres of various dimensions. The estimated activity as function of time is reported and fitted by an exponential decay curve. The parameters of the exponential which should be equal to the radio-active physical decay constant and thus accuracy of the algorithm was tested against the well-known decay constants for those nuclides.

Mouse heart phantom

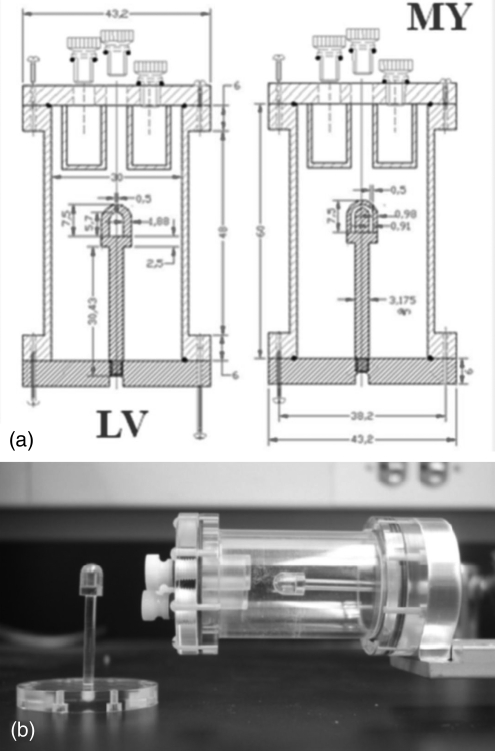
Mouse heart phantoms were designed to mimic the dimension of a mouse heart in shape and dimension. A separate myocardium and left ventricle mouse heart phantoms were created to be scanned separately thereby avoiding the portioning wall between the two fillable cavities. The myocardium phantom was made of acrylic and was composed of two pieces placed concentrically to create a fillable region with a cylindrical and hemispherical hollow component. The fillable area depicting the myocardium wall had a 3 mm diameter and a thickness of 0.90 mm. The second left ventricle phantom has a cavity of 3 mm in diameter (see Fig. 1). The phantoms were filled independently with ¹¹C and ¹⁸F to estimate the recovery coefficients and spill-over fractions (F_bb represents the recovery coefficient of the blood pool  =  ratio of measured blood pool activity over known value in the left ventricle phantom, F_mm represents the recovery coefficient of the myocardium  =  ratio of measured myocardium activity over known value in the myocardium phantom, F_bm represents the spill-over fraction of the blood pool onto the myocardium  =  ratio of measured myocardium activity over known value of blood pool in left ventricle phantom, and F_mb represents the spill-over fraction of the myocardium onto the blood pool  =  ratio of measured blood pool activity over known myocardium value in myocardium phantom). In a separate experiment, the mouse myocardial phantom was filled with a mixture of ¹¹C and ¹⁸F initially in an equal ratio of activity concentration (at the time of scanning). The heart phantoms were inserted into the image quality phantom and imaged for 2 h. The list-mode data file was then sorted into a dynamic sequence of 30 × 120 s frames and 15 × 240 s frames. A measured transmission image using the rotating Co-57 point source (2 passes for 15 min) was used to calculate the attenuation correction file using the segmentation technique. The decay rates and activity concentrations were estimated by fitting a two-exponential function to the nondecay corrected average intensity in the images. The list-mode file was further reprocessed to create a dynamic sequence containing one tenth of the counts from the original scan, and the same analysis was performed.

Figure 1.

(a) Schematic drawing of the mouse left ventricle (LV) and myocardium (MY) phantoms placed inside the image quality phantom; the dimensions are in mm. (b) Actual picture of the phantoms with the left ventricular phantom shown detached.

Animal experiment

A normal mouse was employed to evaluate the accuracy of the blood time activity concentration extracted from left ventricle ROIs (the largest pool of blood in the animal) as compared to actual blood activity concentration measured from arterial blood sampling. The Balb/C mouse was anesthetized, and a cannula was inserted into the aorta (microcatheter 1.2F, 0.4 mm OD × 0.15 mm ID). A second port was installed in the left leg vein for activity injection. The animal was then placed on the imaging pallet in the scanner by centering the heart in the imaging FOV. Approximately, 18 MBq (500 μCi) of ¹⁸F-FDG was injected, and the scanning was simultaneously started for a duration of 1 h. The list-mode data file was then sorted as dynamic sequence of 40 frames, shorter at the beginning of the scan and longer toward the end to capture optimally the kinetic of the tracer. Manual blood sampling was performed by withdrawing approximately 5 μl at set time points. Blood samples were collected in preweighted 10 μl centrifuge tube that were then weighted and finally counted in a gamma counter (Beckman 8000 Gamma counter); see Ref. 25 for further details. The dead-space of the cannula was removed in between each sample.

Electrocardiogram (EKG) leads were attached to the two front paws and 1 hind limb, and the QRS-wave signal (i.e., the electrocardiographic deflection representing ventricular depolarization; the initial downward, upward, and the following downward deflections are termed Q, R, S, respectively) was used as a cardiac trigger to the microPET. In postacquisition reconstruction, the list-mode data file was also sorted as dynamic-gated sinograms with 40 dynamic frames, and the heart cycle was divided into 8 time segments. The sinograms corresponding to the segments of diastolic phase of the beating cycle were added together at each time frame to constitute a sequence of dynamic sinogram data at diastole. Data were then reconstructed with the standard corrections using a measured attenuation correction (1 pass with ⁵⁷Co rotating point source) and with the 2D-FBP and 3D-MAP (b  =  0.05) algorithm. Four series of images corresponding to 2D-FBP and 3D-MAP, noncardiac gated and cardiac-gated (at diastole) acquisitions were thus reconstructed using the same EKG gated sinograms. A small ROI was drawn on a zoomed PET image showing the left ventricle of the heart. Image based blood input function were compared to the manual blood sampling.

RESULTS

Spatial resolution and noise

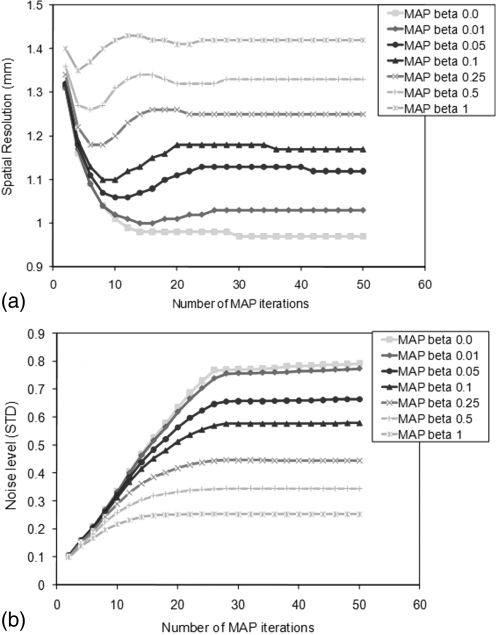
Figures 2a, 2b presents the spatial resolution extracted from the FWHM in the capillary phantom images reconstructed with MAP at the centre of the FOV and the average noise estimated by the standard deviation over the mean in a large ROI traced in the uniform area, respectively, as a function of the number of iterations. The plots show for β values ranging from 0 to 1. The spatial resolution has been observed to reach a stable value after 20 iterations. The resulting resolution ranges from 0.97 to 1.42 mm depending on the β value. As shown in Fig. 2b, the noise in the image reaches a stable value faster (i.e., with fewer iterations) for a higher β value. As will be discussed later, the contrast also converges at 20 iterations. Consequently, the optimal number of MAP iterations has been confirmed to be 20 (18 iterations is suggested by the manufacturer) and was used throughout the studies in this work.

Figure 2.

(a) Spatial resolution and (b) noise level for MAP reconstructions for various numbers of iterations and for several values of the β hyper parameter. The noise level was estimated by the standard deviation of an ROI traced in the uniform background region, and the average value over 11 consecutive planes was calculated.

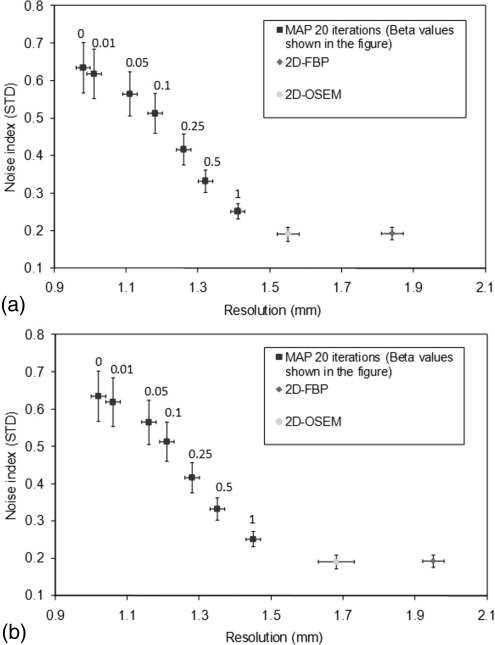
Figures 3a, 3b presents the spatial resolution in the capillary phantom reconstructed with 2D-FBP, 2D-OSEM, and 3D-MAP at the center of the FOV [Fig. 3a] and at 8 mm radial offset [Fig. 3b]. The data are presented along with the average noise in the images. Error bars indicate the standard deviation of the measured spatial resolution and of the image plane standard deviation over 11 adjacent planes. This plot indicates that better spatial resolution is achieved by 3D-MAP with similar level of noise (image roughness) at a value of β around 1.0 as compared to 2D-FBP and 2D-OSEM reconstructions. The spatial resolution obtained with 3D-MAP reaches a value of 1.4 mm with a β of 1.0 while the 2D-FBP has a value of 1.8 mm and 2D-OSEM has a value of 1.5 mm. Lower values of β produce better resolution along with higher noise for 3D-MAP. The resolution with 3D-MAP reaches a value of 1.0 mm with a β of zero. 2D-OSEM presents a spatial resolution and a noise property comparable to 3D-MAP employed with a value of β of 1.0 for a source located close to the center of the FOV. However, spatial resolution with 2D-OSEM at 8 mm is strongly reduced. The line source located at 8 mm from the centre of the FOV showed an appreciably poorer spatial resolution with 2D-OSEM and 2D-FBP as compared to the results from the 3D-MAP algorithm.

Figure 3.

Noise versus resolution plots (a) at the CFOV and (b) at 8 mm offset for 2D-FBP, 2D-OSEM, and 3D-MAP with various β values.

Quantitative accuracy

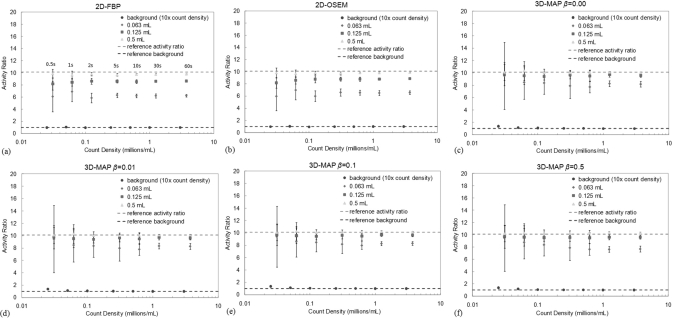
The results of the quantitative accuracy analysis are shown in Figs. 4a, 4b, 4c, 4d, 4e, 4f for 2D-FBP, 2D-OSEM, and 3D-MAP. The MAP reconstructions were performed with four values of the hyperparameter β as indicated in the figures. The error bars on these plots indicate the standard deviation of estimated ratios over the 10 or 20 images of the same frame duration. The count densities for the background area were multiplied by 10 on the figures for display purposes. The estimated activity concentration in the largest sphere had the expected concentration relative to the background area for all three algorithms (2D-FBP, 2D-OSEM, and 3D-MAP with any β). This ratio is also shown to be independent of the count density. For the MAP reconstructions, the 0.125 ml sphere has a ratio of activity concentration of 9.56 corresponding to 94% recovery coefficient for this sphere, while the smallest sphere has an average ratio of activity concentration of 8.12 (78.2% recovery) for the longest frame duration. The 2D-OSEM and 2D-FBP do not perform as well, yielding recovery coefficients lower than those observed with 3D-MAP. The estimated activity ratios from 2D-FBP with the longest frame duration are: 8.64 (83.9% recovery) for the 0.125 ml sphere and 6.24 (57.5% recovery) for the smallest sphere; ratios obtained from 2D-OSEM are: 8.87 (86.4% recovery) for the 0.125 ml sphere and 6.58 (61.3% recovery) for the smallest sphere. The reference activity ratio (hot contrasts) for this experiment is 10.11. The improvement in activity ratio achieved by 3D-MAP relative to 2D-FBP and 2D-OSEM is similar to what was observed in Ref. 11 though the overestimated activity ratio by 3D-MAP for the large spheres as shown in Ref. 11 was not observed here due to the smaller ROI used in the estimation of the activity ratio.

Figure 4.

Activity concentration ratio between spheres and surrounding background area for (a) 2D-FBP, (b) 2D-OSEM, (c) 3D-MAP β = 0, (d) 3D-MAP β =  0.01, (e) 3D-MAP β = 0.1 and (f) 3D-MAP β =  0.5) with various scan durations. Error bars indicate statistical uncertainty over the different realizations. A ratio of 10.11 indicates complete recovery of the activity. The count densities in the background area were multiplied by 10 for this presentation.

The recovery coefficients for MAP are all very similar regardless of the choice of the hyperparameter β except for the largest value of β at 0.5 where the recovery coefficients are slightly lower. However, a small positive bias is observed for frames of short duration (with the lowest number of counts). This bias is present in the uniform area for count density of less than 0.05 × 10⁶ counts/ml. Statistically significant biases in the uniform areas are 37% and 17% for the count densities of 0.025 and 0.05 × 10^− 6 counts/ml (p-values < 0.05). The positive bias was only visible within the smallest sphere of 0.063 ml at an average count density of 0.031 ×  10⁶ counts/ml. The magnitude of this bias is of the order of 11% and is smaller than the statistical uncertainty of a single measurement. This bias is found not be statistically significant after averaging many measurements (p-value > 0.05). No positive biases are observed for 2D-FBP and 2D-OSEM (note that the FORE rebinning produces 2D sinograms with more counts per bin (less number of bins) as compared to 3D sinograms, and the positive bias is likely to present at a lower count density for 2D-OSEM as was observed in Ref. 34).

The error bars shown in Fig. 4 represent the standard deviation on the calculated recovery coefficients and represent the spread of the average activity concentration measurements or the inherent uncertainty of a measurement. The standard error on the average activity concentration upon successive repetition of the experiment is approximately 4.5 times lower. The standard deviations for the lowest count densities are larger than the positive bias introduced by the reconstruction algorithm. Essentially, this indicates that in those very low count experiments, the total error in the activity ratio is not only affected by the positive systematic bias due to the non-negativity constraints of the iterative algorithm but mostly by the precision error due to low counting statistics as indicated by the error bars.

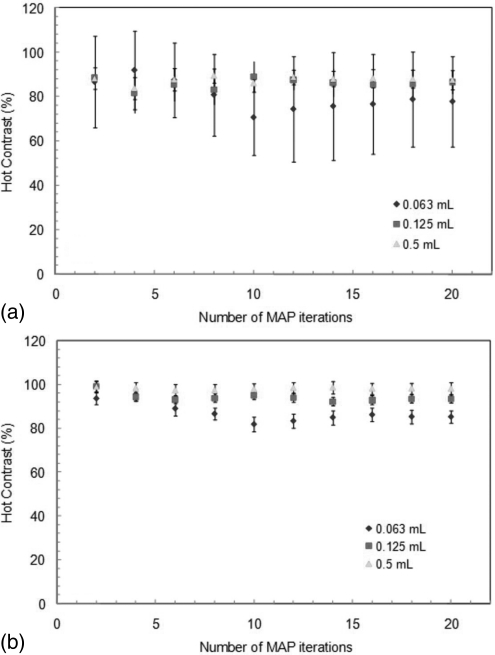
In Figs. 5a, 5b, the contrast recovery of the three different sizes of spheres is plotted as a function of the number of iterations for the MAP reconstruction. The contrasts were observed to become constant after 10–12 iterations (β = 0.05). Figures 5a, 5b correspond to a low statistics (2 s frames) and high statistics case (60 s frames), respectively. For both cases, the same number of iterations is needed to achieve constant contrasts (87.9% in the 2 s frames and 98.2% in the 60 s frames for the largest sphere). Again, error bars represent the standard deviation among 10 or 20 frames of the same duration. The small difference in contrast observed is smaller than the statistical uncertainty and is found not to be of statistical significance (p-value > 0.05).

Figure 5.

Contrast recovery of the three different sizes of sphere obtained from the MAP reconstruction (β  =  0.05) as a function of number of iterations for (a) 0.03  ×  10⁶ counts/ml and (b) 3  ×  10^− 6 counts/ml.

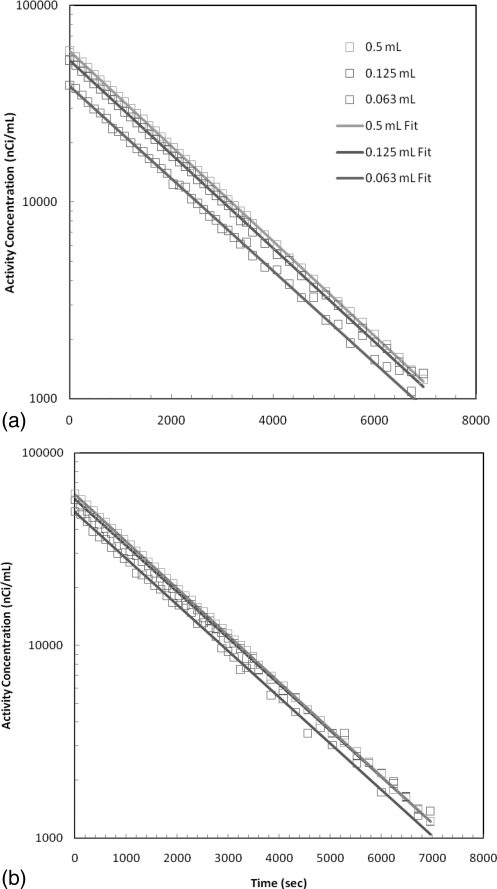
In the second experiment with this phantom, the spheres contained ¹¹C while the uniform area was filled with ¹⁸F. Data were acquired over a period of 2 h and subdivided in frame duration of 2 minutes for the first hour and then 4 min for the second hour. Images were then reconstructed with 2D-FBP, 2D-OSEM, and 3D-MAP (20 iterations, β  =  0.01, 0.05, and 0.5). A plot of the estimated activity concentration as a function of time is presented in Figs. 6a, 6b for 2D-FBP and 3D-MAP algorithms. The fitting parameters are gathered in Table TABLE I. for 2D-FBP, 2D-OSEM, and 3D-MAP reconstructions with different β hyperparameter values along with the contrast recovery coefficients and T_1/2 deviation from the nominal values. Generally, larger activity concentration was obtained from all spheres with MAP algorithm indicative of the more accurate quantitative accuracy. For all reconstructions, the slope of the distribution is in agreement with the expected half-life for ¹¹C and the choice of β parameter does not have a significant impact on the estimated activity concentrations and on the fitted parameters.

Figure 6.

Activity concentration of the spheres filled with ¹¹C and background area filled with ¹⁸F solution plotted as a function of time for (a) 2D-FBP and (b) 3D-MAP (20 iterations and β  =  0.05).

TABLE I.

Measured activity concentration and measured nuclide half-lives in the spheres filled with ¹¹C with comparison to the known nominal values. The recovery coefficients (activity coefficient divided by the nominal value) and the half-life deviation (in %) are also presented. The values are listed in the order the smallest sphere to the largest sphere (i.e., 1st: 0.063 ml, 2nd: 0.125 ml, and 3rd: 0.5 ml).

Algorithm	11C Activity(nCi/ml)	T1/2(min)	Recovery coefficients (%)	T1/2Deviation(%)
Nominal values	65220	20.38	—	—
2D-FBP	38945 ± 77	21.38 ± 0.04	60	4.9
	52396 ± 89	21.05 ± 0.03	80	3.3
	58548 ± 94	20.77 ± 0.03	90	1.9
2D-OSEM	40410 ± 78	21.25 ± 0.0	62	4.3
	52991 ± 89	21.03 ± 0.03	81	3.2
	58583 ± 94	20.78 ± 0.03	90	2.0
3D-MAP β  =  0.01	47286 ± 85	21.29 ± 0.04	73	4.5
	55968 ± 92	21.02 ± 0.03	86	3.1
	61230 ± 97	20.60 ± 0.03	94	1.1
3D-MAP β  =  0.05	48482 ± 85	21.30 ± 0.04	74	4.5
	56395 ± 92	21.01 ± 0.03	86	3.1
	61204 ± 97	20.57 ± 0.03	94	0.9
3D-MAP β  =  0.5	49500 ± 87	20.82 ± 0.03	76	2.2
	57554 ± 93	20.87 ± 0.03	88	2.4
	61063 ± 77	20.55 ± 0.03	94	0.8

The estimated radio-activity half-lives in the spheres are all very close to the nominal ¹¹C half-life regardless of the reconstruction algorithm. The estimated activity concentrations are also higher with MAP indicating better recovery of the activity due to the gain in spatial resolution. This improvement is mostly apparent for the smallest sphere size. The values of recovered activity are also very similar for different values of β and vary slightly.

Mouse heart phantom

Images of the ¹¹C myocardium mouse phantom reconstructed with 2D-FBP and 3D-MAP (20 iterations, β  =  0.05) are presented in Fig. 7. Table TABLE II. presents the estimated recovery coefficients and spill-over fractions for ¹¹C and ¹⁸F, and for both 2D-FBP and 3D-MAP reconstructions. As expected, higher recovery coefficients (blood pool recovery coefficient, F_bb and myocardium recovery coefficient, F_mm) and lower spill-over fractions (spill-over from blood pool to myocardium, F_bm and spill-over from myocardium to blood pool, F_mb) are observed with ¹⁸F than with ¹¹C due to the shorter positron range. MAP reconstructions also provide better recovery coefficients (close to 100), but the spill-over fractions are not zero indicating residual spill-over from incomplete recovery of the activity.

Figure 7.

Transverse and coronal images of the mouse myocardial phantom filled with ¹¹C and reconstructed with (a)–(b) 2D-FBP and (c)–(d) 3D-MAP (20 iterations, β  =  0.05).

TABLE II.

Recovery coefficients (F_bb of the blood pool and F_mm of myocardium areas) and spill-over fractions (F_bm and F_mb) from the mouse heart phantoms for ¹¹C and ¹⁸F.

	2D-FBP		3D-MAP
	11C	18F	11C	18F
Fbb	68	73	100	100
Fbm	27	18	21	16
Fmb	21	18	11	1
Fmm	40	46	67	83

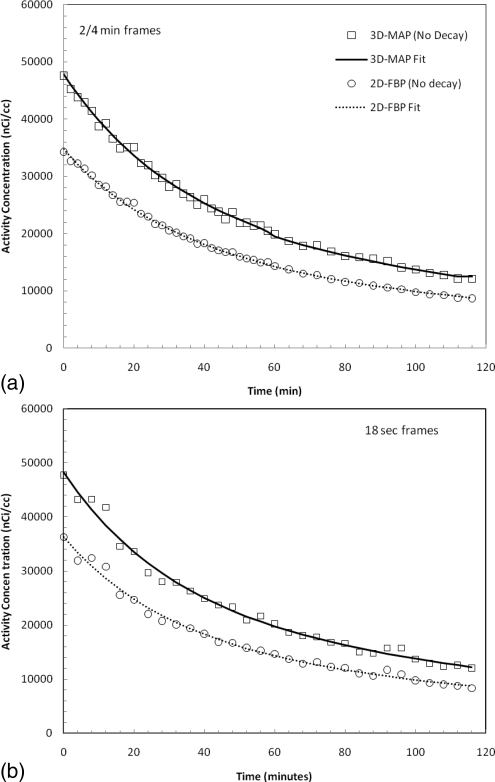
The results of the mix nuclide experiment are presented in Figs. 8a, 8b. The nondecay corrected intensity from the myocardium phantom filled with ¹¹C and ¹⁸F mixture was fitted by a sum of two exponentials where the parameters of the fits along with the standard errors are presented in Table TABLE III.. The decay constants are well within the expected values considering the error on the estimates and are in agreement with the half-lives of ¹⁸F and ¹¹C for both image reconstructions. The estimated activity concentrations with MAP are also higher for all time points, indicative of higher recovered activity values. In Fig. 8b, dynamic sequence of images was created from resampling the same list-mode file, and the same analysis was performed on the images with approximately 10% of the statistics. The result of the fit is shown on the figure and the fitted parameters are presented in Table TABLE III..

Figure 8.

Estimated activity concentration in the myocardial chamber of the mouse heart phantom filled with a mixture of ¹¹C and ¹⁸F, for (a) 2/4 min frames and (b) 18 s frames. The dash line represents a double exponential fit used to estimate recovery ratios and decay constants.

TABLE III.

Measured activity concentrations and half-lives from the heart phantom filled with a solution of ¹¹C and ¹⁸F. The standard error of the half-lives is presented in square-bracket.

Algorithm	11C Activity (nominal T1/2  =  20.38 min)		18F Activity (nominal T1/2  =  109.8 min)
2/4 min frames	(nCi/ml)	Measured T1/2 (min)[Standard error]	(nCi/ml)	Measured T1/2 (min)[Standard error]
2D-FBP	17402	20.18 [0.98]	18022	108.5 [1.16]
3D-MAP	25438	20.65 [1.32]	25237	110.87 [1.00]
18 s frames
2D-FBP	18861	20.14 [1.18]	17399	110.32 [0.50]
3D-MAP	23886	20.15 [1.13]	24382	110.87 [1.00]

Animal data

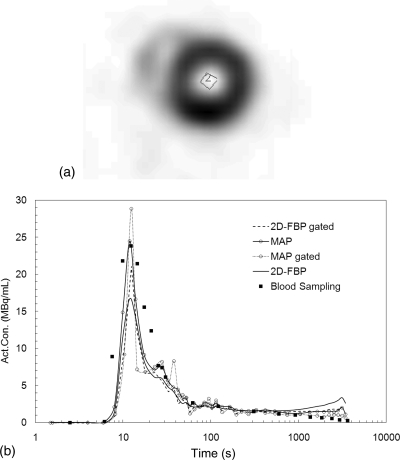
Figure 9b shows the time activity curves of the blood activity concentration extracted from a small ROI traced inside the left ventricle from one animal dataset as seen on the microPET images [Fig. 9a]. The time activity curves obtained from the 2D-FBP, 2D-FBP (gated), 3D-MAP, 3D-MAP (gated) images are plotted and compared to the blood sampling data. Good agreement between MAP reconstructions of gated heart at diastole and blood sampling is observed except at the later time points where the reconstructed activity in the myocardium is higher than the blood activity concentration. The discrepancy at early time points (around the peak) is likely due to the limitation in the manual sampling process leading in error in the sampling time and to diffusion of the activity in the cannula. ¹⁸F-FDG accumulates substantially into the myocardium and creates spill-over into the left ventricle due to the limited spatial resolution to contaminate the time activity concentration of the blood from an ROI traced over the left ventricle of the heart. Nevertheless, MAP performed better than FBP with less spill-over from the myocardium into the left ventricle.

Figure 9.

(a) The MAP gated image showing the small ROI traced inside the left ventricle of a mouse injected with 0.5 mCi (18.5 MBq) of ¹⁸F-FDG. (b) Blood activity concentrations derived from the ROI shown in (a). Images were reconstructed with 2D-FBP and 3D-MAP (20 iterations, β  =  0.05). EKG data (at diastole) are also presented.

DISCUSSION

The main objective of this work was to study the accuracy on the recovery of the activity concentration in hot lesions relative to background as a function of object size, statistics, number of iterations, and choice of the β parameter in 3D-MAP with comparisons to established reconstruction algorithms such as 2D-FBP or 2D-OSEM used with their standard parameters. 2D-FBP is the standard image algorithm which is expected to provide the gold-standard for accuracy comparison. However, this algorithm produces noisier/rougher images in low count experiments. It is known that iterative reconstruction converges more slowly, i.e., likely need more iterations, for cold regions (regions devoid of activity compared to the surrounding). This image feature was not studied in this work as the intent was to study the recovery coefficients of small hot lesions under various conditions.

The imaging performance of MAP was first established by the evaluation of the spatial resolution for various values of the β parameter controlling the smoothness of the images and for various numbers of iterations using a phantom that allows the resolution and the noise in the images to be measured simultaneously. We observed that the spatial resolution is dependent on the choice of the β hyperparameter (as expected) and that better resolution can be achieved by 3D-MAP as compared to 2D-FBP and 2D-OSEM at the expense of increase in image noise. However, at equivalent noise level, 3D-MAP still provides higher spatial resolution.

Disselhorst et al.³⁵ studied the recovery coefficients of 1–5 mm rods on a cold background using the NEMA-2004 image quality phantom and compared the performance of 3D-MAP with 2D-FBP using ¹⁸F and other nuclides. An improvement in count recovery of 36% with 3D-MAP was observed with respect to 2D-FBP (and 2D-OSEM). In their paper, the number of iterations and hyperparameter was set at 18 and 0.1, respectively. From Figs. 4a, 4b (2D-FBP and 2D-OSEM) and Figs. 4c, 4d, 4e, 4f (3D-MAP with β = 0, 0.01, 0.1, 0.5), we note that the recovery coefficient of the 0.063 ml sphere increases from approximately 60% to slightly more than 80%. This is therefore a gain in recovery consistent with Disselhorst’s measurement.

An examination of the reproducibility of a PET measurement (i.e., contrast recovery) was performed by studying similarly acquired frames of equal duration in a dynamic procedure which is equivalent to repeating the experiment multiple times. This experiment first demonstrated that the full resolution is not recovered by the resolution recovery technique implemented in MAP in very small objects. This fact was also indicated in Ref. 5 and is shown here as well with a more recent scanner capable of higher resolution. We observed that the recovery coefficients were higher (closer to 100%) with 3D-MAP as compared to 2D-FBP and 2D-OSEM but not 100% for the very small objects. MAP was found to be accurate for high contrast objects (10:1) that are larger than 3 mm in diameter. The resolution recovery algorithm does not recover completely the loss of resolution from the crystal size, photon noncollinearity, and intercrystal scatter for such small size objects. The precision estimates reported here were obtained by dividing a single list-mode file into a number of frames of equal duration. This technique is not identical to repeating the experiments multiple times as the phantom is not repositioned in between each scan as was done in Ref. 15. Therefore, the more realistic reproducibility can be expected to be lower. However, the intent of the study was to focus on the reproducibility from statistical origin and not on counting error due to varying local sensitivity arising from slight difference in positioning of the phantom. Both Figs. 45 show that the activity ratio or contrast recovery is less accurate for the smaller spheres and less reproducible for lower count situations though the same number of MAP iterations was required to achieve a stable contrast value independent of the counting statistics as depicted in Fig. 5.

For noisy data, such as in frames of very short duration, a small positive bias exists in MAP reconstruction possibly due to the non-negativity constraint of the algorithm. However, this occurs in situations where the count density is extremely low, rarely encountered in practice. For example, in Fig. 4, we showed a bias for counts density lower than 0.03 × 10⁶ counts/ml for the smallest sphere. This number of events would be acquired in 0.86 s for an injection of 17.5 MBq (0.5 mCi) in a 20 g mouse with assumptions such as a camera sensitivity of 4% and a uniform activity distribution.

The decay experiment using the phantom with spheres (Fig. 6) and the dynamic heart phantom (Fig. 8) showed that MAP and FBP performed equally well at measuring the half-life of the nuclides. This indicates that the hot lesion quantification obtained from MAP reconstruction is accurate over a wide range of activity level. Figs. 3a, 3b also indicated similar spatial resolution with MAP for sources located at 0 and 8 mm central offset positions. This indicates that myocardium recovery and spill-over fractions to be independent of the heart position in the field of view. This is not to be expected with 2D-FBP or 2D-OSEM. The ¹⁸F-FDG dynamic study in the mouse heart showed a small spill-over from the myocardium into the left ventricle at late time points. Reasonable agreement between manual blood sampling and the MAP reconstructions with cardiac gating (diastole) was observed (i.e., within ∼15% in average for the late time-frames). All other reconstructions led to larger contamination due to spill-over from the myocardium into the left ventricle. ¹⁸F-FDG accumulates substantially into the myocardium even in fasted mice; therefore, this compound represents an extreme case of large signal in the myocardium for a correspondingly weak signal in the blood. Other tracers might not have such a high myocardial uptake; as a result, an ROI over the left ventricle may be able to accurately predict the blood input function. In addition, the agreement between the early time points and blood sampling is poor due to limitations in the manual blood sampling which needs to be fast and due to diffusion in the tube required for sampling. The limitation of the manual sampling has been recognized before^{36, 28} and has been a motivation for the development of imaged based techniques^{27, 37, 38, 28} or automated blood sampling apparatus.^{26, 39, 40}

The above reconstruction used the 3D-MAP iterative algorithm where each frame was independently reconstructed. Novel 4D algorithms promise to reduce the noise in the evaluation of kinetic parameters by imposing a constraint to ensure the time evolution of the pixel intensity is smooth. These should not have an impact on the accuracy of the activity concentration estimate over long frames but may have an impact for frames of short duration such as in a dynamic sequence. The data shown here for the phantom experiments revealed that accurate decay constants were obtained. The application of 4D PET algorithm might have consequence on the errors relative to these estimates. Kinetic compartment modeling is plagued by large uncertainty especially when the data are noisy. Therefore, 4D PET will be likely to help in providing kinetics parameters of higher precision.

For the specific conditions examined in this work which is on the recovery of activity of hot lesion compared to the background counts, MAP has been demonstrated to be quantitative in small animal PET imaging; however, in the case of cold regions surrounded by warm background, the results might be different; e.g., more MAP iterations might be required to reach a stable cold contrast, and the performance of the cold contrast recovery might be worse than that of the hot contrast.

CONCLUSIONS

This study examined the spatial resolution and count recovery of warm lesions for the MAP algorithm on the microPET scanners and compares to generally adopted algorithms. Although the MAP algorithm does not completely recover the loss of spatial resolution, the images are quantitative in the sense that the average value of activity are correctly reconstructed without bias apart from the expected residual partial volume effect. MAP reconstruction seems to be at least as quantitative as FBP but with higher recovery coefficients and lower spill-over fraction in small objects over a wide range of count statistics. The recovery of the loss of spatial resolution is not complete and small objects are still affected by the partial volume effects. A small positive bias was observed at very low count density, but this bias was small as compared to the statistical fluctuations observed in repeated experiments.