Robust optimization of intensity modulated proton therapy

Abstract

Purpose: Intensity modulated proton therapy (IMPT) is highly sensitive to range uncertainties and uncertainties caused by setup variation. The conventional inverse treatment planning of IMPT optimized based on the planning target volume (PTV) is not often sufficient to ensure robustness of treatment plans. In this paper, a method that takes the uncertainties into account during plan optimization is used to mitigate the influence of uncertainties in IMPT.

Methods: The authors use the so-called “worst-case robust optimization” to render IMPT plans robust in the face of uncertainties. For each iteration, nine different dose distributions are computed—one each for ± setup uncertainties along anteroposterior (A-P), lateral (R-L) and superior–inferior (S-I) directions, for ± range uncertainty, and the nominal dose distribution. The worst-case dose distribution is obtained by assigning the lowest dose among the nine doses to each voxel in the clinical target volume (CTV) and the highest dose to each voxel outside the CTV. Conceptually, the use of worst-case dose distribution is similar to the dose distribution achieved based on the use of PTV in traditional planning. The objective function value for a given iteration is computed using this worst-case dose distribution. The objective function used has been extended to further constrain the target dose inhomogeneity.

Results: The worst-case robust optimization method is applied to a lung case, a skull base case, and a prostate case. Compared with IMPT plans optimized using conventional methods based on the PTV, our method yields plans that are considerably less sensitive to range and setup uncertainties. An interesting finding of the work presented here is that, in addition to reducing sensitivity to uncertainties, robust optimization also leads to improved optimality of treatment plans compared to the PTV-based optimization. This is reflected in reduction in plan scores and in the lower normal tissue doses for the same coverage of the target volume when subjected to uncertainties.

Conclusions: The authors find that the worst-case robust optimization provides robust target coverage without sacrificing, and possibly even improving, the sparing of normal tissues. Our results demonstrate the importance of robust optimization. The authors assert that all IMPT plans should be robustly optimized.

INTRODUCTION

Intensity modulated proton therapy (IMPT) is a powerful tool to design and efficiently deliver highly conformal and homogeneous dose distributions to the target, while at the same time sparing the adjacent organs at risk (OARs) to a greater degree compared to either intensity modulated x-ray therapy (IMRT) or passively scattered proton therapy (PSPT).^{1, 2} This is made possible due primarily to the flexibility of arbitrarily setting nonuniform intensities of “beamlets” of a sequence of energies of multiple beams incident from different directions. A beamlet in our terminology is a thin scanning pencil beam of protons entering and exiting from the nozzle and incident on the patient. The largest fraction of the dose due to each beamlet is deposited around its terminal end in a region called the “spot.” In this paper, we will use the term spot and beamlet interchangeably.

The intensity distributions for each of a group of beams are derived using standard inverse treatment planning techniques that optimize an objective function with respect to the intensities of individual beamlets. Various strategies have been proposed for designing IMPT plans.³ The two most prominent ones are (1) the single field uniform dose method and (2) 3D intensity modulation. In the former, intensities of beamlets of each beam are optimized individually without considering other beams, with the objective of producing, per beam, uniform dose distribution within the target volume, and minimum dose outside. We call this method “single field optimized” IMPT, or SFO-IMPT. [SFO is often referred to as single field uniform dose (SFUD) optimization.] In the latter, intensities of all beams are optimized simultaneously to balance the dose and dose-volume objectives of normal tissues and the target volumes. We call this method “multifield optimized” IMPT, or MFO-IMPT, and it is the proton spot scanning equivalent of IMRT. For obvious reasons, it has the greatest flexibility to produce optimum dose distribution patterns, especially for complex anatomic geometries. The work reported in this publication is focused on the MFO-IMPT. For brevity, we will use the term IMPT to refer to MFO-IMPT in the remainder of the document unless otherwise necessary for clarity.

The effectiveness of IMPT may be greatly diminished by range and patient setup uncertainties.^{4, 5, 6, 7, 8, 9, 10} Range uncertainties arise from multiple sources, such as CT number uncertainties, tumor shrinkage, patient weight gain or loss, and conversion from CT numbers to stopping powers. Appreciable degradation of the delivered dose distributions may also occur from setup uncertainties due to the misalignment of incident beams and the patient anatomy and due to the realignment of internal heterogeneities among themselves and with respect to the target volume. Intrafractional organ motion, e.g., in the proton therapy of lung cancer, may also cause significant changes in patient geometry¹¹ and consequently to dose distributions. These uncertainties mean that the delivered IMPT dose distribution may be quite different from what is seen on the treatment plan, may be of questionable reliability and may lead to unforeseen outcomes.

For MFO-IMPT, the intensities of spots placed in the target volume and the corresponding dose distributions per beam are, in general, highly inhomogeneous. In many situations, beamlets from a given beam direction may not even reach the distal edge of the target. Inhomogeneous dose distributions within the target for individual beams are compensated for by dose deposited by beamlets from other directions. Therefore, the uncertainties in range may lead to either overshooting, i.e., beamlets producing hot spots in the target volume, or undershooting, i.e., beamlets producing cold spots. This makes IMPT even more sensitive to uncertainties.⁴

In conventional photon radiotherapy (3D conformal or IMRT), setup uncertainties are handled by adding margins around the clinical target volume (CTV) to form a planning target volume (PTV). The PTV margin is chosen with the implicit assumption that the CTV will remain covered with the prescribed isodose surface with high probability (e.g., 95%) in the presence of uncertainties. This is a good assumption for photons since, as pointed out by Meleike et al.,¹² the spatial nature of photon dose distributions is minimally perturbed by uncertainties. In other words, a photon dose distribution is relatively robust in the face of uncertainties. Meleike et al. have used the term “static dose cloud” to describe a photon dose distribution.

For proton therapy, dose distributions are affected significantly by various factors mentioned above,^{1, 11, 13, 14} which significantly perturb dose distributions not only distally and proximally from the target volume but also within it and, as a result, affect the robustness of proton dose distributions. Presence of complex heterogeneities in the path of protons could further exacerbate the perturbation of dose distributions. The traditional concept of PTV with setup uncertainty-based expansion of the CTV is not applicable to proton therapy. Proton dose distributions are not appreciably affected by rigid body shifts along the beam direction, but they are affected by lateral shifts and by anatomic variations. For PSPT, an effective method to reduce the impact of uncertainties, especially for relatively homogeneous anatomies (e.g., prostate), is the use of appropriate beam-specific distal and proximal margins (coupled with smearing of range compensators). The lateral margins used are the same as those for defining the traditional PTV for photon therapy. It is commonly assumed that the same practice is appropriate for SFO-IMPT, although there is no equivalent of smearing in SFO. However, because of the arbitrarily irregular beamlet intensity distributions within the target volumes for MFO-IMPT, the practice of assigning beam-specific distal and proximal margins is not meaningful.

In the absence of a suitable method to account for uncertainties, the current, though unsatisfactory, practice of MFO-IMPT has been to expand the CTV into traditional PTV (Ref. ¹⁵). In the context of this approximation, it is assumed that anatomic changes and tumor motion have a negligible impact on the dose distribution in space.⁸ The resulting dose distributions may be significantly deficient in robustness, i.e., the dose distribution actually delivered may be quite different from what is planned.⁴ This lack of robustness leads to a lack of confidence in the dose distributions seen on the MFO-IMPT plans even though they are often the best that can be achieved with proton therapy. Concern about robustness has been an impediment in the broader clinical use of MFO-IMPT. Therefore, the development of suitable methods to improve robustness (i.e., robust optimization) is vital to exploit the full potential of this important modality.

There are several published reports on robust optimization of MFO-IMPT. Probabilistic and robust linear programming approaches have been proposed for both an idealized two-dimensional geometry to account for range uncertainties⁹ and a clinical paraspinal case to account for both range and setup uncertainties.⁸ Similarly, a robust optimization approach based on the so-called “worst-case dose distribution” (described in Sec. 2) was applied in a clinical case (for a tumor near the spinal cord) by Pflugfelder et al.⁷ Most recently, Fredriksson et al.¹⁶ have reported a study using “minimax” optimization to incorporate range and setup uncertainties in IMPT. In order to make the optimization process tractable for clinically relevant cases, a nonlinear constrained program is used in their implementation. Their implementation is computationally demanding and requires an optimization solver that can deal with nonlinear constraints. The resulting treatment plans showed reduced sensitivity to uncertainties.

In this report, we have used an approach similar to the one used by Pflugfelder et al.⁷ A modification of the objective function to penalize hot spots within the target, which could potentially occur due to range uncertainties, leads to improved target dose homogeneity. We have applied this method to a number of clinical cases and demonstrate that it leads to MFO-IMPT dose distributions that are considerably less sensitive to setup and range uncertainties than the traditional PTV-based optimization. Only one illustrative case each of nonsmall cell lung cancer (NSCLC), base-of-skull (BOS), and prostate cancer are presented in this paper. An important finding of our work is that robust optimization may also result in improved quality of plans in terms of greater sparing of normal tissues and more homogeneous target dose distributions. It is important to recognize that, since robust optimization and PTV-based optimization (or other traditional methods) incorporate uncertainties differently, comparison of results must utilize plans that incorporate uncertainties in the same manner.

We should mention that MFO-IMPT, in particular robust optimization, is highly CPU time and memory intensive. To achieve acceptable optimization time and to meet memory requirements, we parallelized computations in the beamlet domain using memory-distributed parallelization on a large multiprocessor system. A compressed sparse matrix format is used to save the memory usage for every processor. Work on improving the storage and computational efficiency is continuing and will be reported in a separate publication.

The remainder of the paper is organized as follows. In Sec. 2, we introduce the worst-case robust optimization algorithm, patient data, beam configurations, and robustness quantification technique. In Sec. 3, we describe application of robust optimization to three clinical cases to demonstrate the efficacy of the method. Interpretation of results and the discussion of principles explaining our observations, including improved OAR sparing achieved by robust optimization compared to the PTV approach are given in Sec. 4. Finally, we conclude in Sec. 5.

METHODS

The focus of this work is to evaluate the effectiveness of an approach to robust optimization of MFO-IMPT by comparing its results for a set of clinical cases with the optimization using the traditional “PTV-based” approach.

Worst-case robust optimization algorithm

In the following description of our method, the intensity, i.e., weight, of beamlet j is denoted by the non-negative quantity ${\omega }_j^2$. Thus, the constrained optimization problem with respect to weights is turned into an unconstrained one of optimizing the square root of the beamlet weights instead of optimizing the beamlet weight directly. The weight array ${\omega }_j^2$ (or the intensity map) is optimized by minimizing the objective function.

For the PTV-based MFO-IMPT optimization, we used the standard quadratic objective function employed commonly for conventional IMRT planning.^{17, 18, 19} The PTV-based optimizations do not consider range uncertainties. It considers setup uncertainties implicitly as they are incorporated into the PTV definition but ignores the perturbation of dose distributions caused by them. As is done conventionally for IMRT planning, the PTV-based method optimizes dose distribution in the PTV taking into consideration normal tissue constraints. The objective function used is given by

$$\begin{array}{c}{F}_{\mathrm{PTV}}({\omega }_j)=\sum _{i\in \mathrm{PTV}}{p}_{\mathrm{PTV}}{(D_i-D_{0,\mathrm{PTV}})}^2\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}+\sum _{i\in \mathrm{OARs}}{p}_{\mathrm{OARs}}H(D_i-D_{0,\mathrm{OARs}}){(D_i-D_{0,\mathrm{OARs}})}^2,\end{array}$$ (1)

where p terms denote the penalty weights of the corresponding terms and $D_0$ terms are the prescribed doses or constraints for the corresponding organs. The Heavyside function $H(D_i-D_0)$ is defined conventionally, i.e., it is unity if $D_i>D_0$ but zero if $D_i\le D_0$. The dose $D_i$ at the voxel i can be calculated as $D_i=\sum _j{k}_{i,j}{\omega }_j^2$, where the influence matrix (or the dose deposition coefficient) $k_{i,j}$ is calculated using an in-house dose calculation engine for proton pencil beams of a finite size.^{20, 21} In our current study, we used only dose constraints, which were adjusted by trial and error to meet the dose-volume constraints used in our clinic. Dose-volume constraints may be incorporated using the method described by Wu and Mohan,¹⁸ which we plan to do in our future studies.

As may be obvious, the definition of PTV for photons is intended to effectively make photon dose distributions in the CTV robust in the face of uncertainties. During the course of treatment the CTV is expected to reside within the PTV. The PTV dose distribution and dose-volume histogram represents the “worst that can happen” to the CTV. The same does not hold for protons in part because of range uncertainties and in part because of the fact that proton dose distributions are perturbed by uncertainties.²² However, a corresponding “worst-case” dose distribution, the PTV dose distribution analog for protons, can be defined. Furthermore, MFO-IMPT can be optimized based on worst-case dose distribution, the results of which will ostensibly be robust in the face of uncertainties.

Following the strategy published by Lomax,²³ a simple worst-case dose distribution may be computed as follows: For the same beam arrangement, the nominal dose distribution (i.e., without consideration of uncertainties) and dose distributions incorporating (1) setup uncertainties by shifting the patient’s CT image, and (2) range uncertainty by scaling the nominal beamlet ranges by +/− range uncertainty (e.g., 3.5%) are computed. For incorporating setup uncertainties, the isocenter of patients is shifted along anteroposterior (A-P), superior–inferior (S-I), and lateral (R-L) directions yielding six dose distributions and the corresponding influence matrices. For range uncertainties, stopping power ratios are modified by −3.5% and 3.5% to generate two additional influence matrices, corresponding to maximum and minimum proton ranges respectively. The worst-case dose distribution is then represented by the minimum of the nine doses in each voxel in the CTV and the maximum of the nine doses in each voxel outside the CTV. Note the use of CTV for the worst-case dose distribution calculations instead of the PTV. The worst-case dose distribution is not physical but it serves as a lower bound for the worst possible treatment plan.⁷

For robust optimization, an objective function $F_{\mathit{Robust}}({\omega }_j)$ similar to the one in expression (1) is used

$$\begin{array}{c}{F}_{\mathrm{Robust}}({\omega }_j)=\sum _{i\in \mathrm{CTV}}{p}_{\mathrm{CTV},\min }{(D_{i,\min }-D_{0,\mathrm{CTV}})}^2\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}+\sum _{i\in \mathrm{OARs}}{p}_{\mathrm{OARs}}H(D_{i,\max }-D_{0,\mathrm{OARs}})\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}\times {(D_{i,\max }-D_{0,\mathrm{OARs}})}^2.\end{array}$$ (2a)

Note again that in robust optimization, the optimization target is the CTV. The terms $D_{i,\min }=\underset{m}{\min }(D_i^m)$ and $D_{i,\max }=\underset{m}{\max }(D_i^m)$ indicate the minimum and maximum dose among m (=9) possible doses $D_i^m$ in voxel i, which are calculated using $D_i^m=\sum _j{k}_{i,j}^m{\omega }_j^2$ in each iteration. The m influence matrices $k_{i,j}^m$, incorporating range and setup uncertainties, are precalculated. Pflugfelder et al.⁷ used the same worst-case dose distribution concept in their robust optimization implementation and demonstrated that it led to plans with reduced sensitivity to uncertainties. However, uncertainties may lead to hot spots (e.g., due to beamlet range overshoot) in the target, which may not be adequately controlled by the objective function (2a). While hot spots may be acceptable for some tumor sites (e.g., small tumors of the lung and brain), in general they are considered undesirable. To minimize such hot spots, we have introduced another term in the objective function

$$\begin{array}{c}{F}_{\mathrm{Robust}}({\omega }_j)=\sum _{i\in \mathrm{CTV}}{p}_{\mathrm{CTV},\min }{(D_{i,\min }-D_{0,\mathrm{CTV}})}^2\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}+\sum _{i\in \mathrm{CTV}}{p}_{\mathrm{CTV},\max }{(D_{i,\max }-D_{0,\mathrm{CTV}})}^2\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}+\sum _{i\in \mathrm{OARs}}{p}_{\mathrm{OARs}}H(D_{i,\max }-D_{0,\mathrm{OARs}})\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}\times {(D_{i,\max }-D_{0,\mathrm{OARs}})}^2.\end{array}$$ (2b)

One could argue that the first term in this expression constrains both hot and cold spots as is the case in conventional optimization. In robust optimization using worst-case dose distribution, it affects only the minimum in each target voxel. The second term is necessary in order to constrain the maximum dose in each target voxel.

As with some other methods of robust optimization,^{7, 8, 16} our method considers both range and setup uncertainties. An assumption implicit in the worst-case optimization method is that each uncertainty affects dose distribution independently. In reality, the dose distributions may be affected simultaneously by multiple changes in position and range. Second, the computation of worst-case dose distributions employing the maximum values of the setup and range changes assumes that these occur by the same magnitude for every fraction. In reality, there is a distribution of setup variations. Both of these assumptions lead to results that may be conservative in terms of target coverage and normal tissue sparing. However, they are consistent with the use of PTV in photons.

Patient data

We applied our robust optimization method to three clinical cases: one lung (stage III B nonsmall cell lung cancer), one BOS (clivus chordoma), and one prostate (adenocarcinoma) (Table TABLE I.). For the lung case, three beams in the transverse plane at gantry angles of 180°, 230°, and 320° were used. Setup uncertainties of ±5 mm and range uncertainty of ±3.5% of the beams’ nominal ranges were assumed (Table TABLE I.). For the BOS case, two beams in the transverse plane at gantry angles of 75° and 270° and one beam at gantry angle of 300° and couch angle of 90° were used. The setup and range uncertainties were assumed to be ±3 mm and ±3.5% respectively (Table TABLE I.). For the prostate case, two beams in the transverse plane at gantry angles of 90° and 270° (parallel-opposed fields) were used. Setup uncertainties of ±5 mm and range uncertainty of ±3.5% of the beams’ nominal ranges were assumed (Table TABLE I.). The dose grid resolutions for the three cases were 2.5, 2.5, and 1.0 mm, respectively.

TABLE I.

Margins used for PTV-based and robust optimization.

Case	Optimization method	PTV and lateral margins (mm)	Range uncertainty (field-specific) (mm)
Lung	PTV-based	5	N/A
	Robust	5	5.1
			8.1
			5.7
Base-of-skull	PTV-based	3	N/A
	Robust	3	8.9
			7.8
			8.6
Prostate	PTV-based	5	N/A
	Robust	5	8.0
			8.1

For PTV-based optimization, in general, the CTV-to-PTV margins are the same as those used for conventional IMRT planning. For robust optimization, there is no CTV-to-PTV margin; however, as explained above, the dose distributions are calculated by shifting the beam configuration through setup uncertainties and changing the ranges.

For both PTV-based and robust optimization, a margin for “penumbra” is added to allow for the lateral fall-off of dose. CTV-to-PTV margin is only for uncertainties. In the design of treatment plans, an additional margin is assigned for penumbra to ensure that the PTV is covered with the prescribed dose (or to an acceptable level, e.g., 95% of the prescribed dose). For IMRT or IMPT, this margin is usually smaller than the margin that would be required for 3D photon or proton treatments. This is due to the fact that intensity modulation has the ability to increase the fluence in the boundary regions to sharpen the penumbra. IMRT and IMPT penumbra margins are determined empirically and can be functions of number of beams and tumor characteristics.

Based on the requirements and characteristics of our scanning beams, which use the discrete spot scanning mechanism to deliver IMPT, spots are placed uniformly within the margin for the penumbra at selected spacing. IMPT is delivered energy-layer-by-energy-layer. The number of energy layers, selected from a discrete set characteristic of our delivery system, depends on the depth and the dimension of the target along the beam path.

Table TABLE II. shows the spot scanning characteristics of each of the beams used for each example shown in this paper. The penumbra margin is selected based on the average energy, which determines the size of the spot at the surface of the patient and at depth. The σ of the incident spot in our system varies from approximately 5 mm for the highest energy (222 MeV) to approximately 12 mm for the lowest (72 MeV). The spot size increases further in the medium to approximately 8 mm for the highest energy and to 13 mm for the lowest energy. For the BOS case, a bolus of approximately 10 cm was used to reduce spot size and the number of energy layers. This should explain the larger range uncertainties in Table TABLE I. and the higher energies and relatively small number of energy layers in Table TABLE II. for the BOS.

TABLE II.

Beam parameters used in the optimization of IMPT plans.

Lung	Penumbra margin (cm)	Energy range (MeV)	Number of layers	Spot spacing (cm)
Field 1	0.6	84.7–146.9	49	0.5
Field 2	0.6	94.2–188.2	55
Field 3	0.6	88.8–155.3	48
Base-of-skull
Field 1	0.5	168.8–201.0a	14	0.5
Field 2	0.5	148.8–183.4a	16
Field 3	0.5	155.3–195.6a	18
Prostate
Field 1	1.2	148.8–190.5	19	0.5
Field 2	1.2	148.8–190.5	19

^aFor the base-of-skull case, a bolus with water equivalence thickness of approximately 10 cm is used to reduce spot size and the number of energy layers.

Robustness evaluation

It should be pointed out that the nominal dose distributions (i.e., without consideration of any uncertainties) from the PTV-based optimized IMPT plans do not reflect the dose distributions actually realized in the face of uncertainties. To a considerably lesser degree, the same may be true of the robustly optimized plan. Therefore, to compare the results of PTV-based optimization and robust optimization, the uncertainties must be incorporated into dose distributions, which mean that the worst-case dose distributions must be computed for both types of plans. We term this process robustness evaluation.

RESULTS

In this section, three cases (one each of stage III NSCLC, clivus chordoma and a cancer of the prostate) are selected to illustrate our method. Plans were optimized using both the PTV-based and robust approaches. To intercompare the results of the two methods, robustness was quantified by computing worst-case dose distribution for each approach. In addition, families of DVHs for each uncertainty (e.g., setup, range) for all structures of interest were displayed along with the nominal DVHs (i.e., without consideration for uncertainties). The “bands” of DVHs are an effective means to illustrate the sensitivity to uncertainty²⁴—the wider the band, the greater the sensitivity.

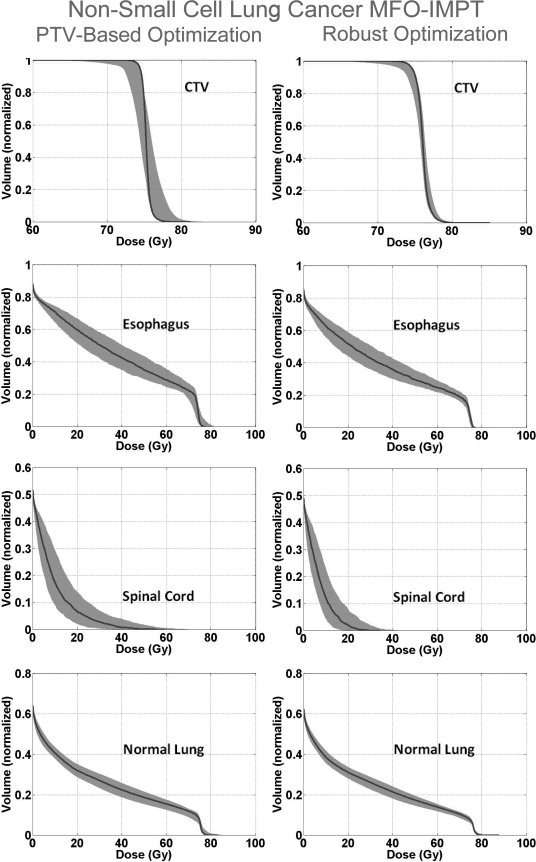
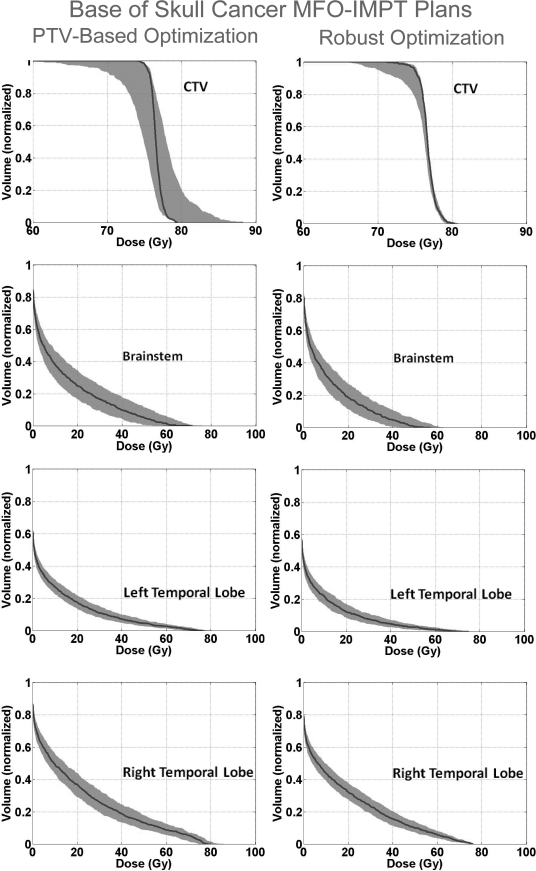
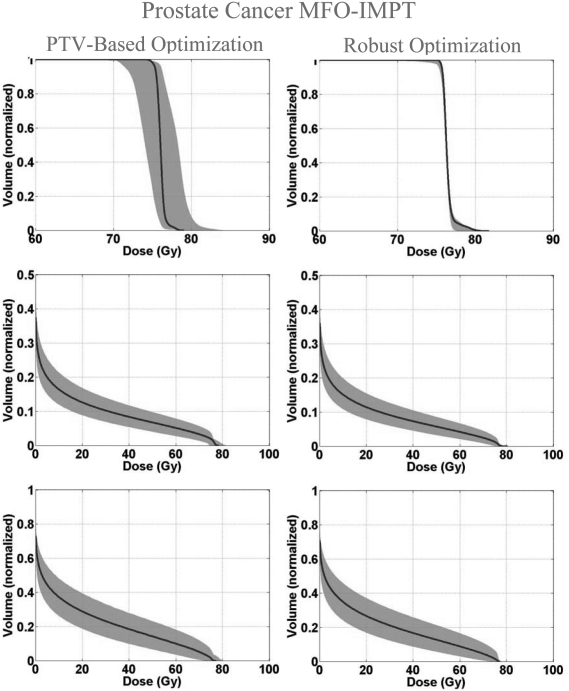
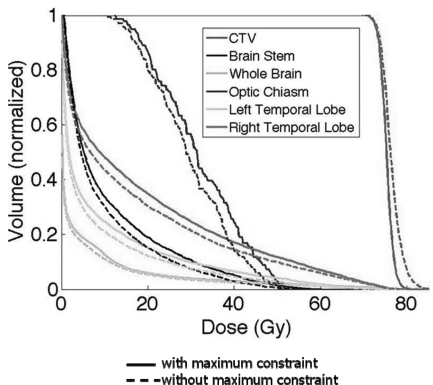
Figure 1 shows the DVH bands of the CTV, normal lung, esophagus, and spinal cord for the lung case; Fig. 2 shows the DVH bands of the CTV, brainstem, right temporal lobe, and left temporal lobe for the BOS case and Fig. 3 shows the DVH bands of the CTV, bladder, and rectum for the prostate case. The PTV-based plan and robustly optimized plan were optimized using the same dose constraints, the same penalties, and the same initial conditions. The dose constraints and penalties used in the robust optimization and robustness evaluation are listed in Table TABLE IV.. For fair comparison, we renormalized plans for the lung and BOS cases to have at least 98% of CTV covered by the prescription dose (74 Gy) in the nominal dose distribution and changed other dose distributions accordingly. It is apparent that the CTV DVH bands are narrower for the robustly optimized plans than for the PTV-based plans, indicating the reduced sensitivity of the former to setup and range uncertainties, which is exactly what the goal of robust optimization is. In addition, we notice that the falloff of the CTV DVH bands is steeper, and the maximum dose is lower for the robustly optimized plan. This is presumably the consequence of the additional term in Eq. 2b to limit the maximum dose in each target voxel, which promotes greater target dose homogeneity. This is further illustrated in Fig. 4, which compares DVHs of the nominal dose distributions with and without constraints on the maximum target voxel doses for the robust optimization for the BOS case. The optimizer allowed higher doses in the target volume to achieve better normal tissue protection. The homogeneity index (HI) is degraded from 9.9% to 14.9% without the maximum dose constraint. The HI is defined as the difference between the dose to 1% CTV volume and the dose to 99% CTV volume, divided by the prescription dose (74 Gy).

Figure 1.

Color wash represents the DVH bands for dose distributions covering all setup and proton range uncertainties for CTV and various organs for the robustly optimized plan (right column) and the PTV-based plan (left) for the NSCLC case. The solid lines are the DVHs for the nominal dose distribution (i.e., without consideration of uncertainties). The narrowness of CTV band for the robustly optimized plan indicates improved robustness. At the same time, the sparing for the esophagus, spinal cord, and normal lung is perceptibly improved.

Figure 2.

DVH bands for dose distributions covering all setup and proton range uncertainties for CTV and various organs for the robustly optimized plan (right column) and the PTV-based plan (left) for the base-of-skull case. As for the lung case, the solid lines are DVHs for the nominal dose distribution, and it is apparent that the CTV coverage for the robustly optimized plans is less sensitive to uncertainties and the normal tissue sparing is improved.

Figure 3.

DVH bands for dose distributions for the prostate case with the solid lines indicating the nominal dose distribution. Robustness of prosate dose distribution and the sparing of the bladder and rectum are improved.

TABLE IV.

Penalty terms p and dose constraints D₀ (Gy) used in robust optimization [Eq. 2b] and robustness evaluation [Eqs. 3a, 3b].

Lung	TARGET constraint (min)	TARGET constraint (max)	Heart constraint	Cord constraint	Esophagus constraint	Normal lung constraint
p	1.0 × 105	1.5 × 105	8.0 × 102	6.0 × 103	8.0 × 102	8.0 × 102
D0(Gy)	74	74	10	0	35	35

Base-of-skull	TARGET constraint (min)	TARGET constraint (max)	Optical chiasm constraint	Brain–CTV constraint	Brainstem constraint	R temporal lobe constraint	L temporal lobe constraint	Whole brain constraint
p	2.0 × 105	2.0 × 105	8.0 × 102	2.0 × 103	1.0 × 104	2.0 × 103	8.0 × 103	3.0 × 103
D0(Gy)	74	74	0	0	10	0	10	0

Prostate	TARGET constraint (min)	TARGET constraint (max)	Bladder constraint	Rectum constraint	Femoral heads constraint
p	1.0 × 105	1.0 × 105	8.0 × 102	8.0 × 102	8.0 × 102
D0(Gy)	76	76	40	40	5

Figure 4.

Comparison of base-of-skull case CTV, brainstem, whole brain, optic chiasm, left temporal lobe, and right temporal lobe DVHs for the robustly optimized plan with constraint on the maximum dose in each target voxel [solid lines, Eq. 2b] vs without maximum dose constraint [dashed lines, Eq. 2a]. The constraint makes CTV dose distribution more homogenous but at the cost of reduced normal tissue sparing.

An interesting, and perhaps counterintuitive, finding is that for both lung and BOS cases, sparing of normal tissues is improved. One might expect that the robust optimization would lead to treatment plans that reduce uncertainty to the dose distribution in the CTV but at the cost of reduced normal tissue sparing. An explanation of this observation is given in the Sec. 4.

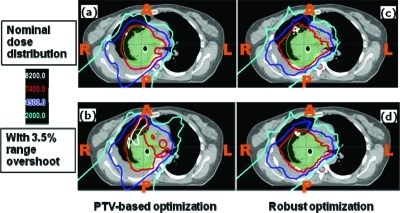
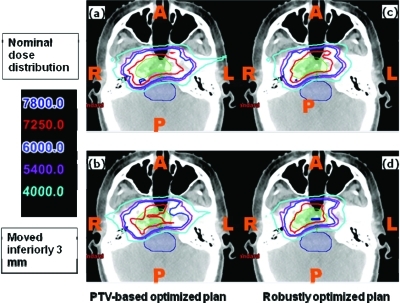
Figures 56 show the transverse dose distributions for the lung and BOS cases respectively. Panels (a) and (b) are for the PTV-based plans and panels (c) and (d) are for the robustly optimized plans. For the lung case, panels (a) and (c) are for the nominal plans (i.e., without any uncertainties considered), whereas in panels (b) and (d) the range uncertainty (3.5% range overshoot) has been applied to all beams. It is clear that the dose distribution in the robustly optimized plan is essentially unaffected compared to the PTV-based plan (note the red 74 and cyan 20 Gy (RBE) isodose lines). For the BOS case, the patient is moved inferiorly by 3 mm. The shift affects the PTV-based plan to a significantly greater degree than the robustly optimized plan.

Figure 5.

Dose distributions in the transverse plane for the lung case illustrating that robustly optimized plan is relatively insensitive to range uncertainty. Left panels: PTV-based plans. Right panels: robustly optimized plans. Top row: with nominal range. Bottom row: with 3.5% higher range. CTV: green color wash; spinal cord: purple color wash.

Figure 6.

Dose distributions in the transverse plane for the base-of-skull case illustrating that robustly optimized plan is relatively insensitive to set-up uncertainty. Left panels: PTV-based plans. Right panels: robustly optimized plans. Top row: nominal position. Bottom row: with patient shifted inferiorly by 3 mm. CTV: green color wash; brainstem: purple color wash.

Figure 7 shows the transverse dose distributions for the prostate case. Panel (a) is the PTV-based plan whereas panel (b) is the robustly optimized plan. It is apparent that the prescription isodose surface covers a larger volume in the former. In spite of smaller volume enclosed within the prescription dose surface in the robustly optimized plan, the CTV remains appropriately covered in the face of set-up uncertainties as illustrated in panel (c), where the patient is moved posteriorly by 5 mm; in (d), where the patient is moved to the right by 5 mm; and in (e), where beam ranges are decreased by 3.5%. Panel (c), (d), and (e) are all for the robustly optimized plan. Thus, the robust optimization algorithm makes the “effective” safety margin as small as necessary to account for uncertainties around the CTV while ensuring adequate coverage.

Figure 7.

Panel (a) is the nominal dose distribution for the PTV-based prostate plan. The remaining panels are the dose distributions for the robustly optimized plan: (b) nominal, (c) with patient shifted posteriorly by 5 mm, (d) shifted to the right by 5 mm, and (e) with beam range decreased by 3.5%. Red is the prescription isodose contour lines (76 Gy), green line is the PTV and blue line is the CTV. Letters O and O’ indicate original and shifted positions of the isocenter. Comparison of panel (a) with other panels illustrates that the prescription isodose surface encloses a larger volume for the PTV-based optimization vs robust optimization. At the same time, the CTV remains covered with the prescription dose in the face of uncertainties.

Table TABLE III. compares total scores (values of objective function) and subscores of individual structures of the worst-case dose distributions derived from the PTV-based and robustly optimized plans. The subscores for the target (CTV/GTV) are calculated using

$$\begin{array}{c}{\mathrm{Score}}_{\mathrm{TARGET}}=\sum _{i\in \mathrm{TARGET}}{p}_{\mathrm{TARGET},\min }{(D_{i,\min }-D_{0,\mathrm{TARGET}})}^2\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}+\sum _{i\in \mathrm{TARGET}}{p}_{\mathrm{TARGET},\max }{(D_{i,\max }-D_{0,\mathrm{TARGET}})}^2,\end{array}$$ (3a)

while the subscores for the OARs are calculated using

$${\mathrm{Score}}_{\mathrm{OAR}}=\sum _{i\in \mathrm{OAR}}{p}_{\mathrm{OAR}}{(D_{i,\max }-D_{0,\mathrm{OAR}})}^2.$$ (3b)

The total score is the sum of the subscore of the targets and OARs. The scores represent deviation from the individual constraints. If a dose constraint is met, the subs-score would be zero. Values of subscores depend on the values of the penalty parameters and on the number of points in the structure. Therefore, it is meaningful to compare subscores for different optimization methods only for the same structure. The penalty terms p and the dose constraints to the target and OARs are listed in Table TABLE IV.. In all cases the total scores for the robustly optimized plans are lower than the corresponding PTV-based plans. In addition, with the exception of optic chiasm for the BOS case, subscores for CTVs and all normal structures are lower for the robustly optimized plans, further indicating that robust optimization not only makes CTV dose distribution less sensitive to uncertainties but may also lead to improved sparing of normal tissues.

TABLE III.

Comparison of the total score and subscores for individual anatomic structures for the worst-case dose distributions for the PTV-based and robustly optimized plans. The subscores for the target (CTV/GTV) are calculated using Eq. 3a, while the subscores for the OARs are calculated using Eq. 3b. The total score is the sum of the subscore of the targets and OARs. The scores represent deviation from the individual constraints. If a dose constraint is met, the subs-score would be zero. Values of subscores depend on the values of the penalty parameters and on the number of points in the structure. Therefore, it is meaningful to compare subscores for different optimization methods only for the same structure. The penalty terms p and the dose constraints to the target and OARs are listed in Table TABLE IV..

Lung	Total	GTV	CTV	Heart	Cord	Esophagus	Normal lung
PTV-based solution	5.58 × 106	9.45 × 105	2.18 × 106	4.39 × 105	1.29 × 106	4.67 × 105	2.61 × 105
Robust optimization	3.86 × 106	6.47 × 105	1.83 × 106	3.60 × 105	4.15 × 105	3.77 × 105	2.27 × 105

Base-of-skull	Total	CTV	Optical chiasm	Brain-CTV	Brainstem	R temporal lobe	L temporal lobe	Whole brain
PTV-based solution	8.72 × 106	2.35 × 106	1.10 × 106	3.01 × 105	2.84 × 106	1.46 × 106	1.55 × 105	5.14 × 105
Robust optimization solution	7.21 × 106	2.16 × 106	1.16 × 106	2.59 × 105	1.90 × 106	1.18 × 106	1.06 × 105	4.47 × 105

Prostate	Total	CTV	Bladder	Rectum	Femoral heads
PTV-based solution	1.53 × 106	9.04 × 105	9.79 × 104	1.67 × 105	3.61 × 105
Robust optimization	1.07 × 106	5.04 × 105	8.76 × 104	1.57 × 105	3.23 × 105

DISCUSSION

We reiterate that, due to the characteristics of proton dose deposition (e.g., sharp distal fall-off and lateral scattering), proton dose distributions are more sensitive to various forms of uncertainties than photon dose distributions. For passively scattered proton therapy, sensitivity to uncertainties is reduced by the use of such techniques as smearing of compensators and assignment of beam-specific distal and proximal margins. For scanning beam proton therapy using SFO, distal and proximal margins are similarly assigned for range uncertainty, but there is no equivalent of smearing other than the finite spot size. Thus, SFO is more sensitive to uncertainties than PSPT. For multifield, or 3D, optimization, energy and fluence distributions are such that dose distributions per beam within the target may be highly inhomogeneous. Dose contributions due to individual beams are blended in such a way that the sum of all beams results in the desired uniform dose distributions in the target and the best possible compromise in normal tissues. Although MFO dose distributions are (apparently) the best in terms of optimality, they are also predisposed to being perturbed in regions of junctions or overlap and are, therefore, most sensitive to uncertainties.

Rationale of optimization and evaluation of IMPT plans using worst-case dose distributions

Conventional approaches for intensity modulated treatment planning employing PTV cannot explicitly consider the impact of range uncertainty per beamlet or compensate for dose perturbation caused by changes in anatomy and setup. In this paper, we have attempted to demonstrate that, with the incorporation of setup and range uncertainties into the optimization process, one can reduce sensitivity of the resulting treatment plans to uncertainties.

The robust optimization method we have chosen uses the worst-case dose distribution to compute the objective function value in each iteration. Our method is similar to the method used by Pflugfelder et al.⁷ and reinforces their findings with regard to improved robustness of the resulting plans. Additionally, we have modified the worst-case objective function to constrain target dose heterogeneity by limiting the maximum dose in each target voxel.

In general, without appropriate testing, it is not possible to ascertain how robust an arbitrary IMPT plan is. Robustness may depend on multiple factors including optimization algorithm, severity of constraints, the number and directions of beams, etc. However, it is important to reemphasize that, when evaluating and comparing proton dose distributions, it is necessary to build robustness into the plan by incorporating the impact of uncertainties. We achieve this in our work by computing the worst-case dose distributions for the competing plans. This is analogous to the use of PTV for photons, which implicitly represents the worst-case dose distribution for the CTV. The worst-case dose distribution considers setup uncertainty not only for the target but also for normal structures. Additionally, it considers range uncertainty and, more importantly, perturbation of dose distribution. Worst-case dose distributions are also appropriate data to be used when dose distributions are to be added, for instance, when a part of the treatment is delivered with photons and the rest with protons, or when treatment plans from different modalities are to be compared.

It should be mentioned that the method of comparison of robustly and conventionally optimized plans we used is different from those used by many of the other investigators,^{7, 8, 9, 10} who either designed the conventional plans based on CTV and/or compared robustly optimized plans with CTV-based plans. In this work the PTV is chosen as the target for the conventional PTV-based plan, whereas the CTV is chosen as the target for the robustly optimized plan. We then compare the plan quality and robustness of these two plans. However, in the previous work such as that of Pfugfelder et al.,⁷ the CTV is used as the target for both conventional optimization and robust optimization. Then, the plan quality and robustness of the two plans are compared. We believe that the comparison of robustly optimized plan with CTV-based optimized plan is not valid since the latter does not incorporate uncertainties.

The validity of worst-case techniques for plan evaluation and for optimization may be questioned since it corresponds to the maximum extent of uncertainty (more correctly to the uncertainty that covers, say, ∼95% of the distribution). In reality, the actual uncertainty over the course of therapy and over the population of patients is represented by a distribution; and margins used for planning and evaluation are such that, typically, there is a ∼95% probability that the target will remain covered or that normal structures will be spared adequately. The PTV-based planning and plan evaluation for photons similarly assume this maximum extent of uncertainty. For lack of better methods, PTV-based techniques continue to be used in proton plan evaluation and in IMPT optimization; however, their validity is limited.

The concept of PTV for photons and of worst-case dose distributions for both protons and photons may also be justifiable on biological grounds. Underdosing caused by marginal misses or in-field dose perturbations in a small number of fractions may lead to appreciable risk of local failure. The CTV must receive the prescribed dose distribution for all or almost all the fractions.

Optimality of plans and sparing of normal tissues

We have applied our method to multiple clinical cases and included one case each of lung, BOS and prostate in this paper. An interesting general finding is that, with robust optimization, compared to PTV-based optimization, not only is the target dose distribution more robust in the face of uncertainties, but the plan quality, particularly in terms of normal tissue sparing is also improved. This may seem counter-intuitive. There are three possible explanations for this observation.

In robust optimization, the optimizer attempts to compensate for perturbations caused by any of the uncertainties that may lead to deviations in individual voxels from the prescribed dose in the target or in exceeding the limits of normal tissues. This makes the target dose distribution less sensitive to uncertainties and, when observed in the worst-case scenario, to be more homogeneous and with greater normal tissue sparing. On the other hand, in the PTV-based case, the worst-case dose distribution shows underdosing in the target, and renormalization to achieve the required coverage may lead to increase in normal tissue doses.

Another factor may be that in PTV-based optimization, spots are placed in a larger fixed PTV volume, whereas in the worst-case robust optimization, the spots are placed in the CTV, albeit in its multiple instances. This means that, in the latter case, a larger volume of normal tissues is competing against a smaller volume of the target; and since there is considerable degeneracy in the optimization process, the optimizer is likely to achieve the desired CTV coverage at increased normal tissue sparing. While the goal of PTV-based optimization is to assure that the prescribed isodose surface covers the PTV, the robust optimization may lead to a reduced volume of the prescribed isodose surface that still covers the CTV in the face of the uncertainties. This is illustrated for the prostate example in Fig. 7.

An additional point is that robust optimization considers uncertainties for the target as well as for all normal structures, where as the PTV-based optimization considers only the target. If the PTV-based optimization were to incorporate planning volumes at risk (PRVs) also, the competition between the target and organs at risk may also lead to additional sparing for the latter, but probably not to the same extent as for robust optimization.

Limitations of the worst-case approach to robust optimization and robustness evaluation

Just like the use of PTV (and PRVs) for photons, the worst-case approach as described here is a reasonable first step in incorporating uncertainties in proton plan evaluation and optimization. However, it is only an approximate approach. For example, it assumes that interfractional variations are of rigid body type and does not consider deformations and changes in positions of anatomic structures relative to each other. Second, it assumes that each uncertainty can be considered independently of others. In reality, multiple uncertainties can occur simultaneously. For instance, the patient’s position may shift along A-P, H-F, and R-L directions, and range uncertainty may exist simultaneously. It is possible to simultaneously consider all uncertainties by sampling them from distributions, but it would require the computation of a very large number of dose distributions, which may not be practical for routine use. Nevertheless, it would be appropriate in a future study to carry out such computations for a small number of cases to assess the consequences of treating the uncertainties as being independent of each other.

In principle, the methodology described in this paper can also be extended to incorporate uncertainties related to intrafractional respiratory motion. One could include the dose distributions corresponding to maximum inhale and maximum exhale images in the family of dose distributions used to compute worst-case dose distributions. It is important to note, however, that deformations of anatomy caused by respiration would need to be explicitly considered for each of nine dose distributions.

In spite of these limitations, we believe that the method described here is a practical step in the right direction.

CONCLUSIONS

In this paper, we have demonstrated that robust optimization of IMPT plans based on worst-case dose distributions improves robustness and at the same time improves sparing of normal tissues compared to conventional methods of optimization based on PTV. Before comparing dose distributions of different methods, it is, however, essential to incorporate uncertainties in the resulting plans. Our results confirm the findings of other investigators with regard to improved robustness. The addition of this term, along with our optimization approach leads to improvement in sparing of normal tissues in the robustly optimized plan as compared to PTV-based plans. For limitations of space, we have included only illustrative examples in this paper; however, we have conducted a robust optimization study for 20 cancer patients including 9 H&N, 7 lung, and 4 prostate cancer patients. Results andconclusions are consistent with those reported in this paper.

We acknowledge that our worst-case dose distribution approaches used for optimization and evaluation of plans has limitations; however, they are essentially analogous to the use of PTV and PRV in IMRT. More sophisticated approaches are possible but would require further research and considerable increase in computational resources. In such approaches, all uncertainties should be considered simultaneously and sampled from distributions of uncertainties. We expect to carry out these investigations. We also expect to extend our methods to include intrafractional respiratory motion. Inclusion of anatomic deformations and variations in positions of anatomic structures relative to each other in robust optimization is far more challenging and may be of interest in the more distant future.