Linking extinction–colonization dynamics to genetic structure in a salamander metapopulation

Abstract

Theory predicts that founder effects have a primary role in determining metapopulation genetic structure. However, ecological factors that affect extinction–colonization dynamics may also create spatial variation in the strength of genetic drift and migration. We tested the hypothesis that ecological factors underlying extinction–colonization dynamics influenced the genetic structure of a tiger salamander (Ambystoma tigrinum) metapopulation. We used empirical data on metapopulation dynamics to make a priori predictions about the effects of population age and ecological factors on genetic diversity and divergence among 41 populations. Metapopulation dynamics of A. tigrinum depended on wetland area, connectivity and presence of predatory fish. We found that newly colonized populations were more genetically differentiated than established populations, suggesting that founder effects influenced genetic structure. However, ecological drivers of metapopulation dynamics were more important than age in predicting genetic structure. Consistent with demographic predictions from metapopulation theory, genetic diversity and divergence depended on wetland area and connectivity. Divergence was greatest in small, isolated wetlands where genetic diversity was low. Our results show that ecological factors underlying metapopulation dynamics can be key determinants of spatial genetic structure, and that habitat area and isolation may mediate the contributions of drift and migration to divergence and evolution in local populations.

1. Introduction

A major goal of population genetics is to understand the ecological and evolutionary drivers of spatial genetic structure, which can provide insight into the demographic history and evolutionary potential of populations [1,2]. From an evolutionary perspective, the degree of neutral genetic divergence (e.g. F_ST) among populations depends mainly on the relative forces of genetic drift and migration [3,4]. Although genetic drift increases divergence among populations, migration opposes drift by genetically homogenizing populations. Importantly, the strength of genetic drift decreases as population size increases, and migration is related positively to the frequency of dispersal. Thus, environmental factors associated with population size and dispersal should have important roles in shaping both demographic patterns and spatial genetic structure [1,2,5–7].

For species in fragmented landscapes, population size and dispersal can vary substantially among habitat patches, and species may experience frequent extinctions and colonizations within local patches while persisting at a regional scale [8]. In systems with population turnover, spatially realistic metapopulation theory predicts that extinction probability decreases as patch area increases, and colonization probability decreases as patch isolation increases [9,10]. Habitat heterogeneity is also predicted to affect turnover dynamics, both by influencing habitat quality within patches [11–13], and by influencing the likelihood of dispersal among patches [14]. Area, isolation and habitat heterogeneity have been shown to predict turnover dynamics in a wide array of systems [15–19].

Unlike spatially realistic models of metapopulation dynamics, most metapopulation genetic models are spatially implicit and assume that patches are identical with respect to ecological characteristics. Under an island model, metapopulation genetic theory predicts that founder effects associated with patch recolonization play the primary role in creating genetic divergence [20–22]. Specifically, divergence among local populations is predicted to increase as a result of founder effects when the number of colonists arriving at unoccupied patches is similar to the average number of migrants among extant populations, and colonists are derived from a small number of source populations [23]. Empirical studies of some metapopulations have supported these predictions by demonstrating that F_ST among newly colonized populations is greater than F_ST among established populations [24–26] (but see [27–29]).

Although population age (i.e. newly colonized versus established) may predict part of the genetic divergence seen in metapopulations, age alone does not account for spatial and ecological factors driving turnover dynamics, and thus potentially affecting genetic divergence. Patch area, isolation and habitat quality mediate population size and dispersal, thereby producing metapopulation-scale extinction and colonization dynamics [9,11]. Because genetic drift and migration also depend on population size and dispersal, ecological factors related to demographic turnover should affect spatial patterns of genetic divergence and diversity. For example, extinction-prone patches characterized by small area or poor quality may have high rates of genetic drift owing to low population size or recurring founder events, resulting in high divergence. In contrast, patches spatially connected to other patches via dispersal may have high colonization probability and gene flow, leading to low divergence and high diversity. Migration can also counteract drift in small or low-quality sites via rescue effects [22,30,31].

The area-isolation and habitat paradigms have been critical for understanding metapopulation dynamics [13], but these principles are rarely used to understand metapopulation genetic structure. Specifically, there is a lack of empirical studies testing whether known predictors of metapopulation dynamics also predict genetic structure, which has limited our understanding of the ecological mechanisms that shape patterns of genetic divergence and diversity. We hypothesized that the ecological factors underlying metapopulation dynamics of the eastern tiger salamander (Ambystoma tigrinum tigrinum, Ambystomatidae) were also important predictors of genetic structure. Ambystoma tigrinum is a pond-breeding amphibian that prefers breeding in fishless ponds with hydroperiods long enough (greater than 12 weeks) to ensure larval development and metamorphosis. Juveniles become sexually mature within 2 years and are the primary contributors to among-pond dispersal [32].

We evaluated genetic diversity and divergence among 41 breeding wetlands (hereafter referred to as populations) in an A. tigrinum metapopulation in northern Illinois. A 3-year study of metapopulation dynamics indicated that extinction and colonization events are common in this system [33]. To test whether founder effects associated with turnover influenced metapopulation genetic structure, we first evaluated whether F_ST differed between newly colonized and established populations. Next, we tested whether genetic divergence and diversity were related to ecological factors known to affect metapopulation dynamics. Colonization probability is related negatively to fish presence and positively to wetland area and connectivity (the inverse of isolation), whereas extinction probability is related positively to fish presence and negatively to connectivity [33]. Although wetland hydroperiod was not a strong driver of turnover during our study because of above-average precipitation [34], short hydroperiod can lead to low survival and low reproductive success in dry years [32]. These results suggest that genetic drift should be strongest in wetlands with predatory fish, short hydroperiod and low connectivity, whereas immigration should be greatest in fishless wetlands with large area and high connectivity. Thus, we predicted that genetic divergence of populations would increase with fish presence and decrease with wetland area, connectivity and hydroperiod. We also predicted that genetic diversity would be greatest in large, connected wetlands with long hydroperiods and without predatory fish.

2. Material and methods

(a). Study sites and tissue collection

This study was conducted in a 9300 ha area in northern Illinois, USA, centred at the Richardson Wildlife Foundation property (West Brooklyn, IL: 41°42′26.6″ N, 89°11′25.0″ W). The landscape is dominated by row-crop agriculture with fragmented patches of forest, wetland and sand prairie. Marsh ponds and open wetlands with variable hydroperiods make up 0.8 per cent of the landscape. We collected tissue samples from A. tigrinum individuals at 41 wetlands (figure 1), which were part of a study on metapopulation dynamics conducted between 2007 and 2009 [33]. The median wetland area was 0.97 ha (range: 0.07–3.8 ha), and the median Euclidean distance between wetlands was 2861 m (range: 82–8487 m).

Figure 1.

Spatial distribution of 41 wetlands in an Ambystoma tigrinum metapopulation in northern Illinois. Circles and squares represent wetlands where A. tigrinum tissue samples were collected. Populations were classified as newly colonized (circles) or established (squares). Symbol size is proportional to wetland area, and colour gradation represents local F_ST [35].

For tissue collection, minnow traps were used to capture A. tigrinum individuals at wetlands for either three or four consecutive days between May and early August during 2008 and 2009. We collected an average of 18 tissue samples per site (range: 14–27; electronic supplementary material, table S1) from larvae by removing a small (less than 5 mm) piece of the tail. We collected samples from 37 sites in 2008 and 4 sites in 2009. Tissues samples were preserved in 95 per cent ethanol and stored at −80°C before DNA extraction.

(b). Microsatellite amplification and scoring

Total genomic DNA was extracted from tissues using the Qiagen DNeasy Blood and Tissue kit (Qiagen, Inc., Valencia, CA). We genotyped individuals at 13 microsatellite loci developed for other Ambystoma species and subspecies: AcalD001, AcalD021, AcalD031, AcalD032, AcalD088, AcalD098, AcalD108 and AcalB142 [36], AmaD321 [37], AjeD23 and AjeD422 [38], At52.6 [39], and ATS5-7 [40] (see electronic supplementary material, table S2 for PCR conditions). PCR products were visualized using an ABI Prism 3730xl Analyzer, and alleles were scored manually with Genemapper v. 3.7 software (Applied Biosystems, Foster City, CA).

We used Microchecker v. 2.2.3 to identify genotyping errors and assess whether null alleles were present [41]. Microchecker indicated that null alleles were present for three loci across sites AcalB142, AjeD23 and AjeD422, so we excluded those loci from the analyses. Because the presence of full siblings in larval samples can bias allele frequencies [42], we used the program Colony v. 2.0 to identify full siblings within each population [43]. One individual of each full-sibling pair was randomly removed from the dataset. There was an average of 17 individuals per site (range: 13–26) after exclusion of full siblings (electronic supplementary material, table S1). Qualitatively, our results were not sensitive to the inclusion or exclusion of full siblings (B. J. Cosentino 2011, unpublished data).

(c). Standard genetic analyses

We calculated the number of alleles per locus (N_A) and average observed (H_O) and expected (H_E) heterozygosities across loci for each population using Genalex v. 6.41 [44]. Allelic richness corrected for sample size was calculated using Fstat v. 2.9.3 [45]. We tested for departures from Hardy–Weinberg and linkage equilibrium within populations using exact tests in Genepop v. 4.0 (Markov chain method, 10 000 dememorization steps, 1000 batches, 10 000 iterations per batch [46]). To evaluate inbreeding within populations and genetic divergence among populations, we used Fstat v. 2.9.3 to calculate mean F_IS and F_ST [47] across all populations by jackknifing across loci [45]. We calculated F_ST between all population pairs, and the significance of pair-wise F_ST values was calculated using a permutation test (16 400 permutations [45]). We also tested for isolation-by-distance (electronic supplementary material, text S1). In cases where multiple statistical tests were performed (e.g. Hardy–Weinberg, linkage and pair-wise F_ST), we applied a sequential Bonferroni correction to p-values for a family-wise error rate of α = 0.05 [48].

(d). Effect of population age and ecological factors on genetic structure

First, to isolate the influence of founder effects on genetic divergence, we tested the key prediction that F_ST among newly colonized populations was greater than F_ST among established populations [25,49]. Data on wetland occupancy from 2007 to 2009 allowed us to distinguish newly colonized and established populations [33]. Newly colonized populations were defined as sites at which tissues were collected in the year in which a site was colonized by A. tigrinum (i.e. the wetland was vacant the previous year). In contrast, established populations had been occupied for greater than or equal to 1 year when tissues were collected. Our classification of population age was based on naive occupancy, which was reliable given our high detection rates: average daily detection probability of A. tigrinum using minnow traps was 0.82 [33]. Because sites were surveyed for a minimum of 3 consecutive days each year, the cumulative probability of detecting A. tigrinum at a wetland each year (p_c) was ≥0.99 using the equation

where 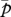is the average daily detection probability and n is the number of surveys [50]. We used Fstat v. 2.9.3 to calculate F_ST among newly colonized and established populations separately, and a permutation test (10 000 permutations) to examine whether F_ST was greater among newly colonized populations than among established populations.

Next, we tested the hypothesis that the genetic divergence of populations was influenced by ecological factors driving extinction–colonization dynamics. We used the program Geste v. 2.0 to implement a hierarchical Bayesian formulation of the F-model [51] to estimate population-specific F_STs (hereafter ‘local F_STs’) and relate F_STs to environmental factors using generalized linear models [35]. Local F_STs represent the degree to which populations are genetically differentiated from the metapopulation as a whole [35,51,52]. The F-model is more realistic than the island model [3] in that it allows for variation in rates of migration and drift among populations. Environmental factors are used to explain variation in F_ST resulting from different rates of migration and drift in each population. This method is robust to deviations from migration-drift equilibrium when the ‘separation-of-timescales’ approximation is met [51], which occurs in metapopulations with turnover [53], like our study system [33]. Our sample sizes (e.g. number of loci, individuals per population and populations) were adequate for model determination and parameter estimation [35].

We evaluated effects of five factors on local F_STs: (i) wetland area, (ii) connectivity, (iii) fish presence, (iv) wetland hydroperiod and (v) population age (newly colonized versus established). Wetland area and connectivity metrics were measured using ArcMap v. 9.3 (ESRI, Redlands, CA). To measure wetland connectivity, we used a metric that includes a negative exponential dispersal kernel and accounts for distances to potential source wetlands [9,54]. The connectivity (C_i) of wetland i was measured as:

where p_j is the probability of occupancy of source wetland j, α is a parameter scaling the effect of distance on dispersal (1/α is the average dispersal distance) and d_ij is the Euclidean distance between target wetland i and source wetland j. Euclidean distance was a better predictor of occupancy and extinction probabilities compared with distances that account for matrix structure [33]. We calculated C_i by setting α equal to 0.0022 [33], and p_j depended on wetland occupancy for A. tigrinum between 2007 and 2009. We set p_j equal to 0 for source wetlands in which A. tigrinum was undetected in all 3 years, 0.33 for source wetlands occupied in 1 year, 0.67 for source wetlands occupied in 2 years, and 1 for source wetlands occupied in all 3 years. We used the full set of 90 wetlands in our study area to calculate C_i (see fig. 1 in [33]). Fish presence represented whether or not a site was occupied by predatory fish at least once between 2007 and 2009. We documented predatory fish in 10 of the 41 sites over the 3-year period [33]. The most common predatory fish encountered were yellow bullhead (Ameiurus natalis), green sunfish (Lepomis cyanellus) and bluegill (Leopomis macrochirus). Finally, we used an ordinal rank ranging from 1 to 4 to record hydroperiod for each wetland (1, most ephemeral; 4, most permanent). Hydroperiod ranks were based on observations during repeated occupancy surveys for A. tigrinum at each site between 2007 and 2009.

Geste introduces the observed genetic data through the likelihood function to estimate allele frequencies in each population, and local F_STs are related to environmental factors with regression models using a lognormal prior [35]. Each model includes a constant term and parameters representing the effect of environmental factors on local F_ST (α_i = regression coefficient for factor i). An error term (σ²) is estimated for each model as well. The model set consists of a single model with constant and error terms only, and additional models representing all possible combinations of environmental factors to explain variation in F_ST. With five factors, our model set consisted of 32 total models. There was no evidence of strong multicollinearity among continuous predictor variables (all r < 0.28). Newly colonized wetlands tended to be smaller than established wetlands, but there was significant variation in size within age classes (means ± 1 s.d.: newly colonized = 0.7 ± 0.7 ha; established = 1.3 ± 1.0 ha).

A reversible jump Markov chain Monte Carlo approach was used to estimate the model-averaged posterior means of local F_STs and the posterior probability and parameters for each model. The model with the highest posterior probability is most supported. Overall support for individual factors was evaluated by summing posterior probabilities across models including a given factor. We used the following parameter settings: 10 pilot runs of 5000 iterations to estimate parameters of the proposal distribution, 500 000 iterations of additional burn-in, a thinning interval of 50 and a sample size of 30 000 to obtain parameter estimates. We report the mean posterior parameter estimates for α_is, whereas we report the mode for σ² because its posterior distribution was highly asymmetric [35].

To evaluate the effect of ecological factors on genetic diversity within populations, we used PROC GENMOD in SAS to build linear models of allelic richness using a normal probability distribution and an identity link function (SAS v. 9.2; SAS Institution, Inc., Cary, NC). Wetland area, connectivity, fish presence, hydroperiod and population age (newly colonized versus established) were used as predictor variables. We built 15 models that included additive effects of up to two predictor variables, and we included an intercept-only model. Model support was evaluated using the Akaike information criterion corrected for small sample size (AICc) [55].

3. Results

(a). Standard genetic analyses

We found no evidence of linkage disequilibrium between loci within populations after Bonferroni corrections. Furthermore, genotypes at individual loci deviated from Hardy–Weinberg proportions in only five of 410 cases. Because deviations were not consistent for individual loci across populations, we retained all 10 loci for further analyses. Allelic richness, standardized for sample size, averaged 6.7 alleles per locus within populations (range: 4.3–7.8; electronic supplementary material, table S1), and the average expected heterozygosity (H_E) was 0.73 (range: 0.63–0.77; electronic supplementary material, table S1). Across all populations, the number of alleles per locus averaged 10.8 (range: 2–20; electronic supplementary material, table S2). There was no indication of non-random mating within populations (mean F_IS: 0.016, s.e.: 0.024).

(b). Effects of population age and ecological factors on genetic structure

The overall F_ST among all sites was 0.036 (s.e.: 0.002). Pair-wise F_ST ranged from 0 to 0.16 (electronic supplementary material, table S3), and there was a significant pattern of isolation-by-distance (electronic supplementary material, figure S1). Genetic divergence was greater among newly colonized populations than among established populations (newly colonized F_ST: 0.046; established F_ST: 0.025; p: 0.033), supporting the prediction that founder effects influence spatial genetic structure in the metapopulation.

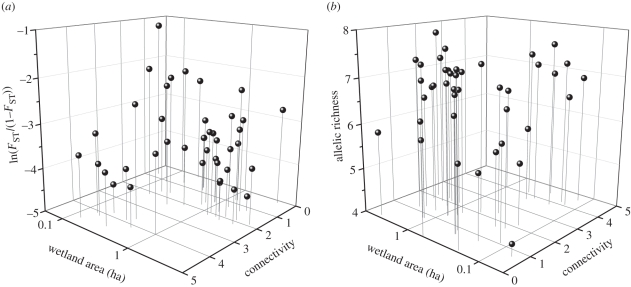
The model of genetic divergence with the highest posterior probability included effects of wetland area and connectivity (table 1). Local F_ST was negatively related to both area and connectivity (figure 2a; regression coefficients for the top model: area = −0.40, connectivity = −0.33; error term = 0.47). Relative to area and connectivity, hydroperiod and age had weak effects on F_ST (table 1). F_ST decreased marginally with hydroperiod and age (regression coefficients for the most-supported models including each term: hydroperiod = −0.20, age = −0.17). The intercept-only model had low posterior probability (0.033), and models with fish presence were not supported (table 1).

Table 1.

Posterior probabilities for the five most-supported models of genetic divergence (local F_ST) of Ambystoma tigrinum populations and sum of posterior probabilities of models with a given factor.

most probable models		sum of posterior probabilities
model	posterior probability	factor	sum
area + connectivity	0.58	area	0.87
area	0.09	connectivity	0.84
area + connectivity + hydroperiod	0.08	age	0.13
area + connectivity + age	0.06	hydroperiod	0.11
area + connectivity + fish	0.03	fish	0.06

Figure 2.

Relationships of (a) genetic divergence (ln (F_ST/(1 − F_ST))) and (b) allelic richness to wetland area and connectivity for 41 populations in an Ambystoma tigrinum metapopulation. Data for wetland area are plotted on a log scale. Axis scales in (a) are reversed for the purpose of presentation.

Consistent with patterns of genetic divergence, the most-supported model of genetic diversity included wetland area and connectivity (electronic supplementary material, table S4). Allelic richness was positively related to wetland area and connectivity (figure 2b; regression coefficients for top model ± 1 s.e.: area = 0.37 ± 0.09; connectivity = 0.25 ± 0.07). Although allelic richness was marginally greater in established wetlands than in newly colonized wetlands (means ± 1 s.e.: newly colonized = 6.38 ± 0.19; established = 6.97 ± 0.10), population age was not an important predictor of allelic richness compared with area and connectivity (electronic supplementary material, table S4).

4. Discussion

In accordance with demographic predictions from metapopulation theory, our results show that metapopulation genetic structure depended on patch area and isolation. Genetic divergence was greater among newly colonized populations than among established populations, suggesting that founder effects influenced genetic structure in this A. tigrinum metapopulation. However, population age was an inadequate measure of the strength of drift and migration. Compared with population age, genetic divergence was more strongly influenced by wetland area and spatial connectivity, two factors also predictive of A. tigrinum metapopulation dynamics [33]. Area and connectivity were also the only important predictors of allelic richness, corroborating patterns of genetic divergence. Thus, our results support the hypothesis that ecological factors underlying metapopulation dynamics also shape spatial genetic structure. Consistent with our predictions, genetic divergence was greatest in small, isolated wetlands. Because small wetlands with low connectivity also had low allelic richness, our results suggest that habitat geometry may constrain the long-term response of local populations to selection [56]. Contrary to our prediction, wetland hydroperiod and presence of predatory fish were not strong predictors of genetic divergence.

Greater genetic divergence among newly colonized populations than established populations indicated that founder effects associated with turnover had a role in generating spatial genetic structure. Previous studies have found a similar pattern in plants [25,49], beetles [24,57] and copepods [26], but we are unaware of comparable studies on vertebrates in a metapopulation context. In metapopulations with demographic turnover, theory predicts that F_ST increases among sites due to turnover when

where k is the number of colonists of newly established populations, N_m is the number of migrants among extant populations and ϕ is the probability that any two alleles among colonists have the same population of origin [23]. In our system, sites were probably colonized by a small number of individuals (k < 2N_m), which resulted in low allelic richness in newly colonized sites compared with established sites. Given that A. tigrinum is dispersal-limited [33], our results suggest that, on average, newly colonized wetlands were founded by A. tigrinum dispersers from a small number of nearby source populations (i.e. high ϕ). Colonization by long-distance dispersers can increase F_ST within metapopulations with high extinction rates [58], but a stronger isolation-by-distance pattern for newly colonized populations than established populations suggests that colonization by long-distance dispersers was rare (electronic supplementary material, figure S2).

Although genetic divergence varied between newly colonized and established populations, population age was not an important predictor of local F_STs relative to ecological variables underlying turnover dynamics. This outcome probably reflects the failure of population age to account for environmental factors influencing genetic drift and gene flow [25]. For example, wetlands with high spatial connectivity had greater allelic richness and were less differentiated than isolated sites (figure 2), indicating that the number and origin of colonists probably depend on spatial context. Genetic drift owing to founder effects may be buffered in sites with high connectivity due to a greater number of colonists, or lower probability of common origin among colonists when compared with isolated sites. Even in the case of extreme founder effects (i.e. very low k), connected sites should receive gene flow subsequent to initial colonization, which can decrease F_ST over time [22,30]. The weaker pattern of isolation-by-distance for established populations than newly colonized populations indicates that occasional long-distance gene flow may decrease divergence over time as well (electronic supplementary material, figure S2).

For A. tigrinum, wetland area may have affected both gene flow and genetic drift. A previous study supported a target effect for A. tigrinum in which colonization probability was related positively to wetland area [33]. Thus, the negative effect of wetland area on genetic divergence may be explained by a greater rate of gene flow to large wetlands than to small wetlands. Wetland size also had a positive effect on immigration of marbled salamanders (Ambystoma opacum) [59]. If population size is related positively to wetland area, genetic drift should be weaker in large wetlands, which would also reduce genetic divergence. In our system, wetland area had a positive effect on occupancy probability for A. tigrinum [33], suggesting that large wetlands may support larger, more stable breeding populations than small wetlands. Effective population size of a related species, Ambystoma californiense, was found to be positively related to the size of vernal pools [60].

Overall, few metapopulation genetic studies have evaluated the relationship between habitat area and spatial genetic structure [6]. Spawning area had a negative effect on F_ST for Atlantic salmon (Salmo salar), and this effect was attributed to the limited impact of genetic drift when spawning area is large [61]. Genetic divergence was also related negatively to pool volume for Daphnia longispina, owing to either weak genetic drift or strong gene flow in large pools [26]. Interestingly, the level of genetic diversity within populations of the herb Geum urbanum depended on an interaction between population size and connectivity in which connectivity increased genetic diversity only in small populations [29]. Hence, populations in large patches may have high genetic diversity even when connectivity is low owing to the weak effect of drift [29].

Wetland area and connectivity were important predictors of F_ST, but fish presence and wetland hydroperiod were not. Predatory fish have negative effects on amphibian survival, abundance and distribution [62–64], and wetlands with short hydroperiods can decrease adult survival and the probability of successful recruitment in A. tigrinum [32]. We predicted sites with predatory fish and short hydroperiod would be subject to strong genetic drift owing to low population size, bottlenecks or recurring founder events following extinction, which should all result in high local F_ST [6,65]. Hydroperiod had a weak negative effect on F_ST, suggesting that long hydroperiod may partly limit the effect of genetic drift. However, fish presence was not predictive of F_ST. In our study system, A. tigrinum populations are maintained in sites with fish by a rescue effect in which immigration prevents local extinction [33]. Thus, gene flow from connected source populations may maintain genetic diversity in sites with predatory fish (i.e. genetic rescue) [31]. Predatory fish also exhibited surprisingly high rates of colonization and extinction in our study system [33]. Therefore, the effects of predation on A. tigrinum population size may have been mitigated by short persistence time of fish in individual wetlands.

Patch area and isolation are important determinants of species distributions in fragmented landscapes, but occupancy and metapopulation dynamics can also depend strongly on habitat heterogeneity [66]. For A. tigrinum, area and isolation were clearly better predictors of metapopulation genetic structure and genetic diversity than current habitat quality, as represented by hydroperiod and presence of predatory fish. These measures of habitat quality are, however, important determinants of demography and metapopulation dynamics [32,33]. This uncoupling of demographic and genetic responses to habitat heterogeneity may have important implications for adaptive evolution. Specifically, hydroperiod and fish presence should impose strong selection on traits that minimize desiccation and predation risk during the larval stage (e.g. growth rate) [67]. In heterogeneous landscapes, however, local adaptation to predators or hydroperiod may be constrained by population connectivity and resulting gene flow from fishless or permanent wetlands [68]. Strong genetic drift in small wetlands may limit the effectiveness of selection as well [69]. More broadly, our results suggest that patch connectivity and area—two factors that form the basis of spatially realistic metapopulation theory—may mediate adaptive divergence in metapopulations. Further study is needed to evaluate how variable selection pressures interact with habitat geometry to influence trait evolution in A. tigrinum and in other metapopulations.