High dispersal ability inhibits speciation in a continental radiation of passerine birds

Abstract

Dispersal can stimulate speciation by facilitating geographical expansion across barriers or inhibit speciation by maintaining gene flow among populations. Therefore, the relationship between dispersal ability and speciation rates can be positive or negative. Furthermore, an ‘intermediate dispersal’ model that combines positive and negative effects predicts a unimodal relationship between dispersal and diversification. Because both dispersal ability and speciation rates are difficult to quantify, empirical evidence for the relationship between dispersal and diversification remains scarce. Using a surrogate for flight performance and a species-level DNA-based phylogeny of a large South American bird radiation (the Furnariidae), we found that lineages with higher dispersal ability experienced lower speciation rates. We propose that the degree of fragmentation or permeability of the geographical setting together with the intermediate dispersal model are crucial in reconciling previous, often contradictory findings regarding the relationship between dispersal and diversification.

1. Introduction

Through its influence on gene flow [1,2], geographical range expansion and colonization [3–5], dispersal ability can have opposing effects on the diversification process. Lineages distributed over larger geographical areas are prone to subdivision by barriers [6–8], suggesting that greater dispersal ability stimulates speciation. However, dispersal can inhibit speciation by maintaining genetic cohesion among populations [6,8–11].

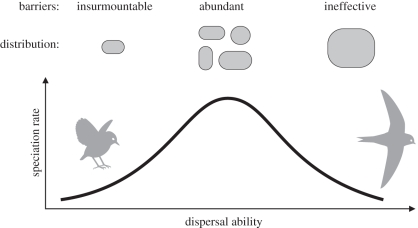
An ‘intermediate dispersal’ model combines the stimulatory and inhibitory effects of dispersal on diversification [6,12–15] (figure 1). Lineages with low dispersal ability are geographically restricted and thus have few opportunities for geographical speciation. At the other extreme, lineages with high dispersal ability are distributed over wide areas but experience reduced speciation rates due to genetic homogenization via gene flow. This model predicts that lineages with intermediate dispersal abilities experience a blend of range expansion and geographical subdivision that maximizes speciation rates.

Figure 1.

Basic elements of the intermediate dispersal model, which predicts a unimodal relationship between dispersal ability and speciation rates. Lineages with low dispersal ability are restricted to small areas where opportunities for geographical subdivision are few, resulting in low chances of speciation. Lineages with intermediate dispersal ability expand their geographical range and differentiate across barriers. Lineages with high dispersal ability maintain high levels of gene flow across extensive geographical ranges.

Empirical evidence for the relationship between dispersal ability and speciation, and for the intermediate dispersal model in particular, remains scarce [13,15–17]. Difficulties in determining the effect of dispersal on diversification include the use of crude indicators of dispersal propensity, indirect measures of speciation rates and analyses capable of detecting only monotonic changes in diversification [12–16,18,19].

Here, we analyse the relationship between dispersal ability and diversification in a large, continental radiation of Neotropical passerine birds: the ovenbirds and woodcreepers (Furnariidae). Furnariids are of special interest in the study of dispersal and diversification for two main reasons. First, furnariids represent a continental adaptive radiation of over 290 species [20]; therefore, they may shed light on the processes that generate high biological diversity. Second, they encompass a wide range of dispersal abilities, from poor dispersers with small distributions to those that have colonized oceanic islands up to 800 km from the continent [21].

A major difficulty in addressing the relationship between dispersal and diversification is that dispersal is exceptionally difficult to quantify [3,22]. The assessment of dispersal ability based on phenotypic traits has been used in large-scale studies in plants [18,19,23,24], marine organisms [2,15,25] and anurans [17]. Here, we use an index of wing shape that, because of its relationship with flight performance, can be used as a surrogate for dispersal ability in birds. We then analyse the relationship between dispersal ability and diversification rates using an explicit phylogenetic modelling framework [26]. We provide not only the first quantitative analysis of the relationship between dispersal ability and diversification in a radiation of birds, but also the first test of the intermediate dispersal model in continental organisms.

2. Material and methods

(a). Wing shape

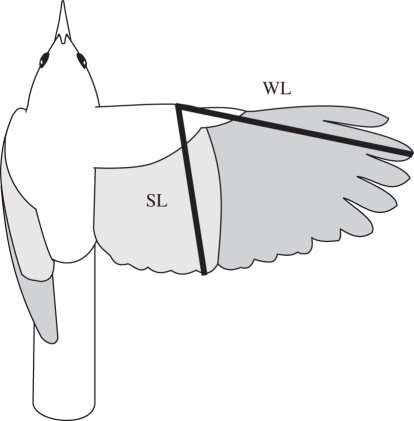
According to aerodynamic models of avian flight, wings with high aspect ratio are the key to efficient long-distance flight [27]. Consequently, we used an index of wing shape related to the aspect ratio of the wing [28,29] (figure 2):

where WL is the standard length of the closed wing and SL is the distance from the carpal joint to the tip of the first secondary feather. Because WL is related to the extent and SL to the width of the wings (figure 2), the standardized difference between WL and SL is related to the aspect ratio of the wing. The hand-wing index is equivalent to the index developed by Kipp [28] except that we used the difference between WL and SL instead of direct measurements of the distances between feather tips; we found that WL and SL were easier to measure reliably.

Figure 2.

Linear measurements used to calculate the hand-wing index: (WL) ‘wing length’ from the carpal joint to the tip of the longest primary feather; (SL) ‘secondary length’ from the carpal joint to the tip of the first secondary feather. Both measurements were taken on closed wings without flattening their natural curvature. Here, WL and SL are traced on a wing outline of Xenops rutilans (University of Washington Burke Museum 77 384) to show their relationship with the extent and width of the wing.

Empirical evidence supports the hand-wing index as a valid surrogate for flight and dispersal ability in birds. Flight performance (see the electronic supplementary material), migratory behaviour [29,30], natal dispersal distance [31] and genetic differentiation [32] are all correlated with this index. Because the index varies on a continuous scale, it can be used to study higher order relationships between dispersal and diversification like the intermediate dispersal model.

We estimated the hand-wing index in Furnariidae using museum specimens. SC measured WL and SL in 1174 specimens representing 282 species (96% of the species in the family). Most specimens were measured with digital calipers at the Louisiana State University Museum of Natural Science (LSUMNS) but additional specimens were measured from the following institutions: American Museum of Natural History, Field Museum of Natural History, Museo de Historia Natural Universidad Nacional Mayor de San Marcos (Lima), Museo Argentino de Ciencias Naturales (Buenos Aires), Academy of Natural Sciences (Philadelphia), Museo Nacional de Historia Natural (Montevideo), Yale University Peabody Museum of Natural History, University of Washington Burke Museum of Natural History, Natural History Museum of Los Angeles County and University of Kansas Natural History Museum.

(b). Phylogeny

We used a calibrated species-level phylogeny of the Furnariidae inferred using ca 7000 base pairs from multiple DNA loci [33]. We used the maximum clade credibility tree based on a partitioned Bayesian search of topology and divergence times in BEAST [34]. The tree was calibrated using the age of the split between tyrannoids and furnarioids [35] and multiple biogeographical calibrations based on the last rapid uplift of the northern Andes and the formation of the isthmus of Panama. For further details on phylogenetic reconstruction and calibration, see [33]. For the present analyses, the final tree was pruned to delete taxa included only for rooting or calibration. An additional species, Asthenes luizae, was also removed because we lacked wing shape data.

(c). Hand-wing index and aspect ratio

To evaluate the relationship between the hand-wing index and aspect ratio, we estimated the aspect ratio of 35 furnariid species. We used specimens deposited at the LSUMNS and the University of Washington Burke Museum of Natural History for which wingspan was measured at the time of preparation and a spread-wing or a tracing of its outline was preserved. Only fully spread wing preparations with a straight leading edge were used. We used digital photographs of spread wings or scanned wing tracings to calculate the area of a single wing using the software ImageJ v. 1.42q [36]. Then, we estimated aspect ratio as wingspan²/area, in which the area includes not only twice the area of a single wing but also the ‘root box’ between the wings [27]. We evaluated the relationship between the hand-wing index and aspect ratio statistically using a phylogenetic generalized least-squares (PGLS) approach in which the strength of the phylogenetic effect on the correlation between variables is estimated and used to fit an optimal model [37]. R [38] code for fitting PGLS models was kindly provided by Robert P. Freckleton (University of Sheffield). The phylogeny used in PGLS was obtained by pruning the species-level phylogeny of the Furnariidae down to the 35 species needed for this analysis.

(d). Mode of hand-wing evolution

To investigate the mode of wing shape evolution we used likelihood models of continuous trait evolution [39,40]. We used function fitContinuous in the GEIGER library in R [41] to obtain maximum likelihood values and parameter estimates for four models of evolution: Brownian motion, change concentrated at the tips (lambda), speciational (kappa), accelerating or decelerating (delta) [39] and constrained random walk (Ornstein–Uhlenbeck process with a single optimum) [42]. The lambda model was also used to assess levels of phylogenetic signal in the hand-wing index [37]. One advantage of an index with high phylogenetic inertia is that it can provide information on dispersal abilities at large temporal scales, an important property of a measure of dispersal for the study of diversification [2]. Because measurement error and intraspecific variation can inflate estimates of interspecific variation and affect model estimates [37,43,44], we estimated the standard error of the hand-wing index for each species. For three species represented by a single specimen (Acrobatornis fonsecai, Automolus rufipectus, Schizoeaca perijana), we used the average standard deviation across furnariids as a substitute for the standard error. Squared standard errors are then added to the diagonal of the expected covariance matrix before model estimation [40,43,45]. We assessed the degree of support for each model using an information-theoretic approach based on the second-order estimator of the Akaike information criterion (AICc), which balances model fit and model complexity [46]. Differences in AICc values between models indicate relative differences in information, and from these differences the probability that a given model is the best model can be calculated (w, also called Akaike weight) [46]. Finally, we reconstructed ancestral values of hand-wing index across the phylogeny using maximum likelihood methods [47] after transforming the phylogenetic tree according to the model that best described hand-wing index evolution [39]. We used functions in the GEIGER library [41] for tree transformations and ancestral reconstructions.

(e). Relationship between the hand-wing index and diversification

We used the ‘quantitative state speciation and extinction’ method (QuaSSE) [26] to investigate the relationship between the hand-wing index and diversification in the Furnariidae. This method models diversification as a birth–death process in which speciation and extinction rates are arbitrary functions of a continuous variable that evolves according to a diffusion process. The method does not depend on predetermined ancestral reconstructions. Instead, trait evolution and cladogenesis are evaluated simultaneously in a phylogenetically explicit maximum-likelihood framework. We constructed various likelihood functions representing different models for the relationship between the hand-wing index and speciation: (i) a model in which the speciation rate is constant and independent of the values of the index; (ii) a linear relationship between the index and speciation rates; (iii) a sigmoid relationship; and (iv) a unimodal relationship represented by a vertically offset Gaussian function [26]. Because a relationship between wing shape and net diversification rates can also be mediated by a relationship between dispersal and extinction risk, we evaluated models in which extinction was absent, constant, or a linear function of the hand-wing index. Functions for creating QuaSSE models and finding maximum likelihood estimates are part of the Diversitree library in R. We compared models using likelihood ratio tests and using an information-theoretic approach as before [46]. The relative support for particular parameters across models was assessed by summing the probabilities of the models in which a particular parameter was present.

A directional tendency in trait evolution may also influence the number of species with lower or higher values of a trait, and may represent an alternative to trait-dependent speciation [48,49]. Directional tendencies cannot be detected using a simple diffusion model on an ultrametric tree [50]; thus, a model with a directional tendency alone cannot be evaluated using directional tendency alone. However, QuaSSE models can detect directional tendencies, especially if the tendency opposes trait-dependent speciation (e.g. trait values tend to increase along lineages, but lineages with higher values experience lower speciation rates) [26]. Detecting a directional tendency that opposes species selection would indicate that trait-dependent speciation is an important component of the model. Because of the difficulties in estimation and interpretation, we evaluated a single model including a directional tendency a posteriori by adding a directional parameter to the best model determined by the information-theoretic approach.

3. Results

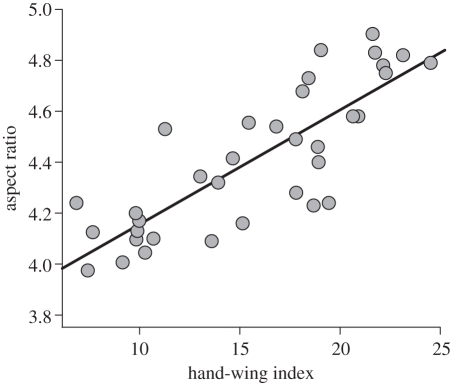
We found a significant positive relationship between the hand-wing index and aspect ratio in the Furnariidae (figure 3, see electronic supplementary material, table S3), thus confirming its utility as a surrogate for flight performance. Hand-wing indices in the Furnariidae are comparatively low, on average, but highly variable (minimum = 5.9, 1st quartile = 12.3; median = 15.7; 3rd quartile = 18.8, maximum = 36.9, see electronic supplementary material, table S4). In contrast, those of most European passerines, many of which are highly migratory, are in the 20–40 range, and only two species have indices well under 20 [28].

Figure 3.

Relationship between aspect ratio and the hand-wing index in 35 species of Furnariidae. Regression line from a phylogenetic generalized least-squares model (R² = 0.66, F = 68.4, d.f. = 1, p < 0.001): aspect ratio = 0.045 (±0.005) × hand-wing index + 3.7 (±0.01).

A simple Brownian motion process was sufficient to describe wing shape evolution in the Furnariidae (table 1). Other models received moderate support but estimated parameters made them essentially equivalent to a Brownian process (i.e. λ, δ, and κ ∼ 1, α ∼ 0). The delta model showed the greatest departure from a Brownian process, suggesting that wing shape evolution may be decelerating over time (δ = 0.81). The lambda value close to 1 indicates strong phylogenetic signal in wing shape data [37].

Table 1.

Models, parameters, and model selection statistics for the evolution of the hand-wing index in Furnariidae. σ², Brownian rate of trait evolution, followed by model-specific parameters (an additional parameter common to all models, the estimated ancestral state, is not shown); log-Lik, logarithm of the maximized likelihood; k, total number of parameters in the model; AICc, second-order estimator of the Akaike information criterion; ΔAICc, difference in AICc values between a model and the best model; w, model probability or Akaike weight.

model	parameters	log-Lik	k	AICc	ΔAICc	w
Brownian	σ2 = 0.84	−714.0	2	1432.0	0	0.38
lambda	σ2 = 0.81 λ = 0.99	−713.6	3	1433.3	1.3	0.20
delta	σ2 = 1.00 δ = 0.81	−713.9	3	1433.9	1.9	0.15
speciational	σ2 = 0.84 κ = 1.00	−714.0	3	1434.1	2.0	0.14
constraint	σ2 = 0.84 α = 1.5 × 10−8	−714.0	3	1434.1	2.0	0.14

The distribution of hand-wing indices on the phylogeny shows that clades with high values (i.e. high dispersal ability) tend to be species-poor, whereas clades with low values tend to be species-rich (figure 4), suggesting a negative relationship between dispersal ability and diversification. The best QuaSSE model included a sigmoid relationship between the speciation rate and the hand-wing index, and a linear relationship between extinction rates and the hand-wing index (table 2, parameter estimates in the electronic supplementary material, table S5), but a model with a unimodal relationship between speciation and wing shape received nearly equal support (ΔAICc = 0.4). Most models that included trait dependent speciation received considerable support (ΔAICc < 4, w > 0.05) as opposed to models of constant speciation (ΔAICc > 5, w < 0.02). The nine best models were the nine models with varying speciation rates. These had a cumulative probability of 0.98 (sum of w), thus defining a 98% confidence set [46]. Even a simple model with a linear relationship between speciation and the hand-wing index and no extinction was significantly better than a model in which speciation rates did not depend on wing shape (likelihood ratio test: χ² = 5.6, d.f. = 1, p = 0.017).

Figure 4.

Species-level phylogeny of the Furnariidae (Bayesian maximum clade credibility tree [33]) showing hand-wing index values for extant species as well as maximum likelihood ancestral reconstructions.

Table 2.

Models and model-selection statistics for the relationship between wing shape and diversification rates in the Furnariidae from QuaSSE analyses. log-Lik, logarithm of the maximized likelihood; k, total number of parameters in the model; AICc, second-order estimator of the Akaike information criterion; ΔAICc, difference in AICc values between a model and the best model; w, model probability or Akaike weight.

speciation	extinction	log-Lik	k	AICc	ΔAICc	w
constant		−1539.7	2	3083.4	5.7	0.02
linear		−1536.9	3	3079.9	2.2	0.09
sigmoid		−1535.0	5	3080.1	2.5	0.08
unimodal		−1534.8	5	3079.9	2.3	0.09
constant	constant	−1539.7	3	3085.4	7.8	0.01
linear	constant	−1535.6	4	3079.4	1.8	0.11
sigmoid	constant	−1535.0	6	3082.2	4.6	0.03
unimodal	constant	−1534.8	6	3082.0	4.4	0.03
constant	linear	−1539.7	4	3087.4	9.8	0
linear	linear	−1535.6	5	3081.5	3.8	0.04
sigmoid	linear	−1531.6	7	3077.6	0	0.28
unimodal	linear	−1531.8	7	3078.1	0.4	0.22

All supported models indicated lower speciation rates for lineages with hand-wing indices above 15 (figure 5), but the exact functional relationship between speciation rates and wing shape was undetermined given the small differences in model fit (table 2) and the fact that the combined support for the three different trait-dependent speciation models was similar (combined probabilities: linear = 0.25, sigmoid = 0.38, unimodal = 0.34).

Figure 5.

Relationship between the hand-wing index and speciation rates in the Furnariidae as inferred from quantitative state speciation and extinction models (QuaSSE). The nine models with varying speciation rates are shown in shades of grey proportional to their probability w (table 2) (some model predictions overlap so only six lines are shown). The black line represents the model-averaged prediction.

To represent the overall relationship between the hand-wing index and speciation rates in the face of high levels of model uncertainty we computed model-averaged predictions in which the expected speciation rate is an average across models weighted by their probability w [46]. The resultant model-averaged prediction (log-likelihood = −1531.8) showed an overall negative relationship between the hand-wing index and speciation rates but with the highest speciation rates at hand-wing values around 10 and an abrupt drop in speciation rates at 15 (figure 5).

Evidence for a role of extinction was ambiguous. The two best supported models included a linear relationship between extinction rates and wing-shape in which extinction is extremely high for lineages with a hand-wing index lower than eight but quickly drops to zero for higher values of the index (electronic supplementary material, figure S2). Models with no extinction or constant extinction also received considerable support (combined probabilities: no extinction = 0.28, constant = 0.18, linear = 0.54), and estimated constant extinction rates were lower than 10⁻⁷ Ma⁻¹ (electronic supplementary material, table S5).

The addition of a directional tendency improved the fit slightly (log-likelihood = −1529.8, likelihood ratio test: χ² = 3.6, d.f. = 1, p = 0.06). The directional parameter estimate (0.15) indicated a tendency toward increasing hand-wing indices along lineages, thus opposing species-selection (lower speciation rate in lineages with higher hand-wing index). This suggests that directional trends in wing shape evolution are not confounding the patterns created by trait-dependent speciation in the Furnariidae.

4. Discussion

We found that furnariid lineages with greater dispersal ability showed lower speciation rates, suggesting that the homogenizing effect of gene flow inhibited speciation in this continental radiation of passerines. This result is consistent with population-level studies, which have found a negative association between gene flow and genetic differentiation [2,32,51]. Although range expansion certainly plays an important role in diversification [6], the potentially stimulating effects of colonization and range expansion [7,52] may have been overshadowed by the inhibitory effect of increased levels of gene flow in the Furnariidae. Our results support the notion that barriers to gene flow played a prominent role in the process of diversification in South America [53–56] and in continental radiations in general [57–59].

Although we found an overall negative effect of aspect ratio on speciation rates, we could not determine the exact functional relationship. Simulations showed that even with large phylogenies and strong effects of a trait on speciation rates it may be difficult to recover the exact functional relationship between traits and speciation rates [26]. We detected an overall decreasing relationship between the hand-wing index and speciation rates that could be produced by a negative linear relationship, a sigmoid relationship or a unimodal relationship in which speciation rates peak at low values of the hand-wing index (figure 5). Therefore, we could not distinguish between a monotonically decreasing relationship between dispersal ability and speciation and the intermediate dispersal model.

Extinction may play a role in the relationship between dispersal and diversification rates. Because of its effects on local persistence, recolonization and geographical range size, high dispersal is hypothesized to decrease extinction risk [60–62] resulting in a positive relationship between dispersal and net diversification rates. However, we found low support for an effect of extinction on diversification patterns in the Furnariidae (see also [33]). Although extinction may be difficult to estimate from molecular phylogenies [26,63] our finding of a negative relationship between dispersal and diversification suggests that the effects of extinction, if any, were overshadowed by the effects of dispersal on speciation.

An underappreciated issue is that the relationship between dispersal and diversification probably depends on the scale and configuration of the geographical setting. The degree of fragmentation of the geographical setting or its permeability to dispersal may determine whether the relationship is positive or negative, or, in the context of the intermediate dispersal model, it may determine the values of dispersal at which speciation rates are maximized. Therefore, in continuous landscapes, where opportunities for isolation may be rare, the negative effect of dispersal on speciation may prevail, speciation rates may peak at low levels of dispersal, and the relationship between dispersal and diversification becomes predominantly negative. On the other hand, in highly fragmented landscapes, such as archipelagos and continental aquatic systems, opportunities for isolation are relatively common, and the positive effect of dispersal on diversification may dominate, producing a peak of cladogenesis at high levels of dispersal and predominantly positive relationships between dispersal and diversification.

An intermediate dispersal model adjusted by the dimensions and configuration of the geographical setting can reconcile previous findings concerning the association between dispersal and diversification in birds. An analysis of bird families of the world found a positive relationship between dispersal propensity and diversification [16]. This is consistent with the idea that when dispersal distances are small in relation to the extent of the geographical realm, increased dispersal ability can stimulate diversification. The avifauna of northern Melanesia archipelagos was the first example of the intermediate dispersal pattern [12,13]. Although some species engage in long flights over water and can disperse across the archipelago, others do not and are restricted to single islands. Therefore, the two extreme dispersal scenarios described by the intermediate dispersal model are represented in northern Melanesia. As a result, the intermediate dispersal pattern becomes evident.

Finally, we found that the Furnariidae, which is restricted to a single biogeographic realm, shows a predominantly negative relationship between dispersal and diversification. Because dispersal is generally easier within a continent than in archipelagos, even low levels of dispersal may inhibit speciation. We predict that most continental avifaunas would show a negative relationship between dispersal and diversification. A few furnariid clades with extremely low dispersal ability allowed the detection of a unimodal relationship between dispersal and diversification but, because these clades lie at the lower end of the avian dispersal ability spectrum, most continental birds may show the predominantly negative relationship predicted by the right-half side of the intermediate dispersal model (figure 1). Further evaluation of the intermediate dispersal model and its ability to predict speciation rates in birds will require the analysis of a diverse sample of avian groups in different geographical regions.

Studies in other organisms are more difficult to reconcile. Recent large-scale studies in angiosperms suggested that dispersal mode, as inferred from fruit characteristics and pollination agents, does not influence cladogenesis [19,23], but a unimodal relationship consistent with the intermediate dispersal model was not analysed. Seed dispersal by ants, conferring comparatively low dispersal ability, may have increased diversification [64]. The fossil record of marine invertebrates suggests a negative effect of dispersal on diversification in which taxa with pelagic larvae (greater potential for dispersal) experienced lower rates of cladogenesis [25], but current distributions in the Pacific Ocean suggest that diversification peaks at intermediate levels of dispersal [15]. Some of these findings may need to be reassessed using better estimates of dispersal potential and new analytical tools. In addition, analyses should not be restricted to positive or negative relationships; the intermediate dispersal model should be evaluated as a candidate model.

By using information on the biomechanics of locomotion, a comprehensive morphological dataset and a species-level phylogeny, we demonstrated how the relationship between dispersal and diversification can be studied in birds and other volant organisms. Variation in flight ability and wing morphology in birds is related to foraging strategies [65–67], migratory behaviour [29,68,69] and predation avoidance [70]. Therefore, dispersal ability in furnariid lineages may be a byproduct of adaptation to particular ecological roles and migratory strategies. As a result, our findings suggest cause–effect links between adaptation, dispersal ability and patterns of diversification.