Relevance of evolutionary history for food web structure

Abstract

Explaining the structure of ecosystems is one of the great challenges of ecology. Simple models for food web structure aim at disentangling the complexity of ecological interaction networks and detect the main forces that are responsible for their shape. Trophic interactions are influenced by species traits, which in turn are largely determined by evolutionary history. Closely related species are more likely to share similar traits, such as body size, feeding mode and habitat preference than distant ones. Here, we present a theoretical framework for analysing whether evolutionary history—represented by taxonomic classification—provides valuable information on food web structure. In doing so, we measure which taxonomic ranks better explain species interactions. Our analysis is based on partitioning of the species into taxonomic units. For each partition, we compute the likelihood that a probabilistic model for food web structure reproduces the data using this information. We find that taxonomic partitions produce significantly higher likelihoods than expected at random. Marginal likelihoods (Bayes factors) are used to perform model selection among taxonomic ranks. We show that food webs are best explained by the coarser taxonomic ranks (kingdom to class). Our methods provide a way to explicitly include evolutionary history in models for food web structure.

1. Introduction

The consumer–resource interactions, which are the basis of food webs and ecosystems, are determined by the coevolutionary dynamics of the traits of the interacting species [1,2]. Some interactions are relatively recent—e.g. relationships between exotic invaders and native species—while other have arisen deep within the tree of life (e.g. plant–herbivorous insect trophic interactions), but all interactions have an evolutionary signature related to the evolution of species traits. The occurrence of an interaction is influenced by traits, such as body size, metabolism, defensive strategies, environmental tolerances and behaviour of both the consumer and the resource. Even though understanding the structure of ecosystems has been one of the great challenges in ecology [3–5], models for food web structure have so far focused only on one or few, albeit important, traits (e.g. body size: [6–10]). However, it has repeatedly been suggested that several traits have to be taken into account in order to fully understand food web structure [9,11,12].

Because of shared evolutionary history, closely related species typically have similar traits [13], which in turn determine their trophic interactions. As such, similar species are more likely to consume or be consumed by similar species [8,14,15]. Evolutionary history could possibly then be used as a surrogate for trophically important traits. Therefore, it is likely that we could detect a signature of evolutionary history in the structure of food webs where closely related species should have specific patterns of interactions. Of course, evolutionary relatedness may not fully summarize all the traits determining species interactions, as species are plastic and are not entirely constrained by their evolutionary history. For example, species have to adapt to their specific environment and differentiate themselves from close relatives owing to competition [8,16]. Nonetheless, evolutionary history provides the objective, a priori hypothesis, that closely related species share similar consumer–resource interactions and clades can be categorized into distinct trophic groups.

Initially, models for food web structure have disregarded this issue, but the topic has recently received more attention. The ‘nested-hierarchy’ model [8] implicitly models phylogenetic similarity among species, whereas other models include evolutionary dynamics for the species [14,17–24]. Rezende et al. [15] analysed compartments (sets of species that tend to interact preferentially within the set and not between sets) in a Caribbean food web [25], and found that, depending on the taxonomic group (bony fishes versus cartilaginous fishes), some of the identified compartments in the food web tended to predominantly contain either closely related or distantly related species. Also, in mutualistic networks a strong phylogenetic signal has been detected, with important consequences for biodiversity [26–28].

Here, we explore the influence of evolutionary history on species interactions by using species' taxonomic classification and exploiting the recently proposed ‘group model’ [29]. In the group model, the species are assigned to non-overlapping groups, and the probability that two species i and j interact is fully determined by the groups to which i and j belong. The model has been previously used to perform unsupervised classification of species into groups [29,30]. However, it can be used when the partition into groups is given, as in this case. We divide species according to evolutionary history, approximated by their taxonomic classification. For example, we divide the species according to kingdoms and recover the likelihood that such a model would produce the empirical network. We can do the same for species grouped by phylum, class, order and so forth. The same type of analysis can be performed based on species phylogenies, where at each bifurcation species are partitioned anew—at the root, species are divided into two groups, at the next deepest bifurcation into three groups and so on until each species is in a distinct group. We can associate a likelihood with each partition, to estimate how well current food web structure is explained through evolutionary time. Using model selection, we can then find the age at which most of the currently observed trophic structure was determined. This tracking of likelihoods in evolutionary time is somewhat blurred when we use taxonomy, but clearly division in coarser ranks (e.g. kingdom) should pre-date that into finer subdivisions (e.g. family).

Using the group model and partitioning species by taxonomy or phylogeny, we address the hypothesis that closely related species can be categorized into trophic groups. We want to answer two basic questions: (i) how much of the food web structure can be explained by the evolutionary history of species? and (ii) which taxonomic ranks can better explain species interactions (i.e. identify the taxonomic level that provides a balance between information on food web structure and number of parameters used)?

2. Methods

(a). Food webs

We analysed nine published food webs: Caribbean [25], El Verde [31], Little Rock [32], Mill Stream (Ledger, Edwards & Woodward, unpublished data, see [11]), Stony Island [33], Tuesday Lake [34],Weddell Sea [35] and two versions of Ythan Estuary [36]. The difference between the two versions of the Ythan Estuary is that in the version from 1996 parasites are included, whereas in the 1991 version they are not.

Empirical data for each network comprise a binary adjacency matrix, indicating consumer–resource interactions and a species list. The species lists can contain Latin binomials or other coarse-grained classifications, such as ‘crabs’, ‘detritus’, etc., as well as unidentified species. In fact, the level of resolution in published webs varied considerably both between webs and within webs, where some nodes were resolved at the species level, whereas others were coarse aggregates of taxa. Because taxonomic resolution is crucial for our exercise, we analysed a large set of webs, and kept only those that displayed a sufficient level of taxonomic detail. The method used for constructing the networks is also of importance, because there is a risk of having a circular argument in which taxonomy is used to build the network and then to perform inference. All the webs we analyse have been built using a variety of methods: Weddell Sea, gut contents and published reports; Caribbean, published reports; Little Rock, expert knowledge; Ythan Estuary (both versions), gut contents and predation observations; Tuesday Lake, gut contents; Mill Stream and El Verde, gut contents, predation observations and published reports; and Stony Island, gut contents. Even though it is likely that taxonomy played some role in the link assignment in the food webs that were assembled using ‘expert knowledge’ and ‘published reports’, none of the original articles explicitly state that this was the main method used for deciding feeding interactions.

For each food web, we compiled the taxonomy for each node. To this end, we searched the Integrated Taxonomic Information System online database (www.itis.gov) using the information contained in the species list. In each web, we kept only those nodes for which we recovered a valid kingdom, phylum, class, order, family and genus. The links between species were kept only if both the resource and the consumer were completely classified.

Many of the webs we analysed were heavily simplified by this procedure. Because the quality of the data is critical for our analysis, we chose to analyse only the nine webs for which we recovered a full taxonomy (to genus level) for more than 65 nodes and for which we retained more than 200 links. These constraints are strict, and relaxing them could influence the results (see §2e). However, it is worth noting the so-called third generation food webs [5], which are currently being published, typically do contain hundreds of species-resolved nodes and thousands of links. Therefore, we are justified in keeping high standards as they would apply to the more recent data. The results of the classification are presented in table 1. Thus, we can produce six taxonomic partitions for each web, dividing the species into kingdom, phylum, class, order, family and genus, respectively.

Table 1.

Statistics for the food webs before and after the search for species with defined taxonomy down to genus level. (Shows the original (SOr) and final (SFin) number of species, and the original (LOr) and final (LFin) number of links. The last columns show the number of kingdoms (nK), phyla (nP), classes (nC), orders (nO), families (nF) and genera (nG) represented in the final food webs.)

food web	SOr	SFin	LOr	LFin	nK	nP	nC	nO	nF	nG
Weddell Sea	488	364	15880	9655	3	20	41	89	170	258
Caribbean	249	203	3313	1901	1	1	2	17	60	120
Little Rock	181	156	2375	1832	3	13	16	35	64	137
Ythan96	134	100	598	415	1	7	12	34	58	80
Tuesday Lake	73	66	410	309	3	9	10	20	35	47
Ythan91	92	74	421	299	1	4	9	27	46	62
Mill Stream	80	67	367	280	2	5	9	22	40	54
El Verde	156	70	1510	268	2	4	9	22	40	56
Stony Island	113	74	832	224	2	6	8	22	36	52

(b). The group model

A food web can be codified as an adjacency matrix A in which A_i,j = 1 means that species i is consumed by j. The food web contains S nodes (species) and L connections (trophic interactions). In the group model [29], the probability that i is a resource for consumer j is defined as:

2.1

where G is a partition of the S nodes in γ non-empty groups. Interactions are therefore determined by Bernoulli trials that use γ² probabilities (q_Gi,Gj, one for each combination of groups).

This model is based on the idea of ‘trophic roles’: species in the same group have consistent interaction patterns with other groups (e.g. in an aquatic food web, species in the ‘benthic herbivores’ group interact with high probability with the ‘benthic macrophytes’ group as consumers and with ‘benthic carnivores’ as resources, but do not interact with each other).

For any given partition of the species into γ groups, we can set the γ² probabilities q_Gi,Gj to their maximum-likelihood estimates (MLEs):

2.2

where L_Gi,Gj is the number of interactions (those in the adjacency matrix) originating from the species in group G_i and terminating in species belonging to group G_j, whereas Z_Gi,Gj is the number of interactions not occurring (the zeros in the matrix) between resources in group G_i and consumers in group G_j. The likelihood for this model (i.e. the probability of the model generating exactly the empirical matrix A) can be written as:

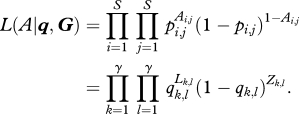2.3

Note that in the model all links originating from group i and terminating in group j are distributed independently and identically.

In our model, the partition G is defined by the taxonomic classification at a particular rank. For example, suppose that we have only two kingdoms (Plantae: group 𝒫 and Animalia: group 𝒜). Then, we need to parametrize four probabilities (q_𝒜𝒜,q_𝒜𝒫,q_𝒫𝒜,q_𝒫𝒫). We can set each one to its MLE. For example, we can compute the MLE for q_𝒫𝒜 by counting how many links go from plants to animals and dividing by the number of plants times the number of animals. Once we computed the four MLE, we can use the formula above to recover the maximum likelihood for the network given the partition into kingdoms.

(c). Randomizations, likelihoods and overlaps

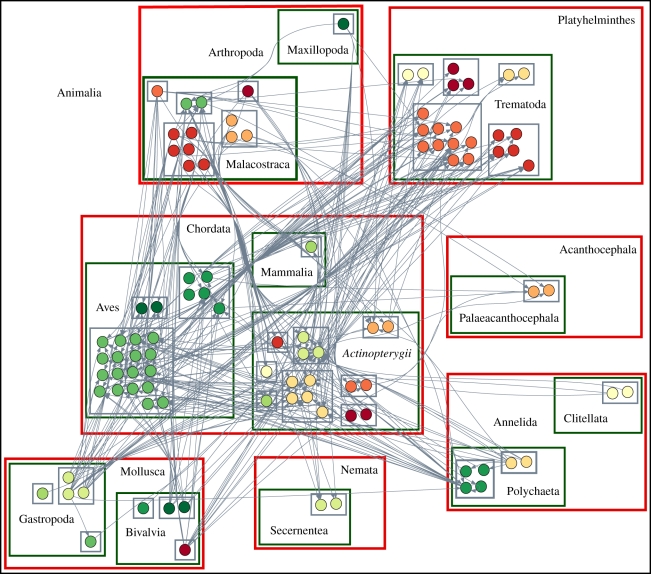
For each of the nine webs and the six taxonomic partitions, we computed the maximum likelihood as specified above. We then produced 10⁶ partitions at random. The random partitions conserved the number and size of the groups. For example, the Ythan Estuary food web (the version from 1996, here named Ythan96) consists of 100 species and seven phyla: Chordata (43 nodes), Platyhelminthes (22 nodes), Arthropoda (14 nodes), Mollusca (nine nodes), Annelida (eight nodes), Acanthocephala (two nodes) and Nemata (two nodes; figure 1). In the randomizations, we generated random partitions of the 100 species in seven groups of size 43, 22, 14, 9, 8, 2 and 2, respectively. For each randomization, we computed the associated maximum likelihood. We then used the distribution of likelihoods from the randomized partitions to measure the probability of obtaining a better likelihood than that produced by the taxonomic split. For the Ythan Estuary (1996) food web, none of the one million randomizations based on the phyla group number and sizes produced a likelihood higher than that associated with the partition into phyla.

Figure 1.

Graphical description of Ythan96 [36] food web. Nested boxes stand for kingdom (black box), phylum (red boxes), class (green boxes) along with their names and order (different colours). For a matrix description of the same food web, see the electronic supplementary material, appendix.

In the case of the Ythan Estuary (1996) food web, we can claim that the split into phyla contains important information on species interactions. For this taxonomic rank, the result is clear: the majority of the feeding interactions are between different phyla, for example Platyhelmintes consumed by Chordata. Some interactions are also within one phylum, for example Chordata. If we analyse the division into kingdoms, then the result is quite obvious: Monera and Plantae act as a resource for the Animalia, while they do not interact with each other and do not have internal connections. Animals, on the other hand, can eat each other.

In order to measure the amount of information captured by the different partitions based on taxonomy, we calculated the proportion of links each model is able to predict correctly [11]. If a model proposes K links of which M are present in the empirical data, then the proportion of correctly proposed links is Ω = M/K. We also derive a p-value for the Ω using the method by Allesina [37].

(d). Model selection

Models based on different taxonomic ranks have different complexities. The number of parameters of the model, in fact, can only increase when moving from kingdom to genus (given that taxonomic ranks are nested). When models differ in the number of parameters, we cannot simply compare the likelihoods, but rather we have to balance the goodness of fit with model complexity. To this end, various measures have been devised, including Akaike information criteria, Bayesian information criteria, and other information criteria [38], all of which hold asymptotically. However, because the group model is quite simple, we can analytically derive its marginal likelihood, which provides an efficient Bayesian model-selection technique descending directly from Bayes theorem.

Suppose we have a model M₁, and the prior probability of the model is P(M₁). We can use the data A to update the posterior probability of the model using Bayes formula:

2.4

where P(M₁|A) is the posterior probability of M₁, P(A) is the probability of the data and P(A|M₁) is the probability of the data given the model (the likelihood). This formulation directly translates in Bayes factors [30,39]. For example, if we have two models, then we can write:

2.5

which, assuming we have a uniform prior on the models, simply becomes:

2.6

Thus, to select among models, we need to compute P(A|M_i), the marginal likelihood of the data conditioned on the model M_i. If the model requires a set of parameters Θ, then the (prior) marginal likelihood can be written as a weighted average of the likelihoods P(A|M_i, Θ_i):

2.7

where P(Θ_i|M_i) is the prior for the parameters and the integral is taken across all possible values of all the parameters.

An example can help clarify this concept. Suppose we have a random-directed graph (i.e. we connect any two nodes with probability p). By assuming a uniform (U[0,1]) prior on p, the marginal likelihood of the data becomes:

2.8

where L is the number of ones in the matrix (the links in the network), Z is the number of zeros and β(·,·) is the beta function. The marginal likelihood can therefore be seen as the expected likelihood when parameters are drawn from their prior distribution.

For the group model, we can write:

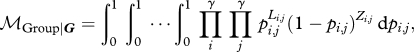2.9

which is the expectation for a product of independent random variables (the likelihoods of the various sub-matrices). The expected value of the product of independent random variables is the product of the expectations. Therefore, we can solve analytically:

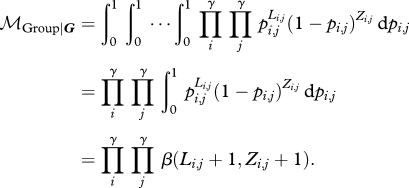2.10

The marginal likelihood penalizes complex models in a very natural way. For each network and taxonomic rank, we computed the marginal likelihood using uniform priors as specified above and used the values to select among taxonomic ranks for each web, with higher values characterizing better models. We repeated the same exercise using a different prior (electronic supplementary material, appendix): the choice of prior did not affect our results.

(e). Simplification of the food webs

One technical problem with the method presented here is that the analysed food webs were more or less simplified by the initial filter, depending on the number of nodes we were able to define up to the genus level. Another concern is that the exclusion of nodes could be biased as the resolution is usually lower at lower trophic levels [5], and a larger proportion of nodes should therefore be excluded at those levels. In order to investigate whether this problem affected our results, we performed two complementary analyses. First, we relaxed the requirements for node-inclusion (taxonomy up to family) in order to exclude fewer nodes for the two webs being most affected by the filter (El Verde and Stony Island). Second, we randomly removed additional nodes in the largest web (Weddell Sea). We found that these variations did not affect the outcome: the same taxonomic classification as in the original setting was chosen to be the ‘best’ grouping (electronic supplementary material, appendix).

(f). Using phylogeny

In order to investigate the robustness of our findings, we additionally examined a more detailed description of species evolutionary history. For this test, we chose the Caribbean food web. We were able to partition the Caribbean food web into phylogenetically defined groups based on a published phylogeny of the species [15]. The Caribbean food web comprised entirely marine fish trophic interactions. Rezende et al. [15] were able to produce a phylogenetic topology (i.e. a phylogeny with arbitrary branch lengths) for 116 of the fishes in the dataset. We dated as many nodes as possible on the topology based on Hedges & Kumar [40] and Steinke et al. [41], and then used the bladj function of Phylocom [42] to distribute the undated nodes evenly among the dated nodes to produce a dated phylogenetic tree with branch lengths in units of millions of years ago. We then partitioned the food web data at each of the 115 nodes in the tree and calculated marginal likelihoods for each.

3. Results

Grouping the species of food webs according to taxonomic ranks yielded much better likelihoods than what one would expect at random (table 2). In fact, besides the trivial (non-significant) results for kingdoms and phyla in the webs where only one kingdom (Caribbean, Ythan91 and Ythan96) or phylum (Caribbean) is represented, all webs but El Verde produced highly significant results up to the genus level (table 2). El Verde did not yield significant results for kingdom (as the web contains only one plant), nor for phylum (as 90% of the species belong to Chordata). Mill Stream and Ythan91 did not yield significant results for the genus level, whereas the other networks did.

Table 2.

Log likelihoods (L) and p-values obtained from the randomizations experiments. (Low values mean that the likelihood obtained from the taxonomic split into kingdom (K), phylum (P), class (C), order (O), family (F) and genus (G), can be rarely matched or surpassed at random.)

food web	LK	pK	LP	pP	LC	pC
Weddell Sea	−31823.1	0	−23891.4	0	−17706.46	0
Caribbean	−7704.5	1	−7704.5	1	−5223.3	0
Little Rock	−5592.3	0	−4362.9	0	−3720.3	0
Ythan96	−1726.8	1	−1366.6	0	−1237.5	0
Tuesday Lake	−811.8	0	−607.7	0	−527.01	0
Ythan91	−1160.1	1	−951.18	0	−830.74	0
Mill Stream	−632.8	0	−608.3	0	−586.2	0
El Verde	−1033.8	5.72E−01	−1023.5	7.69E−01	−817.3	1.30E−05
Stony Island	−581.7	0	−529.2	0	−518.1	0
food web	LO	pO	LF	pF	LG	pG
Weddell Sea	−12679.65	0	−6759.9	0	−2675.8	0
Caribbean	−4840.6	0	−3176.1	0	−2045.5	4.37E−04
Little Rock	−2721.1	0	−1708.3	0	−336.7	0
Ythan96	−858.0	0	−510.4	0	−276.9	8.74E−03
Tuesday Lake	−335.47	0	−214.63	0	−134.99	0
Ythan91	−547.3	0	−300.8	2.00E−06	−159.0	5.67E−02
Mill Stream	−500.9	0	−303.3	7.30E−05	−192.8	1.55E−01
El Verde	−553.0	0	−240.9	0	−100.1	1.07E−04
Stony Island	−479.5	8.20E−05	−280.5	8.00E−06	−162.1	1.59E−03

These results show that including information on taxonomic rank can illuminate the patterns of interaction in the networks. While this is quite trivial for the kingdom level, we note that most models for food web structure do not discriminate between plants and animals [6–12] (but see Rossberg et al. [14,43]).

We then computed the marginal likelihood for each web and taxonomic rank (table 3). For all webs, the maximum marginal likelihood was achieved at coarser taxonomic ranks. For four of the nine food webs we found that the partition based on class produced the maximum marginal likelihood, whereas for three webs the maximum was achieved for the division into phyla and for two at the kingdom level.

Table 3.

Marginal likelihoods for each food web and partition into kingdom (K), phylum (P), class (C), order (O), family (F) and genus (G). (The last column indicates the taxonomic level giving the highest marginal likelihood.)

food web	K	P	C	O	F	G	best
Weddell Sea	−31866.8	−25244.0	−22508.9	−28588.9	−44541.6	−65375.1	C
Caribbean	−7710.4	−7710.4	−5243.0	−5573.1	−10010.8	−18317.1	C
Little Rock	−5647.6	−4837.2	−4425.2	−5116.8	−7342.1	−15110.5	C
Ythan 96	−1732.1	−1544.6	−1637.9	−2782.3	−4302.7	−5792.2	P
Tuesday Lake	−853.4	−845.4	−805.0	−1059.3	−1769.2	−2278.2	C
Ythan 91	−1164.9	−1014.7	−1051.7	−1650.3	−2516.3	−3318.2	P
Mill Stream	−655.3	−682.4	−759.1	−1227.2	−1979.7	−2684.6	K
El Verde	−1046.8	−1063.3	−1009.7	−1249.6	−2020.2	−2758.6	C
Stony Island	−603.8	−626.4	−692.7	−1313.2	−1986.0	−2809.2	K

The proportion of correctly assigned links in the models based on the different taxonomic partitions is between 12 per cent and 44 per cent for the partitions chosen as the best from the model-selection procedure (table 4). Naturally, a larger amount of links are correctly predicted using finer taxonomic ranks (as overlap does not balance goodness of fit with model complexity).

Table 4.

The overlaps between the feeding links predicted by the models and the feeding links provided by the data. (Values in bold represent the models chosen by the model selection. Triple asterisks indicate a p-value less than 0.001.)

food web	ΩK	ΩP	ΩC	ΩO	ΩF	ΩG
Weddell Sea	0.11***	0.27***	0.42***	0.57***	0.76***	0.90***
Caribbean	0.046	0.046	0.29***	0.32***	0.46***	0.63***
Little Rock	0.12***	0.30***	0.37***	0.53***	0.69***	0.93***
Ythan 96	0.042***	0.12***	0.16***	0.36***	0.59***	0.77***
Tuesday Lake	0.19***	0.34***	0.44***	0.64***	0.76***	0.85***
Ythan 91	0.055***	0.13***	0.19***	0.42***	0.66***	0.81***
Mill Stream	0.263***	0.28***	0.31***	0.41***	0.64***	0.76***
El Verde	0.056	0.059	0.16***	0.36***	0.70***	0.88***
Stony Island	0.19***	0.25***	0.27***	0.32***	0.58***	0.74***

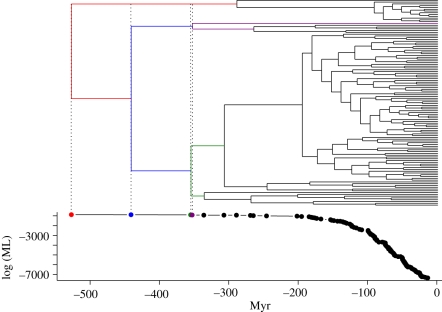
The best fit for the phylogenetic partitioning model for the Caribbean web matched the taxonomic results, which indicated the class-partitioning model as best fit (figure 2). In fact, we found the highest marginal likelihood for the phylogenetic model that split the food web at the root between bony and cartilaginous fishes (i.e. between classes Actinopterygii and Chondrichthyes).

Figure 2.

Phylogenetic tree for 116 species in the Caribbean food web. We report, using the same time axis, the log marginal likelihood for each split in the tree. The first four split and corresponding likelihoods are highlighted.

4. Discussion and conclusions

We here provide a theoretical framework for evolutionary relatedness that can be used to infer community structure. Our results clearly indicate that closely related species tend to interact in a specific way with other groups of closely related species. This is probably because close relatives share similar traits and thus are likely to form a similar pattern of interactions to other groups of close relatives. Evolutionary history is thus highly relevant to food web structure.

Our results also suggest that very basic traits could illuminate the role species take in ecosystems. Partitioning species by taxonomy could possibly be recovered using a combination of traits/characteristics such as metabolic type, habitat preference and feeding mode. Take for example the two webs yielding the maximum marginal likelihood for kingdom (Mill Stream and Stony Island). These two webs display a vast majority of plant–herbivore interactions. Of all the links, 95 per cent of them are of this type in Stony Island and 98 per cent in Mill Stream. It is not surprising, then, that model selection chooses the kingdom partition: as a first approximation, plants only interact with animals and vice versa, forming a quasi-bipartite network. But this distinction between plants and animals could have been found without recurring to taxonomic units. For example, identifying species that could photosynthesize would produce the same split. In other networks that are not almost bipartite, on the other hand, phylum and class yield better results. However, basic distinctions between species could yield similar results. For example, in the Caribbean network, the best split (class) separates the sharks (belonging to the class Chondrichthyes) from the bony fishes (Actinopterygii). Sharks could have been separated based on other characteristics (e.g. respiratory system or type of skeleton). Similarly, in the Ythan Estuary webs, the distinction between Chordata, Mollusca, Arthropoda and so forth could have been produced using a combination of non-taxonomic species traits.

Most of the information on the occurrence of trophic interactions can be recovered using basic taxonomic distinctions (table 4) or, equivalently, with carefully chosen combinations of species traits. Species could be grouped a priori based on shared traits and then those groups could be fitted to food web data using the methods we present here. The group model is especially suited for discrete traits, such as habitat preference or metabolic type, rather than continuous traits, such as body size. On the other hand, taxonomic and phylogenetic partitioning could be performed first to identify significant trophic groupings, and then one could work backwards formulating hypotheses to be tested based on the characteristics that also define those groups.

Our result shows that the more complex food webs (measured as the number of links in the food web after the simplification procedure) often show a higher taxonomic level as the most predictive one (table 4; electronic supplementary material, table S2). For the three most complex food webs, the model selection chooses class. This indicates that sampling effort could play a role in the determination of the ‘best’ taxonomic level. It has been predicted that as species are removed from food webs, the phylogenetic signal should become weaker [19]. This is akin to analysing less and less-resolved webs.

It is worth pointing out that there is a non-negligible part of the food web structure that is not captured by taxonomy. This means that there are additional traits needed to fully explain food web structure.

Other studies have shown that phylogenetic effects are important determinants of community structure [15,26,43–45]. Rezende et al. [15] showed that phylogenetic patterns in food webs may be owing to traits such as body size and habitat selection. However, their results (based on the Caribbean food web) differ fundamentally from those presented here. Rezende and co-workers analysed the modularity of the food web. Modules are defined as groups of species with dense within-module interactions and sparse between-modules connections. They suggested that the food web is highly compartmentalized and that closely related species tend to belong to different modules. Here, we show that when we adopt the more general definition of ‘trophic group’, clustering similar species together can yield important insights into trophic structure.

Cattin et al. [8] constructed a pioneering model where the diet of all species is a consequence of a combination of phylogenetic constraints and adaptation. They could therefore construct food webs with structures relatively close to empirical data. Bersier & Kehrli [46] further explored the relationship between trophic and taxonomic similarity of species in several food webs using the correlation between trophic and taxonomic similarity matrices. They found that phylogeny and food web structure are closely linked. Interestingly, they also found that the correlation differed between consumers and resources, so that closely related resources tended to be preyed upon by similar sets of consumers, whereas closely related consumers tended to prey upon more diverse sets of resources. This skewed signal has also been detected in analyses of the intervality in food webs (measuring to what extent the species in a food web can be ordered in a way such that predators consume adjacent species) [47] and in the strengths of host–parasitoid associations [44]. In the group model, the role of predators and prey of the same group of species are kept distinct (i.e. are modelled by two distinct probabilities), allowing for this differential behaviour.

Rossberg et al. [47] investigated the number of trophic niche dimensions, i.e. species traits, needed to maximize intervality. They showed that when evolutionary aspects were taken into account, food web intervality could be reproduced with relatively few traits compared with when phylogenetic constraints were excluded. Additionally, the same authors provided a framework in which not only the position of a feeding link between two species, but also its strength can be determined using species phylogeny [48]. This suggests that species evolutionary history could also capture finer details of food web structure.

The results from the analysis including species phylogenies for the Caribbean food web matched those obtained with taxonomy: class provides the most parsimonious explanation. This indicates that the bulk of trophic interactions arose early in the diversification of species, owing to evolution of species-specific traits. Producing phylogenetic trees for larger and more diverse webs could further refine the results found using taxonomy.

It is also relevant to ask the question of how good the grouping of species based on taxonomy is, compared with grouping based on other relevant traits. A reasonable grouping could be, for example, based on body size. However, this is not a trivial comparison to preform because taxonomy provides clear splits between the groups, whereas body mass is described on a continuous scale that requires a different splitting method. We preformed a preliminary analysis of groupings based on body size (data available for three webs) and trophic level (all webs, see the electronic supplementary material, appendix). The results are inconclusive: groups based on trophic level and body size can preform better or worse than the corresponding taxonomic case.

The evolutionary history of species in food webs clearly provides important information on their trophic role in the community and thereby important information about food web structure as a whole. The taxonomy of species can be used as a simple surrogate to summarize evolutionary relationships. The methods described here enable the search for biologically relevant groups based on other traits and thus defining which traits, or combination of traits, are of most importance for food web structure.