Effects of male fecundity, interindividual distance and anisotropic pollen dispersal on mating success in a Scots pine (Pinus sylvestris) seed orchard

Abstract

Quantifying the effect of pollen dispersal and flowering traits on mating success is essential for understanding evolutionary responses to changing environments and establishing strategies for forest tree breeding. This study examined, quantitatively, the effects of male fecundity, interindividual distance and anisotropic pollen dispersal on the mating success of Scots pine (Pinus sylvestris), utilizing a well-mapped Scots pine seed orchard. Paternity analysis of 1021 seeds sampled from 87 trees representing 28 clones showed that 53% of the seeds had at least one potential pollen parent within the orchard. Pronounced variation in paternal contribution was observed among clones. Variations in pollen production explained up to 78% of the variation in mating success, which was 11.2 times greater for clones producing the largest amount of pollen than for clones producing the least pollen. Mating success also varied with intertree distance and direction, which explained up to 28% of the variance. Fertilization between neighboring trees 2.3 m apart was 2.4 times more frequent than between trees 4.6 m apart, and up to 12.4 times higher for trees downwind of the presumed prevailing wind direction than for upwind trees. The effective number of pollen donors recorded in the seed orchard (12.2) was smaller than the theoretical expectation (19.7). Based on the empirical observations, a mating model that best describes the gene dispersal pattern in clonal seed orchards was constructed.

Introduction

Gene dispersal, genetic drift and natural selection are the major forces determining the magnitude and direction of microevolution within populations (Hartl and Clark, 2007). In a rapidly changing environment, for example, when ecological changes occur faster than the length of a species' generation, a direct description of contemporary gene flow within and among populations is needed to predict the potential evolutionary responses of plant populations. Such information is also of great practical value in forestry and forest tree breeding. Male and female reproductive successes are influenced by several factors including patterns of pollen dispersal, flowering phenology and fecundity traits (Burczyk and Prat, 1997; Burczyk et al., 2004). Variance in individual reproductive success generated through those factors can either reduce or enhance the genetic value and adaptability of seed orchard crops depending on the seed orchard layout and background pollen contamination (Harju et al., 1996; Lindgren et al., 2009; Torimaru et al., 2009). Knowledge of pollen dispersal and flowering traits is essential for evaluating seed orchard functioning and the implementation of management practices to optimize the gain and diversity of seed orchard crops.

In tree species, characterization of pollen-mediated gene flow relies on evaluation of mating systems and pollen dispersal patterns (Burczyk et al., 1996; Burczyk and Prat, 1997). Inferences about paternity (or parentage) using genetic markers with high levels of polymorphism and codominant expression have provided a powerful approach to evaluate the mating parameters and patterns of pollen dispersal in both natural and breeding populations (Moriguchi et al., 2005; Robledo-Arnuncio and Gil, 2005; Slavov et al., 2005; Gerard et al., 2006; Bacles and Ennos, 2008; Shimono et al., 2011). Such studies have revealed large interindividual differences in mating success, resulting in restricted local breeding neighborhoods (Slavov et al., 2005; Klein et al., 2008). Most studies have reported that interindividual distance explains the heterogeneous contributions to the gene pool (reviewed by Austerlitz et al., 2004). In addition, anisotropic pollen dispersal (that is, directional effects) is also expected to affect mating patterns in wind-pollinated tree species, as wind direction is rarely uniform or random. Anisotropic patterns of pollen dispersal have been reported in some studies (Burczyk et al., 1996; Burczyk and Prat, 1997; Lian et al., 2001; Bacles et al., 2005; Austerlitz et al., 2007), but other studies have failed to detect such effects in natural populations of wind-pollinated tree species (Dow and Ashley, 1996; Streiff et al., 1999; Hanaoka et al., 2007; Pluess et al., 2009). As the spatial arrangements of individuals with varying degrees of fecundity (for example, flower numbers per individual) are evidently nonrandom in natural populations (Itoh et al., 2003; Kanno and Seiwa, 2004; Hosaka et al., 2008), anisotropic pollen dispersal will be masked if trees that produce small quantities of pollen can transfer pollen grains to other trees effectively with the aid of directional air movement. Strong anisotropic pollen dispersal patterns are expected to violate the assumption of random mating in plant populations, resulting in more restricted local breeding neighborhoods than expected. In addition, variation in pollen production among individuals and families is expected to result in heterogeneous paternal contribution to subsequent generations. However, there have been few quantitative evaluations of the genetic consequences of anisotropic pollen dispersal and male fecundity variation, as distinct from the directional effects of nonrandom spatial fecundity, in plant populations.

The aims of this study were to evaluate the effects of male fecundity, interindividual distance and anisotropic pollen dispersal effects on male reproductive success, and to establish a model that, quantitatively, best describes the gene dispersal pattern in clonal seed orchards. To do so we selected a well-mapped Scots pine (Pinus sylvestris) seed orchard in which each clone had a unique multilocus genotype (Torimaru et al., 2009), and the pollen production of each clone had been measured. Mating system parameters and the variance in male reproductive success among the clones were estimated by paternity assignment of open-pollinated seeds. Whereas simple paternity assignment methods seem sufficient for estimating clonal contribution to the total sample of offspring, identifying factors influencing effective pollen dispersal patterns is difficult, as pollen donor locations cannot be conclusively identified in clonal seed orchards. In this regard, a mating model approach, which represents paternal contribution as function forms, can partition the probability of paternity among the ramets of a compatible clone fractionally in relation to intertree distance and direction, and fecundity (see, for example, Burczyk and Prat, 1997). This would enable us to identify the factors affecting the male reproductive success of individual trees. The empirical mating data, fecundity measurements and physical distances were fitted into different mating models to test which combinations of factors (male fecundity, intertree distance or anisotropic pollen dispersal) best explain the observed variance in male reproductive success. Observed male reproductive successes were then compared with estimates from the best-fitting model to quantify their relative importance.

Materials and methods

Seed orchard

A Scots pine seed orchard in Västerhus (63°18′N, 18°32′E) in northern Sweden was selected for the study. This seed orchard covers 13.7 ha and includes 28 clones represented by 3811 grafted trees. It was established in 1991 and reached the commercial production stage in 2005. In 2006, when 15 years old, there was good seed production and satisfactory pollen production (25 kg ha^–1). It is the most genetically advanced Scots pine seed orchard in Sweden, established with tested clones of known breeding values; the predicted genetic gain is the highest among all Scots pine seed orchards in Sweden. The seed orchard was designed using ‘linear deployment' (Lindgren and Matheson, 1986), meaning the ramet number was intentionally varied among clones (ranging from 1 to 9% of the total), with greater numbers of clones of high breeding value. This concept is now commonly applied in the establishment of new seed orchards in Sweden.

Scions from the selected clones were grafted on rootstocks from a seed orchard with a similar origin to Västerhus. The trees were planted in a semirandomized design to maximize the distance between ramets of the same clone. The spacing at the time of planting was 7 m between rows and 2.3 m between successive trees in a given row. The seed orchard is situated on a southwest slope toward a river. It is surrounded by a 30 m corridor of broadleaved trees to the south and open fields in other directions. The closest Scots pine trees to the seed orchard are more than 500 m away. A seed orchard inventory in 2007 found that 3811 of the initially planted 4640 grafts were still alive and 46 rootstocks were recorded (Torimaru et al., 2009).

Cone and needle collection

In June 2007, needles were collected from three ramets of each of the 28 clones for genotyping (two and four ramets were collected for one and four clones, respectively; thus, 87 trees were genotyped in total). To ensure representative sampling, ramets of each clone were selected from across the seed orchard, although there was some clustering around ramets of rare clones. The needles were placed in sealed plastic bags and stored at −20 °C prior to DNA analysis. Cones were collected from the same trees in October 2007 and seeds were extracted during the following 3 weeks. During the entire process, the cones and seed-lots from each ramet were kept separate. Seeds were stored at −20 °C.

Estimation of pollen production

In 2006, the number of pollen strobili (SN) and their mean length (SL) were measured for half of the tree crowns in the experimental block (ca. 0.42 ha) in the orchard. The pollen production (in grams) of the trees was then estimated as 2 × SN × SL × 0.028; 0.028 g is the average yield of pollen for 1 cm of pollen strobili of Scots pine (Koski, 1975). Between 1 and 17 ramets per clone (mean±s.d., 6.8±4.5) were measured and pollen production was averaged for each clone.

Pollen production per clone in the seed orchard was estimated by multiplying the pollen production per ramet per clone and the frequencies of ramets of each clone. Variance component analyses were conducted to quantify the variation in pollen production among ramets within each clone.

DNA extraction and microsatellite genotyping

The method used for the extraction of DNA from the embryos of germinated seeds is described in Torimaru et al. (2009). In this study, we used nine microsatellite loci for genotyping, namely LOP1 (Liewlaksaneeyanawin et al., 2004), PtTX2146, PtTX3025, PtTX3107, PtTX3116, PtTX4001 (Auckland et al., 2002), SsrPt_ctg1376 and SsrPt_ctg4363 (Chagne et al., 2004) and SPAC12.5 (Soranzo et al., 1998). The PCR conditions for each locus, the method of allele identification and the size distribution of alleles and their frequencies in the Scots pine clones in this seed orchard have been described previously by Torimaru et al. (2009). Using these nine loci, the total exclusion probability of there being a second potential parent (pollen parent) was 0.999 for the 28 clones (rootstocks not being genotyped) in the seed orchard (Torimaru et al., 2009). In this study, 10–13 open-pollinated seeds were genotyped from each of the 87 trees: a total of 1021 seeds (22–48 seeds per clone) were genotyped. To minimize genotyping error, all the electrophenograms of each sample were double checked, and ambiguous samples were re-amplified and re-run to obtain reproducible genotypes.

Data analysis

Paternity analysis and mating system parameters

Paternity of each seed was assigned based on a null-assuming simple exclusion method, as described in Torimaru et al. (2009). In this method, when both the maternal and seed genotypes appeared to be homozygous at a locus that exhibits null alleles, they are treated as heterozygous possessing one null allele. In such cases, we cannot exclude paternal candidates with homozygous genotypes that are different from the seed because of the presence of the null allele. If the genotype of a seed did not match any of the 28 clones, it was considered to have been sired by a father outside the seed orchard, thus indicating external pollen contamination. When all but one candidate clone genotype could be excluded (an exact match), we designated the remaining clone as the father. Our previous simulation study demonstrated that, for the clones in the Västerhus seed orchard, paternity assignment using this simple exclusion method assigned paternities better than the maximum likelihood method (Wang et al., 2010). The confidence of the paternity assignment for each of the exactly matched seeds was evaluated on the basis of a likelihood ratio, that is, a paternity index, as used in human paternity tests (Pena and Chakraborty, 1994) and the posterior likelihood using Bayes' theorem (that is, probability of paternity; Evett and Weir, 1998), which were calculated using the method developed for cases where the genotypes of mothers are known and null alleles are considered (Brenner, 1997; Evett and Weir, 1998; Torimaru et al., 2009). Furthermore, a correction factor for cryptic gene flow, that is, the proportion of seeds fertilized by pollen from trees other than the seed orchard clones but not recognized as such, was incorporated to obtain corrected contamination rates for each clone and the orchard. Using the background allele frequency estimated from genotypes of seeds (see Appendix 1), this factor was estimated to be 0.005, and the number of seeds that matched unrelated fathers in the orchard clones by chance could be estimated by multiplying the correction factor by the number of seeds with a paternal parent from the seed orchard clones (see details including the method in Torimaru et al., 2009).

Observed paternal contributions of each clone were calculated as follows: for each of the mother trees, proportions of open-pollinated seeds sired by different clones were calculated based on the result of paternity analysis, and then weighted and averaged across 87 ramets by the proportion of sampled seed per ramet relative to the total number of seeds sampled (that is, 1021 seeds).

Modeling the pollen dispersal and male fecundity effect

Pollen dispersal: We modeled pollen dispersal in terms of distance and direction of mating pairs. The first represents a function of pollen dispersal decreasing with distance from the focal male. To achieve this, we used a two-parameter (a and b) bivariate exponential-power function (p_jkl^ep) to describe the probability of a pollen grain released from the lth ramet of the kth clone contributing to the fertilizing pollen pool of the jth maternal tree (Clark, 1998) as follows:

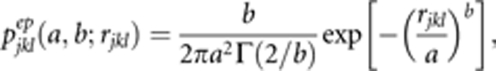where Γ is the classically defined gamma function; r_jkl is the distance between the lth ramet of the kth clone and the jth maternal tree sampled; a is the scale parameter; and b is the shape parameter affecting the ‘fatness' of the tail of the dispersal distribution. When b<1, the dispersal kernel is fat tailed (Clark, 1998), that is, the long-range decay of the probability is slower than for the exponential distribution (b=1) and considerably slower than for a normal distribution (b=2), indicating an increased probability of long-distance dispersal events. Conversely, when b>1, the dispersal is thin tailed, with a rapid decrease of the dispersal function, implying that there are much fewer long-distance dispersal events than when b<1 (see Austerlitz et al., 2004 for further details).

Second, we assessed the effect of direction on pollen dispersal (that is, anisotropic dispersal) within the seed orchard (Burczyk et al., 1996; Burczyk and Prat, 1997). For this, the von Mises function p_jkl^vM, also known as the circular normal distribution (Mardia and Jupp, 2000), was used (see also Chybicki and Burczyk, 2010), as follows:

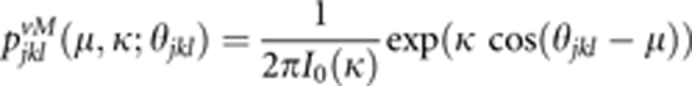where I₀ is the modified Bessel function of order zero; θ_jkl is the direction to the lth ramet of the kth clone from the jth maternal tree; μ is the prevailing direction in which pollen disperses (the distribution is clustered around μ); and κ is a measure of concentration.

Male fecundity: In the present study, equal fecundity among different ramets of the same clone was assumed. In order to obtain flexible responses for male fecundity of the kth clone to the fertilizing pollen pool, from a linear response to nonlinear changes, the logistic function was used as follows: f_k=1/[1+exp(c₁+c₂ × x_k)], where x_k represents the pollen production per ramet of the kth clone measured in 2006 (Table 1), and c₂ corresponds to the correlation between the amount of pollen produced and effective fecundity, such that if the correlation between them is positive, c₂<0, otherwise c₂>0. The amount of pollen when trees have a 50% probability of effective fecundity can be estimated to be –c₁/c₂.

Table 1. Total number of ramets, number of sampled ramets, pollen production per ramet and per clone, number of seeds sired by each clone and global number of effective pollen donors (N_ep).

Clone ID	No. of ramets	No. of sampled ramets	Pollen production per ramet (g)	Pollen production per clone (kg)	No. of seeds sired	Global Nepa
AC1006	254	3	45	11.3	16	14.1	(13.1, 15.1)
AC1075	61	3	39	2.3	18	13.0	(11.3, 14.4)
AC2047	55	3	81	4.5	4	9.9	(7.8, 11.9)
AC2064	170	3	38	6.4	54	10.8	(9.5, 12.3)
AC3015	48	3	59	2.8	2	11.8	(10.0, 13.9)
AC3033	49	3	66	3.3	13	14.0	(11.9, 15.9)
AC3040	127	3	56	7.2	18	12.2	(10.7, 13.7)
AC3056	338	3	24	8.2	40	11.8	(11.0, 12.6)
AC3065	45	3	16	0.7	1	13.0	(11.0, 15.2)
AC4221	64	3	22	1.4	6	14.5	(12.1, 16.5)
X4203	67	4	8	0.5	3	9.8	(8.3, 11.8)
Y2004	63	3	45	2.8	5	10.0	(7.9, 12.0)
Y2005	310	3	28	8.8	9	8.5	(7.6, 9.3)
Y3001	165	3	22	3.6	3	10.7	(9.5, 11.9)
Y3012	230	4	84	19.4	80	12.3	(11.0, 13.3)
Y3014	190	3	79	15.0	35	11.8	(10.5, 12.8)
Y4016	276	3	25	7.0	17	13.8	(12.6, 14.6)
Y4103	41	3	67	2.8	21	12.4	(10.1, 14.9)
Y4507	215	3	224	48.3	102	17.1	(15.5, 18.2)
Y4508	107	3	35	3.8	3	14.2	(12.7, 15.7)
Z2081	210	4	57	12.0	14	12.1	(11.0, 13.1)
Z3007	221	2	61	13.4	37	14.1	(13.1, 15.2)
Z3009	89	3	30	2.7	9	13.7	(12.2, 14.9)
Z3029	91	3	41	3.8	6	13.1	(11.2, 14.8)
Z4003	107	3	50	5.4	17	13.4	(11.8, 14.8)
Z4019	61	3	46	2.8	2	14.7	(12.5, 16.7)
Z4022	122	3	20	2.4	6	15.0	(13.6, 16.7)
Z4032	35	4	49	1.7	3	12.3	(9.9, 14.7)
Total	3811	87		204.3	544	13.7	(13.3, 13.9)

^aCalculated by assuming all trees (that is, 3811 grafts) to be mother trees with equal numbers of seeds (12 seeds), and by applying the parameters for pollen dispersal and mating system in the best-fitting model. The mean values of 100 simulations are reported. The 95% confidence intervals are given in parentheses.

The expected contribution of the kth clone to the local fertilizing pollen pool of the jth mother clone (π_jk) and over to the global sampled pollen pool of the sampled mothers (π_•k) were calculated as follows:

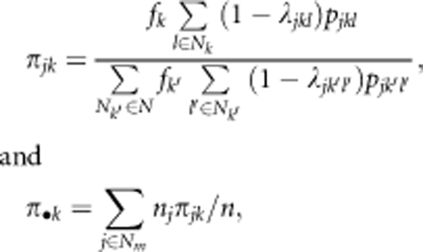where λ_jkl is defined such that if the jth mother clone and the lth ramet of the kth clone are the same clone, then λ_jkl=1, but if they are different, λ_jkl=0. The term p_jkl represents the probability that a pollen grain emitted from the lth ramet of the kth clone travels to the jth mother clone, calculated from the dispersal function (p_jkl^ep, p_jkl^vM, or p_jkl^ep × p_jkl^vM); n_j is the number of seeds sampled from the jth mother; n is the total number of sampled seeds; N, N_m and N_k are the numbers of all grafts in the seed orchard (that is, 3811 grafts, excluding rootstocks), the number of mother ramets sampled (that is, 87 ramets) and the numbers of grafts of the kth clone in the seed orchard, respectively. Note that unlike the situation in natural populations, we have an unknown intermate distance and direction for every offspring in a clonal seed orchard, and π_jk represents the summation of probabilities of paternal contribution to the jth mother clone over ramets of the kth clones.

Identifying the factors that influence mating outcome

To investigate the effects of the environment surrounding a mother tree on its self-fertilization and outcrossing, the probability of self-fertilization (s_j) and outcrossing with pollen from outside the seed orchard or rootstock within the orchard (m_j) for each seed sampled from the jth maternal trees are expressed by the function of variables of interest using an approach applied to link functions in generalized linear models (McCullagh and Nelder, 1989), as follows:

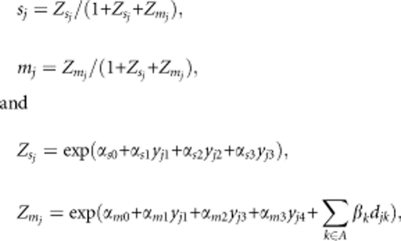where y_j1 represents the amount of auto-pollen (that is, the amount of pollen produced by a tree itself), y_j2 is the self-fertilizing pollen from the ramets of each clone, y_j3 is the outcrossing pollen received from the seed orchard clones (not including pollen from the rootstocks) and y_j4 is the outcrossing pollen from the rootstocks within the seed orchard. The term d_jk represents the distances to the eight angular edges of the seed orchard from the jth maternal tree (that is, eight azimuths); A represents the eight equal angular sectors.

In the present study, the amount of auto-pollen of the jth maternal tree (y_j1) was assumed to be equal among ramets of the same clone, and was represented by pollen production per ramet per clone (see Table 1). On the other hand, the amounts of self-fertilizing (y_j2) and outcrossing (y_j3) pollen received from the clones surrounding the jth maternal tree were assumed to be proportional to the sum of estimates obtained from male fecundities weighted by the pollen dispersal functions as follows:

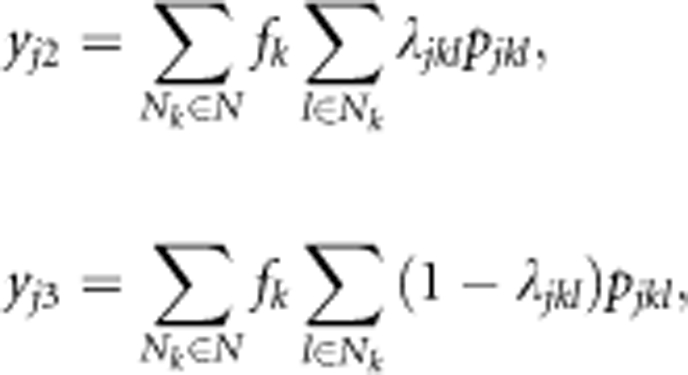The amount of pollen received from the rootstocks surrounding the jth maternal tree (y_j4) is assumed to be proportional to the sum of estimates obtained only from the pollen dispersal functions, that is, 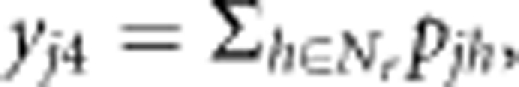where p_jh represents the probability that a pollen grain emitted from the hth rootstock travels to the jth mother clone (p_jh^ep, p_jh^vM or p_jh^ep × p_jh^vM) and N_r represents the number of rootstocks (that is, 46 grafts). All of the variables (y_j1, y_j2, y_j3, y_j4 and d_jk) are standardized to enhance the efficiency of searching for the optimal values of regression coefficients. The ‘slopes' of Z_sj (α_s1, α_s2, and α_s3) and Z_mj (α_m1, α_m2, α_m3, and β_k) describe how self-fertilization and outcrossing by pollen from trees other than the seed orchard clones change with the corresponding variables. When none of the ‘slopes' differ significantly from zero, the model reduces to a ‘standard' mating model with constant rates of self-fertilization and outcrossing by pollen from trees other than the seed orchard clones.

Fitting of mating models

The mating patterns in the seed orchard were analyzed using a modified version of the neighborhood model (Burczyk et al., 1996; Burczyk and Prat, 1997), which is based on the principle of Mendelian segregation between offspring and parents. Each seed sampled from the jth mother clone with genotype M_j could have been produced by self-pollination (with probability s_j), by outcrossing with pollen from trees other than the seed orchard clones (with probability m_j), or through fertilization by pollen from clonal trees within the seed orchard (with probability 1−m_j−s_j). Following this rationale, the probability of observing a specific multilocus diploid genotype (g_ij) in the ith seed of the jth mother clone with genotype M_j is:

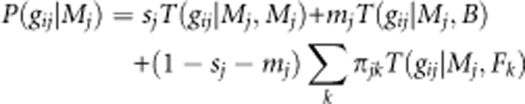where T(g_ij∣M_j, M_j), T(g_ij∣M_j, B), and T(g_ij∣M_j, F_k) are the transition probabilities of an offspring having a diploid genotype g_ij when the mother of genotype M_j is self-fertilized, fertilized by pollen from non-seed orchard trees (that is, background pollen, B) or fertilized by pollen from a tree of genotype F_k different from the genotype M_j in the seed orchard, respectively (Devlin et al., 1988). As two loci were found to have a null allele (Torimaru et al., 2009), all the transition probabilities were adjusted accordingly (see Appendix 2 for calculation). In order to calculate T(g_ij∣M_j, B), background pollen allele frequencies (B) are needed (Burczyk et al., 2002; Oddou-Muratorio et al., 2003). Without knowledge of the background pollen, estimates in the mating model can be biased, particularly if the background pollen allele frequency is assumed to be equal to that of the local population (for example, the seed orchard; Burczyk and Chybicki, 2004). Thus, in this study, background allele frequencies were derived from the identified contaminating pollen in the open-pollinated seed crop (see Appendix 1 for estimate).

Under the above models, the log-likelihood function for all 1021 seeds from the 87 trees is as follows:

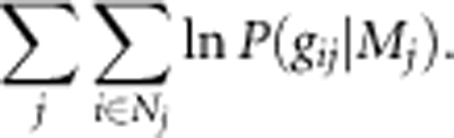The function was maximized by optimizing the parameter sets of mating (α_s0, α_s1, α_s2, α_s3, α_m0, α_m1, α_m2, α_m3 and β_k), dispersal kernels (a, b, μ and κ) and the coefficients of male fecundity effects (c₁ and c₂), by a quasi-Newton method using the function ‘optim' in R. 2.8.0 software (R Development Core Team, 2008). As the sinusoidal functions in the joint density, as well as many parameterizations, cause the maximization programs to become trapped at local maxima, we modified the maximization process as follows. We partitioned (0, 2π) into five equal subintervals. In each subinterval, the maximum of the likelihood function and the maximum likelihood estimators of the parameters were obtained. The global maximum likelihood estimation was then obtained by taking the maximum of these local maxima. We conducted 10 independent runs with different initial values to confirm that all runs converged to the same parameter values with the same maximum likelihood. Beginning with the simplest model, that is, no spatial effect and no male fecundity effect as the null hypothesis, we tested the models with various sets of combinations of spatial structure and male fecundity, and the optimized models were compared using the Akaike Information Criterion (AIC; Akaike, 1973):

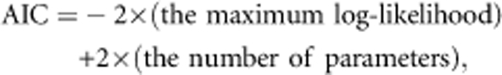AIC values enabled us to make comparisons between models: models with smaller AIC values are more appropriate explanations of the observed data (Burnham and Anderson, 2002). The differences between the AIC values obtained for each of the models and the minimum AIC value from the best-fitting model (ΔAIC) were calculated, and each model with a ΔAIC value ⩽2 was considered to be one of the most parsimonious, and was thus selected as one of the best models (Burnham and Anderson, 2002). This allowed an assessment of the relative importance of the factors male fecundity, dispersal distance and direction for describing the mating patterns observed in the seed orchard. To search effectively for the best-fitting model over 2¹⁹ possible models, we first looked at the set of mating system parameters with the lowest AIC value with no spatial and fecundity effects. We then applied the three dispersal functions (p^ep, p^vM p^ep × p^vM) with and without the effect of male fecundity (f) to search for the best model. After selecting the best-fitting model, we used it to simulate genotypes for each of the 87 sampled trees: the number of genotypes was the same as the number of seeds, and we sampled from each ramet; these genotypes were then used to re-estimate the parameters. This procedure was repeated 100 times and the 95% confidence intervals for the estimated parameters in the best-fitting model were constructed by means of parametric bootstrapping (Manly, 1997).

In addition, we computed the proportion of variability in male mating successes explained by each mating model (r²) as follows (Oddou-Muratorio et al., 2005):

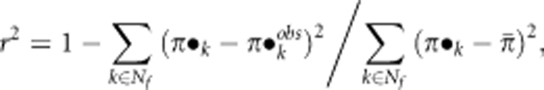where π_•k^obs represents the observed paternal contribution of the kth clone (see the section on paternity analysis); and 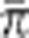is the average observed paternal contribution per clone over 28 clones.

Effective number of pollen donors and pollen dispersal distance

The effective number of pollen donors, N_ep, in the observed pollen pool was calculated. The N_ep is equivalent to the number of male parents in the seed orchard under an ideal situation where the fertility of all males in the seed orchard is equal (Burczyk et al., 1996). This value was calculated as the inverse of the probability of paternal identity for two seeds drawn at random from the 1021 sampled seeds and adjusted for unequal sample size of seeds per mother as follows:

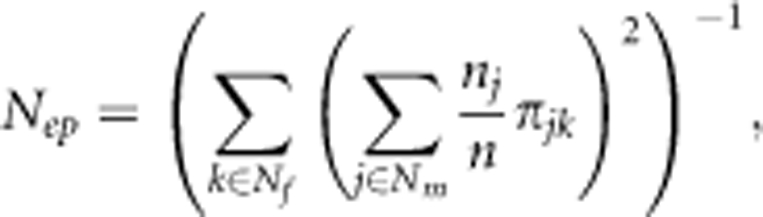where N_f represents the number of paternal clones (that is, 28 clones) (Klein et al., 2008). The 95% confidence interval was constructed based on 100 simulations. The global N_ep was calculated by assuming that all trees (that is, 3811 grafts) were mother trees that produced equal numbers of seeds, and applying the parameters of pollen dispersal and mating system from the best-fitting model. The N_ep over the seed orchard was adjusted by dividing it by the effective number of clones (19.7 from Fries et al., 2008) to remove the effects of uneven clonal replication. Similarly, the global N_ep for the jth clone was calculated as follows:

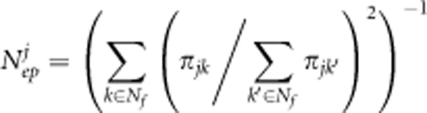Finally, the male fertilities estimated according to the best-fitting model (using the parameters for the full model in Table 2) were used to calculate the mean distance of effective pollen dispersal (δ) between mother clones and their outcrossing mates (not including rootstocks) within the seed orchard, in which intertree distances are weighted by paternal contribution of clones and the number of seeds sampled per mother tree, as follows (Burczyk et al., 1996, 2002):

Table 2. Maximum-likelihood estimates of the best-fitting neighborhood mating model (in bold type) and its submodels obtained by removing one effect each.

Distance	Direction	Fecundity	Variation in mating system	b	δexp	μ	κ	c1	c2
Effects				Mating success parameters
×	×	×	×	0.199 (0.116, 0.391)	73.5 (30.4, 240.2)	312.5 (297.8, 327.0)	1.26 (0.84, 1.90)	2.58 (2.19, 2.92)	−0.03 (−0.04, −0.02)
×	×	—	×	0.23	57.9	312.6	1.27	—	—
—	×	×	×	—	—	288.1	1.27	2.64	−0.03
×	—	×	×	0.313	45.3	—	—	2.59	−0.03
×	×	×	—	0.193	77.2	312.8	1.27	2.58	−0.03
				Mating system parameters			−LogL.	AIC	ΔAIC
				αs0	αm0	αm1
×	×	×	×	−3.23 (−3.73, −2.95)	—	−0.21 (−0.39, −0.07)	16 375.51	32 767.03	0
×	×	—	×	−3.23	—	−0.21	16 479.62	32 971.25	204.2
—	×	×	×	−3.22	—	−0.21	16 427.96	32 867.92	100.9
×	—	×	×	−3.23	—	−0.21	16 391.52	32 795.03	28
×	×	×	—	−3.26	−0.06	—	16 379.65	32 775.31	8.3

Abbreviations: AIC, Akaike's information criterion; ΔAIC, the differences between the AIC values obtained for each of the models and the minimum AIC value from the best-fitting model; −LogL, negative of the natural logarithm of the likelihood function with the optimized parameters.

Mating success (b, δ_exp, μ, κ, c₁ and c₂) and mating system (α_s0, α_m0 and α_m1) parameters were optimized. The 95% confidence intervals of the parameters estimated under the best-fitting model are given in parentheses based on 100 parametric bootstraps. δ_exp=aΓ(3/b)/ Γ(2/b), the mean distance of effective pollen dispersal estimated from a bivariate exponential power function only. Note that μ was measured clockwise from north and transformed into arc degree.

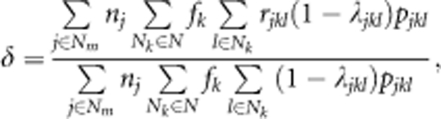where r_jkl represents the distance between the jth mother clone and the lth ramets of the kth clone. Note that the average direction of effective pollen dispersal was equal to the maximum estimate of μ in the best-fitting model.

Results

Pollen production and mating system in the seed orchard

The Scots pine seeds harvested in 2007 were the result of pollination in spring 2006. Pollen production in the Västerhus seed orchard (Table 1) was, on average, 50.6 g per ramet (range 8–224 g) and 7.3 kg per clone (range 0.5–48.3 kg). The variance component analysis indicated that there was minor within-clone variation in pollen production per ramet (4.8%), and major between-clone variation (95.2%). This demonstrates that pollen production is similar among different ramets of the same clone but varies profoundly between different clones. Thus, male fecundity is a strong genotype-specific trait in Scots pine.

Paternity analysis showed that 544 out of 1021 seeds from the Västerhus seed orchard (53%) had at least one candidate pollen parent within the seed orchard (Table 1). The remaining 477 seeds did not match any of the multilocus genotypes of seed orchard clones and were probably sired by pollen from outside the orchard or from rootstocks within the orchard. The estimated contamination rate in the orchard was 47%, after correction for cryptic pollen flow. The number of seeds from cryptic pollen flow (because of mating with pollen from the rootstocks or trees outside the orchard) for each orchard clone was <0.16. The pollen contamination rates per ramet ranged from 0.8 to 100%, and the variance component analysis indicated that variation in contamination rate among clones (63.3%) was significantly larger than that among ramets within the same clone (36.7% P<0.05).

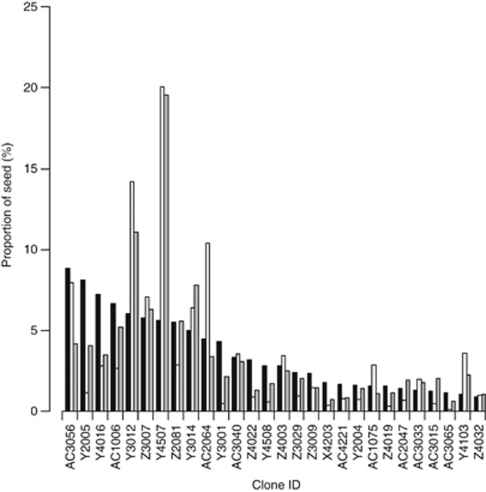
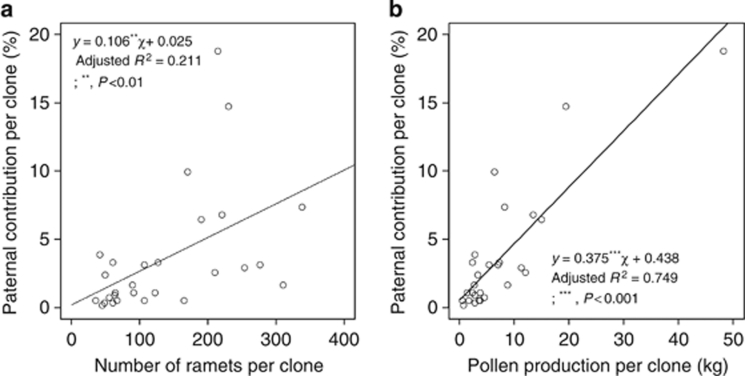
Of the 544 seeds apparently sired by seed orchard clones, 541 (that is, 99%) had a single exactly matched father, and 501 of these had probabilities of assigned paternity exceeding 0.95, indicating high confidence in the assignment of fathers. For the remaining 40 seeds, the probabilities of paternity ranged from 0.438 to 0.949. Only three seeds were compatible with two candidate fathers in the seed orchard. Based on the determined paternity, large variations in paternal contributions (as effective fertilizing male gametes) between the 28 clones were observed (Figure 1). Five clones (AC3015, AC3065, X4203, Y3001 and Z4019) contributed little to the fertilizing pollen pool. The clone that made the greatest contribution was Y4507; it fertilized 20% of the 544 seeds. The top five clones (Y4507, Y3012, AC2064, AC3056 and Z3007) collectively accounted for 60% of the paternity of the seed crop from mating among orchard clones. As anticipated, on the basis of the seed orchard design with unequal ramet frequencies among clones, the paternal contribution per clone increased with the number of grafts per clone and with pollen production per clone, which accounted for ∼21% and 75% of the variation in paternal contributions, respectively (Figure 2).

Figure 1.

Proportions of open-pollinated seeds sired by different clones. The expected values based on the proportion of the clones among all grafts are indicated by the black columns. The observed values are shown by the white columns. The predictions of the best-fitting mating model (π_•k, see text for details of the calculation), which incorporates the effects of male fecundities, intertree distances and anisotropic pollen dispersal, are indicated by the gray columns.

Figure 2.

Relationships between the number of ramets per clone (a) and pollen production per clone (b) in 2006 and actual paternal contribution. The paternal contribution of each clone is represented by the proportion of open-pollinated seeds sired by its pollen. The pollen production per clone was estimated on the basis of the number of ramets per clone multiplied by the mean pollen production per ramet within the clone (see also Table 1).

Among 1021 seeds, 20 (2%) were classified as resulting from self-fertilization, and this was observed in 10 of the 28 clones, varying from 3 to 11% (Supplementary Material S1). The variance component analysis indicated that variation in self-fertilization rate among clones (65.4%) was significantly larger than that among ramets within a clone (34.6% P<0.05). The effective number of pollen donors (N_ep) in the seed orchard estimated from the 87 mother trees was 12.2, with a 95% confidence interval of 10.3–13.9. The global N_ep, which was estimated from 3811 trees using the best-fitting mating model, ranged from 8.5–17.1 among clones (Table 1), with an average across the clones of 13.7 and a 95% confidence interval of 13.3–13.9. These estimates were significantly lower than the theoretical value for random mating within the seed orchard (N_ep=19.7), in which the contribution of each clone to the fertilizing pollen pool is assumed to be proportional to its number of grafts in the seed orchard. The ratio of the observed effective number of pollen donors to the number if random mating was assumed was 0.70.

Mating model evaluation

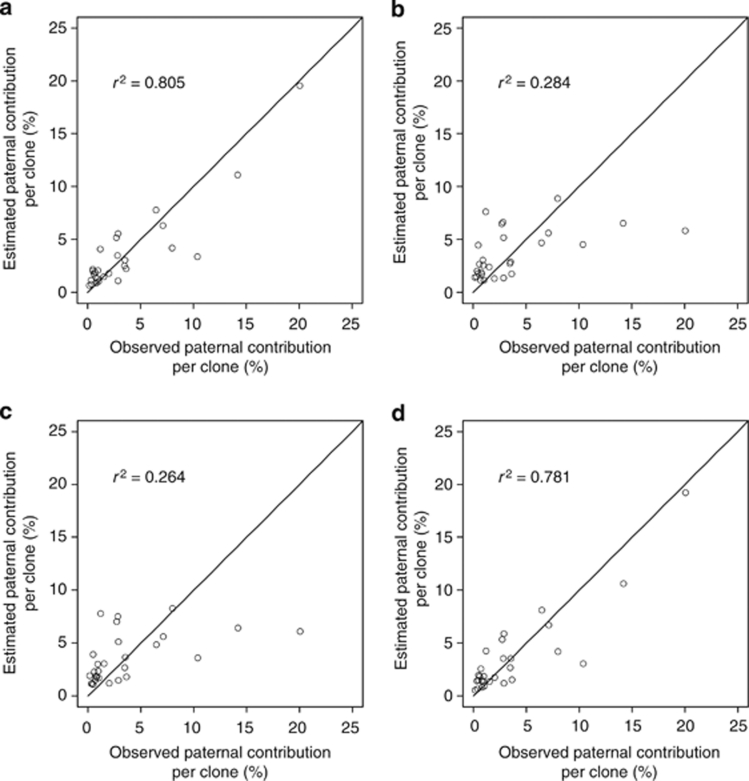
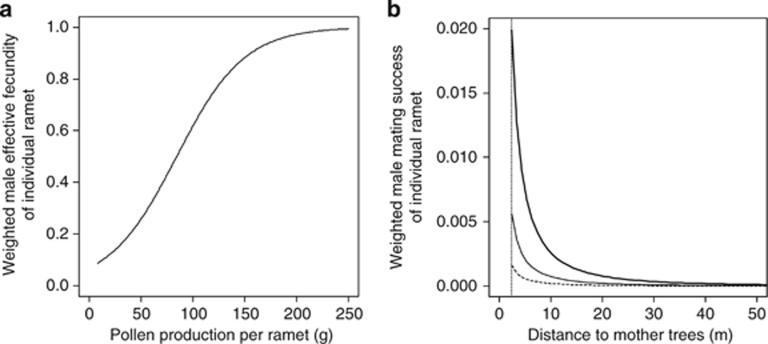
The performance of the best-fitting mating model, as well as the relevant submodels, is summarized in Table 2. The mating model that incorporated the effects of distance, direction, male fecundity and among-tree variation in mating system (that is, self-fertilization and outcrossing rates) appeared to have the lowest AIC value, and explained ca. 81% of the variability of observed paternal contribution per clone (Figure 3a). The model that considered only the effect of male fecundity performed reasonably well and explained 78% of the variability in male mating success (Figure 3d). The model that excluded the effect of male fecundity exhibited the greatest reduction in AIC values (ΔAIC=204.2) of the four effects tested (Table 2). This means that male fecundity is the most important variable in predicting male mating success. In the best-fitting model, the optimized parameters (c₁ and c₂) indicated that clones with high pollen production achieved high levels of mating success (Figure 4a); the amount of pollen production associated with trees that had a 50% probability of effective fecundity was estimated to be 86.0 g (=−2.58/−0.03). This model predicts that the mating success of the clone with the highest pollen production (Y4507) is 11.2 times greater than the clone with the lowest pollen production (X4203), when all other parameters are equal. In the best-fitting model, the mean distance of effective pollen dispersal (δ) between mother clones and their outcrossing mates was 36.3 m with a 95% confidence interval of 26.7–44.4 m. In contrast, the average distance to randomly selected trees (where ramets of the same clone were excluded) from each mother tree was 151.0 m.

Figure 3.

Comparison of observed paternal contribution per clone with values predicted by the mating models: (a) the best-fitting model assuming the effects of male fecundity, distance and direction; (b) distance effect only; (c) directional effect only; and (d) fecundity effect only. Diagonals represent the estimated paternal contribution identified to the observed ones. The r² represents the proportion of variability in male mating success explained by the model under consideration.

Figure 4.

Predicted values of weighted male effective fecundity (a) and mating success (b) of individual ramets. (a) The effects of pollen production on the effective fecundity, weighted according to the logistic function: f=1/[1+exp(c₁+c₂ × x)], where x represents the pollen production per ramet for a clone, and c₁ and c₂ correspond to the coefficients of male fecundity effects on mating success. In this study, c₁=2.58, c₂=−0.03 (see Table 2). The curve started from the minimum observed pollen production per ramet in the seed orchard. (b) The effects of distances and directions to mother trees. Thick, thin and dashed lines represent the relative mating success in azimuth directions of maximum (313°), moderate (43° and 223°) and minimum (133°) dispersal. The dotted vertical line indicates the minimum distance between trees (that is, 2.3 m) in the seed orchard. Optimized parameters in the best-fitting model were used (see Table 2).

The model that did not include any distance effect resulted in the second largest reduction in AIC value (ΔAIC=100.9), indicating that intertree distance also predicts variations in male mating success. We simulated 1021 genotypes of seeds using the optimized mating model with exponential decay in pollen dispersal with distance (that is, shape parameter b=1), and these genotypes were then applied to a model including an exponential power decay function. The maximum likelihood estimate of the 95% confidence interval for b was 0.517–2.063 (mean=0.959), indicating that the observed distribution of pollen dispersal (b=0.199) was significantly leptokurtic and fat tailed (Figure 4b). This implies, for example, that mating success will be 2.4 times higher between nearest neighbor trees (2.3 m apart) than between second-nearest neighbors (4.6 m apart), but that the mating ratios between trees >100 m apart will be close to unity and the differences in distance between distant trees have no significant impact on mating success. Thus, there is an equal probability of pollen arriving from anywhere further than 100 m away.

The model that did not account for directional effect had a weaker impact on ΔAIC (28.0) than that which excluded distance effect, indicating that pollen dispersal direction has a moderate effect on male mating success. The concentration parameter (κ) was used to compare the mating success of males located in different directions relative to the maternal trees, when all other parameters were set to be equal (Figure 4b). The best-fitting model predicted that pollen dispersal was greatest to the northwest (313°) and the mating success of males located southeast (that is, 133°) of maternal ramets was 12.4 times higher than those located northwest of maternal ramets and 3.5 times higher than those to the northeast (43°) and southwest (223°) when intermating distance was set to the minimum intertree distance (that is, 2.3 m) for the orchard plantation. Both models that considered only the effect of spatial components (distance and direction) performed poorly in explaining the variability in male mating success (28% and 26%, respectively, Figures 3b and c) as compared with the best-fitting model. These estimated proportions, however, were slightly higher than that for the null model based only on the ramet frequencies of clones (r²=0.240).

The model that did not take into account variation in mating system parameters had little impact on the ΔAIC value (Table 2). The best-fitting model predicted that an increase in pollen production of individual ramets reduced the impact of pollen from non-seed orchard clones. However, when the three outliers for high pollen production (Y4507, Supplementary Material S2) were excluded from the analysis, the pollen production per ramet was no longer an effective predictor of male mating success, and the model with a constant proportion of pollen from non-seed orchard clones was supported (data not shown). The amount of pollen from the surrounding trees (clonal or rootstocks) of a mother, as well as its distance to the seed orchard's edges, had almost no effect on its self-fertilization rate or the pollen contamination rate.

Discussion

The paternal contribution of clones to the seeds sampled was very skewed, in accordance with previous studies in seed orchards (Moriguchi et al., 2005; Slavov et al., 2005). The effective number of pollen donors (N_ep=12.2) detected in this study was higher than recorded in seed orchards of other wind-pollinated species such as Picea abies (N_ep=6.7, Burczyk et al., 2004) and Pseudotsuga menziesii (N_ep=5.7–11.0, Burczyk and Prat, 1997). Because of the high proportion of effective pollen donors relative to the number of potential fathers in the seed orchard (0.7), the genetic diversity of the seed orchard crops is being maintained to an acceptable level. The deployment of better clones, achieved by intentionally increasing their proportion in the orchard, did not severely reduce the level of diversity. This information about the genetic function of ‘linear deployment' should be helpful in future seed orchard programs that aim at maximizing the gain without compromising diversity too much.

We found that the number of ramets of each clone positively correlated with their paternal contribution. This is to be expected if each ramet contributes additively to the fertilizing pollen pool. However, deviations from expectations were detected in a few cases because of variations in clonal pollen production (Figure 2a). Mating model analysis revealed that pollen production per clone can be used as a good predictor for male reproductive success even without spatial information (Figure 3d), suggesting that male fecundity was an essential determinant of male reproductive success in the seed orchard. This has also been found in other clonal seed orchards (Burczyk and Prat, 1997; Burczyk et al., 2004), and in some natural populations (Burczyk et al., 1996; Goto et al., 2006) of wind-pollinated species.

The estimated value for the mean distance of effective pollen dispersal (δ=36.7 m) was much shorter than that assuming random mating (δ=151.0 m). This spatial proximity had a moderate influence on male reproductive success, in accordance with previous studies of Scots pine, which indicated that 25–31% of mating is among nearest neighbors (Shen et al., 1981; Robledo-Arnuncio and Gil, 2005). However, the fat-tailed pattern of the pollen dispersal curve indicated that long-distance dispersal events also occur in the seed orchard. These results are also in accordance with observations of mating patterns in other wind-pollinated tree species such as Fraxinus mandshurica (Goto et al., 2006), Populus trichocarpa (Slavov et al., 2009), Pinus densiflora (Lian et al., 2001) and Quercus species (Streiff et al., 1999; Nakanishi et al., 2004).

The directional bias with respect to pollen dispersal found within the seed orchard was probably because of wind strength and direction during the flowering season, a feature that has been reported in other studies (Burczyk et al., 1996; Lian et al., 2001; Bacles et al., 2005; Austerlitz et al., 2007). In the region where the Västerhus seed orchard is located, the prevailing daytime winds blow toward the northeast during the flowering period (data obtained from the Skagsudde weather station located 25 km from the seed orchard). Our results, however, suggest that the bias of pollen dispersal was toward the northwest. This discrepancy between the direction of pollen dispersal and the regional prevailing wind has been found in a few other cases (Burczyk et al., 1996, 2004; Robledo-Arnuncio and Gil, 2005). As pointed out by Burczyk et al. (1996), the local topography and vegetation surrounding the study site could modify the prevailing wind direction.

Flowering phenology is probably one of the most important factors affecting outcrossing patterns. Burczyk and Prat (1997) demonstrated in a seed orchard of P. menziesii that mating success is positively correlated with male fecundity for intermediate and later flowering trees, but not for early ones. The outcrossing patterns in the Västerhus seed orchard could be affected, to some degree, by such an unmeasured effect as the function represented is nonlinear in form (Figure 4a).

Most previous studies have identified the factors that contribute to male reproductive successes; these include interindividual distance and direction and fecundity. Few studies, however, have quantified their relative importance; this is because of the limited accessibility of such ecological and biological measurements in natural populations. Artificial plantations provide a good opportunity to validate hypotheses that are not testable in natural populations. Our approach combined paternity assignment using microsatellite markers with mating models that incorporated ecological factors, and provided a quantitative assessment of the roles of fecundity and spatial characteristics on mating success in a population of a wind-pollinated species. The models developed in this study could facilitate quantitative dissection of the complex interactions in the mating systems of forest trees.

Appendix 1

Estimation of background allele frequency

The probability model underlying the estimation of background allele frequencies assumes unlinked loci and no correlated paternity. The first assumption is valid in our study as no linkage disequilibrium was found (data not shown). Significant correlated paternity seems unlikely given the large number of potential candidate fathers, all of which were a considerable distance away from the seed orchard.

The Kronecker operator is defined such that if two alleles A_i and A_j in a locus are the same, then δ_ij=1, whereas δ_ij=0 if they are different. For allele k at a locus, the probability that this allele is transmitted to the progeny, given a parent with genotype A_iA_j, is:

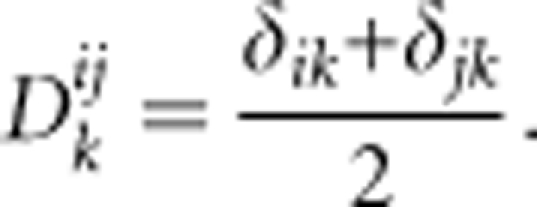In the case of a locus without null alleles, the probability of producing progeny of genotype A_kA_l from background (contaminating) pollen is formulated as follows (Ritland, 2002):

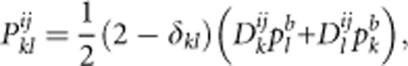where p_l^b and p_k^b represent the allele frequencies in the background pollen pool. For a locus with null alleles, the expected proportion of the maternal genotype among the heterozygous genotypes possessing the visible allele A_i and the null allele A_n in the maternal population q_i^m is:

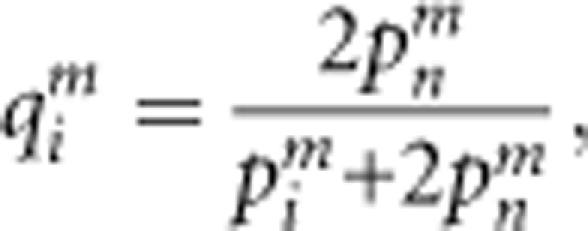where p_i^m and p_n^m represent the visible and null allele frequencies in the maternal population, respectively. When the possibility of apparent homozygous genotypes being heterozygous with one null allele is considered, the probabilities of p_kl^ij should be separately calculated for the four cases as follows:

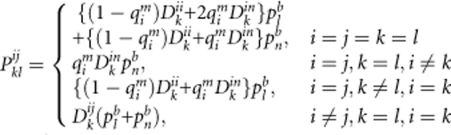where p_n^b represents the null allele frequency in the background pollen pool. In the remaining cases, the formula is same as that for a locus without null alleles. Under the assumption of unlinked loci, the log likelihood over L loci and N progenies sampled is calculated as follows:

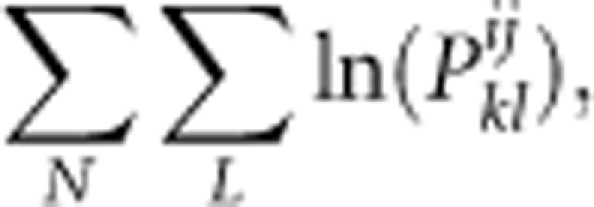Allele frequencies maximizing the log likelihood were estimated numerically by a quasi-Newton method using the function ‘optim' in the R. 2.8.0 software (R Development Core Team, 2008). We conducted 10 independent runs with different initial values and confirmed that all runs converged to the same allele frequencies at every locus, with the same maximum likelihood.

Appendix 2

Transition probability for a locus with null alleles

Apparently, in cases where both parents have heterozygous genotypes, it is not necessary to correct the transition probability. Thus, we consider the situation in which either or both parents have homozygous genotypes at a locus that can contain null alleles. When the parent has the apparent homozygous genotype A_iA_i, the expected proportion of the true genotype among the heterozygous genotypes possessing the null allele A_n (q_i) is:

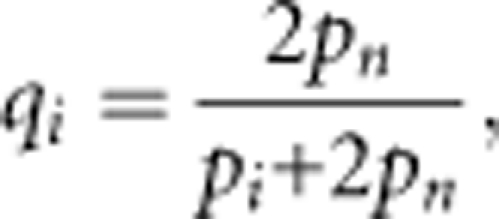where p_i and p_n represent the visible and null allele frequencies in the parental population. Then, when the mother and candidate clone, respectively, have the genotype A_iA_j and A_kA_l (i=j or k=l), the probability of them producing offspring with genotype g_o, T(g_o∣ M, F) is as follows:

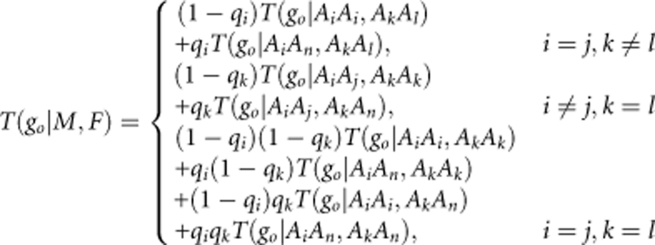where T(g_o∣…, …) on the right-hand side of the equation is the same as the ordinary transition probability (Devlin et al., 1988).

The authors declare no conflict of interest.