Abstract
Behavioral, neuropsychological, and neuroimaging data support the idea that numbers are represented along a mental number line (MNL), an analogical, visuospatial representation of number magnitude. The MNL is left-to-right oriented in Western cultures, with small numbers on the left and larger numbers on the right. Left neglect patients are impaired in the mental bisection of numerical intervals, with a bias toward larger numbers that are relatively to the right on the MNL. In the present study we investigated the effects of optokinetic stimulation (OKS) – a technique inducing visuospatial attention shifts by means of activation of the optokinetic nystagmus – on number interval bisection. One patient with left neglect following right-hemisphere stroke (BG) and four control patients with right-hemisphere damage, but without neglect, performed the number interval bisection task in three conditions of OKS: static, leftward, and rightward. In the static condition, BG misbisected to the right of the true midpoint. BG misbisected to the left following leftward OKS, and again to the right of the midpoint following rightward OKS. Moreover, the variability of BG’s performance was smaller following both leftward and rightward OKS, suggesting that the attentional bias induced by OKS reduced the “indifference zone” that is thought to underlie the length effect reported in bisection tasks. We argue that shifts of visuospatial attention, induced by OKS, may affect number interval bisection, thereby revealing an interaction between the processing of the perceptual space and the processing of the number space.
Keywords: mental number line, neglect, pseudoneglect, optokinetic stimulation, spatial attention, number processing, bisection, nystagmus
Introduction
Number processing is a fundamental skill for everyday living. Indeed, numbers are necessary for many basic activities such as achieving financial interactions and management, telling the time, selecting the correct bus, making a phone call, performing scientific measurements, and so on. Thus, a brain without numbers could make little sense of its internal and external environment, given that various and important everyday activities involving processing of numbers should be compromised (see Dehaene, 1997; Butterworth, 1999, for comprehensive reviews).
An essential question is how knowledge of number is represented in the brain. How, for example, can we decide quickly and effortlessly which of two numerals expresses the greater magnitude or which of two sets contains the smaller number of elements? This has been an important challenge for cognitive neuroscientists during the last decades and encouraging theoretical proposals have been formulated on various empirical grounds. Indeed, recent research on numerical processing in animals and humans converge on the view that knowledge of numbers constitutes a domain-specific cognitive ability, with a specific neural substrate located in the left and right inferior parietal cortices (see Dehaene, 2003).
A far more complex issue, however, is that of the nature of these representations. Dehaene and Cohen (1995) have proposed a comprehensive cognitive–anatomical model to explain various aspects of mathematical cognition. In this model, mathematical information is represented by three distinct codes: an Arabic code, a verbal code, and a code consisting in a continuous, analogical left-to-right oriented mental number line (MNL), where small numbers are represented on the left and progressively larger numbers are represented on the right. According to Dehaene and Cohen (1995), the three codes have different representational and functional properties. The first two codes, for example, are notation-dependent (Arabic vs. verbal). More precisely, the verbal code is responsible for the recognition and production of number words (spoken and written), for the retrieval of rote-memorized arithmetic facts (e.g., the multiplication table, the results of frequent one-digit additions and subtractions, etc.), and for counting. The Arabic code is implicated in the recognition and production of Arabic digits, in parity judgment (i.e., decide if a number is odd or even), and in multi-digit written calculations. The third code (the MNL), in contrast, is supramodal (i.e., notation-independent) and, thus, it can be activated both by numerals (Arabic digits, spoken number words, written number words, etc.) and by directly perceived numerosities of distinct elements in the environment (objects, people, animals, etc.). The principal role of the MNL is to represent the meaning both of numerals and of perceived numerosities by translating them into a continuous and analogical magnitude code (Dehaene et al., 2003). Thus, the MNL supports number comparison (e.g., “is 5 bigger than 6?”) and approximate calculation (e.g., “does the operation 3 + 4 equals 15?”).
It has been shown that each of these codes has a specific cerebral localization (Dehaene and Cohen, 1995). More precisely, the Arabic code is implemented in the inferior mesial occipital–temporal cortices bilaterally, whereas the perisylvian circuits of the left hemisphere support the verbal code. Finally, the analogical code is subserved by the inferior parietal cortices bilaterally. The three codes are coordinated by general-purpose executive systems localized in the prefrontal cortices bilaterally (Dehaene and Cohen, 1995; Dehaene, 2003).
Although the notion of MNL is widely accepted in the numerical cognition literature, what remains controversial is whether the MNL has a truly spatial nature (for reviews, see Dehaene et al., 2003; Hubbard et al., 2005; Umiltà et al., 2009). Dehaene et al. (1990) were the first to report experimental evidence in favor of the spatial format of the MNL. In their study, participants were asked to decide, by pressing either a right-sided or a left-sided key, whether Arabic digits displayed at fixation were larger or smaller than a fixed reference number (i.e., 65). Although key order was counterbalanced, Dehaene et al. (1990) observed that participants were more efficient in pressing the left-sided key for responding “smaller” (Arabic digits <65) and the right-sided key for responding “larger” (Arabic digits >65). Hence, there seemed to be an effect of spatial correspondence between the effector of the response and the position of the processed number on the MNL (i.e., left or right with respect to the reference number). In a second study, Dehaene et al. (1993) observed that there was a left-sided key advantage for small numbers and a right-sided key advantage for larger numbers, even in a task that did not require direct manipulation of number magnitude. In this study, participants were presented with centrally displayed Arabic digits, and they were asked to perform parity judgments by pressing a left-sided or a right-sided key. The results revealed that participants were significantly faster and more accurate in responding to relatively small numbers with their left hand, whereas they were more accurate and fast in responding to relatively large numbers with their right hand. This correspondence between the position of a number on the MNL and the spatial position in which the response to that number took place was termed the spatial numerical association of response codes (SNARC) effect.
The SNARC effect, however, might be also explained by other recent theories that dispense with the spatial coding of numbers (see Gevers et al., 2006; Proctor and Cho, 2006). For example, Gevers et al. (2006) developed a computational account of the SNARC effect, in which “a specific number is not coded as left or right but (…) is coded as either small or large, which in turn activates left or right responses.” The account of Proctor and Cho (2006; see also Santens and Gevers, 2008) is based on the idea that stimuli and associated responses in binary choice tasks are coded with positive and negative polarities. Proctor and Cho (2006) suggested that the SNARC effect may be the result of coding large numbers as positive and small numbers as negative, which would then produce match or mismatch with the polarity coding of responses (negative for left and positive for right). We think, however, that the notion of polarity correspondence does not run against the notion of a spatial representation of numbers. The minus (−) and plus (+) signs are systematically associated with Cartesian coordinates in order to represent spatial positions to the left (−) or to the right (+) of a reference point (i.e., zero). Kosslyn (1994, for review) has proposed a dual system for coding space in the human brain: coordinate spatial codes (e.g., Cartesian coordinates), implemented in the right hemisphere, and categorical spatial codes (e.g., left, right, above, below, etc.), implemented in the left hemisphere. Thus, polarity correspondence might simply involve Kosslyn’s categorical spatial coding. Nevertheless, the graded nature of the SNARC effect (i.e., a linear progression from left-sided response advantage to right-sided response advantage as magnitude increases; e.g., Fias et al., 1996; Priftis et al., 2006) cannot be explained if coding were only categorical.
Further evidence in favor of the spatial format of the MNL has been reported in studies on neurological patients. Zorzi et al. (2002) investigated whether the MNL has a left-to-right spatial organization, by exploring the way numbers are represented in patients affected by left neglect. These patients, more frequently following a right parietal lesion, fail to report, orient to, or verbally describe stimuli in the contralesional side of space (i.e., the left side; for review, see Halligan et al., 2003). When neglect patients are asked to bisect physical lines, they systematically misbisect to the right of the true midpoint of the line, as if they were ignoring its leftmost part. Halligan and Marshall (1988; also see Marshall and Halligan, 1989) observed that this rightward misbisection is directly proportional to the length of the physical line. That is, the longer the physical line, the greater the misbisection to the right of the true midpoint, although leftward misbisection was observed for very short physical lines (i.e., the “crossover” effect).
To investigate whether the MNL has spatial features similar to those of physical lines, Zorzi et al. (2002) asked left neglect patients to mentally bisect numerical intervals (e.g., “Which number is halfway between 1 and 9?”). The results showed that left neglect patients misbisected to the “right” of the true midpoint of longer number intervals (e.g., responding that “7” is halfway between “1” and “9”), but they misbisected to the left of the true midpoint of shorter number intervals (e.g., responding that “6” is halfway between “7” and “9”). Thus, the overall pattern observed in mental number interval bisection resembled that of left neglect patients during the bisection of physical lines. The findings of Zorzi et al. (2002) have been replicated and extended in a number of recent studies reporting effects of neglect on number processing (Rossetti et al., 2004; Vuilleumier et al., 2004; Doricchi et al., 2005; Priftis et al., 2006, 2008; Zorzi et al., 2006; Cappelletti et al., 2007; Zamarian et al., 2007; Hoeckner et al., 2008; Loftus et al., 2008; Yang et al., 2009; for review see Umiltà et al., 2009). The converse relation has been also reported; that is, number processing can modulate left neglect. Bonato et al. (2008) have reported that the presence of small numbers ameliorates physical line bisection in left neglect patients. Loftus et al. (2008) have shown that processing of small numbers overcomes left neglect in a perceptual task. Finally, a reliable “leftward” bias (i.e., “pseudoneglect”) has been reported in healthy participants engaged in various numerical tasks (Longo and Lourenco, 2007; for review, see Umiltà et al., 2009). This bias mirrors, in the number space, the well-known asymmetries observed when healthy participants deploy their visuospatial attention in the physical space (for a review on pseudoneglect in physical space, see Jewell and McCourt, 2000).
Nevertheless, in a recent paper reporting the case study of a patient with right-sided neglect following left hemisphere damage, van Dijck et al. (2011) have proposed that the misbisection pattern observed in neglect patients during number interval bisection is due to a deficit in processing the initial items in a sequence to be held in verbal working memory, rather than a consequence of neglect (also see Fias et al., 2011, for review). If this were the case, one would expect that manipulation of spatial variables should not affect neglect for the number space, given that these manipulations do not affect verbal working memory. There are two published studies that are difficult to reconcile with the verbal working memory account. First, Rossetti et al. (2004) showed that the overall rightward bias of left neglect patients in bisecting mental number intervals can be ameliorated following adaptation to rightward-shifting prisms, a well-known and widely used technique for rehabilitating visuospatial attention deficits of neglect patients. Second, Salillas et al. (2009) reported that leftward, coherent dot movement can improve the difficulties of left neglect patients in judging the magnitude of numbers, which are smaller (e.g., 4) than a reference number (e.g., 5). Note that this task is minimally based on verbal working memory resources, because participants must remember only one item (i.e., the reference number) for performing the task.
The aim of the present study was to investigate whether optokinetic stimulation (OKS) – a technique inducing visuospatial attention shifts by means of elicitation of the optokinetic nystagmus (for review, see Kerkhoff, 2003) – would influence mental number interval bisection in a way similar to the way OKS affects physical line bisection. Indeed, Pizzamiglio et al. (1990) have shown that, with respect to a static OKS condition, leftward OKS improves physical line bisection, whereas rightward OKS deteriorates physical line bisection. Pizzamiglio et al. (1990) showed that these effects were particularly strong and evident in neglect patients with respect to controls. We tested one left neglect patient (BG) and four right-hemisphere damaged control patients without neglect. We postulated that if a deficit in verbal working memory was the reason underlying number interval misbisection, then OKS should have no effects on the performance of the left neglect patient. In contrast, if neglect was the core deficit, leftward OKS should improve number interval bisection, whereas rightward OKS should deteriorate it. Finally, in contrast with Salillas et al. (2009) who used coherent dot motion, in the present study OKS consisted in fast-moving vertical stripes, a visuosensory manipulation which elicits the optokinetic nystagmus (see below).
Materials and Method
Case description
BG, a 64-year-old, right-handed man with 4 years of education, suffered a right-hemisphere ischemic stroke. He had negative neurological and psychiatric history. A computed tomography (CT) scan, performed immediately after his stroke, evidenced a hypodense area in the temporo-parietal region of the right cerebral hemisphere that was extended subcortically to the ventricular-thalamic regions. A second CT scan revealed an extensive hypodense right cerebral lesion accompanied by non-homogeneous, paraventricular-thalamic areas of hypodensity; median structures were in axis. Another CT scan reconfirmed the presence of the same hypodense areas. During hospitalization, BG was complied with physical therapy for left body hemiparesis and neuropharmacological treatment. At the moment of testing, BG was able to take short walks with the help of a tripod, but he mainly used the wheelchair to move himself.
BG underwent formal neuropsychological evaluation. He was alert and collaborative, and oriented to personal information, even if he was only partially oriented in time and space. He had no memory or communication difficulties in everyday life, despite his hypoacusia, which was present even before his stroke. His social, behavioral, and emotional control remained well adapted. Clinical signs of left neglect, consisting in spontaneous head and gaze deviation toward the ipsilesional hemispace, were present. His score on the conventional part of the Behavioral Inattention Test (BIT; Wilson et al., 1987) was below the cut-off, revealing that BG was affected by left neglect. BG gave his informed consent in order to participate in the study, according to the Declaration of Helsinki. Demographic, clinical, and psychometric data of BG are reported in Table 1.
Table 1.
Demographic, clinical, and psychometric data of the participants.
| BG | SL | BGA | CP | CL | |
|---|---|---|---|---|---|
| Sex | M | FE | M | M | M |
| Age (years) | 64 | 55 | 71 | 72 | 54 |
| Education (years) | 4 | 8 | 5 | 18 | 10 |
| Handedness | R | R | R | R | R |
| Lesion site | TPThPv | FTP | FP | BN | Th |
| Lesion etiology | IS | IS | IS | HS | IS |
| MMSE | 23.4/30 | 30/30 | 28.3/30 | 30/30 | 24/30 |
| BIT CONVENTIONAL SUBTESTS | |||||
| Line crossing | 36/36 | 36/36 | 36/36 | 36/36 | 36/36 |
| Letter cancelation | 11/40 | 40/40 | 36/40 | 40/40 | 38/40 |
| Star cancelation | 40/54 | 54/54 | 54/54 | 53/54 | 54/54 |
| Figure copy | 0/3 | 2/3 | 2/3 | 3/3 | 2/3 |
| Shape copy | 1/1 | 1/1 | 1/1 | 1/1 | 1/1 |
| Line bisection | 6/9 | 9/9 | 9/9 | 9/9 | 9/9 |
| Spontaneous drawing | 1/3 | 1/3 | 0/3 | 2/3 | 1/3 |
| Total score | 95/146 | 143/146 | 138/146 | 144/146 | 141/146 |
M, male; FE, female; MCA, middle cerebral artery territory; F, frontal; T, temporal; P, parietal; Th, thalamic; Pv, paraventricular; BN, basal nuclei; R, right; IS, ischemic stroke; HS, hemorrhagic stroke.
Right-hemisphere damaged control patients
Four patients (SL, BGA, CP, CL; mean age 63 years, SD 9.83, mean education 10.25 years, SD 5.56) with right-hemisphere stroke, but without left neglect (hereafter RBDN-group) took part in the study, after giving their informed consent according to the Declaration of Helsinki. Inclusion criteria comprised absence of dementia, substance abuse, and psychiatric disorders. Left neglect was assessed through the conventional part of the BIT (Wilson et al., 1987): all control patients obtained a score above the cut-off (129/146). The MMSE (Magni et al., 1996) was also administered to exclude the presence of general cognitive impairments. Demographic, clinical, and psychometric data of control patients are reported in Table 1.
Mental number interval bisection task
Stimuli
Stimuli and procedure were the same as those used by Zorzi et al. (2002; see also Priftis et al., 2006). Forty-eight forward (e.g., 1–9) and 48 backward (e.g., 9–1) number pairs were orally presented to the participants. Each trial was presented once, in random order. Each number pair defined a specific number interval, whose length was three (e.g., 1–3), five (e.g., 1–5), seven (e.g., 1–7), or nine (e.g., 1–9). Each number interval was presented within the units (e.g., 1–5), the teens (e.g., 11–15), and the twenties (e.g., 21–25). The complete set of number pairs is reported in Table 2.
Table 2.
The complete set of number intervals.
| Length | Units | Teens | Twenties |
|---|---|---|---|
| 3 | 1–3, 2–4, 3–5, 4–6, 5–7, 6–8, 7–9 | 11–13, 12–14, 13–15, 14–16, 15–17, 16–18, 17–19 | 21–23, 22–24, 23–25, 24–26, 25–27, 26–28, 27–29 |
| 5 | 1–5, 2–6, 3–7, 4–8,5–9 | 11–15, 12–16, 13–17, 14–18, 15–19 | 21–25, 22–26, 23–27, 24–28, 25–29 |
| 7 | 1–7, 2–8, 3–9 | 11–17, 12–18, 13–19 | 21–27, 22–28, 23–29 |
| 9 | 1–9 | 11–19 | 21–29 |
| Total | 16 | 16 | 16 |
Optokinetic stimulation
Stimuli
Optokinetic stimulation consisted of moving white vertical stripes (width: 1 cm, height: 11.5 cm, luminance: ∼76 cd/m2), presented against a black background (luminance: 0.42 cd/m2) at the speed of 8.4 cm/s. The inter-stripe distance was 1 cm.
Apparatus and procedure
A notebook (Intel® Pentium® M, CPU: 1.86 GHz, RAM: 512 MB, graphics card: 128 MB, 15′′ screen, refresh rate: 60 Hz, 32 bit colors, 1400 × 1050 pixel resolution) was used to display the OKS. All participants were tested in the same room and under the same luminance condition. The experiment was composed by a preliminary session followed by an experimental session. In the preliminary session, participants sat in front of the screen. A chinrest was used to keep the eyes of the participants at a distance of 40 cm from the screen. Participants were asked to fixate the center of the screen while either leftward or rightward OKS was presented. All participants had normal optokinetic nystagmus, characterized by a slow phase of eye movement toward the direction of the OKS and a rapid phase opposite the direction of the OKS. In the experimental session, participants remained positioned in front of the screen, with their head fixed in the chinrest. Participants were asked to look at the center of the screen. The experimenter sat behind the screen out of the participants’ view and controlled, using a camcorder, whether the participants showed the nystagmus and whether they maintained their gaze on the screen. During the presentation of the OKS conditions (static, leftward, rightward), participants were presented with spoken number pairs and they were asked to say aloud which number was halfway between the first and the second number of each pair (e.g., the experimenter asked: “What number is halfway between 1 and 9?”). There was no time limit for the participants to perform the task. The number pairs were repeated to the participants whenever required. OKS was presented to the participants in three separate blocks (static, leftward, rightward) in three consecutive days (one block on each day).
Results
For each participant and for each number interval, the mean difference between observed (O) and correct (C) responses (dO–C) was calculated (see Table 3). For each participant and condition, responses above and below 3 SD from the mean were excluded from the statistical analyses. The resulting number of outliers was very small (BG: static 2.83%, leftward 2.83%, rightward 0%; RBDN: static 0.26%, leftward 2.08%, rightward: 0.78%).
Table 3.
For each participant the mean dO–C and the associated SE is reported, as a function of number interval length and OKS.
| Length | 3 | 5 | 7 | 9 | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | SE | Mean | SE | Mean | SE | Mean | SE | |
| STATIC OKS | ||||||||
| Patient BG | 0.049 | 0.324 | 0.133 | 0.266 | 1.118 | 0.624 | 3.667 | 4.080 |
| RBDN-1 | 0.000 | 0.000 | −0.167 | 0.097 | −0.222 | 0.173 | 0.167 | 0.307 |
| RBDN-2 | 0.000 | 0.000 | 0.000 | 0.000 | 0.056 | 0.151 | −0.500 | 0.224 |
| RBDN-3 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.081 | −0.333 | 0.211 |
| RBDN-4 | 0.000 | 0.000 | −0.133 | 0.063 | −0.111 | 0.137 | −0.667 | 0.211 |
| LEFTWARD OKS | ||||||||
| Patient BG | 0.317 | 0.417 | 0.233 | 0.257 | 0.471 | 0.550 | 1.167 | 1.721 |
| RBDN-1 | 0.000 | 0.000 | −0.033 | 0.102 | −0.056 | 0.235 | 1.000 | 0.365 |
| RBDN-2 | 0.000 | 0.000 | 0.000 | 0.000 | −0.056 | 0.171 | 0.000 | 0.258 |
| RBDN-3 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| RBDN-4 | 0.000 | 0.000 | −0.103 | 0.076 | −0.278 | 0.195 | 0.333 | 0.422 |
| RIGHTWARD OKS | ||||||||
| Patient BG | 0.095 | 0.243 | 0.400 | 0.265 | 0.667 | 0.443 | 3.333 | 0.333 |
| RBDN-1 | 0.000 | 0.000 | 0.000 | 0.096 | −0.167 | 0.167 | 0.500 | 0.500 |
| RBDN-2 | 0.000 | 0.000 | 0.000 | 0.000 | −0.167 | 0.185 | 0.333 | 0.333 |
| RBDN-3 | 0.000 | 0.000 | 0.000 | 0.000 | −0.056 | 0.098 | 0.000 | 0.000 |
| RBDN-4 | 0.220 | 0.096 | −0.414 | 0.195 | 0.500 | 0.167 | 0.000 | 0.365 |
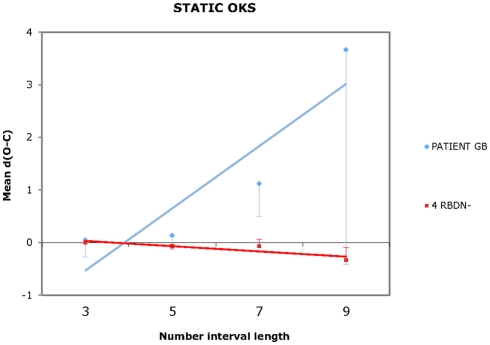
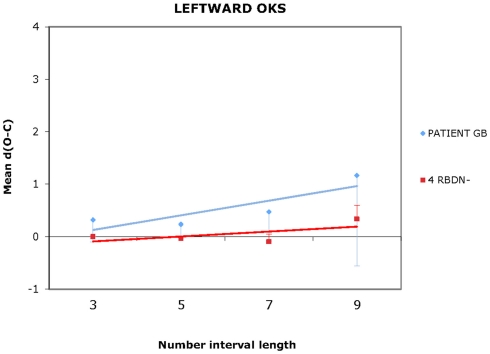
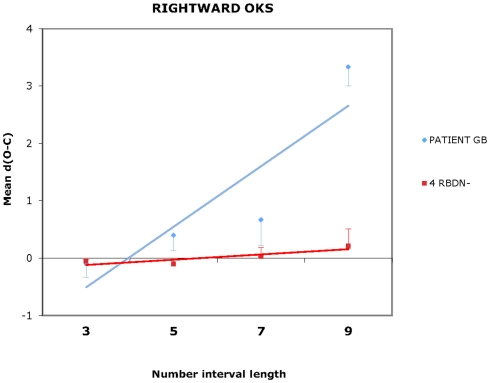
For each participant and each condition of OKS (static, leftward, rightward), Pearson’s r coefficients were calculated (number interval length vs. dO–C). We used specific tests for comparing the Pearson’s r coefficient of BG with those of the RBDN-group (Crawford et al., 2003). In the static condition (see Figure 1), BG misbisected significantly to the right of the true midpoint (r = 0.25), as a function of number interval length, t(3) = 3.527, dO–C = 0.019, one-tailed, showing the typical pattern of mental number interval bisection observed in left neglect patients. Leftward OKS (see Figure 2) improved the performance of BG, which became not significantly different (r = 0.07) from that of RBDN-controls, t(3) = 0.271, p = 0.402, one-tailed. Finally, rightward OKS (see Figure 3) induced BG to misbisect again to the right of the true midpoint, as a function of number interval (BG: r = 0.41), t(3) = 2.551, p = 0.042, one-tailed.
Figure 1.
In the static OKS condition, BG misbisected to the right of the true midpoint, as a function of number interval length.
Figure 2.
In the leftward OKS condition, BG bisection did not differ from that of controls. Even for length 9 the mean dO–C of RBDN – did not differ from 0, t(3) = 1.663, p = 0.194.
Figure 3.
In the rightward OKS condition, BG misbisected to the right of the true midpoint, as a function of number interval length. Even for length 9 the mean dO–C of RBDN – did not differ from 0, t(3) = 1.414, p = 0.252.
Leftward and rightward OKS appeared to induce a reduction of the SE in BG (SE across interval lengths = static: 1.323, leftward: 0.736, rightward: 0.321; also see Figures 1–3). Therefore, we performed further analyses to assess whether the change in variability in BG’s performance, as a function of OKS condition, was different from that of controls. To this aim we used the revised standardized difference test (Crawford and Garthwaite, 2005), which is designed to test the difference of a patient’s performance in two conditions, with respect to that of controls. With respect to the static condition, both leftward and rightward OKS decreased BG’s SE [static vs. leftward OKS, t(3) = 19.049, p = 0.0003, two-tailed; static vs. leftward OKS, t(3) = 15.386, p = 0.0006, two-tailed]. Finally, BG’s SE was smaller in the rightward than in the leftward OKS condition, t(3) = 8.831, p = 0.0003.
Discussion
BG, a left neglect patient, misbisected to the right of the true midpoint of number intervals. His performance significantly improved following leftward OKS given that it became indistinguishable from that of control patients. BG misbisected again to the right of the true midpoint of the number intervals following rightward OKS. Although it may appear that rightward OKS did not affect BG’s performance in comparison to the static condition (compare Figures 1 and 3), we found that rightward OKS strongly decreased variability of response with respect to the static condition.
Neglect patients’ response variability in visual line bisection is attributed to a pathologically extended “indifference zone” (Marshall and Halligan, 1989; Olk et al., 2004; Bonato et al., 2008). The “indifference zone” theory suggests that the bisection bias is due to an increased Weber fraction, which increases, in turn, the discrepancy between two lines, which are judged as equal in length. This accounts for the effect of line length (Marshall and Halligan, 1989) and for the inconsistent perception of the line center in neglect (Olk et al., 2004). Neglect severity is directly related to the size of the “indifference zone” (Bonato et al., 2008). The notion of “indifference zone” can be also applied to number interval bisection. In BG, both rightward and leftward OKS decreased variability with respect to the static condition. Thus, we suggest that the effect of biasing visuospatial attention in either direction through the OKS was to decrease the “indifference zone” and to make BG’s responses more consistent than in the static condition. Note that variability in the rightward OKS condition was even smaller than that in the leftward OKS condition; this suggests that BG responded in the most consistent way when the attention bias induced by rightward OKS had the same direction of the pathological attention bias (i.e., rightward) due to left neglect. The smaller variability in the rightward OKS condition also explains why the Pearson’s r coefficient (correlation between dO–C and interval length) was larger in this condition compared to the static condition (r = 0.41 vs. r = 0.25), even though the mean dO–Cs were similar. Moreover, the fact that rightward OKS did not increase BG’s bias in terms of dO–C over and above his dO–C in the static condition, is likely to reflect a ceiling effect.
Thus, OKS can influence not only the perceived space (for review, see Kerkhoff, 2003), but also the imaginal space of the MNL. Our findings run against the recent proposal that the misbisection pattern observed in neglect patients during mental number interval bisection is not due to neglect, but to a deficit in processing the initial items in a sequence to be held in verbal working memory (Fias et al., 2011; van Dijck et al., 2011). If this were the case, OKS should have not affected number interval bisection in BG, because the same verbal working memory resources were required in all the three OKS conditions (i.e., static, leftward, rightward) to perform the task. In contrast, the finding that the manipulation of visuospatial attention influenced BG’s performance can be only explained by the hypothesis that his misbisection pattern was due to left neglect for the number space.
Our findings are in favor of a functional isomorphism (or homeomorphism) between the perceived space and the imaginal space of the MNL, as originally proposed by Zorzi et al. (2002). Indeed, the two spaces must have similar metrics (e.g., can be defined according to Cartesian coordinates) and can be modulated by the deployment of similar – though independent – spatial attention mechanisms. The independence of the number space from the perceived space is confirmed by double dissociations, which have been reported when left neglect patients bisect physical lines vs. mental number intervals (see Rossetti et al., 2004; Zorzi et al., 2004; Doricchi et al., 2005). Nonetheless, performance of left neglect patients in the two tasks is remarkably similar (Zorzi et al., 2006; Cappelletti et al., 2007) and can be correlated (Yang et al., 2009; see also Longo and Lourenco, 2007, for evidence of pseudoneglect). Furthermore, interactions between the perceived space and the imaginal space of the MNL have been revealed by the effects of spatial variables on number processing (for studies on left neglect patients, see Rossetti et al., 2004; Salillas et al., 2009; for studies on neurologically healthy participants, see Loetscher et al., 2008; Stoianov et al., 2008; Nicholls and McIlroy, 2010; Cattaneo et al., 2011; Kramer et al., 2011) and by the effects of numerical variables on spatial processing (for studies on left neglect patients, see Bonato et al., 2008; Loftus et al., 2008; for studies on neurologically healthy participants, see Fischer et al., 2003; Galfano et al., 2006; Casarotti et al., 2007; Cattaneo et al., 2009).
We conclude that our findings confirm and expand those of other studies revealing the presence of robust interactions between the deployment of attention in the perceived space and the deployment of attention in the imaginal space of the MNL. These interactions challenge both the verbal working memory account of number space in neglect patients (Fias et al., 2011; van Dijck et al., 2011) and the non-spatial accounts of number–space interactions that have been proposed by Gevers et al. (2006) and by Proctor and Cho (2006).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We would like to thank all participants for their time and effort. Konstantinos Priftis and Marco Pitteri contributed equally to this work. This study was supported by a grant (PRIN 2008) from the Italian Ministry of Education, University, and Research to Marco Zorzi. Marco Pitteri was supported by a grant from CARIPARO Foundation to Konstantinos Priftis.
References
- Bonato M., Priftis K., Marenzi R., Zorzi M. (2008). Modulation of hemispatial neglect by directional and numerical cues in the line bisection task. Neuropsychologia 46, 426–433 10.1016/j.neuropsychologia.2007.08.019 [DOI] [PubMed] [Google Scholar]
- Butterworth B. (1999). The Mathematical Brain. London: Macmillan [Google Scholar]
- Cappelletti M., Freeman E. D., Cipolotti L. (2007). The middle house or the middle floor: bisecting horizontal and vertical mental number lines in neglect. Neuropsychologia 45, 2989–3000 10.1016/j.neuropsychologia.2007.05.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casarotti M., Michielin M., Zorzi M., Umiltà C. (2007). Temporal order judgment reveals how number magnitude affects visuospatial attention. Cognition 102, 101–117 10.1016/j.cognition.2006.09.001 [DOI] [PubMed] [Google Scholar]
- Cattaneo Z., Fantino M., Silvanto J., Vallar G., Vecchi T. (2011). Tapping effects on numerical bisection. Exp. Brain Res. 208, 21–28 10.1007/s00221-010-2451-8 [DOI] [PubMed] [Google Scholar]
- Cattaneo Z., Silvanto J., Battelli L., Pascual-Leone A. (2009). The mental number line modulates visual cortical excitability. Neurosci. Lett. 462, 253–256 10.1016/j.neulet.2009.07.027 [DOI] [PubMed] [Google Scholar]
- Crawford J. R., Garthwaite P. H. (2005). Testing for suspected impairments and dissociations in single-case studies in neuropsychology: evaluation of alternatives using Monte Carlo simulations and revised tests for dissociations. Neuropsychology 19, 318–331 10.1037/0894-4105.19.3.318 [DOI] [PubMed] [Google Scholar]
- Crawford J. R., Garthwaite P. H., Howell D. C., Venneri A. (2003). Intra-individual measures of association in neuropsychology: inferential methods for comparing a single case with a control or normative sample. J. Int. Neuropsychol. Soc. 9, 989–1000 10.1017/S1355617703970032 [DOI] [PubMed] [Google Scholar]
- Dehaene S. (1997). The Number Sense. New York: Oxford University Press [Google Scholar]
- Dehaene S. (2003). The neural basis of the Weber-Fechner law: a logarithmic mental number line. Trends Cogn. Sci. (Regul. Ed.) 7, 145–147 10.1016/S1364-6613(03)00055-X [DOI] [PubMed] [Google Scholar]
- Dehaene S., Bossini S., Giraux P. (1993). The mental representation of parity and numerical magnitude. J. Exp. Psychol. Gen. 122, 371–396 10.1037/0096-3445.122.3.371 [DOI] [Google Scholar]
- Dehaene S., Dupoux E., Mehler J. (1990). Is numerical comparison digital: analogical and symbolic effects in two-digit number comparison. J. Exp. Psychol. Hum. Percep. Perform. 16, 626–641 10.1037/0096-1523.16.3.626 [DOI] [PubMed] [Google Scholar]
- Dehaene S., Piazza M., Pinel P., Cohen L. (2003). Three parietal circuits for number processing. Cogn. Neuropsychol. 3, 487–506 10.1080/02643290244000239 [DOI] [PubMed] [Google Scholar]
- Dehaene S., Cohen L. (1995). Towards an anatomical and functional model of number processing. Math. Cogn. 1, 83–120 [Google Scholar]
- Doricchi F., Guariglia P., Gasparini M., Tomaiuolo F. (2005). Dissociation between physical and mental number line bisection in right hemisphere brain damage. Nat. Neurosci. 8, 1663–1665 10.1038/nn1563 [DOI] [PubMed] [Google Scholar]
- Fias W., Brysbaert M., Geypens F., d’Ydewalle G. (1996). The importance of magnitude information in numerical processing: evidence from the SNARC effect. Math. Cogn. 2, 95–110 10.1080/135467996387552 [DOI] [Google Scholar]
- Fias W., van Dijck J. F., Gevers W. (2011). “How number is associated with space? The role of working memory,” in Space, Time and Number in the Brain: Searching for the Foundations of Mathematical Thought, eds Dehaene S., Brannon E. M. (Burlington, MA: Elsevier/Academic Press; ), 133–148 [Google Scholar]
- Fischer M. H., Castel A. D., Dodd M. D., Pratt J. (2003). Perceiving numbers causes spatial shifts of attention. Nat. Neurosci. 6, 555–556 10.1038/nn1066 [DOI] [PubMed] [Google Scholar]
- Galfano G., Rusconi E., Umiltà C. (2006). Number magnitudes orients attention, but not against one’s will. Psychon. Bull. Rev. 13, 869–874 10.3758/BF03194011 [DOI] [PubMed] [Google Scholar]
- Gevers W., Verguts T., Reynvoet B., Caessens B., Fias W. (2006). Numbers and space: a computational model of the SNARC effect. J. Exp. Psychol. Hum. Percept. Perform. 32, 32–44 10.1037/0096-1523.32.1.32 [DOI] [PubMed] [Google Scholar]
- Halligan P. W., Fink G. R., Marshall J. C., Vallar G. (2003). Spatial cognition: evidence from visual neglect. Trends Cogn. Sci. (Regul. Ed.) 7, 125–133 10.1016/S1364-6613(03)00032-9 [DOI] [PubMed] [Google Scholar]
- Halligan P. W., Marshall J. C. (1988). How long is a piece of string? A study of line bisection in a case of visual neglect. Cortex 2, 321–328 [DOI] [PubMed] [Google Scholar]
- Hoeckner S. H., Zauner H., Moeller K., Wood G., Haider C., Gaßner A., Nuerk H. C. (2008). Impairments of the mental number line for two digit numbers in neglect. Cortex 44, 429–438 10.1016/j.cortex.2007.09.001 [DOI] [PubMed] [Google Scholar]
- Hubbard E. M., Piazza M., Pinel P., Dehaene S. (2005). Interactions between number and space in parietal cortex. Nat. Rev. Neurosci. 6, 435–448 10.1038/nrn1684 [DOI] [PubMed] [Google Scholar]
- Jewell G., McCourt M. E. (2000). Pseudoneglect: a review and metaanalysis of performance factors in line bisection tasks. Neuropsychologia 38, 93–110 10.1016/S0028-3932(99)00045-7 [DOI] [PubMed] [Google Scholar]
- Kerkhoff G. (2003). “Modulation and rehabilitation of spatial neglect by sensory stimulation,” in Neural Control of Space Coding and Action Production, eds Prablanc C., Pélisson D., Rossetti Y. (Amsterdam: Elsevier; ), 257–271 [DOI] [PubMed] [Google Scholar]
- Kosslyn S. M. (1994). Image and Brain: The Resolution of the Imagery Debate. Cambridge, MA: MIT Press [Google Scholar]
- Kramer P., Stoianov I., Umiltà C., Zorzi M. (2011). Interactions between perceptual and numerical space. Psychon. Bull. Rev. 18, 722–728 10.3758/s13423-011-0149-y [DOI] [PubMed] [Google Scholar]
- Loetscher T., Schwarz U., Schubiger M., Brugger P. (2008). Head turns bias the brain’s internal random generator. Curr. Biol. 18, R60–R62 10.1016/j.cub.2007.11.015 [DOI] [PubMed] [Google Scholar]
- Loftus A. M., Nicholls M. E. R., Mattingley J. B., Bradshaw J. L. (2008). Numerical processing overcomes left neglect for the greyscales task. Neuroreport 19, 835–838 10.1097/WNR.0b013e3282ff0fa8 [DOI] [PubMed] [Google Scholar]
- Longo M. R., Lourenco S. F. (2007). Spatial attention and the mental number line: evidence for characteristic biases and compression. Neuropsychologia 45, 1400–1407 10.1016/j.neuropsychologia.2006.11.002 [DOI] [PubMed] [Google Scholar]
- Magni E., Binetti G., Padovani A., Cappa S. F., Bianchetti A., Trabucchi M. (1996). The Mini-Mental State Examination in Alzheimer’s disease and multi-infarct dementia. Int. Psychogeriatr. 8, 127–134 10.1017/S1041610296003250 [DOI] [PubMed] [Google Scholar]
- Marshall J., Halligan P. (1989). When right goes left: an investigation of line bisection in a case of visual neglect. Cortex 25, 503–515 [DOI] [PubMed] [Google Scholar]
- Nicholls M. E. R., McIlroy A. M. (2010). Spatial cues affect mental number line bisections. Exp. Psychol. 57, 315–319 10.1027/1618-3169/a000037 [DOI] [PubMed] [Google Scholar]
- Olk B., Wee J., Kingstone A. (2004). The effect of hemispatial neglect on the perception of centre. Brain Cogn. 55, 365–367 10.1016/j.bandc.2004.02.048 [DOI] [PubMed] [Google Scholar]
- Pizzamiglio L., Frasca R., Guariglia C., Incoccia C., Antonucci, G (1990). Effect of optokinetic stimulation in patients with visual neglect. Cortex 26, 535–540 [DOI] [PubMed] [Google Scholar]
- Priftis K., Piccione F., Giorgi F., Meneghello F., Umiltà C., Zorzi M. (2008). Lost in number space after right brain damage: a neural signature of representational neglect. Cortex 44, 449–453 10.1016/j.cortex.2007.08.009 [DOI] [PubMed] [Google Scholar]
- Priftis K., Zorzi M., Meneghello F., Marenzi R., Umità C. (2006). Explicit vs. implicit processing of representational space in neglect: dissociations in accessing the mental number line. J. Cogn. Neurosci. 18, 680–688 10.1162/jocn.2006.18.4.680 [DOI] [PubMed] [Google Scholar]
- Proctor R. W., Cho Y. S. (2006). Polarity correspondence: a general principle for performance of speeded binary classification tasks. Psychol. Bull. 132, 416–442 10.1037/0033-2909.132.3.416 [DOI] [PubMed] [Google Scholar]
- Rossetti Y., Jacquin-Courtois S., Rode G., Ota H., Michel C., Boisson D. (2004). Does action make the link between number and space representation? Visuo-manual adaptation improves number bisection in unilateral neglect. Psychol. Sci. 15, 426–430 10.1111/j.0956-7976.2004.00696.x [DOI] [PubMed] [Google Scholar]
- Salillas E., Graná A., Juncadella M., Rico I., Semenza C. (2009). Leftward motion restores number space in neglect. Cortex 45, 730–737 10.1016/j.cortex.2008.09.006 [DOI] [PubMed] [Google Scholar]
- Santens S., Gevers W. (2008). The SNARC effect does not imply a mental number line. Cognition 108, 263–270 10.1016/j.cognition.2008.01.002 [DOI] [PubMed] [Google Scholar]
- Stoianov I., Kramer P., Umiltà C., Zorzi M. (2008). Visuospatial priming of the mental number line. Cognition 106, 770–779 10.1016/j.cognition.2007.04.013 [DOI] [PubMed] [Google Scholar]
- Umiltà C., Priftis K., Zorzi M. (2009). The spatial representation of numbers: evidence from neglect and pseudoneglect. Exp. Brain Res. 192, 561–569 10.1007/s00221-008-1623-2 [DOI] [PubMed] [Google Scholar]
- van Dijck J. P., Gevers W., Lafosse C., Doricchi F., Fias W. (2011). Non-spatial neglect for the mental number line. Neuropsychologia 49, 2570–2583 10.1016/j.neuropsychologia.2011.05.005 [DOI] [PubMed] [Google Scholar]
- Vuilleumier P., Ortigue S., Brugger P. (2004). The number space and neglect. Cortex 40, 399–410 10.1016/S0010-9452(08)70918-3 [DOI] [PubMed] [Google Scholar]
- Wilson B., Cockburn J., Halligan P. W. (1987). The Behavioural Inattention Test. Bury St. Edmunds, UK: Thames Valley Test Company [Google Scholar]
- Yang Q., Tian Y. H., Wang K. (2009). Spatial nature of mental number line in neglect patients. Zhonghua Yi Xue Za Zhi 89, 610–613 [PubMed] [Google Scholar]
- Zamarian L., Egger C., Delazer M. (2007). The mental representation of ordered sequences in visual neglect. Cortex 43, 542–550 10.1016/S0010-9452(08)70248-X [DOI] [PubMed] [Google Scholar]
- Zorzi M., Priftis K., Meneghello F., Marenzi R., Umiltà C. (2004). “Dissociations in the bisection of visual lines and number lines in neglect,” in Poster Presented at the First Congress of the European Neuropsychological Societies, Modena [Google Scholar]
- Zorzi M., Priftis K., Meneghello F., Marenzi R., Umiltà C. (2006). The spatial representation of numerical and non-numerical sequences: evidence from neglect. Neuropsychologia 44, 1061–1067 10.1016/j.neuropsychologia.2005.10.025 [DOI] [PubMed] [Google Scholar]
- Zorzi M., Priftis K., Umiltà C. (2002). Brain damage: neglect disrupts the mental number line. Nature 417, 138–139 10.1038/417138a [DOI] [PubMed] [Google Scholar]