Positional and temporal clustering in serial order memory

Abstract

The well-known finding that responses in serial recall tend to be clustered around the position of the target item has bolstered positional-coding theories of serial order memory. In the present study, we show that this effect is confounded with another well-known finding—that responses in serial recall tend to also be clustered around the position of the prior recall (temporal clustering). The confound can be alleviated by conditioning each analysis on the positional accuracy of the previously recalled item. The revised analyses show that temporal clustering is much more prevalent in serial recall than is positional clustering. A simple associative chaining model with asymmetric neighboring, remote associations, and a primacy gradient can account for these effects. Using the same parameter values, the model produces reasonable serial position curves and captures the changes in item and order information across study-test trials. In contrast, a prominent positional coding model cannot account for the pattern of clustering uncovered by the new analyses.

Associative chaining and positional coding constitute the two classic models of serial order memory. Although associative chaining was the implicit theory in Ebbinghaus’ (1885/1913) seminal studies of serial learning, early scholars also recognized that people can remember the positions of list items, and that this positional information was often used to aid the learning process (Ladd & Woodworth, 1911). During the 1950s and 1960s, a great deal of research was focused on identifying the functional stimulus in serial learning—the prior item, as predicted by chaining theory, or the item’s position, as predicted by positional coding theory. This work was generally inconclusive, with various experiments lending partial support to one or the other account (for a review, see Young, 1968).

In recent decades, as the emphasis shifted from the study of multitrial serial learning to the study of immediate serial recall, theorists have largely rejected the possibility that chaining plays an important role in serial-order memory (Burgess & Hitch, 2006; Farrell & Lewandowsky, 2002; Henson, Norris, Page & Baddeley, 1996.) Instead, most modern accounts of serial order memory emphasize the importance of positional information as the major retrieval cue.

One of the major sources of evidence for the positional coding view is the phenomenon of positional clustering (also known as positional gradients, and the locality constraint). While many recalled list items appear in their correct serial positions, items that are recalled out of order tend to migrate to neighboring serial positions (e.g., Estes, 1972; Lee & Estes, 1977; Nairne, 1992). This phenomenon would be expected if the retrieval cue is a memorial representation of each item’s list position. When the positional cue fails to correctly retrieve the appropriate item, it activates items from neighboring list positions.

In addition to positional clustering, other critical evidence for position-based models comes from findings of protrusions (erroneous recall of an item from the same position in a prior list) and confusions among phonologically similar items occurring in distinct list positions (e.g., Baddeley, 1968). Although some experiments have demonstrated a role for associative processes in serial learning (e.g., Kahana, Mollison, & Addis, 2010; Serra & Nairne, 2000), the striking effects of positional clustering seen in all serial recall tasks suggest that any contributions of associative chaining are secondary to the more prominent role of positional information.

Recent work has shown that serial recall also exhibits a high degree of temporal clustering, with responses tending to come from positions near that of the just-recalled item (Bhatarah, Ward, & Tan 2006; Klein, Addis, & Kahana, 2005). Whereas positional clustering lends support to position-based models, the temporal clustering effect lends support to chaining-based models. In the present article, we examine the interaction between these effects and show that they are confounded. We alleviate the confound by examining a subset of responses, and find that temporal clustering, rather than positional clustering, is more prevalent in serial recall. Moreover, we show that a simple strength-based chaining model provides a better fit to the overall pattern of positional and temporal clustering than does a positional coding model (Burgess & Hitch, 2006).

Method

To reevaluate the positional and temporal clustering effects in serial recall, we focused on three studies (Golomb, Peelle, Addis, Kahana, & Wingfield, 2008; Kahana & Caplan, 2002, Experiment 2; Kahana et al., 2010). All three studies had participants study and vocally recall lists of common words. Table 1 contains a summary of these studies. For details, see the Appendix.

Table 1.

Summary of the analyzed studies

Presentation Modality	Response Modality	Number of Lists	List Length	Study-Test Trials
Golomb et al., (2008)
Visual	Spoken	1,296	10	1
Kahana and Caplan (2002)[Exp. 2]
Spoken	Spoken	1,200	19	Criterion
Kahana et al., (2010)
Spoken	Spoken	189	13	Criterion
Spoken	Spoken	189	19	Criterion

Clustering analyses performed on the two studies that use longer lists (Kahana & Caplan, 2002; Kahana et al., 2010) focused on the middle list items (4–16 for 19-word lists, and 4–10 for 13-word lists). Edge items were excluded because they cannot appear at all of the distances that were analyzed. However, including all items produced comparable results. Clustering analyses performed on the Golomb et al. (2008) study, which used shorter lists, included all items.

Results

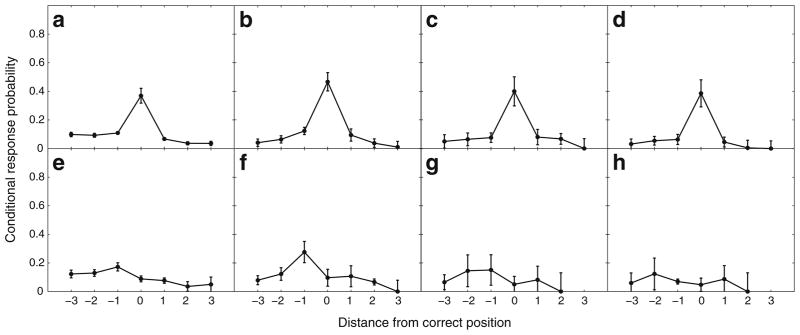
Estes (1972) reported that list items are more likely to be recalled in their correct serial position than in any other output position. Furthermore, items recalled in the wrong position cluster closely around the correct position. This result may be seen in the top row of Fig. 1, which shows that the probability of recalling an item decreases as a function of its distance from the correct position. The probability of recalling an item at each distance was conditioned on the number of times each distance was available. As an illustrative example, consider a list with four items. If a participant recalls all four items in their correct order, the items would all be at distance 0 because their output positions would match their list positions. On the other hand, if a participant recalls the sequence 1–2–4, the fourth item would be at distance -1 because it appears one position early. Similarly, if the participant recalls the sequence 1–3–2, then the second item would be at distance +1 because it appears one position late.

Fig. 1.

Probability of recalling an item as a function of its distance from its correct position. Negative values correspond to recalling an item too early, and positive values correspond to recalling an item too late. Missing data points indicate that the corresponding condition did not occur. Error bars indicate 95% confidence intervals computed using the method of Loftus and Masson (1994). Panels in the top row were computed based on all recalls, while panels in the bottom row were computed based only on recalls following the first order error. Each column is based on data from a different experiment. a and e Golomb et al. (2008) b and f Kahana and Caplan (2002, Experiment 2) c and g Kahana et al. (2010, 13-word lists) d and h Kahana et al. (2010, 19-word lists)

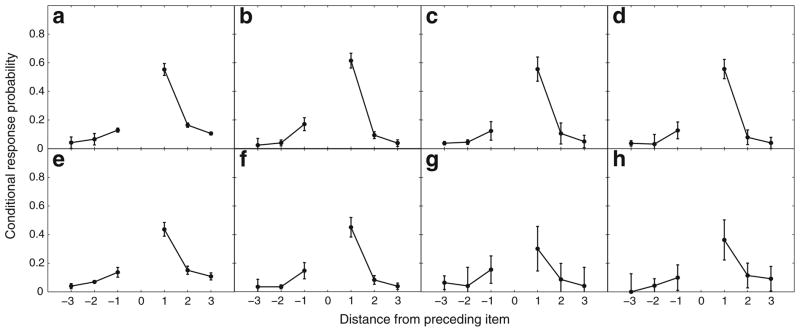
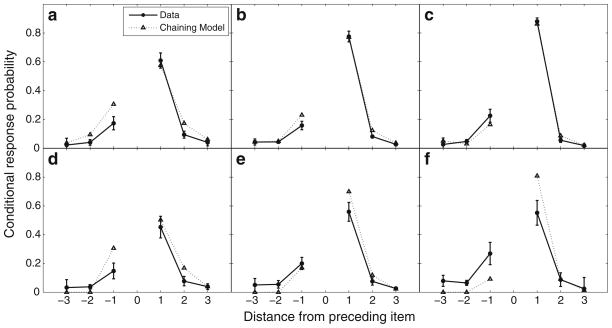
Klein et al. (2005) reported that in serial learning tasks, participants exhibit a strong temporal clustering effect analogous to the forward-asymmetric contiguity effect frequently reported in studies of free recall. This can be seen in the top row of Fig. 2, which shows the degree of temporal clustering around prior recalls. Here, a distance of +1 means that a recalled item had the same predecessor both in the recall sequence and in the list. A distance of +2 means that there was one item in the list separating the recalled item from the preceding recall, and so forth. Negative distances correspond to filling in skipped over items. As before, the probability of recalling an item at each distance was conditioned on the number of times each distance was available. The strong temporal clustering effect illustrated in the top row of Fig. 2 has also been demonstrated in other serial recall experiments (Bhatarah et al., 2006; Bhatarah, Ward, & Tan, 2008; Klein et al., 2005).

Fig. 2.

Probability of recalling an item as a function of its distance from the prior recall. Negative values correspond to recalling an earlier item from the list, and positive values correspond to recalling a later item from the list. Error bars indicate 95% confidence intervals computed using the method of Loftus and Masson (1994). Panels in the top row were computed based on all recalls, whereas panels in the bottom row were computed based only on recalls following the first order error. Each column is based on data from a different experiment, as in Fig. 1

Joint findings of strong positional and temporal clustering may seem contradictory given that the two phenomena have been associated with very different theoretical models. However, it is important to recognize a critical confound in this comparison. Consider what happens after a participant recalls the first two items of a four-item list. If the participant recalls Item 3 next, its distance from the correct output position would be 0, and its distance from the preceding response would be +1.If, instead, the participant recalls Item 4 next, its distance from the correct output position would be −1, and its distance from the preceding response would be +2. In general, for recalls up to and including the first-order error, there is a one-to-one relationship between each item’s distance from the correct output position and from the prior recall, given by the function

$$D_{\mathit{prior}}=-D_{\mathit{pos}}+1$$

Fortunately, one can alleviate the confound by restricting the clustering analyses to items following the first-order error on each trial.¹ For example, in the recall sequence 1–3–4, Item 4 is included because Item 3 was recalled early. Plots of positional and temporal clustering for items following the first-order error are displayed in the bottom rows of Figs. 1 and 2, respectively. Figure 1 shows that such recalls do not cluster around the correct list position. On the other hand, Fig. 2 shows that, although attenuated, the temporal clustering effect is preserved. After committing the first-order error, participants tend to pick up with the list item that follows the item recalled out of order.

Strength-based associative chaining model

We next asked whether an associative chaining model that lacks any direct representation of positional information can account for this pattern of positional and temporal clustering. In previous work, associative chaining models (e.g., Lewandowsky & Murdock, 1989) have been successfully applied to several key features of serial recall and serial learning data, but have generally not been applied to the positional clustering effects that have been a critical source of evidence for positional coding theories (although see Shiffrin & Cook, 1978)

To address this question, we developed a reduced form chaining model that incorporates the two classic assumptions of associative chaining theory: (a) that the strength of association between items is a (exponentially) decreasing function of their distance, and (b) that forward associations (i.e., those between earlier and later items in the chain) are encoded more strongly than backward associations (Ebbinghaus, 1885/1913; Raskin & Cook, 1937). Consistent with other models, we assume a primacy gradient in item encoding strength to simulate participants’ tendency to allocate greater attention to early list items (Brown, Preece, & Hulme, 2000; Henson, 1998; Jensen, 1962; Lewandowsky & Murdock 1989; Page, & Norris, 1998). At test, the model simulates recall probabilistically according to a Luce choice rule (Luce, 1959) and can choose to stop at any position. As in other strength-based recall models, we use matrices to store the strengths of interitem associations (e.g., Kimball, Smith, & Kahana, 2007; Sirotin, Kimball, & Kahana, 2005); we do not explicitly model item representations themselves.

In addition to asking whether our associative chaining model can account for the pattern of positional and temporal clustering, we sought to examine whether the model could simultaneously account for two other critical aspects of serial recall and learning data, specifically: the multi-trial serial position curves (Ward, 1937) and the gains and losses of item and order information across trials (Addis & Kahana, 2004).

In most modeling studies, different experiments from the literature are used to illustrate different empirical phenomena. As such, separate model parameters are estimated for each experiment, and one cannot be sure whether it is the model’s mechanisms or its free parameters that are doing the work of fitting the empirical regularities. In order to assess whether the model can account for each of the findings using a single set of parameter values, we fit data from a single experiment (Kahana & Caplan, 2002, Experiment 2).

Participants in this experiment learned each list to a criterion of one perfect recall (see the Appendix). Because the number of study-test trials varied across lists, we restricted our analyses to the first three study-test trials and excluded lists that were learned in fewer than three trials.

Summary of parameters

As an illustrative example of the model’s dynamics, consider the list in Fig. 3. During study, each item is bound to all of the preceding items. The strength of the associations between nearest neighbors has a Gaussian distribution with an exponentially decaying mean (the primacy gradient; c_s controls the gain, d_s the decay rate, and min_as the lower bound) and with variance σ_as. The primacy gradient allows the model to mimic the way in which participants learn lists: Items from the beginning of the list are remembered on the first trial, and items from later in the list are progressively added on subsequent trials (Slamecka, 1964).

Fig. 3.

Illustration of direct and remote associations in the chaining model

The strength of associations between nonadjacent items decays exponentially as a function of distance. The rate of the decay is Gaussian with parameters μ_bs and σ_bs (note the increasingly lighter shades of gray between nonadjacent items in Fig. 3). Remote associations allow the model to skip ahead and later return to omitted items. Without remote associations, the only type of errors the model would be able to produce are errors of omission. The strengths of backward associations are scaled to w_b times the strengths of forward associations, where 0 < w_b < 1.

In addition to being bound to one another, list items are bound to an additional nonlist item that marks the beginning of a list. During recall, this start marker serves as the initial retrieval cue. Retrieval is probabilistic and follows a Luce choice rule with softmax parameter γ (see Eq. 5). When γ = 1, the probability of retrieving an item is proportional to the strength of the association between the retrieval cue and the item. As γ approaches ∞, only the item that is most strongly associated with the cue will be recalled (i.e., the winner takes all).

If a list item is successfully retrieved, it then serves as the retrieval cue for the subsequent position. Recall may also terminate at any list position if a second competing nonlist item is selected. The strength of this item is controlled by the parameter stop and is independent of the retrieval cue.

Table 2 provides a summary of the model’s parameters together with their best-fitting values. A formal description of the model can be found in the Appendix.

Table 2.

Model parameters

Parameter	Value
cs	0.945
ds	0.318
minas	0.000
σas	0.645
μbs	5.473
σbs	9.930
wb	0.134
stop	0.001
γ	9.169

Modeling positional and temporal clustering

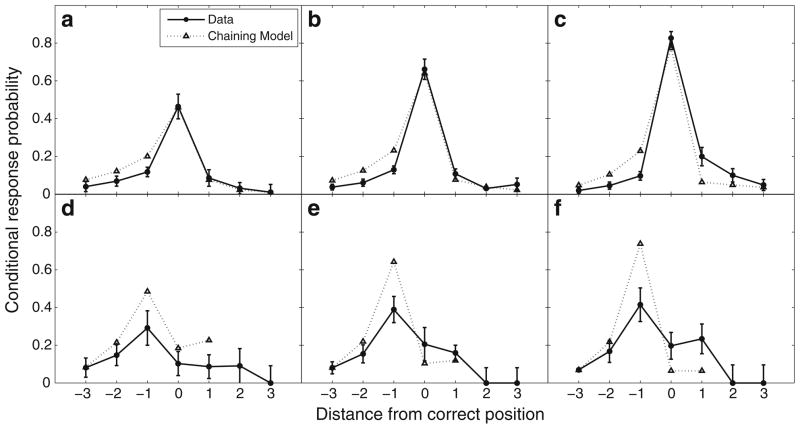
Figures 4 and 5 show that the chaining model can capture the major qualitative features of both positional and temporal clustering, computed in the standard way (top rows), and conditional on the prior recall being an order error (bottom rows). Although the model lacks a direct representation of positional information, it can successfully account for the positional clustering effect because of the confound with the temporal clustering effect.

Fig. 4.

Probability of recalling an item as a function of its distance from its correct position. Negative values correspond to recalling an item too early, and positive values correspond to recalling an item too late. The solid curve was computed based on the data from Kahana and Caplan (2002, Experiment 2), and the dotted curve was computed based on data simulated using the chaining model. Model parameters are given in Table 2. Error bars indicate 95% confidence intervals computed using the method of Loftus and Masson (1994). The three columns correspond to the first three trials of each list. a–c Based on all recalls. d–f Based only on recalls following the first order error

Fig. 5.

Probability of recalling an item as a function of its distance from the prior recall. Negative values correspond to recalling an earlier item from the list, and positive values correspond to recalling a later item from the list. The solid curve was computed based on the data from Kahana and Caplan (2002, Experiment 2), and the dotted curve was computed based on data simulated using the chaining model. Model parameters are given in Table 2. Error bars indicate 95% confidence intervals computed using the method of Loftus and Masson (1994). The three columns correspond to the first three trials of each list. a–c Based on all recalls. d–f Based only on recalls following the first order error

The chaining mechanism, together with the parameter values shown in Table 2, provide a simple and direct account of these results. The mean rate at which the strength of remote associations decays as a function of distance (μ_bs) is high throughout the list. On average, the strength increment between an item and another item more than two positions away is very low (<0.0001). Combined with strong forward asymmetry (w_b), these values result in a strong temporal clustering effect. The model slightly overestimates the magnitude of the effect as compared with the data, especially in later trials. Because the first order error most often involves skipping over a single item (see Fig. 10a), temporal clustering and positional clustering are still partially confounded, leading the model to also overestimate the percentage of items recalled one position early (bottom row of Fig. 4).

Fig. 10.

a Probability of committing the first-order error as a function of distance from the correct position. Negative values correspond to recalling an item too early, and positive values correspond to recalling an item too late. b Probability of recalling an item as a function of its distance from the prior recall, based only on recalls following the first-order error on trials in which the error did not involve skipping over a single item

Modeling serial position curves over trials

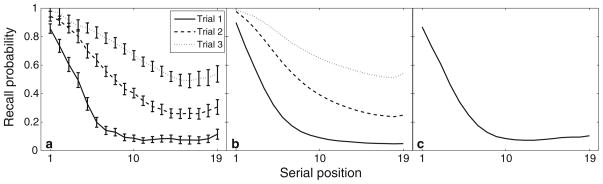
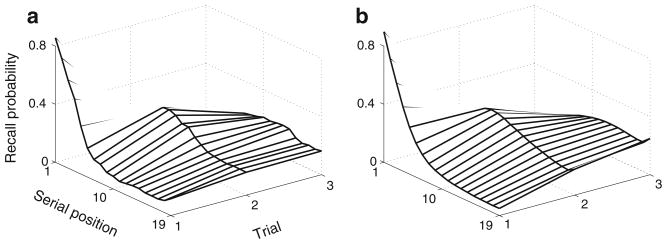
Serial position curves for the data are shown in Fig. 6a. Values for these curves were computed using relative order scoring (i.e., a recalled item was considered correct if the prior recall was the item’s immediate predecessor in the list). This scoring method is well suited to the experimental paradigm that we are modeling. Rather than being forced to make a response at each serial position (e.g. saying “pass” for serial positions that cannot be recalled), participants were free to recall only the words that came to mind. Using relative order scoring allows items from later serial positions to be marked correct even if items from earlier serial positions were omitted (a common occurrence for long lists using spoken recall). In contrast, absolute, or strict, positional scoring (i.e., considering an item to be correct only if it is recalled in the same position in which it was studied) heavily penalizes recall of midlist and end-of-list items.

Fig. 6.

a Serial position curves for Trials 1–3 of a 19 word list (Kahana & Caplan, 2002, Experiment 2). Error bars indicate 95% confidence intervals computed using the method of Loftus and Masson (1994). b Simulated values obtained using the chaining model. Model parameters are given in Table 2. c Simulated values obtained using the Burgess and Hitch (2006) positional coding model. Only the first trial is modeled

As shown in Fig. 6b, the chaining model captures the extended primacy effect and the change in both the level and shape of the serial position curve across trials. The primacy effect is a result of: (a) the inherent interdependencies that exist between items, and (b) the primacy gradient in encoding strengths. On the first trial, midlist items exhibit low levels of recall because the stop item acts as a formidable contender. Although the value of the stop parameter is low (see Table 2), it has a strong influence, on average, because the variance of strength increments (σ_as) is relatively high in comparison. This effect is progressively reduced in later trials as interitem associations are reinforced. Learning is a result of the variability in encoding strength (σ_as and σ_bs), coupled with a closed-loop learning rule (see the Appendix).

The primacy gradient is not necessary to fit the general shape of the serial position curve. Because successful retrieval of each item is dependent on the successful retrieval of the previous list item, chaining provides a natural account of the progressively lower levels of recall seen in later list positions. We tested this notion by fixing the parameters c_s and d_s to 0 and fitting the model with the reduced set of parameters. Although the fits were not quite as good, the model was still able to capture the qualitative features of the serial position curves and the pattern of clustering.

Modeling gains and losses of item and order (GLIO)

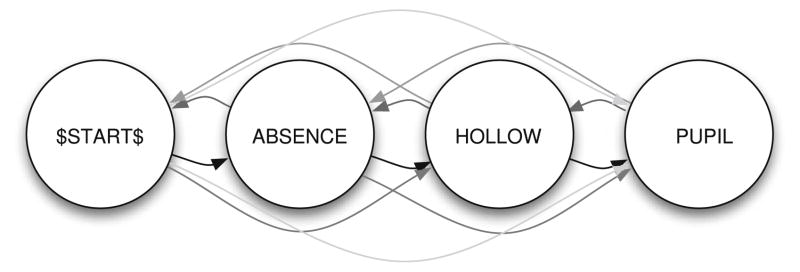
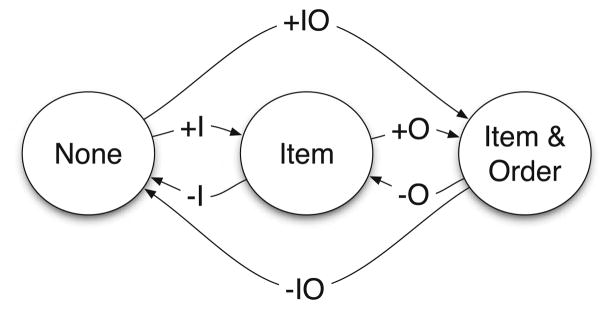
There are two types of information a participant can recall about an item: its membership in the list (item information) and its position in the list (order information). Each type of information may be gained, lost, or stay the same between two consecutive trials (Fig. 7). For example, if an item is recalled on the first trial in the wrong serial position (using relative order scoring, as in the previous section), it follows transition+I from state none to state item. If an item is recalled in the correct position, it follows transition+IO and ends up in state item and order. If item information, order information, or both are lost in a later trial, the item transitions back to one of its previous states. In all, there are six transitions of interest:

Fig. 7.

State diagram representing the possible gains and losses of item and order information between consecutive trials. The three states correspond to omitting an item, recalling an item out of order, and recalling an item in the correct order. Items transition between states in response to changes in item and order information. It is also possible that no change takes place, in which case an item stays in the same state (not shown)

+IO	Gaining item and order information
+I	Gaining item information, incorrect order information
+O	Gaining order information, maintaining item information
−IO	Losing item and order information
−I	Losing item information, did not have order information
−O	Losing order information, maintaining item information

Figure 8a shows the probability of gaining item and order information together (+IO) at each serial position on the first three trials. The data show a large primacy effect and small recency effect on Trial 1 (this is equivalent to the Trial 1 serial position curve shown in Fig. 6a). In later trials, a primacy effect is no longer apparent² and instead there is an increase for groups of items from progressively later in the list. As is shown in Fig. 8b, the model is able to capture the pattern of combined item and order gains for beginning and midlist items. The primacy items are learned first due to the interdependent nature of interitem associations and the gradient in encoding strength. Further strength increments on later trials allow the midlist items to be learned.

Fig. 8.

a Probability of gaining item and order information together at each serial position on Trials 1–3 of a 19-word list (Kahana & Caplan, 2002, Experiment 2). b Simulated values obtained using the chaining model. Model parameters are given in Table 2

The probability of gaining item and order information separately is below 0.15 at almost all serial positions. We aggregate these results across serial positions and summarize them in Table 3. Here we see a trade-off occur over trials, with some items gained out of order in earlier trials and then supplemented with order information in later trials.

Table 3.

Probabilities of gaining and losing item and order information

	Trial	Beh. Data	Simulation
+IO	1	0.232	0.223
	2	0.218	0.222
	3	0.154	0.168
+I	1	0.114	0.126
	2	0.079	0.079
	3	0.041	0.036
+O	1	—	—
	2	0.061	0.050
	3	0.083	0.062
−IO	1	—	—
	2	0.011	0.004
	3	0.016	0.007
−I	1	—	—
	2	0.012	0.013
	3	0.010	0.010
−O	1	—	—
	2	0.012	0.005
	3	0.017	0.010

As is shown in Table 3, the model is able to capture the low levels of separate item and order gains compared with the higher levels of combined gains. The proportion of combined gains relative to separate gains is controlled by the parameter w_b, which determines the likelihood of backward transitions, the parameters μ_bs and σ_bs, which control the strength of remote associations, and the parameter γ, which controls the frequency with which weakly associated items are selected for recall. The low value of w_b (see Table 2) and the high values of μ_bs, σ_bs, and γ together make combined gains more frequent.

The probability of losing information of any type is below 0.05 at all serial positions. We aggregate these results across serial positions as well, and also summarize them in Table 3. Once an item is placed in its correct position, that position is seldom lost. Item information by itself is also seldom lost and is instead supplemented with order information on a later trial. In the model, the same parameters that make combined item and order gains most frequent also ensure that there is very little chance of retrieving a remote item or the stop marker once the associations between nearest neighbors are sufficiently strong.

Comparison with a positional coding model

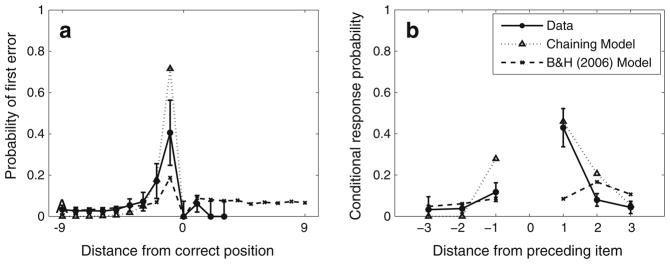
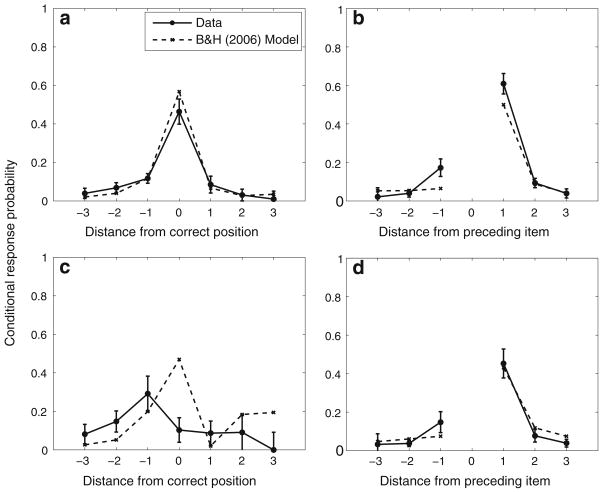
We also examined whether a prominent positional coding model (Burgess & Hitch, 2006) could fit the pattern of positional and temporal clustering. The Burgess and Hitch (2006) model features a neural network architecture in which different contexts, items, and phonemes are represented in separate layers of the network. During study, items become bound to a slowly varying list context, with proximal items bound to overlapping context signals. At test, the list context is played back and used as the retrieval cue. Because the Burgess and Hitch (2006) model has not been applied to multitrial serial learning data, we restrict our analysis to the first study-test trial.

The serial position curve predicted by the model is shown in Fig. 6c. The model captures the extensive primacy, the attenuated recency, and the overall level of recall seen in the data. Shown in the top row of Fig. 9, the model is also able to capture the major qualitative features of the traditional positional and temporal clustering effects. The model fails, however, to capture the pattern of conditional positional clustering (Fig. 9c). Instead, it incorrectly predicts that after committing an order error, participants are still most likely to recall the item from the proper list position.

Fig. 9.

a Probability of recalling an item as a function of its distance from its correct position. The solid curve was computed based on the data from Kahana and Caplan (2002, Experiment 2), and the dashed curve was computed based on data simulated using the model of Burgess & Hitch (2006). Error bars indicate 95% confidence intervals computed using the method of Loftus and Masson (1994). b Probability of recalling an item as a function of its distance from the prior recall. c–d same as in a–b, respectively, but based only on recalls following the first order error

Although one would not ordinarily expect a positional coding model to predict the conditional temporal clustering effect, the Burgess and Hitch (2006) model provides a very good fit to the data (Fig. 9d). We can gain insight into the model’s ability to fit this effect by examining the probability that the first-order error is a given distance from the correct position (Fig. 10a). Here, we see that the first-order error most frequently involves skipping over a single list item and recalling the next item one position early. Although we did not fit either model to this aspect of the data, both the chaining model and the Burgess and Hitch model can account for this effect. With the Burgess and Hitch model, an error of this kind represents a special case in which the subsequent recall is dependent on the identity of the error item. Consider what happens after the Burgess and Hitch model recalls the sequence 1–2–4. After recalling each item, the model inhibits the corresponding item node. The contextual retrieval cue most strongly matches the item from the fourth list position, but that item was recently recalled and inhibited, and is unlikely to be retrieved again. Because the context signal is autocorrelated, the item to most likely be recalled next is Item 5 (lag +1), followed by Item 3 (lag −1), and so on, producing the pattern of temporal clustering shown in Figure 9d. Such a dependence between consecutive recalls is not a general property of the Burgess and Hitch model. If the model recalled any item other than Item 4 in the third output position, Item 4 would not undergo inhibition and would be the item to most likely be recalled next, regardless of which item was recalled in the third output position.

In order to examine the predictions of both models outside of this special case, we repeated the conditional temporal clustering analysis, but this time excluding trials in which the first order error involved skipping over a single list item. Figure 10b shows that while the chaining model still correctly predicts the temporal clustering effect, the Burgess and Hitch (2006) model does not. It is possible that the Burgess and Hitch model could fit the pattern of results shown in Fig. 10b using another set of parameter values. In order to test for this possibility, we refit the model, this time including the results of Fig. 10b. The best-fitting parameter values were similar to those of the initial fit, leaving the pattern of results shown in Fig. 10b unchanged.

General discussion

In recalling sequences of items, people tend to cluster their responses around the correct list position. Items are most likely to be recalled in the correct position and are progressively less likely to be recalled in positions that are further away. This positional clustering effect has been well documented in many recall paradigms and has been used to support the positional coding theory of serial recall. According to positional coding theory, people associate each list item with a positional marker and use those markers as cues to guide recall.

In contrast to positional coding theory, the chaining theory of serial order memory posits that people associate each list item with the preceding item or items, and that during recall, the items serve as a cue for their neighbors. Consistent with this account of serial-order memory, people show a strong temporal clustering, or contiguity, effect. In serial recall, this is seen in the tendency for recalls to be items studied in proximity to the just-recalled item. Because positional information does not play an explicit role in chaining theory, it has generally been assumed that chaining models are unable to account for the positional clustering effect (although see Shiffrin & Cook, 1978).

The presence of prominent temporal and positional clustering in serial recall would seem to support a role for both chaining and positional coding. However, the analyses reported here demonstrate that positional and temporal clustering are highly confounded. Much of the confound is driven by the first several recalls on each trial, which both appear in their correct serial positions (distance 0 in Figs. 1 and 4) and are by definition each one list position away from the prior recall (distance +1 in Figs. 2 and 5). A similar ambiguity exists for the first item on each trial recalled in the wrong serial position. For these items, it is unclear whether recall is driven primarily by positional or by temporal information. An associative chaining model that makes no explicit use of positional information can exhibit significant positional clustering (see Figure 4a–c), providing a good fit to the levels observed in the data. Likewise, a positional coding model (Burgess & Hitch, 2006) that makes no explicit use of temporal information can exhibit significant temporal clustering (see Fig. 9b).

Conditioning the positional and temporal clustering analyses on an incorrect prior recall allowed us to alleviate the confound. We found that while the temporal clustering effect persists following an order error, the positional clustering effect is no longer apparent (see the bottom rows of Figs. 1 and 2). After making an order error, participants were most likely to recall the item on the list following the just-recalled item and not the item from the proper list position. Because chaining theory posits that each recall serves as the subsequent retrieval cue, our chaining model is also able to capture these effects (see Figs. 4d–f and 5d–f). However, because retrieval in the Burgess and Hitch (2006) model is driven primarily by positional information, their model incorrectly predicts that recalls following the first order error cluster around the correct list position (see Fig. 9c).

Surprisingly, the Burgess and Hitch (2006) model was able to capture the conditional temporal clustering effect (see Fig. 9d). We were able to better understand the model’s ability to fit this aspect of the data by analyzing the probability of committing the first-order error as a function of its distance from the correct position (Fig. 10a). Consistent with the data, the first-order error most often involves skipping over a single list item and recalling the next list item one position early. However, because items recalled by the Burgess and Hitch model are inhibited following recall, an item that is recalled one position early is unlikely to be repeated in the next output position, even though it best matches the positional retrieval cue. Instead, the next recall depends on the identity of the item that was recalled early, with higher weight given to neighboring items in the list. This type of dependence between adjacent recalls is not a general property of positional coding models or of the Burgess and Hitch model in particular, but rather, represents a special case of the model’s behavior. Repeating the conditional temporal clustering analysis while excluding the trials on which this type of order error occurred showed that the Burgess and Hitch model cannot match the pattern of temporal clustering beyond this special case.

Our findings point to a contiguity-based associative mechanism as the primary factor underlying positional clustering effects in serial recall. However, these findings do not exclude the possibility that positional information would assert itself in other aspects of serial order memory, especially situations in which interference caused by similarity or item repetitions must be overcome (Baddeley, 1968; Chance & Kahana, 1997; Henson et al. 1996; Kahana & Jacobs, 2000). Furthermore, contiguity-based associations may be indirect. For example, in the temporal context model (Howard & Kahana, 2002; Polyn, Norman, & Kahana, 2009; Sederberg, Howard, & Kahana, 2008), list items are associated with an overlapping context signal similar to the Burgess and Hitch (2006) model. However, unlike the Burgess and Hitch model, where contextual drift is independent of the list items that are experienced (i.e., either studied or recall), in the temporal context model, the context previously associated with each experienced item is incorporated into the model’s time varying context signal. In this way, each list item becomes indirectly bound to its predecessors. Future work will need to investigate the potential of such hybrid models to bridge the gap between the results that we have presented and previous work suggesting the need for positional information.

Appendix

Associative chaining model

In this appendix, we provide a concise description of our strength-based associative chaining model of serial recall and serial learning. MATLAB computer code used to run the simulations can be obtained from http://memory.psych.upenn.edu.

Study phase

Our chaining model uses two matrices to hold the strengths of associations between items, one for forward associations and one for backward associations. For simplicity, we assume that list words are not semantically related and that there are no associations across lists, so we set the initial strengths to zero. Similar to the Lewandowsky and Murdock (1989) model, a start marker is used to simulate the way in which participants access the beginning of a list. The start marker acts as list item 0 and is associated with each subsequent item.

Following the study of list item i on trial T, we increment the strength of the forward association from the immediately preceding item, i − 1, according to the storage equation:

$$\mathrm{\Delta }F{(i-1,i)}_T=a_s[1-F{(i-1,i)}_{T-1}],$$ (1)

where F(i − 1, i)_T−1 is the strength of the association on the previous trial and a_s is a random variable (Gaussian with parameters μ_as and σ_as) that controls the change in strength on the current trial. We do not allow the model to unlearn previous strength increments, so we clamp negative values of a_s to zero. We assume a primacy gradient in encoding strength and reduce the mean of a_s exponentially across serial positions to an asymptotic minimum of min_as:

$${\mu }_{a_s}=c_s{e}^{-d_s(i-1)}+{\mathit{min}}_{a_s},$$ (2)

where i indexes the serial position of the item. σ_as in Eq. 1 and c_s, d_s, and min_as in Eq. 2 are model parameters.

Equation 1 implements a closed-loop learning rule (Lewandowsky & Murdock, 1989): The increment in strength is proportional to the amount of association already in memory. The strength of the backward association from item i to item i − 1 is computed by scaling the forward increment by w_b, a parameter that ranges from 0 to 1:

$$\mathrm{\Delta }B{(i,i-1)}_T=w_b·\mathrm{\Delta }F{(i-1,i)}_T$$ (3)

This allows the model to mimic the forward asymmetry that is typical of serial recall (Bhatarah et al., 2006, 2008; Golomb et al., 2008; Klein et al, 2005).

In addition to forming associations between nearest neighbors, our model also forms remote associations by incrementing the strength between item i and each earlier list item, i − x, according to the more general storage equation:

$$\mathrm{\Delta }F{(i-x,i)}_T=a_s[1-F{(i-x,i)}_{T-1}]e^{-b_s\mid x-1\mid }$$ (4)

Here, a_s is the same as above, and b_s is a random variable (Gaussian with parameters μ_bs and σ_bs) that determines the strength of remote associations relative to nearest neighbors. The minimum value b_s can take is clamped to one. μ_bs and σ_bs are both model parameters. Note that when x = 1, this equation reduces to Eq. 1. During list study, a_s is sampled once for each item and b_s is sampled once for each list. The strength of remote associations is reduced exponentially as a function of the lag, x, which ranges from the previously studied item (x = 1) to the start marker (x = i). As with nearest neighbor associations, we assume that remote associations are formed in both the forward and backward directions, with the backward strength increment scaled by w_b.

Test phase

At test, the start marker serves as the first retrieval cue for each list. After the first position, each successfully retrieved item serves as the cue for the next position. Assuming that the model recalled item i, the next item, j, is chosen by the Luce choice rule (Luce, 1959):

$$P(j\mid i)=\frac{S{(i,j)}^{\gamma }}{{\sum }_{k}S{(i,k)}^{\gamma }+{\mathit{stop}}^{\gamma }},$$ (5)

where S = F + B, k ranges over all unrecalled items, and stop sets the probability of retrieval failure. Both stop and γ are model parameters. Our assumption that items are not repeated does not preclude the use of inhibition or other more realistic repetition suppression mechanisms. We have purposefully left this aspect of our model underspecified in order to focus on the role that is played by the chaining mechanism itself. For this same reason, we have also excluded learning during the test phase.

A numerical example

Consider the behavior of the model on the first trial of a four item list, using the following parameter values: w_b = 0.15, min_as = 0.10, d_s = 0.55, c_s = 0.60, μ_bs = 1.20, stop = 0.02, γ = 1.00. For simplicity, variability of encoding is omitted. All associations are set to zero at the beginning of the simulation. We begin the study phase by applying Eq. 2 to determine the increment in associative strength between the start marker and the first item:

$${\mu }_{a_s}(1)=0.60·e^{-0.55·0}+0.1=0.700,$$

Equation 4 is used to update the strength matrix. Since there is no encoding variability and no prior learning, the increment is exactly 0.700 in the forward direction and 0.105 in the backward direction (0.700·w_b). The rest of the list is presented in a similar manner, and Table 4 shows the resulting associative strength matrices. Here, we combine the forward (F, located in the upper triangle) and backward (B, located in the lower triangle) matrices for ease of presentation.

Table 4.

Associative strengths following the first trial study phase of a sample simulation

	$	1	2	3	4
$	—	.700	.134	.027	.006
1	.105	—	.446	.090	.020
2	.020	.067	—	.300	.065
3	.004	.014	.045	—	.215
4	.001	.003	.010	.032	—

At test, the probability of retrieving the first item is computed using Eq. 5:

$$P(1\mid \$)=\frac{0.700}{0.700+0.134+0.027+0.006+0.020}=0.789$$

The probability of retrieving each of the remaining items is computed in a similar fashion, and an item is selected by sampling from this distribution. If an item is successfully retrieved (i.e., the stop marker is not sampled), the next recall is selected by sampling from the distribution formed by conditioning the remaining items on the first recall. Recall proceeds in this manner until either the stop marker is selected or all of the items are recalled. In the case of choosing the stop marker, the study-test cycle is repeated (for a maximum of ten trials). If the list is correctly recalled, the strength matrix is reset to zero and simulation of the next list begins.

Parameter estimation

The chaining model parameters shown in Table 2 were found by using a genetic algorithm (Mitchell, 1996) to minimize the mean root-mean squared deviation (RMSD) between the data and the model for the three aspects of the data described in the main text (the clustering measures, the serial position curves, and the gains and losses of item and order information). We evolved a population of 20,000 initially random parameter values for 10 generations. We then reduced the size of the population to 1,000 and ran the algorithm for 20 more generations. The parameter values that were in the top 10 percent of each generation were carried over to the next, and new parameter values were computed by sampling from and perturbing the surviving values. The best-fitting parameter values are shown in Table 2, and the simulations described in the main text were performed using these values.

We fit the model of Burgess and Hitch (2006) to the clustering measures and to the first trial serial position curve using the same approach, varying all of the parameters listed in Table A1 of Burgess and Hitch (2006) except for n_a2 and α (these two parameters relate to the grouping of items during presentation, which we do not consider here).

Experiment details

Golomb et al. (2008)

Thirty-six young and 36 older adult participants performed the experiment over two sessions. Half of the participants performed a free recall task during the first session and a serial recall task during the second session, and the other half performed the tasks in the reverse order. We focused our analysis on the data from the younger participants performing serial recall.

Words were drawn from a collection of 846 two-syllable nouns (for details, see Golomb et al., 2008). Each list consisted of 10 words, with each word appearing on the screen for 1 s. ISIs were either 800 ms, 1,200 ms, or 2,400 ms, and were constant within each list. At test, participants were given up to 1 min to vocally recall the list in the presented order.

Participants received four practice lists, followed by 36 test lists. The practice lists were not included in our analysis. Because lists in the Golomb et al. (2008) study were shorter than the lists in the other two studies, we included all items in our analysis, including edge items, in order to maximize the amount of data on which each result is based.

Kahana and Caplan (2002), Experiment 2

Sixty participants performed the experiment over the course of five sessions. The first session consisted of one 10-word, one 15-word, and two 19-word practice lists, which were not included in our analysis. The remaining four sessions each consisted of five 19-word lists. Words were drawn from the Toronto Word Pool (Friendly, Franklin, Hoffman, & Rubin, 1982) without replacement and were presented aurally at a rate of 1.5 s. After studying a list, participants were asked to vocally recall the list in the presented order. The cycle of study and test was repeated for each list until it was recalled perfectly.

In order to avoid edge artifacts, we focused our analysis on list positions 4–16. Comparisons across trials (see the section strength-based associative chaining model) were restricted to the first three trials of each list. Lists that were learned in fewer than three trials (about 17%) were excluded.

Kahana et al. (2010)

Forty-two participants performed the experiment over the course of four sessions. Each list consisted of 7, 13, or 19 words drawn from the Toronto Word Pool (Friendly et al, 1982) without replacement and were presented aurally at a rate of 1 s. At test, participants were given 1 min to vocally recall the list in the presented order, and the study and test cycle was repeated for each list until it was recalled perfectly.

The experiment consisted of two conditions. In the constant start condition, participants studied each list in the usual manner, starting at the same list position. In the spin-list condition, participants studied each list starting in a random position on each trial. We conducted our analysis on the data from the constant start condition only.

The first session of the experiment consisted of practice lists and was not included in our analysis. Subsequent sessions consisted of three lists of each possible length under one of the two starting conditions (the order of conditions was counterbalanced across participants). Four subjects were excluded because they failed to learn any lists within a predetermined maximum number of trials. In order to avoid edge artifacts, we focused our analysis on positions 4–10 for lists of length 13 and positions 4–16 for lists of length 19. We excluded lists of length 7 because they did not yield enough data to condition the clustering analyses on the prior recall being an order error.