Friction Modeling in Concentric Tube Robots

Abstract

Concentric tube robots are a novel class of continuum robots that are constructed by combining pre-curved elastic tubes such that the overall shape of the robot is a function of the relative rotations and translations of the constituent tubes. Frictionless kinematic and quasistatic force models for this class of robots have been developed that incorporate bending and twisting of the tubes. Experimental evaluation of these models has revealed, however, a directional dependence of tube rotation on robot shape that is not predicted by these models. To explain this behavior, this paper models the contributions of friction arising from two sources: the distributed forces of contact between the tubes along their length and the concentrated bending moments generated at discontinuities in curvature and at the boundaries. It is shown that while friction due to distributed forces is insufficient to explain the experimentally observed tube twisting, a simple model of frictional torque arising from concentrated moments provides a good match with the experimental data.

I. INTRODUCTION

Concentric tube robots are currently being designed for a broad range of minimally invasive surgeries since they can be constructed with diameters of several millimeters and lengths of 20-30 cm. Several specific applications are intracardiac surgery, neurosurgery and lung surgery [10]. They can be easily designed and constructed to navigate along 3D curves through body lumens as well as tissue and can manipulate tip-mounted tools. Fig. 1 depicts an example composed of three tubes with tip-mounted forceps.

Fig. 1.

Concentric tube robot composed of three telescoping sections with tip-mounted forceps.

In the last few years, substantial progress has been made in developing this technology [1]-[7]. Mechanics models have been derived for computing the kinematics [1]-[3] and deformation due to external loading [4],[5]. Solution of the anatomically-constrained inverse kinematic problem has been considered in [9],[10]. Real-time implementations of position control [2],[6], and stiffness control [7],[7] have been demonstrated in the laboratory and in beating-heart intracardiac animal trials.

In all publications relating to kinematics, however, a variety of phenomena have been neglected in order to simplify the modeling, but with the acknowledgement that these effects are not necessarily negligible [1],[2]. An important member of this group is friction, and the evidence suggesting its importance can be seen in experimental data measuring the relative twist of a pair of tubes of equal curvature and stiffness. While the frictionless model predicts a single twist angle, experimental results reveal an envelope of twist angles whose boundaries are produced by different directions of relative rotation [1],[2]. Neglecting the existence of this envelope can produce tip position errors of about 10% of the length of the tube pair. For 20 cm long tubes, this is a tip error of 2 cm, which would be unacceptable for most medical applications.

The kinematic models [1]-[3] predict two types of interactions forces between the tubes of the robot. The first consists of the distributed forces along the lengths of the tubes. The second type consists of concentrated moments that are applied between the tubes at their ends and at points of pre-curvature discontinuity. These moments force all tubes to share a common central axis – an assumption that is only exact as the clearance between the tubes goes to zero. Both types of interaction forces can be sources of friction.

The contributions of this paper are as follows. First, Coulomb friction torque due to the inter-tube distributed contact forces is incorporated into the kinematic model. Second, it is demonstrated that this frictional torque is bounded and is insufficient to explain the experimentally observed tube twisting. Third, while detailed analysis of friction due to concentrated moments must incorporate the inter-tube clearances and is beyond the scope of this paper, an approximate lumped Coulomb-type model is proposed and is shown to provide a good match of experimental results. Furthermore, this model can be efficiently implemented in a controller and is appropriate for practical robot designs comprised of telescoping arrangements of fixed and variable curvature sections as proposed in [2].

The paper is arranged as follows. The next section presents the friction models. First, the frictionless model is summarized. It is then modified to include the Coulomb friction torque arising from the distributed contact forces between the tubes. Its effect on tube twisting is examined in the subsequent subsection. Finally, a lumped model is proposed for friction torque due to concentrated moments that enters the distributed model as a boundary condition. The third section presents an experimental evaluation of the lumped model. Conclusions appear in the final section.

II. FRICTION MODELING

There are many possible friction models that can be employed in the control of robotic systems. Selection of the appropriate model depends both on the machine and its operating conditions [11]. As currently used in surgical procedures, concentric tube robots possess lubricated sliding interfaces that experience mm-scale displacements at low velocities. Thus, it is likely that a Coulomb model will provide sufficient accuracy for current tasks and such a model is assumed in this paper.

The kinematic models are derived here using the notation of the frictionless model presented in [1],[2]. It includes bending and torsion for an arbitrary number of tubes whose curvature and stiffness can vary with arc length. Effects that are neglected include shear of the cross section, axial elongation and nonlinear constitutive behavior. It is also assumed here that no external loads are applied to the robot.

In the remainder of the paper, subscript indices i = 1,2,...,n are used to refer to individual tubes with tube 1 being outermost and tube n being innermost. Arc length, s, is measured such that s = 0 at the proximal end of the tubes. The total length of each tube is designated by L_i.

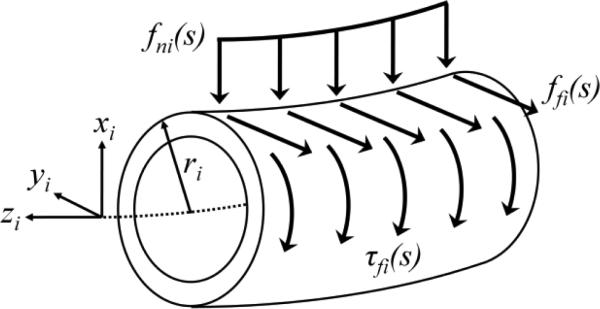
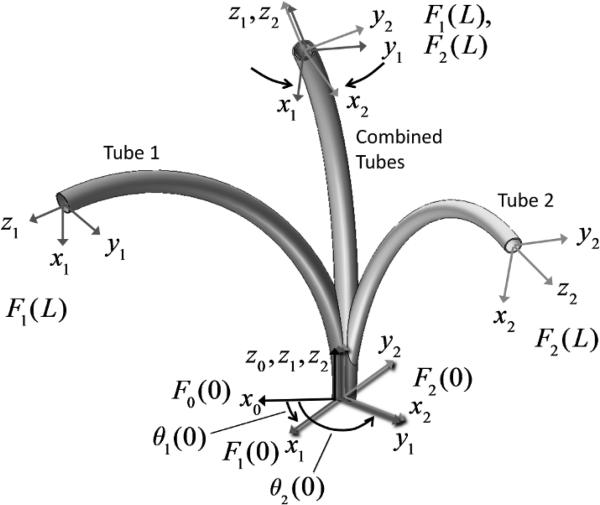
As illustrated in Fig. 2, insertion of one tube inside the other causes each to bend and twist along their length. For each tube, material coordinate frames for each cross section can be defined as a function of arc length s along tube i by defining a single frame at the proximal end, F_i(0), such that its z axis is tangent to the tube's centerline. Under the unrestrictive assumption that the tubes do not possess initial material torsion, the frame F_i(s) is obtained by sliding F_i(0) along the tube centerline without rotation about its z axis (i.e., a Bishop frame [12]). As the tubes move, bend and twist, these material frames act as body frames tracking the displacements of their cross sections. It is also useful to define a reference frame, F₀(s), which displaces with the cross sections but does not rotate about its z axis under tube torsion.

Fig. 2.

Distributed forces and torques applied to tube i by outer neighbor tube i + 1

As the i^th tube's coordinate frame F_i(s) slides down its centerline, it experiences a body-frame angular rate of change per unit arc length given by

$$u_i\left(s\right)={\left[u_{ix}\left(s\right)u_{iy}\left(s\right)u_{iz}\left(s\right)\right]}^T$$ (1)

in which (u_ix,u_iy) are the components of curvature due to bending and u_iz is the curvature component due to torsion. A circumflex on a curvature component is used to designate the initial pre-curvature of a tube.

The kinematic input variables consist of the rotation and translation of each tube about and along the common centerline of the combined tubes. The rotation angle, θ_i(s, is defined as the z-axis rotation angle from frame F₀(s) to frame F_i(s). The translation variable, l_i, is defined as the arc length distance from frame F₀(0) to the initially coincident frame F_i(0). In the rest of the paper, all vector , quantities associated with tube i , e.g., u_i(s), are written with respect to frame F_i(s).

In the subsection below, the frictionless kinematic model of [1],[2] is summarized. The two friction models are then developed in the context of this model.

A. Frictionless Model

The frictionless kinematic equations can be derived by combining four equations – (1) a constitutive model relating bending moments to changes in curvature of individual tubes, (2) a compatibility equation relating the individual curvatures of the assembled tubes to their combined curvature, (3) the equilibrium of bending moments and shear forces on the cross sections of the assembled tubes, and (4) a differential equation that expresses how shear force and bending moment propagate along a curved rod. These are summarized below along with the resulting model from [1],[2].

(1) Constitutive Model

When a tube with initial curvature û_i(s) is deformed to a different curvature u_i(s), a bending moment is generated. Assuming linear elastic behavior, the bending moment vector m_i(s) at any point s along tube i is given by

$$m_i\left(s\right)=K_i(u_i\left(s\right)-{\widehat{u}}_i\left(s\right))$$ (2)

Given the coordinate frame convention described above, all vectors are expressed with respect to frame F_i(s), and K_i is the frame-invariant stiffness tensor given by

$$K_i=\left[\begin{array}{ccc}\hfill k_{ix}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill k_{iy}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill k_{iz}\hfill \end{array}\right]=\left[\begin{array}{ccc}\hfill E_i{I}_i\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill E_i{I}_i\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill J_i{G}_i\hfill \end{array}\right]$$ (3)

in which E_i is the modulas of elasticity, I_i is the area moment of inertia, J_i is the polar moment of inertia and G_i is the shear modulus of tube i.

(2) Compatibility of Deformations

Assuming that the clearance between each pair of adjacent tubes is just sufficient to enable relative motion, all tubes must conform to the same final x-y (bending) curvature. For this to be true, we assume that concentrated moments are generated over negligibly short lengths at discontinuities in pre-curvature and at the ends of tubes.

Each tube is free, however, to twist independently about its z axis. The z component of curvature, ${\phantom{\mid }{u}_i\left(s\right)\mid }_z$, equates to the rate of change of twist angle with respect to arc length, ${\stackrel{.}{\theta }}_i\left(s\right)$,

$${\stackrel{.}{\theta }}_i\left(s\right)={\phantom{\mid }{u}_i\left(s\right)\mid }_z.$$ (4)

The resulting bending curvatures can be equated when written in the same frame. Expressing tube curvatures in terms of the robot frame curvature, u₀, results in

$$u_i\left(s\right)=R_z^T\left({\theta }_i\right)u_0\left(s\right)+{\stackrel{.}{\theta }}_i\left(s\right)e_z$$ (5)

in which R_Z(θ_i)∈ SO(3) is a rotation about the z axis by angle z angle θ_i and e_z = [0 0 1]^T.

(3) Equilibrium of Bending Moments

On each cross section, the bending moments in each tube must sum to the robot's net bending moment, m₀(s), which is zero absent external loading.

$$m_0\left(s\right)=\sum _{i=1}^n{R}_z\left({\theta }_i\right)m_i\left(s\right)=0$$ (6)

As in (5), R_Z(θ_i) is used to transform tube bending moments from frame F_i(s) to frame F₀(s).

(4) Propagation of Shear Force and Bending Moment

The equilibrium equation of the special Cosserat rod model [13]-[15] provides body-frame equations for a curved rod undergoing distributed loading of $\tau \in {\mathbb{R}}^3$ torque per unit length and force per $f\in {\mathbb{R}}^3$ unit length. It can be applied to each tube.

$$\left[\begin{array}{c}\hfill {\stackrel{.}{m}}_i\left(s\right)\hfill \\ \hfill {\stackrel{.}{n}}_i\left(s\right)\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\tau }_i\left(s\right)\hfill \\ \hfill f_i\left(s\right)\hfill \end{array}\right]-\left[\begin{array}{cc}\hfill \left[u_i\left(s\right)\right]\hfill & \hfill \left[v_i\left(s\right)\right]\hfill \\ \hfill 0\hfill & \hfill \left[u_i\left(s\right)\right]\hfill \end{array}\right]\left[\begin{array}{c}\hfill m_i\left(s\right)\hfill \\ \hfill n_i\left(s\right)\hfill \end{array}\right]$$ (7)

Derivatives are with respect to arc length along the rod, s, and $m_i,n_i\in {\mathbb{R}}^3$ are the bending moment and shear force vectors acting on the tube's cross section. Here, and in the remainder of the paper, the square brackets on any vector denotes the skew-symmetric form

$$\left[u_i\right]=\left[\begin{array}{ccc}\hfill 0\hfill & \hfill -u_{iz}\hfill & \hfill u_{iy}\hfill \\ \hfill u_{iz}\hfill & \hfill 0\hfill & \hfill -u_{ix}\hfill \\ \hfill -u_{iy}\hfill & \hfill u_{ix}\hfill & \hfill 0\hfill \end{array}\right]$$ (8)

Consistent with the previous notation, $u_i\left(s\right),v_i\left(s\right)\in {\mathbb{R}}^3$ are the angular and linear strain rates per unit arc length, respectively, experienced by the tube's cross section. Thus, as described previously, u_i(s) has the units of curvature. Similarly, the x and y components of v_i(s) are the shear strain components of the cross section while the z component is v_iz = 1 + ε_iz in which ε_iz is the longitudinal strain. Given the assumptions of negligible shear and longitudinal strain,

$$v_i\left(s\right)={\left[001\right]}^T$$ (9)

In (7), the frictionless assumption together with the tight-clearance assumption used in compatibility constrain the interaction forces and torques that the tubes can exert on each other along their length. The distributed force, f_i(s) , exerted between a pair of tubes must be directed radially with respect to the cross section and so f_iz(s) = 0. Furthermore, the tubes cannot apply distributed moments to each other and so τ_i(s) = 0. Recall, however, the compatibility does require the existence of concentrated moments generated over negligibly short lengths at discontinuities in pre-curvature and at the ends of tubes. These concentrated moments enter (7) as boundary conditions.

Combining (2)-(9) results in the following second order system of differential equations in the n twist angles, θ_i, of the individual tubes.

$$\begin{array}{cc}\hfill {\stackrel{.}{\theta }}_i\left(s\right)& ={\phantom{\mid }{u}_i\left(s\right)\mid }_z\hfill \\ \hfill {\stackrel{.}{u}}_{iz}\left(s\right)& =(1+\nu )\left(u_{ix}\left(s\right){\widehat{u}}_{iy}-u_{iy}\left(s\right){\widehat{u}}_{ix}\right)\hfill \end{array}$$ (10)

For simplicity it is assumed that neither the initial curvatures nor the stiffnesses vary with tube length. In (10), the bending curvatures of the tubes are described by the algebraic equations,

$$\begin{array}{cc}\hfill {\phantom{\mid }{u}_0\left(s\right)\mid }_{x,y}& ={\left[\sum _{i=1}^n{K}_i\left(s\right)\right]}^{-1}{\phantom{\mid }\left[\sum _{i=1}^n{R}_z\left({\theta }_i\left(s\right)\right)K_i\left(s\right){\widehat{u}}_i\left(s\right)\right]\mid }_{x,y}\hfill \\ \hfill {\phantom{\mid }{u}_i\left(s\right)\mid }_{x,y}& ={\phantom{\mid }{R}_z^T\left({\theta }_i\right)u_0\left(s\right)\mid }_{x,y}.\hfill \end{array}$$ (11)

The boundary conditions for the state variables $\{{\theta }_i,{\stackrel{.}{\theta }}_i\}$ are split between the proximal and distal ends of the robot.

$$\begin{array}{cc}\hfill {\theta }_i\left(0\right)& =\text{actuator positions}\hfill \\ \hfill {\stackrel{.}{\theta }}_i\left(L\right)& =0\hfill \end{array}$$ (12)

The boundary condition ${\stackrel{.}{\theta }}_i\left(L\right)=0$ indicates that no torques are applied to the distal ends of the tubes.

Note that when referring to a robot consisting of only two tubes it is occasionally convenient to use the values:

$$\begin{array}{cc}\hfill \alpha & ={\theta }_2-{\theta }_1\hfill \\ \hfill \stackrel{.}{\alpha }& ={\stackrel{.}{\theta }}_2-{\stackrel{.}{\theta }}_1\hfill \end{array}$$ (13)

B. Modeling Friction Torque Due to Distributed Forces

We consider here the effect of frictional forces associated with rotation of the tubes. Fig. 3 shows the distributed forces and torques applied to a tube by its outer neighbor. With respect to (7), the total distributed force f_i(s) is given by

$$f_i\left(s\right)=f_{ni}\left(s\right)+f_{fi}\left(s\right)$$ (14)

The normal contact force f_ni(s) is the only force that the tube experiences in the frictionless case.

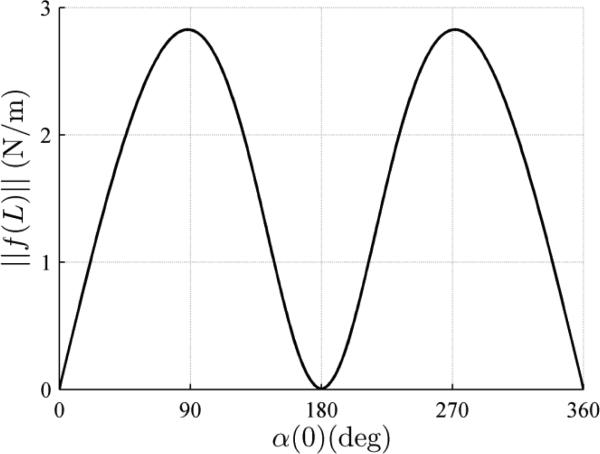
Fig. 3.

Distributed force magnitude at s = L versus relative rotation angle at s = 0 for tube pair B.

For ease of exposition, the notation for the remainder of the paper will not reference the arc length (s) in variables.

Assuming that the relative rotation of tube i with respect to tube i + 1 is about the z-axis, Coulomb friction introduces both a force and torque at the interface given by

$$\begin{array}{cc}\hfill f_{fi}& =\left(\mu \mathrm{sgn}\left({\stackrel{.}{\theta }}_i-{\stackrel{.}{\theta }}_{i+1}\right)\right)\left[v\right]f_{ni}\hfill \\ \hfill {\tau }_{fi}& ={\left[00-r\Vert f_{fi}\Vert \right]}^T\hfill \end{array}$$ (15)

Given this description, the distributed forces and torques have the following nonzero components.

$$f_i={\left[f_{ix}{f}_{iy}0\right]}^T$$ (16)

$${\tau }_i={\left[00{\tau }_{iz}\right]}^T$$ (17)

Combining equations (14),(15) and taking the magnitude,

$$\Vert f_i\left(s\right)\Vert =\Vert f_{ni}\Vert \sqrt{1+{\mu }^2}$$ (18)

Thus (15) can be rewritten purely in terms of f_i:

$${\tau }_{fiz}=-\frac{\mu }{\sqrt{1+{\mu }^2}}{r}_i\Vert f_i\Vert \mathrm{sgn}\left({\stackrel{.}{\theta }}_i-{\stackrel{.}{\theta }}_{i+1}\right)$$ (19)

To modify the governing equations to include the friction force and torque, we need to incorporate their effect into the expression for u̇_iz(s) in (10).

From [1] and [2], this expression was obtained using the z component of the moment equation in (7) with m_i and ṁ_i replaced by u_i and u̇_i, respectively obtained from the constitutive model (2). This results in

$${\stackrel{.}{u}}_{iz}=\left(1+\nu \right)\left({\tau }_{iz}+u_{ix}{\widehat{u}}_{iy}-u_{iy}{\widehat{u}}_{ix}\right)$$ (20)

Substituting τ_iz = τ_fiz to combine (19) and (20) yields

$${\stackrel{.}{u}}_{iz}=\left(1+\nu \right)\frac{-\mu }{\sqrt{1+{\mu }^2}}{r}_i\Vert f_i\Vert \mathrm{sgn}\left({\stackrel{.}{\theta }}_i-{\stackrel{.}{\theta }}_{i+1}\right)+\left(1+\nu \right)\left(u_{ix}{\widehat{u}}_{iy}-u_{iy}{\widehat{u}}_{ix}\right)$$ (21)

We now need an expression for computing f_i. Recall the shear force equation from (7),

$${\stackrel{.}{n}}_i=f_i-\left[u_i\right]n_i$$ (22)

In this equation we first solve for n_i using the rearranged moment equation of (7),

$$\left[v\right]n_i=-K_i{\stackrel{.}{u}}_i+{\tau }_i-\left[u_i\right]K_i\left(u_i-{\widehat{u}}_i\right)$$ (23)

Due to fact that n_i here is premultiplied by [v], this equation only yields explicit values for n_ix and n_iy. The value of n_iz can be found by integrating the z component of the shear force equation,

$${\stackrel{.}{n}}_{iz}=u_{ix}{n}_{iy}-u_{iy}{n}_{ix}$$ (24)

using the values of n_ix and n_iy found above. Note that this adds a new state variable per tube to the overall integration. We now solve for f_i by premultiplying (22) by [v],

$$\left[v\right]{\stackrel{.}{n}}_i=\left[v\right]f_i-\left[v\right]\left[u_i\right]n_i,$$ (25)

taking the derivative with respect to arc length of (23),

$$\left[v\right]{\stackrel{.}{n}}_i=-K_i{\ddot{u}}_i-\left[{\stackrel{.}{u}}_i\right]K_i(u_i-{\widehat{u}}_i)-\left[u_i\right]K_i{\stackrel{.}{u}}_i$$ (26)

and finally setting the right-hand sides equal to yield:

$$\left[v\right]f_i=-K_i{\ddot{u}}_i-\left[{\stackrel{.}{u}}_i\right]K_i(u_i-{\widehat{u}}_i)-\left[u_i\right]K_i{\stackrel{.}{u}}_i+\left[v\right]\left[u_i\right]n_i$$ (27)

Note that only the x and y components of ü_i are required to solve for f_i and recall that the curvature at a give cross-section is given by

$${\phantom{\mid }{u}_0\mid }_{x,y}={\left[\sum _{j=1}^n{K}_j\right]}^{-1}{\phantom{\mid }\sum _{j=1}^n{R}_z\left({\theta }_j\right)K_j{\widehat{u}}_j\mid }_{x,y}$$ (28)

Using the formula for the rotation matrix derivative about z,

$$\frac{d}{dt}{R}_z\left(\theta \right)=\stackrel{.}{\theta }\left[e_z\right]R_z\left(\theta \right),$$ (29)

the derivative with respect to arc length of (28) is

$${\phantom{\mid }{\stackrel{.}{u}}_0\mid }_{x,y}={\left[\sum _{j=1}^n{K}_j\right]}^{-1}{\phantom{\mid }\sum _{j=1}^n{\stackrel{.}{\theta }}_j\left[e_z\right]R_z\left({\theta }_j\right)K_j{\widehat{u}}_j\mid }_{x,y}$$ (30)

and the second derivative is:

$${\phantom{\mid }{\ddot{u}}_0\mid }_{x,y}={\left[\sum _{j=1}^n{K}_j\right]}^{-1}{\phantom{\mid }\left(\sum _{j=1}^n{\ddot{\theta }}_j\left[e_z\right]R_z\left({\theta }_j\right)K_j{\widehat{u}}_j+{\stackrel{.}{\theta }}_j^2{\left[e_z\right]}^2{R}_z\left({\theta }_j\right)K_j{\widehat{u}}_j\right)\mid }_{x,y}$$ (31)

The value in the i^th tube's own frame is:

$$\begin{array}{cc}\hfill {\phantom{\mid }{\stackrel{.}{u}}_i\mid }_{x,y}& ={R^T}_z{\phantom{\mid }\left({\theta }_i\right){\stackrel{.}{u}}_0\mid }_{x,y}+{\phantom{\mid }{\stackrel{.}{R}}_z^T\left({\theta }_i\right)u_0\mid }_{x,y}\hfill \\ \hfill {\phantom{\mid }{\ddot{u}}_i\mid }_{x,y}& ={\phantom{\mid }{R^T}_z\left({\theta }_i\right){\ddot{u}}_0\mid }_{x,y}+{\phantom{\mid }2{\stackrel{.}{R}}_z^T\left({\theta }_i\right){\stackrel{.}{u}}_0\mid }_{x,y}+{\phantom{\mid }{\ddot{R}}_z^T\left({\theta }_i\right)u_0\mid }_{x,y}\hfill \end{array}$$ (32)

Substituting (31)-(32) into (27) gives an equation for f_i in which the only unknown is u̇_iz. When combined with (21), the result is an implicit equation in u̇_iz that must be solved (presumably by root-finding) at each step of the integration.

C. Effect of Distributed-force Friction on Tube Twisting

Simulation was used to evaluate the frictional kinematic model derived above for pairs of tubes comparable to those described in the experiments of section III. These tubes are of equal pre-curvature and bending stiffness. Consequently, their combined curvature varies between the pre-curvature value and zero as they are rotated with respect to each other. It was found that as frictional torque due to distributed forces is varied (0 ≤ μ ≤ ∞), there is little change in the twisting of the tubes.

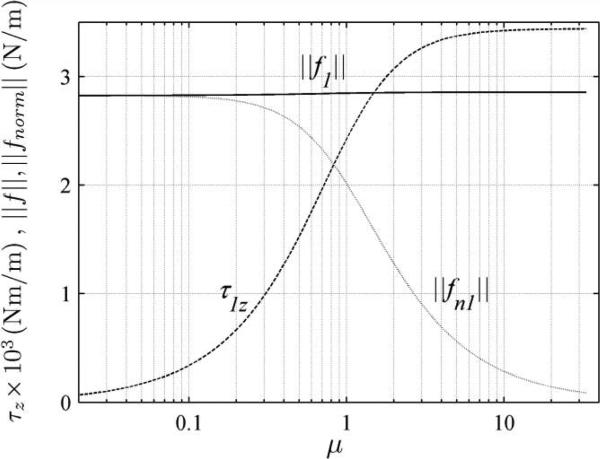
As an example, the tube parameters of tube pair B given in Table 1 and Table 2 were used to compute the configuration in which the tubes are rotated by π/2 with respect to each other at their base. As shown in Fig. 3 for the frictionless case, the distributed forces between the tubes are close to their maximum values and, consequently, the effect of friction due to these forces should also be maximized. Using the equations from section II.B, the total distributed force, f₁, distributed normal force, f_n1, and distributed friction torque, τ_1z, were computed and their magnitudes are plotted as a function of friction coefficient in Fig. 4. It can be observed that, as the friction coefficient μ is increased, the distributed normal force magnitude asymptotically approaches zero while the distributed friction torque asymptotically approaches a finite value. Surprisingly, the total distributed force magnitude remains constant.

Table 1.

Tube Stock Used in Experiments.

Tube	1	2
Outer Diameter (mm)	2.77+/-0.01	2.41+/-0.01
Inner Diameter (mm)	2.55+/-0.01	1.97+/-0.01

Table 2.

Tube pair parameters.

Tube Pair	A	B
r1 (mm)	231	154
r2 (mm)	243	154
Stiffness (tube 1 / tube 2)	0.0334/0.427	0.0334/0.0511

Fig. 4.

Numerically computed values of distributed friction torque,τ_1z ×10³ (dashed line), total distributed force, $\Vert f_1\Vert$ (solid black line) and normal distributed force, $\Vert f_{n1}\Vert$ (grey line), versus friction coefficient μ. Values are for the tip of tube pair B(s = L)when rotated to α(0) = π/2.

Examining the normal and tangential components of the distributed force vector reveals that, as the friction coefficient increases, the components vary so as to maintain the direction and magnitude of the total distributed force vector on the cross section. This is depicted in Fig. 5.

Fig. 5.

Distributed normal, tangent, and total forces on a cross section for two values of friction coefficient. Total force direction and magnitude is preserved.

Further study of the simulation data revealed that the distributed friction torque when integrated over the length of the tubes was two orders of magnitude less than the torque applied at s = 0 to produce the tube rotation α(o) = π / 2.

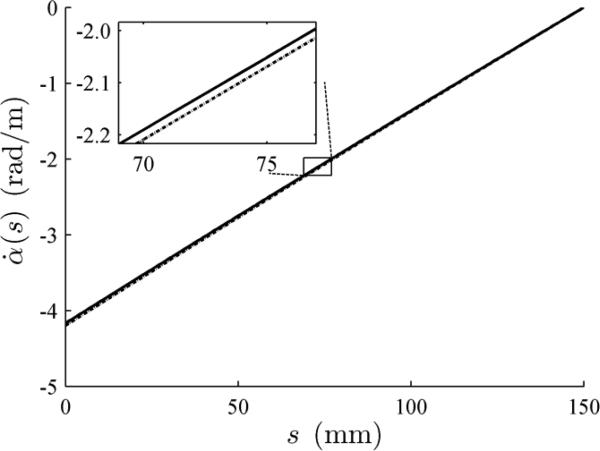
This is illustrated in Fig. 6 that plots tube twist rate, $\stackrel{.}{\alpha }\left(s\right)$, (proportional to cross sectional torque) as a function of arc length. Despite an unrealistically large friction coefficient of μ =10⁵, the change in twist rate produced by friction is negligible.

Fig. 6.

Simulated tube twist rate, $\stackrel{.}{\alpha }\left(s\right)$, without friction (solid)and with friction (dashed, μ = 10⁵)versus arc length, s, for α(0) = π/2. Tube parameters are from experimental tube pair B.

Finally, we numerically examined the effect of large distributed frictional torques on the robot's tip position and similarly showed no appreciable difference.

In summary, for the tubes pairs considered, the frictional torque due to distributed forces has negligible effect on the shape of the tubes. This conclusion is reinforced by the observation that when manually twisting a pair of tubes of equal curvature and stiffness, the maximum friction force is experienced at α(0) = α(L) = π when the curvatures oppose each other and the tubes are straight.

As shown in Fig. 3, however, the magnitude of the distributed force at the tip (also along the entire length of the tubes) is zero at this configuration. Recall that the kinematic model also prescribes that each tube apply concentrated bending moments to the other at their ends. These moments, proportional to the change in curvature of a tube, take on their maximum values when the tubes are straight.

D. Lumped Model for Frictional Torques Due to Concentrated Moments

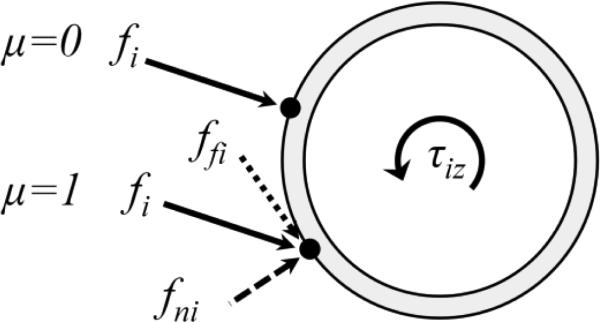
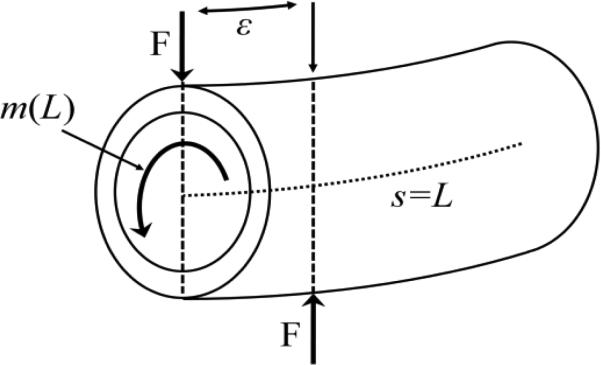
The second potential source of friction torques are the concentrated moments that arise from the compatibility condition at the boundaries of the tubes and at points of discontinuous pre-curvature. A concentrated bending moment is, of course, an idealization that follows from the modeling assumptions. As shown in Fig. 7 for the end of a tube pair (s = L), a concentrated bending moment can be produced by a force couple acting over a small length of the tubes.

$$m\left(L\right)=F\epsilon$$ (33)

In the limit of zero clearance between the tubes, the force goes to infinity and the moment arm goes to zero such that the product produces a finite bending moment given by (33).

Fig. 7.

Distal end of tube pair showing concentrated moment modeled as a force couple.

Each of these concentrated forces will produce a concentrated frictional torque acting on the tubes. The magnitudes of both are inversely proportional to changes in the moment arm, ε. To accurately solve for both F and ε would involve modeling the finite clearances between the tubes and solving for where along the length contact occurs between the tubes.

A simpler alternative approach is to make the assumptions that the moment arm ε is both small and approximately constant as the tubes are rotated. The force magnitudes can then be taken as proportional to the bending moment. This results in a very simple formulation for computing friction torque arising from the concentrated bending moments

$$\begin{array}{cc}\hfill {\tau }_{fi}& ={{\mu }_i}^{\prime }\Vert m_i\Vert \mathrm{sgn}\left({\stackrel{.}{\theta }}_i-{\stackrel{.}{\theta }}_{i+1}\right)\hfill \\ \hfill {{\mu }_i}^{\prime }& =\frac{2{\mu }_i{r}_i}{{\epsilon }_i}\hfill \end{array}$$ (34)

Since this torque is applied at the ends of the tubes and at points of discontinuous curvature, it enters the equations as a boundary condition with the second equation of (12) replaced by

$$\begin{array}{cc}\hfill {\stackrel{.}{\theta }}_i\left(L\right)& ={\tau }_i∕k_{iz}\hfill \\ \hfill {\stackrel{.}{\theta }}_i\left(L\right)& =\frac{{\mu }^{\prime }}{k_{iz}}\Vert m_i\Vert \mathrm{sgn}\left({\stackrel{.}{\theta }}_i-{\stackrel{.}{\theta }}_{i+1}\right)\hfill \end{array}$$ (35)

As with standard friction coefficients, the value of ${{\mu }_i}^{\prime }$ should be estimated from experimental data.

III. EXPERIMENTS

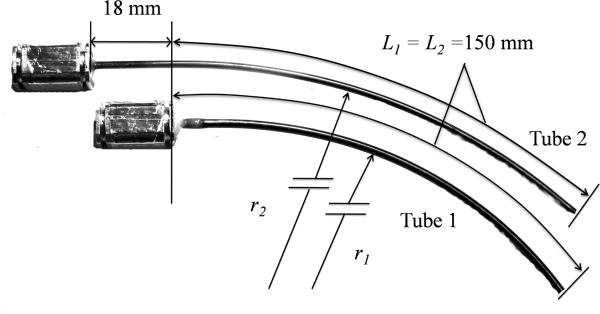
A sequence of experiments was performed to compare the predictions of the frictionless model with the lumped friction model of section II.D. Two tube pairs of nearly equal curvature and stiffness were used as depicted in Fig. 9. The diameters of the tubes are given in Table 1 and the dimensions of the fabricated tubes are given in Fig. 8 and Table 2. To solve the forward kinematics, [1],[2] require the bending and torsional stiffnesses of the tubes. Given that the tubes are of the same alloy and were processed similarly, the stiffness of the tubes should be computable from moments of inertia and the Young's modulus. Stacking the tolerances for inner and outer diameters of tube pairs, however, produces large variations in stiffness ratio. Instead, the stiffnesses of the outer tubes were computed as above and the stiffnesses for the inner tubes were calculated from the calibrated stiffness ratios. These calibrated stiffness ratios were computed by measuring the individual tube pre-curvatures and the pair-wise combined curvature for α_i(s) = π using a camera measurement system (Vision Appliance, Dalsa, Inc.).

Fig. 9.

Tube pair showing graduated disk, twist pointer and tangent pointer.

Fig. 8.

Dimensions of tube pairs

For these tube dimensions, tip deflection due to gravity (< 0.3 mm) was within the measurement error of the camera system (±0.5 mm) and so its effects were neglected in the experiments.

Experiments were performed on two tube pairs (labeled A and B) of identical cross sections (Tube 1 and 2 stock) and length, but of different pre-curvatures as shown in Fig. 8 and described in Table 2. Each tube is glued into a collar as shown and mounted in the motor drive system as shown in Fig. 9. Motor positioning accuracy is better than 0.1 degrees. It is necessary to relate α₂(0) measured at the proximal end of the curved portion of the tubes to the relative angle measured by the motor encoders at the tube collars, α_2m.This is given by

$${\alpha }_{2m}={\alpha }_2\left(0\right)-{\stackrel{.}{\alpha }}_2\left(0\right)\left(18\mathrm{mm}\right)k_{1z}∕(k_{1z}+k_{2z})$$ (36)

To measure the twist at the distal end of the tubes,α₂(L), a circular graduated disk was attached over the last 2 mm of the outer tube (Fig. 9). A 2 cm long straight wire was attached to the tip of the inner tube to enable measurement of the tip tangent direction. A twist pointer was attached perpendicular to this wire adjacent to the disk for twist measurement and zeroed for the configuration in which the curvature of the tubes is aligned. The error in measuring tip angle was estimated to be ±2 degrees.

The relative error of the models in predicting tube tip position and tangent direction was measured using a stereo camera system (Vision Appliance, Dalsa, Inc.) during the twist experiments described above. The tangent direction at the tip was computed from the coordinates of the points at the base and tip of the tangent pointer of Fig. 9.

Experimental data for tip twisting, position, and orientation was collected by rotating the tube pairs quasistatically through a complete revolution in the positive and negative directions at steps of ${\alpha }_{2m}=\{0°,10°,20°\dots \}$.

Poisson's ratio (ν) controls how flexible the tubes are in bending versus torsion. This value is commonly reported as 0.3-0.35 for solid Nitinol specimens. It was determined, however, that a value of ν = 0.6 provides a much better fit to the frictionless torsional model as shown in Fig. 10 and so this value was used for the evaluation of the friction model.

Fig. 10.

Effect of Poisson's ratio on relative torsional twist angle versus motor angle. Calculated using the frictionless kinematic model for Tube pair B. v = 0.6 (solid black line) and v = 0.3 (dashed line).

A. Torsional Twisting of the Tubes

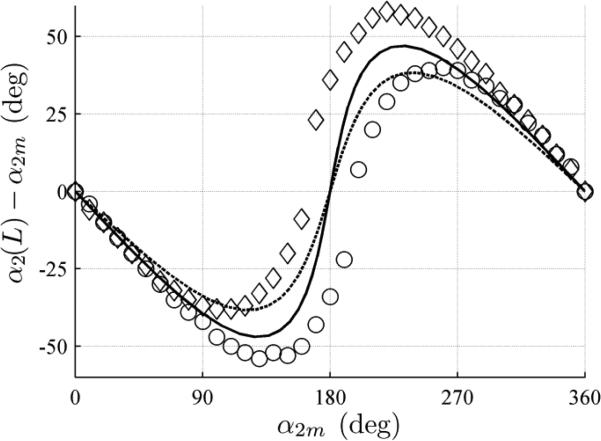
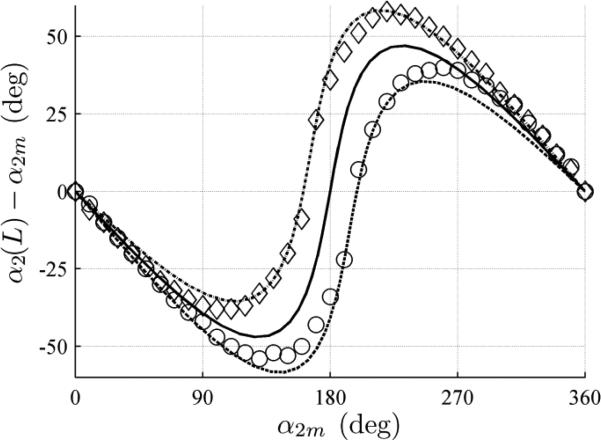
Fig. 11 and Fig. 12 show the collected data and model predictions for the torsional twisting from the base to the tip of the tubes. The frictional model is dependent on the direction of rotation, and thus produces a pair of s-shaped ‘envelope’ curves. These predictions match well the experimental envelope that is also shown in the figures.

Fig. 11.

Effect of boundary friction modeling on relative torsional twist angle versus motor angle for tube pair A. Circles are data collected with clockwise rotation, diamonds are data collected with counterclockwise rotation. The middle solid s-curve represents the frictionless torsional model and the lower and upper dashed lines represent the frictional model with clockwise and counterclockwise rotation respectively.

Fig. 12.

Effect of boundary friction modeling on relative torsional twist angle versus motor angle for tube pair B. Data and curves as in Fig. 11.

These figures clearly demonstrate the predictive capability of the frictional model in comparison to the frictionless torsional model. They also validate that the experimental ‘envelope’ can be explained in large part by tip friction.

B. Tip Position and Tangent Direction

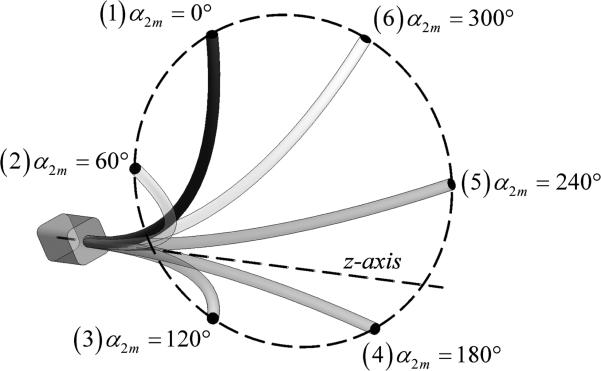
Table 3 reports position and tangent direction error for the two sets of tubes at six values of α_2m. The mean, standard deviation and maxima are also reported for the complete data sets of Fig. 11 and Fig. 12. To visualize the workspace of the tube pairs, Fig. 13 depicts the torsionally rigid solutions [2] for Tube Pair B at the six values of α_2m reported in the table.

Table 3.

Tube Pair Tip Position and Tangent Error. Note that “All” refers to all points in Fig. 11 and Fig. 12

		Tube Pair A frictionless model error		Tube Pair B frictionless model error
		friction model error		friction model error
Point	α2m (deg)	Position (mm)	Tangent (degrees)	Position (mm)	Tangent (degrees)
1	0	$\frac{1.1}{1.1}$	$\frac{2.4}{2.4}$	$\frac{2.4}{2.4}$	$\frac{1.2}{1.2}$
2	60	$\frac{1.2}{1.3}$	$\frac{3.0}{3.2}$	$\frac{3.2}{3.1}$	$\frac{2.5}{2.5}$
3	120	$\frac{1.5}{1.7}$	$\frac{0.8}{1.7}$	$\frac{5.0}{4.6}$	$\frac{4.0}{3.5}$
4	180	$\frac{2.2}{0.7}$	$\frac{2.9}{1.0}$	$\frac{13.4}{2.2}$	$\frac{13.4}{1.7}$
5	240	$\frac{1.7}{1.1}$	$\frac{3.7}{2.7}$	$\frac{4.6}{2.8}$	$\frac{4.9}{3.1}$
6	300	$\frac{1.1}{1.1}$	$\frac{3.4}{3.2}$	$\frac{5.3}{5.3}$	$\frac{4.0}{3.9}$
All (mean)		$\frac{1.8}{1.4}$	$\frac{3.1}{2.7}$	$\frac{5.4}{3.7}$	$\frac{4.3}{2.7}$
All (std dev)		$\frac{0.9}{0.6}$	$\frac{1.5}{1.3}$	$\frac{3.3}{1.8}$	$\frac{3.2}{1.2}$
All (max)		$\frac{4.2}{2.9}$	$\frac{6.0}{5.3}$	$\frac{17.5}{7.8}$	$\frac{18.1}{5.6}$

Fig. 13.

Illustration of six points shown in Table 3 as calculated by the torsionally rigid frictionless model for tube pair B.

As can be seen from Table 3, the frictional and frictionless models are in agreement at α_2m = 0, while they diverge significantly at α_2m = π where the concentrated bending moments at the tips of the tubes, and hence friction, are largest. Note also that the frictional model shows both a larger absolute and relative improvement over the frictionless model in tube pair B (which has a larger pre-curvature).

IV. CONCLUSIONS

In this paper, the frictional contributions of two types of tube interaction forces have been studied. It has been shown that the frictional torques arising from distributed contact forces between the tubes can be included in the kinematic model at the expense of solving a root finding problem at each step of integration with respect to arc length. It was also observed, however, that this source of friction produced a negligible amount of tube twisting and so could not explain the experimentally observed behavior.

A second model was also introduced to predict the frictional torque associated with concentrated bending moments. In this case, the frictional torques are incorporated into the kinematic model as boundary conditions. For the experimental tube pairs, this model provides an improvement in overall position and orientation accuracy, and greatly reduces maximum error.

Fig. 1.

Tube coordinate frames are denoted F_i(s). The relative z-axis twist angle between tube frame F₀(s) and frame F_i(s) is θ(s).