Marginal Structural Models for Case-Cohort Study Designs to Estimate the Association of Antiretroviral Therapy Initiation With Incident AIDS or Death

Abstract

To estimate the association of antiretroviral therapy initiation with incident acquired immunodeficiency syndrome (AIDS) or death while accounting for time-varying confounding in a cost-efficient manner, the authors combined a case-cohort study design with inverse probability-weighted estimation of a marginal structural Cox proportional hazards model. A total of 950 adults who were positive for human immunodeficiency virus type 1 were followed in 2 US cohort studies between 1995 and 2007. In the full cohort, 211 AIDS cases or deaths occurred during 4,456 person-years. In an illustrative 20% random subcohort of 190 participants, 41 AIDS cases or deaths occurred during 861 person-years. Accounting for measured confounders and determinants of dropout by inverse probability weighting, the full cohort hazard ratio was 0.41 (95% confidence interval: 0.26, 0.65) and the case-cohort hazard ratio was 0.47 (95% confidence interval: 0.26, 0.83). Standard multivariable-adjusted hazard ratios were closer to the null, regardless of study design. The precision lost with the case-cohort design was modest given the cost savings. Results from Monte Carlo simulations demonstrated that the proposed approach yields approximately unbiased estimates of the hazard ratio with appropriate confidence interval coverage. Marginal structural model analysis of case-cohort study designs provides a cost-efficient design coupled with an accurate analytic method for research settings in which there is time-varying confounding.

Marginal structural models (1) are used increasingly to estimate the total, joint (2), or direct/indirect (3) associations of exposures with an outcome of interest. Using inverse probability weighting, such structural models can be employed to consistently estimate exposure associations when 1 or more time-varying confounders are affected by a prior time-varying exposure. Marginal structural Cox proportional hazards regression models (4) are commonly used when the outcome is time-to-event (5–8).

The case-cohort design is an efficient approach for estimating the hazard ratio accurately when obtaining exposure or covariate information is costly (9–12). In this design, exposure or covariate information is collected only for a random subcohort, as well as for all participants who have experienced the event of interest (and henceforth are cases). Cost savings are obtained by not collecting exposure and covariate information on noncases outside the subcohort. A case-cohort analysis typically proceeds with a standard Cox regression model for the subcohort, augmented with the cases outside the subcohort to improve precision (13, 14). Prior methodological work suggests that case-cohort designs may be analyzed using methods for causal inference based on potential outcomes (15, 16). However, to date, there has not been an example analysis of a case-cohort design using marginal structural models. Here we illustrate this approach with an analysis of the association between highly active antiretroviral therapy (HAART) initiation and incident acquired immunodeficiency syndrome (AIDS) or death (7).

MATERIALS AND METHODS

Study cohort

This analysis used data from the Multicenter AIDS Cohort Study (17) and the Women’s Interagency HIV Study (18). Beginning in 1984, the Multicenter AIDS Cohort Study enrolled 6,972 homosexual and bisexual men in Baltimore, Maryland; Chicago, Illinois; Pittsburgh, Pennsylvania; and Los Angeles, California. Beginning in 1994, the Women’s Interagency HIV Study enrolled 3,772 women in New York, Chicago, Los Angeles, San Francisco, and Washington, DC. Approximately every 6 months, participants in both studies underwent a physical examination, completed an extensive interviewer-administered questionnaire that obtained information on use of antiretroviral therapy, and provided a blood sample. Positive enzyme-linked immunosorbent assays with confirmatory Western blots were used to determine seropositivity for human immunodeficiency virus type 1 (HIV-1). Institutional review boards approved all protocols and informed consent forms, which were completed by participants in both cohorts.

The cost of these semiannual study visits varied by cohort, by site within each cohort, and over time, but the cost in 2007 was approximately $1,560 per participant per visit. Approximately $600 of the $1,560 was required for determination of covariate information based on biomarkers (e.g., CD4 cell count, HIV-1 RNA viral load), and this $600 may be saved for visits where covariate information is not required. However, the balance of the $1,560 is required in order to conduct the visit and obtain and store biologic specimens, regardless of whether the covariate information is needed presently. These costs will be used to quantify savings for the case-cohort design.

Analyses presented here included the 950 men and women who were alive, HIV-1-seropositive, and not using antiretroviral therapies in April 1995, just before effective therapy became available (the first highly active regimen was approved by the US Food and Drug Administration on December 6, 1995). Each participant contributed a maximum of 24 study visits, beginning with the first semiannual visit after April 1995 (the baseline visit). For the present report, participants were followed until: 1) incident AIDS or death, 2) initiation of non-HAART treatment, 3) dropout (i.e., 2 consecutive missed visits), or 4) study completion in September 2007. For participants who were missing baseline data on any time-varying covariate but remained eligible, baseline was redefined as the first visit with complete data. This approach is analogous to the inclusion of late entries in survival analysis (19) and assumes that such late entries are noninformative (20).

An illustrative subcohort was selected as a 20% simple random sample without replacement from the 950 participants. Among the 190 participants chosen for the subcohort, 41 (22%) were cases. The case cohort was defined as the subcohort of 190 participants plus the 170 cases (211 − 41 = 170) outside the subcohort.

Measurements

The endpoint of interest was first diagnosis of clinical AIDS or death from any cause, as recently described (21). The exposure of interest was initiation of HAART, versus no antiretroviral therapy. Data on a number of fixed and time-varying covariates were recorded.

Levels of T-lymphocyte subsets were determined by immunofluorescence using flow cytometry in laboratories participating in the National Institute of Allergy and Infectious Diseases Quality Assurance Program. T-lymphocyte subsets were measured in purified peripheral blood mononuclear cells or ethylenediaminetetraacetic acid-anticoagulated whole blood by staining with fluorescent dye-conjugated monoclonal antibodies that were specific for CD4 lymphocytes (Becton Dickinson, Mountain View, California) (22).

Plasma HIV-1 RNA viral load levels were measured in laboratories participating in the proficiency testing program of the National Institute of Allergy and Infectious Diseases Virology Quality Assurance Laboratory. To harmonize viral load detection limits, which varied from 50 copies/mL to 400 copies/mL across cohorts and over time, we set values below 400 copies/mL to a value of 200 copies/mL. Missing time-varying covariate information after the baseline visit (9%) was carried forward from the most recent prior observed value.

Statistical methods

In this article, capital letters represent variables and lowercase letters represent possible values of the variables or constants. Let T be the time from study entry to AIDS or death. Due to study completion, dropout, or inadequate therapy initiation, T may be right-censored. Let T_s be the potential time from study entry to AIDS or death under the regimen of HAART initiation at time s. Letting $h_{T_s}\left(t\right)$ denote the hazard at time t for the random variable T_s, a marginal structural Cox proportional hazards model is $h_{T_s}\left(t\right)=h_0\left(t\right)\exp \left[x\right(t\left)\mathrm{\beta }\right]$, where h₀(t) is the hazard for participants not exposed by time t (i.e., all T_s where s > t), and x(t) = 1 if t > s and x(t) = 0 otherwise. For this model, β is the log hazard ratio comparing the regimens previously exposed to treatment with those not exposed to treatment by time t. The specification of exposure to HAART is a simple initiation indicator and does not depend on time since initiation or cumulative exposure, which is in keeping with most (7, 8, 23) but not all (21) prior reports. We also consider structural models for cumulative average exposure to HAART.

Cohort and subcohort estimation.

In Appendix 1, we describe standard methods for drawing inference assuming the above model using data from the full cohort. Methods for the analysis of the subcohort follow directly from those for the full cohort. The only distinction is that the subcohort analysis is conducted using only the data from the 190 (out of 950) participants chosen at random for the subcohort. This restriction to the 190 subcohort participants also applies for calculation of the inverse probability weights described in Appendix 1.

Case cohort.

For case-cohort designs, the Cox partial likelihood must be adjusted to account for sampling of covariate information from only a subset of participants. Here we extend Prentice’s approach to estimation of the hazard ratio from a case-cohort study design (12). Assuming no tied failure times, for the case-cohort design the contribution to the weighted partial likelihood corresponding to participant i failing at time t_i is

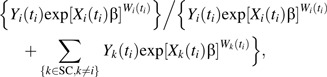where Y, X, and W are as defined in Appendix 1 and SC denotes the 190 participants in the subcohort. The distinction between the contributions to the weighted partial likelihood for the full cohort and those shown here is that the sum in the denominator of the weighted partial likelihood is taken over the members of the subcohort and the case, rather than the full cohort membership.

For the case-cohort design, the inverse probability weights are estimated using the subcohort set SC as well as cases outside the subcohort. Contributions to the models for the inverse probability weights were themselves weighted inversely to the sampling probability for the case-cohort design. Specifically, cases (inside or outside the subcohort) were given a weight of 1, while noncases inside the subcohort were given a weight of 5 (1/0.2 = 5). Noncases outside the subcohort were not used to estimate the inverse probability weights.

Unadjusted and adjusted hazard ratio estimates were obtained for comparison from standard unweighted Cox models without and with adjustment for the same set of variables as used in the marginal structural model. A Monte Carlo simulation experiment is presented in Appendix 2. The simulation examines some finite-sample properties of the proposed method. All analyses were conducted with SAS, version 9.2 (SAS Institute, Inc., Cary, North Carolina), using robust variance estimates (24) to calculate 95% confidence intervals and P values for all case-cohort designs and marginal structural models (see Appendix in Cole et al. (25)).

RESULTS

At study entry, the 950 cohort participants had a mean age of 39 years (standard deviation (SD), 8), a CD4 cell count of 498 cells/mm³ (SD, 279), and a viral load of 4.5 log₁₀ copies/mL (SD, 0.7) for the 74% participants with detectable values; 61% were women, and 59% were African-American. The 190 subcohort participants had similar characteristics at study entry (Table 1).

Table 1.

Characteristics of the Cohort (Men and Women Infected With HIV Type 1) and the 20% Subcohort at Baseline and During Follow-up, Multicenter AIDS Cohort Study and Women’s Interagency HIV Study, 1996–2007

Characteristic	Cohort (n = 950)			Subcohorta (n = 190)
	%	Mean (SD)	No.	%	Mean (SD)	No.
At baseline in 1996
Mean age, years		39 (8)			38 (8)
Female sex	61		578	57		108
African-American race	59		560	54		102
Mean CD4 cell count, no. of cells/mm3		498 (279)			489 (283)
Mean log10 HIV-1 RNA level, no. of copies/mL		4.5 (0.7)b			4.5 (0.7)c
Over follow-up between 1996 and 2007
No. of person-years			4,456			861
No. of exposed person-years			2,974			590
No. with incident AIDS or death			211			41

Abbreviations: AIDS, acquired immunodeficiency syndrome; HIV, human immunodeficiency virus; SD, standard deviation.

^aThe subcohort comprised 20% of 950 cohort participants chosen at random.

^bAmong 705 detectable measurements.

^cAmong 145 detectable measurements.

Over the course of follow-up, the 950 cohort participants contributed 4,456 person-years, of which 2,974 person-years were accrued after antiretroviral therapy initiation. During follow-up, 180 cases of incident AIDS and 31 AIDS-free deaths were observed, 259 participants were censored at inadequate therapy initiation, 173 participants were lost to follow-up, and 307 participants completed the study event-free.

The 190 subcohort participants contributed 861 person-years, of which 590 person-years were accrued after antiretroviral therapy initiation. During follow-up, 34 cases of incident AIDS and 7 AIDS-free deaths were observed, 94 participants were censored at inadequate therapy initiation or lost to follow-up, and 55 participants completed the study event-free (Table 1).

The inverse probability weights for the cohort had a mean of 0.95 (SD, 0.65) with a range of 0.14–9.60 and first and 99th percentiles of 0.22 and 4.12, respectively. The inverse probability weights for the subcohort had a mean of 0.98 (SD, 0.66), with a range of 0.09–4.91 and first and 99th percentiles of 0.15 and 3.77, respectively. The inverse probability weights for the case cohort had a mean of 0.98 (SD, 0.65), with a range of 0.10–7.29 and first and 99th percentiles of 0.16 and 3.26, respectively.

Consistent with prior research (7), in the full cohort the unadjusted hazard ratio for AIDS or death was 1.02 (95% confidence interval (CI): 0.72, 1.43), and the adjusted hazard ratio was 0.96 (95% CI: 0.68, 1.36). The inverse probability-weighted hazard ratio for AIDS or death was 0.41 (95% CI: 0.26, 0.65) (Table 2). For the inverse probability-weighted hazard ratio, the ratio of the upper confidence limit to the lower confidence limit, a measure of precision, was 2.5. As expected (26), when we truncated the inverse probability weights at the first and 99th percentiles, the hazard ratio was somewhat muted yet slightly more precise (hazard ratio = 0.48, 95% CI: 0.31, 0.74); untruncated inverse probability weights were used henceforth. The treatment initiation association appeared to increase over follow-up time, with a hazard ratio of 0.61 (95% CI: 0.22, 1.66) before 2 years and a hazard ratio of 0.38 (95% CI: 0.23, 0.61) after 2 years from study entry (P for homogeneity = 0.39). Two years was chosen as the point at which approximately half of the events had occurred; henceforth, this possible departure from proportional hazards was disregarded.

Table 2.

Cohort, 20% Subcohort, and Case-Cohort Analyses of the Association Between Highly Active Antiretroviral Therapy and Incident AIDS or Death Among 950 Men and Women Infected With HIV Type 1, Multicenter AIDS Cohort Study and Women’s Interagency HIV Study, 1996–2007

Analysis and Model	Hazard Ratio	95% Confidence Interval	Standard Errora
Cohort
Unadjusted	1.02	0.72, 1.43	0.176
Adjustedb	0.96	0.68, 1.36	0.178
Weightedb	0.41	0.26, 0.65	0.231
Subcohort
Unadjusted	1.27	0.57, 2.86	0.412
Adjusted	1.37	0.60, 3.17	0.426
Weighted	0.53	0.23, 1.24	0.436
Case-cohort
Unadjusted	0.97	0.61, 1.54	0.238
Adjusted	1.09	0.69, 1.73	0.235
Weighted	0.47	0.26, 0.83	0.293

Abbreviations: AIDS, acquired immunodeficiency syndrome; HIV, human immunodeficiency virus.

^aStandard error for log hazard ratio; robust standard error for case-cohort and weighted models.

^bAdjusted and weighted models both controlled for time-varying prior CD4 cell count and HIV-1 RNA level, specified as restricted cubic splines.

As expected, results for the subcohort were less precise than those for the full cohort. The unadjusted hazard ratio for AIDS or death was 1.27 (95% CI: 0.57, 2.86), and the adjusted hazard ratio was 1.37 (95% CI: 0.60, 3.17). The inverse probability-weighted hazard ratio for AIDS or death was 0.53 (95% CI: 0.23, 1.24) (Table 2). For the inverse probability-weighted hazard ratio, the ratio of upper to lower confidence limits was 5.39, or 2.16 times that of the full cohort precision.

Finally, results for the case-cohort design recovered much of the precision lost in the subcohort design. The unadjusted hazard ratio for AIDS or death was 0.97 (95% CI: 0.61, 1.54), and the adjusted hazard ratio was 1.09 (95% CI: 0.69, 1.73). The inverse probability-weighted hazard ratio for AIDS or death was 0.47 (95% CI: 0.26, 0.83) (Table 2). For the inverse probability-weighted hazard ratio, the ratio of upper to lower confidence limits was 3.19, or 1.28 times that of the full cohort precision.

Table 3 summarizes dollar and precision costs relative to the full cohort. While the costs for the full cohort design would be about $14.5 million, the costs for the subcohort and case-cohort designs would be about $10 million and $10.5 million, respectively. For the subcohort design, the dollar savings are more than offset by the decreased precision, as seen by the proportional precision costs’ being larger than unity. However, for the case-cohort design, the dollar savings are offset by the decreased precision, such that the proportional precision costs remain below unity and therefore in favor of the case-cohort study design under a fixed budget.

Table 3.

Costs and Precision Costs for Cohort, 20% Subcohort, and Case-Cohort Marginal Structural Analyses of Highly Active Antiretroviral Therapy and Incident AIDS or Death Among 950 Men and Women Infected With HIV Type 1, Multicenter AIDS Cohort Study and Women’s Interagency HIV Study, 1996–2007

Analysis and Visit Type	No. of Visits	Cost, dollarsa	Proportional Costs	Precision Costsb	Proportional Precision Costs
Cohort
Full	9,172	14,308,320
Partial	0	0
Total		14,308,320	1c	3.31	1c
Subcohort
Full	1,766	2,754,960
Partial	7,406	7,109,760
Total		9,864,720	0.69	4.30	1.30
Case-cohort
Full	2,891	4,509,960
Partial	6,281	6,029,760
Total		10,539,720	0.74	3.09	0.93

Abbreviations: AIDS, acquired immunodeficiency syndrome; HIV, human immunodeficiency virus.

^aCosts of a full study visit were approximated at $1,560 and costs of a partial study visit at $960 (excluding biomarker determinations).

^bPrecision costs were defined as costs (in millions of dollars) × standard error.

^cProportional costs and precision costs were taken with respect to the full cohort.

Similar results were obtained when modeling the cumulative average exposure. For instance, using the full cohort, the unadjusted, adjusted, and marginal structural model estimates of the hazard ratio for cumulative average exposure to HAART were 0.73 (95% CI: 0.44, 1.21), 0.84 (95% CI: 0.50, 1.42), and 0.24 (95% CI: 0.12, 0.47), respectively. In the case-cohort marginal structural model analysis, the hazard ratio estimate was 0.30 (95% CI: 0.12, 0.73).

Monte Carlo simulation results are provided in Appendix 2. Briefly, the simulations demonstrated that the proposed case-cohort approach yields approximately unbiased estimates with appropriate confidence interval coverage and recovers a large portion of the precision present in the full cohort design (Appendix Table 1).

DISCUSSION

Using a combination of a case-cohort study design and a marginal structural Cox model analysis, we estimated that relative to no antiretroviral therapy, initiation of HAART decreased the hazard of AIDS or death by 53%. A similar result was found using the combination of a full cohort design and a marginal structural Cox model analysis, but a dramatically attenuated result was found using standard analytic methods for both the case-cohort and full cohort designs. The combination of a case-cohort design with marginal structural model analysis was found to be favorable in terms of a combination of monetary cost and precision for the present example. In settings where there is a larger cost savings associated with not collecting exposure or covariate information from persons outside the subcohort or where the outcome is less frequent, the case-cohort study design will be even more advantageous.

While we are unaware of any prior work on marginal structural models for case-cohort designs, Joffe and Rosenbaum (15) and Mansson et al. (16) describe case-cohort studies using propensity scores, which have features in common with the present work but are restricted to time-fixed exposures.

There are several competing approaches to estimating the hazard ratio from a case-cohort design. Early work by Kupper et al. (10) and Miettinen (11) dealt with estimation of the incidence density ratio under the dual assumptions of the hazards’ being proportional across exposure groups and constant over time, both assumptions being within levels of measured variables. Modern approaches, since the work of Prentice (12), allow the hazards for exposure groups to be nonconstant over time but continue to assume proportionality across exposure groups. Borgan and Samuelsen (27) reported Monte Carlo simulations showing that Prentice’s approach (12) and Barlow’s approach (28), the latter using inverse probability of sampling weights, provide similar inferences when the subcohort is of reasonable size relative to the full cohort (i.e., ≥15% of the full cohort), as is the case in our setting. Further details on differences between these approaches are discussed by Barlow et al. (13), Borgan and Samuelsen (27), Langholz and Jiao (29), and Kulathinal et al. (30).

The present results should be interpreted with consideration of the following limitations. First, like all observational analyses, the estimates have a causal interpretation only under the assumption of no unmeasured confounding. This assumption probably holds approximately here, because the most important clinical and laboratory information used by physicians as indications for therapy initiation was collected and used in the models for the estimation of the weights (31). As described previously (7, 26), numerous additional functional forms for the weight models were explored (e.g., longer covariate histories, more flexible splines), as well as a broader set of covariates (e.g., age, race, body mass index, HIV-related symptoms, use of Pneumocystis jiroveci pneumonia prophylaxis, and red blood, platelet, CD3, and CD8 cell counts), but such alternative model specifications did not appreciably alter the results. If the assumption of no unmeasured confounders is correct and the model used to create the treatment weights is correctly specified, then weighting creates a pseudopopulation in which the probability of therapy initiation is not a function of the time-varying covariates (i.e., no confounding exists), but the association of therapy initiation with AIDS or death is the same as in the actual study population.

Second, and as in all prospective analyses with right-censoring, the results are based on the assumption that right-censoring is ignorable, conditional on measured covariates. Neither the present analyses nor past analyses (5, 7, 25, 32) suggested that there was notable selection bias due to measured variables in these data.

Third, the results rely on the assumptions that therapy initiation and time to AIDS or death are measured without error. There are 3 pertinent subpoints. Firstly, we did not account for therapy cessation in these analyses. The inverse probability-weighted analysis was therefore estimating an “intention-to-treat effect” (32) of therapy initiation versus no antiretroviral therapy in a hypothetical randomized clinical trial in which 1) participants were randomly assigned to begin continuous therapy at different visits, 2) all participants initially complied and began therapy at their assigned visit, and 3) a portion later discontinued therapy. Secondly, the timing of therapy initiation may have been misreported. Cole et al. (21) have described methods with which to account for such measurement error. Thirdly, these results may have been sensitive to the relative infrequency of data collection (i.e., 6-month intervals). Misclassification due to this coarse measurement (with respect to time) could have reintroduced some confounding, which could have biased the estimated hazard ratios in either direction (26). Indeed, therapy is initiated during the interval between study visits by physicians who have access to information beyond that collected for the study. Therefore, a sensitivity analysis to deviations from the no-unmeasured-confounding assumption is appropriate but was beyond the scope of this article.

Fourth, the inferences rely on correct model specification. There are 2 pertinent subpoints. Firstly, we assume that the most recent prior observed value is a reasonable substitute for the 9% missing time-varying covariate information that was carried forward. Given the relatively small amount of missing time-varying covariate data, one would expect results to be robust to violations of this assumption. Secondly, inferences rely on correct specification of the final structural model relating HAART exposure to incident AIDS or death. We fitted a simple initiation indicator, as well as cumulative average exposure, and found similar results.

Fifth, our approach to implementing a marginal structural model for the case-cohort design is not fully efficient. One way to improve the efficiency would be to use information from the full cohort that is currently ignored. Recently, Breslow et al. (33, 34) discussed stratified case-cohort studies in the context of 2-stage study designs (35, 36). They demonstrated that use of the full cohort in the analysis of case-cohort studies may improve precision for estimation of covariate associations in the full cohort, as well as product terms between these covariates and the exposure of interest. In our setting, a modification of the association of therapy with incident AIDS or death by baseline CD4 cell count has been reported (7). This may be a topic of future work.

Finally, we assume both consistency (37, 38) and positivity (37, 39), which would be granted by design in a randomized trial but are subject to possible violations in observational studies. For causal contrasts to be interpretable, either there must be a single route to the exposure or the multiple routes must yield similar effects. This consistency assumption is likely to hold approximately in the present setting, where the exposure is a treatment (40, 41). Valid use of inverse probability weights requires that there not be a probability of 0 or 1 that participants are exposed at any level of the confounders (26). This positivity assumption was met in theory in our study, as some participants with high CD4 cell counts and low viral loads initiated therapy while others with low CD4 cell counts and high viral loads did not, and this assumption was not violated in practice, as previously discussed (26).

In conclusion, the association of HAART initiation with incident AIDS or death using a marginal structural model analysis of a full cohort design was approximated well using an analogous analysis of a case-cohort design. The combination of the cost-efficient case-cohort design with accurate analytic methods based on potential outcomes provides the epidemiologist with a useful tool for etiologic inference.

Glossary

Abbreviations

AIDS

acquired immunodeficiency syndrome

CI

confidence interval

HAART

highly active antiretroviral therapy

HIV-1

human immunodeficiency virus type 1

SD

standard deviation

APPENDIX 1.

Standard Analysis of a Marginal Structural Cox Model

The hazard ratio, exp(β), may be estimated consistently in the full cohort under the dual assumptions of no unmeasured confounders and no unmeasured informative censoring (42) by maximizing a weighted partial likelihood as described below. Let S be the time from study entry to highly active antiretroviral therapy (HAART) initiation for persons who initiate HAART before T, and S = T otherwise. Note that S is interval-censored because therapy initiation is known only to occur between semiannual study visits: We take the right side of the interval as S.

Assuming no tied failure times, for the full cohort design the contribution to the weighted partial likelihood corresponding to participant i failing at time t_i is

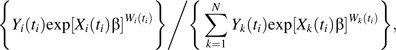where Y_i(t) is an indicator of participant i’s being in the risk set at time t, X_i(t) = 1 if t > S_i and X_i(t) = 0 otherwise, and the inverse probability weights are $W_i\left(t\right)=W_i^X\left(t\right)W_i^C\left(t\right)$, defined below.

Let J denote the number of follow-up study visits for an individual, let v_j equal the time from baseline to follow-up visit j = 1 to J, and let v₀ = 0. In the case where acquired immunodeficiency syndrome (AIDS) occurs during the interval (v_j−1, v_j], the time of AIDS replaces the visit time v_j. In the case where death occurs after visit J, the time of death replaces the visit time v_J. Let X(v_j) = 1 indicate exposure initiation in the interval (v_j−1, v_j]; by design, X(v₀) = 0. Let L(v_j) be the vector of covariates measured at visit j, with baseline covariates denoted as L(v₀). Let C(v_j) = 1 indicate that the participant was censored because of dropout or initiation of non-HAART therapy during the interval (v_j−1, v_j]; by design, C(v₀) = 0. Overbars are used to denote histories, such that $\widehat{X}\left(v_j\right)=\left\{X\right(v_0),X(v_1),X(v_2),\mathrm{\dots },X(v_j\left)\right\}$; $\widehat{L}\left(v_j\right)$ and $\widehat{C}\left(v_j\right)$ are defined analogously. The inverse probability weights are defined as

and

where P[ | ] is the conditional probability function. The denominator for each term in W^X(t) is the probability that a participant received her own observed treatment at time v_j given her past exposure and covariate history and that she remained uncensored.

The estimate of β was obtained in 2 steps: First, the inverse probability weights were estimated for each individual at each failure time, and then the weighted partial likelihood was maximized conditional on the estimated weights. We estimated the components of the inverse probability weights using pooled logistic regression models (43), as previously described (25). In the pooled logistic regression model, baseline covariates included age, sex, CD4 cell count, and log₁₀ viral load. Time-varying covariate histories were modeled as restricted cubic splines with 4 knots located at the 5th, 33rd, 67th, and 95th percentiles for CD4 cell count and log₁₀ viral load, both taken at visit j − 1. Using SAS, the time-varying inverse probability weights (and exposure) were accommodated with a counting process style of data input, with entry and exit times given as v_j−1 and v_j for j = 1 to J. Inverse probability weights were calculated in the same manner for cumulative average HAART, but the marginal structural Cox model replaced X(t) with ${\displaystyle {\sum }_{v_j\le t}X\left(v_j\right)}/{\displaystyle {\sum }_{v_j\le t}1}$. This cumulative average could be generalized to allow for unequal visit intervals.

APPENDIX 2.

Simulation design

We conducted 5,000 simulations each of 1,000 participants for 2 scenarios: β = 0 and β = log(1/2). We first describe a method for simulating data such that the marginal structural Cox model given in the main text holds when there are 2 possible exposure times, at times t = 0 and t = t₁ > 0. We assume here that β ≤ 0, such that exposure is not harmful. Let T₀, $T_{t_1}$, and $T_{\mathrm{\infty }}$ denote the potential survival times corresponding to regimens where the first exposure is at t = 0, the first exposure is at t = t₁, and there is never exposure, respectively. Note that T_∞ has the corresponding hazard $h_{T_{\mathrm{\infty }}}\left(t\right)=h_0\left(t\right)$ and that we do not assume $T_{t_1}>t_1$. The steps needed to generate the potential survival times are:

1. Draw T_∞ from an exponential distribution with hazard h₀(t) = λ and survival function S₀(t) ≡ Pr(T_∞ > t) = exp(−λt).

2. Let T₀ = T_∞exp(−β).

3. Let$T_{t_1}=T_{\mathrm{\infty }}I(T_{\mathrm{\infty }}<t_1)+(T_0-\mathrm{\theta })I(T_{\mathrm{\infty }}\ge t_1)$,where $\theta =t_1\left[\exp \right(-\mathrm{\beta })-1]$ and I(.) is the indicator function, equal to 1 when the condition (.) is true and 0 otherwise.

A proof that this method yields potential outcomes satisfying the marginal structural Cox model is available from the authors.

We set λ = 1 and t₁ = 0.1. For each participant, we set the baseline covariates to constant values 0, so they may be ignored without consequence. We generated a baseline exposure as Bernoulli with a probability of 1/3. Next, we generated a first time-varying confounder as Bernoulli with a marginal probability of 0.5 dependent on baseline exposure by an odds ratio of 8 and the potential survival time under no exposure (T_∞) by an odds ratio of 5 per unit of time. Then, we generated a second time-varying confounder as a standard normal dependent on baseline exposure (with a mean difference of 2 for exposed) and the potential survival time under no exposure (with a mean difference of 0.5 per unit of time). Finally, for the approximately two-thirds of subjects who were unexposed at baseline, we generated a time-varying exposure at t₁ = 0.1 as Bernoulli with a marginal probability of 0.5 dependent on the first time-varying confounder by an odds ratio of 0.1 and on the second time-varying confounder by an odds ratio of 0.75 per unit. The observed survival time was assigned as the potential survival time that coincided with the observed exposure history. We set survival times longer than the 25th percentile as administratively censored, such that there were 25% events. For subcohort analysis, we selected a 20% subsample at random without replacement.

Simulation analysis

For each scenario and each of the 5,000 simulations, we conducted 5 analyses with the following models: 1) an unadjusted Cox proportional hazards model using the full cohort; 2) a Cox model using the full cohort, adjusting for the 2 time-varying confounders in the linear predictor; 3) a marginal structural Cox model using the full cohort; 4) a marginal structural Cox model using only data from the subcohort; and 5) a marginal structural Cox model using the cases and the cohort, as described in the main text.

For each of the 5 analyses, we calculated bias, 95% confidence interval coverage, statistical power, and root mean squared error. Bias was computed as the average difference between an estimator and the true log hazard ratio. Confidence interval coverage was computed as the proportion of times the confidence interval contained the true hazard ratio. Statistical power was computed as the proportion of simulations in which the 95% confidence interval excluded the null value of unity. The empirical variance was defined as the square of the empirical standard error (i.e., the standard deviation of the 5,000 estimates). The root mean squared error was calculated by taking the square root of the sum of the square of the bias and the empirical variance for the estimator.

Simulation results

Neither unadjusted Cox models nor adjusted Cox models provided unbiased estimates of the hazard ratio. The mean stabilized inverse probability weights for the cohort and case-cohort designs were 1.00 and 1.02, respectively. For all 3 designs (i.e., cohort, subcohort, and case-cohort), the marginal structural Cox model provided an approximately unbiased estimate of the hazard ratio, approximately valid type 1 error when testing the null hypothesis of a hazard ratio equal to 1, and appropriate 95% confidence interval coverage (Appendix Table 1).

The empirical standard errors differed notably across the designs. In scenario 2 (alternative hypothesis), the empirical standard error for the inverse probability-weighted cohort was 0.144, while for the 20% random subcohort, precision was lost, such that the empirical standard error was 0.332. This difference accords with theory in that, with sample sizes of 1,000 and 200, the ratio of the standard errors should be approximately 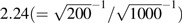and was observed to be 2.31 (0.332/0.144 = 2.31). In the case-cohort design, the empirical standard error was improved over the subcohort design to 0.225.

From another perspective, also in the alternative scenario, the statistical power for the inverse probability-weighted results across the 3 designs is notable, because this difference illustrates the advantage of the case-cohort design over the subcohort design. The cohort design had approximately 99% statistical power, while the subcohort design had only 52% statistical power. The case-cohort design had statistical power of approximately 90% and therefore recovered much of the information available in the full cohort.

Appendix Table 1.

Results From 5,000 Cohort, Subcohort, and Case-Cohort Marginal Structural Analyses^a for Null and Alternative Scenarios

	Cohort Analysis			Subcohort Analysis (IP-Weighted)	Case-Cohort Analysis (IP-Weighted)
	Unadjusted	Adjusted	IP-Weighted
Scenario 1: null hypothesis
Bias	0.336	0.113	0.001	0.006	−0.015
Average standard error	0.143	0.156	0.162	0.363	0.212
Empirical standard errorb	0.138	0.150	0.157	0.363	0.228
95% CI coverage, %	33.4	90.1	95.8	94.7	93.4
Type 1 error, %	66.6	9.9	4.2	5.3	6.6
Root MSE	0.363	0.188	0.157	0.363	0.228
Relative root MSE			1	2.31	1.45
Scenario 2: alternative hypothesis
Bias	0.671	0.146	0.001	0.004	−0.004
Average standard error	0.139	0.156	0.156	0.351	0.217
Empirical standard errorb	0.131	0.138	0.144	0.332	0.225
95% CI coverage, %	<0.1	87.3	96.7	96.2	94.0
Statistical power, %	4.3	95.9	99.4	51.5	89.6
Root MSE	0.684	0.201	0.144	0.332	0.225
Relative root MSE			1	2.31	1.56

Abbreviations: CI, confidence interval; IP, inverse probability; MSE, mean squared error.

^a1,000 participants per cohort with 25% events; 200 participants per subcohort.

^bStandard deviation of 5,000 log hazard ratio estimates.