Screening of chemicals for human bioaccumulative potential with a physiologically based toxicokinetic model

Abstract

Human bioaccumulative potential is an important element in the risk assessment of chemicals. Due to the high number of synthetic chemicals, there exists the need to develop prioritisation strategies. The purpose of this study was to develop a predictive tool for human bioaccumulation risk assessment that incorporates not only the chemical properties of the compounds, but also the processes that tend to decrease the concentration of the compound such as metabolisation. We used a generic physiologically based toxicokinetic model that based on in vitro human liver metabolism data, minimal renal excretion and a constant exposure was able to assess the bioaccumulative potential of a chemical. The approach has been analysed using literature data on well-known bioaccumulative compounds and liver metabolism data from the ECVAM database and a subset of the ToxCast phase I chemical library—in total 94 compounds covering pharmaceuticals, plant protection products and industrial chemicals. Our results provide further evidence that partitioning properties do not allow for a reliable screening criteria for human chemical hazard. Our model, based on a 100% intestinal absorption assumption, suggests that metabolic clearance, plasma protein-binding properties and renal excretion are the main factors in determining whether bioaccumulation will occur and its amount. It is essential that in vitro metabolic clearance tests with metabolic competent cell lines as well as plasma protein-binding assays be performed for suspected bioaccumulative compounds.

Electronic supplementary material

The online version of this article (doi:10.1007/s00204-011-0768-0) contains supplementary material, which is available to authorized users.

Introduction

To prevent cases in which the use of a chemical can result in unacceptable consequences for human health or for the ecosystems, it is generally agreed that risk analysis has to be carried out. However, due to the large number of existing chemicals and, for many of them, the lack of detailed information on their properties, their fate, their environmental concentrations and their human exposure pathways, it is generally accepted that screening approaches are necessary to prioritize and to select chemicals of concern for whose a more detailed risk characterization and analysis should be performed (Muir and Howard 2006; Daginnus et al. 2011). Risk assessment is based on two aspects: firstly the hazard of a given chemical, which is function of its physico-chemical properties, and secondly its exposure levels to ecosystems and to humans. A comparison of exposure levels and safe chemical doses/concentrations is then carried out and the risk evaluated. The chemical hazards of a substance are evaluated according to its persistence (P) in the environment, long-range transport potential (LRTP), bioaccumulation (B) characteristics and toxicity (T) (Klasmeier et al. 2006). Substances identified during a screening phase as PBT or vPvB (very persistent, very bioaccumulative) are normally subjected to a detailed risk assessment.

Bioaccumulation refers to the continuous increase in the concentration of a chemical in an organism, compared to the chemical’s concentration in the environmental media to which the organism is exposed, i.e., air, water, soil, food, etc. Bioaccumulative potential is an important element in all exercises of chemical prioritization and in all existing regulations (US EPA 1998; CEPA 1999; ECHA 2008). The potential of a chemical to bioaccumulate has to be considered for the assessment of its long-term effect. Bioaccumulation is the result of mass-balance processes and may be seen as a competition between the uptake and depuration/metabolism/excretion rates. Due to the lack of bioaccumulation data for the majority of substances, there is a strong interest for the use of predictive methods. The development of predictive tools is now encouraged by many international policies, and it is expected that the use of in silico and reliable in vitro methods will continuously increase in environmental and human risk-assessment exercises. Most of the predictive approaches developed so far, when no experimental data are available, are mainly based on the calculation of the lipophility of the substance, sometimes using empirical correlations between a certain bioconcentration factor (BCF, commonly defined as the ratio of concentrations of the chemical in the organism and in water, freely dissolved, at equilibrium) or bioaccumulation factor (BAF, considering also the food, i.e., \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{BAF}} = {\text{BCF}} \cdot \prod\nolimits_{i = 1}^{n} {{\text{BMF}}_{i} } $$\end{document}, where BMF is the biomagnification factor expressed as the ratio of the concentration in the predator to the concentration in the diet –prey-, and the index i refers to the trophic position in the food chain) and the octanol–water partition coefficient (K _OW) for a certain organism (Mackay 1982). Even though this approach takes into account the fact that high hydrophobic compounds tend to bioaccumulate in lipids, it does not consider the processes that will tend to decrease the concentration of the compounds, such as excretion, depuration and/or metabolisation processes, with the possible scenario of a relatively low lipophilic compound that is not metabolised or excreted, i.e., high affinity to certain proteins, and under repeated exposure will reach higher concentrations inside the organism. In addition, bioaccumulation potential was evaluated mainly in fish (Veith et al. 1979; Van der Oost et al. 2003; Arnot and Gobas 2003) and aquatic species (Carafa et al. 2009; Zaldívar et al. 2011), with few attempts to evaluate it in terrestrial food chains (Kelly and Gobas 2001; Gobas et al. 2003). Furthermore, only very recently several approaches have been developed to include also bioaccumulation in humans (Czub and McLachlan 2004a, b; Undeman et al. 2011).

Bioaccumulation is the result of the conservation of mass in a living system where a substance that enters the system either leaves it or accumulates within the system. However, as mentioned above, the biotransformation has been poorly taken into account in previous studies. Whereas several approaches have been developed to consider it in fish (Arnot et al. 2008), few attempts have been proposed for human. In a recent paper, McLachlan et al. (2011), in a theoretical framework, have shown that chemicals with similar partitioning properties may have a complete different bioaccumulation potential, being metabolisation and/or excretion the main factors responsible for this behaviour.

One of the main reasons, for the fact that metabolism and elimination have not been taken into account when evaluating bioaccumulation potential, is that these processes are difficult to evaluate and quantify. However, due to the last developments on in vitro and high-throughput techniques, it is now possible to quantify these aspects and to integrate them into a mechanistic description of the kinetic processes that monitor the bioaccumulation. Therefore, it becomes possible to evaluate quantitatively to which extent a substance bioaccumulates in humans using physiologically based pharmacokinetic/toxicokinetic models (PBPK or PBTK).

A PBTK model consists of a series of mathematical equations that based on the specific physiology of an organism and on the biophysical properties of a substance are able to describe the absorption, distribution, metabolism and elimination (ADME) of the compound within this organism (Andersen 1981). The solution of these equations provides the concentration of the chemical compound and its metabolites over time in the modelled organs and allows for a sound mechanistic description of the kinetics processes including the kinetics of accumulation.

In this work, we have used a generic PBTK model that, based on in vitro liver metabolism data, minimal renal excretion and a chronic exposure, is able to assess the bioaccumulative potential of a chemical. The approach has been analysed using literature data for some well-known bioaccumulative compounds, data from the ECVAM (European Centre for the Validation of Alternative Methods) database, and for a subset of the ToxCast phase I chemical library.

Materials and methods

Selected chemicals

The final list is mainly based on the merger of two lists: 55 organic chemicals, mostly drugs and pesticides, which is a subset selected from the list of an international ICCVAM validation (2009), and a subset of 35 substances (Rotroff et al. 2010), mostly pesticides, of the ToxCast Phase I chemical library (http://www.epa.gov/nccttoxcast/chemicals.html). For the ECVAM database chemicals, liver metabolism and unbounded fraction data were taken from Pelkonen et al. (2009) and Rousu et al. (2010), whereas a similar data for the chemicals in ToxCast phase I have been published in Rotroff et al. (2010). When more than one value was provided, we used the average value. The lists had two duplicate compounds: diuron and parathion. In this case, we used Rotroff et al. (2010) data. However, similar results were obtained. In addition, we had included, subject to the availability of data in the literature, several compounds: PCBs, PFOS and DDT (Parham and Portier 1998; Loccisano et al. 2011; Yamazaki et al. 2010). The list of selected chemicals as well as their physico-chemical parameters has been provided in the Supplementary Material, Table 1. For the estimation of physico-chemical properties, we used EPI Suite v4.0 form US EPA (2011) and, for pKa, Simulations Plus ADMET predictor (2011).

Simulated conditions and BCF prediction

For each substance, a mechanistic physiologically based toxicokinetic model was developed using a generic population-based ADME model (Jamei et al. 2009). The Simcyp software (Simcyp Limited, Sheffield, UK) in its minimal version, the portal vein, the systemic circulation and the liver (Rowland Yeo et al. 2010), was used (see Fig. 1a for a schematic representation and Supplemental Material, section 1 for details on the simulation). The PBTK input data and the predicted parameters used in the present study have been provided in the Supplementary Material, Table 1.

Fig. 1.

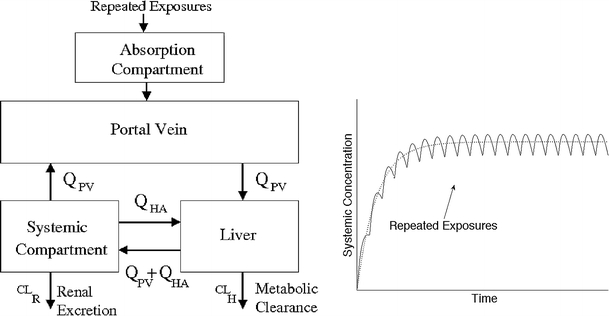
PBTK model and simulations. a Schematic representation of the generic PBTK model used to simulate perfusion-limited uptake of compound under a chronic exposure. b Typical time profile of the systemic compartment concentration where the successive bumps induced by repeated exposures have been exemplified. The dotted line is the trajectory of the averaged-PBTK model. See Supplementary Material, Sections 2 and 3 for more details

One difficulty in evaluating the BCF for human is the multiple sources of exposure. The calculation of the human bioconcentration factor cannot be as easily defined as the ratio of the concentration in blood and in water. It has been suggested that bioaccumulation should refer to an increase in blood concentration with repeat exposures. The successive administrations of small doses induce small fluctuations of the concentration of substrate in the systemic circulation and, at a coarser time scale, the compound progressively bioaccumulates, see Fig. 1b. The simulations were performed until the concentrations reach a steady state. These values have been used to calculate the human bioconcentration factors, hBCF, defined as:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{hBCF}} = \alpha \frac{{C_{\text{sys}}^{*} }}{{{D \mathord{\left/ {\vphantom {D T}} \right. \kern-\nulldelimiterspace} T}}} $$\end{document} 1

where \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ C_{\text{sys}}^{*} $$\end{document} (mg/l) is the steady-state blood concentration of the chemical in the systemic circulation, D (mg) is the dose and T (h) is the time elapses between two successive exposures. The ratio D/T mimics a constant flow and may be seen as the result of a constant exposure scenario. The parameter α in Eq. 1 is a normalizing factor that leads to a dimensionless bioconcentration factor. Here, we take α = V _PV/t where V _PV is the volume of the portal vein and t has a unit of time and is set at 1 h.

The time profile of the concentration in the systemic compartment is recorded, and a first-order saturating process is used to approximate its global shape. The Simcyp-computed trajectory is approximated by a transitory regime characterized by a time constant, τ _sys, followed by the saturating regime described by the steady-state value \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ C_{\text{sys}}^{*} $$\end{document}. The numerical value of the couple \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ (C_{\text{sys}}^{*} ,\tau_{\text{sys}} ) $$\end{document} is computed for all the selected compounds, and the \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ C_{\text{sys}}^{*} $$\end{document} value is used to compute hBCF according to Eq. 1. The time constant τ _sys is used to evaluate the bioaccumulation half-life noted T _acc and defined as T _acc = τ _sys ln 2. Because we were describing the time profile of the systemic concentration caused by successive exposures, the bioaccumulation half-life used here is different from the biological half-life commonly used in pharmacokinetic studies that describes the increase of drug concentration following a single uptake with a first-order kinetic models and refers to the time it takes for the blood plasma concentration to halve its steady state. It is also different from the well-known elimination half-life that is used to describe the decay of a substance.

Characterization of the hBCF

A direct and straightforward estimation of the hBCF based solely on a limited number of compound characteristics is highly desirable for prioritization exercises and may provide an efficient pre-screening criterion for a rapid assessment. In this sense, we have developed a simplified mapping based on two parameters to assess the bioaccumulation potential of compounds. The derivation of the expression is based on the averaging of the generic Simcyp-PBTK model and provides an analytical approximation of the hBCF. Comparison with the hBCF obtained with the complete PBTK model is done.

The proposed measure of hBCF is derived from the steady state reached by the PBTK model after successive exposures. To explore other bioaccumulation metrics, we investigate a possible characterization of the hBCF based (1) on the bioaccumulation half-time and (2) on the structure of the PBTK model that describes the toxicokinetics of the compound. For the latter, we calculated for each compound the distance between the actual PBTK model that describes the toxicokinetic of the compound and a virtual PBTK model without clearance, i.e., a PBTK model for which the compound fully bioaccumulates in the body without biotransformation or excretion. We called this model the virtual trap PBTK model. The proposed measure is obtained from the singular value decomposition of the PBTK matrix that describes the kinetics of the compound (see Supplementary Material, Section 4). A comparison of the results obtained using the different approaches in terms of bioaccumulation potential assessment is done.

Assessment of PBTK model results

To assess the validity of our modelling approach, published pharmacokinetic data were collected and compared with our model results (see Supplementary Material, Section 1).

Results and discussion

PBTK model validation

In Table 1, the results of our model for twelve chemicals were compared with published pharmacokinetic/toxicokinetic data and published PBTK model predictions. Our results agree with the results obtained by Rotroff et al. (2010) concerning 2,4-dichlorophenoxyacetic acid, oxytetracycline dehydrate, triclosan, bisphenol A and parathion. Our simulated results, 40 h, agree with experimental data on plasma elimination half-lifes of warfarin for the two enantiomers: R-warfarin 46 ± 7 h and S-warfarin 36 ± 13 h, respectively. The prediction of the maximum plasma concentration for chlorpyrifos and propranolol hydrochloride was similar to human kinetic studies and published PBPK model results. In the last case, also the data on the time at which C _max was reached are gathered and compared with the simulation, i.e., 2 h in the two experiments (10 and 20 mg day⁻¹ oral dose) and 2.1 h in the simulations. Apart from the well-known persistent compounds such as PCBs, DDT and PFOS were uncertainty on the estimations (Simcyp could only run for 200 days, and we extrapolated the values), and the experimental variability (e.g. for PCB-153, we have found published values between 5 and 27.5 years) tends to be higher, the main discrepancy is obtained for thioridazine where the predicted elimination half-life value is much higher than the experimental one: an elimination half-life that oscillates around 26 h has been reported while we predicted 87 days. This points out a limitation of our approach due to the fact that we consider only liver metabolism and minimal renal excretion, whereas the main excretion route of thioridazine seems to be through the faeces. A similar limitation holds for oxytetracycline where the observed overprediction of the concentration possibly lies in the fact that a 100% oral absorption has been considered, whereas a low oral bioavailability has been reported for this compound (Nielsen and Gyrd-Hansen 1996). However, as stated before, our main interest is in developing a fast screening procedure to estimate human bioaccumulation potential for risk assessment and, as a conservative approach, false-positive predictions are not our main concern.

Table 1.

Comparison of our model simulations with literature human data and published PBTK model results

Compound	Css (steady-state concentration) for 1 mg kg−1 day−1 dose (μM)	Present study
2,4- Dichlorophenoxyacetic acid	9.05–90.05	44.47
Oxytetracycline dehydrate	0.36	2.31
Triclosan	2–10	2.18
Bisphenol A	<0.13	0.31
Parathion	0.17	0.24

	Plasma elimination half-life	Present study
Thioridazine	26 (h)	87 (days)
Warfarin	(R-isomer) 46 ± 7(h) (S-isomer) 36 ± 13 (h)	40 (h)
DDT	5–8 (years)	2 (years)
PCBs	10–15 (years)	7 (years)
PFOS	2.4–21.7 (years)	2.5 (years)

	Cmax (maximum concentration) (μM)	Present study
Chlorpyrifos	~0.01a	0.013
Propranolol	0.15b 0.23c	0.12 0.24

^afor 1 mg kg⁻¹ day⁻¹ dose; ^b for 10 mg day⁻¹ dose; ^c for 20 mg day⁻¹ dose

Estimation of the hBCF

In Table 2, the human bioaccumulation factor is shown for the top twenty of the selected compounds (a complete table is provided in the Supplementary Material, Table 2). Qualitatively, some of the estimations are in agreement with the results reported in the literature concerning well-known human bioaccumulative compounds, i.e., PCBs, PFOS and the DDT (Cho et al. 2011; Kärrman et al. 2006). Concerning pharmaceuticals, only two compounds appear at the lower end of the top list: thioridazine, which is an antipsychotic agent with central nervous system activity, and warfarin, which is an anticoagulant. There are some evidence of accumulation of thiroidazine and its metabolites in brain, a factor of five when compared with plasma (Svendsen et al. 1988). However, unlike warfarin for which the PBTK model results were in agreement with published data (see Table 1), the results for thioridazine should be subject to caution due to the overestimation of the compound half-life and, therefore, an expected overprediction of its concentration levels. As stated before, one explanation is that we have not considered the main route of elimination for this compound.

Table 2.

Estimated human bioconcentration factor (hBCF) for the top twenty compounds. The octanol–water partition coefficient and the nature of the compound are also reported (PPP is for plant protection products)

Compound name	CAS number	Log KOW	hBCF	Main category
PFOS	1763-23-1	6.28	926.4	Industrial Chem.
Emamectin	155569-91-8	5.0	325.4	PPP (insecticide)
Buprofezin	69327-76-0	4.3	44.9	PPP (insecticide)
PCB80	33284-52-5	6.6	44.5	Industrial Chem.
PCB77	32598-13-3	6.63	44.5	Industrial Chem.
PCB153	35065-27-1	7.75	44.2	Industrial Chem.
PCB155	33979-03-2	7.55	44.1	Industrial Chem.
PCB136	38411-22-2	7.65	44.1	Industrial Chem.
Fenvalerate	51630-58-1	6.2	20.2	PPP (insecticide)
Bentazone	25057-89-0	2.34	11.1	PPP (pesticide)
DDT	50-29-3	6.91	8.11	PPP (insecticide)
Parathion	56-38-2	3.83	7.05	PPP (insecticide)
Cyprodinil	121552-61-2	4.0	6.73	PPP (fungicide)
Pyraclostrobin	175013-18-0	5.45	5.28	PPP (fungicide)
2,4- Dichlorophenoxy acetic acid	94-75-7	2.81	5.24	PPP (pesticide)
Fipronil	120068-37-3	4.0	2.64	PPP (insecticide)
Thioridazine	50-52-2	5.9	2.64	Pharmaceutical (antipsychotic)
Warfarin	81-81-2	2.7	2.44	Pharmaceutical (anticoagulant)
Bromacil	314-40-9	2.11	2.33	PPP (herbicide)
Fenoxycarb	72490-01-8	4.3	2.33	PPP (insecticide)

Two agricultural chemicals appear at the top of the list, emamectin and buprofezin. The higher values obtained for both compounds are due to two different reasons: in the first case due to the low clearance rate and in the second due to the low unbounded fraction value that decreases our calculated renal clearance. For emamectin, there is some evidence of low bioaccumulation in aquatic species, with a BCF of 80 for the whole Bluegill Sunfish (Chukwudebe et al. 1996), which, therefore, classifies the compound as nonbioaccumulative. In the same paper, it is also reported that similar results have been found in mammals (rats and goats), but the authors refer to unpublished data. The potential to bioaccumulate predicted by our analysis for emamectin suggests that further review for this compound may be warranted.

Comparing to emamectin, a higher BCF value for fish has been reported for buprofezin (BCF = 509 whole fish) and also for fenvalerate (BCF = 1,664), parathion (BCF = 97), cypronidil (BCF = 393), pyraclostrobin (BCF = 706), fipronil (BCF = 202), whereas lower values have been reported for bentazone (BCF = 21), 2,4-D (BCF = 3.16) and bromacil (BCF = 3.2), data from EPI Suite™ (US EPA 2011) and the Footprint Database (EUP 2009). However, these values are not sufficient to classify these substances as bioaccumulative. According to the European Chemicals Agency (ECHA 2008) and previous legislation, the criteria to be classified as Bioaccumulative (B) or very Bioaccumulative (vB) are the following:

• BCF > 2,000 l kg⁻¹ and BCF< 5,000 l kg⁻¹→ B

• BCF > 5,000 l kg⁻¹→ vB

Concerning mammal species, there are few data discussing bioaccumulation potential, and the results obtained for a particular species cannot be directly extrapolated to another species. For example, some bioaccumulation potential from fipronil has been reported in beef cattle, whereas rapid metabolisation seems to occur in rats (Tingle et al. 2003). Here, fipronil appears in the top twenty list suggesting a bioaccumulative potential for human.

Questioning of the hydrophobicity paradigm

The octanol–water partition coefficient has been commonly used as the main screening criterion for the assessment of the bioaccumulation potential with the idea that this value is a surrogate for the tendency of a compound to partition to tissue lipid. The overwhelming majority of works have focused on the applicability of this approach for fish, with recent approaches considering other properties, such as size, ionization potential, potential metabolism, etc. However, it is not clear to which extend a predictive method based on the octanol–water partition coefficient is relevant for terrestrial life, as already discussed by Gobas et al. (2003), and more specifically for human bioaccumulation assessment. To analyse these aspects, we have plotted in Fig. 2a, the logarithm of the predicted human bioconcentration factor, log hBCF, as a function of log K _OW. The relative weak influence of the octanol–water partition coefficient is clearly illustrated (r ² = 0.18), despite a substantial correlation of the log K _OW with the bioaccumulation factors for fish (Fig. 2b, r ² = 0.81 for the experimental values, r ² = 0.79 for Method 1 EPI Suite™ values and r ² = 0.77 for Method 2 EPI Suite™ values (US EPA 2011). Therefore, this approach has a limited domain of applicability and appears to be inconclusive for human prediction. The comparison between the log hBCF and the log BCF obtained from experiments and EPI Suite™ values (see Fig. 2c) indicates a strong discrepancy between human and fish. Even if a small correlation exists between the log BCF for fish and for human (r ² = 0.22), the bioaccumulation assessment for human cannot be obtained from studies on fish. These results suggest that the determinants for human and fish bioaccumulation are quite different, and bioaccumulation potential should be evaluated for humans in chemical risk-assessment reports.

Fig. 2.

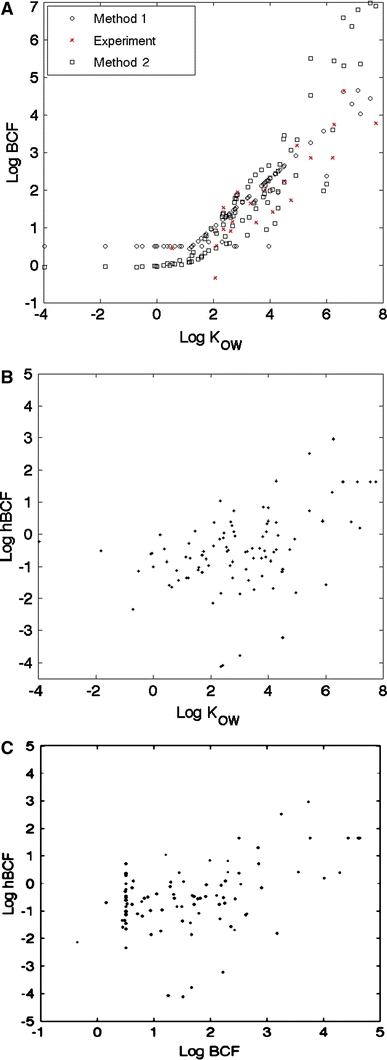
Influence of partitioning on bioaccumulation. a Plot of the bioconcentration factor for fish as a function of the octanol–water partition coefficient for the selected compounds. Method 1 and Method 2 refer to predicted values from EPI Suite™ algorithms and values depicted with red crosses indicated experimental data. Panels b and c are plots of the human bioaccumulation factor as a function of: b the octanol–water partition coefficient and c the bioconcentration factor for fish

The weak influence of K _OW observed here corroborates recent studies (Czub and McLachlan 2004a, b; McLachlan et al. 2011) and strongly encourages the investigation of new criteria for human bioaccumulation. It has been suggested that the susceptibility to biotransformation is the principal determinant of bioaccumulation in humans. Even for aquatic life, the estimation of bioaccumulation from K _OW is valid as far as there is no transformation or degradation of the compound. Recent QSAR modelling approach has been developed to consider the limitation of bioaccumulation due to metabolism (Dimitrov et al. 2005). However, it remains unclear how to incorporate such adjustment factors and alternative predictive methods are therefore desirable. Mass-balance models used here offer a powerful conceptual framework that allows the integration of the kinetics processes that monitor bioaccumulation together with a mechanistic understanding of the underlying processes and therefore seem to be more appropriate for bioaccumulation assessment.

The importance of elimination

To evaluate the role of elimination in the biaccumulative potential of a substance, we derived an approximation of the hBCF as a function of the intrinsic hepatic clearance and the renal excretion (see Supplementary Material, section 3, Eq. 6). Figure 3 shows the plot of the logarithm of the approximated hBCF in the (Log(CLu_int), Log(fu)) state space where CLu_int (l h⁻¹) is the intrinsic metabolic clearance and fu is the unbound fraction in plasma. Each colour represents a change of half an order of magnitude of the bioaccumulation factor. This simplified mapping was generated by running the program for all the possible combinations of liver clearance values and unbounded fraction. Recall that the intrinsic clearance accounts for metabolism and is used to derive the hepatic clearance, whereas the free fraction in plasma is directly related to the renal excretion through the minimal excretion model. The rank previously obtained with the complete model is placed on the mapping near the corresponding compounds. The classification obtained from this mapping is in line with the one obtained with the complete PBTK model. A more detailed comparison is done Fig. 4a where the hBCF for the different compounds is plotted versus its approximation. All the points lie on the diagonal except the points associated to PCBs and PFOS that show a significant difference, but these compounds are still classified as bioaccumulative with the two approaches.

Fig. 3.

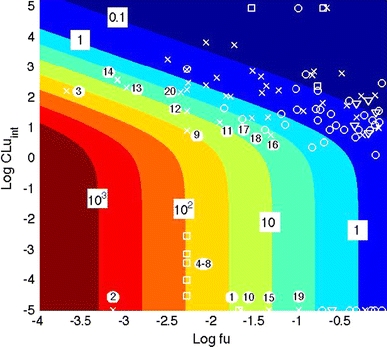
The simplified mapping. Determination of the human bioconcentration factor (hBCF) as a function of the unbound intrinsic hepatic clearance CLu_int (l h⁻¹) and the free fraction in plasma, fu. The logarithmic scale of hBCF is marked on the boundaries separating the coloured fields. The predictions are done using an approximation of the hBCF value computed with the PBTK model for the 96 selected compounds. For the sake of comparison, the top twenty ranking obtained with the complete model is indicated (filled white circle). Compounds are represented using the following labelling: circles, ‘open circle’, are for pharmaceutical compounds, crosses, ‘multiple sign’, are for plant protection products (insecticide, pesticide,…) squares, ‘open square’, are for industrial chemicals and triangles, ‘inverted filled triangle’, are for natural products (alkaloid, hormone, …). Compounds without liver clearance, i.e., CLu_int = 0, are arbitrary placed on the map at a log value of −5

Fig. 4.

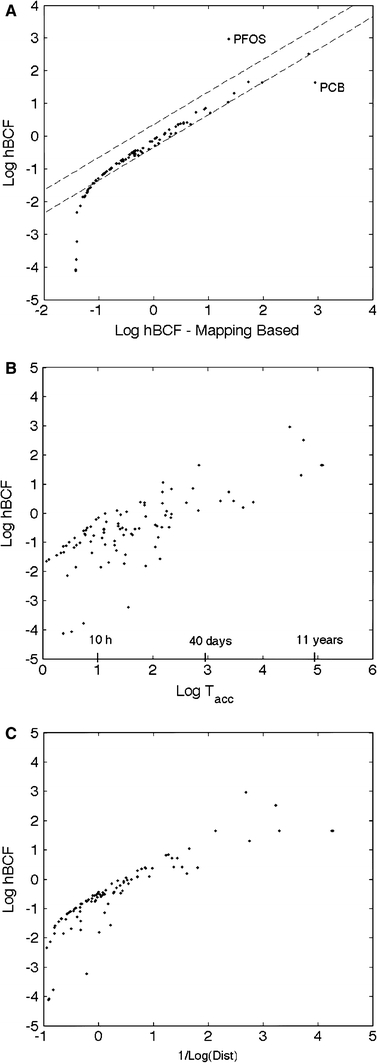
A Assessment of the accuracy of the simplified mapping. The human bioconcentration factor predicted by the PBTK model is compared with the prediction given by the simplified mapping shown in Fig. 3. An interval of ±0.35 around the identity has been plotted that could account for the variation experimentally observed on the replicated measures of BCF. b–c. Alternative characterizations of human bioaccumulation. Log–log plot of the human bioconcentration factor as a function of b the bioaccumulation half-life and c the inverse of the distance to the virtual trap PBTK model, i.e., the PBTK model without excretion

The simplified mapping summarizes the results obtained for the analysed compounds using Simcyp when placed on the developed plot using the analytical expression. The compounds have been divided into several classes: pharmaceuticals, plant protection products (PPP), industrial chemicals and natural products. Compounds crossing the zero line have a bioaccumulative potential. As it can be observed, pharmaceutical compounds do not tend to bioaccumulate or have low values. This is expected since they have been designed to be active and easily degradable. Conversely, a considerable amount of PPP and industrial chemicals show some bioaccumulative potential.

The ability to describe the bioaccumulative potential of a compound through the metabolism combined with the renal excretion shows that the clearance is the main determinant factor for human bioaccumulation. We believe that this approach offers a fast and reliable approach to assess human bioaccumulative potential in a high-throughput set-up by performing two in vitro tests: one to calculate the chemical binding to plasma proteins using standard techniques such as equilibrium dialysis (Waters et al. 2008), ultrafiltration (Zhang and Musson 2006) or ultracentrifugation (Nakai et al. 2004) and the other to estimate the liver clearance by in vitro measuring the metabolite formation and/or the substrate depletion of the compound using human hepatocytes (Pelkonen et al. 2009; Rotroff et al. 2010).

Alternative assessment of hBCF

The method used above to predict the bioaccumulation potential of a substance is based on the steady-state reaches by the corresponding PBTK model. To evaluate to which extent the time-signature of a compound could also provide an indication about its bioaccumulative potential, we compared Fig. 4b the bioconcentration factor as a function of the bioaccumulation half-file (T _acc). Compounds that have a high hBCF value tend to have a high bioaccumulation half-life. A correlation of r ² = 0.59 is found between the two logarithmic values. This inter-dependence stems from the ability of the bioaccumulation half-time to describe the elimination kinetics, specifically for compounds with a slow kinetics where the toxicokinetics is essentially described with one compartment. For instance, for PFOS, we found a bioaccumulation half-life of 2.5 years which is identical to the elimination half-life predicted by our model. Warfarin has a shorter bioaccumulation half-life, 42 h, which is still quite similar to the predicted value for the elimination half-life, 40 h.

The comparison of the top twenty hBCF-based ranking previously obtained with the one based on the bioaccumulatiom half-life shows an overlap for sixteen compounds (see Supplementary Material, Table 3). However, despite the bioaccumulation potential is entangled with the bioaccumulation half-life, the time profile of the compound obtained with repeated exposures only provides a partial criteria and does not allow a reliable identification of bioaccumulative chemicals since a difference of several orders of magnitude for hBCF values is observed for compounds with close bioaccumulation half-life. Moreover, etoxazole, isoxaben, zoxamide and amitriptyline appear in the top twenty ranking based on T _acc, whereas their hBCF values are, respectively, 1.6, 1.22, 0.93 and 0.70 which rank them at the place 23, 25, 29 and 34. Conversely, some compounds with a high bioaccumulation potential do not appear at the top of the list based on bioaccumulation half-life.

The bioaccumulation half-life is a synthetic measure of the time-evolution of a compound that tends to reduce the dynamic to a single compartment model. However, the actual toxicokinetics of the selected compounds is not likely to be consistent with a first-order kinetic model. We found that a preferable metric is based on the distance of the actual PBTK model to the virtual trap PBTK model. A correlation of r ² = 0.71 between the hBCF (log) and proposed distance (log) is found (see Fig. 4c). Using the ranking based on this measure, the top twenty list is almost completely recovered, and the two rankings only differ from two compounds (see Supplementary Material, Table 4). Fenoxycarb and warfarin do not appear in this new ranking but are located at the end of the hBCF-based list. Conversely, etoxazole (pesticide) and isoxaben (herbicide) are at position 12 and 20, whereas they are ranked 23 and 25 according to their hBCF. Note that a high bioaccumulation potential (for fish) has been reported for etoxazole, whereas a low bioaccumulative potential in mammals has been suggested for isoxaben (NPIC 2011). This theoretical measure provides a reliable characterization of the bioaccumulation potential of a substance that has the twofold advantage of being independent of the exposure and being obtained efficiently with a well-established algorithm on matrix computation without requiring the computation of all the time-dependent concentrations of the PBTK models. Therefore, this approach could provide a valuable tool for fast screening in large databases.

Conclusions

The vast majority of the approaches to predict the bioaccumulation potential consider only the partitioning of the chemical and not the biotransformation potential of the organism. The results obtained in this study suggest that it is possible to have a pre-assessment of the human potential bioaccumulation by performing two in vitro tests: one to calculate the chemical binding to plasma proteins and the other to estimate the liver clearance by in vitro measuring the metabolite formation and/or the substrate depletion of the compound using human hepatocytes. Both types of tests are suited to high-throughput analysis and therefore can be used for screening purposes for the prioritisation of new compounds. However, there are several aspects that should be considered carefully in this approach. First, it is assumed that the in vitro measurements adequately describe the in vivo activity. Second, the experimental conditions in the in vitro tests should have been properly selected, e.g., compounds concentration low enough to avoid saturation when measuring substrate depletion. Third, concerning the in vitro clearance, it is assumed that there is no further biotransformation in the gastrointestinal track and, in addition, metabolism occurs only in the liver. Normally, all these assumptions are conservative, and therefore, it is more probably to obtain false positives than false negatives as it can be observed in the compounds that deviate in the comparison between experimental data and predictions. Finally, there is the need to develop sensitive throughput analytical techniques that can allow a better understanding of the kinetics aspects in in vitro experiments. This would also help in determining a general procedure for performing in vitro–in vivo extrapolation (IVIVE) and being able to move from concentration to dose response without the use of animal experiments (Adler et al. 2011). Our research is continuing along these lines.

Electronic supplementary material

Below is the link to the electronic supplementary material.