Experience-dependent firing rate remapping generates directional selectivity in hippocampal place cells

Abstract

When rodents engage in irregular foraging in an open-field environment, hippocampal principal cells exhibit place-specific firing that is statistically independent of the direction of traverse through the place field. When the path is restricted to a track, however, in-field rates differ substantially in opposite directions. Frequently, the representations of the track in the two directions are essentially orthogonal. We show that this directionally selective firing is not hard-wired, but develops through experience-dependent plasticity. During the rats' first pass in each direction, place fields were highly directionally symmetric, whereas over subsequent laps, the firing rates in the two directions gradually but substantially diverged. We conclude that, even on a restricted track, place cell firing is initially determined by allocentric position, and only later, the within-field firing rates change in response to differential sensory information or behavioral cues in the two directions. In agreement with previous data, place fields near local cues, such as textures on the track, developed less directionality than place fields on a uniform part of the track, possibly because the local cues reduced the net difference in sensory input at a given point. Directionality also developed in an open environment without physical restriction of the animal's path, when rats learned to run along a specified path. In this case, directionality developed later than on the running track, only after the rats began to run in a stereotyped manner. Although the average population firing rates exhibited little if any change over laps in either direction, the direction-specific firing rates in a given place field were up-or down-regulated with about equal probability and magnitude, which was independent in the two directions, suggesting some form of competitive mechanism (e.g., LTP/LTD) acting coherently on the set of synapses conveying external information to each cell.

Introduction

Principal neurons in the hippocampus proper exhibit activity correlated with the location in which an animal is located (O'Keefe and Dostrovsky, 1971). In an open environment, when an animal is moving around in a random path, such as while foraging for food, the majority of place cells fire at rates that are independent of the direction in which the animal is passing through the cell's “place field” (Muller et al., 1987). These findings are consistent with the predominant view of the hippocampus encoding an allocentric representation of space (O'Keefe and Nadel, 1978). It is clear that the hippocampus is necessary for spatial memory (e.g., Morris et al., 1982); however, the degree to which this structure encodes changes in sensory cues or behavioral contingencies occurring in a single spatial environment is still debated (e.g., Eichenbaum et al., 1999).

One view is that the selection of which hippocampal cells fire at a given location is initially determined by path integration mechanisms (McNaughton et al., 1996), whereas sensory information that may vary at that location may become associatively linked to the selected cells, thus enabling future correction of path integrator errors. Such associative linking would typically not involve changing the membership of the active population (which would be considered “global remapping”), but could affect their relative firing rates (“rate remapping”; Leutgeb et al., 2005). Global remapping is typically induced when a rat is transferred between separate, distinct, recording rooms (Leutgeb et al., 2004), when the rat locomotes between two boxes (Skaggs and McNaughton, 1998; Colgin et al., 2010), or when a large mismatch is introduced between its path-integrated heading direction and familiar visual landmarks (Knierim et al., 1998; Fuhs et al., 2005). In addition to local sensory information, internal information such as working memory, current goals, behavioral set, and possibly even circadian rhythms may also affect firing rates without significantly changing the locations at which the hippocampal cells fire (O'Keefe and Conway, 1978; Hetherington and Shapiro, 1997; Wood et al., 2000; Leutgeb et al., 2005, 2006; Sparks et al., 2010).

A long unresolved problem with the mainly allocentric view of hippocampal place cells has been that whereas, in an open environment, a large majority of place cells exhibit firing that is not direction specific (Muller et al., 1994; Markus et al., 1995), on a track that is repeatedly traversed along a specific path, the activity of place cells in each direction differs substantially (McNaughton et al., 1983; Muller et al., 1994). In addition to the configuration of the traversable portion of the environment, the task the animal is performing also affects directionality of place cells: if the animal is repeatedly running a path between specified goal locations even in an open environment, the place cells show distinct directional firing (Markus et al., 1995). Interestingly, the presence of many local cues on the track reduces the difference in firing between the two running directions (Battaglia et al., 2004), but the complexity of distal room cues appears not to affect directionality (Markus et al., 1995).

Recent findings suggest that the firing of “grid cells” in the medial entorhinal cortex is generated by path integration and is the primary source of relative position information to the hippocampus (Hafting et al., 2005; Fyhn et al., 2007). Also notably, under conditions that induce rate remapping in hippocampal cells, grid cells do not exhibit changes in firing location or relative firing rate; however, conditions that induce global remapping in hippocampal cells also induce global remapping in grid cells (Fyhn et al., 2007). Overall, current data suggest that path integration occurs in the medial entorhinal cortex (McNaughton et al., 2006), and this information is then passed on to the hippocampus, which can combine it with other information, such as landmarks or other spatial cues, and task demands or other internal state variables, to form a conjunctive code for locations and the events that occur there (Leutgeb et al., 2005).

Path integration by the medial entorhinal cortex does not, however, explain why the place cell activity in two running directions on a track is so different, while the activity in an open environment is essentially independent of direction of travel. In the current study, we recorded from hippocampal cells while a rat traversed a circular track in both directions, beginning with the very first time that the rat had experienced the track in a given spatial context. We observed that, while the track was novel to the animal, the two running directions were in fact highly correlated. During repeated traversals of the track, the firing rates of place cells changed in both running directions, becoming highly dissimilar by the end of the session, as previous studies had shown. We present evidence that, unlike the expression of place fields per se, directional selectivity is an experience-dependent phenomenon driven by gradual changes in the response of a cell to external sensory cues and/or internal variables such as goals or recent trajectories which occurs when the traversal of a path becomes stereotyped.

Methods

Subjects

Five male rats (four Brown Norway-Fisher hybrids and one Brown Norway) were used for this study. The rats were housed individually and kept on a 12 h dark/12 h light schedule. Training and experiments occurred during the dark phase. During pre-training, and then again during recording, they were kept at ∼85% of their free-feeding body weight, in order to be motivated to run for food rewards. All animal protocols complied with National Institutes of Health guidelines and Canadian Council for Animal Care (CCAC) regulations under the guidance of the University of Arizona Institutional Animal Care and Use Committee (IACUC) or the institutional animal care committee at the University of Lethbridge.

“hyperdrive” assembly and implant

Rats were implanted with a “hyperdrive” consisting of 14 individually movable tetrodes. Each tetrode consisted of four strands of insulated 13 μm nichrome wire twisted together, and was inserted in silica tubing and secured with cyanoacrylate glue to a drive cannula. The drive cannula was coupled by a plastic nut to a drive screw, so that rotation of the nut allowed vertical movement of the tetrodes through another (30 gauge) guide cannula. The 14 guide cannulae were placed within the inverted conical core of the hyperdrive, evenly spaced and angled at 30° from the vertical axis at the top, and bundled together and vertical to the brain surface at the bottom of the hyperdrive, where they would be contacting the brain. For rats 1–3, the guide cannulae were bundled into a 2 × 7 linear array, to be placed along the proximal-distal axis of dorsal CA1. The remaining two animals (rats 4 and 5) were implanted with hyperdrives with a bundle forming a circle, and lowered to dorsal proximal-mid CA3. A more detailed explanation of the hyperdrive, implantation, and recording techniques is published in Gothard et al. (1996a).

Surgery was performed under Isofluorane anesthesia. A 3 mm in diameter craniotomy was opened above the right dorsal hippocampus (coordinates of the center of the craniotomy differed slightly between rats, between 3.3–3.8 mm posterior and 2.0–3.0 mm lateral). The Dura was removed, the hyperdrive bundle was centered above the craniotomy, with guide tubes just touching the surface of the brain, and the craniotomy was sealed with Kwik-Sil and then cemented in place with dental acrylic anchored by dental screws spread over the rest of the dorsal surface of the skull. After surgery rats were administered 26 mg of acetaminophen orally for pain relief, and given Ampicillin in their food for 10 days or given subcutaneous injections of Metacam and Tribrissen to prevent infection. All tetrodes were lowered into the brain immediately following surgery by turning the screws three full turns (954 μm).

Recording procedures

Twelve tetrodes were lowered over the course of 2–4 weeks to CA1 (rats 1–3) or CA3 (rats 4 and 5). The remaining two tetrodes were lowered to the corpus callosum, to serve as a reference, and the hippocampal fissure as an EEG recording probe. For recording, the hyperdrive was connected to a unity-gain headstage (Neuralynx, Bozeman, MT) which allowed low noise transmission of signals from each of the four channels of each tetrode, via a multi wire cable and a commutator mounted on the ceiling, to digitally programmable amplifiers and then to the Neuralynx Cheetah system. Local field potential activity was continuously sampled from one channel of each tetrode at 2.4 kHz, amplified 500–1000 times, filtered between 1 and 300 Hz, and recorded. For this analysis, only the LFP signal from the tetrode with the largest number of cells on each day (the one most likely to be in the cell body layer) was used (filtered off-line at 6–10 Hz to determine the theta signal). Spike signals from each channel of the 12 hippocampal tetrodes were referenced against the corpus callosum electrode signal, amplified 1000–5000 times and filtered between 600–6000 Hz. Signals were digitized at 32 kHz, and a 1ms sample was recorded when the signal reached a pre-determined threshold. The thresholds were adjusted manually for each channel, depending on the noise level and spike amplitude on that channel. The headstage also contained a circular array of LEDs that were detected by an overhead camera and recorded by the Cheetah system along with the neural signals to allow tracking of the position of the rat on the maze. Video spatial resolution was approximately 3 pixels/cm.

After the completion of recordings, the location of the tetrodes was ascertained by creating a small electrolytic lesion at the tip of each tetrode (by passing 5 μA current for 10 s). Histological sections were Nissl stained to localize the lesions. Based on coronal sections from the 3 CA1 rats, it was determined that the recordings of rats 1 and 2 came from a wide range of proximal-distal coordinates in CA1, and rat 3 was found to have most tetrodes in proximal CA1, one tetrode in CA2, and 2 tetrodes in distal CA3. Thus, the day 1 recordings included 183 CA3 cells, 22 CA2 cells, and 83 CA1 cells (51 from the proximal half).

Pre-training and behavioral tasks

All rats were pre-trained prior to hyperdrive surgery to run laps back and forth between food dishes on a circular track, as well as to forage for randomly sprinkled food rewards in an open-field environment. All pre-training sessions occurred in a different room than the room in which recording took place. The track used during recording was usually different from the one used during pre-training, or when the same track was used, a different surface was placed on the track.

The first behavioral task involved the rats running on a circular track. Two rats ran on a track 120 cm in diameter, one rat on a 115 cm track and one on a 152 cm diameter track. A barrier was placed at one end of the track, with food dishes on either side of it, so the rat would have to turn around and run back to get the next food reward. Small objects and textures were placed on half of the track (“cue-rich”), and the other half had a uniform surface with no nearby objects (“cue-poor”). Each running session lasted 25–30 min, and was preceded and followed by 30 min–1 h of rest in a small pot near the track. Because the rats were pre-trained to perform this task, three of the rats showed good enough behavior during their very first exposure to the track to allow us to analyze individual laps. Rat 3, however, did not run on the track during his very first exposure, and ran too slowly and too few laps (6) during his second exposure for that data to be analyzed. Thus, the data analyzed as rat 3's “session 1” is actually his third day being placed on the track. Nevertheless, this data showed very similar results to the actual first exposure of the other three animals, and so was included in this study. The second task involved the rats running on a circular open platform. One rat ran on a platform 115 cm in diameter, and the other rat on a 142 cm platform. A three-walled box was placed at the edge of the platform, and the rat was acclimated to this environment for 5 min prior to each running session, by being confined to the box with a barrier placed along the opening. Once the barrier was removed, the rat was expected to run to the food dish on the opposite edge of the platform, pick up a food reward, and return to the box to eat the reward. The task was designed to be able to manipulate the speed of the rat as he returned with food rewards of different sizes. That aspect of the task, however, was not important to this study. Each running session lasted 30 min. The rats also foraged for randomly distributed food rewards in the same environment every day for 30 min (prior to the shuttle task, with a 30 min rest between tasks). It took the rats 2–4 days to learn the shuttle task, but once they learned it, they were running over 20 laps per session, most of them directly between the box and the food dish. Only the spikes occurring along a direct path were analyzed, and laps in which the rat diverged from a direct path to the food dish for more than 20% of the run in either direction were excluded from the analysis.

Spike sorting

Spikes recorded during the entire recording session (2–3 rest periods and 1–2 running epochs) were sorted based on energies and first two principal components of the waveforms recorded on each electrode of a tetrode, using a semi-automated procedure. An automated algorithm (KlustaKwik, K. D. Harris, http://klustakwik.sourceforge.net/) was used to find clusters, which were then merged and adjusted manually using a modified version of MClust 3.1 (A. D. Redish, http://redishlab.neuroscience.umn.edu/MClust/MClust.html).

Position tracking

The position during the running epochs was extracted at each video frame by fitting a circle to the ring of LEDs on the headstage. The position determined during previous frames was used to eliminate active pixels at a distance of greater than 20 pixels, which could not have been from the headstage, but were a result of other spurious light sources. This 2D position was then deconstructed into a 1D representation along the track. For the circular track task, a circle was fit to the position data, and the coordinate along the diameter of the track was determined for each frame (with the barrier assigned a position of 0). For the shuttling task, principal component analysis on the XY coordinates was used to find the axis of the “track” and the coordinates along that axis were used (with the outer edge of the home box assigned a position of 0). Periods when the rat was stopped on the track were removed, by finding any periods when the rat was moving at less than 2 cm/s. Velocity was calculated by smoothing XY position with a 1-s hamming window, and then calculating the distance moved between subsequent frames. For the shuttling task, periods when the rat diverged from the track (the coordinates along the axis orthogonal to the “track” crossed a threshold value in either direction) were also removed from the analysis. If the rat diverged from the “track” for more than 20% of the distance in either direction, the whole lap (both directions) was removed from the analysis. Laps were identified by finding the turn-around points at the ends of the track.

Field analysis

Individual fields were delineated by smoothing (with a hanning window of five bins) the firing rate in (2 cm) position bins and automatically finding the peaks and troughs on either side of those peaks. Peaks at a minimum of 0.8 Hz were considered fields, and the first trough away from the peak that had a firing rate of less than 0.05 of the peak rate was considered the field boundary. Fields that had two peaks that were separated by a trough of at least 0.6 of the smaller peak rate were split in two. Fields were outlined individually in each running direction, and then combined if the majority of the field overlapped with the field in the opposite direction. This way all the spikes from fields that had shifted in the forward running direction would be considered. If a field was not found in the opposite direction, the spikes occurring in the same position bins were considered as the opposite direction field. All field boundaries were checked manually on a phase precession plot (Figure 1), and overlapping fields, fields that did not show phase precession in at least one running direction, or overlapped with food dish locations were excluded. Approximately 30% of the fields found by the automated algorithm were deleted in the manual step, most of these because they included few spikes and did not show phase precession, or they overlapped with a food dish location. The phase precession criterion was not applied very stringently, instead it was used in conjunction with the other criteria, for example to differentiate low firing rate fields from spurious spikes, or to determine if overlapping fields could be successfully separated with a single boundary or should not be used. The boundaries of approximately 30% of the remaining fields were adjusted manually, because the automated algorithm did not identify the full phase precession of a field (especially low firing rate fields), or it included some noise spikes from outside of a field. Spikes occurring within the boundaries thus set were then considered for the lap-by lap analysis of each field. See Table 1 for the number of cells and fields analyzed from each animal.

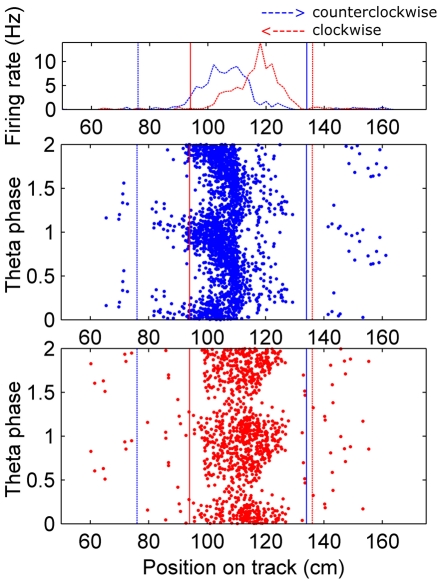
Figure 1.

Assigning boundaries around fields. Top: Occupancy normalized firing rate for an example cell is plotted on the coordinates of the circular track (the barrier was at 0 cm, which wraps around to 361.3 cm, and the food dishes were near that, at ∼10 cm and 351 cm). The firing rate in the clockwise direction (right to left on this plot) is colored red, and the counter-clockwise direction is in blue. Fields were identified by an automated algorithm, which found peaks (in each direction separately) in the smoothed version of this plot, and set boundaries at the troughs around those peaks. If the majority of the field found in one direction overlapped with a field in the opposite direction the two fields were combined, and the spikes within the boundaries outlined in each direction were considered for further analysis. The boundaries were set separately for each direction to account for the shifting of fields in the backwards running direction. If a field did not overlap with one in the opposite direction, any spikes occurring in the same position bins were considered as the opposite direction field. Dotted vertical lines indicate the beginning and solid lines the end of the field. Bottom: All fields identified were visualized on a theta phase plot, to ensure they exhibited phase precession. Fields that did not show complete phase precession in at least one direction, overlapped with another field, or showed truncated phase precession because of overlap with a food dish location were eliminated from the analysis.

Table 1.

Statistics of each session analyzed.

Rat	Session	Full, direct laps run	Cells	Fields in analysis
CUE-RICH CUE-POOR CIRCULAR TRACK
1	1	24	50	63
	2	12	72	80
	3	15	74	82
2	1	14	13	20
	2	7	43	39
	3	11	26	33
3	1	25	69	79
	2	7	65	28
	3	20	69	45
5	1	34	156	32
	2	20	175	22
	3	19	137	42
SHUTTLING TASK
3	1	13	47	9
	2	53	48	13
	3	77	39	18
4	1	20	94	15
	2	21	69	10
	3	29	81	14

Two tasks were performed by five rats. Each rat ran a task for at least three days, and the first three sessions were analyzed. (Rat 1 ran on the circular track twice a day, so the afternoon session of day 1 was considered session 2 and analyzed with the other rats' day 2, and the morning session of day 2 was session 3). The numbers of laps completed by the rat, cells recorded, and fields analyzed are displayed for each rat and session. The smallest number of laps traversed by any of the rats during a given session was analyzed.

Directionality index

The directionality of cells was determined by counting the number of spikes fired in each direction within each field, because this measures rate remapping better than a correlation. Spatial correlations are also influenced by the fact that fields are often offset in the two running directions (Battaglia et al., 2004). Thus, we calculated a “directionality index,” which was the difference in number of spikes fired in each running direction divided by the total spikes in both directions on each lap, based on the rate remapping difference ratio in Leutgeb et al. (2005). The difference between the higher firing rate direction (on average over the whole session) and the lower firing rate direction was used instead of the absolute value of the difference, because this way the same direction is being subtracted for all laps. Negative DI values resulted when the running direction in which more spikes occur switched between laps. When a cell spiked only in one running direction, the DI was 1.

Results

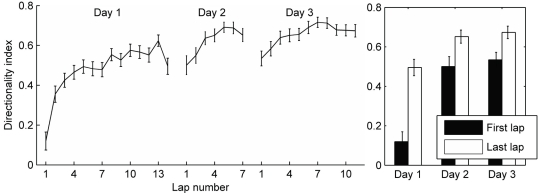
To study whether and how the directionality of place cells changes during initial experience on a track, we compared firing rates during passes through place fields in either direction across laps during the animal's first session on the track. For each cell, each place field was delineated (see Figure 1 and Methods), and all spikes that occurred within the field boundaries on each lap were counted. The “directionality index” (DI) of each field was calculated for each lap. The “higher firing rate direction” is defined as the direction in which, over the whole session, the number of spikes fired is greater. The DI is the number of spikes fired in the higher firing rate direction minus the lower firing rate direction, divided by the total number of spikes in both directions, and is the same as the rate remapping difference ratio used by Leutgeb et al. (2005). The average DI increased from a very low value (cells show almost identical firing in both directions) to a high value in about five laps of experience on the track (Figure 2), even though the average firing rates of the population stayed the same (Figure 4A). During the second and third sessions of experience on the track, the DI was already high on the first lap, but still increased slightly during the next few laps (Figure 2). There was a significant difference between the DI on the first lap compared to the last lap on all three days (paired t-tests, day 1: p < 0.0001, day 2: p < 0.05, day 3: p < 0.01). This was true for both the CA1 and CA3 cells in our analysis, although, consistent with the more robust rate remapping in CA3 reported by Leutgeb et al. (2005), the CA3 cells showed higher directionality at the end of the session (CA1 DI during last lap: 0.42, ± SEM 0.056, CA3 DI during last lap: 0.66 ± SEM 0.074, t-test: p < 0.05). We cannot, however, rule out individual differences between rats in this case, because the CA3 and CA1 samples came largely from different animals. While the average pattern clearly shows that the directionality of place cells increases from the first few laps to the end of the first session, individual cells showed different patterns of firing rate changes within different fields (discussed below). Some examples of firing rate changes in individual fields are shown in Figure 3.

Figure 2.

Development of directionality on a circular track. The number of spikes occurring within the field boundaries in each running direction was analyzed. The directionality index was calculated for each field on each lap as the difference in number of spikes fired in the preferred and non-preferred running directions divided by the total spikes in both directions (see Methods). The mean directionality index for all fields is plotted for each lap and each session. Error bars represent standard error of the mean. Laps are cut off at the least number of laps run by the four rats in a given session. Right: Comparing the directionality index during the first lap and the last lap in each session shows a significant increase from beginning to the end of each session.

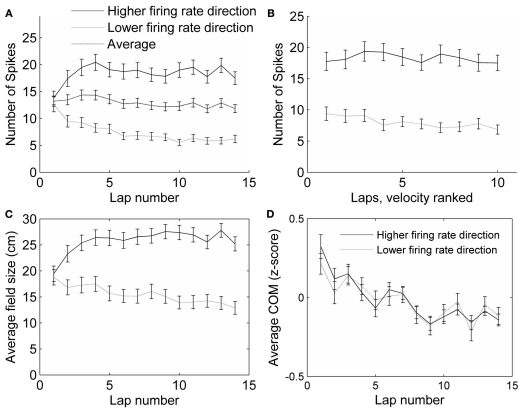
Figure 4.

Control analyses. (A) The average number of spikes fired in all fields did not change with lap number, even though the firing rates in each direction did. (B) The number of spikes fired within a field decreased slightly with running speed, but not differentially for the two running directions. The average number of spikes fired on the slowest pass through each field, the next slowest, and so on until the fastest pass, was calculated. The first four laps were excluded from this analysis, because the running speed was highly correlated with lap number in these laps. The slowest passes through each field (excluding the first four laps) were on average 17.7 cm/s (SEM = 0.53), and the fastest passes were on average 31.0 cm/s (SEM = 0.75), covering a range of the same size to the range of the passes during laps 1–10. (C) Average field size (measured as the distance from the first spike to the last spike) changed in each running direction across laps by about 35%, but not as much as the number of spikes fired (A). (D) The center of mass (COM) of place fields shifted backwards, in both preferred (higher firing rate) and non-preferred (lower firing rate) directions.

Figure 3.

Examples of firing rate changes in individual cells on day 1. (A) A proximal CA1 cell from rat 3 expressing a field on the cue-rich side of the track showed a typical pattern of directionality increase. Many cells (those falling in the category shown in Figure 5B) showed a directionality increase such as this. (B) Some cells expressed fields that started with significant directionality in the first few laps, such as the highlighted field of the intermediate CA1 cell shown here. Like this example, many cells in the category shown in Figure 5C increased their directionality even more after the first few laps. (C) An intermediate CA1 cell from rat 1 expressing a field on the cue-rich part of the track showed a small directionality increase. Many cells remained bi-directional throughout the session. (D) A few cells started directional and became less so, or reversed their preferred direction of firing (cells in the categories in Figure 5E,F). This intermediate CA1 cell from rat 1 didn't start firing until the return (clockwise) direction on the first lap, and then, over the next two laps, increased its firing rate in the counter-clockwise direction, eventually firing more spikes in that direction.

The average running speed of the rats tended to increase throughout the session, as the rats explored the track relatively slowly during the first few laps and later ran faster, now purely to receive their rewards (from 14.2 cm/s, SEM = 0.25 on lap 1 to 26.7 cm/s, SEM = 0.78 on lap 10). It is known that the firing rate of place cells increases with running speed (McNaughton et al., 1983); however, as the rat runs faster, he passes through each field more quickly, which compensates for the higher firing rate, and the total number of spikes fired during the pass through the field is approximately the same (Ekstrom et al., 2001). In our results, the number of spikes fired during each pass through a field actually decreased slightly with running speed (analysis of variance of the effect of velocity rank on number of spikes: F = 7.3, p < 0.01; Figure 4B). A decrease in the number of spikes in both directions would not, however, affect the DI, because this measure compensates for the total number of spikes. The number of spikes did, in fact, decrease with velocity similarly in both running directions (interaction between running direction and velocity rank: F = 0.2, p > 0.1; Figure 4B), but changed in opposite directions with chronological lap number (interaction between running direction and chronological lap number, F = 9.53, p < 0.01; Figure 4A). Thus, the observed change in firing rates over the first few laps cannot be accounted for by the effects of different running speeds seen during those laps.

Even though the track was narrow (∼10 cm), it is possible the rats were following slightly different paths in the clockwise vs. counter-clockwise directions. To study whether a possible difference in paths could have affected place cell firing rates and contributed to the DI, we analyzed the effect of the difference in paths taken through a field on the DI. The difference in position along the width of the track of paths taken on two subsequent passes through a single field was on average 1.67 cm, and varied with a standard deviation of 1.86 cm. We found that the difference between position along the width of the track during passes in either direction accounted for only 0.2% of the variability in directionality indexes (R² = 0.0023, p = 0.015) on day 1. During subsequent days, when the DI was greater, the effect of difference in position between passes on DI was not significant (day 2: R² = 0.00017, p = 0.1; day 3: R² = 0.00036, p = 0.1). Thus, the differences in firing rates in the two running directions are barely, if at all, affected by differences in paths traversed.

The change in relative firing rate within place fields in the two running directions has the characteristics of rate remapping, because changes in rate occurred without overall changes in firing location. To confirm this assessment, we analyzed several parameters that would indicate global remapping. First, global remapping would predict that many fields would appear in a novel location which did not show firing during the first few laps. During the first three laps, no spikes were fired only in 10 fields (5.2 percent), and six or fewer spikes were fired in 26 (13 percent) fields in those first three laps. When these fields were removed from the analysis, the average DI did not change noticeably (DI on lap 1 including all fields: 0.12 ± SEM 0.045, including only fields that exhibited more than six spikes in the first three laps: 0.14 ± SEM 0.045). Second, global remapping would predict that many cells stopped firing completely in one running direction; however, even during rate remapping the changes in rate can be sufficient to cause a few cells to have firing probabilities that approach zero in a given location in one or other condition (Leutgeb et al., 2005). Forty-eight fields (25 percent) ended with no spikes in at least one running direction. Removing these fields from the analysis reduced the DI both at the beginning and end of the session, but the change in directionality was still significant, both for the fields that ended with spikes in both directions, and for the fields that ended with no spikes in one direction (paired t-test between DI on first and last lap, p < 0.001 in both cases). Additionally, the size of each place field was measured on each lap, as the distance between the first and last spike (within the field boundaries) during that lap. The average field sizes did not change very much (about 35%—Figure 4C, compared to a 50% change in firing rates—Figure 3A, and only 20% when fields with no spikes are not included). To check for stability in the locations of place fields, we analyzed the center of mass (COM) of each field on each lap. The average COM of the fields shifted in the direction opposite to the direction of running, as has been observed previously (Mehta et al., 1997), but no other shifting of individual fields was observed (average COM shift from first to last lap was 4.6 ± 12.6 cm, SEM = 0.83; Figure 4D). Interestingly, the experience-dependent backwards COM shift was observed both in the direction in which the field was becoming stronger, as well as in the direction in which the field was becoming weaker. The COM shift was observed for both CA3 and CA1 cells on day 1, and also observed on days 2 and 3 in the preferred firing direction of CA1 cells, but not CA3 cells (similar to previous data of Lee et al., 2004).

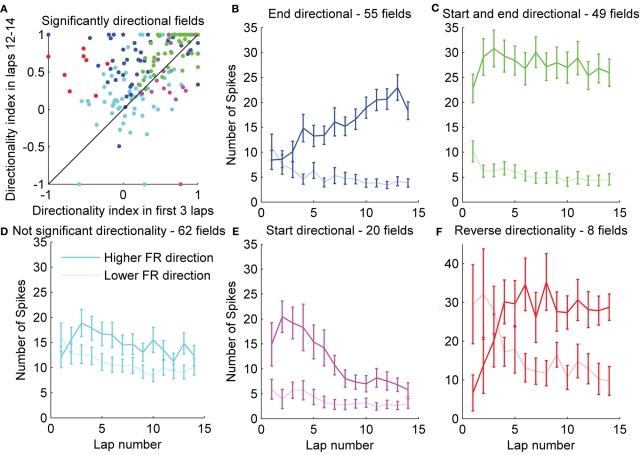
To understand how individual fields changed as the rat gained experience in the environment, we plotted the DI during the first three laps versus the DI during the last three laps for each individual field (Figure 5A). This plot shows that while, on average, the DI increased with lap number, individual fields exhibited a wide range of directionality indices both at the start of exposure to the environment as well as after repeated runs. Consistent with the average results, many fields showed a substantial increase in DI during the behavior session, while many fewer fields showed a decrease in DI. To check the significance of the DI for each individual field, we calculated the chi square statistic comparing the number of spikes in each running direction for each field, both in the first three laps, and in the last three laps. Of the 194 total fields expressed on day 1, 77 showed significantly directional firing during laps 1–3, and 111 showed significant directionality during the last three laps. Fifty-six of these showed directional firing both at the beginning and end of the session. Of those 56 fields, 42 showed an increase in DI from the first three to the last three laps. The last 62 fields did not show significant directionality at the beginning or end of the session. Interestingly, of the 77 fields that showed significantly directional firing at the start of the session, eight exhibited a reversal in the preferred firing direction. At the beginning of the session, the firing rate in these eight fields was higher in the direction that became the lower firing rate direction when averaged over the session (the “lower firing rate,” or “non-preferred” direction). By the end of the session, seven of these fields showed a significant directionality in the preferred direction, while one of them did not show significant directionality. We plotted the number of spikes per lap separately for each of five categories of fields: fields that showed directional firing only at the end of the session (Figure 5B, blue), fields that showed directional firing (in the preferred direction) both at the start and end of the session (Figure 5C, green), fields that never showed directional firing (Figure 5D, cyan), fields that showed significant directional firing (in the preferred direction) only at the start of the session (Figure 5E, magenta), and fields that showed significant directional firing in the non-preferred (lower firing rate) direction at the start of the session (Figure 5F, red). Separating the fields into groups that exhibit similar directionality changes during the first session shows that even though different cells exhibit different amounts of directionality throughout the session, there was an average tendency to increase their firing rate in the preferred direction and decrease their firing rate in the non-preferred direction during the first few laps. A substantial number of cells, however, exhibited decreases in firing in the preferred direction or increases in firing in the non-preferred direction while nevertheless increasing overall directionality, due to even greater changes in the opposite direction.

Figure 5.

Remapping in individual fields. (A) To observe the amount of rate remapping exhibited within individual fields, the directionality index during the first three laps was plotted against the directionality index during the last three laps. Significance of the directionality in individual fields was assessed with a χ² test. Fields were classified based on whether they exhibited significant (p < 0.05) directionality at the beginning or end of the session or both, and are color-coded based on this classification. (B–F) For each group of fields, the average firing rates in each running direction are also displayed. Error bars represent standard error of the mean. Additionally, eight fields were identified that showed significant directionality in the non-preferred direction at the beginning of the session.

We addressed the question of whether there may be some form of competition involved in the change in firing rates over the first few laps by assessing whether directionality tended to increase in the direction that was preferred on lap 1. In other words, we tested the hypothesis that initially stronger inputs tended to get stronger while initially weaker ones tended to get weaker. The average directionality during lap 1 was small, but significant (0.12 ± SEM 0.045, t-test: p < 0.05). We computed the signed DI (CW rate – CCW rate)/(CW rate + CCW rate) for each field for laps 1 and 14 on day 1 and performed a regression analysis. There was a weak tendency for directionality to increase in the direction of the initial bias (R² = 0.084, F = 13.1, p < 0.001). This tendency was true even for the three rats that were actually visiting the track for the first time (R² = 0.081, F = 8.05, p < 0.01).

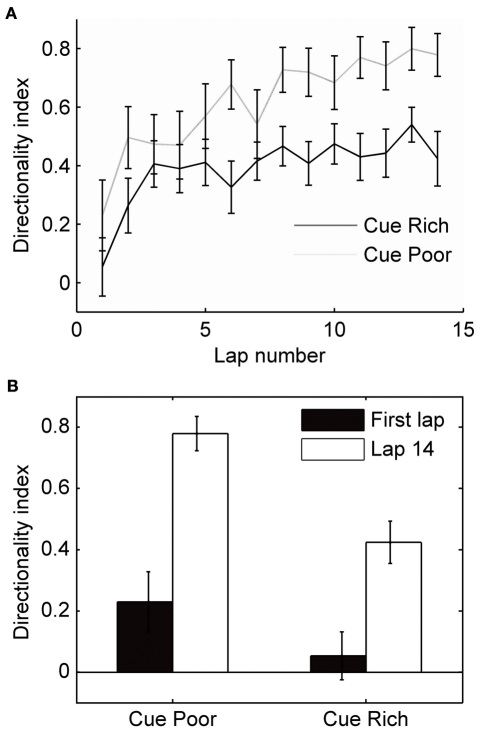
Place cells are known to express more bidirectional place fields when local cues are present on the track (Battaglia et al., 2004). To assess how local cues affected the development of directional firing in our experiment, half of the track had small objects or textures on it, and the other half was bare. During the first lap, fields on either side of the track did not differ significantly (t-test, p = 0.16), but by the end of the first session, fields expressed on the cue poor half of the track showed higher directionality than fields expressed on the half of the track rich in cues (t-test, p < 0.001; Figure 6). An analysis of variance showed a significant effect of cue condition on the DI (F = 4.39, p < 0.05), and a significant interaction between lap number and cue condition (F = 5.93, p < 0.05). Another possible difference between the two halves of the track was the rats' behavior: they ran slower on the cue-rich part of the track, and stepped over and around certain objects and textures in stereotyped ways (running speed through fields on cue-rich part of the track: 18.2 ± 4.56 cm/s, cue-poor part of track: 29.5 ± 7.99 cm/s, t-test: p < 0.001). The specific stereotyped movements and the sequence of movements, however, was different between the two running directions on the cue-rich part of the track, and more similar (involving fewer specialized movements) on the cue-poor part of the track.

Figure 6.

Local cues and the development of directionality. Half of the circular track was enriched with small objects and textures (local cues). (A) The mean directionality index is plotted for fields expressed on the cue-rich and cue-poor halves of the track. (B) During the first lap, field directionality on the cue-rich and cue-poor halves of the track did not differ significantly (t-test, p = 0.16). Over the session, fields on both parts of the track became significantly more directional (paired t-tests, p < 0.01); however, fields on the cue-rich part of the track increased directionality less than fields on the cue-poor side, and directionality was significantly different between regions on the last lap (t-test, p < 0.001).

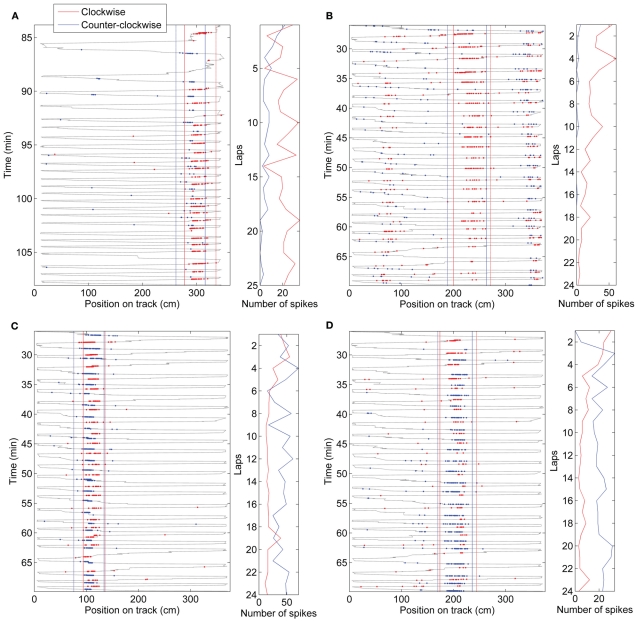
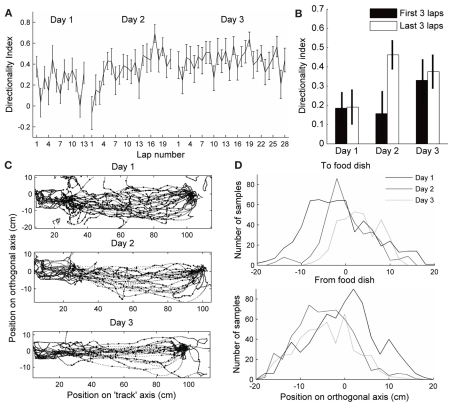
Directional firing of place cells has also been shown when a rat's path was not physically restricted to a track, but the rat was trained to run a specified path in order to receive rewards at known locations (Markus et al., 1995). To determine whether directional firing in this case also develops from initially omni-directional place fields, we trained rats to run back and forth between a home-box location and a food dish on a circular open-field platform. It took the rats 2–4 days to learn the task, but as soon as they were running >20 laps, we analyzed the directionality of their place fields. On the first day the rats ran more than 20 laps, the DI of the fields was low and did not significantly change during the session (Figure 7A). The day after that, however, the DI started low and increased by the end of the session (Figure 7A,B; paired t-test between first three laps and last three laps: p < 0.01). The following days the DI started as high as at the end of day 2, and did not change throughout the session. As in the circular track task, the speed of running through a field affected the number of spikes fired during that pass slightly, but did not affect passes in the two directions differentially. To determine why directionality only developed on the second day of performing the shuttling task, we analyzed the variability of the paths the rats took to the food dish (the paths for one rat are plotted in Figure 7C). The first 13 direct laps were analyzed on each day for each rat. The position was sampled five times per second during traverses to and from the food dish (excluding times the rat was in the box or at the food dish). The position along the axis orthogonal to the most direct path from home box to food dish (the “track” axis) was analyzed. On the first day, the distribution of positions visited by both rats during their runs was wider than on the following days (Brown–Forsythe test for equality of variances: p < 0.001, multiple comparison test shows that day 1 is significantly different from days 2 and 3, but day 3 is not different from day 2). Even though the paths were more stereotyped when directionality developed, and were different between the two running directions, the difference in the paths did not predict the DI, as in the circular track data. These results show that the differential rate remapping in opposite running directions can develop not only on tracks that constrain the animal's trajectory, but also in an open-field environment that is repeatedly traversed along a particular path. In an open-field environment, however, the rate remapping develops only once behavior becomes stereotyped.

Figure 7.

Directionality in an open-field. (A–B) Directionality index in fields expressed on an open-field platform during performance of a shuttle task. Day 1 is the first day each rat ran more than 20 laps (This was actually day 2 in the environment for one rat, and day 4 for the other rat. On this day, rat 3 ran 22 laps, 13 of which were direct, and rat 4 ran 25, 20 of which were direct). The day after that, the rats ran 53 and 21 direct laps, respectively, and the directionality index started low and increased by laps 18–21. On the following day (3), the directionality index started as high as at the end of day 2, and did not change throughout the session. (B) Directionality index during the first three and last three laps of each session. (C) Paths run by one of the rats during the first 13 direct passes between the start box (left) and the food dish (right). The position was sampled five times per second, excluding the times when the rat was in the box or at the food dish, to test for variability (large dots). (D) Distribution of positions along the axis orthogonal to the direct path from food dish to box at the sampled times is plotted for both rats. Paths toward the food dish and away from the food dish are plotted separately. The distribution is wider on day 1 in both directions.

Discussion

The main finding is that, in rats running on a track, the firing of hippocampal place cells is initially bidirectional, and gradually becomes highly unidirectional. This large increase in directional selectivity involves gradual changes in firing rates in either or both running directions, during approximately the first 5–10 laps on the first day of exposure to the track. This effect is almost entirely due to positive and negative changes in direction-specific firing rates of the neurons, and not to changes in the locations in which the neurons fire (i.e., rate remapping). Thus, while retaining information about the allocentric location of the animal, the network gradually differentiates the direction in which it is traveling on the track. This finding clarifies a long standing question of why the firing of hippocampal neurons is different in different directions when the rat is following a specified path (McNaughton et al., 1983; Muller et al., 1994), but the same in each direction when the rat is following random paths (Muller et al., 1987).

The formation of place fields has been hypothesized to depend on one of two separate mechanisms: learning of the sensory details of the environment to construct a map and triangulate one's location in it, or a continuous updating of one's movement trajectory to calculate allocentric position in the environment (path integration), or some combination of the two mechanisms. Models relying on the first mechanism rely on the learning of associations between place cells and their sensory inputs in order to form non-directionally specific place fields. For example, Sharp (1991) modeled a network with sensory inputs relating to the egocentric distance and direction of landmarks projecting to entorhinal and then hippocampal cells, and used competitive learning to establish place fields. A prediction of this model was that place fields would initially be directional, but become direction-independent after exploration in multiple directions. Because exploration was restricted to two directions on a track, place fields on a track would never become omni-directional in this model. Our data, however, show a pattern opposite to that predicted by this model; place fields are initially omni-directional, and increase their direction-specificity with experience. The current findings are more consistent with models that rely on some form of path integration to determine the initial location of place fields.

The assertion that path integration determines the formation of place fields is well supported with previous experimental evidence (reviewed in McNaughton et al., 1996, 2006). For example, symmetry of sensory cues in an environment does not result in symmetrical place cell firing (Sharp et al., 1990) and identical sensory environments located at 180° rotated orientations (Fuhs et al., 2005), or in different rooms (Leutgeb et al., 2005) result in global remapping of place representations. Further, place fields do not change location when lights are turned on or off (O'Keefe and Speakman, 1987; Quirk et al., 1990; Markus et al., 1994). The inhibition (Kentros et al., 1998) or deficiency (Barnes et al., 1997) of LTP does not disrupt the formation of place fields, but does disrupt the recall of place cell associations with previously visited environments. Global remapping is instantaneous when a large mismatch between sensory cues and vestibular information occurs (Knierim et al., 1998), as is place field realignment to moved landmarks (Gothard et al., 1996a), further supporting that learning is not necessary for the establishment of novel or changed place cell representations.

In the framework of path integration models, earlier hypotheses to account for directionality along restricted paths involved a switch of “reference frames” or maps (now referred to as global remapping) at the arm ends; however, attempts to observe the predicted complete discontinuity in firing patterns at arm-ends were generally unsuccessful (Redish et al., 2000). The symmetrical firing observed during the first traversal of a path, is consistent with typical, non-directional firing during random foraging behavior, and also with the evidence that the selection of which hippocampal neurons are able to fire at a given location is determined on the basis of path integration rather than exteroceptive cues (presumably by inputs from the medial entorhinal cortex). When the animal travels the same route multiple times, however, it appears that the firing of hippocampal cells gradually becomes conjunctive for the path integrator coordinates and the direction-specific “local view” (McNaughton et al., 1991).

The most plausible source of external landmark information to the hippocampus proper is via the lateral entorhinal cortex (LEC) (Burwell and Amaral, 1998; Si and Treves, 2009; Renno-Costa et al., 2010; Deshmukh and Knierim, 2011). LEC projects to the outer portions of the dendrites of DG and CA3 uniformly along the transverse axis of hippocampus, and to the distal (i.e., nearest to subiculum) CA1 cells. We observed strong increases in directional tuning in both CA3 and CA1 (including the cells located in proximal CA1, which only get direct inputs from MEC and CA3), raising the possibility that the directionality increase in CA1 is largely driven by changes in CA3 itself or in Schaffer collateral synapses.

At present, one can only speculate about the possible mechanisms of the increased directionality. The data appear to be generally compatible with the observation that LEC inputs are capable of bidirectional weight changes (LTP/LTD; McNaughton et al., 1978; Abraham and Goddard, 1983) and support the hypothesis that the LEC to CA3 (and/or DG) connections which are active in a given direction either increase or decrease according to some form of competition. Plausibly, the initial mean weights of synapses driven by the novel cues, being drawn effectively at random from an existing weight distribution, would be approximately equal in the two directions (central limit theorem). Whether the mean weights would increase or decrease might depend on some form of competition (e.g., BCM rule), by which inputs causing strong activation are strengthened whereas those causing weaker activation are weakened. We did observe a slight tendency for directionality to increase in the direction of initial preference, but it accounted for only 8% of the directionality variance by the end of session 1. It is also possible that competition is influenced by the timing of inhibitory inputs from interneurons driven at short-latency by other pyramidal cells (Csicsvari et al., 1998; Marshall et al., 2002; Maurer et al., 2006). In addition, the firing rates of some hippocampal interneurons are strongly modulated by novelty (Wilson and McNaughton, 1993; Nitz and McNaughton, 2004), which may have an important impact on plasticity over the first few laps. In any case, if the magnitude and direction of weight change is a random variable that is correlated over the active population of inputs onto a given hippocampal cell for a given running direction, then the firing in opposite directions would tend to diverge, resulting in increased directional bias.

On average, there was about a 50% increase or decrease in firing rate over time in a given direction (Figure 4A); however, there were cases of cells either starting out or ending up with zero spikes in one direction. If the observed changes in firing are indeed due to changes in LEC synaptic efficacy, the complete lack of firing in one direction implies that, at least in some cells, MEC inputs alone are not sufficient to drive spiking. Since MEC inputs are also known to exhibit plasticity, however, it is also possible that both sets of inputs may undergo experience-dependent changes. The effect of local cues on the track, however, which would likely reduce the net difference in external input in the two directions, appears to indicate that the main changes are driven by external inputs.

Other studies have shown that rate remapping occurs when the behavioral goals or context, or internal state of the animal changes (e.g., Frank et al., 2000; Wood et al., 2000; Bower et al., 2005). By teaching the rats a shuttling task, we modified their behavioral goals. This change in behavioral context could explain why remapping occurred in the same environment when the task changed from foraging for randomly placed rewards and running between predictable reward locations (Markus et al., 1995). In our results, this rate remapping didn't occur until the task was so well learned that it was performed stereotypically. This indicates that the development of directionality in the hippocampus does not drive the change in behavioral strategy; instead it may be driven by the shift to a different behavioral state. Some of the studies of rate remapping at identical locations during running toward different goals have been interpreted to mean that mnemonic coding, when it is task-relevant, exists in the hippocampus in addition to spatial coding (Berke et al., 2009). Another interpretation, based on our results, is that the “context” encoded by the hippocampus can include the particular trajectory being traversed, if traversal of the trajectories becomes highly stereotyped. Studies of the initial place cell activity in these tasks should be performed to differentiate between these two hypotheses. If the rate remapping occurs after the task is well learned, it would suggest that task demands, including goal locations, are actually learned by a different structure, such as the striatum, and remapping in the hippocampus is driven later by input relating to the task context. Some findings support this second hypothesis, including that Berke et al. (2009) did not see rate remapping in the initial learning trials of their cued goal maze task, even though in those trials the rat was using its prior positions to plan a future route. Additionally, rate remapping of overlapping positions in a sequence task does not occur when the overlapping parts of the trajectories include more than one arm (Lenck-Santini et al., 2001; Bower et al., 2005), and is not necessary for a rat to learn complex sequences (Bower et al., 2005).

Mehta et al. (1997) reported an experience-dependent place field expansion in CA1, with a COM shift in the direction opposite the direction of travel, when rats ran unidirectionally around a track. This effect was subsequently shown to occur also in CA3, in a more long lasting form (Lee et al., 2004) and to be dependent (at least in CA1) on NMDA receptor function (Ekstrom et al., 2001). The accepted view of the mechanism of this experience-dependent expansion and shift is that it reflects the development of what Hebb (1949) referred to as a “phase sequence.” Synapses from cells that fire earlier in a sequence onto cells firing later become asymmetrically strengthened through spike-timing dependent LTP. In their discussion, Mehta et al. (1997) commented: “A natural question is whether the observed asymmetry would cancel out if the rat ran repeatedly back and forth along a route in both directions. It turns out that this experiment is not possible because, under such circumstances, the hippocampus encodes the forward and return journeys using different sets of place cells.” The present results show that this conjecture was incorrect; the forward and return journeys apparently are encoded by the same set of place cells, but with substantially direction-dependent firing rates, and we did observe a COM shift in both the preferred and the non-preferred directions, on the first day. The fact that field expansion in both directions didn't cancel out the asymmetric COM shift, could be explained by local feedback inhibition, an after-hyperpolarizing current, or another form of depression in each place cell that does not allow a place cell that has recently fired to be activated by connections from other currently active place cells. Another possible implication of this result is that the synapses that mediate rate remapping are not the same as the synapses that mediate the place field shift. Rate remapping typically resulted in fewer spikes fired in the non-preferred direction, suggesting a synaptic depression, yet the field shift is generally attributed to synaptic enhancement.

On the second and third days on the track, place field shift occurred only in CA1 cells, and only in the preferred direction, while directionality increased only slightly, and in both CA1 and CA3 cells. The fact that place field expansion does not occur in CA3 on later days is consistent with previous results (Lee et al., 2004) which suggest that the underlying plasticity is more persistent in CA3 than CA1. A possible explanation for the lack of expansion in the non-preferred direction in CA1 on days 2 and 3 may be that there was insufficient depolarization on the cells to induce LTP in the feed-forward synapses from CA3. Of course, the foregoing proposals are speculative. Understanding the specific mechanisms involved in these phenomena await further study.

In summary, during the first few traverses of a fixed route in space, place cell activity is almost entirely determined by allocentric position; later the activity becomes modulated by other factors, without significantly affecting the position dependence (rate remapping). The shift is likely due to sensory information at a given position, but could also be partially driven by internal state variables such as memory or goals, or the behavior of the animal at particular locations. We presented evidence that directionality does not develop until behavior becomes stereotyped, suggesting that the performance of a specific task in an environment contributes to changes in place cell activity. Both sensory and motor information makes its way into the hippocampus, in a highly processed form, however. Recordings from the input structures to the hippocampus (especially MEC and LEC) during performance of directional tasks in a novel environment are needed to elucidate what drives the development of directionality of place cells.

Conflict of interest statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.