Paradoxical Physiological Transitions from Aging to Late Life in Drosophila

Abstract

In a variety of organisms, adulthood is divided into aging and late life, where aging is a period of exponentially increasing mortality rates and late life is a period of roughly plateaued mortality rates. In this study we used ∼57,600 Drosophila melanogaster from six replicate populations to examine the physiological transitions from aging to late life in four functional characters that decline during aging: desiccation resistance, starvation resistance, time spent in motion, and negative geotaxis. Time spent in motion and desiccation resistance declined less quickly in late life compared to their patterns of decline during aging. Negative geotaxis declined at a faster rate in late life compared to its rate of decline during aging. These results yield two key findings: (1) Late-life physiology is distinct from the physiology of aging, in that there is not simply a continuation of the physiological trends which characterize aging; and (2) late life physiology is complex, in that physiological characters vary with respect to their stabilization, deceleration, or acceleration in the transition from aging to late life. These findings imply that a correct understanding of adulthood requires identifying and appropriately characterizing physiology during properly delimited late-life periods as well as aging periods.

Introduction

Age-specific mortality rates in humans, fruit flies, and other organisms increase exponentially during early adulthood, but then sometimes decelerate and plateau at advanced adult ages.^1–7 (For review, see ref. 8). The initially exponential increase in mortality rates, often modeled by Gompertz equations,⁹ defines the “aging” period of adulthood.^10,11 At late adult ages, not only do mortality rates decelerate and no longer follow the Gompertz equation, fecundity deterioration also decelerates and approaches a plateau at later ages.¹² Therefore, we have proposed that there are two demographically distinct periods of adulthood, namely aging and late life.^13,14 The deceleration or plateauing of mortality rates at late adult ages implies that the early-adult, sustained, age-dependent deterioration of age-specific fitness components, which is defined as aging by evolutionary biologists (e.g., ref. 11), can slow or stop in late adulthood.

The phenomenon of mortality rate plateaus in late life has been primarily, although not exclusively, explained by two main types of theories—lifelong demographic heterogeneity theories and evolutionary theories based on the force of natural selection (reviewed in refs. 14 and 15). In lifelong heterogeneity theories, cohorts are modeled as collections of subsidiary groups, each with its own characteristic Gompertzian function of accelerating mortality rates.^16,17 In these lifelong heterogeneity theories, hypothetical individuals that are less robust throughout life are expected to die off at earlier ages, compared to hypothetical individuals that are more robust throughout life. Therefore, lifelong heterogeneity theories imply that, at very late chronological ages, individuals with life-long superiority in robustness should be present in larger numbers than more frail individuals. If this lifelong heterogeneity is far more extreme than any that has yet to be observed in a naturally configured population, it could then result in a slowing of demographic mortality rates at late ages.^14,16–18

One major scientific problem with lifelong heterogeneity theories is that the robustness character that these theories rely on is unspecified, allowing for infinite variants of the theory specifically devised to fit any particular set of experimental data (for review, see ref. 15). In addition, experiments have shown that mortality plateaus persist, even when genetic and environmental variations are reduced or eliminated.^3,19,20 For example, experiments with highly inbred lines of Drosophila melanogaster have shown that genetic variation is not required for mortality plateaus.^3,19 Furthermore, Khazaeli et al.²⁰ have shown that mortality plateaus persist even when preadult heterogeneity among individuals is significantly reduced for highly inbred Drosophila cohorts. Numerical analysis of large-scale changes in the environment of adult Drosophila has shown that environmental effects are unlikely to generate enough lifelong heterogeneity to explain mortality plateaus.^14,21 Additionally, lifelong heterogeneity theories require strong positive correlations between survival probabilities among adult ages; there is evidence that such correlations do not generally exist (for review, see refs. 11, 14, and 22).

Female fecundity is another life history character that undergoes a pronounced deceleration at late ages.^12,23 These late-life fecundity plateaus are not as readily explained by lifelong heterogeneity theories.²⁴ It is conceivable that flies that are capable of surviving into late life have low, stable fecundities compared to flies that die before reaching late life. This possibility is based on the assumption of trade-offs between reproduction and mortality. But such trade-offs do not always occur, nor do they always have the same form when they do occur.^25–27 Finally, and perhaps least equivocally, Rauser et al.²⁴ found that late-life fecundity deceleration also occurs among individual females, and they further found that the fecundity plateaus of individual females could not be predicted by any type of lifelong heterogeneity model.

Alternative evolutionary theories for late life are based on the forces of natural selection. In 1966, Hamilton²⁸ derived the result that the force of natural selection acting on mortality is given by s(x)/T, where x is chronological age and T is a measure of generation length. The function s at age x is given by

(1)

where r is the Malthusian parameter, or the growth rate of the population, associated with the specified l(y) survivorship and m(y) fecundity functions. The s(x) function scales according to the impact on fitness of a change in an individual's future reproduction, after age x, arising from a change in survival probability at that age. Before the first age of reproduction, s is always equal to 1; once reproduction has ended, and for all subsequent ages, s is equal to 0; during the reproductive period, s(x) progressively falls, causing a loss of adaptation with age over this range of ages (for review, see ref. 29). Thus, early in life, before the first age of reproduction in a population, this scaling function implies that mortality rates are not expected to change systematically with age. Similarly, when the force of natural selection acting on mortality rates converges with zero late in adulthood, mortality rates should stabilize, albeit at high levels, because natural selection will no longer discriminate among genetic effects acting at these late ages, and this pattern has been produced in explicit numerical models of the evolutionary process.^14,30 Criticisms of such numerical simulations have suggested that their observed plateaus in mortality rates could be transient states under the assumed mutation model^31,32; but Mueller et al.¹⁴ have provided formal counter-examples showing that such criticisms are not generally valid. There are other evolutionary models for mortality deceleration (e.g., refs. 33 and 34; reviewed in ref. 35), with some differences among them. More theoretical work needs to be done to place evolutionary explanations of late life on firmer theoretical foundations, although some significant advances have recently been made.¹⁴

But more importantly for scientists, the entire group of evolutionary models for mortality deceleration^33,34 based on the Hamilton forces of natural selection are experimentally falsifiable. Predictions of the Hamiltonian theories of late life have been corroborated experimentally in heavily replicated laboratory studies (e.g., refs. 7 and 36; reviewed in ref. 15), unlike the poor record of experimental corroboration for lifelong heterogeneity theories, reviewed above and elsewhere (e.g., ref. 14). A critical distinction between lifelong heterogeneity theories of late life and evolutionary theories of late life is that, in the lifelong heterogeneity theories, all individuals in a population are assumed to continue aging until death and the late-life mortality plateau is explained as an aggregate demographic effect. This is in contrast to the evolutionary theories of late life, in which it is possible for individuals in a population to cease aging at very late adult ages. In these evolutionary theories, late life is a distinct third phase in the individual's life history that occurs after development and aging; it is not just a demographic effect.

Because age-specific mortality and fecundity stabilize in late life (e.g., refs. 2 and 24), it is conceivable that the trajectories of physiological characteristics that underlie fitness may also be different after the transition from aging to late life. In this study, we tested for differences in physiology between aging and late life using populations of Drosophila melanogaster.

We distinguish between three broad hypotheses regarding late-life physiology. (1) Deterioration in all functional characters continues at the same rate through both aging and late life, without deceleration or interruption. This result would provide evidence against the evolutionary theories of late life discussed above. (2) Late life generally converges on a state of “quiescence,” in which all functional characters stabilize, much as mortality and fecundity characters do. This type of result is intuitively in keeping with both the lifelong heterogeneity theories and the evolutionary theories. (3) Late life is complex, such that functional characters vary with respect to their continued deterioration, stabilization, or even partial recovery. Thus, the present experiments put the evolutionary theories of late life at risk of falsification; as we explain elsewhere, it is difficult to falsify the indefinitely elastic lifelong heterogeneity theories using experiments of the type that we report here.¹⁴

Methods

Study system

Six replicate populations of D. melanogaster were tested for differences between the aging and late-life periods of adulthood. The populations used were the IV population that was collected from the wild by P.T. Ives³⁷ and five populations that were derived from the IV population but maintained under the same exact conditions as the ancestral IV population, called B₁, B₂, B₃, B₄ and B₅.^38,39 All six of these replicate populations were maintained in the Rose Laboratory on 14-day generation cycles in 24 hr of light at ∼25°C. The five B populations did not differ from the IV population in how they were maintained; they only differed in that they have been genetically isolated from each other since 1980. The six experimental cohorts were studied at different times of the year, in two different laboratories, from January, 2008, to September, 2008.

Mortality assays

We used an average of 2,100 flies per replicate population in the mortality assays. Of these flies, on average the first 68% of deaths were used to characterize the mortality pattern for each replicate population. Flies were aged in cages at densities of ∼800 flies per cage with mixed sexes. The food in the cages was replaced with fresh food every other day, with mortality recorded on Mondays, Wednesdays, and Fridays.

Functional assays

The physiological characters that we studied are demonstrably related to age-specific mortality and age-specific reproduction. Selection on life-history characters strongly affects these physiological characters; and when selection is imposed on some of these physiological characters, life-history characters respond strongly.^40–43 The specific characters were: Desiccation resistance, starvation resistance, time spent in spontaneous motion, and negative geotaxis. For each replicate population, approximately 7,500 flies, half males and half females, were maintained in cages under identical conditions to the mortality cages (densities of 800 flies/cage, fresh food every other day, dead flies removed every other day, and equal levels of CO₂ exposure). At each assay age, sample flies were removed at random from the cages using light CO₂ anesthesia. Forty-eight flies per sex per population were removed from the cages at random three times each week. Twenty-four of these flies were used in the desiccation resistance assays. The other 24 flies were used in the starvation resistance, time spent in motion, and negative geotaxis assays (each fly was tested for all three characters). These assayed flies were not returned to their cohort's population cages. The protocols for the individual assays follow.

Desiccation resistance

Flies were placed in 8-dram glass vials in groups of 4 males or 4 females (never mixed). A short foam-plastic plug was used to enclose the flies in the bottom of the vial. Three grams of Drierite desiccant was then added on top of the sponge, and the vial was sealed with two layers of parafilm to keep moisture from entering the vial. The vials were checked every hour and the number of dead flies was recorded. Death was inferred from a fly's lack of movement on mechanical provocation.

Time spent in motion

This assay tests for a fly's spontaneous locomotor activity in a set time interval. Flies were lightly anesthetized using carbon dioxide. Individual flies were placed in 8-dram glass vials and confined to the bottom 1 cm of the vial using a plug. The vial was inverted so that the fly was clearly visible when viewed from above. Each fly was given 10 min to fully recover from the carbon dioxide anesthesia. Then a stopwatch was used to time the spontaneous movement of each fly in a 2-min time interval. To improve the accuracy of the measured time in motion, each fly was tested twice back-to-back by two separate experimenters with about 30 sec between measurements. The two measurements were averaged to give the time in motion for each fly.

Negative geotaxis

For the same flies that were used in the time in motion assay, the sponge in the vial was moved to the top of the vial, allowing 8 cm of space from the bottom of the vial. The vial was tapped onto the bench to cause the fly to fall to the bottom of the vial. A stopwatch was started when each fly was at the bottom of the vial. The percentage of flies that reached the top of the vial in an allotted 1-min time interval was recorded. All of the flies that made it to the top did so in under 15 sec. The negative geotaxis assay measures the fly's innate escape response. Similar negative geotaxis assays have been used previously in other laboratories (e.g., refs. 43 and 44).

Starvation resistance

For the same flies that were used in the time in motion and negative geotaxis assays, the sponge at the top of the vial was pushed down into the vial so that an absorbent rayon ball could be placed above the sponge. Next 5 mL of distilled water was added to the rayon ball, and the vial was covered with two layers of parafilm and inverted. Deaths from starvation were recorded every 4 hr.

Data analysis

Our focus on late life is motivated by the Hamiltonian evolutionary theory of late life.^14,30 Under that theory, mortality is expected to increase in an approximately exponential fashion through the first part of the adult life span and then level off at some advanced age. The age at which this leveling of mortality rates occurs is, under this evolutionary theory, the start of late life. Thus, our primary interest in cohort mortality data is not to arrive at the best fitting model but rather to provide an estimate of the onset of late-life.

The simplest model that captures the essential features of the evolutionary model of late life is a two-stage Gompertz function. If we let u(x) be the instantaneous mortality at age x, then the functional form of the two-stage Gompertz is,

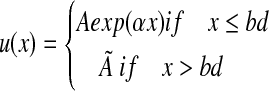(2)

The parameter bd of the two-stage Gompertz (Equation [2]) is called the breakday, and its value is used as an estimate of the boundary between the aging and late-life phases of life.

When age-specific mortality over a fixed period of time obeys a binomial distribution, our previous research has shown that the parameters of Equation (2) are best estimated by a maximum likelihood technique.⁴⁵ There are several different ways maximum likelihood may be implemented for the estimation of parameters in Equation (2). A method we proposed previously,⁴⁵ and refer to here as the “deaths-per-census-period” method, uses the total number of deaths that occur between each census period. Mueller et al.⁴⁵ pointed out that because models like Equation (2) are continuous-time models, but deaths are recorded over discrete intervals, there are some key advantages to the deaths-per-census-period method. One of these is that the number of deaths is known exactly, whereas the age-at-death is only known approximately.

A second technique, called here the “age-at-death” method, uses the age-at-death of each individual in a cohort to estimate the maximum likelihood function.⁴⁶ In fact, a software program called WinModest⁴⁶ is used quite widely to implement the age-at-death method. While Pletcher⁴⁶ recognizes that transforming experimental survival data to mortality or survival rates can result in biased parameter estimates, he suggests this is not the case if one uses the age-at-death method. But, as first pointed out by Mueller et al.,⁴⁵ using the age-at-death method is fraught with danger, because it is not known exactly or with what level of inaccuracy age-at-death will be a function of the time between census points, or for that matter a function of the overall longevity of the organism.

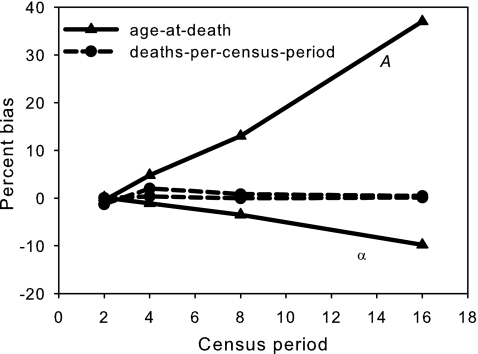
To illustrate the differences between these two maximum likelihood techniques, we conducted a simple computer simulation using the Gompertz equation: u(x)=Aexp(αx). We generated 100 independent cohorts of 1,000 individuals. The age-at-death of each individual was determined by the inverse transform method⁴⁷ using the Gompertz equation with a fixed set of parameter values (see legend to Fig. 1). These ages-at-death were then rounded off to the next census date to mimic the type of data actually used in a cohort-survival experiment, like the ones conducted in this paper. With these raw data, we then used both the deaths-per-census-period and the age-at-death maximum likelihood procedures to estimate the demographic model parameters. From the 100 simulations, we then determined the level of bias for each of the two estimated Gompertz parameters, measured as: (Mean parameter estimate) − (true parameter value). As anticipated in Mueller et al.,⁴⁵ the bias of the age-at-death method gets worse the longer the census period. Accordingly, we conclude the age-at-death technique is unacceptable unless census intervals are very short relative to average life span, and we have only used deaths per census period in the demographic analysis of our experimental data. However, as we discuss next, implementation of the deaths-per-census-period maximum likelihood technique is not always straightforward.

FIG. 1.

Estimation bias in the two Gompertz model parameters, A and α. One hundred independent cohorts of 1,000 individuals were generated to estimate this bias. Age-at-death for each individual was determined by the inverse transform method⁴⁷ and the Gompertz equation with parameter values A=0.00096, and α=0.099. To mimic a survival experiment, we assumed there was a census of dead individuals take every 2, 4, 8, or 16 days. For the age-at-death maximum likelihood procedure, dead individuals were assumed to have died at the midpoint of the census interval of their death. If these 1000 deaths were d₁, d₂,…, d₁₀₀₀, then the likelihood function for the age-at-death method was, 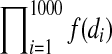, where f(x) is the density function of the Gompertz equation, 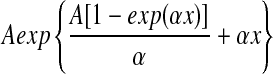Let n₁, n₂, ., n_k be the number of deaths at each of k-census periods and S₁, S₂,…, S_k be the number of live individuals at the start of each census period. The age of individuals at the start of census period j is t_j. Then the maximum likelihood function for the number-of-deaths-per-census period method is, 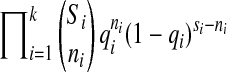where q_i is the Gompertz-predicted probability of dying during census period i, which equals 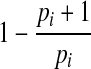and . 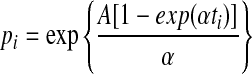The age-at-death estimates are evidently much more biased, particularly with longer census periods.

If individuals of the same age vary in the chance of dying, or if there are sources of variability in addition to binomial sampling effects, then a deaths-per-census-period maximum likelihood technique that assumes a binomial distribution of mortality rates in each census period might be wrong. Although the evolutionary theory of late life assumes that the forces of natural selection and drift are primarily responsible for late life plateaus, this theory does not require that there be no variation in mortality rates between individuals. If there is variation in mortality rates due to genetic differences between individuals or environmental differences, then there might be a range of probabilities of death. This could be described by distributions like, say, a beta-binomial. However, in addition to the mean probability of death, the beta-binomial also has two shape parameters that would have to be estimated. As individuals die, the parameters of this beta-binomial would be changing, making the successful estimation of the extra parameters of the beta-binomial very difficult. In light of these difficulties then, it might be more appropriate to use another estimation procedure, like least-squares regression. In addition to the issue of which method should be used to estimate the parameters of the two-stage Gompertz, there is a second concern with regard to the level at which these estimates should take place. It is possible to provide separate estimates for each sex and each population. However, any differences in the estimated breakdays, dividing aging and late life, between populations may not be meaningful given their similar evolutionary history. Pooling all populations, but keeping the sexes separate, also results in a larger sample, which is better for estimating mortality patterns late in life.

One would hope that the results would not vary substantially among these different types of analyses, but this cannot be assumed in advance. Accordingly, we have used two very different statistical approaches in our data analysis, to evade potential statistical artifacts arising from just one. The first data analysis pooled all individuals of each sex from the six populations. We then used the deaths-per-census-period maximum likelihood technique to estimate the breakday for females and males. In the second data analysis, we estimated the breakday for each sex and population with the regression technique. In both data analyses, the estimated breakdays were used to classify the different age ranges as either “aging” or “late life.” We should note that both methods could yield an estimated breakday that is at or after the last census date, should a simple Gompertz model be better than the two-stage Gompertz model of equation.²

With the data analysis based on the first statistical strategy, the parameters, A, α, 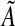, and bd were estimated by maximum likelihood.⁴⁵ The numerical routines that search for this maximum may converge on a local maximum or fail to converge if the maximum is on a relatively flat region of parameter space. Accordingly, we searched a grid of 4,560 points in parameter space to see if there was a parameter combination with greater likelihood than our optimization function found. Our second data analysis estimated the parameters, A, α, 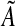, and bd by weighted nonlinear regression using the nls procedure of the R statistical program.⁴⁸

The maximum likelihood analysis of mortality yielded a male cohort breakday that was beyond the ages we tested. Consequently, our statistical comparisons of the physiological patterns in the aging and late-life phases of life were only done for females in our first analysis. The regression analysis gave usable breakdays for both males and females, so the tests of physiological characteristics split between aging and late-life phases using regression analysis took sex into account.

For the analysis of female physiological data based on a maximum-likelihood separation of aging and late life, the physiological data were analyzed using the linear mixed-effects package, lme in R. For each physiological measurement, a vector of independent variables was recorded. These include the fly's age (i=2, 5, 7,…max.age), stage (j=0 (aging), 1 (late life), population (k=IV, B₁, B₂,…, B₅), and vial (l=1, 2,…, max.vial). With this notation, we modeled each physiological measurement with the following linear model,

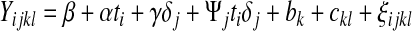(3)

In Equation (3), the main effects of age and stage are measured by α and γ, respectively. The effect of stage on the slope is measured by Ψ. δ_x is the indicator random variable that equals 1 if x=1 and 0 otherwise. There are three sources of random variation in Equation (2): Variation due to population is measured by b_k, vials within populations by c_kl, and residual variation by ξ_ijkl. These three sources of variation are assumed to be normally distributed independent random variables with a mean of 0, but different variances as estimated from the observations. Our key statistical test is to compare the age-dependent slope in the aging phase, α, to the slope in the late life phase, α+Ψ.

For the analysis of female and male physiological data based on a regression-partition of aging and late life, the physiological data were analyzed using the linear mixed-effects package, lme in R. For each physiological measurement, a vector of independent variables was recorded. These include the fly's age (i=2, 5, 7,…max.age), sex [j=0 (female) or 1 (male)], stage [k=0 (aging), 1 (late life)], population (l=IV, B₁, B₂,…, B₅), and vial (m=1, 2,…, max.vial). With this notation, we modeled each physiological measurement with the following linear model,

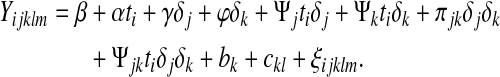(4)

In Equation (4), the main effects of age, sex, and stage are measured by α, γ, and φ, respectively. The effect of sex on the slope is measured by Ψ_j. The effect of stage on the slope is measured by Ψ_k. The interaction of sex and phase on the slope is measured by Ψ_jk. δ_x is the indicator random variable that equals 1 if x=1 and 0 otherwise. There are three sources of random variation in Equation (4): Variation due to population is measured by b_k, vials within populations c_kl, and residual variation ξ_ijklm. These three sources of variation are assumed to be normally distributed independent random variables with a mean of 0, but different variances as estimated from the observations. Our key statistical test in this case is to compare the age-dependent slope in the aging phase, which is α for females and α+Psi;_j for males, to the slope in the late life phase, which is α+Ψ_k for females and α+Ψ_j+Ψ_k+Ψ_jk for males. In other words, we determine if the difference in these slopes is significantly different from 0. The degrees of freedom for these test statistics were equal to the number of observations minus the number of estimated parameters. These were large, as the number of observations for the physiological experiments was between 2,239 and 2,807.

Results

Maximum likelihood analysis

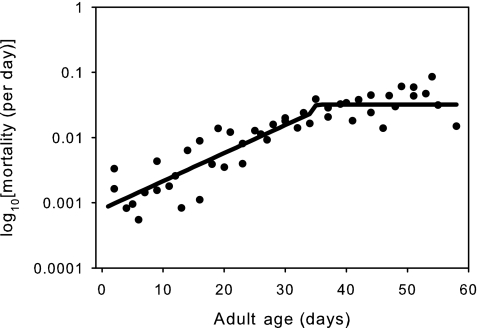
Our first analysis was based on estimates of the parameters of the two-stage Gomperz equation obtained from maximum likelihood. For females, as shown in Fig. 2, the estimated plateau in mortality starts at day 34, the breakday separating aging from late life, whereas for males the inferred plateau does not start until the last day data was collected for mortality (day 55). Accordingly, we have limited our maximum-likelihood analysis of the physiological traits to females. At the time the male mortality assay was stopped, there were still 1,546 males alive of the original 7,990 or 19% of the male population. We stopped the mortality assay early because we only collected physiological data until day 56 and afterward did not have enough flies to test for physiology. The purpose of this study was to compare physiology between aging and late life, so it would have been meaningless to collect more mortality data when no corresponding physiology data could be obtained.

FIG. 2.

The observed mortality (circles) of females from all six populations. The estimated mortality (line) is from the two-stage Gompertz equation obtained by maximum likelihood estimation using the number of deaths per census period. The estimated mortality plateau starts at 34 days.

For each physiological trait, we fit the linear model of Equation (3) to the female data. Physiological measurements made on or before day 34 were considered to be in the aging phase of life and those after day 34 were relegated to late life. Female flies continue to develop and mature after pupation, which leads to an increase in starvation resistance at early adult ages. This is because female flies continue to grow and increase their starvation resistance in early adulthood, which obscures the effect of aging.⁴⁹ To eliminate the effect of this continued development on our results, we looked at female starvation resistance by removing data from the first four assay ages, which was the period of time when female starvation resistance was increasing with age. The slopes of the age-dependent linear functions for each physiological character before and after the breakday are given in Table 1.

Table 1.

The Slopes before and after the Mortality Breakday (Day 34) for Females and Four Physiological Measurements

Trait	Slope before breakday	Slope after breakday	p
Desiccation resistance	−0.234	−0.106	<10−6
Time in motion	−0.969	−0.240	<10−6
Negative geotaxis	−0.00152	−0.00797	<10−6
Starvation resistance	−0.967	−1.06	0.55

The significance of the difference in these slopes based on a t-test with over 2,000 degrees of freedom is given in the last column.

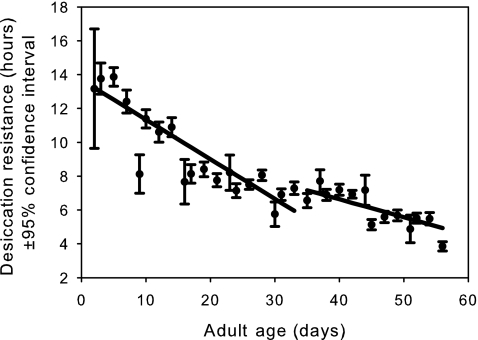
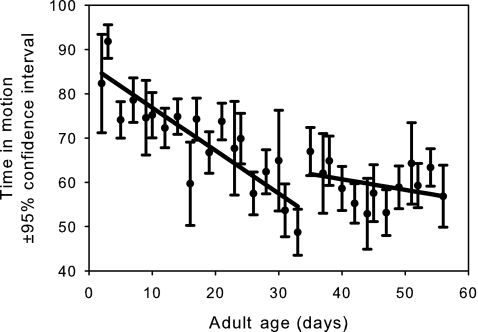
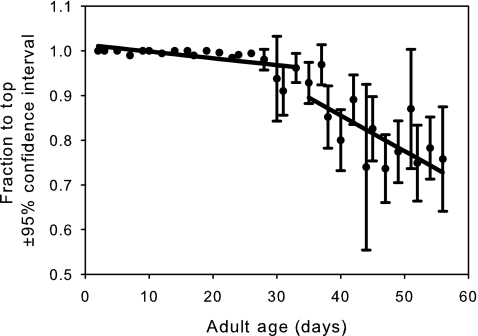
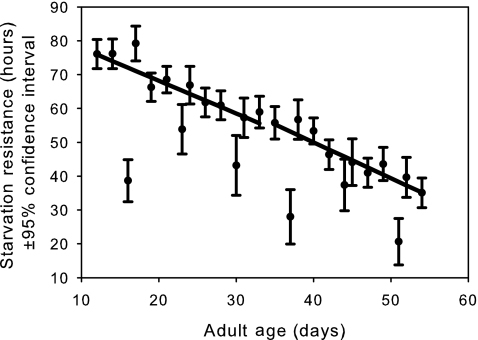
Desiccation resistance (Fig. 3) shows a significant slowing in its age-dependent decline after the maximum likelihood breakday (p<10⁻⁶; Table 1). A similar pattern is observed for time-in-motion (Fig. 4, p<10⁻⁶; Table 1). However, negative geotaxis shows a strikingly different pattern, at least with respect to slope (Fig. 5), which becomes more negative in the late-life phase (p<10⁻⁶; Table 1). This suggests that the late-life flies are probably moving less and hence fewer are making it to the top of the vial in the fixed time interval allotted for this assay. After removing the first four sample points, we see that female starvation resistance shows no significant change in slope before and after the breakday (Fig. 6, p=0.55, Table 1).

FIG. 3.

The mean observed desiccation resistance (circles) with 95% confidence intervals for females from all six populations. The linear age-specific predictions before and after the breakday are shown as solid lines. The slope before the breakday is significantly more negative than the slope after the breakday (p<10⁻⁶).

FIG. 4.

The mean observed time in motion (circles) with 95% confidence intervals for females from all six populations. The linear age-specific predictions before and after the breakday are shown as solid lines. The slope before the breakday is significantly more negative than the slope after the breakday (p<10⁻⁶).

FIG. 5.

The mean observed negative geotaxis (circles) with 95% confidence intervals for females from all six populations. The values are the fraction of the population that have made it to the top of the vial. The linear age-specific predictions before and after the breakday are shown as solid lines. The slope before the breakday is significantly more negative than the slope after the breakday (p<10⁻⁶).

FIG. 6.

The mean observed starvation resistance (circles) with 95% confidence intervals for females from all six populations. The linear age-specific predictions before and after the breakday are shown as solid lines. The slopes before and after the breakday are not significantly different (p=0.55).

Regression analysis

We also estimated the mortality-rate breakdays of each population and sex using nonlinear regression. On the basis of these estimates of when late-life begins, we repeated the analysis of physiological traits using Equation (4). The slopes describing the age-specific change of the four physiological traits (Table 2) in females are the same as those found in our previous maximum-likelihood analysis (Table 1). The males also show the same qualitative patterns as the females for time in motion, desiccation resistance, and negative geotaxis (Table 2). With either estimate of breakday, females show no significant difference in slopes for starvation resistance (p=0.55 in Table 1, and p=0.10 in Table 2), whereas the male starvation resistance data show a significant decrease of slope in late-life (p<10⁻⁶ ; Table 2).

Table 2.

The Slopes before and after the Mortality Breakday for Males and Females and Four Physiological Measurements

Sex	Trait	Slope before	Slope after	p
Female	Desiccation resistance	−0.213	−0.0829	<10−6
	Time in motion	−0.757	0.0489	<10−6
	Negative geotaxis	−0.00201	−0.00956	<10−6
	Starvation resistance	−0.944	−0.830	0.10
Male	Desiccation resistance	−0.0988	−0.0621	<10−6
	Time in motion	−0.787	−0.466	<10−6
	Negative geotaxis	−0.00393	−0.0173	<10−6
	Starvation resistance	−0.326	−0.177	<10−6

The significance of the difference in these slopes based on a t-test with over 2,000 degrees of freedom is given in the last column.

Discussion

Age-specific mortality and fecundity plateau at late adult ages,^{5,6,14,18,24,35,50} defining a period that is sometimes called “late life” [(e.g., ref. 24). The existence of a late-life period at very late ages suggests that functional aging must stop, in aggregate, at these old ages. Therefore, an intuitive expectation might be that physiology should stabilize in late life.

Drapeau et al.⁴ found that the rate of decline in starvation resistance slows in late life in D. melanogaster, but that the decline in desiccation resistance is not affected by the transition from aging to late life. However, their physiological data did not extend very far into late life. Contradicting these results, Nghiem et al.⁵¹ found that desiccation resistance does seem to stop declining in late life. These mixed results demonstrated the need to study what happens to organismal physiology during late life on a larger scale.

In this study, using ∼57,600 D. melanogaster of cohorts derived from six evolutionarily distinct populations, we tested four physiological characteristics that decline during aging^40–43—desiccation resistance, starvation resistance, time spent in motion, and negative geotaxis. We examined the transition of these physiological characters from aging to late life.

As the cohorts demographically transitioned from aging to late life, the qualitative patterns of change in physiology were not the same for all the characters tested. Time spent in motion and desiccation resistance declined at slower rates in late life, a result that conforms to a scenario in which physiology stabilizes in late life.

But the results for negative geotaxis were paradoxical. In negative geotaxis assays, flies are banged to the bottom of a vial, which induces an escape response. Flies then move up the side of the vial using legged-climbing.⁵² Negative geotaxis has been shown to decline with age both when measured as a rate of climbing and when measured as a percentage of flies that make it to the top.^53–55 In contrast to the time in motion and desiccation results, negative geotaxis declined at a faster rate in late life compared to its rate of decline during aging. The importance of this result is that it goes against the general notion that late life should be a period of physiological stabilization. During late life, at least one aspect of functional physiology deteriorates at a faster rate than it does during aging. This is counterintuitive, given that life-history characters deteriorate much less rapidly during late life compared to their deterioration during aging.

Time spent in motion and negative geotaxis are both measures of locomotor behavior in D. melanogaster. Such locomotor behaviors have been shown to decline with age in flies (for review, see refs. 56 and 57). Given that decreased mobility is one of the most common complaints among the elderly,⁵⁸ and that older individuals are sometimes more concerned with improving their mobility than with extending their lives,⁵⁹ studying changes in mobility at late adult ages is of particular importance. In this study, the two measures of locomotor behavior are dependent on mortality in different ways, suggesting that declines in these two measures could result from deterioration in different organ systems. Or these two measures might trade off against each other. It is also possible that the deterioration of at least some functional traits could be independent of mortality patterns (e.g., ref. 60).

The results for the starvation resistance character were more complex. Starvation resistance declined less quickly statistically in late life, compared to its rate of decline during aging, in males. However, in females, starvation resistance did not significantly change in its rate of decline from aging to late life. Age-specific starvation resistance has previously proven a particularly complex character to analyze in adult cohorts (see ref. 39), and this appears to be another example of its complexity.

In summary, our results show that: (1) Late life physiology is distinct from the physiology of aging, in that there is not necessarily a continuation of the physiological trends which characterize aging; and (2) late life physiology is complex in its differences from the physiology of aging, in that different physiological characteristics that deteriorate during aging vary with respect to their stabilization, deceleration, or acceleration in late life.

In the Hamiltonian analysis of aging, any character that underlies an age-specific fitness component that is subject to genetic variation is liable to deterioration during aging as a result of the strongly declining age-specific forces of natural selection shaping survival and reproduction during the first part of adulthood. But in late life, the forces of natural selection are extremely weak and there are no consistent changes in the forces of natural selection acting on age-specific survival or fecundity. Therefore, it makes sense that age-related changes in functional physiology might differ between aging and late-life stages, in light of Hamiltonian reasoning. If all the consistent physiological declines observed during aging continued unremittingly after the transition to demographic late life, then the Hamiltonian theory for late life would be rendered implausible.

However, because Hamiltonian theory only makes clear predictions for individual age-specific mortality and fecundity characters, but not their underlying physiology, it does not make predictions about the specific direction of change for any physiological characteristic in the transition from aging to late life. It is possible then, as Shahrestani et al.¹⁵ already suggested and as found in the present study, that distinct physiological characters might vary in their trajectories during the transition from aging to late life, some continuing to deteriorate at an accelerated or decelerated rate, others stabilizing, and perhaps some even improving with age in late life.

Our results are consistent with Hamiltonian theory, but we should also point out that they are not inconsistent with alternative theories for late-life mortality plateaus, such as the lifelong heterogeneity theories. In the latter theories, because there is no necessary expectation for the relationships between functional physiological characters and hypothesized lifelong differences in demography, a transition between aging and late life produced by extreme lifelong heterogeneity can lead to a wide spectrum of trajectories for physiological characters. In explicit simulations of changes in age-specific physiological characters over the course of adult life, when these simulations assume lifelong heterogeneity for robustness, a variety of patterns can be produced: Reversal of functional aging, alternating waves of increase and decrease in functional physiology, continuing physiological deterioration during late life, accelerating deterioration during late life, and so on.¹⁴ There is extensive evidence against specific versions of lifelong heterogeneity theories (for review, see ref. 14). But the entire class of lifelong heterogeneity theories is difficult to refute in toto. Indeed, what allows lifelong heterogeneity theories to generate a great diversity of possible patterns for the physiological transition from aging to late life is precisely their collective lack of specificity.

Given that the physiology of late life is observably distinct from that of aging, future research on adult physiology should take the late-life period into consideration. A complete understanding of adulthood requires identifying and studying physiology in the late-life period, as a phase that has distinct properties from those of aging. More physiological studies of the present kind are needed, and should be done not just with Drosophila, but also with other model organism cohorts, to better characterize late-life physiology across the spectrum of biological diversity.

Acknowledgments

We thank the dozens of undergraduate researchers in the lab of M.R.R. who were involved in conducting these experiments, especially Andrew Nguyen, Daisy Lankarani, Garen Abedi, Thien-Tuan Tran, Thuy Tran, and Souseh Zamani. This work was supported by a DDIG Grant NSF-DEB-0910362 awarded to P.S. and M.R.R., a GAANN Fellowship awarded to P.S. from the Department of Education, and numerous UCI UROP Fellowships awarded to our undergraduate students.

Author Disclosure Statement

The authors have no financial interests to declare.