Substitution and pooling in crowding

Abstract

Unless we fixate directly on it, it is hard to see an object among other objects. This breakdown in object recognition, called crowding, severely limits peripheral vision. The effect is more severe when objects are more similar. When observers mistake the identity of a target among flanker objects, they often report a flanker. Many have taken these flanker reports as evidence of internal substitution of the target by a flanker. Here, we ask observers to identify a target letter presented in between one similar and one dissimilar flanker letter. Simple substitution takes in only one letter, which is often the target but, by unwitting mistake, is sometimes a flanker. The opposite of substitution is pooling, which takes in more than one letter. Having taken only one letter, the substitution process knows only its identity, not its similarity to the target. Thus, it must report similar and dissimilar flankers equally often. Contrary to this prediction, the similar flanker is reported much more often than the dissimilar flanker, showing that rampant flanker substitution cannot account for most flanker reports. Mixture modeling shows that simple substitution can account for, at most, about half the trials. Pooling and nonpooling (simple substitution) together include all possible models of crowding. When observers are asked to identify a crowded object, at least half of their reports are pooled, based on a combination of information from target and flankers, rather than being based on a single letter.

Electronic supplementary material

The online version of this article (doi:10.3758/s13414-011-0229-0) contains supplementary material.

Introduction

In daily life, visual crowding often prevents recognition of objects in clutter. It is impossible to recognize objects that are too close together, and the critical spacing for recognition grows proportionally with eccentricity (Bouma, 1970; Levi, 2008; Pelli & Tillman, 2008). Crowding wrecks object recognition, but what remains in its wake? Analyzing observers’ mistakes during crowding might elucidate how crowding happens, by revealing how the mistaken report depends on the stimulus. Observers who are asked to identify a crowded target often mistakenly report a flanking object instead (Chastain, 1982; Estes, Allmeyer, & Reder, 1976; Huckauf & Heller, 2002; Krumhansl & Thomas, 1977; Põder & Wagemans, 2007; Strasburger, 2005; Strasburger, Harvey, & Rentschler, 1991; Vul, Hanus, & Kanwisher, 2009; Wolford & Shum, 1980). This basic finding is consistent with two different accounts of crowding: substitution and pooling. In the substitution account, observers merely confuse the locations of the flanker and target objects, perhaps due to positional uncertainty or failure of attentional selection, and the report is based on a single object, from the wrong place (Chastain, 1982; Estes et al., 1976; Huckauf & Heller, 2002; Strasburger, 2005; Strasburger et al., 1991; Vul et al., 2009; Wolford & Shum, 1980). In the pooling account, observers combine features across several objects and sometimes report a flanker, because that (flanker) object is similar to (i.e., shares features with) the pooled result (Dakin, Cass, Greenwood, & Bex, 2010; Greenwood, Bex, & Dakin, 2009; Parkes, Lund, Angelucci, Solomon, & Morgan, 2001; Prinzmetal, 1995; Treisman & Schmidt, 1982; van den Berg, Roerdink, & Cornelissen, 2010; Wolford & Shum, 1980).

Any model of crowding must receive the stimulus as input and produce the appropriate kind of observer response (e.g., a letter or a word). That is a vast space of possible models. Particular models—for example, substitution and pooling—have been carved out of that space. Here, we carefully define pooling to divide the space in two: pooling and nonpooling. Pooling models take input from more than one object and may perform any computation to produce the response. All other crowding models, forming the complement to pooling, are nonpooling. Nonpooling models (which we also call simple or unpooled substitution) take input from only one (or none) of several presented objects and may perform any computation on that input to produce the response. Pooling and nonpooling, together, make up the space of all possible models of crowding.

Intuition may suggest other ways of breaking up this space—for example, whether or not there is migration of objects. However, we do not know how to test that. The particular division we study here allows for strong tests and conclusions that sorely discredit all the unpooled models (to one side of the border) and, thus, recommend the complement: pooling (on the other side of the border). Psychophysical testing of models typically requires a nearly full specification of the model, and, thus, rejects only a tiny part of the model space. We discovered that nonpooling is so strong a condition that it has a recognizable, testable signature in the model behavior, even though we allow the model to perform any computation whatsoever upon the restricted input.

Our division is pooling versus nonpooling. We will show that pooling is needed to model crowding; unpooled substitution is not enough. Unpooled substitution is simple substitution, but there are other, more complicated substitution models whose responses depend on multiple letters, and they are thus pooling models, by our definition. For example, Wolford (1975) and Wolford and Shum (1980) described a model in which the response is sometimes based on a (whole) flanker that replaces the target (i.e., unpooled substitution) and at other times based on a few features of the flanker that have migrated into and combined with the target (feature perturbations) (i.e., pooling). Van den Berg et al. (2010) proposed a feature integration model of crowding based on population codes that exhibits substitution-like behavior—for example, source confusion. This model uses information from all objects and thus, by our definition, is a pooling model, not simple substitution. Our definition of pooling is broad, including any model that uses information from more than one object, and thus includes all the crowding models that average a stimulus parameter (e.g., orientation, position) across multiple objects (Dakin et al., 2010; Greenwood et al., 2009; Parkes et al., 2001; van den Berg et al., 2010).

Evidence for pooling in crowding appears in two literatures: crowding (in spatial vision) and illusory conjunction (in cognitive psychology). Each has its own favorite stimuli. Both literatures demand that the experimenter know the features of the stimuli.

Spatial vision studies of crowding have used lines or gratings (Dakin et al., 2010; Greenwood et al., 2009; Parkes et al., 2001). These studies have varied a single continuous feature (orientation or position) of the target and flankers. The perceived position (or orientation) of a crowded target is biased toward the average position (or orientation) of the target and flankers. This demonstrates a simple form of pooling (averaging) and rejects simple substitution of these parameters in these stimuli. Gratings and lines are useful because their features—orientation and position—are easily specified and pooling can be modeled as averaging over those features. However, that virtue comes at a cost: The experimental paradigms and the averaging models are specific to estimating a scalar parameter of the target. It is hard to imagine how the paradigms and models might be generalized to cope with arbitrary tasks and objects, for which the stimulus-specific pooling rules do not apply. For example, what is the “average” identity of several letters?

Cognitive psychology studies have described pooling in illusory conjunction, which is the false perception of an object that is not present yet is composed of “features” from objects that are present (Prinzmetal, 1995; Robertson, 2003; Treisman, 1996; Treisman & Schmidt, 1982). For example, an observer glimpsing a green next to a red might report seeing a red . Many studies have characterized illusory conjunctions for color, letter identity, lines, and simple geometric shapes (Ashby, Prinzmetal, Ivry, & Maddox, 1996; Cohen & Ivry, 1989; Donk, 1999; Gallant & Garner, 1988; Ivry & Prinzmetal, 1991; Kanwisher, 1991; Keele, Cohen, Ivry, Liotti, & Yee, 1988; Lasaga & Hecht, 1991; Prinzmetal, 1981; Prinzmetal, Henderson, & Ivry, 1995; Prinzmetal & Keysar, 1989; Prinzmetal, Presti, & Posner, 1986; Rapp, 1992; Treisman & Schmidt, 1982; Wolford & Shum, 1980). Illusory conjunctions arise when presentation time is brief, attention is diverted, or stimuli are presented close together in the periphery (Prinzmetal, 1995; Prinzmetal, Diedrichsen, & Ivry, 2001; Robertson, 2003; Treisman & Schmidt, 1982). The third case is the one most commonly reported. Illusory conjunction is pooling, and most published reports of illusory conjunction are due to crowding, so they demonstrate pooling in crowding (Pelli, Palomares, & Majaj, 2004). But, as with the spatial vision studies, all the demonstrations of pooling in illusory conjunction require the experimenter to first specify the features.

The studies on pooling rely on knowing the features, but the multiple features of ordinary objects are usually unknown, so these studies cannot tell us about pooling of ordinary objects. To skirt the hurdle of having to define and specify the “features” of most ordinary objects, which has limited the scope of previous work, we introduce a new paradigm that instead asks, for any kind of object, whether the observer’s response draws information from a single object (simple substitution) or both the target and a flanker (pooling).

As usual in psychophysics, we have access only to the stimulus and the observer’s overt report. We assessed whether the similarity of target to flanker affected that report. Similarity is a second-order property (Sperling, Chubb, Solomon, & Lu, 1994), a relation between two objects that is meaningless for a single object. Thus, effects of similarity on errors can be used to show that the report is based on information from more than one letter. This approach is reminiscent of multiple-report paradigms in which observers are asked to make second guesses and the frequencies of various kinds of error are used to infer properties of the precategorized representation of the stimulus (Macmillan & Creelman, 2005; Sperling, 1960; Swets, Tanner, & Birdsall, 1961).

Letters are good objects, by design. They are familiar, meaningful, named things (Pelli et al., 2009). We presented three letters side by side, a target between two flankers, and asked the observer to identify the target by pressing that key on the keyboard. We manipulated the similarity between the flankers and the target to control crowding (Fig. 1), and we characterized the roles of substitution and pooling in crowding through error analysis and mixture modeling.

Fig. 1.

Demonstration of crowding. While fixating the square on the left, try to identify the middle letter in the triplet below. This is hard. We think that you will agree that, if you had to name it, you would be more likely to call the jumbled middle letter M than I. This is the effect of similarity on errors that we measured in our experiment. Now fixate the square on the right and try to identify the middle fruit in the triplet below. (This fruit demo works best in color.) Once again, we think that you will agree that you would be more likely to call the jumbled middle fruit an apple than a lemon. Actually, it’s a peach. Our experiments used letters, but the effect of similarity on errors applies to any kind of object

According to the (simple) substitution model, as defined here, the observer’s response is based on information from a single letter taken from one of several locations (either target or flanker), as determined by spatial uncertainty or attention. Having taken only one letter, the substitution process knows only its identity, not its similarity to the target. Thus, the substitution process must report both kinds of flankers—similar and dissimilar—equally often. As we will show, contrary to this prediction, the similar flanker is mistakenly reported much more often than the dissimilar flanker. This refutes the (simple) substitution model.

However, we wanted more. Models evolve. Our aim was to discredit simple substitution in general, so it could never return. We defined pooling as taking information from more than one letter. We defined simple substitution as taking no more than one letter from the stimulus. Simple substitution means not pooling. Disproving simple substitution proves pooling. However, what if the observer substitutes on some trials and pools on others? Such a mixture model cannot be utterly rejected, but we can show that, even in this most favorable setting, simple substitution provides little help in explaining the human results.

This study’s approach to modeling may seem unfamiliar to some readers. Psychology studies usually present a particular model that fits the data. The model is a story, a plausible account of the results. Such models are often not worth much. Weakly supported, they change every time new data appear, and they fade away as time passes and modeling fashions change. Fitting the data usually provides only weak support, unlike the strong rejection that would result from failing to fit. Thus, a particular model that fits is merely a maybe: a specific account that might be true. Here, we use mixture modeling to achieve a strong conclusion that transcends particular fully specified models and must be true of any viable account of the phenomenon.

We present three experiments. Rather than point to a single best value for the key parameter, it turns out that our mixture model is compatible with a range of values, so our results are presented as upper and lower bounds. Experiment 1 is a direct attack on the simplest form of simple substitution, flanker-based substitution, in which the response is based on only one flanker. The results put an upper bound on the frequency of flanker-based substitution. Encouraged by the success of Experiment 1, we raise our sights in Experiment 2 to challenge the most general version of substitution. We introduce a mixture model and an enhanced experimental design. The results put an upper bound on the frequency of both target- and flanker-based substitution and, thus, put a lower bound on the frequency of pooling. Finally, Experiment 3 establishes our paradigm’s excellent sensitivity, finding that eliminating crowding greatly reduces pooling.

Method

Observers

Three experienced observers, 24–32 years old, with normal or corrected-to-normal vision, participated in the experiments. Observer A.W. was naive as to the hypothesis; the other 2 observers were the authors J.F. and R.C.

Stimuli

All stimuli were produced using the Psychtoolbox extensions in MATLAB and were presented on a 19-in. ViewSonic monitor placed 57 cm from the observer (Brainard, 1997; Pelli, 1997), with 1,024 × 768 pixels at a spatial resolution of 28 pixel/deg and a frame rate of 100 Hz.

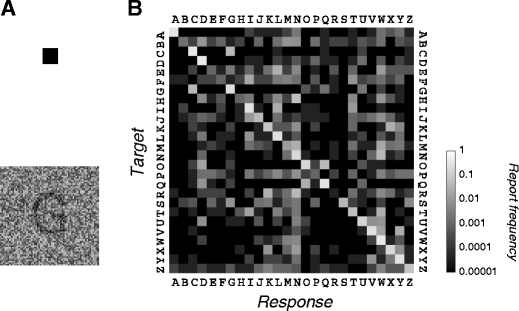
On each trial, the observer was asked to identify a letter presented on the screen (alone or flanked, central or peripheral). Fig. 2 shows typical stimuli for Experiments 1–3. The details and the observers differ depending on the set of measurements: confusion matrices (J.F., A.W., and R.C.), Experiment 1 (J.F., A.W., and R.C.), Experiment 2 (J.F. and R.C.), and Experiment 3 (J.F. and R.C.). The confusion matrix and Experiment 1 used the 26-letter uppercase alphabet in the Courier font: ABCDEFGHIJKLMNOPQRSTUVWXYZ. Experiments 2 and 3 used a six-letter alphabet: LTINMW. We varied two parameters (eccentricity and spacing) slightly among observers to equate overall accuracy. Letter size (height of an uppercase X) was always 0.9º. Depending on the measurement, the target was presented either unflanked (alone) or flanked (in a triplet, between two flankers). When flankers were used, the center-to-center spacing of the letters was 1.5° (observer A.W.) or 1° (J.F., R.C.). Depending on the measurement, the target was presented either at fixation or in the periphery. When letters were presented in the periphery, the eccentricity of (the center of) the target was 8º (R.C.) or 10º (A.W., J.F.), and the target was centered on the vertical meridian in the lower visual field.

Fig. 2.

Typical stimuli for Experiments 1–3. Each black square is a fixation mark. The letter triplet is peripheral (center is 8° to 10° in the lower visual field) in Experiments 1 and 2 and central (0°) in Experiment 3. In Experiment 1, the two flankers are different: similar and dissimilar to the target. In Experiments 2 and 3, they are the same: Both are similar or dissimilar to the target

The stimulus timing in Experiments 1 and 2 was as follows (the timing differed for Experiment 3; see below). At the start of each trial, the observer fixated a small black square (0.25º wide) at the center of the screen, and the stimulus was presented below fixation for 150 ms, after which the letters disappeared but the fixation square remained. In all three experiments, at the end of each trial, the observer selected a response (a letter) by pressing that key on the keyboard. The observers took as long as they liked to respond. There was no feedback. Each observer performed 200 trials. Further details of Experiments 1–3 are presented below.

Similarity

For our experiments, we sought flanker letters that were either similar or dissimilar to the target. We measured letter-to-letter similarity by asking each observer to identify a letter in noise in the peripheral visual field (Fig. 3). We tabulated the observer’s reports in a confusion matrix (Bouma, 1971; Townsend, 1971). For each presented letter, the matrix gave the probability of each letter report. We imagine that the more features any two letters share, the more similar they are, and the more frequently they are confused. Confusion matrices were similar across observers (average pairwise correlation coefficient between confusion matrices was .78 ± .04, mean ± standard deviation across 3 observers). There are many other ways that one could measure similarity, including subjective rating, and we imagine that they would all yield comparable results. Manipulating similarity is an effective and convenient way to control crowding (Kooi, Toet, Tripathy, & Levi, 1994; Põder, 2007). But it is not the only way. Our paradigm’s conclusions about pooling depend only on the fact that some letter pairs are much more crowded than others.

Fig. 3.

Similarity. a The observer fixated a small black square at the center of the screen. A dark uppercase letter of size (height) 0.9º was presented for 150 ms. It was centered on the vertical meridian in the lower visual field at an eccentricity of 10º (A.W., J.F.) or 8º (R.C.). Independent noise drawn from a zero-mean uniform distribution was added to each pixel of a 2.25º × 2.25º square region containing the letter. In the experiment, the background was gray (42 cd/m²), matched to the mean luminance of the region containing the letter, but in this illustration, the background is white. The task was to identify the target letter. The noise level (range of the uniform distribution from which the noise is drawn) was adjusted to roughly match accuracy across observers (41% ± 5% frequency of correct responses, average ± standard error across 3 observers; chance performance was 4%). While fixating the black square, one would find it hard to tell the letter. It could be a G, a C, a Q, or an O. After being displayed for 150 ms, the target and fixation square disappeared, and after a 200-ms delay, a response screen showed all 26 letters as possible responses. The observer moved the mouse-controlled cursor to select a response, after which the response screen disappeared. The feedback tone was high-pitched for correct and low-pitched for incorrect. After another 200-ms delay, the fixation square reappeared, and after 1 s, the next letter appeared. In a single session, each letter was presented 20 times, for a total of 520 trials. Observers did four separate sessions, for a total of 80 trials per letter. b We measured a confusion matrix for each observer. The confusion matrix for observer J.F. is shown on the right. Each row of the matrix corresponds to a different target letter (A–Z). The gray level of each cell indicates the fraction of trials on which the target was reported as a particular letter (A–Z)

To analyze the similarity of absent letter reports in Experiment 1, we first normalized each row of the confusion matrix to eliminate variability due to accuracy differences across letters. Specifically, for each possible target letter, we took the corresponding row of the confusion matrix, set the entry corresponding to the target to 0, and divided the rest of the entries by their maximum value. This produced a measure of normalized similarity for each possible response, ranging from 0 (least similar) to 1 (most similar).

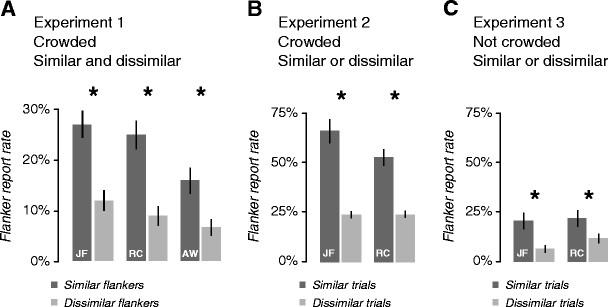
This normalized similarity measure was also used to assess the similarity of the similar and dissimilar flankers used in Experiment 1. For that experiment, we chose flankers that were as similar (or dissimilar) to each target while satisfying the additional requirements that all 26 similar flankers should be unique (no repeats), all 26 dissimilar flankers should be unique, and pairs of (dissimilar) targets should share the same pair of flankers: similar and dissimilar for one target versus dissimilar and similar for the other target (Fig. 4). These lists were constructed by first picking a similar flanker for each target, ensuring uniqueness. Then the targets were grouped into pairs; any such grouping fully specified the dissimilar flanker for each target, because of the requirement that pairs of targets should share the same pair of flankers. Different groupings into pairs were tried until the average dissimilarity was close to 0. All of these constraints resulted in slightly less similarity (and more dissimilarity) than would be obtained without these requirements. The average normalized similarity of the similar flankers was .74 ± .08, and for the dissimilar flankers, it was .02 ± .02 (as compared with the values of 1 and 0, respectively, that would be obtained without constraints) (mean ± standard deviation across 3 observers).

Fig. 4.

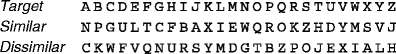
The two flankers, similar and dissimilar, used with each target in Experiment 1. These are for observer J.F., based on his confusion matrix (Fig. 3). Lists for the other observers were much like these. The list was constructed by choosing flankers that were as similar (or dissimilar) to each target while satisfying the requirements that all 26 similar flankers should be unique (no repeats), all 26 dissimilar flankers should be unique, and pairs of targets (e.g., A and G) should share the same pair of flankers (e.g., N and C), similar-and-dissimilar for one target versus dissimilar-and-similar for the other target. Thus, each flanker pair—for example, N and C—was equally likely to be similar-and-dissimilar as dissimilar-and-similar. This symmetrical distribution of the flankersmade the joint distribution of the two flankers independent of the similarity of the flankers to the target. On each trial, the target was randomly selected (A–Z) and displayed between the similar and dissimilar flankers specified here, placed randomly left and right or right and left of the target. Thus, on each trial, each of the three letters could be any letter A–Z with equal probability

Mixture modeling

According to the simple substitution (or nonpooling) model defined here, the observer’s response is based on information from a single letter unwittingly taken from one of several locations, as determined by spatial uncertainty or attention. That is the only constraint on the (simple) substitution model’s computation.  On some trials, the substitution model takes in a target, which it need not report faithfully; we call that target substitution. Otherwise, the substitution model takes in a flanker, which it need not report faithfully; we call that flanker substitution. On every trial, the model takes in a target or a flanker. The measured performance is an average across trials whose reports are flanker and target based. In general, the reported letter is only statistically related to the letter taken in, like reporting a letter in noise. So, even if it takes in the target, the substitution model may erroneously report another letter. In Experiment 1, the substitution model could report a flanker by (unwittingly) taking in that flanker and reporting it faithfully or by taking in the other flanker or the target and reporting it unfaithfully.

(Simple) substitution is a special case of a completely general model, which we call general pooling. General pooling is constrained only to receive the stimulus and give a response of the kind demanded by the task. The response may have any deterministic or statistical dependence on the stimulus. General pooling includes, as special cases, all models of crowded and masked target identification that we can imagine, including simple substitution. As we will see, simple substitution fails to fit the results, and general pooling, of course, fits perfectly. How well would a mixture of these two models fit? The goal here is to assess the explanatory power of the substitution model without insisting that it explain every trial. After all, we are explaining the responses of an intelligent willful observer who might change strategy unpredictably from trial to trial. We do not want to reject substitution just because the observer occasionally does something else. To that end, trying to be realistic, we assume a very general framework—a mixture model—in which either substitution or general pooling occurs randomly on each trial (see “Mixture Model,” 2011, in Wikipedia). The mixture model creates the most favorable possible condition for substitution, assigning it as many of the trials as possible, supposing that the rest are performed by general pooling. Our pooling model is deliberately vague (i.e., general) in order to provide a generous test of substitution. It needs to be general to serve the purpose of giving substitution its best chance to flower. By fitting the human results (minimizing a cost that includes the fraction of trials assigned to general pooling), we discover how large a role substitution can play and still allow the mixture model to fit well.

This model mixes three processes: a flanker-based process, a target-based process, and a target-and-flanker-based process. The two single-letter processes substitute, and the multiple-letter process pools. We will occasionally refer to the mixture of the two single-letter processes as the substitution process. We are particularly interested in the flanker-based substitution process because it is the simplest way to explain mistaking the target for a flanker. Flanker-based substitution is the heart of the substitution account, as the advocates of substitution and pooling—subbers and poolers—agree. When observers report flankers, as they often do, how many of those reports are due to flanker-based substitution? The mixture model is presented in the Appendix.

Experiment 1: Crowded. Similar and dissimilar

Experiment 1 was a classic crowding task. Three observers participated (J.F., A.W., and R.C.). At the start of each trial, the observer fixated a small black square at the center of the screen, and the target was presented in the lower visual field (centered on the vertical meridian), with a flanker on either side. The observer was told that a triplet of letters would be presented in the periphery, a target between two flankers, and that he or she should identify the target, ignoring the flankers.

We used each observer’s confusion matrix to tailor the triplets to the observer. The confusion matrix was based on identifying letters in noise (Fig. 3). Each target was assigned two flankers, one that was similar to the target and one that was dissimilar (Fig. 4). Pairs of targets shared the same pair of flankers: similar and dissimilar for one target, and dissimilar and similar for the other. On each trial, the two flankers were randomly placed next to the target (left and right or right and left). The assignment of flankers (Fig. 4) ensured that, on each trial, the letter at each location could be any letter A–Z, with equal probability. A single letter told nothing about similarity among the letters in the triplet.

Similarity proof

Here follows a proof that if the observer's response is based solely on one flanker, the probability of reporting a flanker similar to the target must equal the probability of reporting a flanker dissimilar to the target. In Experiment 1, each trial presented a target letter between two flanker letters, one similar and one dissimilar to the target. The pair of flankers was determined by the target, but their left–right ordering in the display was random. Each flanker’s distribution (A–Z) was independent of its similarity to the target. Thus, if the response depended solely on one flanker, the probability of reporting that flanker would be independent of its similarity to the target. Furthermore, the joint distribution of the two flankers was independent of their similarity to the target. Thus, if the response depended only on one flanker, the probability of reporting the other flanker would be independent of the similarity of the two flankers to the target. Flanker substitution cannot distinguish similarity.

Table 1 presents the fraction of trials on which the observer reported the target or (wrongly) reported a similar flanker, dissimilar flanker, or absent letter (neither target nor flanker). As was expected, crowding made all 3 observers perform poorly. They averaged only 32% ± 4% correct identification of the target, but this was still well above chance, which was 1/26 = 4%. They often reported the flankers (32% of trials), confirming previous studies (Krumhansl & Thomas, 1977; Strasburger, 2005). Do flanker reports favor the similar flanker? If flanker substitution accounts for all flanker reports, then the two flankers (similar and dissimilar) are equally likely to be reported. In fact, we found that observers far more frequently reported the similar (23%) than the dissimilar (9%) flanker (Table 1 and Fig. 5a). Each observer’s data disprove the prediction that the two flankers are equally likely to be reported (p < .01 for each observer individually, two-sided permutation test, for 3 observers). The frequency of similar-flanker reports was also significantly greater than the frequency of dissimilar-flanker reports in a random-effects analysis across observers [p = .026, t(2) = 6, two-sided paired t-test]. In this experiment, unless the target was known, the flanker identity provided no hint as to whether it was similar or dissimilar to the target. Thus, the observed preference for similar over dissimilar flankers proves that at least some of the observer’s mistaken reports were at least partly based on the target.

Table 1.

Response rates in Experiment 1: Crowded. Similar and dissimilar

	Average	J.F.	R.C.	A.W.
Target	32% ± 4%	25%	32%	38%
Similar flanker	23% ± 3%	27%	25%	16%
Dissimilar flanker	9% ± 1%	12%	9%	7%
Absent letter	36% ± 1%	36%	34%	39%
Total	100%	100%	100%	100%

Experiment 1: Average ( ± standard error across 3 observers) and individual frequency of the four kinds of responses produced by the observer when asked to identify a crowded target: the target, the similar flanker, the dissimilar flanker, or an absent letter (neither target nor flanker). The stimulus was a target flanked by a similar and a dissimilar letter, one on either side, such as CGE. Percentages are rounded to the nearest integer. Where necessary, rounding is adjusted to ensure that the percentages for the four different types of responses add up to 100%. These data reject flanker substitution as a complete explanation. As part of a mixture model, a flanker substitution process can account for, at most, 55% of the trials that produced these results (see the Results section and the Appendix, Eq. 4).

Fig. 5.

The effect of crowding on flanker reports. a Flanker report rates in Experiment 1 for similar flankers (dark bars) and dissimilar flankers (light bars). All 3 observers reported the flanker that was similar to the target much more often than the one that was dissimilar. The error bars extend from the 16th to 84th percentiles of the bootstrapped distribution. The difference is significant for every observer and disproves the prediction of flanker substitution that similar and dissimilar reports are equally likely (*p < .01, two-sided permutation test). As part of a mixture model, flanker substitution can account for, at most, 55% of the trials (see the Results section, Table 1, and the Appendix, Eq. 4). b Flanker report rates in Experiment 2 on trials where the flankers were similar to the target (dark bars) and dissimilar (light bars). Both observers reported the flanker more than twice as often on similar than on dissimilar trials. The difference is significant for both observers (*p < .001, one-sided permutation test). Fitting all trials with a mixture model, we find that flanker substitution accounts for 29% of trials and target substitution accounts for 28%. The remainder (43%) require pooling (see the Results secion, Table 2, and the Appendix, Eq. 7). c Flanker report rates in Experiment 3, in which the letter triplets were presented at fixation to eliminate crowding. Without crowding, flanker reports are greatly reduced. In the mixture model, target substitution accounts for 84% of all trials, and substitution, of any kind, accounts for 92% (see the Results section, Table 3, and the Appendix, Eq. 22). Pooling (8%) is still needed to account for the discrepancy between similar and dissimilar trials

This rejects flanker substitution as a full account. Maybe that’s a straw man, but we now raise our sights to challenge the most general form of (simple) substitution.

From these results, the Appendix derives an upper bound on the frequency of flanker substitution. To maximize the supposed role of the flanker substitution process, our mixture model attributes all the dissimilar-flanker reports (9%) to flanker substitution. This process is blind to similarity (since it sees only one letter), so it will produce similar-flanker reports at the same rate, which accounts for less than half of the similar-flanker reports (23%). Thus, even though the flanker substitution process was invented to explain flanker reports, it accounts for less than half of the similar-flanker reports. Something other than flanker substitution, either target substitution or pooling, must account for the rest.

Even though this experiment used a classic crowding task, it is conceivable that something else, such as acuity or lateral masking, might account for some of the mistakes. Did the observer have enough acuity to identify the target alone? With the stimulus parameters of Experiment 1, observers accurately identified an unflanked letter in the periphery or a flanked letter at fixation. We quantified this in one observer (J.F.). The observer identified an isolated (unflanked) letter in the periphery. Everything was the same as in Experiment 1 for observer J.F., except that there were no flankers. The observer did 100 trials. We find that accuracy for an unflanked target was 96% (as compared with 34% flanked), which shows that acuity accounts for very few mistakes, if any.

To test for possible lateral masking effects other than crowding, the observer identified a target between two flankers at fixation. [Everything was the same as in Experiment 1 for observer J.F., except that the triplet was presented centrally (at 0°) instead of peripherally; the fixation square disappeared during stimulus presentation. The observer did 100 trials.] Many different mechanisms of lateral masking have been proposed, and it would be hard to rule them all out one-by-one, but crowding is unique in that it is negligible at fixation, whereas the other effects have little dependence on eccentricity. We eliminated crowding from the experiment by moving the stimulus to fixation, which abolished crowding while preserving the other lateral masking effects. Crowding goes away because the letter spacing far exceeded the tiny 0.06º critical spacing at fixation (Toet & Levi, 1992). When we did this, performance rose from 34% to 99%, indicating that practically all mistakes at the original peripheral location were due to crowding.

Experiment 1 places an upper bound on the frequency of flanker substitution by showing that more than half of similar-flanker reports depend on the target (see the Appendix). However, the remaining trials could still be due to either target-based substitution or pooling. As was mentioned above, the only constraint on the substitution processes (either target or flanker based) is that they use information from only one letter location, selected unwittingly. Thus, flanker reports, especially similar-flanker reports, could be mistaken responses to the target, as a result of target substitution.

Recall that target substitution means that the observer’s response is based solely on the target, but the report might not be faithful (i.e., it can be wrong). It may be like reporting a target in noise. Perhaps the observers’ responses are all due to target substitution and the higher rate of similar-flanker reports occurs because target substitution reports letters that are more similar to the target. If this were the primary cause of similar-flanker reports, we might also expect absent letter reports to be similar to the target. To check for this, we asked, on absent letter reports, how similar the reported absent letter was to the target. We assessed these similarities using each observer’s confusion matrix. The average similarity between absent letter and target was .27 ± .05, only slightly higher than the value of .19 one would expect if the observer was randomly guessing (n = 3).1 However, this is inconclusive about the role of target substitution, because perhaps target substitution favors only the most similar letter, which is always present and, thus, not among the possible “absent” letters responses. So we enhanced the experimental paradigm to assess target substitution.

Experiment 2: Crowded. Similar or dissimilar

Experiment 1 tested each flanker with various targets; Experiment 2 additionally tested each target with various flankers. Experiment 1 tested flanker substitution; Experiment 2 also tested target substitution. Flanker substitution is ignorant of the target, and target substitution is ignorant of the flankers.

Two observers participated in Experiment 2 (J.F. and R.C.). Size, spacing, eccentricity, and the method of response were identical to those in Experiment 1. On each trial of Experiment 2, the target was surrounded by two flankers, which were identical to each other. The target and flanker were drawn independently from the same six-letter alphabet containing two groups of three letters (L T I N M W). The letters were similar within each group but dissimilar across groups. On each trial, the target and flanker were each selected randomly and independently from the six-letter alphabet, so the flanker could be identical (17%), similar (33%), or dissimilar (50%) to the target. Across many trials, each flanker appeared with various targets, and, unlike in Experiment 1, each target appeared with various flankers. The observer knew the six possible letters, and the response had to be one of them.

As in Experiment 1, the flanker-substitution process saw only a flanker, so its probability of faithfully reporting the flanker was independent of the flanker’s similarity to the target. However, we found that the flanker was reported much more frequently when it was similar (60%) than when it was dissimilar (24%) (average of 2 observers; see Table 2 and Fig. 5b). Supposing that all flanker reports are due to flanker substitution predicts that flanker reports are equally likely on the two types of trial. Data from each observer disproved this prediction (p<.001 for each observer individually, one-sided permutation test, for 2 observers).

Table 2.

Response rates in Experiment 2. Crowded. Similar or dissimilar

	Identical Trial	Similar Trial	Dissimilar Trial
Target	88% ± 1%	23% ± 7%	47% ± 4%
Flanker	n/a	60% ± 6%	24% ± 1%
Absent	12% ± 1%	17% ± 1%	29% ± 4%
Total	100%	100%	100%

Experiment 2: Average ( ± standard error across 2 observers) frequency of the three kinds of responses produced by the observer when asked to identify a crowded target: the target, the flanker, or an absent letter (neither target nor flanker). The stimulus was a target between two identical flankers. On each trial, the target and flanker were independent random samples from the same six-letter alphabet: L T I N M W. The three types of trials were flanker identical to target (e.g., WWW; 17% of trials), similar to target (MWM; 33%), and dissimilar to target (LWL; 50%). Substitution can account for, at most, 57% of the trials that produced these results (see the Results section and the Appendix, Eq. 7).

More important, because each flanker was presented with various targets and each target was presented with various flankers, Experiment 2 allowed us to place an upper bound on the frequencies of both target- and flanker-based substitution. Specifically, we implemented the mixture model to estimate the contributions of the three processes (see the Appendix). The observer’s performance in each condition (each entry in Table 2) was modeled as a linear combination of the probabilities that each of the three processes (target substitution, flanker substitution, and pooling) would be invoked. The model fitting minimized the weighted sum of total squared error and the probability of pooling. Recall that our modeling effort is asymmetric, by design. (Simple) substitution is specific (with few degrees of freedom), and general pooling is completely general (with as many degrees of freedom as the human data). The goal was to discover how large a role substitution could play and still allow the mixture model to fit well. Fitting the data from Experiment 2 indicates that no more than 57% of the trials in this experiment were due to target- or flanker-based substitution (Appendix, Eq. 7). Pooling must account for the remaining 43% of the trials and can explain all of them, whereas simple substitution is not needed and can explain, at most, 57% of the trials. When observers were asked to identify a crowded object, nearly half of their reports were pooled, on the basis of a combination of information from target and flankers, rather than being based on a single letter.

(Simple) substitution, with its few degrees of freedom, might seem to deserve praise for having accounted for about half of the trials in our mixture model of Experiment 2. However, much of the credit for this achievement should go to pooling, which uses its many degrees of freedom to account for the aspect of human performance that substitution cannot. The human observer response depends on similarity between letters, and substitution’s does not. The mixture model manages to attribute about half the trials to substitution only because pooling graciously accommodates substitution’s blindness to similarity by using its many degrees of freedom to never report a target among similar flankers and never report a dissimilar flanker. If we intervene, setting more-plausible nonzero lower bounds for such reports by the pooling process (Appendix, Eqs. 17 and 18), the maximum role of substitution is reduced from 57% to 32% of trials.

Experiment 3: Not crowded. Similar or dissimilar

In a third experiment, we established our paradigm's excellent sensitivity to crowding. Specifically, if the stimulus conditions are changed so that observers still make mistakes but the mistakes are not due to crowding, we would expect to attribute far fewer of them to pooling. The control experiment described above for Experiment 1 presented the stimulus centrally, instead of peripherally, to eliminate crowding. It found very few errors and, thus, ruled out the contribution of lateral masking to the observer’s mistakes. Experiment 3 also presented the stimulus centrally to rule out crowding but introduced other factors (reduced duration, post-mask) to cause errors, and we show that the errors do not reflect pooling.

Two observers (J.F. and R.C.) participated in Experiment 3. The size, spacing, method of response, alphabet, and trial types were identical to those in Experiment 2. However, instead of presenting letter triplets in the periphery (at 10º, as in Experiments 1 and 2), letters were presented at fixation (the target was centered at 0º) to eliminate crowding. There was no crowding of this stimulus at fixation, because the letter spacing far exceeded the tiny 0.06º critical spacing (Toet & Levi, 1992). To restore difficulty to the task, we reduced the stimulus duration from 150 ms to either 70 or 80 ms (adjusted to roughly match performance between observers), and the triplet was immediately followed by a post-mask. The post-mask was a triplet of three randomly chosen letters (from the 26 letters A–Z), presented with the same size, location, and duration as the target and flankers. Without these manipulations, performance would be nearly perfect. These conditions yielded performance of 57% ± 6% correct target identification (n = 2). The fixation square was on at all times, except for when the triplet and the post-mask were presented.

As is reported in the Appendix, we fit the same model as that in Experiment 2 to the observer’s data in each condition (each entry in Table 3) and found that pooling on only 8% of the trials was enough to account for the measured performance, leaving the rest to substitution (primarily target substitution). Performance in Experiment 3 thus primarily reflected responses based solely on the target (which could be either correct or incorrect, just as a single letter in noise can be reported correctly or not). This 8% lower bound on pooling without crowding was less than a quarter of the 43% lower bound on pooling with crowding found in Experiment 2. Without crowding, substitution accounted for 92% of the trials. These data demonstrate the sensitivity of our paradigm: When factors other than crowding impair performance (e.g., brief duration and post-mask), we find very little pooling, and substitution reigns.

Table 3.

Response rates in Experiment 3: Not crowded. Similar or dissimilar

	Identical Trial	Similar Trial	Dissimilar Trial
Target	63% ± 2%	52% ± 3%	60% ± 8%
Flanker	n/a	22% ± 1%	10% ± 3%
Absent	37% ± 2%	27% ± 3%	33% ± 4%
Total	100%	100%	100%

Experiment 3: Much like Experiment 2 (Table 2), except that the stimulus (target and flankers) was at fixation instead of in the periphery. Shown are the average (±standard error across 2 observers) frequencies of the three kinds of responses produced by the observer when asked to identify the target letter: the target, the flanker, or an absent letter (neither target nor flanker). Unlike in Experiment 2, the target was not crowded, because it was presented at fixation. To restore difficulty, despite the central presentation, the stimulus was presented briefly (70 or 80 ms), and was followed by a post-mask. Substitution accounted for 92% of the trials that produced these results (see the Results section and the Appendix, Eq. 22)

Discussion

Our findings refute past suggestions of rampant unpooled substitution during crowding (Chastain, 1982; Estes et al., 1976; Huckauf & Heller, 2002; Strasburger, 2005; Strasburger et al., 1991; Vul et al., 2009; Wolford & Shum, 1980) and extend existing evidence for pooling in crowding (Dakin et al., 2010; Greenwood et al., 2009; Parkes et al., 2001; Prinzmetal, 1995; Treisman & Schmidt, 1982; van den Berg et al., 2010; Wolford & Shum, 1980) to ordinary objects whose features are not known. Many studies of crowding have shown that flanker similarity increases the effect of crowding on target identification performance, and these effects motivated our use of similarity to manipulate crowding (Andriessen & Bouma, 1976; Estes, 1982; Kooi et al., 1994; Krumhansl & Thomas, 1977; Põder, 2007). Studies of illusory conjunction have also shown that such binding errors increase with similarity (Ivry & Prinzmetal, 1991), and in so far as these errors likely reflect crowding (Pelli et al., 2004), these studies also show that similarity increases crowding. Our key finding, however, is not that similarity affects the frequency of making a mistake, but that it systematically influences the identity of the mistake and that the resulting pattern of errors constrains a substitution model in which the observer draws information from only one object. Flanker reports during crowding are old news. Our paradigm reveals that the flanker reports reflect pooling and cannot be explained by unpooled substitution alone. Thus, although we manipulated the similarity of letters (and fruit) to control crowding (Fig. 1), this article is not about similarity, letters, or fruit. It is about crowding. We find that flankers that crowd more are reported more. This severely limits the potential role of unpooled substitution in crowding. It shows that crowding is pooling.

This article has considered a low-level substitution process that unwittingly takes in a stimulus letter, before crowding, before any lateral interaction. A clever proposal from an anonymous reviewer instead attributes the results of Experiment 1 to the observer’s intentionally taking a letter from his crowded internal representation. The reviewer notes that the dissimilar flanker will be less crowded by the target than will the similar flanker. Thus, the observer may often see one identifiable letter next to a two-letter jumble. It might be a good strategy to report a letter unlike the identifiable one. We asked our observers, and they denied using this strategy, but they might yet have done so without realizing it. This puts a new light on the results of Experiment 1, but the reviewer's proposal is inapplicable to Experiment 2, in which the left and right flankers are the same. Any model that incorporates effects of similarity is getting information from several letters and is thus a pooling model, by our definition.

Our results refer to the pooling of unknown features across letters, whereas several previous descriptions of pooling in crowding (and rejections of substitution) have dealt exclusively with simple, known features (Dakin et al., 2010; Greenwood et al., 2009; Parkes et al., 2001; van den Berg et al., 2010). Results obtained with such stimuli, such as lines and gratings, do not readily predict the characteristics of flanker reports during the perception of ordinary crowded objects. Our method provides a way to prove that when objects are crowded, observers use information from more than one object. The paradigm is applicable to any object, and the demo in Fig. 1 indicates that the results found with letters generalize at least to fruit.

To reach a lasting conclusion, our simple substitution model (i.e., unpooled) assumes only the essential: taking at most one letter, possibly from the wrong place. To assess that idea, without insisting that it explain every trial, we introduce the general pooling process to handle the rest of the trials. Altogether, this is a mixture model. The probability of using the general pooling process is a parameter. The cost minimized by the fitting includes that parameter. Fitting this mixture model to our experimental results reveals an upper bound on the fraction of trials (about half) that can be attributed to unpooled substitution—that is, any report process that takes in only one letter. This conclusion is strong (based on rejection), and broad, applying to all models that do not pool.

The reader may be impressed that with few degrees of freedom, unpooled substitution accounts for half of the trials. However, credit where credit is due. One should acknowledge that the unpooled substitution process abuses the generous hospitality of the mixture model and demands too much from the accommodating general pooling process. The observer is affected by similarity, and unpooled substitution is not. The mixture model fits well only because the general pooling process, with its many degrees of freedom, is very accommodating. To make up for unpooled substitution’s blindness to similarity, the general pooling process never reports the target on similar trials and never reports the flanker on dissimilar trials. Supposing that any plausible pooling process must occasionally give these responses, and specifying plausible lower bounds severely curtails the degree to which pooling can make up for unpooled substitution’s deficiencies, reducing the maximum role of unpooled substitution from 57% to 32% of trials (Appendix E).

Conclusion

The simple substitution model once provided an elegant and parsimonious account of existing results. Its proponents divided the space of possible explanations, paving the way for experiments, like ours, that distinguish the two sides. Illusory conjunction and averaging of orientation and position are obviously pooling, not simple substitution, but these vivid demonstrations are restricted to cases in which one knows the features. Our results reject simple substitution—defined as taking information from at most one object, possibly from the wrong place—as a complete account. Incorporated into the mixture model, simple substitution can account only for, at most, about half of the trials, relying on general pooling, with its many degrees of freedom, to take up the slack. Furthermore, supposing substitution on half the trials demands implausible contortions of the general pooling process to account for the other half. Substitution’s weak contribution to the mixture model is embarrassing, showing that it fails to account for the errors it was invented to explain. Simple substitution accounts for fewer than half of the similar-flanker reports. Pooling is needed to account for the rest. Despite its elegant simplicity, supposing simple substitution detracts from parsimony if its explanatory burden is in addition to, rather than instead of, the cost of explaining pooling.

Crowding is quickly emerging as a fundamental limit to the recognition of all objects (Pelli & Tillman, 2008). This study manipulated the similarity of letters to control crowding. We found that flankers that crowd more are reported more. This severely restricts the possible role of unpooled substitution in crowding. On its own, unpooled substitution cannot account for crowding. It is not enough. Pooling is required. Pooling takes information from more than one letter. Unpooled substitution is nonpooling (taking information from no more than one letter). Disproving unpooled substitution proves pooling.

Electronic supplementary materials

Below is the link to the electronic supplementary material.

Appendix Mixture modeling

A. Introduction

The main text defines pooling as taking in more than one object and (simple) substitution as nonpooling, taking in at most one object. (We abbreviate simple substitution to just substitution throughout the Appendix.) Here, we derive upper bounds on the frequency of flanker substitution, target substitution, and both. We were pleasantly surprised to obtain these bounds on substitution, despite allowing it to perform any computation. The key is mixture modeling. Measured human performance is an average over many trials. The mixture model supposes that each trial, randomly, is mediated by one of several simple processes. On each trial, one of the three processes F, T, or TF is invoked with corresponding probability p _F, p _T, or p _TF, where p _F + p _T + p _TF = 1. (F and T stand for flanker and target. The TF process takes in the target and all the flankers.) The random selection of a process is independent on each trial and independent of the stimulus. It might seem artificial to suppose mixing, but, in fact, it comes with the territory. The substitution process, as defined here, receives only one letter, unwittingly taken from one of several locations, as determined by spatial uncertainty. The letter received is either the target (with probability p _T) or a flanker (with probability p _F). That implies that the substitution processes’ performance is a mixture of target and flanker substitution processes. The F (flanker substitution) process produces a response based solely on a flanker. The T (target substitution) process produces a response based solely on the target. The two processes are otherwise identical and have the same fidelity: The substitution is faithful when it reports the letter received, with probability s _eq. Otherwise, it is unfaithful, with probability 1–s _eq. The TF (general pooling) process produces a response based on the target and flankers. If substitution gives a full account, then p _F + p _T = 1 and p _TF = 0. Except for the restriction of stimulus information, these processes are unconstrained and may perform any computation. Thus, the general pooling process (TF) is utterly unconstrained, and we invoke it here only to take up the slack (using its several degrees of freedom, p ₁, p ₂, . . .), accounting for the trials that substitution cannot. We do not insist that substitution provide a full account. A partial account will do. But how much can it account for?

Our mixture model assigns distinct processes to substitution of target and flanker but supposes that the two processes are identical (implemented by the same processor), transforming the input letter with no regard to where it came from.

Our analysis of Experiments 1 and 2 finds that substitution can account for, at most, 60% of the trials, leaving pooling to account for the rest, which it has enough degrees of freedom to do. However, the necessary values may seem implausible: Maximizing the role of substitution requires that pooling never reports a dissimilar flanker and never reports the target when the flanker is dissimilar. If one supposes that the pooling process must have nonzero rates for these reports then the maximum possible role of substitution is correspondingly reduced (Appendix E).

B. Experiment 1: With crowding. Similar and dissimilar

There are two ways of going about this. We can reason about particular constraints, writing a discrete equation for each one, or we can put all the constraints into a single matrix equation and ask the computer to solve it for us. Each approach has its merits, so we present both.

The mixture model supposes that each human response probability is a linear combination of the response probabilities of the three processes. For Experiment 1 (Table 1), we have

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \begin{array}{*{20}{c}} {Data} \hfill & {} \hfill & {Response\;Probability} \hfill & {} \hfill & {Process\;Response\;Probability} \hfill & {Process\;Probability} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {\begin{array}{*{20}{c}} {{\text{T}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} & {{\text{F}}\;\;\;\;\;\;\;\;\;\;\;\;} & {\text{TF}} \\ \end{array} } \hfill & {} \hfill \\ {\left[ {\begin{array}{*{20}{c}} {0.32} \\ {0.23} \\ {0.09} \\ {0.36} \\ \end{array} } \right]} \hfill & \approx \hfill & {\left[ {\begin{array}{*{20}{c}} {P\left( {target\;response} \right)} \hfill \\ {P\left( {similar - flanker\;response} \right)} \hfill \\ {P\left( {dissimilar - flanker\;response} \right)} \hfill \\ {P\left( {absent - letter\;response} \right)} \hfill \\ \end{array} } \right]} \hfill & = \hfill & {\left[ {\begin{array}{*{20}{c}} {{P_T}\left( {t.r.} \right)} \hfill & {{P_{\text{F}}}\left( {t.r.} \right)} \hfill & {{P_{\text{TF}}}\left( {t.r.} \right)} \hfill \\ {{P_{\text{T}}}\left( {s.f.r.} \right)} \hfill & {{P_{\text{F}}}\left( {s.f.r.} \right)} \hfill & {{P_{\text{TF}}}\left( {s.f.r.} \right)} \hfill \\ {{P_{\text{T}}}\left( {d.f.r.} \right)} \hfill & {{P_{\text{F}}}\left( {d.f.r.} \right)} \hfill & {{P_{\text{TF}}}\left( {d.f.r.} \right)} \hfill \\ {{P_{\text{T}}}\left( {a.l.r.} \right)} \hfill & {{P_{\text{F}}}\left( {a.l.r.} \right)} \hfill & {{P_{\text{TF}}}\left( {a.l.r.} \right)} \hfill \\ \end{array} } \right]} \hfill & {\left[ {\begin{array}{*{20}{c}} {{p_{\text{T}}}} \hfill \\ {{p_{\text{F}}}} \hfill \\ {{p_{\text{TF}}}} \hfill \\ \end{array} } \right].} \hfill \\ \end{array} $$\end{document} 1

Every cell is a probability, between 0 and 1, and every column adds up to 1.

In Experiment 1, an upper bound on the role of flanker substitution is set by the dissimilar-flanker report rate (9%). The report rates of the other two processes (T and TF) cannot be negative, so the observed report rate of the human observer is an upper bound on the report rate of the flanker substitution process (F).

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ 0.09 \approx P\left( {dissimilar - flanker\;response} \right) \geqslant {p_{\text{F}}}{P_{\text{F}}}\left( {{\text{d}}{\text{.f}}{\text{.r}}{.}} \right) $$\end{document} 2

Flanker substitution F is ignorant of the target, so it must report similar and dissimilar flankers at the same rate. This assumes, as in our experiments, that any given flanker letter is equally likely to be similar or dissimilar to the target. Flanker substitution with a 9% report rate accounts for less than half of the similar-flanker reports (23%).

Above, we consider only one constraint of the model and derive an upper bound. One can wonder whether that upper bound is achievable, since other constraints might intrude. For that we implement all the constraints in our linear model, somewhat arbitrarily filling in a few unspecified details (s _sim and s _dis) to show that at least this instantiation of the model does, in fact, achieve that upper bound.

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \begin{array}{*{20}{c}} {Data} \hfill & {} \hfill & {Response\;Probability} \hfill & {} \hfill & {Process\;Response\;Probability} \hfill & {Process\;Probability} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {\begin{array}{*{20}{c}} {\;\;{\text{T}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;} & {{\text{F}}\;\;\;\;\;\;\;\;\;\;\;\;} & {\text{TF}} \\ \end{array} } \hfill & {} \hfill \\ {\left[ {\begin{array}{*{20}{c}} {0.32} \\ {0.23} \\ {0.09} \\ {0.36} \\ \end{array} } \right]} \hfill & \approx \hfill & {\left[ {\begin{array}{*{20}{c}} {P\left( {target\;response} \right)} \hfill \\ {P\left( {similar - flanker\;response} \right)} \hfill \\ {P\left( {dissimilar - flanker\;response} \right)} \hfill \\ {P\left( {absent - letter\;response} \right)} \hfill \\ \end{array} } \right]} \hfill & = \hfill & {\left[ {\begin{array}{*{20}{c}} {{S_{\text{eq}}}} \hfill & {\frac{{{S_{\text{sim}}}12 + {S_{\text{dis}}}13}}{2}} \hfill & {{p_1}} \hfill \\ {{S_{\text{sim}}}/12} \hfill & {\frac{{{S_{\text{eq}}} + {S_{\text{dis}}}/13}}{2}} \hfill & {{p_2}} \hfill \\ {{S_{\text{dis}}}/13} \hfill & {\frac{{{S_{\text{eq}}} + {S_{\text{dis}}}/13}}{2}} \hfill & {{p_3}} \hfill \\ {1 - {\Sigma_3}} \hfill & {1 - {\Sigma_3}} \hfill & {1 - {\Sigma_3}} \hfill \\ \end{array} } \right]} \hfill & {\left[ {\begin{array}{*{20}{c}} {{p_{\text{T}}}} \hfill \\ {{p_{\text{F}}}} \hfill \\ {{p_{\text{TF}}}} \hfill \\ \end{array} } \right],} \hfill \\ \end{array} $$\end{document} 3

where Σ₃ is shorthand for the sum of the three cells immediately above in that column, fidelity s _eq is the probability of reporting the letter received, s _sim is the probability of reporting any of the 12 letters most similar to it, and s _dis = 1 – s _eq – s _sim is the probability of reporting any of the 13 letters most dissimilar to it. Thus, substitution has four degrees of freedom, p _T, p _F, s _eq, and s _sim, and general pooling has three: p ₁, p ₂, and p ₃. We used Excel with the Solver add-in

(http://www.solver.com/mac/dwnmacsolver.htm) to find the solution that maximizes p _F:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {0.32} \\ {0.23} \\ {0.09} \\ {0.36} \\ \end{array} } \right]} \hfill & \approx \hfill & {\left[ {\begin{array}{*{20}{c}} {P\left( {target\;response} \right)} \hfill \\ {P\left( {similar - flanker\;response} \right)} \hfill \\ {P\left( {dissimilar - flanker\;response} \right)} \hfill \\ {P\left( {absent - letter\;response} \right)} \hfill \\ \end{array} } \right]} \hfill & = \hfill & {\left[ {\begin{array}{*{20}{c}} {0.00} \hfill & {0.03} \hfill & {0.68} \hfill \\ {0.00} \hfill & {0.16} \hfill & {0.32} \hfill \\ {0.00} \hfill & {0.16} \hfill & {0.00} \hfill \\ {0.00} \hfill & {0.65} \hfill & {0.00} \hfill \\ \end{array} } \right]} \hfill & {\left[ {\begin{array}{*{20}{c}} {0.00} \hfill \\ {0.55} \hfill \\ {0.45} \hfill \\ \end{array} } \right].} \hfill \\ \end{array} $$\end{document} 4

Specifically, Solver finds the solution that minimizes the cost, which is the fraction of trials not carried out by flanker substitution plus the squared error of the model’s fit to the data: \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ 1 - {p_{\text{F}}} + {10^5}\sum\limits_{{\forall r}} {{{\left( {{P_{\text{data}}}(r) - {P_{\text{model}}}(r)} \right)}^2}} $$\end{document}, where r is the kind of response, one for each row in the second matrix in Eq. 4. Note that there is no target substitution p _T = 0 (top of rightmost matrix), so ignore the first column of the big matrix. Attaining the upper bound, flanker substitution is responsible for all the dissimilar-flanker reports, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {p_{\text{T}}}{P_{\text{T}}}\left( {d.f.r.} \right) = {p_{\text{TF}}}{P_{\text{TF}}}\left( {{\text{d}}{\text{.f}}{\text{.r}}{.}} \right) = 0 $$\end{document}. Thus, flanker substitution accounts for \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {p_F}{P_F}\left( {{\text{s}}{\text{.f}}{\text{.r}}{.}} \right)/P\left( {{\text{s}}{\text{.f}}{\text{.r}}{.}} \right) = 0.55 \times 0.16/0.23 = 38\% $$\end{document} of the similar-flanker reports.

Experiment 1 tested each flanker with various targets, which is a revealing test of the flanker substitution process. However, this experiment did not test each target with various flankers, so it does not tell us much about the target substitution process. Experiment 1 provides a useful upper bound on p _F, but not p _T. Experiment 2 does that.

Note that Eqs. 1–4 apply to Experiment 1 and that Eqs. 5–7 apply to Experiment 2. The Excel spreadsheets used to solve Eqs. 3 and 6 are provided in the online Supplement.

C. Experiment 2: With crowding. Similar or dissimilar

In Experiment 2, the two flankers were the same. The six-letter alphabet consisted of two 3-letter groups: L T I N M W. Letters were similar within a group and dissimilar across groups. On each trial, the target and the flanker were independent random samples from the alphabet. Thus, there were three kinds of trials: identical (e.g., WWW), similar (MWM), and dissimilar (LWL).

The mixture model supposes that each human response probability in Experiment 2 (Table 2) is a linear combination of the response probabilities of the three processes.

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \begin{array}{*{20}{c}} {\text{Data}} \hfill & {} \hfill & {{\text{Response}}\;{\text{probability}}} \hfill & {} \hfill & {{\text{Process}}\;{\text{response}}\;{\text{probabilty}}} \hfill & {{\text{Process}}\;{\text{probability}}} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {\begin{array}{*{20}{c}} {\;\;{\text{T}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \hfill & {{\text{F}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \hfill & {\text{TF}} \hfill \\ \end{array} } \hfill & {} \hfill \\ {\left[ {\begin{array}{*{20}{c}} {0.88} \hfill \\ {0.12} \hfill \\ \hline {0.23} \hfill \\ {0.60} \hfill \\ {0.17} \hfill \\ \hline {0.47} \hfill \\ {0.24} \hfill \\ {0.29} \hfill \\ \end{array} } \right]} \hfill & \approx \hfill & {\left[ {\begin{array}{*{20}{c}} {P\left( {{\text{target}}\;{\text{response}}\;{\text{on}}\;{\text{identical}}\,{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{absent}}\;{\text{response}}\;{\text{on}}\;{\text{identical}}\;{\text{trial}}} \right)} \hfill \\ \hline {P\left( {{\text{target}}\;{\text{response}}\;{\text{on}}\;{\text{similar}}\;{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{flanker}}\;{\text{response}}\;{\text{on}}\;{\text{similar}}\;{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{absent}}\;{\text{response}}\;{\text{on}}\;{\text{similar}}\;{\text{trial}}} \right)} \hfill \\ \hline {P\left( {{\text{target}}\;{\text{response}}\;{\text{on}}\;{\text{dissimilar}}\;{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{flanker}}\;{\text{response}}\;{\text{on}}\;{\text{dissimilar}}\;{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{absent}}\;{\text{response}}\;{\text{on}}\;{\text{dissimilar}}\;{\text{trial}}} \right)} \hfill \\ \end{array} } \right]} \hfill & = \hfill & {\left[ {\begin{array}{*{20}{c}} {{P_{\text{T}}}\left( {{\text{t}}{\text{.r}}{\text{.o}}{\text{.i}}{\text{.t}}{.}} \right)} \hfill & {{P_{\text{F}}}\left( {{\text{t}}{\text{.r}}{\text{.o}}{\text{.i}}{\text{.t}}{.}} \right)} \hfill & {{P_{\text{TF}}}\left( {{\text{t}}{\text{.r}}{\text{.o}}{\text{.i}}{\text{.t}}{.}} \right)} \hfill \\ {{P_{\text{T}}}\left( {{\text{a}}{\text{.r}}{\text{.o}}{\text{.i}}{\text{.t}}{.}} \right)} \hfill & {{P_{\text{F}}}\left( {{\text{a}}{\text{.r}}{\text{.o}}{\text{.i}}{\text{.t}}{.}} \right)} \hfill & {{P_{\text{TF}}}\left( {{\text{a}}{\text{.r}}{\text{.o}}{\text{.i}}{\text{.t}}{.}} \right)} \hfill \\ \hline {{P_{\text{T}}}\left( {{\text{t}}{\text{.r}}{\text{.o}}{\text{.s}}{\text{.t}}{.}} \right)} \hfill & {{P_{\text{F}}}\left( {{\text{t}}{\text{.r}}{\text{.o}}{\text{.s}}{\text{.t}}{.}} \right)} \hfill & {{P_{\text{TF}}}\left( {{\text{t}}{\text{.r}}{\text{.o}}{\text{.s}}{\text{.t}}{.}} \right)} \hfill \\ {{P_{\text{T}}}\left( {{\text{f}}{\text{.r}}{\text{.o}}{\text{.s}}{\text{.t}}{.}} \right)} \hfill & {{P_{\text{F}}}\left( {{\text{f}}{\text{.r}}{\text{.o}}{\text{.s}}{\text{.t}}{.}} \right)} \hfill & {{P_{\text{TF}}}\left( {{\text{f}}{\text{.r}}{\text{.o}}{\text{.s}}{\text{.t}}{.}} \right)} \hfill \\ {{P_{\text{T}}}\left( {{\text{a}}{\text{.r}}{\text{.o}}{\text{.s}}{\text{.t}}{.}} \right)} \hfill & {{P_{\text{F}}}\left( {{\text{a}}{\text{.r}}{\text{.o}}{\text{.s}}{\text{.t}}{.}} \right)} \hfill & {{P_{\text{TF}}}\left( {{\text{a}}{\text{.r}}{\text{.o}}{\text{.s}}{\text{.t}}{.}} \right)} \hfill \\ \hline {{P_{\text{T}}}\left( {{\text{t}}{\text{.r}}{\text{.o}}{\text{.d}}{\text{.t}}{.}} \right)} \hfill & {{P_{\text{F}}}\left( {{\text{t}}{\text{.r}}{\text{.o}}{\text{.d}}{\text{.t}}{.}} \right)} \hfill & {{P_{\text{TF}}}\left( {{\text{t}}{\text{.r}}{\text{.o}}{\text{.d}}{\text{.t}}{.}} \right)} \hfill \\ {{P_{\text{T}}}\left( {{\text{f}}{\text{.r}}{\text{.o}}{\text{.d}}{\text{.t}}{.}} \right)} \hfill & {{P_{\text{F}}}\left( {{\text{f}}{\text{.r}}{\text{.o}}{\text{.d}}{\text{.t}}{.}} \right)} \hfill & {{P_{\text{TF}}}\left( {{\text{f}}{\text{.r}}{\text{.o}}{\text{.d}}{\text{.t}}{.}} \right)} \hfill \\ {{P_{\text{T}}}\left( {{\text{a}}{\text{.r}}{\text{.o}}{\text{.d}}{\text{.t}}{.}} \right)} \hfill & {{P_{\text{F}}}\left( {{\text{a}}{\text{.r}}{\text{.o}}{\text{.d}}{\text{.t}}{.}} \right)} \hfill & {{P_{\text{TF}}}\left( {{\text{a}}{\text{.r}}{\text{.o}}{\text{.d}}{\text{.t}}{.}} \right)} \hfill \\ \end{array} } \right]} \hfill & {\left[ {\begin{array}{*{20}{c}} {{p_{\text{T}}}} \hfill \\ {{p_F}} \hfill \\ {{p_{\text{TF}}}} \hfill \\ \end{array} } \right]} \hfill \\ \end{array} $$\end{document} 5

Every cell is a probability, between 0 and 1. For each kind of trial, the total response probability is 1.

Fidelity s _eq is the probability that a substitution process emits the letter it received. Let s _sim and s _dis be the probabilities of emitting a letter similar or dissimilar to that received. That’s enough to allow us to write out all the response probabilities for the T and F processes. The general pooling process TF is unconstrained and has a degree of freedom for each case. Thus, the mixture model for Experiment 2 is

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \begin{array}{*{20}{c}} {\text{Data}} \hfill & {} \hfill & {{\text{Response}}\;{\text{probability}}} \hfill & {} \hfill & {{\text{Process}}\;{\text{response}}\;{\text{probabilty}}} \hfill & {{\text{Process}}\;{\text{probability}}} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {\begin{array}{*{20}{c}} {{\text{T}}\;\;\;\;\;\;\;\;\;} \hfill & {{\text{F}}\;\;\;\;\;\;} \hfill & {\text{TF}} \hfill \\ \end{array} } \hfill & {} \hfill \\ {\left[ {\begin{array}{*{20}{c}} {0.88} \hfill \\ {0.12} \hfill \\ \hline {0.23} \hfill \\ {0.60} \hfill \\ {0.17} \hfill \\ \hline {0.47} \hfill \\ {0.24} \hfill \\ {0.29} \hfill \\ \end{array} } \right]} \hfill & \approx \hfill & {\left[ {\begin{array}{*{20}{c}} {P\left( {{\text{target}}\;{\text{response}}\;{\text{on}}\;{\text{identical}}\,{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{absent}}\;{\text{response}}\;{\text{on}}\;{\text{identical}}\;{\text{trial}}} \right)} \hfill \\ \hline {P\left( {{\text{target}}\;{\text{response}}\;{\text{on}}\;{\text{similar}}\;{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{flanker}}\;{\text{response}}\;{\text{on}}\;{\text{similar}}\;{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{absent}}\;{\text{response}}\;{\text{on}}\;{\text{similar}}\;{\text{trial}}} \right)} \hfill \\ \hline {P\left( {{\text{target}}\;{\text{response}}\;{\text{on}}\;{\text{dissimilar}}\;{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{flanker}}\;{\text{response}}\;{\text{on}}\;{\text{dissimilar}}\;{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{absent}}\;{\text{response}}\;{\text{on}}\;{\text{dissimilar}}\;{\text{trial}}} \right)} \hfill \\ \end{array} } \right]} \hfill & = \hfill & {\left[ {\begin{array}{*{20}{c}} {{S_{\text{eq}}}} \hfill & {{S_{\text{eq}}}} \hfill & {{p_1}} \hfill \\ {1 - {S_{\text{eq}}}} \hfill & {1 - {S_{\text{eq}}}} \hfill & {1 - {p_1}} \hfill \\ \hline {{S_{\text{eq}}}} \hfill & {{S_{\text{sim}}}/2} \hfill & {{p_2}} \hfill \\ {{S_{\text{sim}}}/2} \hfill & {{S_{\text{eq}}}} \hfill & {{p_3}} \hfill \\ {1 - {\Sigma_2}} \hfill & {1 - {\Sigma_2}} \hfill & {1 - {\Sigma_2}} \hfill \\ \hline {{S_{\text{eq}}}} \hfill & {{S_{\text{dis}}}/3} \hfill & {{p_4}} \hfill \\ {{S_{\text{dis}}}/3} \hfill & {{S_{\text{eq}}}} \hfill & {{p_5}} \hfill \\ {1 - {\Sigma_2}} \hfill & {1 - {\Sigma_2}} \hfill & {1 - {\Sigma_2}} \hfill \\ \end{array} } \right]} \hfill & {\left[ {\begin{array}{*{20}{c}} {{p_{\text{T}}}} \hfill \\ {{p_{\text{F}}}} \hfill \\ {{p_{\text{TF}}}} \hfill \\ \end{array} } \right],} \hfill \\ \end{array} $$\end{document} 6

where p _TF = 1 – p _T – p _F and Σ₂ is shorthand for the sum of the two cells immediately above in that column.

Solver finds the solution that minimizes the cost, which is the fraction of trials pooled plus the squared error of the model’s fit to the data: \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {p_{\text{TF}}} + {10^5}\sum\limits_{{\forall r}} {{{\left( {{P_{\text{data}}}(r) - {P_{\text{model}}}(r)} \right)}^2}} $$\end{document}, where r is the kind of response, one for each row in the tall matrices in Eq. 6. The solution has minimum pooling p _TF of 43%. This substitution process has four2 degrees of freedom, p _F, p _T, s _eq, and s _sim, and the general pooling process has five: p ₁, p ₂, p ₃, p ₄, and p ₅. Here is the solution found by Excel and Solver:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {\frac{{\begin{array}{*{20}{c}} {0.88} \hfill \\ {0.12} \hfill \\ \end{array} }}{{0.23}}} \hfill \\ {\frac{{\begin{array}{*{20}{c}} {0.60} \hfill \\ {0.17} \hfill \\ \end{array} }}{{\begin{array}{*{20}{c}} {0.47} \hfill \\ {0.24} \hfill \\ {0.29} \hfill \\ \end{array} }}} \hfill \\ \end{array} } \right]} \hfill & \approx \hfill & {\left[ {\begin{array}{*{20}{c}} {\frac{{\begin{array}{*{20}{c}} {P\left( {{\text{target}}\,{\text{response}}\;{\text{on}}\;{\text{identical}}\;{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{absent}}\,{\text{response}}\;{\text{on}}\;{\text{identical}}\;{\text{trial}}} \right)} \hfill \\ \end{array} }}{{P\left( {{\text{target}}\,{\text{response}}\;{\text{on}}\;{\text{similar}}\;{\text{trial}}} \right)}}} \hfill \\ {\frac{{\begin{array}{*{20}{c}} {P\left( {{\text{flanker}}\,{\text{response}}\;{\text{on}}\;{\text{similar}}\;{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{absent}}\,{\text{response}}\;{\text{on}}\;{\text{similar}}\;{\text{trial}}} \right)} \hfill \\ \end{array} }}{{\begin{array}{*{20}{c}} {P\left( {{\text{target}}\,{\text{response}}\;{\text{on}}\;{\text{disimilar}}\;{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{flanker}}\,{\text{response}}\;{\text{on}}\;{\text{disimilar}}\;{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{absent}}\,{\text{response}}\;{\text{on}}\;{\text{disimilar}}\;{\text{trial}}} \right)} \hfill \\ \end{array} }}} \hfill \\ \end{array} } \right]} \hfill & = \hfill & {\left[ {\begin{array}{*{20}{c}} {\frac{{\begin{array}{*{20}{c}} {0.79} \hfill & {0.79} \hfill & {1.00} \hfill \\ {0.21} \hfill & {0.21} \hfill & {0.00} \hfill \\ \end{array} }}{{\begin{array}{*{20}{c}} {0.79} \hfill & {0.04} \hfill & {0.00} \hfill \\ \end{array} }}} \hfill \\ {\frac{{\begin{array}{*{20}{c}} {0.04} \hfill & {0.79} \hfill & {0.83} \hfill \\ {0.17} \hfill & {0.17} \hfill & {0.17} \hfill \\ \end{array} }}{{\begin{array}{*{20}{c}} {0.79} \hfill & {0.04} \hfill & {0.55} \hfill \\ {0.04} \hfill & {0.79} \hfill & {0.00} \hfill \\ {0.17} \hfill & {0.17} \hfill & {0.45} \hfill \\ \end{array} }}} \hfill \\ \end{array} } \right]} \hfill & {\left[ {\begin{array}{*{20}{c}} {0.28} \hfill \\ {0.29} \hfill \\ {0.43} \hfill \\ \end{array} } \right].} \hfill \\ \end{array} $$\end{document} 7

Thus, if we maximize the role of substitution, it accounts for \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {p_{\text{T}}} + {p_{\text{F}}} = {57}\% $$\end{document} of the trials, and pooling accounts for the remaining p _TF = 43%. However, the mixture model also fits the data well with less substitution, all the way down to none at all, p _T = p _F = 0 and p _TF = 1.

In modeling both experiments, we introduced parameters s _sim and s _dis to describe the distribution of unfaithful responses, but they turn out not to matter for present purposes. They do not constrain the role of substitution.

Note that Eqs. 1–4 apply to Experiment 1 and that Eqs. 5–7 apply to Experiment 2. The Excel spreadsheets used to solve Eqs. 3 and 6 are provided in the online Supplement.

D. Experiment 2: Confirmation

The previous section obtained a nice result. However, minimization is tricky. One might find a local minimum and miss the global minimum. So here we derive the same upper bound on substitution, but in the old-fashioned way, reasoning with discrete equations.

In Experiment 2, an upper bound on the role of flanker substitution is set by the flanker report rate (24%) on dissimilar trials:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {p_{\text{F}}}{P_{\text{F}}}\left( {{\text{flanker}}\;{\text{response}}\;{\text{on}}\;{\text{dissimilar}}\;{\text{trial}}} \right) \leqslant P\left( {{\text{f}}.{\text{r}}.{\text{o}}.{\text{d}}.{\text{t}}.} \right). $$\end{document} 8

Our model (Eq. 6) says that P _F(f.r.o.d.t.) = s _eq and that P(f.r.o.d.t.) ≈ 0.24, so we can substitute

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {p_{\text{F}}}{s_{\text{eq}}} \leqslant 0.{24}. $$\end{document} 9

Similarly, an upper bound on the role of target substitution is set by the target report rate (24%) on similar trials:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {p_{\text{T}}}{P_{\text{T}}}\left( {{\text{target}}\;{\text{response}}\;{\text{on}}\;{\text{similar}}\;{\text{trial}}} \right) \leqslant P\left( {{\text{t}}.{\text{r}}.{\text{o}}.{\text{s}}.{\text{t}}.} \right) $$\end{document} 10

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {p_{\text{T}}}{s_{\text{eq}}} \leqslant 0.{23}. $$\end{document} 11

Summing Eqs. 9 and 11 yields

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \left( {{p_{\text{T}}} + {p_{\text{F}}}} \right){s_{\text{eq}}} \leqslant 0.{47}, $$\end{document} 12

which sets an upper bound on fidelity s _eq. A lower bound is set by the absent-letter rate (12%) on identical trials:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {p_{\text{T}}}{P_{\text{T}}}\left( {{\text{absent}}\;{\text{letter}}\;{\text{response}}\;{\text{on}}\;{\text{identical}}\;{\text{trial}}} \right) + {p_{\text{F}}}\;{P_{\text{F}}}\left( {{\text{a}}.{\text{l}}.{\text{r}}.{\text{o}}.{\text{i}}.{\text{t}}.} \right) \leqslant P\left( {{\text{a}}.{\text{l}}.{\text{r}}.{\text{o}}.{\text{i}}.{\text{t}}.} \right) $$\end{document} 13

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \left( {{p_{\text{T}}} + {p_{\text{F}}}} \right)\left( {{1} - {s_{\text{eq}}}} \right) \leqslant 0.{12}. $$\end{document} 14

Summing Eqs. 12 and 14 yields an upper bound on substitution:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {p_{\text{T}}} + {p_{\text{F}}} \leqslant 0.{59}. $$\end{document} 15

Solving Eqs. 12 and 14 for s _eq yields explicit lower and upper bounds on fidelity s _eq:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {1} - 0.{12}/\left( {{p_{\text{T}}} + {p_{\text{F}}}} \right) \leqslant {s_{\text{eq}}} \leqslant 0.{47}/\left( {{p_{\text{T}}} + {p_{\text{F}}}} \right). $$\end{document} 16

These bounds converge as p _T + p _F increases from zero and coincide when p _T + p _F reaches its maximum of 0.59, at which point 0.8 ≤ s _eq ≤ 0.8.

This result is practically the same as that in Eq. 7. (The upper bound on substitution is 57% in Eq. 7 and 59% in Eq. 15, both about 60%.) The result of the global minimization depends on the somewhat arbitrary cost function, so one should not expect exact agreement.

Thus, if we maximize the role of substitution, it accounts for about 60% of the trials, and pooling accounts for the remaining 40%. However, the mixture model also fits the data well with less substitution, all the way down to none at all, p _T = p _F = 0 and p _TF = 1.

E. Summary

Pooling is needed to account for what substitution cannot. Flanker substitution is blind to the target, so it cannot explain a difference in flanker report rate that depends on flanker–target similarity. Target substitution is blind to the flanker, so it cannot explain a difference in target report rate that depends on flanker–target similarity. This assumes, as was the case in our experiments, that every letter is equally likely to be similar or dissimilar to an unknown target or flanker. Thus, in both experiments, the dissimilar-flanker report rate constrains flanker substitution to account for less than half of the similar-flanker reports. In a similar way, in Experiment 2, the target report rate on similar trials (23%) constrains faithful target substitution to be, at most, 23%, so target substitution accounts for less than half of the target reports on dissimilar trials (47%). This is disappointing. Substitution explains only half of the trials it was designed to explain.

We find that substitution can account for, at most, 57% of the trials, leaving pooling to account for the rest, which it has enough degrees of freedom to do. However, the necessary values may seem implausible: Maximizing the role of substitution requires that pooling never reports the target on similar trials and never reports a flanker on dissimilar trials. If one supposes nonzero minimum frequencies for such reports, the maximum possible role of substitution is correspondingly reduced. We might somewhat arbitrarily suppose that, when the flanker is similar, the frequency of reporting the target ought to be at least half of the frequency of reporting the flanker,

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {P_{\text{TF}}}\left( {{\text{target}}\;{\text{response}}\;{\text{on}}\;{\text{similar}}\;{\text{trial}}} \right) \geqslant {P_{\text{TF}}}\left( {{\text{flanker}}\;{\text{rsponse}}\;{\text{on}}\;{\text{similar}}\;{\text{trial}}} \right)/2, $$\end{document} 17

and that when the flanker is dissimilar, the frequency of reporting it is at least as great as for reporting any given absent letter,

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {P_{\text{TF}}}\left( {{\text{flanker}}\;{\text{response}}\;{\text{on}}\;{\text{dissimilar}}\;{\text{trial}}} \right) \geqslant {P_{\text{TF}}}\left( {{\text{absent}}\;{\text{response}}\;{\text{on}}\;{\text{dissimilar}}\;{\text{trial}}} \right)/4. $$\end{document} 18

In terms of the free parameters of the general-pooling model defined in Eq. 6, this becomes

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {p_2} \geqslant \frac{{{p_3}}}{2} $$\end{document} 19

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {p_5} \geqslant \frac{{1 - {p_4} - {p_5}}}{4}. $$\end{document} 20

Adding these two plausible constraints (in Solver) reduces the (maximum possible) substitution rate p _T + p _F from 57% down to 32% of the trials. (The spreadsheet in the online Supplement makes these options available.)

In conclusion, pooling (with many degrees of freedom) is needed to explain 100% – 57% = 43% of the trials and can explain them all. Substitution (with fewer degrees of freedom) is not needed and can explain, at most, 57% of the trials. (Adding mild constraints, Eqs. 17 and 18, to ensure the plausibility of the general-pooling process reduces the upper bound on substitution from 57% down to 32%.) Since we have to suppose pooling, parsimony favors dispensing with substitution and its extra explanatory burden.

We have shown that when observers are asked to identify a crowded object, nearly half of their reports are based on a combination of information from target and flankers, rather than being based on a single letter.

F. Experiment 3: Without crowding. Similar or dissimilar

Experiment 3 is analyzed in the same way as Experiment 2, using the same three-process mixture model (Eq. 21). However, the conditions and results are different, so different model constraints are revealed when the same model is fit to the new data. Experiments 1 and 2 were done peripherally, and we expected crowding, but Experiment 3 was done centrally, so we do not expect crowding.

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \begin{array}{*{20}{c}} {\text{Data}} \hfill & {} \hfill & {{\text{Response}}\;{\text{Probability}}} \hfill & {} \hfill & {{\text{Process}}\;{\text{Response}}\;{\text{Probability}}} \hfill & {{\text{Process}}\;{\text{Probability}}} \hfill \\ {} \hfill & {} \hfill & {} \hfill & {} \hfill & {\begin{array}{*{20}{c}} {\;{\text{T}}\;\;\;\;\;\;\;\;} \hfill & {{\text{F}}\;\;\;\;\;\;\;} \hfill & {\text{TF}} \hfill \\ \end{array} } \hfill & {} \hfill \\ {\left[ {\begin{array}{*{20}{c}} {0.63} \hfill \\ {0.37} \hfill \\ \hline {0.52} \hfill \\ {0.22} \hfill \\ {0.26} \hfill \\ \hline {0.60} \hfill \\ {0.10} \hfill \\ {0.30} \hfill \\ \end{array} } \right]} \hfill & \approx \hfill & {\left[ {\begin{array}{*{20}{c}} {P\left( {{\text{target}}\;{\text{response}}\;{\text{on}}\;{\text{identical}}\;{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{absent}}\;{\text{response}}\;{\text{on}}\;{\text{identical}}\;{\text{trial}}} \right)} \hfill \\ \hline {P\left( {{\text{taget}}\;{\text{response}}\;{\text{on}}\;{\text{similar}}\;{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{flanker}}\;{\text{response}}\;{\text{on}}\;{\text{similar}}\;{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{absent}}\;{\text{response}}\;{\text{on}}\;{\text{similar}}\;{\text{trial}}} \right)} \hfill \\ \hline {P\left( {{\text{target}}\;{\text{response}}\;{\text{on}}\;{\text{dissimilar}}\;{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{flanker}}\;{\text{response}}\;{\text{on}}\;{\text{dissimilar}}\;{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{absent}}\;{\text{response}}\;{\text{on}}\;{\text{dissimilar}}\;{\text{trial}}} \right)} \hfill \\ \end{array} } \right]} \hfill & = \hfill & {\left[ {\begin{array}{*{20}{c}} {{S_{\text{eq}}}} \hfill & {{S_{\text{eq}}}} \hfill & {{p_1}} \hfill \\ {1 - {S_{\text{eq}}}} \hfill & {1 - {S_{\text{eq}}}} \hfill & {1 - {p_1}} \hfill \\ \hline {{S_{\text{eq}}}} \hfill & {{S_{\text{sim}}}/2} \hfill & {{p_2}} \hfill \\ {{S_{\text{sim}}}/2} \hfill & {{S_{\text{eq}}}} \hfill & {{p_3}} \hfill \\ {1 - {\Sigma_2}} \hfill & {1 - {\Sigma_2}} \hfill & {1 - {\Sigma_2}} \hfill \\ \hline {{S_{\text{eq}}}} \hfill & {{S_{\text{dis}}}/3} \hfill & {{p_4}} \hfill \\ {{S_{\text{dis}}}/3} \hfill & {{S_{\text{eq}}}} \hfill & {{p_5}} \hfill \\ {1 - {\Sigma_2}} \hfill & {1 - {\Sigma_2}} \hfill & {1 - {\Sigma_2}} \hfill \\ \end{array} } \right]} \hfill & {\left[ {\begin{array}{*{20}{c}} {{p_{\text{T}}}} \hfill \\ {{p_{\text{F}}}} \hfill \\ {{p_{\text{TF}}}} \hfill \\ \end{array} } \right]} \hfill \\ \end{array} $$\end{document} 21

Here is the solution found by Excel and Solver:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {0.63} \hfill \\ {0.37} \hfill \\ \hline {0.52} \hfill \\ {0.22} \hfill \\ {0.26} \hfill \\ \hline {0.60} \hfill \\ {0.10} \hfill \\ {0.30} \hfill \\ \end{array} } \right]} \hfill & \approx \hfill & {\left[ {\begin{array}{*{20}{c}} {P\left( {{\text{target}}\;{\text{response}}\;{\text{on}}\;{\text{identical}}\;{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{absent}}\;{\text{response}}\;{\text{on}}\;{\text{identical}}\;{\text{trial}}} \right)} \hfill \\ \hline {P\left( {{\text{target}}\;{\text{response}}\;{\text{on}}\;{\text{similar}}\;{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{flanker}}\;{\text{response}}\;{\text{on}}\;{\text{similar}}\;{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{absent}}\;{\text{response}}\;{\text{on}}\;{\text{similar}}\;{\text{trial}}} \right)} \hfill \\ \hline {P\left( {{\text{target}}\;{\text{response}}\;{\text{on}}\;{\text{dissimilar}}\;{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{flanker}}\;{\text{response}}\;{\text{on}}\;{\text{dissimilar}}\;{\text{trial}}} \right)} \hfill \\ {P\left( {{\text{absent}}\;{\text{response}}\;{\text{on}}\;{\text{dissimilar}}\;{\text{trial}}} \right)} \hfill \\ \end{array} } \right]} \hfill & = \hfill & {\left[ {\begin{array}{*{20}{c}} {0.61} \hfill & {0.61} \hfill & {0.82} \hfill \\ {0.39} \hfill & {0.39} \hfill & {0.18} \hfill \\ \hline {0.61} \hfill & {0.10} \hfill & {0.00} \hfill \\ {0.10} \hfill & {0.61} \hfill & {1.00} \hfill \\ {0.28} \hfill & {0.28} \hfill & {0.00} \hfill \\ \hline {0.61} \hfill & {0.06} \hfill & {1.00} \hfill \\ {0.06} \hfill & {0.61} \hfill & {0.00} \hfill \\ {0.33} \hfill & {0.33} \hfill & {0.00} \hfill \\ \end{array} } \right]} \hfill & {\left[ {\begin{array}{*{20}{c}} {0.84} \hfill \\ {0.08} \hfill \\ {0.08} \hfill \\ \end{array} } \right]} \hfill \\ \end{array} $$\end{document} 22

Starting at the left, the first matrix in Eqs. 21 and 22 is the human result. The second matrix is our model for it. Each element in the third matrix is the probability, given that a particular process is active, that it will emit a particular response on a particular kind of trial. The fourth matrix, last on the right, is the probability of each kind of process being active on any given trial. Note that, in this fit, we discover that the pooling process (when invoked) always reports a flanker on similar trials (p ₃ = 1.00) and always reports the target on dissimilar trials (p ₄ = 1.00).

In Experiment 2, we found that all three processes were similarly active: pooling, 43%; target substitution, 28%; and flanker substitution, 29%. Here, in Experiment 3, 84% of the trials are target substitution, and only a small fraction are pooling (8%) or flanker substitution (8%). Substitution accounts for 92% of the trials.