Exploring the Energy Landscapes of Protein Folding Simulations with Bayesian Computation

Abstract

Nested sampling is a Bayesian sampling technique developed to explore probability distributions localized in an exponentially small area of the parameter space. The algorithm provides both posterior samples and an estimate of the evidence (marginal likelihood) of the model. The nested sampling algorithm also provides an efficient way to calculate free energies and the expectation value of thermodynamic observables at any temperature, through a simple post processing of the output. Previous applications of the algorithm have yielded large efficiency gains over other sampling techniques, including parallel tempering. In this article, we describe a parallel implementation of the nested sampling algorithm and its application to the problem of protein folding in a Gō-like force field of empirical potentials that were designed to stabilize secondary structure elements in room-temperature simulations. We demonstrate the method by conducting folding simulations on a number of small proteins that are commonly used for testing protein-folding procedures. A topological analysis of the posterior samples is performed to produce energy landscape charts, which give a high-level description of the potential energy surface for the protein folding simulations. These charts provide qualitative insights into both the folding process and the nature of the model and force field used.

Introduction

Approximately 50 years ago, Anfinsen and colleagues (1) demonstrated that protein molecules can fold into their three-dimensional native state reversibly, leading to the view that these structures represented the global minimum of a rugged funnel like energy landscape (1–3).

According to the hierarchical folding theory of Baldwin and Rose (4,5), a protein folds by first forming local structural elements, namely, α-helices and β-strands. These secondary structure elements then interact with each other, resulting in the formation of the folded protein. The formation of local structural elements reduces the entropy of the protein (for example, the side chains of helical residues are strongly constrained by the rest of the helix). This loss of entropy is compensated by favorable short-range interactions, including hydrogen bonding and desolvation of backbone polar groups. This is considered to be a fundamental property of proteins, and any model system attempting to simulate protein folding should mimic this property.

Although there has been recent evidence of hierarchical folding in long timescale molecular dynamics simulations made possible by the use of custom designed supercomputers (6), simplified Gō-type models remain an important class of protein models in the investigation of energy landscapes. Gō models assume that nonnative interactions do not contribute to the overall shape of the folding energy surface (7,8). In this work we use an extended Gō-type model, in which a Gō potential captures interactions between contacts of the native state of the protein, but attractive nonnative interactions are also permitted (for example, hydrogen bonds can form between residues that are not in contact in the native state). This addition allows us to explore a more realistic rugged energy landscape compared to the “perfect funnel” found in a standard Gō model (8), while maintaining the ability to perform simulations with limited computational resources.

The energy landscapes of protein-folding simulations are most commonly visualized in terms of two- or three-dimensional plots of microscopic or free energy versus a reaction coordinate, such as the fraction of residue contacts in common with the native state or the root mean-square deviation (RMSD) between a given conformation and the native state (9,10). Originally developed for reduced lattice models, these approaches have since been used for all-atom off-lattice simulations, although, in these more realistic models, they offer only an indirect visualization of the energy landscape at a single scale (11). Projection into the space defined by principal components analysis of the contact map has also been used to provide a two-dimensional visualization of the energy surface (12). Techniques adapted from robotic motion planning have been used to provide a probabilistic roadmap of protein folding, which may be mapped onto a conceptual drawing of the potential energy surface (13). Protein potential energy surfaces and folding funnels have also been visualized by disconnectivity graphs (14) and scaled disconnectivity graphs (15,16). Although these latter methods have the advantage of providing a visualization of the whole energy landscape, they rely on creating a large database of local energy minima of the surface, and are therefore impractical for large systems; they also do not provide information about the entropy of the system (which governs the widths of the conceptual protein-folding funnel).

The funnel like nature of the energy landscape provides a challenging conformational space for computer simulations to explore, because only an exponentially small number of conformations have low energy and low entropy and are found toward the bottom of the funnel; the system also undergoes a first-order phase transition as the protein collapses into its native state. In this work, we use nested sampling to explore the energy landscapes of protein folding simulations. Nested sampling is a Bayesian sampling technique introduced by Skilling (17,18), designed to explore probability distributions where the posterior mass is localized in an exponentially small area of the parameter space. It both provides an estimate of the evidence (also known as the marginal likelihood, or partition function) and produces samples of the posterior distribution. Nested sampling offers distinct advantages over methods such as simulated annealing (19), Wang-Landau sampling (20), parallel tempering (replica exchange) (21), and annealed importance sampling (22), in systems characterized by first-order phase transitions (17,23). The technique reduces multidimensional problems to one dimension and has a single key parameter in the trade-off between cost and accuracy. The calculation of free energies by thermodynamic integration (24) and thermodynamic observables, such as heat capacities, typically involves multiple simulations at different temperatures. Nested sampling provides an efficient framework for computing the partition function and hence thermodynamic observables at any temperature, without the need to generate new samples at each temperature. Hence, it allows us to directly investigate the macroscopic states of the protein-folding pathway and evaluate the associated free energies. Nested sampling has previously been used in the field of astrophysics (25) and for exploring potential energy hypersurfaces of Lennard-Jones atomic clusters (23), yielding large efficiency gains over parallel tempering. Its use in this article represents, to our knowledge, the first application of this technique to a biophysical problem.

Materials and Methods

In general, the energy of a polypeptide, E(Ω,θ), is defined by its conformation, Ω, and arbitrary interaction parameters, θ. These interaction parameters may be as diverse as force constants, distance cutoffs, dielectric permittivity, atomic partial charges, etc. This energy, in turn, defines the probability of a particular conformation, Ω, at inverse thermodynamic temperature β via the Boltzmann distribution

$$P\left(\Omega ,\theta |\beta \right)=\frac{1}{Z\left(\theta ,\beta \right)}\text{exp}\left[-E\left(\Omega ,\theta \right)\beta \right],$$ (1)

$$Z\left(\theta ,\beta \right)=\int d\Omega \text{exp}\left[-E\left(\Omega ,\theta \right)\beta \right],$$ (2)

where Z(θ, β) is the partition function (or evidence, in Bayesian terminology). In the following, energy is expressed in units of RT, the product of the molar gas constant and absolute temperature and β = 1/RT.

In Bayesian statistics, with θ an unknown parameter, D the observed data, and H the underlying model or hypothesis, we have the following relation (Bayes' rule)—posterior × evidence = likelihood × prior—

$$\mathcal{P}\left(\theta |D,H\right)Z=\mathcal{P}\left(D|H,\theta \right)\mathcal{P}\left(\theta |H\right),$$

where Z, the evidence, is defined as

$$Z=\int \mathcal{P}\left(D|H,\theta \right)\mathcal{P}\left(\theta |H\right)d\theta .$$

Nested sampling provides an algorithm for estimating the evidence, Z = P(D|H), and the procedure additionally explores the posterior distribution, allowing its properties to be estimated.

Procedure

We define X(λ) = λ to be the proportion of the prior distribution with likelihood L(X) > λ. Then, following Skilling (17), the evidence is

$$Z={\int }_0^{1}L\left(X\right)dX,$$

where L(X(λ)) = λ and dX = π(θ)dθ, with π(θ) the prior distribution. Fig. 1 shows the graph of L against X (this is not to scale, as normally the bulk of the posterior is in an exponentially small area of the phase space). L is a decreasing function of X, as the restriction on the likelihood becomes tighter as λ increases. The area under the curve is Z. The nested sampling procedure estimates points on this curve (see Algorithm, below) and then uses numerical integration to calculate Z.

Figure 1.

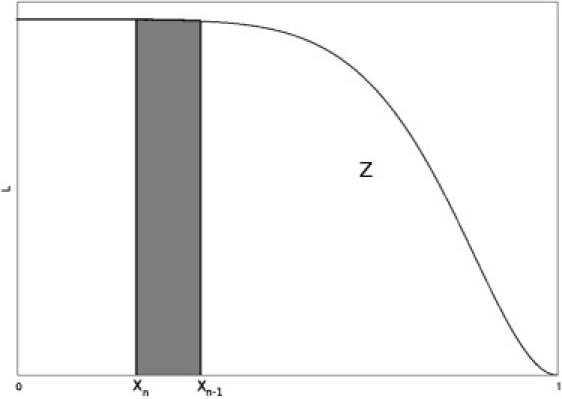
Evidence Z is the area under the function L(X). The sample θ_n represents X_n−1 – X_n of the phase space volume; the proportion of the x axis is shaded. Its weighting for the posterior is L_n (X_n−1 – X_n)/Z; the proportion of Z is shaded.

Algorithm

• 1.Sample (uniformly, with respect to the prior distribution) K points of the parameter space {θ₁…θ_K}, i.e., the “active list”; then calculate their likelihoods: {L(θ₁),…,L(θ_K)}.
• 2.Take the sample point with the smallest likelihood; save it as (L₁, X₁) (see below for an estimate of X); remove this point from the active list.
• 3.Generate a new point θ sampled uniformly (with respect to the prior distribution) from those points with likelihood L(θ) > L^∗ = L₁; then add it to the active list.
• 4.Repeat Steps 2 and 3, generating (L₂, X₂), (L₃, X₃),…,(L₁, X_i),… .

X₁ is located at the largest of N numbers uniformly distributed on (0, X₀), where X₀ = 1. Skilling (17) suggests using the expected value of the shrinkage ratio, X_i/X_i−1, to estimate X_i (the estimate of X for iteration i), where X_i is the largest of N numbers uniformly distributed on (0, X_i−1). The shrinkage ratio has the probability density function f(t) = Kt^K−1, with mean and standard deviation log (t) = (−1 ± 1)/K, and, as each shrinkage ratio is independent, we find, if uncertainties are ignored,

$$\text{log}\left(X_i\right)=\left(-i\pm \sqrt{i}\right)/K\Rightarrow X_i\approx \text{exp}\left(-i/K\right).$$

It is also possible to use the arithmetic expected value to estimate X_i (26). This implies that X_i = αⁱ, where α = K/(K + 1). In the limit of large K, these two approaches are identical and henceforth we will use α = exp(−1/K) or K/(K + 1), and X_n = αⁿ.

Parallel nested sampling

For high-dimensional systems, sampling uniformly (conditional upon the likelihood being above a fixed value, L^∗) is not computationally tractable. In this case, a Markov chain can be used to explore the parameter space (22). To generate a new point, one of the active set of points (not necessarily the one with the lowest likelihood) is chosen to be the start of a short Monte Carlo (MC) run, with all moves that keep the likelihood above L^∗ being accepted.

Starting the MC run from a copy of one of the points of the active set, chosen at random, is crucial to nested sampling. Suppose we have a bimodal likelihood function. Once L^∗ is sufficiently high, the region of the parameter space the chain is allowed to explore will no longer be connected; it will have two disconnected components. Without copying, all active points that enter the subordinate component will be trapped there. With copying, provided at least one enters the dominant mode, then as L^∗ increases, active points in the subordinate mode will be replaced by ones from the dominant mode. This is particularly important for likelihood functions for which the dominant mode splits again at a higher likelihood. In general, for a given K, if the relative phase space volume of a mode is <1 / K in comparison to the rest of the space at the splitting likelihood, the chances of nested sampling exploring the mode is small (23). Therefore, the parameter K controls the resolution of the exploration.

The number of trial MC moves per nested sampling iteration, m, is another key parameter when using nested sampling for higher dimensional systems. If m is too small, the parameter space is inadequately explored; new active set samples and the current conformations they are copied from remain very similar. Setting m too high results in longer than necessary runtimes, as conformations partway through the MC run are already sufficiently different from their starting positions. Hence, K controls which regions of the parameter space are available to the algorithm and m controls how well these regions are explored.

We parallelized the nested sampling algorithm by removing the P points with the lowest likelihood at each nested sampling iteration, one for each processor used. Each processor then runs its own independent MC simulation to replace one of the removed points. For post processing, at each iteration we only store the point that has the P^th lowest likelihood and adjust α accordingly; α = 1 − P/(K + 1).

Running a parallel nested sampling algorithm with K points explores the parameter space more effectively than P serial nested sampling simulations each with K/P points in the active set, while requiring equal computational resources. Consider a likelihood function, which splits n times in the dominant mode (i.e., contains the majority of the evidence), with the probabilities of an exploratory active point falling into the dominant mode being W₁,W₂,…W_n at the critical likelihood (which is the likelihood of splitting). Defining success as exploring the dominant mode at the n^th split in at least one simulation, it can be shown, using an argument similar to that of Sivia and Skilling (18), that

$$\mathbb{P}\left(\text{success}|\text{one}\text{simulation}\text{with}K\text{points}\right)={\Pi }_g\left[1-{\left(1-W_g\right)}^K\right]$$ (3)

and

$$\mathbb{P}\left(\text{success}|P\text{simulations}\text{with}K/P\text{points}\right)=1-{\left(1-{\Pi }_g\left(1-{\left(1-W_g\right)}^{K/P}\right)\right)}^P.$$

For example, if n = 2, W₁ = W₂ = 0.1, K = 32, and P = 4, then ℙ(success|parallel) = 0.933 and ℙ(success|serial) = 0.792.

Posterior samples

The sample points removed from the active set, labeled θ₁, θ₂,…, say, can be used to estimate properties of the posterior distribution. Sample point θ_n represents

$${\omega }_n=X_{n-1}-X_n$$

of the phase space volume (with respect to the prior distribution) and hence

$${\chi }_n=\frac{\left(X_{n-1}-X_n\right)L\left({\theta }_n\right)}{Z}$$

is the relative volume of the posterior space that θ_n represents; see Fig. 1.

In the case of a Boltzmann distribution, at inverse temperature β, L(θ_n) = exp (−E_nβ) and hence, by calculating χ_n(β), a single nested sampling simulation can provide the expectation value of any thermodynamic observable, such as heat capacity, at any temperature. Given a property Q(θ|β) of the posterior,

$$\mathbb{E}\left(Q|\beta \right)\approx \sum _i{\chi }_i\left(\beta \right)Q\left({\theta }_i\right).$$ (4)

In energetic terms, the nested sampling scheme is built from a set of decreasing energy levels, {E_n}, with the energy of conformation Ω_n given by Eq. 5. Each energy level has an associated weight, which is also decreasing. At each energy level, a set of K sample points (or conformations), {Ωⁱ_n}, is obtained by uniform sampling from the energy landscape below E_n: Ωⁱ_n ∼ U(Ω: E(Ω) < E_n). After every iteration, a new lowest energy level E_n+1 is defined to be at a fixed fraction, α, of the current energy distribution. In this way, a fraction αⁿ of the whole phase space has energy below E_n, and a fraction αⁿ⁺¹ has energy below E_n+1. The phase space volume will therefore shrink exponentially, by a factor of α, with every nested sampling iteration, and the algorithm is able to locate exponentially small regions of phase space.

The protein model

The polypeptide model we use is adapted from our previous published work (27–30). It is fully described in the Supporting Material and a summary is provided below.

Our polypeptide model features all-atom representations of the polypeptide backbone and β-carbon atoms. Other side-chain atoms are represented by one or, in the case of branched side chains, two pseudoatoms, following Srinivasan and Rose (31).

For a given protein sequence, R, the Boltzmann distribution defines the probability, P(R, Ω|β), of it adopting a particular conformation, Ω, at inverse thermodynamic temperature β. This probability can be factorized into the product of the sequence-dependent likelihood for a given conformation and the prior distribution of conformations, P(R, Ω) = P(R|Ω)P(Ω). This can be rewritten in energetic terms as

$$E\left(R,\Omega \right)=-\text{ln}P\left(R|\Omega \right)+E(\Omega ),$$ (5)

where sequence-dependent and sequence-independent contributions to the energy are separated. We assume that the sequence-independent term, E(Ω), is defined by short-range interactions among the polypeptide backbone, β-carbon, and pseudo-atoms. At room temperature, van der Waals repulsions and covalent bonding between atoms are extremely rigid interactions that contribute to this energy. Another large contribution comes from hydrogen bonding, but the magnitude of this interaction is vaguely understood. The sequence-dependent part of the potential (the negative log-likelihood) can be approximated by the pairwise interactions between side chains, which make the largest contribution to this term. In this work, these interactions are modeled by a Gō-type potential based on a regularized native contact map (27), which contains lateral contacts in parallel and antiparallel β-sheets and contacts between residues i and i + 3 in α-helices (32,33). Our model also includes a hydrophobic packing term; hydrophobic side chains coming into contact with hydrophobic or amphipathic side chains are rewarded with a decrease in energy (31). The force constants for these side-chain interactions, as well as backbone hydrogen bonding, are optimized using a novel statistical machine learning technique (29).

Nested sampling is initialized with K conformations, uniformly distributed over the space of dihedral angles (i.e., every ϕ_i, ψ_i ∼ U[−180°, 180°]). To generate new sample points we use our implementation of an efficient Metropolis Monte Carlo (MMC) algorithm (28,30), which relies on local Metropolis moves, as suggested in earlier studies (34). In contrast to other programs that rely on local Metropolis moves in the space of dihedral angles, our sampler utilizes local crankshaft rotations of rigid peptide bonds in Cartesian space. An important feature of our model is the elasticity of the α-carbon valence geometry. With flexible α-carbon valence angles, it becomes possible to use crankshaft moves inspired by earlier MMC studies of large-scale DNA properties. The amplitudes of proposed crankshaft rotations were chosen uniformly from [−α₀, α₀] where, at every 2000 nested sampling iterations, α₀ (the maximum allowed proposed amplitude) was recalculated, attempting to keep the acceptance rate at 50% (the trial MC moves used for this calculation were then ignored).

We ran simulations until Z(β) converges for β = 1 (T = 25°C), which implies that we have sampled from the thermodynamically accessible states for all temperatures smaller than β (>T). The nested sampling algorithm marches left across the x axis of Fig. 1. The step size is constant in log X and the larger the K, the smaller the step size. For a given protein and β, we find that simulations terminate at approximately the same point on the x axis (for protein G, with β = 1, this is ∼e⁻⁴⁴⁰). This implies that the total number of iterations is proportional to K, and the total number of MC moves is proportional to mK. The results for protein G shown below are from a simulation with K = 20,000 and m = 15,000, which used 32 processors (Xeon X5650; Intel, Santa Clara, CA), had 1.38 × 10¹¹ MC moves, and took ∼22 h.

Energy landscape charts

We use the algorithm recently introduced by Pártay et al. (23), which uses the output of a nested sampling simulation to generate an energy landscape chart, facilitating a qualitative understanding of potential energy surfaces. It has the advantage of showing the large-scale features of the potential energy surface without requiring a large number of samples.

The output of a nested sampling simulation is a sequence of sample points with decreasing energy. Each sample point (conformation), Ω_n, represents ω_n = αⁿ⁻¹ − αⁿ of the phase space and has energy E_n(Ω_n). A metric defining the distance between two conformations is required, and using this, a topological analysis of the sample points is performed. As the metric, we use the root mean-square deviation of the backbone and side-chain nonhydrogen atoms of a pair of conformations; that is, the sum of the Euclidean distances of corresponding atoms after the two conformations have been translated and rotated in space to minimize the overall distance.

A graph 𝒢 is created with the sample points as nodes and arcs joining a sample to the k nearest samples that have higher energy. In this work, k is chosen to be 15 throughout. We then start with an empty graph (${\mathcal{G}}^{\prime }$), adding nodes one at a time (starting with the lowest energy) to gradually rebuild 𝒢.

Energy landscape charts are produced with energy on the vertical axis, and, at a given energy E_n, the width of the chart is proportional to the sum of the weights of the points below that energy (i.e., ω_n + ω_n+1 + …), that is, the available phase space volume in the prior space, contained at <E_n. On the horizontal scale, the chart is split into different basins corresponding to the disconnected subgraphs that exist when sample n is added to ${\mathcal{G}}^{\prime }$. The relative widths of the basins is given by the ratio of the sum of the weights of the sample points in the disconnected subgraphs. The ordering of the basins horizontally is arbitrary. Due to the rapid shrinking of the available phase space volume with decreasing energy, for better visualization, a horizontal scaling is applied by an exponential function of the energy, similar to Pártay et al. (23). The energy landscape chart represents a potential energy landscape for the system.

We also use a variant of the energy landscape charts where the width of the chart is proportional to the sum of the posterior weights, χ_n = ω_n exp(−E_nβ)/Z(β), i.e., (χ_n + χ_n+1 + …), at inverse temperature β. Hence, the relative widths of the basins correspond to the probabilities of adopting a conformation from one basin or another. These energy landscape charts, therefore, represent the energy landscape as it is experienced by the protein at inverse temperature β. In the following, the two versions will be referred to as prior and posterior energy landscape charts, according to the weights used in the calculation of their basin widths.

Results

To validate the nested sampling procedure, we simulated the folding of an isolated 16-residue polyalanine β-hairpin. We then conducted folding simulations on a number of small proteins that are commonly used for testing protein folding procedures: protein G (PDB code 1PGA), the SH3 domain of Src tyrosine kinase (PDB code 1SRL), and chymotrypsin inhibitor 2 (PDB code 2CI2).

Isolated polyalanine β-hairpin

We used a Gō-like potential to simulate the folding of an isolated 16 residue polyalanine β-hairpin. Fig. S1 in the Supporting Material (bottom panel) shows a snapshot of five (equally spaced along the log(X) axis) conformations from a single simulation with K = 1000, m = 2500 (a total of 1.12 × 10⁸ MC moves). At the beginning there is a rapid decrease in energy, moving from extended conformations (at first those with van der Waals collisions) to hairpinlike structures (A–C). The final part of the simulation moves through the exponentially small volume of the phase space containing hairpinlike structures, gradually decreasing in energy toward a fully formed hairpin (D and E).

We used the hairpin to check the behavior of the nested sampling procedure: Fig. S1 (top panel) shows how α₀ (the maximum proposed crankshaft rotation amplitude) varies with the energy threshold for a simulation with K = 1000. As lower energy is reached, α₀ is reduced to keep the acceptance rate near 0.5. Fig. S1 (second panel) shows the acceptance rate. Fig. S1 (third panel) shows the difference between the start and end points of a single MC chain, specifically the drift per dihedral angle, where the drift is the L₂-norm of the dihedral angles.

The protein model used stabilizes room temperature secondary structure formation; it folds isolated helices and hairpins very effectively. This is reflected in the energy landscape charts that consist of a single funnel (not shown).

Fig. S2 (top) shows the time evolution of the dihedral angles of four residues of the 16-residue polyalanine. The formation of the hairpin can be clearly seen. For example, the dihedral angles of the residues in the strands 4 and 11 converge to the standard β-sheet area of the Ramachandran plot. The Gō-like potential used was designed for a hairpin with a two-residue turn, and this is found to be the case. The dihedral angles of the turn residues 8 (60 ± 15, −90 ± 30) and 9 (−150 ± 30, 0 ± 30) are closest to the values of a type II′ turn ((60, −120) and (−80, 0)) (35). Fig. S2 (bottom) shows the energy of the snapshots (right-hand axis) for nested sampling plotted against time. The monotonic decrease of the energy over a very large energy range allows us to view the formation of the hairpin.

Due to the nature of the model used, the folding pathway of the hairpin is relatively simple to sample, and parallel tempering can also successfully fold the hairpin. However, in this case, we need a very large temperature range to explore the whole parameter space and view the folding pathway in its entirety. For example, Fig. S2 (bottom) shows the energy of two of the parallel tempering chains; room temperature and 300°C. For real proteins, which have more complicated energy landscapes and possibly high energy barriers, it is difficult to know the temperature range required for parallel tempering to explore the entire parameter space and not be trapped in a particular basin. Nested sampling, with its top-down, temperature-independent approach, does not suffer from this problem.

Another of the advantages of nested sampling is that simulations are temperature-independent, and hence can provide estimates of thermodynamic variables at any temperature. Fig. 2 shows the heat capacity (C_v) curve for the 16-residue polyalanine. The curves were calculated using nested sampling (converged down to −25°C, so that the C_v curve does not stop abruptly at room temperature), and parallel tempering. The solid line is calculated using 10 nested sampling simulations each with 1.3 × 10⁹ MC moves. The dashed lines show twice the standard error. The parallel tempering curve shows the heat capacity using 10 parallel tempering simulations (again each with 1.3 × 10⁹ MC moves) with error bars showing twice the standard error. For parallel tempering, the heat capacity is only calculated for discrete temperatures and a procedure such as Boltzmann reweighting (36) is needed to calculate the continuous curve.

Figure 2.

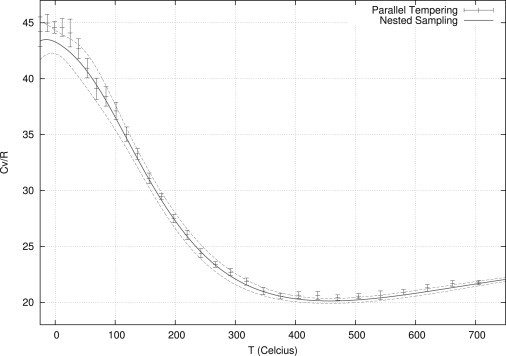
Heat capacity curve for the 16-residue polyalanine. The nested sampling simulations (solid line) use 1.3 × 10⁹ MC moves, with error lines denoting two standard errors from the mean. The parallel tempering uses the same number of MC moves again with error bars showing two standard errors from the mean.

There appears to be good agreement between the methods. Previous results have found nested sampling to be more efficient at calculating the heat capacity curves (23). In this example, we found nested sampling to be of similar efficiency to parallel tempering. We believe this to be because, unlike the system presented in Pártay et al. (23), our phase transition (from coil to hairpin) occurs over a very large energy (and hence temperature) range from which parallel tempering can successfully sample.

Protein G

Protein G is a 56-residue protein consisting of an antiparallel four-stranded β-sheet and an α-helix, with a β-Grasp (ubiquitin-like) fold, which has been extensively studied by a variety of folding simulation techniques (37–40). Its native structure is shown on the left of Fig. S3. All figures of protein G in this article have been oriented so that the first β-strand is the second strand from the right and the N-terminal residue is at the top.

As described above, the nested sampling procedure can be used to estimate the thermodynamic energy of the system at any temperature, using Eq. 4 For protein G, at room temperature (β = 1.0), the thermodynamic energy is −190 units. Fig. S3 shows a sample of four room-temperature, thermodynamically accessible conformations found by a single nested sampling simulation with K = 20,000 and m = 15,000. The conformers have energies −189, −190, −191, and −190, respectively, with backbone RMSDs (from the crystal structure) of 1.93 Å, 2.96 Å, 3.97 Å, and 5.22 Å, respectively. The estimated value of the backbone RMSD at β = 1, calculated using Eq. 5, is $\mathbb{E}\left(\text{RMSD}\right|\beta =1)=3.21\AA$.

Conformers A–D in Fig. S3 have the correct backbone topology, close to the native structure, but there is a reasonable amount of variation in the orientation of the helix with respect to the β-sheet at this temperature. It is important to remember that protein structures are intrinsically flexible (41–43), and the crystal structure (1PGA.pdb) is only one member of an ensemble of conformations that the protein may explore. In the Supporting Material we demonstrate that flexible motion of protein G allows a substantial reorientation of the axis of the helix with respect to the sheet. Conformers A–D in Fig. S3, which differ from the native state principally in the orientation of the helix relative to the sheet, may therefore be more representative of the native state than the RMSD alone suggests.

The first half of the nested sampling simulation is spent exploring high-energy conformations with no noticeable secondary structure and often steric hindrances. In the second half of the simulation, once the long-range quadratic bias potential has pulled the secondary structure elements close together, the short-range hydrogen-bond interaction contributions increase to dominate the bias potential contributions, having a steeper gradient in the last third of the simulation (see Fig. S4 (top)). The short-range hydrophobic interaction contributions are the smallest, but nevertheless not negligible; they ensure the correct packing of the hydrophobic and amphipathic side chains at conformations available at room temperature (see below and Fig. 3). Fig. S4 (bottom) shows a sequence of 10 conformers in order of decreasing energy. These conformers come from the deepest basin of the energy landscape chart of a simulation (higher energy conformers come from the part of the energy landscape chart that contains the deepest basin). The sequence illustrates how the secondary and tertiary structure accrete in the course of a simulation, capturing the essence of the hierarchical folding model. The sequence is not, however, a single folding pathway, in the sense of a molecular dynamics trajectory; there are many conformations in the active set in the same basin. It is possible, though, that Fig. S4 (bottom) represents a plausible sequence of events leading to the native structure.

Figure 3.

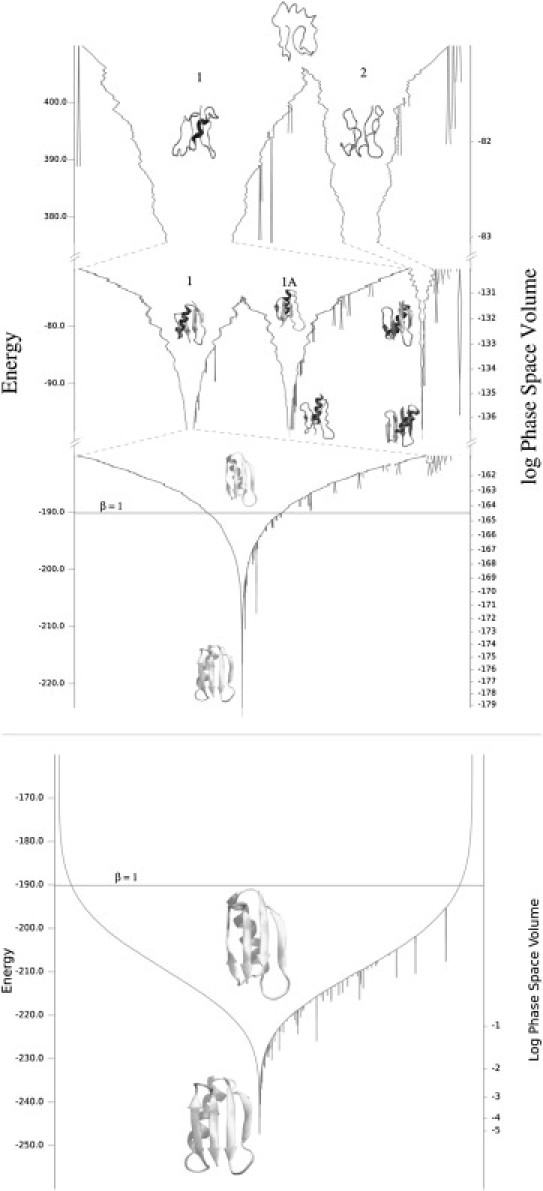
(Top) Prior (potential) energy landscape chart. (Bottom) Posterior energy landscape chart at β = 1, for a nested sampling simulation of protein G using K = 20,000 and m = 15,000. (Left axis) The energy is shown in units of RT, and the width of the chart is proportional to the sum of the prior (top) and posterior (bottom) weights of the nested sampling points below the given energy level (shown on the right axis). The prior energy landscape chart shows the potential energy surface and the posterior energy landscape chart shows, for a given temperature, the probabilities of finding conformations from the different basins. At β = 1 (room temperature), only funnel 1 is accessible. The scaling function used for the prior energy landscape chart is exp(−fE) (with f being 0.1, 0.4, and 0.7 on the top, middle, and bottom panels of the prior energy landscape chart, respectively). Example conformers from the main basins, at various energy levels, are shown on the charts.

Energy landscape charts using the prior and posterior weights for a nested sampling simulation of protein G using K = 20,000 and m = 15,000, calculated using a connectivity number k = 15, are shown in Fig. 3. The volume scale on the right-hand axis shows the proportion of the prior and posterior phase space volume available below the given energy level. The width of the chart uses this scale. Basins that contain <1/1000th of the probability mass at the point of splitting are not shown on the diagram. Conformers have been placed on the chart to provide examples of the samples found in different places of the chart.

Topologically, for energy above 405 units, there is one main basin containing virtually all of the samples. There is little structure in the samples, as shown by the conformer at the top of the chart. However, at energy 405 units, the phase space splits into two main funnels: one with the helix forming on the correct side of the sheet (funnel 1) and one with it forming on the incorrect side (funnel 2). Funnel 1 further splits at energy −75 units, corresponding to conformations where the hydrophobic residues are in the interior of the protein (funnel 1) or on the surface of the protein (funnel 1A). At room temperature (the expected energy corresponding to β = 1 is marked by a horizontal line on both panels of the chart), the phase space volume of both funnels 1A and 2 are <1/1000th of the main funnel and hence the posterior energy landscape chart consists of a single funnel. The inaccessibility of funnel 1A at room temperature indicates the importance of hydrophobic interactions.

Fig. S5 shows two conformers that are placed in the same small basin, branching off the right-hand funnel. The conformer on the left has higher energy than the one on the right. These conformers are very similar, and demonstrate that the topological analysis shows how metastable conformations are formed. The pathway to these states would be obtained by considering conformers found in the same basin.

Discussion

It is interesting to consider how the energy landscape charts vary from simulation to simulation. Topologically, we always find two main funnels in the protein G simulations (funnels 1 and 2 on Fig. 3), corresponding to the packing of the helix on either side of the sheet. The dominant mode with the native like backbone topology (funnel 1) splits again at a lower energy level to two funnels, corresponding to the hydrophobic residues being in the interior (funnel 1) or on the surface (funnel 1A) of the protein. The energy at which funnels 1 and 2 split varies significantly between simulations, from 220 to 580 energy units. This is probably because the RMSD metric is an imprecise way of comparing wildly different conformations. The energy where funnels 1 and 1A split has a much smaller variation, −75 to −55 energy units. This trend in the variation of splitting energies was also observed in the nested sampling simulations of the other modeled proteins. Metrics other than the RMSD might improve the reproducibility of energy landscape charts and would be worthy of investigation.

The relative basin widths of energy landscape charts depend on the size of the nested sampling active set, K. In general, K determines the resolution of exploration. When converging the evidence at lower temperatures, a larger value of K is required. This is because at every splitting of the likelihood function, the probability of exploring the dominant mode decreases, according to Eq. 3. At high energies, the accessible conformational space is connected, and the MMC procedure explores the space effectively. As the energy lowers, the accessible conformational space becomes increasingly disconnected. Because the MMC procedure cannot jump between disconnected components of the conformational space, an increasingly large set of active points is required to sample effectively. As the posterior mass is concentrated at lower energies for lower temperatures, K behaves as an effective minimum temperature. Using too small an active set for a given temperature causes large variation between different nested sampling simulations; for example, the estimates for the evidence and the relative widths of the funnels of energy landscape charts.

In the protein G simulations, we find that K = 20,000 is large enough to produce simulation independent charts for temperatures near β = 1. When using, for example, K = 2500, which is too small for sampling the posterior distribution at β = 1, we find that the active set becomes extremely homogenous and the simulation is, in effect, exploring just one tiny basin in one of the main funnels, by making smaller and smaller crankshaft rotations. Hence, we find a single room-temperature accessible conformation, as opposed to the wide selection that is found when K = 20,000.

The magnitude of m relative to K is problem-specific. It has been suggested that for probability distributions that lack a large number of modes, it is optimal to set K small and use a large m (the cost is proportional to mK) (21). For protein G, we find the energy landscape is so complex that we need a large K to explore all the funnels simultaneously, and a large m to ensure the active set remains heterogeneous, and we therefore choose m and K to have the same order of magnitude. Incorporating nonlocal flexible motions (44) into our MMC procedure may allow a decrease in m without losing heterogeneity and this is a focus of future work. If this proves to be the case, we would choose to increase K relative to m.

In our previous work (27), using MMC with parallel tempering to simulate the folding of protein G with a simpler model (no γ-atoms and hydrophobic interactions were included in this model), the lowest energy structures obtained were similar to those shown at the bottom of funnel 2 of Fig. 3, with the helix packed on the incorrect side of the sheet and a backbone RMSD of 8.6 Å from the crystal structure. This demonstrates the difficulty of using parallel tempering or simulated annealing to reconstruct the native structure, when the energy landscape exhibits two main funnels separated by a large energy barrier. If the annealing proceeds down the incorrect funnel it will be nearly impossible for it to climb back out and down into the correct funnel.

The reason for the double funnel is the symmetry of the protein G topology with respect to the Gō-type bias potential, which is the predominant factor at the beginning of the simulation. The further splitting of the main funnel into funnels 1 and 1A (Fig. 3) is also due to the nature of the Gō-type bias potential. This applies a quadratic potential on the C_β atom contacts, which does not restrict the hydrogen-bond pattern between the individual strands; at high energies, both conformations (with the hydrophobic residues of the β-sheet being in the interior or on the surface of the protein) are similarly likely to be adopted. However, other energy and entropy contributions due to the presence of side chains (e.g., hydrophobic interactions and steric clashes) ensure that only conformations with the nativelike topology are accessible at room temperature. This way, energy landscape charts also reflect the nature of the protein model and force field used. For example, the energy landscape charts for chymotrypsin inhibitor 2, which differs in topology from protein G, but also possesses a similar symmetry with regard to the packing of the α-helix against the β-sheet, also exhibit this double funnel (see the Supporting Material).

It would be interesting to compare energy landscape charts of nested sampling simulations using other protein models and force fields, for example, all-atom representations, and this will be a focus of future work.

Conclusion

This article has described the parallelization of the nested sampling algorithm, and its application to the problem of protein folding in a force field of empirical potentials that were designed to stabilize secondary structure elements in room-temperature simulations. The output of the nested sampling algorithm can be used to produce energy landscape charts, which give a high level description of the potential energy surface for the protein folding simulations. These charts provide qualitative insights into both the folding process and the nature of the model and force field used. The topology of the protein molecule emerges as a major determinant of the shape of the energy landscape, as has been noted by other authors (37). The energy landscape chart for protein G exhibits a double funnel with a large energy barrier, a potential energy surface that parallel tempering struggles to explore fully. The nested sampling algorithm also provides an efficient way to calculate free energies and the expectation value of thermodynamic observables at any temperature, through a simple postprocessing of the output.