Analysis of Molecular Movement Reveals Latticelike Obstructions to Diffusion in Heart Muscle Cells

Abstract

Intracellular diffusion in muscle cells is known to be restricted. Although characteristics and localization of these restrictions is yet to be elucidated, it has been established that ischemia-reperfusion injury reduces the overall diffusion restriction. Here we apply an extended version of raster image correlation spectroscopy to determine directional anisotropy and coefficients of diffusion in rat cardiomyocytes. Our experimental results indicate that diffusion of a smaller molecule (1127 MW fluorescently labeled ATTO633-ATP) is restricted more than that of a larger one (10,000 MW Alexa647-dextran), when comparing diffusion in cardiomyocytes to that in solution. We attempt to provide a resolution to this counterintuitive result by applying a quantitative stochastic model of diffusion. Modeling results suggest the presence of periodic intracellular barriers situated ∼1 μm apart having very low permeabilities and a small effect of molecular crowding in volumes between the barriers. Such intracellular structuring could restrict diffusion of molecules of energy metabolism, reactive oxygen species, and apoptotic signals, enacting a significant role in normally functioning cardiomyocytes as well as in pathological conditions of the heart.

Introduction

Of the different processes active in a functioning cell, there are not many that are unaffected by diffusion. The composition, geometry, and solvent properties of the intracellular environment determine the characteristics of diffusion for everything from the smallest signaling molecules to enzymes to DNA/RNA. Three restrictions for diffusion are generally considered: viscosity of the fluid phase, binding of the diffusing molecule to other molecules or structures, and molecular crowding that effectively reduces the volume available for diffusion (1). In heart and oxidative skeletal muscle cells diffusion of smaller molecules, such as ADP, has been found to be severely restricted when analyzing kinetics of respiration in permeabilized fibers or cells in respirometer (2,3), autofluorescence of single cells (4), sarcoplasmic reticulum Ca²⁺ ATPase (5), and response of ATP-sensitive K⁺ channel (6). Diffusion restrictions estimated from mitochondrial respiration kinetics have partially been attributed to mitochondrial outer membrane (3,7,8).

In addition to outer membrane and submembrane diffusion restrictions (6), there are diffusion obstacles in cardiomyocytes that group ATPases and mitochondria (5). Those diffusion obstacles have been attributed to the regular arrangement of intracellular organelles such as mitochondria (9,10) leading to anisotropic diffusion in rat cardiomyocytes (11) as well as dependence of apparent diffusion coefficient (DC) on diffusion time in lobster muscle fibers (12). The role of diffusion obstacles in heart regulation is not clear. However, it has been established that ischemia-reperfusion injury reduces the overall diffusion restriction regardless of whether ischemia is induced globally (13) or regionally (14), an effect that can be reduced by ischemic preconditioning (15). Such correlation between the state of the heart muscle and diffusion obstacles suggests that obstacles to diffusion play an important role in regulation of intracellular processes and could be a target of therapies in heart failure treatment.

So far, diffusion restrictions have been suggested from indirect measurements such as kinetics of mitochondrial respiration in permeabilized cells and fibers. Although for larger molecules, diffusion has been found to be significantly restricted (1,16–18), direct assessment of diffusion in muscle cells has not confirmed the existence of large diffusion restrictions for smaller molecules, for which intracellular DC was found to be ∼2× smaller than in water (19). In experiments performed using ³¹P-NMR, a small reduction of DC was observed for ATP and phosphocreatine (PCr) when compared to DC in solution at short diffusion distances. It was found, however, that the transverse DC was dependent on diffusion time (12,20). To reproduce ³¹P-NMR data, it was suggested that the diffusion is mainly restricted by intracellular structures with overall cylindrical orientation (12,20), such as sarcoplasmic reticulum (12). Such intracellular diffusion obstacles were not identified in a recent ³¹P-NMR study of the human calf muscle (21). Large influence of intracellular structures on diffusion of smaller molecules in cytoplasm has not been demonstrated using fluorescence-based methods either.

Recently, we extended raster image correlation spectroscopy (RICS) (22–24) to take into account possible anisotropy of diffusion and determined the diffusion coefficient for fluorescently labeled ATP (11). We found only a small reduction of the DC attributable to anisotropy. In that study, however, several limitations emanated from using a commercial confocal microscope. In particular, using an analog photomultiplier tube as a detector demands that long pixel acquisition times be used to avoid interference between pixels (23,11). As a result, only a small amount of pixels is acquired at relatively slow laser scanning speeds, limiting correlation analysis to pixels in the same image line.

In this article, we custom-built a confocal microscope that allowed us to significantly increase the precision of DC estimation. We determined DCs for two different molecules of different size and found that the diffusion of a larger molecule (Alexa647-dextran 10K) was hindered less than that of a smaller one (ATTO633-ATP). To explain such a counterintuitive result, we composed a mathematical model that mimics the diffusion pathway in the heart muscle cell and found parameters describing intracellular diffusion obstacles. Although our main results are discussed in this text, we provide extensive Supporting Material giving an introduction to the RICS method, which includes extended experimental and mathematical method descriptions and a section on statistical analysis of model parameter estimates.

Materials and Methods

Experimental procedures

Adult outbred Wistar rats of both sexes weighing 300–500 g were used in the experiments. Animal procedures were approved by Estonian National Committee for Ethics in Animal Experimentation (Estonian Ministry of Agriculture). Cardiomyocytes (CMs) were isolated as described in Sepp et al. (3).

Solutions and chemicals

The following fluorescent dyes were used in this work: ATTO633-ATP (catalogue No. NU-808-633; Jena Bioscience, Jena, Germany), Alexa647-dextran 10K (catalogue No. D-22914; Invitrogen, Carlsbad, CA), ATTO655-COOH (catalogue No. AD655-21; ATTO-TEC, Siegen, Germany), and MitoTracker Green (catalogue No. M-7514; Invitrogen). Mitotracker Green was used in concentration of 0.25 μM. Dyes for which DCs were estimated were used in a concentration of 8 nM and 16 nM for ATTO633-ATP and Alexa647-dextran 10K, respectively. Solutions are described in detail in the Supporting Material.

Determination of diffusion coefficients using RICS

To perform imaging for RICS, we designed and built a confocal microscope. This allowed us to automate image acquisition under varying laser scanning angles and frequencies. For analysis, triplet states and experimentally obtained point-spread function (PSF) were taken into account. See the Supporting Material for the mathematical and experimental details of RICS analysis and for the setup of the confocal microscope.

Statistics

Raw data were analyzed using homemade software. All results are shown as mean ± SD.

Mathematical model

Stochastic diffusion simulations and data analysis were performed using custom-written Python and C++ code on a computational cluster (96 dual-core AMD Opteron 2216 CPUs). Diffusion in three dimensions was simulated to establish independence of DCs in x, y, and z directions. A faster one-dimensional model was then used for each spatial direction separately. Diffusion was simulated inside a 20 μm × 20 μm × 5 μm region for the three-dimensional model and a 20-μm region for the one-dimensional model. Possible intracellular structures in direction α (α represents any of the directions x, y, and z) were approximated with periodically placed barriers d_α μm apart, having permeabilities p_α (probability for a particle to traverse the wall after an interaction). Diffusion in direction α in the interbarrier space (IBS) was assumed to be reduced by a factor of 0 < λ_α ≤ 1 compared to that in free intracellular solution. Reduction factors λ were considered to be different for ATTO633-ATP and Alexa647-dextran 10K and for distinct spatial directions.

At each timestep Δt = 1 μs, every simulated particle undertook a random displacement in all of the directions x, y, and z, drawn from a normal distribution $\mathcal{N}\left(0,\sqrt{2D_{\alpha }\Delta t}\right),$ where D_α is the DC in direction α. Timestep value 1 μs was chosen to match pixel acquisition timestep in experiments so as to obtain similar images from the stochastic model. Also, a timestep of 1 μs ensured that diffusing particles would have a very low probability of diffusing out of the PSF during acquisition. This was estimated by using the relation of root mean-square displacement to time and diffusion coefficient of the dye in water. If a particle's trajectory intersected with a barrier, it had a probability p_α of passing that barrier and 1−p_α of bouncing back elastically.

Concurrent to simulating diffusion, confocal microscope image acquisition with various scanning speeds and pixel sizes was simulated to obtain images for use in RICS analysis. For the three-dimensional model, we used analysis methods identical to those employed for analyzing experimental data. For the one-dimensional model, theoretical one-dimensional autocorrelation functions used in fitting were derived (see the Supporting Material for details). Obtained apparent DCs in direction α were functions of barrier parameters p_α, d_α, and λ_α values. Comparison of simulated and experimental results yielded sets of model parameters with which simulations for both molecules simultaneously matched experimental data. In subsequent analysis, permeability values were reinterpreted as η-pores of radius R per μm² of barrier surface. This interpretation required knowledge of radii of the diffusing molecules. These were estimated from DCs in salt solution using the Stokes-Einstein relationship, yielding 0.92 nm for the radius of ATTO633-ATP and 4.1 nm for Alexa647-dextran 10K.

Results

RICS extensions

RICS was extended by using multiple scanning speeds and angles during imaging with the aim of altering the contribution of diffusional anisotropy in acquired images. For image acquisition, we used 19 angles uniformly spanning the range from 0 to 360°. Scanning resolution was altered in tandem with scanning axes rotation. This was all done in a random sequence to eliminate bias. As explained in the Supporting Material, these additions were done to maximize the amount of data for fitting with theoretical correlation curves.

We tested the method by estimating DCs of ATTO633-ATP, Alexa647-dextran 10K, and ATTO655-COOH in water and measurement solution. The estimated DC for ATTO655-COOH in water, 454 ± 3 μm²/s at 26°C, is in good agreement with published data: 426 ± 8 μm²/s at 25°C (25). Full results are given in Table 1. According to our results, small anisotropy of diffusion (<20%) is not resolvable with this method. Further technical details concerning our extension to RICS can be found in the Supporting Material.

Table 1.

Diffusion constants (D_TR and D_L in transverse and longitudinal directions, respectively) obtained from raster image correlation spectroscopy at 26°C

				Diffusion			Triplet
Dye	Media	n	Cmp.	Concentration	DTR	DL	T	τ
				nM	μm2/s	μm2/s	Relative	μs
ATTO655-COOH	Water	4		21 ± 2	454 ± 3		0.08 ± 0.01	3.3 ± 0.1
	Water	4		21 ± 2	442 ± 4	483 ± 7	0.08 ± 0.01	3.1 ± 0.1
	Solution	4		22 ± 4	362 ± 4		0.10 ± 0.01	4.3 ± 0.7
	Solution	4		22 ± 4	348 ± 2	403 ± 10	0.09 ± 0.01	3.8 ± 0.7
ATTO633-ATP	Water	4		16 ± 4	326 ± 13		0.10 ± 0.01	4.3 ± 0.1
	Water	4		16 ± 4	322 ± 15	337 ± 12	0.10 ± 0.01	4.2 ± 0.1
	Solution	4		21 ± 4	195 ± 8		0.14 ± 0.01	5.6 ± 0.3
	Solution	4		21 ± 4	183 ± 11	222 ± 3	0.14 ± 0.01	5.5 ± 0.3
	CM	5		86 ± 12	4.0 ± 0.6	4.6 ± 0.9	0.39 ± 0.10	45 ± 5
	CM	5	1	19 ± 4	0.7 ± 0.3	0.8 ± 0.2	0.23 ± 0.04	5.2 ± 2.5
			2	41 ± 10	24 ± 6	35 ± 8
Alexa647-dextran 10K	Water	4		12 ± 3	62 ± 1		0.23 ± 0.01	3.8 ± 0.7
	Water	4		12 ± 3	60 ± 2	65 ± 2	0.23 ± 0.01	3.8 ± 0.7
	Solution	4		12 ± 2	53 ± 1		0.23 ± 0.00	4.0 ± 0.2
	Solution	4		12 ± 2	51 ± 2	57 ± 1	0.23 ± 0.00	4.0 ± 0.2
	CM	7		13 ± 3	16 ± 2	19 ± 3	0.34 ± 0.02	6.6 ± 1.1

Listed values were obtained in water, measurement solution (solution), or CMs. On the basis of n experiments, several parameters were determined in addition to diffusion coefficient(s): concentration, triplet time constant τ, and triplet-state contribution T. Correlations between fluctuation of fluorescence signal were fitted by isotropic model (diffusion coefficient specified only as D_TR), anisotropic model (D_TR and D_L specified), or model with two components (Cmp).

Experimental results

To determine the intracellular DCs of ATTO633-ATP and Alexa647-dextran 10K, the dye has to be present inside the cell. For both our dyes, which are not able to permeate intact sarcolemma, we used a poking procedure demonstrated in Fig. 1, A–E. In short, we introduced small holes (of diameter ∼1 μm) into the cell membrane with a glass pipette, leading to diffusion of the dye from the surrounding solution into the cell. These small holes were open throughout the experiment, resulting in constant exchange of solution with the intracellular environment. For Alexa647-dextran 10K, a higher concentration had to be used to get a sufficient signal for RICS analysis.

Figure 1.

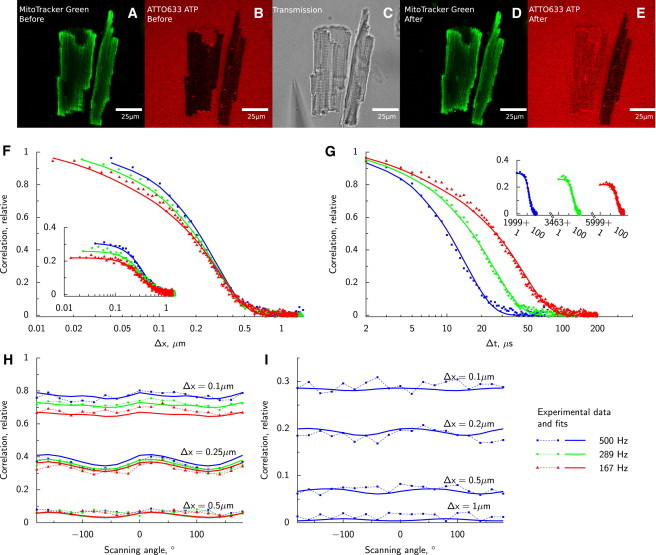
Diffusion of ATTO633-ATP in rat CM analyzed by RICS. In the beginning of the experiment, intact rat CMs labeled with Mitotracker Green are positioned into solution containing ATTO633-ATP (confocal images, A and B). Because cells are intact, ATTO633-ATP does not penetrate sarcolemma and fluorescence is recorded in solution surrounding the cells as well as T-tubules (B). Holes are introduced into sarcolemma by poking one of the cells with a glass pipette (transmission image of approaching pipette in C). As a result, ATTO633-ATP is able to diffuse into the cell (E) while the structure of the cell is intact (D). RICS analysis is presented in F–I. Experimental data (points) acquired at different laser scanning frequencies and directions are fitted by a model (lines). Spatial and temporal components of the correlation function are shown in panels F and G, respectively. On panels F and G, imaging was performed with the laser scanning along a line parallel to axis x at different frequencies (frequencies noted in legend on the right bottom). Correlation along the same line (main graphs of F and G); correlation of the signal between pixels in adjacent lines (insets). Due to the laser backtracking and variation in scan frequencies, temporal component has gaps visible (inset of panel G). Due to asymmetry of PSF, laser scanning in different directions leads to modification of correlation function between pixels in the same line (H) and in the adjacent lines (I). Note how the slow component leads to significant correlation in pixels in adjacent lines (I and insets of F and G).

Representative correlation functions (CFs) estimated for ATTO633-ATP in the cell and the fit with two components are shown in Fig. 1, F–I. The two components represent a slower, bound form of the dye and the freely diffusing form. In case of one component, only the free form is present. See the Supporting Material on how the number of components modifies the form of the theoretical CF. Slower diffusion in the cell can be seen from the relatively high correlation (especially when comparing to CFs in water; see the Supporting Material) between pixels in adjacent lines (inset, Fig. 1, F and G). A slight lack of fit observable in Fig. 1, F and G, is caused by the fact that the fit for only one of the 19 angles recorded in experiment is shown. The optimization process attempts to fit all angles simultaneously (Fig. 1, H and I), resulting in slight per-angle deviations.

Summary of the DCs determined by anisotropic models is presented in Table 1. Note that, when fitting ATTO633-ATP data using a single-component model, the triplet-state time constant increases to >40 μs and has a large contribution to the CF (39%). Such triplet-state parameters in the fit can be explained by an additional diffusing component that is not accounted for in the single-component model. When a two-component model is used, more acceptable triplet-state parameters are obtained. In the two-component model, contribution of the very slow fraction (probably bound fraction) is ∼30%, with the rest attributed to freely moving ATTO633-ATP.

As can be seen from Table 1, the triplet-state time constant for Alexa647-dextran 10K in cells is not as large as obtained with a single-component model for ATTO633-ATP and the single-component fit is sufficient for Alexa647-dextran 10K data. Using saponin permeabilization in lieu of poking did not result in markedly different results from Table 1. DCs obtained with saponin permeabilization were 15 ± 2 μm²/s in the transverse and 19 ± 1 μm²/s in the longitudinal directions (n = 7).

On the basis of our analysis, we conclude that the DC of the freely moving fraction of ATTO633-ATP in CMs is 5.6–8.1× reduced (depending on direction) compared to the coefficient in the measurement solution. For Alexa647-dextran 10K, reduction of the DC was considerably smaller: 2.8–3.5 times. Thus, our experimental results indicate that the diffusion of a smaller molecule is restricted more in the intracellular environment than the larger molecule.

Analysis by stochastic model

To find an explanation for our counterintuitive experimental results, we turned to computational modeling. Diffusion of ATTO633-ATP and Alexa647-dextran 10K was simulated in three dimensions with periodically placed permeable barriers in x, y, and z directions using a stochastic computational model (Fig. 2 A). This geometry was chosen as the simplest and least computationally intensive approximation to intracellular diffusion restrictions. Concurrently with the processes of molecule diffusion and interaction with barriers, confocal microscope data acquisition was simulated and images similar to those in physical experiments were obtained. Apparent diffusion coefficients in the three dimensions were calculated from simulated results by applying numerical methods identical to those employed on experimental data. Our goal was to determine barrier parameters with which DC values obtained from the model coincide with those from experiments.

Figure 2.

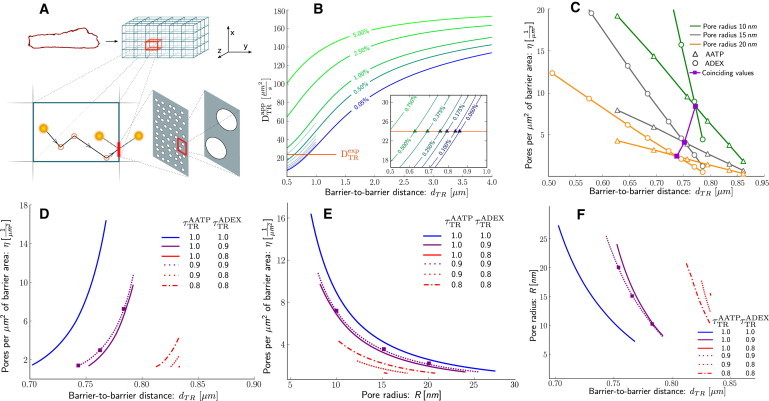
Analysis of diffusion in the cell using the stochastic model. (A) Scheme of the computational model. Intracellular structure of the cell (top left) is approximated by a three-dimensional lattice of barriers that hinder molecule diffusion (top right). Barriers are placed, depending on direction α, d_α μm apart and have permeabilities p_α. Diffusion coefficient in the space between barriers is reduced by a factor λ compared to solution $\left(0<\lambda \le 1\right)$. Stochastically diffusing molecules interact with barriers and have a probability p_α of passing through (bottom left). Permeable barriers correspond to porous walls with η-pores of radius R per μm² of barrier area (bottom right). Apparent diffusion coefficients are estimated over the entire lattice. (B) Apparent diffusion constant values for ATTO633-ATP are obtained from simulations with varying barrier distances (horizontal axis) and permeabilities (indicated by values on curves). (Horizontal solid line) ATTO633-ATP diffusion coefficient estimated from experiment $\left(D_{TR}^{exp}\right)$. (Inset) Region 0.5 … 1 μm, where curves intersect with experimental data. (Triangles) Intersection points. (C) Points of intersection from panel B with permeability converted to pores per μm² for different pore radius values (10, 15, and 20 nm). Intersections of ATTO633-ATP (open triangles) and Alexa647-dextran 10K (open circles) curves of identical pore radius values signify points where model and experiment coincide for both molecules simultaneously (solid squares). Intersections are curves in three-dimensional space (barrier-to-barrier distance versus pore radius versus pores per μm²). (D) View of intersection curves from panel C in barrier-to-barrier distance and pores per μm² axes. (Lines) Different ${\lambda }_{TR}^{AATP}$ and ${\lambda }_{TR}^{ADEX}$ values. (Squares) Example intersection points from panel C. (E) Same as panel D, but for pore radius and pores per μm² values. (F) Same as panel D, but for barrier-to-barrier distance and pore radius values. AATP and ADEX represent ATTO633-ATP and Alexa647-dextran 10K, respectively.

The apparent DC estimated by RICS is a macroscopic variable comprised of two components—diffusion in interbarrier space (IBS) and restrictions from barriers. We assume the x and z axis (both represented by the transverse TR direction) to have identical diffusion restrictions and, consequently, identical barrier parameters. The y axis corresponds to the longitudinal L direction and can have barrier parameters different from the transverse direction.

Barriers in spatial direction α (α is TR or L) are described by two parameters—their permeability (p_α) and barrier-to-barrier distance (d_α). DC in IBS is reduced compared to solution, D_IBS = λ_α · D_sol, where the reduction factor λ_α depends on the direction α and the diffusing molecule. In our simulations, we scan IBS diffusion reduction factors in the whole range 0…1 for all directions and molecules.

We estimated apparent DC values (D_α^app) for various barrier distances, permeabilities, and IBS diffusion reduction factors. From calculations performed with the three-dimensional model, we determined that diffusion in any spatial direction is dependent on barrier parameters in that direction only and is not affected by the existence or properties of barriers in any orthogonal direction. This allowed us to derive and use a computationally faster one-dimensional RICS model to study diffusion in the transverse and longitudinal directions separately.

Results for simulations performed with ${\lambda }_{TR}^{AATP}=0.9$ are shown in Fig. 2 B. Points where computational results intersect with the experimentally obtained $D_{TR}^{exp}$ values give us a combination of barrier parameters in the transverse direction at which the stochastic model is able to reproduce experimental results. Surprisingly, for the model to match experimentally obtained $D_{TR}^{app}$ values, very small permeabilities (p < 0.1%) and closely spaced barriers (d < 1 μm) are necessary.

We performed analogous numerical experiments and analysis for Alexa647-dextran 10K with the intention of finding parameters where simulation results for both ATTO633-ATP and Alexa647-dextran 10K simultaneously match experimental data, and relating these values to physical barrier characteristics. Permeability values obtained for ATTO633-ATP and Alexa647-dextran 10K are not directly comparable. They can, however, be related to the radius of the diffusing molecule (r), the radii of permeable pores in the barriers (R), and the number of pores per μm² (η) by: p = πη(R–r)² (see the Supporting Material for derivation).

Fixing a particular R value for the pore radius, we can convert p values to η and compare barrier characteristics obtained for ATTO633-ATP and Alexa647-dextran 10K (Fig. 2 C). Intersections between ATTO633-ATP and Alexa647-dextran 10K curves now indicate physical parameter values where computational and experimental constraints are satisfied for both molecules simultaneously. By varying R values we get a range of suitable parameters for a combination of λ^AATP and λ^ADEX in both transverse and longitudinal directions. Some combinations of λ^AATP and λ^ADEX do not result in intersections, and are therefore discarded as unsuitable. In addition, we assumed that λ^AATP ≥ λ^ADEX, as diffusion of larger molecules is restricted more by molecular crowding than the small ones (18).

The relationship between R- and η-values in the transverse direction is shown on Fig. 2, D–F, for ${\lambda }_{TR}^{AATP}$, ${\lambda }_{TR}^{ADEX}$ values where intersections occur. Summary of parameters satisfying all constraints is shown in Table 2. Error estimates for the table entries were obtained from Monte Carlo simulations detailed in the Supporting Material. Data in the table represent the mean ± SDs obtained from Monte Carlo simulations. A number of parameter estimates do not follow a normal distribution. For those, the mean ± SDs do not illustrate the actual distribution well and the histograms given in the Supporting Material should be consulted instead. For the DC reduction ratio, the maximum estimate for which no error is given as the result was always 100% of the DC in solution for both ATTO633-ATP and Alexa647-dextran 10K.

Table 2.

Diffusion obstacles predicted by stochastic model on the basis of RICS measurements

Barrier	Direction
	Transverse TR(x,z)		Longitudinal L(y)
	Min	Max	Min	Max
Distance d[μm]	0.68 ± 0.10	0.87 ± 0.07	0.73 ± 0.13	1.02 ± 0.10
Pore radius R[nm]	7.4 ± 2.1	30 ± 8	6.7 ± 1.8	38 ± 10
Pore density η[1/μm2]	1.2 ± 0.1	29 ± 23	1.1 ± 0.1	48 ± 37
λαAATP	0.78 ± 0.13	1.0	0.78 ± 0.13	1.0
λαADEX	0.77 ± 0.14	1.0	0.77 ± 0.14	1.0

Discussion

The major experimental finding of this study is that the diffusion of the freely moving fraction of a smaller molecule (ATTO633-ATP) is hindered considerably more by intracellular diffusion obstacles than the diffusion of a larger molecule (Alexa647-dextran 10K). In general, fractional reduction of the diffusion coefficient is expected to be larger for larger molecules (18). To explain our counterintuitive result, we assumed that diffusion obstacles are formed by permeable barriers arranged in a three-dimensional lattice. The major finding from numerical simulations performed with this assumption is that such diffusion barriers can reproduce the overall DCs of ATTO633-ATP and Alexa647-dextran 10K estimated from experiments conducted on rat CMs. According to our simulations, the diffusion barriers are ≤1 μm apart with relatively few small openings (∼1 … 30 openings per μm² of radius 7 … 30 nm).

Intracellular structures acting as diffusion obstacles

Barrier parameters obtained from our computational model imply that only ∼0.3% of barrier surface is covered with pores. Intuitively, this would appear a prohibitively small percentage for diffusion to be able to have a significant role in cellular metabolism. However, it can be shown that if there are (4R·d)⁻¹ pores of radius R per unit area in a barrier that is at distance d from neighboring barriers, then the diffusion current through the barrier is half of what it would be if there was no barrier at all (26). Substituting our parameters, this means that just ∼1.2% of the barrier would need to be penetrable to obtain half-maximal diffusion current.

The distances found between barriers are consistent with the morphology of rat CMs (Fig. 3). The predicted distance between barriers (∼0.8 μm) is in agreement with the reported transverse distance between T-tubules (27–30). In transversal direction, the distance between centers of adjacent mitochondria is ∼1.8 μm (9), indicating that there are two barriers at this distance. In longitudinal direction, two possible distances between adjacent mitochondria have been found (∼1 μm and ∼1.8 μm) due to the difficulty of distinguishing whether there is one or two mitochondria per sarcomere (9). It is possible to make this distinction, however, from following reactive oxygen species (ROS)-induced depolarization of mitochondria. Although ROS-induced mitochondrial depolarization typically occurs synchronously for mitochondria within the same sarcomere (31), depolarization of a single mitochondrion with half-sarcomere length can occasionally be observed (32). This suggests that there is a pair of mitochondria per sarcomere with ∼1 μm between the centers, similarly to the distance between barriers predicted for longitudinal direction in this work. Thus, distances between diffusion barriers are consistent with the internal periodicity of rat CM morphology.

Figure 3.

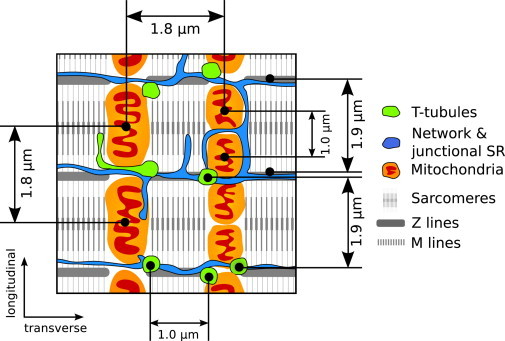
Internal structure of the cardiac muscle cell. A regular arrangement of intracellular structures and organelles is present (30,55,34). Mitochondria are separated 1.8 μm in the transverse direction and 1.0 or 1.8 μm (depending on whether there are one or two mitochondria per sarcomere) in the longitudinal direction (9). Sarcomere Z lines are separated by 1.9 μm in the longitudinal direction identically with T-tubules, whereas in the transverse direction T-tubules are 1.0 μm apart on average (27–29).

It is not clear, however, which structures can cause such obstacles to diffusion. It has been shown that internal membranes can have an effect on intracellular diffusion (33). This raises the possibility that, in restricting diffusion, a role is played by sarcoplasmic reticulum (SR) (that can form planular cisternae (30) and invaginate the space between sarcomeres (34)), or the T-tubular system. Both of these are found with periodicity (Fig. 3) similar to that determined by us. As we found very dense placement of diffusion barriers, we suggest that intracellular proteins in the heart cells could be associated with SR and other inner membrane structures leading to such profound diffusion obstacles. Additionally, enzymes can be associated with M and Z lines of sarcomeres (35,36). This suggestion is in line with our previous analysis of permeabilized fiber measurements using a three-dimensional mathematical model that predicted very small permeability for restrictions imposed by the SR (8).

Model geometry

The model geometry used by us is not the only one able to explain our experimental data. Other more complex geometries can be conceived and modeled. For example, a geometry with volumes accessible only to the smaller molecule could result in the apparent DC reducing more than the DC of a molecule that cannot access these volumes, leading to the same paradoxical smaller relative decrease in DC of a larger molecule. Our choice was motivated by the relative simplicity of the geometry employed and, stemming from this, relatively fast computation times. However, already for this basic model, calculations on our cluster of 96 dual-core machines took several months. More complex geometries would increase this time manifold. We consider our result not to be the definitive indication of wall-like porous barriers in cardiomyocytes, but a useful approximation presenting new questions to be investigated.

Diffusion between barriers

According to Shorten and Sneyd (37), the reduction factors of diffusion (λ−s) of the ATTO633-ATP-sized molecule in sarcomeres are 0.6 and 0.8 in the transverse and longitudinal directions, respectively. We consider IBS to contain sarcomeres, mitochondria, and free cytosolic space (up to 11% (38)) and, based on this, expect hindrance to diffusion in IBS to be less than or equal to that in sarcomeres. As in our study, viscosity in mitochondria has been found to be moderate when intramitochondrial structure with internal membranes is taken into account (39). Our results suggest moderate crowding in IBS, leading to a small influence of crowding on kinetics of reactions in the cell. Additionally, our results are in agreement with the small (5–15%) reduction of DC of unbound PCr and ATP in rat skeletal muscle compared to the value in solution, determined by ³¹P-NMR diffusion spectroscopy (20).

Overall diffusion coefficient

The overall reduction of DC found in this work was larger than the DC reduction determined in Kushmerick and Podolsky (19). The reasons for the differences in results could be related to our use of larger molecules or the morphological differences between rat CMs and frog skeletal muscle. Reduction of ATTO633-ATP DC was considerably larger than the one we previously found for Alexa647-ATP (11). This is probably due to the use of dedicated confocal setup in this work, leading to a more accurate determination of CFs used in analysis.

In this article, we were able to use dedicated hardware. This allowed us to obtain data at a faster time resolution—making it possible to fit several lines of the CF, compared to just one line as it was done in Vendelin and Birkedal (11). Additionally, the faster scan speeds that we can now obtain increase the amount of data that can be fitted. We have also included triplet states in the CF analysis, which were missing earlier. Furthermore, in our earlier study, saponin was kept in the solution throughout the experiment. We speculate that all these aspects contribute to the smaller reduction in DC obtained in Vendelin and Birkedal (11).

Although diffusion of ATP or PCr has been found to be anisotropic in skeletal muscle (20,12), diffusion of larger molecules has been found to be isotropic in rat CMs (16). Here, diffusion was found to be moderately anisotropic for both studied molecules. As a result, distances and permeabilities of diffusion barriers varied for different directions.

We found that ATTO633-ATP has two components when diffusing in the cell—a bound form and a freely diffusing form. This partitioning is indicated by a large triplet-state time constant when using only one component in the fit (Table 1). For Alexa647-dextran 10K only a single, freely diffusing component was necessary. Adding a second component resulted in the slow component having a small contribution to overall signal (∼5% from total concentration, results not shown). Thus, although properties of the used dyes are different, to remove possible bias we compared only freely diffusing components in our analysis.

Technique used

In our analysis we fitted CFs found by RICS using a one- or two-component model, taking into account triplet states of the molecule. During measurements, we varied scanning speed and direction to determine how correlation relates to temporal and spatial components. With this approach, anisotropy of diffusion can be assessed and two DCs can be determined. However, there are several aspects that make the application of our technique nontrivial. For smaller molecules with fast diffusion rates, photon-counting detectors are required to increase the number of acquired data points used in fitting. When studying anisotropic diffusion, measurements have to be performed at different scanning angles. Due to the variation of scanning speeds and angles, measurements take a long time, with typical experiments lasting for 2–3 h.

Our measurements were performed on a dedicated microscope with a custom-built confocal detection unit that allowed us to automate measurements, to randomize scanning speed and angle sequences to avoid bias, and to track movements of the cell to acquire images in the same region. The main advantage of having a custom-built confocal arises from the ability to program it ourselves. Although some commercial confocal software allows the writing of macros, the extendibility of such solutions is limited. Although there are several solutions that allow automating aspects of image acquisition on commercial confocal microscopes, we are not aware of any solution that allows the level of control we require. Furthermore, RICS analysis benefits greatly from having a photon counter instead of an analog detector (11,23). However, we expect that for studying diffusion of larger molecules, commercial microscopes with analog detectors can be adequate and would also allow us to determine DCs in an anisotropic case.

When analyzing the CFs found in RICS measurements, we used the actual PSF of the optical system (40), rather than approximate analytical functions, as PSF asymmetry was found to influence CF's dependence on scanning direction. In calculations of RICS analysis, knowledge of correlation of fluctuations in concentration is required. This information is conveyed by the so-called propagator, which determines the form of the diffusional correlation term G_D given in Eq. S2 in the Supporting Material. The propagator is a function that makes it possible to determine the probability of finding a diffusing particle at a distance from the starting position after a given time period. Although the propagator for the case pertinent to this work is described by simple analytical functions, it may not always be applicable. For example, when employing anomalous diffusion, one has to find solutions for the fractional Fokker-Planck equation or apply numerical approximations (41) to find the propagator. This may be an important limitation that has to be considered when applying our approach.

Physiological implications

Our results suggest small distances between intracellular barriers to diffusion and a limited amount of holes in them in rat CMs. Such partitioning of the cell may have important physiological and pathophysiological implications. Energy transfer can be influenced if the localization of the barriers is such that ATP-consuming and ATP-producing parts of the cell are separated. Such separation would indicate a prominent role for energy transfer systems, such as the creatine kinase shuttle. Because diffusion restrictions are expected to decrease after ischemia (13,14), such positioning of barriers could lead to a change in the role of the energy transfer system in pathologies. Whether it is consistent with modulation of energy transfer depending on the workload, as shown in the analysis of ³¹P-NMR inversion and saturation transfer experiments (42), is not clear and requires further studies.

Alternatively, barriers could group ATP-producing and ATP-consuming parts of the cell together, as suggested by coupling between ATPases and mitochondrial respiration (3,5). In this case, barriers would influence synchronization between different parts of the cell and would restrict local ATP production to local consumption. Prominent diffusion obstacles separating the cell into smaller segments are also consistent with formation of clusters during mitochondrial oscillations (43,44) and may play an important role in pathologies by restricting diffusion of ROS, apoptosis signals, and Ca²⁺ waves (45).