Perceptual interaction of the harmonic source and noise in voice

Abstract

Although the amount of inharmonic energy (noise) present in a human voice is an important determinant of vocal quality, little is known about the perceptual interaction between harmonic and inharmonic aspects of the voice source. This paper reports three experiments investigating this issue. Results indicate that perception of the harmonic slope and of noise levels are both influenced by complex interactions between the spectral shape and relative levels of harmonic and noise energy in the voice source. Just-noticeable differences (JNDs) for the noise-to-harmonics ratio (NHR) varied significantly with the NHR and harmonic spectral slope, but NHR had no effect on JNDs for NHR when harmonic slopes were steepest, and harmonic slope had no effect when NHRs were highest. Perception of changes in the harmonic source slope depended on NHR and on the harmonic source slope: JNDs increased when spectra rolled off steeply, with this effect in turn depending on NHR. Finally, all effects were modulated by the shape of the noise spectrum. It thus appears that, beyond masking, understanding perception of individual parameters requires knowledge of the acoustic context in which they function, consistent with the view that voices are integral patterns that resist decomposition.

INTRODUCTION

Most researchers and clinicians agree that the amount of inharmonic energy (noise) present in a human voice is an important determinant of vocal quality. As a result, a large number of studies (reviewed by Buder, 2000) have proposed different measures of vocal aperiodicity and spectral noise levels, while others have examined correlations between such measures and ratings of specific dimensions of vocal quality. For example, de Krom (1995) reported correlations between the noise-to-harmonics ratio (NHR) and rated breathiness, while Hillenbrand (1988) found a “very strong” relationship between rated breathiness and the NHR, and Eskenazi et al. (1990) found a significant correlation between the NHR and rated roughness. More recently, Shrivastav and Camacho (2010) found that breathiness ratings could be predicted with moderate accuracy (R²= 0.63) from F0, the partial loudness of the harmonic energy in the voice, and the loudness of the noise excitation.

Despite this long research tradition, very little is known about the interaction between the harmonic and inharmonic aspects of the voice source in determining perceived voice quality. The influences of sound intensity on listeners’ perception of pitch (Stevens, 1935) and of sound frequency on the perception of loudness (e.g., Fletcher, 1934) are well known, but similar interactions that occur in voice quality perception are not understood. Noise has been shown to mask pure and periodic complex tones more effectively than such tones mask noise, even when the tones and noise have identical long-term excitation patterns (Gockel et al., 2002, 2003), but these studies explicitly required that listeners hear the tones and noise as two separate sounds, which is not the case in voice stimuli. However, consistent with these findings, previous studies of voice stimuli (Kreiman and Gerratt, 2005; Shrivastav and Sapienza, 2006) have demonstrated that listeners’ sensitivity to noise levels in voice depends in part on the shape of the higher part of the harmonic voice source spectrum, so that more noise energy is needed relative to the amount of harmonic energy present for listeners to perceive a constant noise level in the context of stronger high-frequency harmonic excitation. The details of this interaction have not been established, nor have the effects of NHR levels on perception of harmonic excitation been investigated.

Beyond their importance for models of voice quality, issues of the interaction between harmonic and noise excitation have important implications for interpreting acoustic measures of voice. If the perceptual importance of noise depends on the shape of the harmonic source spectrum, then the perceptual significance of a given NHR value depends on the context in which that noise level occurs, and not merely on the noise level itself. Further, knowledge of the manner in which harmonic and inharmonic excitation interact perceptually has implications for remediation in cases of vocal pathology, for example by indicating cases where an improvement in one dimension requires a simultaneous improvement in another to be perceptible.

In investigating these issues, the present study deviates from the practice of studying the relationship between spectral noise and specific voice qualities like breathiness and roughness. Instead, we examined the influence of the NHR and of the slope of the harmonic source spectrum (from the second harmonic to the highest harmonic; H2–Hn) on each other in a same/different task so that listeners judged the effects of parameter changes in the context of a complete voice pattern, and not with respect to individual quality dimensions. In experiment 1 we measured just-noticeable-differences (JNDs) for the NHR and for H2–Hn, both as functions of varying NHR and H2–Hn. In experiment 2, we examined the perceptual importance of differences in the spectral characteristics of noise; and in experiment 3 we assessed the interaction between noise characteristics and listeners’ sensitivity to the NHR and harmonic spectral slope.

EXPERIMENT 1

Methods

Stimuli

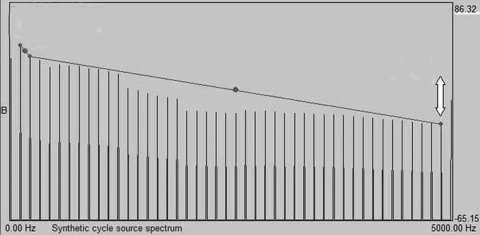
Two synthetic voices (one male and one female) were created using the UCLA voice synthesizer (Kreiman et al., 2010). Stimuli were based on natural tokens of the vowel /a/produced by two normal speakers (Table Table I.), except that a single noise source with a flat spectrum (similar to that used by the KLSYN88 synthesizer; Klatt and Klatt, 1990) was used to model the inharmonic voice source in all tokens. [Note that some NHR measures assess noise separately in different frequency bands (e.g., Lively and Emanuel, 1970), implying that noise spectral shape is perceptually important. This issue is investigated in experiment 2.] Four versions of each of these voices were created by manipulating the slope of the harmonic voice source spectrum from the second harmonic to the highest harmonic (H2–Hn; Fig. 1), so that it equaled −3 dB/octave (a relatively flat spectrum), −6 dB/octave, −9 dB/octave, or −12 dB/octave (a steeply falling spectrum). H1–H2 remained constant across all spectral manipulations.

Table I.

Synthesis parameters for the male and female voice tokens.

Parameter	Male voice	Female voice
F0	126 Hz	192 Hz
F1/B1	545 Hz/136 Hz	953 Hz/145 Hz
F2/B2	1199 Hz/99 Hz	1368 Hz/113 Hz
F3/B3	2708 Hz/118 Hz	2151 Hz/791 Hz
F4/B4	3536 Hz/173 Hz	3138 Hz/127 Hz
F5/B5	4302 Hz/1800 Hz	3929 Hz/261 Hz
Original noise-to-harmonics ratio	−36.6 dB	−22.8 dB
Original overall source spectral slope	−7.35 dB/octave	−10.65 dB/octave
H1−H2	6.38 dB	4.24 dB

Figure 1.

(Color online) Manipulations of the harmonic voice source spectrum. Listeners adjust the slope of H2–Hn by typing the desired slope value into a box (not shown) and then clicking the point labeled with a double arrow. Note that H1–H2 remains constant throughout manipulations of H2–Hn.

Next, four versions of each of these eight synthetic voice samples (four spectral slopes × two original voice samples) were created by setting the noise-to-harmonics ratio (NHR) to −40 dB (noise-free), −30 dB, −20 dB, and −10 dB. Each of these 32 “base” stimuli was then used as the starting point for creating two series of synthetic stimuli. In the first series, the NHR was increased in 20 steps of 1–2 dB while H2–Hn remained constant. Because the NHR is a ratio of noise to harmonic energy, this manipulation resulted in changes in absolute noise levels (without reference to harmonic levels) as well as in noise levels relative to harmonic levels. In the second series, H2–Hn was decreased in 30 steps of 0.5–1 dB while the NHR remained constant. In this case, holding the NHR constant required varying absolute noise levels, in order that noise levels relative to harmonic amplitudes would remain constant across changes in harmonic spectral slope. In both series of stimuli, step size was selected based on pilot studies. This procedure resulted in 64 series of stimuli, as shown in Table Table II.. Prior to presentation to listeners, all stimuli were equalized for peak amplitude and multiplied by 25 ms ramps to eliminate onset and offset click artifacts.

Table II.

Design of Experiment 1.

Test	NHR	Spectral slope (H2–Hn)	Step size
1	Varying, baseline = −40 dB	Constant within a block, 1 block/spectral slope/voice	2 dB (NHR)
2	Varying, baseline = −30 dB	Constant within a block, 1 block/spectral slope/voice	1 dB (NHR)
3	Varying, baseline = −20 dB	Constant within a block, 1 block/spectral slope/voice	1 dB (NHR)
4	Varying, baseline = −10 dB	Constant within a block, 1 block/spectral slope/voice	1 dB (NHR)
5	Constant, = −40 dB	Varying within a block, 1 block/spectral slope/voice	0.5−1 dB (spectral slope)
6	Constant, = −30 dB	Varying within a block, 1 block/spectral slope/voice	0.5−1 dB (spectral slope)
7	Constant, = −20 dB	Varying within a block, 1 block/spectral slope/voice	0.5−1 dB (spectral slope)
8	Constant, = −10 dB	Varying within a block, 1 block/spectral slope/voice	0.5−1 dB (spectral slope)

Listening task

Experiment 1 comprised eight listening tests. Eighty-two normal-hearing listeners participated in this experiment: 10 completed each listening test, except that 12 listeners participated in test 6. Listeners were tested individually in a double-walled sound suite. Stimuli were played at a constant comfortable listening level over Etymotic ER-1 insert earphones (Etymotic Research, Inc., Elk Grove Village, IL), which mimic free-field presentation. No listener participated in more than one test.

Each test included eight blocks of stimuli, as shown in Table Table II.. Within each test, trials were blocked by harmonic slope condition, and blocks were presented in a different random order to each listener. For each block, listeners heard a series of pairs of voices and were asked to judge whether the voices in each pair were the same or different (an AX procedure). One voice in each pair was always the first stimulus in the series, and the other was a test stimulus that differed from the first in either NHR (tests 1–4) or in H2–Hn (tests 5–8), but not both. All other parameters remained constant within and across tests. Voices within a pair were separated by 250 ms. Listeners could play the pair once only in each order (AB and BA) before making their decisions. If the listener correctly distinguished the stimuli in two successive trials, then the difference between stimuli was decreased by one step along the relevant continuum; but if the listener incorrectly responded “same” to either of the two previous trials, then the difference between stimuli was increased by one step (a 1 up, 2 down paradigm; Levitt, 1971). The test proceeded until 12 reversals were obtained, and the just-noticeable difference (JND) for that listener and block was calculated by averaging the difference between the standard and test stimuli at the last eight reversals. This procedure identified the NHR or spectral slope value (depending on test) for which a listener could correctly distinguish the target and test stimuli 70.7% of the time (see Levitt, 1971, for theoretical justification and mathematical derivation).

Prior to beginning the test, listeners heard training stimuli (one male and one female voice) to familiarize them with the contrast being tested. Three stimuli were contrasted for each voice: the standard stimulus and two test stimuli selected so that one was relatively easy to distinguish from the standard, and one was quite similar to the standard. Listeners first heard the two test stimuli several times, until they were confident they could distinguish them. They then heard each test stimulus paired with the standard. Training lasted no more than 5 min, after which the experimental trials began immediately. Total testing time for the eight blocks of trials in each test averaged about 1 h.

Results

Mean JNDs for the NHR as a function of H2–Hn and of baseline NHR are given in Table Table III.. Three-way analysis of variance (ANOVA; H2–Hn × noise baseline × speaker) showed significant main effects of all three independent variables (H2–Hn: F(3, 304) = 27.56, p < 0.01; noise baseline: F (3, 304) = 24.35, p < 0.01; speaker: F(1, 304) = 13.19, p < 0.01), plus a significant interaction between H2–Hn and noise baseline (F(9, 304) = 8.36, p < 0.01). As Table Table III. shows, when H2–Hn was relatively flat (−3 dB/octave), JNDs for the NHR were highly dependent on the amount of noise present in the voice, with JNDs decreasing significantly with increasing noise levels (Tukey post hoc tests, p < 0.05). In other words, it was easier to hear small changes in the NHR when NHR levels were high than when they were very low. However, this dependence decreased with increasingly steep harmonic spectral roll off, and completely disappeared when H2–Hn was steeper than −6 dB/octave. Conversely, when the NHR was high, JNDs for the NHR were independent of H2–Hn, with dependence increasing as the NHR decreased (Tukey post hoc tests, p < 0.05). The main effect of speaker reflects the fact that mean JNDs were slightly but significantly smaller for male voices (4.83 dB, vs 6.14 dB for female voices).

Table III.

JNDs (in dB) for the NHR as a function of NHR baseline and H2–Hn. Standard deviations are given parenthetically.

	NHR
H2–Hn	−40 dB	−30 dB	−20 dB	−10 dB
−3 dB	13.69 (3.74)	9.0 (3.97)	6.62 (4.25)	3.13 (1.66)
−6 dB	8.03 (3.69)	5.48 (3.11)	5.18 (4.46)	3.09 (1.56)
−9 dB	4.13 (2.55)	4.22 (2.30)	4.84 (4.11)	3.12 (1.86)
−12 dB	3.64 (2.28)	4.35 (3.40)	5.95 (4.58)	2.88 (2.33)

Mean JNDs for H2–Hn as a function of baseline H2–Hn and NHR condition are given in Table Table IV.. Three-way ANOVA (baseline H2–Hn × NHR × speaker) showed significant main effects of all three independent variables (baseline H2–Hn: F(3, 288) = 28.49, p < 0.01; NHR: F(3, 288) = 19.99, p < 0.01; speaker: F(1, 288) = 14.92, p < 0.01), along with significant interactions between NHR and baseline H2–Hn (F(9, 288) = 3.91, p < 0.01) and between NHR and speaker (F(3, 288) = 4.10, p < 0.01). With respect to the interaction between NHR and baseline H2–Hn, Table Table IV. shows that when the harmonic spectrum is relatively flat, changes in the NHR have no effect on perception of H2–Hn. However, as spectral roll off becomes increasingly steep, the influence of the NHR on perception of changes in harmonic slope increases proportionally. When H2–Hn rolled off most steeply, each increase in NHR had a significant effect on listeners’ ability to hear changes in spectral slope; but when spectra were flattest, increasing NHR had no significant effect. The NHR/speaker interaction reflects the fact that JNDs for spectral slope were significantly larger for the male stimuli when noise levels were highest than in any other condition (mean JND = 13.34 dB, vs 7.52 dB). No other conditions differed significantly.

Table IV.

JNDs (in dB) for H2–Hn as a function of NHR and H2–Hn baseline. Standard deviations are given parenthetically.

	H2−Hn
NHR	−3 dB/octave	−6 dB/octave	−9 dB/octave	−12 dB/octave
−40 dB	5.80 (2.89)	6.11 (3.24)	5.87 (3.18)	7.57 (3.29)
−30 dB	6.45 (2.48)	5.83 (3.05)	6.88 (3.20)	10.24 (3.35)
−20 dB	5.46 (2.19)	6.09 (2.30)	8.94 (3.70)	12.11 (2.77)
−10 dB	5.93 (3.02)	8.88 (4.67)	13.99 (8.48)	15.74 (9.41)

To estimate listeners’ perceptual sensitivity to the NHR and H2–Hn, we calculated the ratio of the mean JND values obtained here to the range observed for each parameter across the set of 70 normal and pathological voices studied in Kreiman et al. (2007a) This ratio is an index of how perceptually salient each parameter might be in a complete voice pattern: a wide range of variability in a parameter across voices, combined with good listener sensitivity (and hence a small ratio) increases the likelihood that a parameter will be perceptually important. Results are given in Table Table V., along with comparison values for H1-H2, jitter, and shimmer (Kreiman and Gerratt, 2010). Values for jitter and shimmer are based on ranges for normal speakers (Brockmann et al., 2008). Normative data for pathological speakers are not reliable due to the technical difficulties of measuring jitter and shimmer in irregular phonation (e.g., Titze, 1995; Gerratt and Kreiman, 1995). As this table shows, on average, perceptual sensitivity to the NHR and to H2–Hn are high, similar to values for H1-H2, and greatly exceed that for jitter and shimmer [for which the average JND exceeds range (Brockmann et al., 2008; Kreiman and Gerratt, 2005)].

Table V.

Estimated ratio of average JND to range for selected acoustic measures of voice quality, reflecting listeners’ relative perceptual sensitivity to the different parameters. See text for more explanation.

Factor	JND/Range = Index
NHR	5.47 dB/54.9 dB = 0.10
H1−H2	3.19 dB/23.81 dB = 0.13
H2−Hn	8.24 dB/33.6 dB = 0.25
Shimmer	1.99 dB/1.43 dB = 1.39
Jitter	3%/0.85% = 3.53

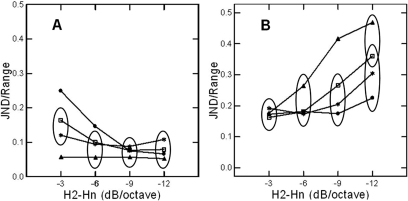
These results are also plotted in Fig. 2. In this figure, the different baseline NHR conditions are plotted with different symbols, so that the relationship among the lines in each panel reflects the main effect of baseline NHR. H2–Hn context is shown on the x axis; and JND/range is plotted on the y axis. Thus, this figure shows the interactions of H2–Hn and NHR in determining the relative perceptual importance of changes in the NHR [Fig. 2a] and H2–Hn [Fig. 2b]. Changes in the NHR [Fig. 2a] remain perceptually salient (i.e., the JND/range ratio remains small) even when effects of H2–Hn on noise perception are strongest (when H2–Hn equals −3 dB/octave and noise levels are low). In fact, the JND/range ratio for the NHR never exceeds 0.3 across all experimental conditions, despite the significant main effects of baseline NHR and H2–Hn on JNDs. Thus, although the NHR interacts significantly with H2–Hn, this interaction affects JNDs only under rather limited circumstances, and to a limited extent. In contrast, the perceptual importance of H2–Hn for the same stimuli is more dependent on context [Fig. 2b]. Perceptual importance is greatest and most constant across H2–Hn conditions when harmonic slopes are flattest and/or the NHR is low. However, when steep harmonic slopes combine with moderate-to-high NHR levels, changes to H2–Hn have more limited perceptual importance, because the change in slope needed to achieve even a minimally perceptible change in quality is large relative to the range of this parameter across voices.

Figure 2.

Variations in sensitivity to changes in NHR and H2–Hn as a function of baseline H2–Hn. The y axis shows the ratio of the JND to range for the NHR (an index of listeners’ overall sensitivity), and the x axis shows baseline H2–Hn. (a) Sensitivity to changes in NHR. (b) Sensitivity to changes in H2–Hn. Values for NHR = −40 dB (noise free) are plotted with filled circles; open squares represent values when the NHR = −30 dB; asterisks show values when the NHR = −20 dB; and filled triangles indicate values when the NHR = −10 dB (very noisy). Ellipses enclose points that do not differ significantly. See text for fuller description.

Discussion

Previous results examining a limited range of stimuli have shown that it is harder to hear changes in spectral noise levels in the presence than in the absence of high frequency harmonic energy, and vice versa (Kreiman and Gerratt, 2005; Shrivastav and Sapienza, 2006), and that noise is a more effective masker of tones than tones are of noise (Gockel et al., 2002, 2003). The results of this experiment are broadly consistent with these findings. Overall JNDs for the NHR decreased with decreasing levels of high-frequency harmonic energy; JNDs for H2–Hn increased with increasing NHR; and increasing noise levels had a greater influence on perception of H2–Hn than changes in H2–Hn did on perception of noise, as Fig. 2 shows, consistent with previous observations of asymmetrical masking. However, all of these effects reflect the interaction of noise and H2–Hn in determining perceptual sensitivity to changes in either. Perceptually meaningful measurements of noise and of harmonic slope in voice thus require knowledge of the relationship between sensitivity to noise levels and perception of spectral slope. (We return to this point in Sec. 9.)

JNDs for the NHR reported here differ substantially from those reported by Shrivastav and Sapienza (2006). Using stimuli created with the KLSYN88 synthesizer (Klatt and Klatt, 1990), Shrivastav and Sapienza (2006) found that listeners needed a 20 dB increase in AH (the amplitude of aspiration noise) to hear a difference in noise level relative to a normal voice, decreasing to about 11 dB at high levels of AH. If we define a “normal” voice as having a harmonic slope of about −6 dB/octave and an NHR between −40 dB and −30 dB, the value obtained in the present experiment is between 5.5 dB and 8 dB, decreasing to about 3 dB at high noise levels (Table Table III.). These values compare fairly well with the JND of 10 dB we reported previously (Kreiman and Gerratt, 2005). Shrivastav and Sapienza (2006) suggested that changes in the spectrum of the aspiration noise in their stimuli might have affected their results, but the spectrum of the noise source is essentially flat and cannot be manipulated in the KLSYN88 synthesizer (Klatt and Klatt, 1990), making this unlikely. These comments, along with our finding of perceptual interactions between harmonic and inharmonic source excitation, do however raise the possibility that differences in noise spectral shape constitute a third factor affecting perceptual sensitivity to the NHR and to H2–Hn. Although some measurement approaches assess the NHR in restricted frequency bands, thus implying underlying differences in noise levels in these bands (e.g., Lively and Emanuel, 1970), relatively little empirical evidence is available regarding the nature or extent of variations in the inharmonic component of the voice source (although see Stevens, 1998, for extended review of theoretical studies of noise spectra). Experiment 2, therefore, begins with descriptive analyses of noise spectra for a sample of pathological voices, and then examines the perceptual importance of these variations.

EXPERIMENT 2

Analyses of noise spectra

Forty samples of the vowel /a/ produced by speakers with vocal pathology (20 male, 20 female) were selected at random from a library of samples recorded under identical conditions. Samples were directly digitized at 20 kHz using a Bruel & Kjær 1/2 in. microphone (model 4193) placed 10 cm from the speaker’s lips at a 45° angle, with 16 bit resolution and a linear phase sigma-delta analog-to-digital converter to avoid aliasing. Noise spectra were derived via analysis-by-synthesis using the methods described in Kreiman et al. (2010). Briefly, recordings were downsampled to 10 kHz, after which the inharmonic part of the voice source (the noise excitation) was estimated through application of a cepstral-domain comb lifter like that described by de Krom (1993; see also Qi and Hillman, 1997), performed on a 204.8 msec segment of the original voice sample. F0 was estimated using an algorithm based on Pearson correlations between successive cycles and was used to construct a lifter to remove the “rahmonics” (the cepstral-domain equivalent of harmonics). This process filtered out the periodic energy in the voice, leaving the noise as shaped by vocal tract filtering. This residual signal was transformed back into the frequency domain and inverse filtered to remove the effects of vocal tract resonances, producing the spectrum of the noise component of the voice.

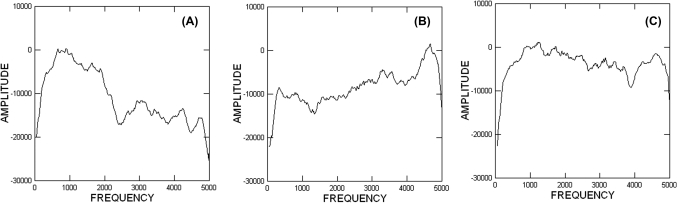
Visual inspection of the resulting noise spectra revealed three different underlying shapes: one with most noise below 3 kHz [a negatively sloped noise spectrum; n = 13; Fig. 3a], a positively sloped noise spectrum [n = 5; Fig. 3b], and a relatively flat noise spectrum [n = 22; Fig. 3c]. One representative spectrum was selected from each of these groups (as shown in Fig. 3) for use in the following experiment.

Figure 3.

Representative noise spectra. Units on the y axis are arbitrary. (a) A typical falling spectrum. (b) A typical rising spectrum. (c) A typical flat spectrum.

Methods

Pilot study

In a pilot test to determine if listeners can discriminate among the three underlying noise shapes, two listeners heard pairs of noise sounds in isolation (not combined with a harmonic component or filtered through a vocal tract model) synthesized with the spectra in Fig. 3. Stimuli were presented over Etymotic ER-1 insert earphones (Etymotic Research, Inc., Elk Grove Village, IL). Listeners also heard an equal number of pairs where stimuli were identical. They judged whether the stimuli were the same or different, and rated their confidence in their responses on a 5 point scale. Both listeners were able to discriminate the isolated noise spectra with 100% accuracy (hit rate = 100%, false alarm rate = 0%) and perfect confidence (mean rating = 1.0).

Stimuli

To determine whether listeners could discriminate among the different noise spectra in natural voice contexts, we created three new synthetic versions of each of the two voices studied in experiment 1. Each version used one of the noise spectra shown in Fig. 3. Apart from noise spectra, the three versions of these voices were identical (Table Table I.). Noise was synthesized as follows. Because the analysis-by-synthesis procedure outputs a noise time series, the noise spectra used for synthesis were derived by analyzing each noise time series with a 512 point FFT with a Hamming window, and then smoothing the resulting spectra with a 20-point moving average. White noise was then passed through a finite impulse response filter modeling each smoothed spectrum to produce three new, synthetic noise time series modeled on the original natural noise spectra.

Next, each synthetic noise time series was combined with four different glottal pulse time series representing four harmonic source slopes (−3 dB/octave, −6 dB/octave, −9 dB/octave, and −12 dB/octave), at 4 NHRs (−40, −30, −20, and −10 dB), for a total of 48 versions of each voice source (3 noise spectra × 4 source spectra × 4 NHR values) and 96 total stimuli. Other synthesis details are identical to those used in experiment 1.

Listeners and listening task

Ten listeners participated in this experiment. All reported normal hearing. They heard stimuli in pairs over Etymotic ER-1 earphones at a constant comfortable listening level. Within a pair, stimuli differed only in the shape of the noise spectrum, with all other synthesizer parameters held constant. For each pair of stimuli, listeners judged whether the stimuli were the same or different, and rated their confidence in their response on a 5-point scale ranging from “positive” to “wild guess.” Each pair was presented twice, along with an equal number of pairs where stimuli were the same, for a total of 192 trials/listener. The task took about 1 h to complete.

Results and discussion

Across conditions, listeners discriminated otherwise identical stimuli with different noise spectra with a hit rate of 59.6% and a false alarm rate of 5.3%. Hit rates varied with the comparison being made, however. When listeners compared flat vs falling noise spectra, the hit rate was 57.5%; for flat vs rising spectra it was 49.1%, and for falling vs rising spectra it was 72.2%.

To provide a more detailed examination of these data, same/different responses were combined with confidence ratings to produce a 10-point scale that ranged from “positive voices are the same” ( = 1) to “positive voices are different” ( = 10). D′ (a measure of discrimination accuracy; e.g., Macmillan and Creelman, 2005) was calculated using these recoded data for each combination of harmonic spectral slope and NHR, for each speaker. Across listeners and conditions, d′ equaled 1.56 (corresponding to a probability of a correct response of approximately 0.66; sd = 1.31; range = −2.33–3.79), substantially less than the perfect performance observed when listeners were asked to discriminate noise spectra in isolation from the natural voice context (which would yield a d′ of approximately 6.93; Macmillan and Creelman, 2005). One-way ANOVA (dependent variable = d′ values) showed that the three noise spectra were equally discriminable from one another, despite differences in hit rates (F(2, 45) = 3.07, p > 0.05), so data were combined for subsequent analyses.

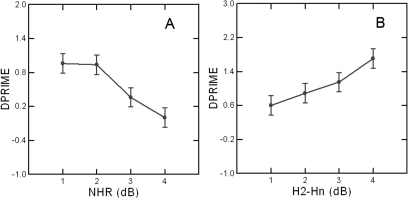
An additional ANOVA examined how changes in NHR and in the slope of the harmonic source spectral shape affected listeners’ ability to discriminate among noise spectral shapes. This revealed significant main effects of NHR (F(3, 144) = 29.09, p < 0.01) and harmonic spectral shape (F(3, 144) = 16.62, p < 0.01), but no interaction between variables (F(9, 144) = 1.99, p > 0.01). These main effects are shown in Fig. 4. When the NHR was greater than or equal to −20 dB, listeners discriminated equally well among the different noise spectra (Tukey post hoc comparisons, p > 0.05; mean d′ = 1.60). Discrimination performance decreased significantly as the NHR decreased below this value, however (Tukey post hoc comparisons, p < 0.05), so that at the lowest NHR levels d′ approached 0. Additional Tukey post hoc comparisons (p < 0.05) indicated that the discrimination task grew more difficult as H2–Hn decreased, so that listeners were most accurate when it equaled −12 dB/octave (d′ = 1.70), and least accurate when it equaled −3 dB/octave or −6 dB/octave (mean d′ = 0.74).

Figure 4.

(Color online) Changes in discrimination accuracy (measured by d′) for the three noise sources, as a function of changes in (a) NHR and (b) H2–Hn. See text for more discussion.

These results indicate that changes in noise spectral shape are harder to hear in the context of a complete voice pattern than in isolation, because vocal tract filtering obscures differences in levels of high frequency excitation while masking by harmonic energy makes remaining differences harder to hear. This result is consistent with findings by Shrivastav and Sapienza (2006) that the spectrum of the aspiration noise in their stimuli after vocal tract filtering affected JNDs for “breathiness.”

Nevertheless, listeners in the present study were still able to discriminate among voices that differed only in noise spectral shape, with better-than-chance accuracy. It follows that the spectrum of inharmonic energy in the voice source contributes significantly to voice quality: Changes in the shape of the noise spectrum produced perceptible changes in the way the voice sounds. This effect depended on both the amount of noise in the voice and on the slope of the harmonic source spectrum, which in turn suggests that patterns of listener sensitivity to these two attributes may depend in turn on the shape of the noise spectrum. Experiment 3 tests this hypothesis.

EXPERIMENT 3

Methods

Experiment 3 comprised two tests, each including eight blocks of trials. Stimuli were created using the methods applied in tests 1 and 8 in experiment 1, except that the flat noise spectrum used in experiment 1 was replaced with the falling spectrum shown in Fig. 3a. In the first test, within each block of trials the NHR increased in 20 steps of 1–2 dB from a baseline of −40 dB. (Step size was determined by pilot study.) H2–Hn remained constant within a block, but across blocks it varied from −3 dB to −12 dB in steps of −3 dB (as in experiment 1, test 1). Four blocks of stimuli were created using the male voice from experiment 1, and four with the female voice. In test 2, the 8 blocks of stimuli again corresponded to the four H2–Hn levels, combined with the male/female voice contexts. Within each block the slope of the harmonic source spectrum changed in 30 steps of 0.5−1 dB (as determined by pilot study) while the NHR remained constant across trials and blocks at −10 dB. All other details of stimulus preparation follow the procedures described for experiment 1.

Twenty-four normal-hearing listeners participated in this experiment, 12 in each test. No listener had participated in any previous test. All training and testing procedures were identical to those used in experiment 1.

Results and discussion

Three-way (noise spectral shape × speaker × H2–Hn) ANOVAs were used to compare JNDs for the NHR and H2-Hn from these two tests to those obtained for stimuli with flat noise spectra in experiment 1 (NHR: test 1; H2–Hn: test 8). For the NHR, this analysis revealed a significant main effect of noise spectral shape (F(1, 160) = 172.73, p < 0.01; Table Table VI.): Listeners were significantly more sensitive to changes in the NHR when the noise spectrum was flat than when it was falling. This analysis also indicated that sensitivity increased as harmonic spectral roll off grew steeper (F(3, 160) = 25.11, p < 0.01), but the pattern of change with H2–Hn depended on the shape of the noise spectrum (F(3, 160) = 2.82, p < 0.05). When the noise spectrum was flat, JNDs for the NHR first decreased significantly but then asymptoted, so that JNDs when H2–Hn equaled −3 dB/octave differed significantly from all other conditions, which did not differ significantly (Tukey post hoc comparisons, p < 0.05). In contrast, when the noise spectrum was falling, JNDs decreased slowly with increasing harmonic spectral roll off, and differences were significant only for the steepest roll off condition, which differed from all others (Tukey post hoc comparisons, p < 0.05). Finally, a significant main effect of speaker was observed (F(1, 160) = 12.11, p < 0.01). Sensitivity to the NHR was slightly greater for the male voice samples than for the female samples (JND = 11.22 dB vs 13.99 dB).

Table VI.

JNDs (in dB) for the NHR as a function of noise spectral shape and H2−Hn, for Experiment 3. Data for flat noise spectra were taken from Experiment 1, test 1. Standard deviations are given parenthetically.

	H2−Hn
Noise shape	−3 dB/octave	−6 dB/octave	−9 dB/octave	−12 dB/octave
Flat	13.69 (3.74)	8.03 (3.69)	4.13 (2.55)	3.64 (2.28)
Falling	12.07 (5.01)	11.51 (4.41)	9.17 (4.28)	6.76 (4.29)

Noise spectral shape also affected listeners’ sensitivity to changes in H2–Hn (three-way ANOVA; F(1, 160) = 13.81, p < 0.01): Listeners were more sensitive to changes in H2–Hn when the noise spectrum was falling than when it was flat (Table Table VII.). Significant main effects were also observed for baseline H2–Hn (F(3, 160) = 24.51, p < 0.01) and for speaker (F(1, 160) = 26.16, p < 0.01), as was a significant interaction between speaker and H2–Hn (F(3, 160) = 3.52, p < 0.02). The main effect of speaker was significant only when H2–Hn equaled −9 or −12 dB/octave), but not when the harmonic spectrum is relatively flat (−3 or −6 dB/octave) (Tukey post hoc comparisons, p < 0.01).

Table VII.

JNDs (in dB) for H2−Hn as a function of noise spectral shape and baseline H2–Hn, from Experiment 3. Data for flat noise spectra were taken from Experiment 1, test 8. Standard deviations are given parenthetically.

	H2–Hn
Noise shape	−3 dB/octave	−6 dB/octave	−9 dB/octave	−12 dB/octave
Flat	5.93 (3.02)	8.88 (4.67)	13.99 (8.48)	15.74 (9.41)
Falling	5.31 (2.24)	7.32 (3.32)	8.22 (3.53)	12.58 (5.54)

GENERAL DISCUSSION

The combined results of these experiments indicate that perception of the harmonic spectral slope and of noise levels in voice (measured by the NHR) is a function of a set of complex interactions between the shape and levels of the harmonic and inharmonic parts of the voice source. These results extend previous findings that listeners’ sensitivity to noise levels in voice depends in part on the shape of the higher part of the harmonic voice source spectrum. JNDs for the NHR vary significantly with both noise level (more noise = smaller JNDs) and with harmonic spectral slope (steeper roll off = smaller JNDs), but NHR had no effect on JNDs for the NHR when harmonic slopes were steepest, and harmonic slope had no effect when NHR levels were highest. Similarly, perception of changes in H2–Hn depended on NHR values and on baseline H2–Hn, so that JNDs increased when spectra rolled off more steeply, with this effect in turn depending on the noise level (relatively more noise = bigger effect of baseline H2–Hn on JNDs for H2–Hn). Finally, all of these effects were modulated by the shape of the noise spectrum. Listeners were more sensitive to changes in H2–Hn when the noise spectrum was falling and to changes in the NHR when the noise spectrum was flat. When noise was flat, sensitivity to the NHR was significantly worse when the harmonic spectrum was flattest, and when noise was falling, sensitivity to the NHR was significantly better when the harmonic spectrum rolled off most steeply.

It thus appears that understanding the perception of these individual parameters requires knowledge of the acoustic context in which they function. Currently available measures of the NHR and/or of the slope of the harmonic voice source do not reflect context effects on perceptual acuity. As a result, the same NHR value measured from two voices with different harmonic sources may correspond to very different levels of perceived “noisiness,” while voices with rather different NHRs may sound similarly noisy. It follows that changes to the NHR as a result of clinical intervention may improve vocal quality to different extents, depending on the overall voice pattern. Similarly for harmonic spectral slope: The perceptual impact of changes in the amount of high-frequency harmonic excitation in a voice depends heavily on the amount and shape of the noise present. These impacts are not trivial: Across experiments, JNDs for the NHR ranged from 2.88 to 13.69 dB, while JNDs for H2–Hn ranged from 5.32 to 15.74 dB, representing substantial variation in the degree of perceptual importance, depending on the acoustic context in which the cue functions.

These results differ somewhat from previous studies using an “auditory model” to quantify the acoustic precursors of breathy voice quality (Shrivastav and Sapienza, 2003). That model accounts for variations in perceived breathiness via two measures: the partial loudness of the harmonic source (as masked by noise) and the loudness of the noise source, unmasked by harmonic energy (Moore et al., 1997). The present data indicate that, although noise masks harmonics much more efficiently than harmonics mask noise (cf. Gockel et al., 2002, 2003), masking of noise by harmonic energy is not in fact negligible, as the auditory model assumes. Note also that psychoacoustic studies of partial loudness (Moore et al., 1997; Gockel et al., 2002, 2003) explicitly require that harmonic and noise energy be perceptually separable, which is not the case with natural voice stimuli, in which noise and harmonics fuse perceptually. This further limits the extent to which results of such studies can be meaningfully generalized to more complex speech stimuli. In fact, in one study, application of the auditory model increased predictive power by only 4% as compared to traditional acoustic measures (Shrivastav and Sapienza, 2003), possibly as a result of the factors discussed above.

Finally, the finding that perception of H2–Hn and NHR are context-dependent has important implications for the issue of how to model voice quality in general. Current approaches to the study of quality can be divided into two broad categories: those that treat quality as a bundle of features, and those that treat quality as a pattern that resists decomposition (see Kreiman and Sidtis, 2011, for extended review). Many clinical voice evaluation protocols require listeners to rate individual voice features (e.g., Kempster et al., 2009; Hirano, 1981; Laver et al., 1981), and thus implicitly assume the first model. However, the present results, as well as results of a number of behavioral and neuropsychological studies (e.g., Van Lancker et al., 1985a,b; Li and Pastore, 1995; Schweinberger et al., 1997; Andics et al., 2010; Melara and Marks, 1990), are more consistent with the second view of quality. For example, in priming experiments (Schweinberger et al., 1997) reaction times to famous voices were significantly faster when listeners had previously heard a different exemplar of the voice. Because the priming effect was produced by a different sample of each voice, it appears that the benefit derives from the complete voice pattern, not from the specific details of a given sample, consistent with the view that voices are processed as patterns, and not as bundles of features. Similarly, acoustic alterations can affect the recognizability of a voice, but it is not possible to predict the extent of the effect from either the context in which a cue occurs or from the value of the parameter alone—the overall perceptual importance of a given acoustic feature cannot be determined a priori, because it depends on the values of the other features in the pattern (Van Lancker et al., 1985a,b; Lavner et al., 2000). Finally, listeners’ difficulty in isolating individual features in complex voice patterns is the major cause of disagreements in voice rating tasks (Kreiman et al., 2007b). The present results add one more piece of evidence that voices are integral patterns: It is impossible to assess the perceptual impact of either harmonic or noise energy independently, without the influence of the other kind of excitation.