Volume Exclusion and H-Bonding Dominate the Thermodynamics and Solvation of Trimethylamine-N-oxide in Aqueous Urea

Abstract

Trimethylamine-N-oxide (TMAO) and urea represent the extremes among the naturally occurring organic osmolytes in terms of their ability to stabilize/destabilize proteins. Their mixtures are found in nature and have generated interest in terms of both their physiological role and their potential use as additives in various applications (crystallography, drug formulation, etc.). Here we report experimental density and activity coefficient data for aqueous mixtures of TMAO with urea. From these data we derive the thermodynamics and solvation properties of the osmolytes, using Kirkwood–Buff theory. Strong hydrogen-bonding at the TMAO oxygen, combined with volume exclusion, accounts for the thermodynamics and solvation of TMAO in aqueous urea. As a result, TMAO behaves in a manner that is surprisingly similar to that of hard-spheres. There are two mandatory solvation sites. In plain water, these sites are occupied with water molecules, which are seamlessly replaced by urea, in proportion to its volume fraction. We discuss how this result gives an explanation both for the exceptionally strong exclusion of TMAO from peptide groups and for the experimentally observed synergy between urea and TMAO.

Introduction

Virtually all organisms use organic osmolytes to counter biochemical stress.¹ The denaturant urea is among those osmolytes and can occur as a stressor, e.g., in the kidney,² but it is also used against osmotic stress.¹ In either case, urea is found in mixtures with at least one other osmolyte, typically a methylamine, such as trimethylamine-N-oxide (TMAO).¹ This compound has generated considerable research interest, not only because it is the strongest known protein stabilizer among the natural osmolytes³ and a crystallizing agent;⁴ it also has been found to correct medicinally significant issues, such as prion aggregation⁵ and cellular folding defects.⁶

It has remained somewhat elusive what the mechanism of TMAO’s action on protein is, and how it counters the denaturing effect of urea. The range of opinions is broad and includes suggestions that TMAO stabilizes proteins by classical preferential exclusion⁷⁻¹⁴ or by altering the structure of water¹⁵⁻¹⁷ and that TMAO counteracts urea by directly interacting with urea,^18,19 by urea-independent preferential exclusion from the protein,^7,20−22 or by reverting changes of the structure of water caused by urea.¹⁵ Since many of these ideas have to do with the bulk solution, it is expedient to focus on ternary mixtures of TMAO with urea in water.

Here we report thermodynamic experiments that are combined with rigorous statistical mechanics²³ to derive structural properties of the solution.²⁴ This so-called Kirkwood–Buff approach provides a link between thermodynamics and preferential interactions on the one side and the structure of the solution on the other.^{11,12,25−27} The basic idea of this approach is that deviations from random distribution of molecules around each other produce characteristic changes in the partial molar volumes and chemical activities of the solution components,²³and that conversely knowledge of these thermodynamic properties allows us to derive information about the proximity of molecules in solution.²⁴ The so-called Kirkwood–Buff integrals (integrated pair correlation functions) are a measure of the excess or deficit of one type of molecule around another.²³

Using this Kirkwood–Buff approach, we find that, in aqueous urea, TMAO behaves as if it were a hard-sphere gas and the effective size of the hard-sphere depends on its occupancy with either water or urea molecules at two mandatory solvation sites. This result gives a rationale for the strong exclusion of TMAO from peptide groups,^9,28 which is substantially enhanced by the water/urea spacers intercalated between TMAO and the peptide group. It also explains the experimentally observed (though small)²⁰ synergy between urea and TMAO, which is caused by the increased exclusion of TMAO from the peptide group, as small spacers (water) are replaced by larger ones (urea).

Results

The primary goal here is to derive the solvation behavior of aqueous mixtures of urea and TMAO, which requires partial molar volumes and chemical activities of the solution components (see eqs 16 and 17).

Volumes

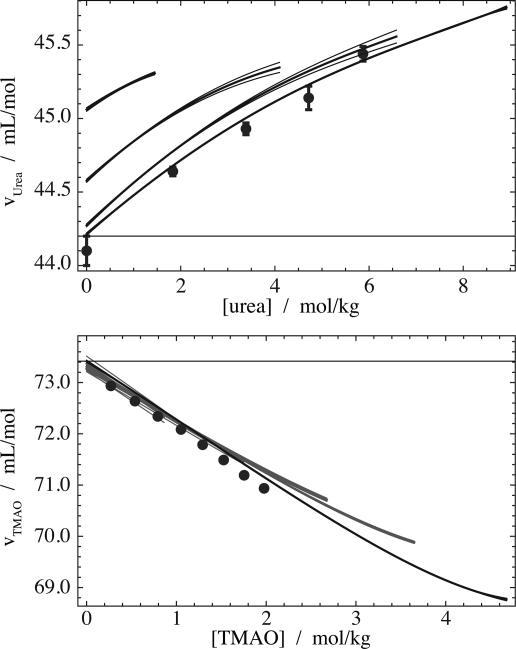
The partial molar volumes are shown in Figure 1, where the horizontal lines represent the limiting values in plain water. The partial molar volumes of both urea (top panel) and TMAO (bottom panel) depend very little on the concentration of the respective other osmolyte within the range of concentrations used in the vapor pressure experiments (∼3 M). The partial molar volume of water is virtually unchanged (not shown). Our data on urea compare favorably with previous data reported by Lee and Chalikian²⁹ (points in the top panel of Figure 1). The partial molar volume of TMAO comes very close to the data reported by Di Michele et al.³⁰ (points in the bottom panel of Figure 1). However, there is a slight offset. This could be due to deviations between the assumed and actual concentrations of TMAO. Di Michele et al. used a very hygroscopic³¹ preparation of anhydrous TMAO without further treatment, and their data become identical with ours if we assume that their TMAO contained 3–4% water.

Figure 1.

Partial molar volumes of urea and TMAO in their ternary mixtures with water. Straight horizontal lines represent limiting partial molar volumes in plain water. Top panel: urea partial molar volume (thick lines) in 0 m, 2 m, 4 m, and 6 m TMAO (bottom to top). Propagated fitting errors are given by thin lines, and points represent previous data.²⁹ Bottom panel: Same for TMAO in 0–15 m urea (3 m steps from bottom to top). Points are literature data.³⁰ The parameters from a fit of the density data to eq 7 are given in Table 1.

Table 1. Density Fitting Results to Eq 7 in mL/mol.

v̅1,0	44.2		v̅0,1	73.4
v̅2,0/(10–3/m)	276		v̅0,2/(1/m)	–1.1
v̅3,0/(10–3/m2)	–48		v̅0,3/(1/m2)	0.11
v̅4,0/(10–3/m3)	7		v̅0,4/(10–3/m3)	7
v̅5,0/(10–3/m4)	–0.5		v̅0,5/(10–3/m4)	0
v̅1,1/(10–3/m)	–41		v̅1,3/(10–3/m3)	–8
v̅1,2/(10–3/m2)	77		v̅2,2/(10–3/m3)	–8
v̅2,1/(10–3/m2)	4		v̅3,1/(10–3/m3)	0.5

Osmotic Coefficient and Activity Coefficients

The osmotic coefficient data are shown in Figure 2 along with the fit (eq 12). Our urea data (thin open circles) compare well with previous data (thick open circles).³² The osmotic coefficient of TMAO (filled circles) is symptomatic for molecules that have repulsion between each other.³³ We decided to sample the osmotic coefficient of a 2:1 mixture of urea:TMAO (triangles), because this is a ratio found in living organisms.^34,35 At this ratio, the osmotic coefficient remains close to unity; i.e., the water behaves close to ideally in the molality scale.

Figure 2.

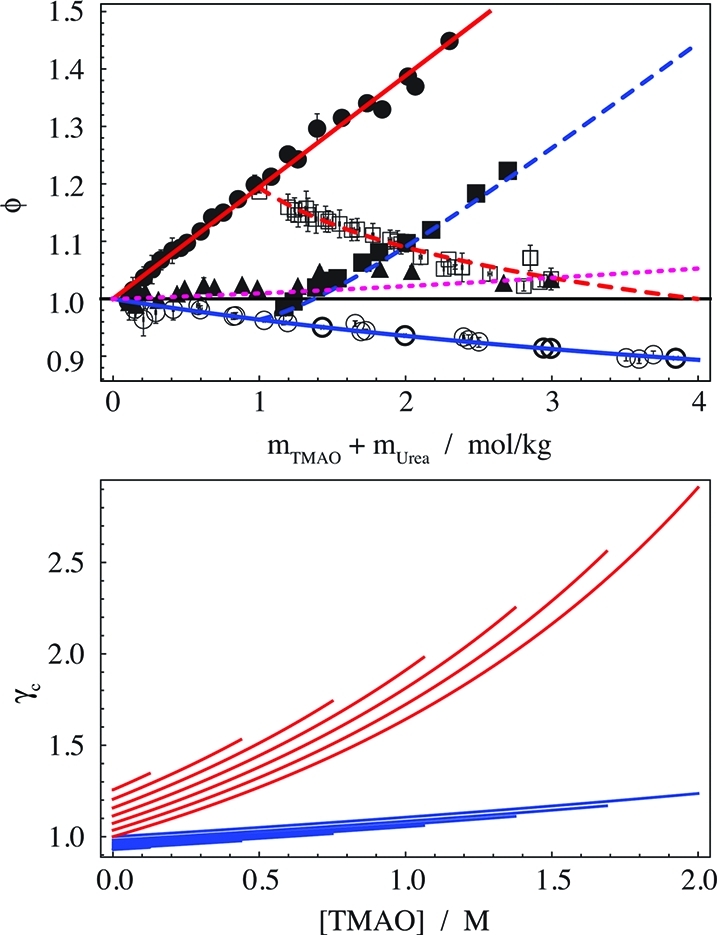
Osmotic coefficients and activity coefficients in aqueous mixtures of urea with TMAO. (Top panel) Osmotic coefficients. Lines are the fit: blue, addition of urea to water (solid) or 1 m TMAO (dashed); red, addition of TMAO to water (solid) or 1 m urea (dashed); magenta, urea/TMAO = 2/1. Data: thin open circles, urea in water (this work); thick open circles, urea in water;³² open squares, urea in 1 m TMAO; filled circles, TMAO in water; filled squares, TMAO in 1 m urea; triangles, urea/TMAO = 2/1. Error bars show the standard deviation of three to nine measurements. (Bottom panel) Molar activity coefficients as a function of the TMAO concentration: red lines, γ_c of TMAO; blue lines, γ_c of urea. The successively shorter lines that are offset relative to unity correspond to 0–3 M urea, spaced by 0.5 M increments.

The molar activity coefficients can be described as previously by³³

1

where i stands for either urea (U) or TMAO (T). The parameters c_1,i and c_2,i are the inverse effective volumes occupied by a single osmolyte and a pair of osmolyte molecules, and g_2,i is an interaction parameter. The parameter γ₀ accounts for the effect of the second osmolyte on the infinite dilution activity coefficient of the first one. All parameters depend on the other osmolyte’s concentration, e.g.,

2

The parameters are given in Table 2.

Table 2. Parameters for the Second-Order Polynomials for Each Parameter in Eq 1, for Either Urea (U) or TMAO (T): Given Are the Zeroth-, First-, and Second-Order Coefficients for a Second-Order Polynomial of the Type Given by Eq 2.

	0th	1st	2nd
c1,T	1.453 M	–0.040	0
c2,T	2.066 M	–0.078	0
g2,T	8.311 M	0.022	0.030/M
γ0,T	1	0.074	0
c1,U	19.84 M	–6.1	1.32/M
c2,U	11.02 M	0	0
g2,U	21.14 M	–3.94	0
γ0,U	1	0.11	0

The resulting molar activity coefficients (Figure 2, bottom panel) depend primarily on the molarity of TMAO, and to a much lesser degree on the molarity of urea. For example, the change in γ_c,U (blue lines) as a function of TMAO (going from left to right) is several fold larger than as a function of urea (going from the uppermost curve to the lowest). For this reason, γ_c is plotted as a function of the TMAO concentration. Both activity coefficients increase upon addition of the respective other osmolyte, suggesting mild mutual exclusion.³³ This effect is, however, small compared to the strong increase of the activity coefficient of TMAO with its own concentration (see bottom panel of Figure 2).

Solvation

From the combined volumetric and osmometric data we derived the Kirkwood–Buff integrals (KBIs) of all components in the ternary mixture, using eq 16. Remember that the KBIs are a measure of the excess or deficit of one type of molecule around another type. The results are shown in Figure 3. The first observation is that again, as in the case of the activity coefficients (Figure 2), all concentration dependencies are almost exclusively due to TMAO. That is, the change along the TMAO axis is generally larger than the urea-dependent offset within each group of curves. Only the self-solvation KBIs of the osmolytes 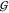_UU and 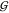_TT depend slightly on the concentration of urea. Thus the cluster of lines corresponding to increasing urea concentration becomes visible in these two cases. The urea concentration increases from the highest line (0 m) to the lowest one (3.6 m) in both cases. The overall level of the TMAO self-solvation, 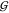_TT, is at least 3 times more negative than expected for an osmolyte of its size. The magnitude of 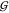_TT is in the order of that of disaccharides.³⁷ But as expected,³⁷ the hydration terms 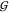_WT, 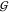_WU, and _WW are small in comparison.

Figure 3.

Solvation in aqueous mixtures of urea with TMAO. The Kirkwood–Buff integrals _ij for hydration of urea (cyan), TMAO (blue), and water (black) are given separately (top panel) to avoid overlap with _UU. The data are given as a function of the TMAO molarity in clusters of curves that correspond to increasing urea concentrations (starting form zero, offset in increments of 0.4 m). The propagated fitting error is smaller than 0.001 L/mol for hydration, and smaller than 0.01 L/mol for osmolyte–osmolyte interaction.

Hard-Sphere-like Behavior of TMAO

Figure 4 demonstrates that TMAO closely follows a solvation pattern expected for a hard-sphere gas, i.e., a system in which the one and only interaction between molecules is hard-core repulsion (molecules cannot overlap each other). At low concentrations, such spheres occupy the space randomly. As the concentration increases, their proximity is determined by the question of how well they can be packed. The lower panel shows 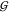_TT at 0 M urea (continuous red line), along with three sets of predictions according to the Carnahan–Starling equation for hard-spheres (eq 23), using the partial molar volumes for TMAO shown in Figure 1. TMAO actually behaves like a hard-sphere of the size of a doubly hydrated TMAO molecule. This solvation pattern makes sense, because it is known that TMAO is strongly hydrated by two water molecules.^22,37,38 Naturally, though TMAO has a very compact shape, it is not literally a perfect sphere. But TMAO shows a remarkable similarity to the solvation expected for an ideal hard-sphere.

Figure 4.

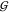Hard-sphere like behavior of TMAO. The upper panel shows the TMAO hydration, _WT (blue), and the water self-hydration, _WW (gray), at 0 M urea, along with the hard-sphere behavior calculated for 0 to 2 hydration waters, using eqs 24 and 25. The lower panel contains the same information for the TMAO self-solvation, 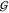_TT (red), at 0 M urea (continuous red line) and in the limit of 0 M TMAO (dashed red line). The latter is shown as a function of the urea molarity, and the dash-dotted line is calculated according to eq 5. The deviations between the best prediction and the data are smaller than the uncertainty in the data (∼10 mL/mol).

The hard-sphere like behavior can be further tested by investigating the TMAO 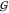hydration, _WT, shown in the upper panel of Figure 4. Also this KBI perfectly matches the model of a hydrated hard-sphere that has the size of a doubly hydrated TMAO molecule (eq 24). The same behavior is found with the water self-hydration, 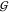_WW (Figure 4, top panel). There is no straightforward way to calculate the other, urea-related KBIs from the hard-sphere model.

Discussion

Much has been written about the interactions among TMAO, urea, and water in solution, and the main focus has been on the water interactions. We start by first considering the hydration of TMAO, and then examine the other (previously more neglected) binary interactions in solution, and close with a discussion of water structure.

Strong, Two-fold Hydration of TMAO

Our finding that aqueous TMAO behaves similarly to a hard-sphere of the size of TMAO dihydrate strongly suggests that TMAO has two mandatory hydration waters. This is supported by various other lines of research. Anhydrous TMAO cannot be produced by evaporating the two hydration waters; rather, TMAO has to be sublimed at high temperature.³¹Ab initio calculations also show tightly coordinated water.³⁹ Dielectric relaxation finds TMAO as a dihydrate in solution, and in the same research the very large enthalpy of H-bond formation was pointed out.³⁷ Based on NMR it was found that all TMAO in water is present as dihydrate.³⁸ A strong hydration of TMAO was also seen in molecular dynamics simulations.⁴⁰ Raman spectroscopy indicates that TMAO has at least three H-bonds from neighboring water,⁴¹ but the mere existence of H-bonded waters does not necessarily imply that all (or even any) of them are mandatory hydration waters. The spectroscopic observation that the solvation shell of TMAO contains slower moving water molecules⁴² may be at least in part due to the solvation sites at the TMAO oxygen. Significantly, small angle scattering measurements found that both water oxygen and urea nitrogen are found around the TMAO oxygen at hydrogen-bonded distances, with one hydrogen atom between.^19,43 Thus, both urea and water snap into hydrogen-bonded positions as they approach the TMAO oxygen.

The Two Mandatory Ligands of TMAO Can Be Water Molecules, Urea Molecules, or Both

It has been found both by Raman spectroscopy³⁰ and neutron/X-ray scattering⁴³ that TMAO does not self-aggregate. We can add now the significant finding to which degree TMAO does not aggregate; viz., its self-solvation _TT is indistinguishable from that of a hard-sphere gas—there is no significant attraction. According to the effective size of the hard-sphere, the TMAO must be doubly hydrated, as discussed above. Upon addition of urea, these waters are progressively replaced by urea molecules,⁴³ and this should lead to an increase of the effective hard-sphere size. Indeed, 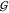_TT changes upon urea addition toward more negative values, which correspond to larger sphere diameters (Figures 3 and 4), as discussed in the following around eq 5.

Water and Urea Are Essentially Equivalent Ligands for TMAO

Is there actual (weak affinity) binding of urea to TMAO? Meersman et al. argued that urea binds to TMAO with an affinity that is comparable to the interaction of urea with peptide groups.⁴³ However, they also pointed out that their analysis was assuming a binding model, rather than the proper exchange model.⁴³ Therefore we reanalyze their data, as shown in Figure 5 as continuous lines. We focus on the first two reported binding events, because a potential third “urea site” is barely populated.⁴³ The reaction model is

3

where T, U, and W represent TMAO, urea, and water, respectively, and K₁ and K₂ are the exchange constants for the two reactions. The populations for each species were calculated and fit to the data numerically. The resulting “affinities” are quite weak, so that the midpoint of the “binding” of the first urea is around 7.5 M urea. In comparison, the midpoint of the binding of urea to a peptide NH is around 4 M.⁴⁴ In the face of such weak affinities the question arises, how do the exchange curves in Figure 5 compare to random occupancy with water and urea? If we take the volume fraction as an approximate model for the likelihood that a site is randomly occupied by a species,⁴⁴ we first need to consider that direct TMAO–TMAO interaction at the oxygen site does not occur (see previous paragraph). So, we normalize the volume fractions of water and urea to refer to the non-TMAO volume (1 – ϕ_T), and obtain for the populations of the three species

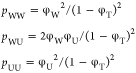4

The resulting curves are shown as dashed lines in Figure 5. The population of the dihydrate, p_WW, closely follows the exchange curve, and thus double occupancy with water is practically random. For the other two species, there is a marginal deviation from random distribution, such that the single urea species is populated slightly less than random, and the double urea species slightly more. This view of nearly random interaction is also supported by recent molecular dynamics simulations, where TMAO was found to be equally H-bonded to water and urea at about 35% by volume of each urea and water,²² and a rough equivalence of both was noted.⁴⁰ The idea of random interaction of water and urea with TMAO is also consistent with the spectroscopic finding that there is no specific urea-TMAO binding.⁴⁵ A computational finding that both urea and water interact strongly with TMAO¹⁸ should then be taken to mean that though both are strongly interacting with TMAO (judged by the fact that the solvation sites are mandatory), they are about equally strongly interacting (judged by the random interaction).

Figure 5.

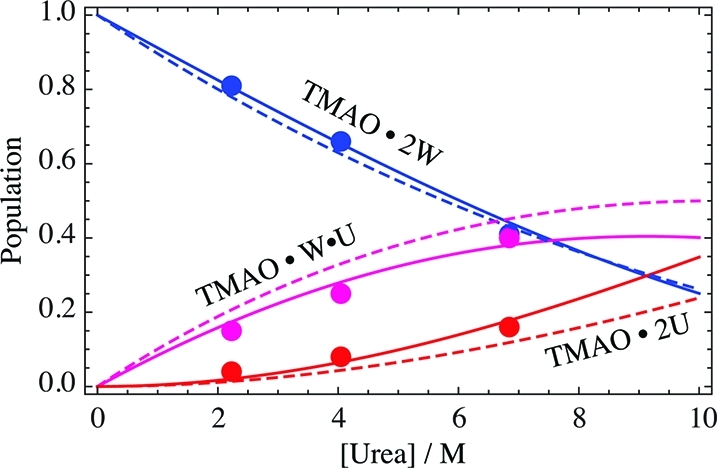
“Binding” of urea to TMAO. Points are previously measured data.⁴³ Continuous lines are global fits of model eq 3 to the data (K₁ = 4.6, K₂ = 2.5). Dashed lines are random encounters calculated according to volume fractions (eq 4).

From the concept of random occupancy we can also predict the change in 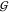_TT upon addition of urea that we observe in Figures 3 and 4. If we take the three populations of differently sized hard-spheres (eq 4) as weights for the KBIs for the three sphere sizes,

5

we get very good agreement between the data and the prediction as shown in Figure 4 (lower panel, red dashed and black dash-dotted lines).

The Urea–TMAO Interaction _UT Is Dominated by Steric Exclusion Effects

From neutron and X-ray diffraction measurements Meersman et al. derived the radial distribution function between a urea nitrogen and the TMAO oxygen as shown in Figure 6 (blue line).⁴³ Although there is a clear first solvation peak corresponding to direct H-bonding, this peak does not exceed unity much, which is indicative of massive steric exclusion. This makes sense, considering that urea can approach the TMAO oxygen only from that hemisphere that is not blocked by the nitrogen and three methyl groups.

Figure 6.

Radial distribution function of urea nitrogen around TMAO oxygen: blue line, data for about 2 M each of urea and TMAO;⁴³ red line, effect of direct steric exclusion between urea and TMAO (eq 6). Top: schematic illustration of the origin of the peaks for (A) direct H-bonding of urea to TMAO and (B) solvent-separated H-bonding. TMAO oxygen and urea nitrogen are boxed. Water atoms are displayed in gray.

How do the data compare to a situation where urea is excluded from TMAO but randomly distributed beyond the limits of the TMAO molecule (in a urea continuum)? Analytic integration of a 3D space with a TMAO-sized spherical hole gives the contribution of the direct steric exclusion to the radial distribution function as

6

where r_min is the minimal distance between urea and the TMAO oxygen (about 1.2 Å),¹⁹ and r_T is the effective radius of dry TMAO (2.66 Å).²⁸ The resulting curve is shown in red in Figure 6. Comparing the data (blue) with the steric contribution (red) reveals more clearly the second solvation peak around 5.5 Å, which may come from both the second urea nitrogen and water-separated urea–TMAO pairs. Beyond this peak the radial distribution function levels off. Significantly, the blue scattering curve integrates within error to the same value as the red curve, viz., the measured _UT ≈ – 90 mL/mol at ∼2 M TMAO. This result highlights the dominance of steric exclusion, where the H-bonding related deviations of the actual g(r) from eq 6 merely have an alignment effect that averages out to zero.

Hydration of Urea and TMAO Is Unchanged upon Mixing

Previous findings support our observation that the hydration of the osmolytes, 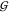_TW and 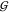_UW, hardly depends on osmolyte concentration (except for the nonspecific hard-sphere-like behavior of 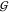_TW as a function of c_TMAO). Near-infrared spectra do not show any evidence that the hydration of either urea or TMAO changes upon mixing.⁴⁵ Also NMR, combined with molecular dynamics, showed that the hydration shell structure of TMAO is maintained over a wide concentration range.⁴⁶

Water Structure

There are two schools of thought on the origin of the behavior of osmolytes, viz. either direct interaction of water/osmolyte with target molecules^7−14,26,27 (preferential interactions) or indirect effects through alterations of the structure of water.^15,16 Typical uses of the term “water structure” refer to just one small aspect of the properties of water. Thus it is not surprising that one can reach diametrically opposite conclusions regarding the effect of osmolytes merely by choosing how the term “water structure” is used.¹³ It has been suggested that the term “water structure” may be even undefinable in view of such issues.²⁶ It is therefore expedient to refer to the actual observations (e.g., H-bond angles) rather than to use a word with multiple disparate uses.

What is the appropriate definition of “water structure” when we want to understand the thermodynamics of the solution? Perhaps the most general definition is given by the KBIs, which provide a rigorous link between the positions of molecules in solution and thermodynamics.²³ The KBIs are directly linked with preferential interactions,^{11,12,25−27} which means that the school of thought that osmolytes act through preferential interaction has a rigorous statistical mechanic backing. Does that mean there is no place for the other school of thought? To answer this question, we have to remember that the KBIs are integrated radial distribution functions, so they are thermodynamically valid descriptions of solution structure as well. And all the other measures of water structure can be equally valid thermodynamically, to the degree to which they explain the form of the KBI.

There are two general aspects of water structure: the bulk water structure (related 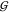to _WW) and the hydration structures of the osmolytes (related to 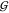_TW and 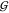_UW). We already discussed some of the latter above, and numerous more could be added.^{10,13,16,17,22,38,47−53} The point is that it is by no means obvious how those findings could be predictive of a significant change in any of the hydration KBIs, 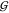_WW, 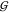_TW, and 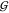_UW. Specifically, Figure 3 shows that the water self-hydration, 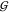_WW, changes very little as osmolyte is added. The effect may be significant in terms of the precision of the data (see Figure 4), but negligibly small compared to the changes seen in the other KBI. Moreover, it has been pointed out that 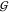_WW does not even appear in the Kirkwood–Buff expressions that describe the impact of osmolytes on protein stability.²⁷ The other two hydration KBI do explicitly occur in those expressions, but 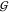_TW seems to be governed by mere packing, as judged by its hard-sphere like behavior.

Conclusions

We have used a combination of our current experimental volume and chemical activity data with Kirkwood–Buff theory to elucidate the behavior of TMAO in aqueous urea. A second look on scattering data provided a strong confirmation and some additional insight. The picture that emerges shows a dominant role of hydrogen bonding along with simple steric exclusion. TMAO is a roughly spherical molecule and behaves as such to a degree that its self-solvation and hydration resemble the properties of a hard-sphere gas. However, it has two mandatory solvation sites that can be occupied by water or urea, substantially enlarging the effective hard-sphere diameter. The hydrogen bonding at these sites is sufficiently strong to prevent both water and urea from approaching the oxygen with anything else other than their hydrogen atoms.

What implications does this have for osmolyte–protein interactions? It is well known that TMAO is strongly excluded from peptide groups.^3,8,9,28 Such preferential exclusion (also termed “osmophobicity” ⁹) favors the native state because the denatured state exposes more surface, leading to more exclusion.⁹ Aqueous TMAO appears to interact with the peptide groups only through its hydration waters.^38,40 Thus, the H-bonds donated to the TMAO from peptide groups must be significantly weaker than those donated from water and urea. So, in the presence of TMAO but absence of urea, the peptide groups will be preferentially hydrated, with at least one water layer between peptide and TMAO—just because TMAO will only hydrogen-bond to the peptide through an intercalated water.

What is then expected upon addition of urea is that the situation does not fundamentally change. The only difference is that now TMAO has the option to interact with the peptide group through either an intercalated urea, or an intercalated water. The mechanism of stabilization by TMAO does not change as urea is added. Only the spacing between TMAO and the peptide groups is increased as the TMAO solvation waters are replaced by urea. That is, TMAO should be more excluded and become a more potent protein stabilizer in the presence of urea than in its absence. Indeed, a slight trend to larger “m-values” of TMAO in the presence of urea has been observed²⁰ (m-values are a measure of how potent an osmolyte is in stabilizing a protein). Conversely, if TMAO becomes a more potent stabilizer in the presence of urea, then urea must become less effective as a denaturant for symmetry reasons (Maxwell relations).^20,54 A similar trend to synergy has been found with mixtures of sarcosine (another methylamine) with urea,⁵⁴ raising the question whether similar principles apply to other osmolytes as well.

Materials and Methods

Densimetry

TMAO dihydrate from Sigma and ultrapure urea from USB were dried at 60 °C for at least 20 h. The masses used to prepare the solutions were measured using a Mettler Toledo AT20 analytical balance equipped with an antistatic device. The densities of the solutions were measured in an Anton Paar DMA 5000M density meter, using automatic viscosity correction.

Vapor Pressure Osmometry

The TMAO dihydrate used for the osmotic coefficient measurements was freshly synthesized and recrystallized.⁵⁵ The water vapor pressure was measured in a Wescor Vapro 5520 osmometer^8,56,57 with modifications described previously.⁵⁸ The measured osmolality values were divided by the total molality of urea and TMAO to obtain the osmotic coefficient, which is a measure of the deviation of the water chemical activity from ideal behavior.

Volume Data Evaluation

The density of the urea TMAO mixtures was measured to obtain the partial molar volumes. Using Wolfram Mathematica, the data were fit to the relation

7

where the numerator is the mass of the solution per kg of water and the denominator the volume per kg of water (note that the molecular weights M_i have to be given in kg/mol). Among the parameters, ρ₀ is the density of plain water, v̅_1,0 and v̅_0,1 are the limiting partial molar volume in plain water (of urea and TMAO, respectively), and the v̅_i,k terms in general are mixed derivatives of the volume with respect to the molalities of urea and TMAO, m_U and m_T. The partial molar volumes of urea and TMAO are then

8

9

and the partial molar volume of water

10

directly follows, knowing the molar concentrations of urea and TMAO (c_U and c_T) and the molecular weights of all species (18.015, 60.06, and 75.11 g/mol), and considering²⁸

11

Vapor Pressure Data Evaluation

The vapor pressure data were used to derive the chemical activities of urea and TMAO through the method of Schönert.⁵⁹ The osmotic coefficient data were fitted to

12

and it was found that terms up to second order are sufficient. There are additional isopiestic data available on the dependence of ϕ on urea concentration in the absence of TMAO.³² Including these data requires terms up to seventh order in urea concentration. Equations for the chemical activities of water, urea, and TMAO follow directly:⁵⁹

13

14

15

Kirkwood–Buff Integrals

Solvation properties can be calculated from the partial molar volumes and chemical activities as follows. The excess or deficit of molecules of type i and j around each other (relative to the bulk) is given by integrated pair correlation functions, the so-called KBIs,²³

16

where the elements of matrix A are given by

17

Here, κ is the compression coefficient, δ_i,j the Kronecker delta, T the absolute temperature, R the gas constant, |A| the determinant of A, and |A|_i,j denotes a cofactor of the matrix. After eq 17 is substituted into eq 16, κ has little impact on 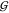_ij. This is because κ is then not in an isolated position in the denominator any more, and is negligibly small for our purposes,⁶⁰ so we just set it to its value in plain water.⁶¹ In order to link the derivatives in this equation back to the vapor pressure results, they are rewritten as either

18

for all cases except when i = k = W, or

19

by use of the Gibbs–Duhem relation.

Kirkwood–Buff Integrals for Hard-Spheres

As shown in the Results section, TMAO behaves like a hard-sphere gas in urea solution. Calculating the KBIs for hard-spheres is conveniently done through the Carnahan–Starling equation.⁶² Though this relation is for a single-component hard-sphere gas, it is possible to infer the implicit properties of the water as follows. In a two-component solution (here, water and TMAO), the KBIs are

20

and

21

for the self-solvation of TMAO and self-hydration of water, and

22

for the hydration of TMAO,³⁶ where a_ii = (∂ ln a_i/∂ ln c_i) and γ_ii = (∂ ln a_i/∂ c_i). The molar activity coefficient of component i is γ_i. From eq 22 we see that a_WW = a_TTv̅_W/v̅_T holds. Taking into account γ_WW = (a_WW – 1)/c_W allows use of eqs 20 to 22 to obtain 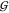_WW and 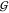_WT from 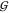_TT, if a_TT and the partial molar volumes are known:

23

24

25

Multiplying the Carnahan–Starling equation for a hard-sphere gas⁶² by the concentration c_S and performing a derivative with respect to c_S gives a_SS(63) as follows:

26

where ϕ = c_Sv̅_S is the volume fraction of the hard-sphere, c_S its molarity, and v̅_S its partial molar volume. Equation 26 can then be used in place of a_TT to calculate the various KBIs (eqs 23–25). When the size of the hard-spheres is different from v̅_T, we change v̅_T in eq 23 accordingly. That is, the partial molar volume of TMAO mono- or dihydrate is larger than that of TMAO itself. However, when it comes to the partial molar volume in the context of 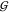_WT, there is no such thing as a mono- or dihydrate. This is because 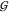_WT considers the spacing between TMAO and the surrounding water molecules independently of whether or not they are mandatory hydration waters. Accordingly, we do not change v̅_T in eq 24 when the size of the hard-spheres is assumed to be different from v̅_T.

Note that in the limit of c_S→0, we recover the classically expected result for the excluded volume (equaling the second virial coefficien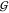t), _WT – 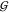_TT = 4v̅_S.⁶³

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States