Using tri-axial acceleration data to identify behavioral modes of free-ranging animals: general concepts and tools illustrated for griffon vultures

Summary

Integrating biomechanics, behavior and ecology requires a mechanistic understanding of the processes producing the movement of animals. This calls for contemporaneous biomechanical, behavioral and environmental data along movement pathways. A recently formulated unifying movement ecology paradigm facilitates the integration of existing biomechanics, optimality, cognitive and random paradigms for studying movement. We focus on the use of tri-axial acceleration (ACC) data to identify behavioral modes of GPS-tracked free-ranging wild animals and demonstrate its application to study the movements of griffon vultures (Gyps fulvus, Hablizl 1783). In particular, we explore a selection of nonlinear and decision tree methods that include support vector machines, classification and regression trees, random forest methods and artificial neural networks and compare them with linear discriminant analysis (LDA) as a baseline for classifying behavioral modes. Using a dataset of 1035 ground-truthed ACC segments, we found that all methods can accurately classify behavior (80–90%) and, as expected, all nonlinear methods outperformed LDA. We also illustrate how ACC-identified behavioral modes provide the means to examine how vulture flight is affected by environmental factors, hence facilitating the integration of behavioral, biomechanical and ecological data. Our analysis of just over three-quarters of a million GPS and ACC measurements obtained from 43 free-ranging vultures across 9783 vulture-days suggests that their annual breeding schedule might be selected primarily in response to seasonal conditions favoring rising-air columns (thermals) and that rare long-range forays of up to 1750 km from the home range are performed despite potentially heavy energetic costs and a low rate of food intake, presumably to explore new breeding, social and long-term resource location opportunities.

Movement ecology and the integration of ecology, behavior and biomechanics

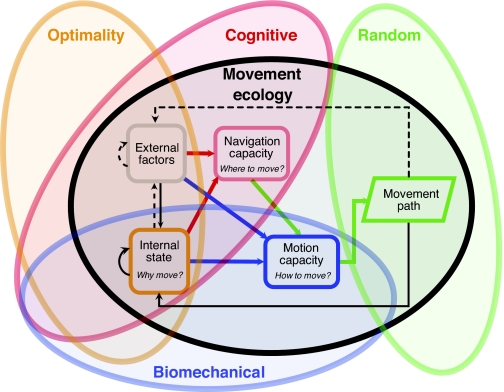
Recent advances in mechanistic modeling and tracking technology have enriched our capacity to disentangle the key parameters affecting movement processes and to characterize movement patterns accurately. These advances set the stage for integrating the four existing paradigms for studying movement – the random, biomechanical, cognitive and optimality approaches (Fig. 1) – in the form of a new cohesive ‘movement ecology’ framework (Nathan et al., 2008). The biomechanical paradigm elucidates the machineries that enable individuals or propagules to move, including their physical mechanics, energetics and physiology, and thus focuses on the study of the motion capacity of individual organisms. The cognitive paradigm explores the mechanisms of gathering, processing and responding to the environment in a way that produces nonrandom movement in time and space and thus focuses on the navigation capacity of the individual. The optimality paradigm examines the relative efficacy of different movement strategies in optimizing some particular fitness currencies (e.g. energy gain or survival) over ecological or evolutionary time-scales, and thus focuses mostly on the external factors affecting the internal state of the individual. The random paradigm analyzes the fit of observed animal tracks to various random walk models to assess, for example, search efficiency and thus focuses exclusively on the movement patterns. The movement ecology framework explicitly combines these basic components of movement and the links among them (Fig. 1) (Nathan et al., 2008), which can be identified across all movement types and taxonomic groups (Holyoak et al., 2008). Thus, this framework offers a template for transdisciplinary integration of the four existing movement research paradigms (Fig. 1) (Nathan et al., 2008) to create jointly the new paradigm of movement ecology, devoted to the comprehensive study of all biological (whole-organism) movement phenomena.

Fig. 1.

A movement ecology framework that integrates four existing paradigms for studying organismal movements. From Nathan et al. (Nathan et al., 2008); © 2008 National Academy of Sciences, USA.

Movement ecology thus aims at unifying organismal movement research and aiding the development of a general theory of whole-organism movements (Nathan et al., 2008). To facilitate this unification, we need tools that can provide simultaneous information about the movement, energy expenditure and behavior of the studied organisms, and the environmental conditions they encounter en route. The primary focus to date has been on integrating movement and environmental data (Boettiger et al., 2011; Dalziel et al., 2008; Fryxell et al., 2008; Getz and Saltz, 2008; Sapir et al., 2011; Vanak et al., 2010; Yott et al., 2011). The link between movement, energy expenditure and behavior has been tested less often in free-ranging animals in the wild (but see Green et al., 2009a; Sapir et al., 2010; Wilson et al., 2006). To facilitate the less-studied link between movement, energy expenditure and behavior, we focus here on a promising tool that uses tri-axial acceleration (ACC) data to assess energy expenditure, and especially to identify the behavioral modes of free-ranging wild animals along large-scale long-term movement pathways, a task that cannot be addressed by means of direct observations.

Movement research has recently experienced a rapid upsurge (Holyoak et al., 2008) with the advent of movement tracking tools and GPS devices in particular (Hebblewhite and Haydon, 2010; Wikelski et al., 2007), as well as various stochastic methods to analyze animal movements (Smouse et al., 2010). Nevertheless, movement data, however accurate, are insufficient on their own to infer links among biomechanical, behavioral and ecological processes driving the movement of individuals. Here, we use simultaneous GPS and ACC measurements to identify both the behaviors and location of the tracked animal, as well as the estimated energy expenditure along the track, to infer the biomechanical, behavioral and environmental drivers along the movement pathway. In the following, we briefly review the use of ACC data to assess energy expenditure and, in particular, to identify behavioral modes. We outline a general protocol for obtaining ACC-based behavioral classification and focus on one crucial step – the identification of behavioral modes by supervised machine learning algorithms. Then, we apply these techniques to classify the behavioral modes of vultures and illustrate the combined use of GPS and ACC data to examine preliminarily several interactions between behavioral, ecological and biomechanical aspects of their movements at relatively long temporal and large spatial scales.

Using acceleration data to identify behavioral modes

Under the general family of biologging techniques (Cooke et al., 2004; Ropert-Coudert and Wilson, 2005; Rutz and Hays, 2009), tri-axial accelerometers are particularly promising in providing data that can elucidate links between biomechanical and ecological processes in the context of movement. The use of accelerometers for studying movement of organisms stems from epidemiological studies, originated in the 1950s, aimed at assessing changes in human physical activity in relation to health status (Chen and Bassett, 2005; Plasqui and Westerterp, 2007; Yang and Hsu, 2010). The technique has been applied more recently to study the movement, behavior and physiology of animals as well (Fahlman et al., 2008; Gleiss et al., 2010; Green et al., 2009b; Halsey et al., 2009a; Halsey et al., 2008; Halsey et al., 2009b; Halsey et al., 2011; Martiskainen et al., 2009; Moreau et al., 2009; Payne et al., 2011; Sakamoto et al., 2009; Scheibe and Gromann, 2006; Shepard et al., 2009a; Shepard et al., 2009b; Shepard et al., 2008; Watanabe et al., 2005; Wilson et al., 2006; Yoda et al., 2001; Yoda et al., 1999).

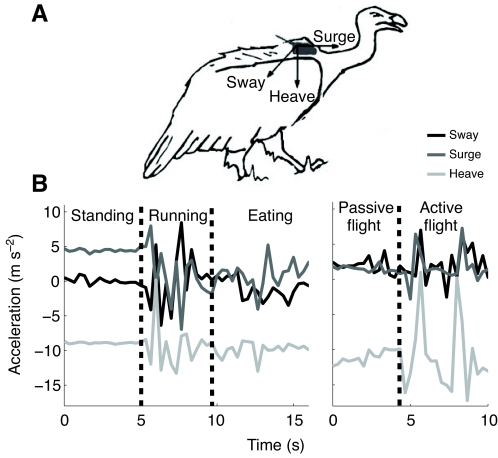
Accelerometers provide measures of two distinct types of acceleration: static and dynamic acceleration. Static acceleration is due to the force of the gravitation field of the Earth (and the orientation of the accelerometer with respect to that field), whereas dynamic acceleration is due to animal movement (Shepard et al., 2008). Advances in micro-electromechanical technology have yielded miniaturized low-cost portable units that are highly reliable in measurement and incurring little variation over time. Hence they can be carried by a wide range of free-ranging animals without impeding movement. Accelerometers can be designed to record acceleration in three directions (Fig. 2A). An important summary statistic that is often used when discussing ACC data series is overall dynamic body acceleration (ODBA), which is a measure of the aggregate acceleration of a subject (Shepard et al., 2008; Wilson et al., 2006). ODBA is calculated by subtracting the static component from the total ACC values for each axis and then summing the resulting dynamic components across axes. Following intensive application of ACC data to quantify human energy expenditure (Bouten et al., 1994; Crouter et al., 2006; Montoye et al., 1983; Plasqui and Westerterp, 2007), the use of ODBA and related measures for assessing energy expenditure of free-ranging animals is progressively being adopted in studies of animal behavior, ecology and physiology (Fahlman et al., 2008; Gleiss et al., 2010; Green et al., 2009b; Halsey et al., 2009b; Halsey et al., 2011; Shepard et al., 2009b; Wilson et al., 2006). As ODBA can help assess energy expenditure, ACC data can contribute to the integration of biomechanics, behavior and ecology. We demonstrate the application of ODBA in one of our empirical examples. As this particular use of ACC data has recently been reviewed and illustrated in various studies (Fahlman et al., 2008; Gleiss et al., 2010; Green et al., 2009b; Halsey et al., 2009b; Halsey et al., 2011; Shepard et al., 2009b; Wilson et al., 2006), other applications of ODBA will not be elaborated here.

Fig. 2.

(A) Schematic representation of a tri-axial accelerometer attached to a vulture, recording linear acceleration along the x (medial–lateral, sway), y (anterior–posterior, surge) and z (inferior–superior, heave) axes. (B) Two illustrative signals recorded by a tri-axial accelerometer (3.3 Hz per axis), demonstrating switches from standing through running to eating and from passive to active flight.

In addition to the determination of physiological processes, ACC data have been used in human health research to classify automatically a subject’s behavioral modes such as sitting, walking or running. These efforts were designed to provide additional data from wearable digital processors able to compute context-specific features in real-time (e.g. DeVaul and Dunn, 2001). Overall, accelerometers have been widely applied to classify human behavior by means of diverse data-analysis tools (Godfrey et al., 2008; Preece et al., 2009).

The application of accelerometers to identifying animal behavioral modes is relatively new; to our knowledge, Yoda and colleagues (Yoda et al., 1999) were the first to apply this technology to free-ranging wild animals. A general protocol for such studies begins with capturing and tagging the animals with GPS–ACC devices. It then continues with collecting the data either directly by retrapping the animal, or by remote data retrieval through radio link, cellular phone networks or satellite communication. In parallel, ACC measurements can be calibrated and ground-truthed by observing tagged animals in the field during ACC measurements. The ground-truthed ACC segments are then used to train classification or machine-learning algorithms that are then validated against independent observations and subsequently used to classify unobserved behaviors from non-ground-truthed ACC data. Individual applications of this protocol can skip some stages or apply different methods at various stages. For example, most studies of free-ranging wild animals, including penguins (Yoda et al., 2001), cormorants (Laich et al., 2008) and raptors (Halsey et al., 2009a), have discriminated behavior by visual observation of the ACC data, without specifically developing a classification function. Other studies have applied several classification techniques such as linear discriminant analysis (LDA), k-means clustering and support vector machines (SVMs) to automatically discern different behaviors of domestic animals such as cats (Watanabe et al., 2005), cows (Martiskainen et al., 2009; Nielsen et al., 2010) and free-ranging wild shags (Sakamoto et al., 2009). The latter study proposed an approach to skip the ground-truthing stage, and yet not all basic behaviors were discernible by the proposed approach.

Machine learning algorithms

Here, we implement and compare five supervised machine-learning algorithms: LDA, SVMs, classification and regression trees (CART), random forest (RF) and artificial neural networks (ANNs). The algorithms selected are those most commonly used for various pattern recognition and classification tasks. We perform a comparative analysis using LDA as a baseline, anticipating that the other methods, through incorporation of nonlinearities or decision trees to separate out categories, are likely to perform better than LDA. We applied these algorithms to our ACC vulture data using the R programming environment. We employed a variety of R packages to implement the various methods, as detailed in supplementary material Table S1. The following list summarizes the methods.

Linear discriminant analysis

LDA reduces the dimensionality of the data by maximizing the variance between the classes while minimizing the variance within the classes. LDA is a parametric method that assumes unimodal Gaussian distributions of classes. Often this is unlikely to be the case. The linear boundaries of LDA are also a restriction. Other variants, such as quadratic discriminant analysis, relax this restriction. In any event, the use of such restrictive assumptions can, in practice, have the beneficial effect of lessening the likelihood of over fitting (which then incorporates the particulars of the noise, thereby degrading predictive performance), and generally LDA is found to perform acceptably well.

Support vector machines

SVMs construct a hyperplane to separate transformed observations, while trying to maximize the distance of observations from this separating hyperplane. These methods were developed in the 1990s and have since become quite popular (Cortes and Vapnik, 1995) because they have a strong theoretical foundation and often produce good results. Fundamentally, SVM is a binary classifier. Multiclass classifications can be implemented by treating such problems as a set of binary ones – for instance, by constructing a set of classifiers, where each classifier compares one of the classes versus all the other classes. SVMs are relatively computationally intensive.

Classification and regression trees

CART methods can be used either for predicting continuous variables or choosing among categories. In the categorical case, a set of hierarchical decision rules is developed that can be used to predict the class of unclassified samples. Each rule can branch into another rule or a terminal category. CART has a number of advantageous features. Its decision rules can be applied very quickly and are also relatively easy to interpret. One of the potential weaknesses of CART is over-fitting, which can be mitigated through a pruning operation that reduces the number of decision rules incorporated in the tree. Another potential issue is the hierarchical partitioning which reduces the effective sample sizes making it more difficult to identify rules and trends in each subsample. Relationships between variables can also be difficult to identify owing to this hierarchical partitioning.

Random forests

RFs are ensemble classifiers in which sets of classification trees are constructed using a procedure similar to CART, but including introduced stochasticity (Breiman, 2001). Instead of potentially using all the variables to determine the best split at each node, only a randomly selected subset of variables is used. RF offers increased accuracy in relation to CART. However, this accuracy comes at a cost: RFs are more computationally expensive to train and to use as predictors; it is no longer possible to display directly and interpret the CART tree (there are many separate and distinct trees); and, given the stochastic nature of the algorithm, each invocation of the algorithm will result in different decision rules and slightly different results.

Artificial neural networks

ANNs are inspired by biological neural networks and are collections of interconnected ‘neurons’ that sum their inputs and release an output that is governed by an activation function (often sigmoidal in shape). Of the many designs for neural networks, this study uses the most common – a single hidden-layer perceptron network. In our implementation, we allowed one input node for each summary statistic derived from the ACC data, as described below, and one output node for each of the classification options (our defined set of possible behavioral modes). The number of nodes we allowed for the hidden layer was 30. ANNs can be very good at learning and can successfully process complex inputs such as raw data that other methods presented here might be unable to handle. However, it has been argued that a fair amount of ‘art’ is required in the process of building an ANN, and its design can be more subjective than the usage of the other methods discussed here because selection of the number of hidden nodes and steepness of the activation function are rather ad hoc. Additionally, the training stage of network construction can be computationally intensive.

Ten-fold cross-validated parameter tuning (i.e. the training data set was one-tenth the size of the testing data set) was implemented to ensure robustness in the performance of each algorithm. It is important to note, however, that this tuning should not be considered exhaustive. In all likelihood, there are ways in which additional, small performance improvements could be gained from each of the algorithms; however, the focus of this paper was a comparative analysis of methods, and minor improvements to all of the methods can be made once one of the methods is selected as the method-of-choice in a particular application. For instance, CART can be slightly improved by performing a principal component analysis (PCA) on the data prior to training. However, one of the primary benefits of CART is that the resulting tree diagram is interpretable. If PCA is applied prior to tree building, then the output is no longer directly interpretable as the decision rules are based on the principal components rather than the original summary statistics. For this reason, we did not conduct a preliminary PCA as we felt that, in the context of our unifying movement ecology paradigm (Fig. 1), our ability to interpret the results biomechanically supersedes any small gains in the accuracy of classifying particular behaviors.

Identifying vulture behavioral modes

We illustrate the general protocol outlined above by using ACC data to classify behaviors of free-ranging griffon vultures (Gyps fulvus, Hablizl 1783). The griffon vulture is of major concern in conservation because many populations have dramatically declined throughout the species range. In Israel, the Nature Protection Authority (NPA) operates a nationwide monitoring and management program that includes massive captures (83±60 new individuals per year, and 120±60 recaptures, based on NPA data from 2006–2010) using walk-in traps during the non-breeding season (October to December) and year-round supplementation of natural feeding through provision of new carcasses every 2–4 days throughout the year at 25 feeding stations. Overall, 43 adult (>4 years old) trapped birds were equipped with the GPS–ACC tags during three field seasons of the years 2008, 2009 and 2010 (10, 11 and 22 tags, respectively). These vultures were also marked with patagial tags and color rings, allowing individual identification in the field. We emphasize that all our tagged birds were adults that were previously marked by the NPA (therefore indicating resident birds), and our tracking data confirmed the general notion that adults in the study populations do not migrate on a regular basis. Young (first- to fourth-year) birds, however, can exhibit migratory movements, given that several satellite-tracked subadult birds tagged in Israel were found to winter in Sudan and Saudi Arabia or originated from Turkey and wintered in Israel (O. Hatzofe, personal communication).

GPS–ACC tags

Vultures were fitted with 160 g GPS–ACC tags, using 30 g harnesses in a backpack configuration (i.e. the unit lies at the center of the back and is tied with a Teflon harness designed to tear apart after several years). The tag plus harness constitute 2.4% of the mean body mass of tagged vultures. The tags (E-Obs GmbH; Munich, Germany) include three independent functions: (1) a GPS device providing the ground speed and the position in three dimensions (longitude, latitude and elevation) for each data-point. GPS accuracy is 5 m (50% of the points are within 5 m from the true location); (2) a 3D accelerometer measuring ACC at three perpendicular axes at a frequency of 3.3 Hz each; and (3) a pinger emitting a tag-specific UHF-signal. The pinger facilitates fieldwork by helping detection of the bird from afar and by signaling the exact time of ACC and GPS measurements, which is essential for precise ACC calibration observations. Data of the GPS and ACC components are stored on board until they are downloaded through UHF communication to a handheld receiver.

Tag sampling protocol

Owing to the diurnal activity regime typical of vultures, transmitters were set to work in a 12 h duty cycle starting 07:00 h for tags deployed in 2008, and for a 13 h duty cycle starting at 06:30 h for tags deployed in 2009 and 2010. During working hours, GPS locations were recorded every 10 min (26 tags, track duration: 304±147 days; mean±s.d.; 73–533 days minimum and maximum duration) or 1 min (17 tags, track duration: 109±56 days; 34–188 days). For the purpose of the analysis presented here, 1 min tags were subsampled at 10 min intervals. Accelerometers were sampled at 10 min intervals for durations of 24.6 s (all tags in 2008 and two 1 min tags in 2009), 20.4 s (9 tags in 2009) or 16.2 s (all tags in 2010). Variation in our sampling protocols across years reflects our trade-off between intensity of data collected along movement paths and the total length of each path, as well as data storage limitations, as we learned more about battery performance and data download frequency throughout our study.

Field and zoo observations

We searched for vultures in the field on a weekly or bi-weekly basis for data retrieval and for behavioral observations required for the ACC classification. Overall, we downloaded data from 43 individuals, comprising 756,764 GPS–ACC measurements obtained across 9783 vulture-days (i.e. almost 27 years). Observations were made using telescopes (Televid 77, Leica, Germany) and binoculars. Behaviors (during the exact times of ACC measurements) were observed at various places, including roosting sites, feeding sites and birds on the wing. In addition, two tags were deployed on captive vultures in the Tisch family Biblical Zoo at Jerusalem for behavioral observations. The dataset includes 905 ground-truthed ACC bouts from which we extracted 1035 segments of seven different behaviors: active flight, passive flight (soaring–gliding), eating, lying down (a horizontal position in which the abdomen is in full contact with the surface), preening, running (including other active behaviors on the ground) and standing.

Data processing (GPS)

Daily movement properties were analyzed from the GPS data: ‘roost departure time’ was calculated as the first non-static point (speed >4 m s^–1) as long as the vulture flew at least 2 km from its initial location during the day. In ∼14% of the days, the vultures did not leave the roost, and, in ∼9% of the days, they left earlier than the first GPS sample (07:00 or 06:30 h). Similarly, ‘roost arrival time’ was defined by the first static point that was within 2 km of the final night location. In ∼4% of the days, the vultures arrived to the roost later than the last GPS point (19:00 or 19:30 h). Overall, the Euclidian distance between the last point of the day and the first point of the following morning was within 5.8 km range for 95% of the nights. The ‘daily traveled distance’ is calculated by summing all distances between successive points, and the ‘maximal displacement’ is defined as the Euclidean distance between the first point and the farthest location of the day. Flight ‘straightness’ is the ratio between travel distance up to this point and the max displacement itself. We preferred this index over the ratio between daily traveled distance and daily displacement (between the start and the end point of the day) as vultures show a tendency to return to the same or to a nearby roost site. This generates a short daily displacement distance that masks any differences in flight pattern. The daily path was also scanned for day-stops, defined as locations where the vulture landed and stayed static (speed <4 m s^–1) and within 400 m for more than 20 min. Vultures usually made one or two day-stops and rarely more than four a day.

Data processing (ACC)

The ACC sensor output in millivolts was transformed to acceleration (m s^–2) units using tag-specific calibration values obtained prior to tag deployment. For each ACC measurement, we classified one of the behaviors using the ANN method. Also the total daily ODBA was calculated using a window size of 6 s (18 data-points per axis). In addition to the ACC-based classification, we used GPS data to enhance the validity of the behavioral classification. For instance, the proportion of flight time spent in active (wing flapping) versus passive (gliding–soaring) flights was calculated only for sections identified as flight by the GPS data (speed and elevation). This maximizes the signal-to-noise ratio in the data by excluding non-flight data points.

Correct identification of unobserved eating events is essential for assessing energy intake. We scanned ACC data recorded when vultures were on the ground (either at their morning or evening roost or during a day-stop) for eating behavior. Vultures usually spend a few hours at a carcass site, during which they eat and fight over the carcass for 30 min or more. Thus, to minimize false-positive errors, we defined an eating event as: (i) more than one ACC measurement during the stop being classified as ‘eating’ (97% of the classified events); (ii) a single ‘eating’ observation being accompanied by two or more ‘running’ measurements (indicating fight and/or hop) within the same stop (2% of the classified events); or (iii) a single ‘eating’ observation that occurred in a specific time and location when and where other tagged vultures were eating (1% of the classified events).

Summary statistics selection

To make the relationship between ACC data and behaviors more interpretable, we calculated summary statistics from the ACC data (after transformation to m s^–2) and used these for the machine-learning algorithms, namely mean, standard deviation, skewness, kurtosis, maximum value, minimum value, autocorrelation (for a displacement of one measurement) and trend (the coefficient for a linear regression through the data). These statistics were calculated for each of the three axes, along with a fourth quantity, q, calculated as the square-root of the sum-of-squares of the three axes (i.e. the length of the diagonal of the x–y–z volume involved). Tests using more-robust versions of statistical measures – median, median absolute deviation – did not yield significant differences.

Additionally the three, pair-wise correlations between the x (sway), y (surge) and z (heave) ACC series were calculated. ODBA was calculated and used as a summary statistic too (Shepard et al., 2008; Wilson et al., 2006). Finally, the inclination (θ=cos^–1[z/q]) and azimuth (φ=tan^–1[y/x]) for the q axis were determined and their circular variances included as summary statistics. Overall, we used 38 summary statistics in our analyses.

A study classifying bovine behavior from ACC data used 28 summary statistics, including, mean, standard deviation, skewness, kurtosis, maximum value, minimum value and energy for each of the three axes of the accelerometer, pairwise correlations between the axes, and vector length (Martiskainen et al., 2009). We did not include vector length in our analysis, as it would be a function of the analysis decisions and not inherent in the data. The Martiskainen et al. energy measure was designed to look at periodic behavior of their data and, in a prior paper, it was determined to be the least important of the summary statistics that were examined (Ravi et al., 2005). Other researchers have looked at relating frequency analyses of ACC data to observed behaviors (Sakamoto et al., 2009; Scheibe and Gromann, 2006; Watanabe et al., 2005). We visually inspected the power spectrum of the ACC time series but could not identify strong patterns in the frequency domain. Possibly, the granularity of our measurements was too coarse (3.33 Hz per axis) to identify these. Studies relating frequency to behavior have used per-axis frequencies ranging from 64 Hz (Sakamoto et al., 2009) through 33.3 Hz (Scheibe and Gromann, 2006) to 16 Hz (Watanabe et al., 2005), which are significantly higher than our sampling frequency and allow much finer determination of frequency behavior. In general, sampling frequency should be at least twice the frequency of the most rapid body movement essential to characterize a behavioral mode to fulfil the Nyquist sampling criterion (Chen and Bassett, 2005).

The choice of summary statistics can be done prior to model training and testing, but it can also be carried out in an iterative manner by examining model results. Supplementary material Fig. S1 tabulates the relative importance of the different summary statistics, as determined by looking at changes to the Gini index used to measure errors across the RF ensemble of trees (see package ‘Random Forests’ at http://stat-www.berkeley.edu/users/breiman/RandomForests). The relative importance of variables can change between the methods, but this analysis is a good indicator of general importance.

All five machine-learning methods were applied to summary statistics of the data. Of the five implement algorithms, only ANNs could be expected to classify behavior efficiently directly from the ACC data before preprocessing into summary statistics. To test the efficiency of ANN in this case, we constructed an ANN using the basic ACC readings directly for a window of 17 points as inputs (∼5 s). This model achieved an accuracy averaging slightly below 80%, which was less than the accuracy of the models we trained using the summary statistics and indicates that, by preprocessing the ACC data into summary statistics, we actually improve ANN classification with the size of the perceptrons we used in our analysis (perhaps improvements could be obtained with more hidden units than we used).

Training and testing

The 905 ground-truthed observations included 1035 segments, each representing a single behavioral category, were taken and treated as distinct units. Using the repeated random subsampling cross-validation procedure, the dataset was split into two subsamples: 70% was used for training the models and 30% was used (after modification, see below) to test the performance of the algorithms. This 70:30 split is an ad hoc measure but is a commonly used division found in other machine-learning applications. Other cross-validation techniques used in human behavior studies include the P-fold and the leave-one-out procedures (e.g. Altun et al., 2010).

Confidence intervals for the estimated accuracy were found by repeatedly generating stochastic 70:30 splits, evaluating model accuracy on them, and treating the resultant set as being governed by the Student’s t-distribution. During prediction, the methods generated a probability or score for the different classes occurring rather than a single result. As a result, the single most likely category determined by this score was used for the calculation of classification errors. In specific applications, where the cost of misclassification is high, it might be beneficial only to accept predictions when the score rises above some threshold and mark other values as ‘Unknown’. Accuracy was calculated as the number of correct calculations divided by the total number of classifications.

Of practical interest are the computational requirements of the algorithms. Using any of the five algorithms presented here to predict a class is extremely fast on modern computing hardware, and the prediction time would probably not be an issue for most users, unless real-time predictions are required or extremely large datasets are involved. Training the algorithms, however, can take significantly longer and is dependent on the size of the training set, the number of summary statistics and the algorithm-specific parameters. Performance is, of course, implementation specific; but in our work we found both the CART and LDA methods to be extremely fast in all cases. SVMs, RFs and ANNs were significantly slower in training, and the ANN training duration appeared to increase the fastest as the sizes of training set and summary statistics increased.

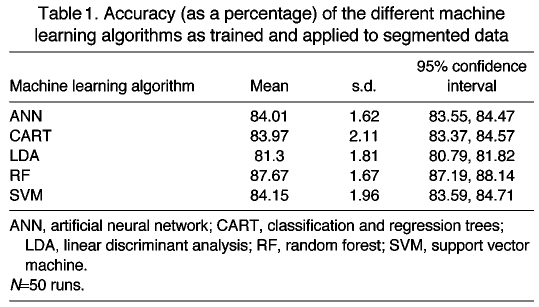
The accuracies for the algorithms when trained and tested on the segmented data are reported in Table 1. The RF algorithm performed the best, whereas LDA performed the worst. Using Tukey’s range test, the differences between LDA and the other algorithms is significant at the 5% level, as is the difference between RF and the other algorithms. The differences between SVM, ANN and CART are not significant at this level. Fifty random subsamplings of observations were used to generate these results.

Table 1.

Accuracy (as a percentage) of the different machine learning algorithms as trained and applied to segmented data

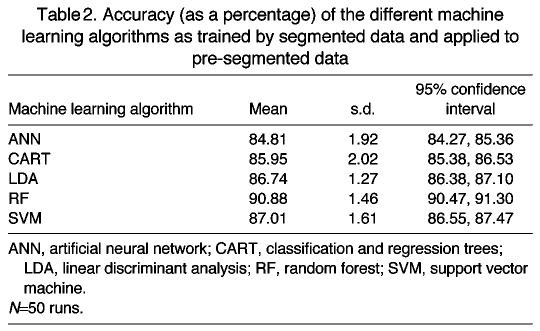
The accuracies reported in Table 1 are the best measure of the relative performance of the different techniques for the selected training dataset. However, because the basic ACC bouts downloaded from the animals are not segmented and can include more than a single behavior, we used the pre-segmented ACC bouts to assess the absolute performance of the different techniques on our dataset. That is, instead of using the ground-truthed segments, each including only one behavior, the algorithms classified behaviors in the validation set using the statistics calculated for the whole ACC measurement bout (of 24.6 s, 20.4 s or 16.2 s; see Tag sampling protocol above). The methods could not be directly trained for this task as the specification of multiple correct classifications during training is not supported by all the algorithms used. However, we could directly test the accuracy of the trained classifiers on these pre-segmented bouts, and a second set of accuracy calculations were performed using these pre-segmented bouts and are reported in Table 2. The accuracy measurements in Table 2 are less indicative for the relative performance of the different classification techniques compared with the results in Table 1 because only in the latter procedure do both the training and the validation subsamples include strict single-behavior segments. However, the results in Table 2 are the best measure of how the methods perform in practice on our large dataset in which 99.9% of the ACC bouts are not segmented to include only a single individual behavior. As can be seen, a slight across-the-board improvement in accuracy is shown in this application compared with the baseline of the training case.

Table 2.

Accuracy (as a percentage) of the different machine learning algorithms as trained by segmented data and applied to pre-segmented data

In addition to examining the overall accuracies, it is often useful in practice to look in more detail at the specific types of errors made by the classification algorithms. These errors can be presented numerically, for example using a confusion matrix, or graphically, as in supplementary material Fig. S2, where mosaic plots are used to illustrate the classification accuracies on a per-behavior basis. The columns indicate the observed behaviors, whereas the rows indicate the predicted behaviors. Correct classifications are shown in the diagonal, green regions; incorrect classifications are shown in the off-diagonal, red regions. The areas of the rectangles are proportional to the number of classifications. This information can be used several ways. For instance, the ‘general preening’ behavior is often incorrectly classified as ‘standing’ by the algorithms. This common error indicates that, to improve the classifications, time might be well be spent focused on developing measures that distinguish between general preening and standing.

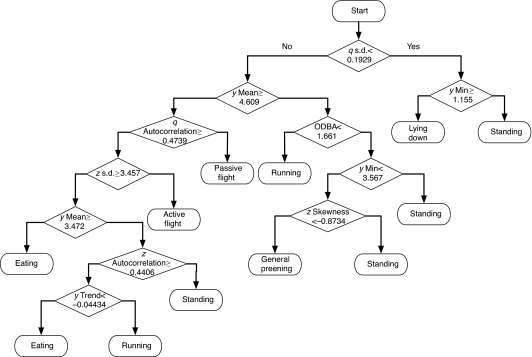
The utility of an algorithm is also determined by its ability to help interpret the classification rules. LDA, RF, ANN and SVM are to some extent ‘black box’ algorithms. Once trained, they can achieve high levels of accuracy, but it is difficult to interpret the internal rules that they use to arrive at their categorization decisions. Important findings can be developed from the decision rules of each method, such as the relative importance of variables, but creating a ‘narrative’ from these rules is generally not feasible. As seen in Fig. 3, the CART algorithm has the benefit that its decision rules are directly interpretable and can yield insights on the classification problem at hand. Take, for example, the initial (first-level) decision rule: whether the standard deviation of the magnitude of the q vector is less than 0.19. As the standard deviation of the q vector is a measure of the overall movement, a low value indicates a low level of movement. When this value is low, the algorithm indicates that the vulture is lying down or standing, both relatively immobile activities compared with running, eating and active flying. Next the two second-level decision rules distinguish activities in which the anteroposterior (head to tail) axis of the body is approximately perpendicular to the ground (standing, running and preening) from activities in which this axis is more parallel to the ground (lying down, flight and eating). To differentiate between lying down and standing, the algorithm considers the minimum value of the surge (y) axis (Fig. 2B), with values greater than 1.2 indicating standing as opposed to lying down. To differentiate between activities with ground-perpendicular versus ground-parallel anteroposterior axis position (standing, running and preening vs flight and eating), the mean value of the surge axis is considered. In summary, both first- and second-level decision rules are reasonable, and a CART algorithm can provide an after-the-fact narrative of how to predict behaviors. Not all the decision rules are so easy to interpret (e.g. the rule based on the skewness of the z axis), but, in general, an examination of these rules can provide a better understanding of the classification problem.

Fig. 3.

CART tree. Decision rules are evaluated downwards to arrive at each category prediction. At each rhombic branch node, a rightward move indicates a ‘yes’ or ‘true’ evaluation of the expression in the rhombus, whereas a leftward move indicates a ‘no’ or ‘false’ evaluation. Only the primary category for each leaf is shown. Probabilities for other categories for each leaf and branching point can also be determined based on the prior distribution of categories.

The analytical protocol suggested here can be further improved by developing and testing algorithms to identify shifts in the ACC signal within non-segmented bouts. For example, the characteristic duration of each behavior can be identified from the ground-truthed dataset, and a moving window of an appropriate length can be deployed to identify matching segments within the ACC bouts. This can be further elaborated by estimating the probability of different behaviors to appear sequentially using a Markov chain model. Such tools, however, await development.

Using ACC and GPS data to link behavior, ecology and biomechanics of griffon vultures

We illustrate the application of the ACC and GPS data for investigating two research questions that link behavior, ecology and biomechanics. First, we examine how characteristics of vulture movements (flight mode and daily travel distance) vary across the year in relation to seasonal changes and the breeding cycle. Second, we examine whether vultures undertaking exceptional long-range forays (LRFs) differ from vultures during routine foraging excursions in their core home range in daily travel distance, energy expenditure and feeding rate.

Variation in vulture flight characteristics across the year

Vultures rely heavily on soaring flight using rising air thermals (Ruxton and Houston, 2004), which are stronger and more frequent in Israel in the summer compared with the winter (Goldreich, 2003). We thus hypothesized that vultures fly longer distances and use less active flapping flights during the summer. In Israel, griffon vultures lay eggs between December and February, incubate their single egg for approximately 55 days during January–April, rear a nestling for ∼110 days until mid-summer, and the post-fledging dependence period lasts ∼75 days until early fall (Mendelssohn and Leshem, 1983; Shirihai, 1996). During the post-fledging period, adults feed their young mostly or only in the nest (Mundy et al., 1992; Sarrazin et al., 1994). Given the high energetic demands of young vultures, the post-fledging period involves significant time and energy demands on the parents. Assuming that the seasonal variation in (the artificially supplied) resource abundance and distribution is low, we expect the daily travel distance to be short during the incubation period and to increase during the nestling rearing period, with yet further increases during the post-fledging dependence period to fulfil the higher feeding demands. In the non-breeding season, we expect vultures to travel longer distances, to explore other colonies and foraging areas.

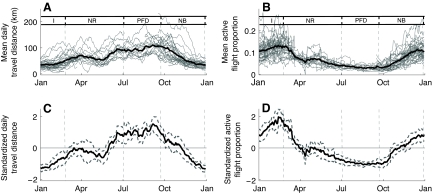
To test these predictions, we used the GPS data to estimate the variation in mean daily travel distance across the year, and the ACC data to distinguish active (flapping) flights from passive (soaring-gliding) flights and thereby to estimate how the proportion of the total daily flight time devoted to active flight varies throughout the year. We found a clear seasonal dichotomy of significantly shorter flights during the winter and longer ones during the summer (Fig. 4A,C). In January, for example, the mean travel distance was ∼35 km day^–1, with low intraspecific variability. By contrast, in the summer (July–September) the daily travel distance was significantly higher at ∼70 km day^–1, with some individuals reaching an average of 80–100 km day^–1 for an entire month. During spring and fall (March–June, October–November), the travel distance of the vultures was not statistically different than the mean.

Fig. 4.

The changes in mean and standardized daily travel distances (A,C) and in mean and standardized proportions of active (flapping) flight of griffon vultures (B,D) across the year. Both parameters were averaged using a running window of 30 days, and the analysis was restricted to individuals tracked over 90 days (N=32). For vultures tracked for more than a year (N=11), overlapping dates of successive years were averaged. Thin gray lines in panels A and B represent individuals and thick dashed gray lines in C and D are 95% confidence intervals; the thick black line represents population averages. To compensate for interspecific differences in the mean and magnitude of variation of each parameter, the values of each individual were normalized to a standard normal distribution with (μ=0, σ=1) to obtain graphs C and D. Abbreviations indicate different phases in the annual cycle of a breeding vulture: I, incubation; NR, nestling rearing; PFD, post-fledging dependence; NB, non-breeding.

A clear pattern was found also for the proportion of flight time invested as active flight (Fig. 4B,D). During summer time, the proportion of active flight was significantly lower than during winter and showed a low variability among individuals. In the winter, the overall proportion was higher and so were the differences among individuals, although vultures spent fewer hours a day flying in this season. Active flight is energetically considerably more demanding than passive flight (Ruxton and Houston, 2004), and typical ODBA values in our dataset are in the order of 6.1 and 1.6 m s^–2, respectively.

The observed patterns match the predictions arising from the hypothesis that environmental conditions in general, and thermal availability in particular, limit the flight activity of vultures. During winter, the days are shorter and colder and the thermals are weaker and less frequent. These conditions force vultures to stay more days in their roost, fly fewer hours a day and work harder by actively flapping to get airborne. By contrast, in the summer, vultures enjoy favorable thermals conditions, with long hot days ideal for soaring flights. Therefore, as expected, during this season vultures spent more hours a day flying, flew longer distances, almost without performing any active flight.

The breeding cycle of the vultures might also account for variation in the daily travel distance across the year, keeping in mind that effects attributed to breeding cycle might also reflect independent effects of seasonality in environmental conditions and vice versa. As expected from the breeding cycle, during the incubation period, flight distances are significantly shorter than the annual average. In the subsequent nestling rearing period, the daily flight distance increases to match the annual average. Later, daily travel distances are significantly longer in the post-fledging dependence period and the weeks following this period when the vultures are not breeding, hence supporting our predictions. After October, flight distances gradually decrease (Fig. 4A,C). The decrease during December, towards the onset of the next breeding season, follows our prediction. Yet, the earlier decrease during October and November departs from our prediction of long travels during the midst of the non-breeding period, presumably owing to the rapidly declining thermal conditions at this time of the year, and especially during November. This, and the finding that the proportion of active flight is significantly higher than the annual average during the incubation period (Fig. 4B,D), presumably reflects the effects of thermal availability rather than the effects of factors associated with this specific breeding stage. These findings, and the significantly low proportion of active flight during the post-fledging dependence period, suggest that the breeding cycle of griffon vultures in this region might be selected to coincide with activities that entail low flight demands (such as incubation) when thermal conditions are unfavorable, and activities that entail high flight demands (such as the training flights of fledglings) occur when thermal conditions are most favorable. This hypothesis, although speculative, merits further investigation.

Flight, feeding and energetic costs during exceptional long-range forays

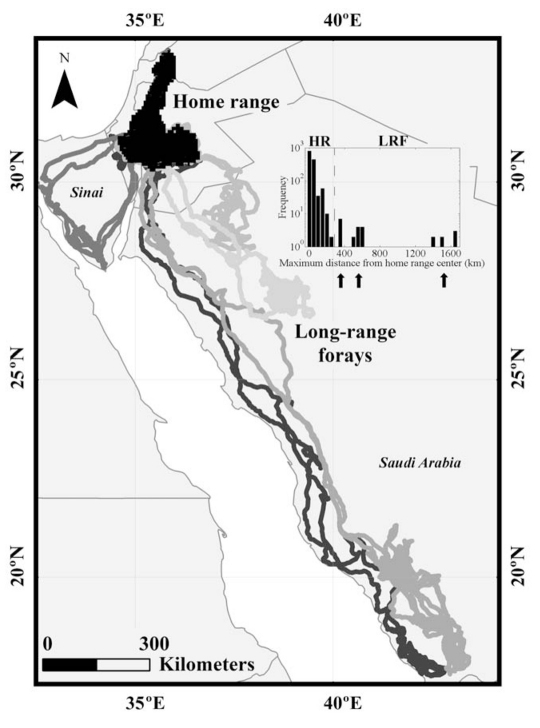
Vultures are highly mobile birds capable of crossing tens and even hundreds of kilometers on a daily basis. Nevertheless, most individuals tend to forage within a limited area and roost in a few locations. On six different occasions, we observed rare long-range forays (LRFs), where vultures left their core home range for a new, geographically remote area (Fig. 5). These forays represent a rare phenomenon of ∼2.5% of our data set (Fig. 5). They are characterized by a distinct pattern of a commuting phase (where the bird performed a long directional flight) to the destination area, followed by a relatively short foraging phase (performing more tortuous flights and roosting in the same area) and then commuting back to the home range. Four different birds left Israel for Saudi Arabia: in two of these cases the birds commuted almost directly south–southeast for 7–9 days, until reaching the border between Saudi Arabia and Yemen, ∼1600 km from their usual activity. They foraged around for 11 and 64 days, respectively, before returning home in a journey lasting 12–13 days. The third bird commuted for 10 days, flying around 600 km towards the southeast and foraged for 68 days. In the fourth case, the direction was more easterly, the range was shorter (400 km) and the commuting phase was 2–6 days in length, with a stay of 30 days. The fifth bird left for Egypt, circled the Sinai Peninsula for approximately one week on two separate occasions; in this case, no foraging phase was performed. An additional tagged bird was trapped in Saudi Arabia in December 2010 and we have not yet obtained the GPS–ACC data (see http://arabnews.com/saudiarabia/article230917.ece).

Fig. 5.

Exceptional long-range forays of individual griffon vultures trapped and tagged in the Judean and Negev Deserts of Israel. The histogram shows the frequency of the maximum displacement of a tracked bird from the center of its home range in non-overlapping intervals of 14 days. The six events defined as long-range forays (indicated by black arrows) are very rare (∼2.5% of the data set; note the log scale of the histogram). In three events, one in Sinai and two in northern Saudi Arabia, the vultures reached distances of 400 to 600 km from the home range center. On two other occasions, the vultures reached the border between Saudi Arabia and Yemen, over 1700 km from their home range center. The vast majority of the 43 tagged birds did not reach more than 200 km from their home range center. The population home range (black area mapped out in Israel and Jordan) is calculated from the entire dataset as the 95% kernel. HR, home range; LRF, long-range foray.

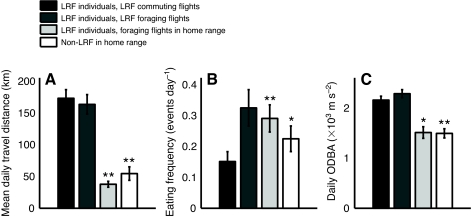
To investigate what could drive vultures to perform LRFs, we explored the mean daily travel distance, the energetic costs (total daily ODBA, summed for 13 activity hours for each tag) and food intake rate (frequency of eating events). Note that ODBA is an indirect and not an ideal proxy for energy expenditure (Halsey et al., 2011), and the use of eating frequency (events day^–1) to estimate food intake rate assumes low variation in the quantity and energetic value of the consumed food among feeding events. To control for both intraspecific variability and possible seasonal effects on vulture behavior, we use a paired design where each commuting phase is compared with: first, the regular foraging phase over the same time interval (e.g. 6 days) of the same individual 2 weeks after it returned to its home range, and second, the foraging phase of another randomly selected individual during the same period of the commuting flight. We also plotted the behavior during the foraging phase of the LRF individuals far from their home range, but the small sample size does not permit a proper statistical comparison with the relevant controls mentioned above.

Vultures performing LRFs achieved much longer daily travel distances than the mean during the commuting phase: four times longer than during normal foraging of the same bird (P<0.01, N=10; paired Wilcoxon test) and three times longer than other birds at the same period of time (P<0.01, N=10; Fig. 6A). Daily eating frequency was on average two- or three-fold lower than that of the controls (P<0.01 and P=0.03, respectively, N=10; Fig. 6B). The total daily ODBA was significantly higher in the commuting phase compared with that of the two controls (P=0.039 and P<0.01, respectively, N=10; Fig. 6C). All reported P-values are after Bonferroni correction for multiple comparisons. All the comparisons with the foraging flights of LRF individuals were not significant, although this lack of significance might be attributable to the small sample size.

Fig. 6.

Pairwise comparisons among three measures – (A) mean daily travel distance, (B) eating frequency and (C) total daily ODBA – derived from the data (±s.d.) for an individual vulture in the following phases of its lifetime movement pathway: commuting phase of a long-range foray (LRF) event (black); foraging phase far from its home range (dark gray), in the home range shortly after return from the long journey (pale gray) and randomly selected conspecifics within the home range during the time of the LRF (white). Control groups that are significantly different from LRF events are marked as follows: ^*P≤0.05; ^**P≤0.01.

Although the very small sample size (N=4) of LRF events that include a foraging phase precludes a proper statistical comparison, inspection of the data reveal that foraging phases embedded in LRFs resemble commuting phases more than foraging phases not embedded in LRFs. Daily travel distances during the LRF foraging phase were as long as during the commuting phase and much longer compared with the controls. Eating frequency was higher than during the commuting phase, but ODBA values were similar.

These surprising results suggest that vultures undertaking LRFs experience notable expenditures of energy without concomitant gains in resource intake, compared with individuals not undertaking such flights: LRF vultures fly more hours, cover much longer distances each day and hence experience elevated levels of energy expenditure during these forays. This high energy cost is not compensated by more frequent feeding; on the contrary, LRF vultures, during both the commuting and foraging phases, feed less frequently than vultures foraging normally within the home range. This implies that LRF vultures are unlikely to maintain their energy balance and are likely to fast for extended periods (Prinzinger et al., 2002). The effects of these extremely deprived conditions can be further appreciated given that one LRF event lasted more than 2 months. Moreover, reduction in energy intake rate might be even more severe if LRF birds have lower social ranking far from the core of their home range. In this case, the accessibility of LRF individuals to carcasses is likely to be lower than local individuals, leading to even smaller energy gains per feeding event occurring at a greatly reduced frequency. Overall, our results strongly suggest that LRF events cannot be explained by optimal foraging considerations, and LFR behavior appears to be energetically very costly. We propose that either social aspects (e.g. a search for a mate) or long-term advantages accruing from knowing resource distributions at locations well beyond current home ranges might account for this extreme and fascinating phenomenon.

Concluding remarks

Our analyses demonstrate the utility of using simultaneous GPS and ACC data along the movement pathways of free-ranging animals in exploring questions at the interface of behavior, ecology and biomechanics. The two data sources are complementary, with ACC data providing insight into behavior and energy expenditure, whereas GPS data enable associating the observed pathway with environmental drivers of the movement of an animal. Combining GPS and ACC data obtained from free-ranging vultures enabled us to suggest that their annual breeding schedule might be selected primarily in response to seasonal conditions favoring rising-air columns, and that rare LRF events are performed despite heavy energetic costs and low rates of food intake. Indeed, ACC-based tools cannot help address all questions at the interface of ecology, behavior and biomechanics, cannot replace all alternative methods of estimating energy expenditure and flight performance and still await significant technological and analytical developments to allow in-depth investigation of the basic biomechanics and energetics of the movements of animals in the wild. However, it should be remembered that such analyses have always been very challenging in free-ranging animals, and especially those that move over long periods and large spatial scales. Byrnes and colleagues (Byrnes et al., 2011), for example, effectively illustrated the power of ACC data recorded at 100 Hz not only to identify climbing and gliding behaviors of free-ranging Malayan colugos, but also to quantify the climbing heights. However, such an application is naturally limited to relatively short times and small spatial scales, depends on physical retrieval of the data-loggers and requires complementary measurements of the horizontal component of movements. Watanabe and associates (Watanabe et al., 2011) used GPS–ACC loggers to classify the flight and diving behaviors of shags and to quantify their movement tracks, wing-beat frequency and the duration and groundspeed of flights. An additional propeller was used to quantify flight airspeed as well, enabling estimation of flight power curves and comparison of flight and diving performance. Altogether, the GPS–ACC family of tools can help integrate biomechanics, ecology and behavior of free-ranging animals. These tools can provide very rich datasets and symbolize the start of a data-rich era in ecological, behavioral and biomechanical research (Nathan et al., 2008). Each data source can be used to address a particular set of questions, but applied together – as we plan to do in future studies – they will bring us closer to a full integrative analysis of movement in the framework of the unifying formulation depicted in Fig. 1.