Skip to main content
PMC home page
The Journal of Physiology logoLink to The Journal of Physiology
. 2011 Nov 7;590(Pt 2):363–375. doi: 10.1113/jphysiol.2011.214528

Human sympathetic outflows to skin and muscle target organs fluctuate concordantly over a wide range of time-varying frequencies

Alan Bernjak 1, Jian Cui 2,3, Satoshi Iwase 2,4, Tadaaki Mano 2,5, Aneta Stefanovska 1, Dwain L Eckberg 6
PMCID: PMC3285071  PMID: 22063627

Abstract

Non-technical summary

Traffic carried over two branches of the sympathetic nervous system can be recorded in cooperative human subjects, with fine needles inserted directly into leg nerves. We made simultaneous recordings of sympathetic activity with two needles inserted into nerve tracts supplying skin and muscles, and used a mathematical method, wavelet phase coherence, to obtain insights into how the brain regulates neural oscillations. Our results document continuously varying and coherently coupled human skin and muscle sympathetic nerve oscillations over time (suggesting that they are driven by other central frequency generators).

Abstract

Frequency-domain analyses of simultaneously recorded skin and muscle sympathetic nerve activities may yield unique information on otherwise obscure central processes governing human neural outflows. We used wavelet transform and wavelet phase coherence methods to analyse integrated skin and muscle sympathetic nerve activities and haemodynamic fluctuations, recorded from nine healthy supine young men. We tested two null hypotheses: (1) that human skin and muscle sympathetic nerve activities oscillate congruently; and (2) that whole-body heating affects these neural outflows and their haemodynamic consequences in similar ways. Measurements included peroneal nerve skin and tibial nerve muscle sympathetic activities; the electrocardiogram; finger photoplethysmographic arterial pressure; respiration (controlled at 0.25 Hz, and registered with a nasal thermistor); and skin temperature, sweating, and laser-Doppler skin blood flow. We made recordings at ∼27°C, for ∼20 min, and then during room temperature increases to ∼38°C, over 35 min. We analysed data with a wavelet transform, using the Morlet mother wavelet and wavelet phase coherence, to determine the frequencies and coherences of oscillations over time. At 27°C, skin and muscle nerve activities oscillated coherently, at ever-changing frequencies between 0.01 and the cardiac frequency (∼1 Hz). Heating significantly augmented oscillations of skin sympathetic nerve activity and skin blood flow, arterial pressure, and R-R intervals, over a wide range of low frequencies, and modestly reduced coordination between skin and muscle sympathetic oscillations. These results suggest that human skin and muscle sympathetic motoneurones are similarly entrained by external influences, including those of arterial baroreceptors, respiration, and other less well-defined brainstem oscillators. Our study provides strong support for the existence of multiple, time-varying central sympathetic neural oscillators in human subjects.

Introduction

Two sympathetic neural outflows, to skin and skeletal muscles, can be recorded directly in conscious cooperative human volunteers. The ability to record traffic travelling in two anatomically distinct nerve fascicles to two functionally distinct target organs opens the possibility that such human recordings might be analysed creatively, to better understand central neurophysiological rhythm-generating mechanisms. Although the number of studies of either skin or muscle sympathetic nerve activities of humans is large, there are only a few publications reporting simultaneous recordings of skin and muscle sympathetic nerve activities, in individuals (Delius et al. 1973; Wallin et al. 1973; Bini et al. 1981; Jänig et al. 1983; Fagius et al. 1985; Vissing et al. 1991), or in small groups of subjects (Saito et al. 1990; Takeuchi et al. 1994; Kodama et al. 1998).

With one exception (Fagius et al. 1985), all studies of simultaneously recorded human skin and muscle sympathetic nerve activities employed time-domain analysis methods. These studies indicate that sympathetic bursts occur at different times in the two neural outflows, and are not obviously coordinated. Skin sympathetic nerve activity may be only loosely coupled to respiration (Hagbarth et al. 1972; Wallin et al. 1974; Boczek-Funke et al. 1992), but muscle sympathetic nerve activity is strongly coupled (Delius et al. 1973; Eckberg et al. 1985). Skin sympathetic nerve activity is not as obviously coupled to cardiac (and presumably, baroreceptor) activity as muscle sympathetic nerve activity. However, Macefield & Wallin (1999) documented cardiac rhythmicity in single-fibre skin sympathetic neurograms with R-wave triggered averages, and Cui et al. (2006) showed that skin sympathetic nerve spectral power covers a wide frequency range which extends to the cardiac frequency. In addition, Bini et al. (1981) and Jänig et al. (1983) reported the emergence of a cardiac rhythm in skin sympathetic neurograms during heating.

The study by Fagius et al. (1985) characterized simultaneously recorded skin and muscle sympathetic nerve activities in one subject with power spectral analysis, in association with anaesthetic blockade of the glossopharyngeal and vagus nerves in the neck. This unique article reports that before local anaesthesia, visual inspection of the time series identified no obvious coordination between skin and muscle sympathetic nerve activities. After neck anaesthesia, however, power spectra of skin and muscle neurograms were similar. This provocative observation suggests that fluctuations of human skin and muscle neural outflows are generated or modulated by a common central oscillator. Under usual circumstances, however, coordination of skin and muscle sympathetic oscillations is obscured by strong arterial baroreceptor influences that affect muscle, but not skin sympathetic motoneurones.

We report wavelet phase coherence analysis of simultaneously recorded skin and muscle sympathetic nerve activities in a group of young men studied at normal room temperature and during whole-body (room) heating. This new method of treating human microneurography signals has major advantages over time- and frequency-domain approaches used previously, in that it yields ongoing high-resolution characterizations of interactions among neural and haemodynamic signals over time, and provides robust, statistically quantifiable indications of both the frequencies of oscillations – low, as well as high – and their coherences. We tested the null hypotheses that human skin and muscle sympathetic nerve activities oscillate congruently, and that whole-body heating affects these neural outflows, their coordination, and consequences in similar ways.

Methods

Subjects

We studied nine young men whose ages averaged (±SEM) 22 ± 1 years, heights 174 ± 2 cm, and weights 64 ± 2 kg. Each subject gave his written informed consent to participate in the study, which was approved by the Human Research Committee, Research Institute of Environmental Medicine, Nagoya University, Nagoya, Japan, and which conformed with the provisions of the Declaration of Helsinki. All subjects were healthy, and none were taking medications.

Measurements

We simultaneously recorded multiunit postganglionic sympathetic nerve activities with insulated tungsten microelectrodes inserted into a skin fascicle of a peroneal nerve, and a muscle fascicle of an ipsilateral tibial nerve. Skin sympathetic bursts were identified by their irregular occurrence and apparent lack of cardiac synchronicity; appearance (with widely varying durations); accentuation by mental activity, somatosensory (sound, pain, light or electrical) stimuli, and deep breathing; and their elicitation of increased sweating or reduced skin blood flow in the innervated area (Hagbarth et al. 1972; Bini et al. 1981). Muscle sympathetic bursts were identified by their position within muscle nerve fascicles; obvious pulse-synchronicity; modulation by respiration (Eckberg et al. 1985); and accentuation by held-expiration (Badra et al. 2001) or Valsalva straining (Delius et al. 1973; Smith et al. 1996). Neural signals were amplified, filtered (bandwidth: 500–5000 Hz), rectified, and integrated by a resistance–capacitance network with a time constant of 0.1 s, to obtain mean voltage displays.

We recorded the electrocardiogram with a bio-electric amplifier (AB-621G, Nihon Kohden, Tokyo, Japan); arterial pressure with a finger photoplethysmograph (Finapres, Ohmeda, Louisville, KY, USA); and respiration with a nasal thermistor. We identified the region of skin innervated by the impaled nerve fascicle by lightly stroking the skin to elicit cutaneous mechanoreceptor discharges. We measured skin blood flow velocity with a laser-Doppler probe (ALF21, Advance, Tokyo, Japan), and sweating with a capacitance hygrometer (Hidrograph AM-2, Fourtion, Nagoya, Japan) placed on the dorsum of the foot in the innervated area. Tympanic membrane and skin temperatures were registered with thermistors. All signals were recorded by a multi-channel FM recorder (KS-616U, Sony Precision Technology, Tokyo, Japan), and were digitized (Spike2, Cambridge Electronics Design, Cambridge, UK) for off-line processing.

Protocol

All experiments were performed with subjects in the supine position in a sound-, light-, temperature-, and humidity-controlled artificial climate room. Subjects breathed at 0.25 Hz with a metronome. Tidal volume was neither measured nor controlled. We recorded data for a minimum of 20 min at an ambient temperature of ∼27°C, and then for 30–40 min as room temperature increased to ∼38°C.

Analyses

All analyses of nerve traffic were made from normalized integrated neurograms. Before analysis, the mean value of the signal was subtracted and then the signal was divided by its standard deviation.

Wavelet transform

We used wavelet transforms with the Morlet mother wavelet to analyse data in the time–frequency domain (Stefanovska et al. 1999). This method (described in detail in the Appendix and in references cited below) characterizes the dynamics of signals over a wide frequency range, from 0.0095 to 2 Hz, with logarithmic resolution. Wavelet power spectra quantify the power of specific oscillatory components, and wavelet phase coherences (Bandrivskyy et al. 2004) identify concordant frequency fluctuations between pairs of neural signals.

Wavelet transforms are projections of signals from the time to the time–frequency domain. Unlike Fourier transforms, which use a window of constant length to calculate spectra, wavelet transforms adjust the length of wavelets during the calculations. Thus, high-frequency components are analysed with short wavelets, and low-frequency components are analysed with long wavelets; this is achieved by shortening or lengthening the wavelets in time. In this way, each frequency component is selectively analysed according to its corresponding period. Use of Morlet wavelet with its complex Gaussian sinusoids yields excellent localizations of oscillations and their coherence in both time and frequency.

Before calculations of wavelet transforms were made, time series were resampled at 10 Hz, and their spectra below 0.0095 Hz were removed by subtracting a moving 110 s average. Use of longer wavelets for lower frequencies (more data samples) enhances the amplitudes of the wavelet transforms at low, compared with high, frequencies. This enables easier identification of low-frequency oscillations, which usually have lower power than high frequency oscillations. Information regarding the strength of particular components is obtained by calculating the wavelet spectral power.

Wavelet phase coherence

Wavelet phase coherence identifies consistent phase relationships, and provides inferential evidence regarding causality between signals. In contrast with cross-spectra, significant phase coherence between signals can be identified even when their common powers are low. This is particularly meaningful for low-frequency components, which make important, but not necessarily large contributions to total power.

To quantify wavelet phase coherences between signals, we first calculated their wavelet transforms. Use of the complex Morlet wavelet permits extraction of instantaneous phase differences at each position in time and frequency. The relative phase differences are then calculated and their variations in time yield wavelet phase coherences (Bandrivskyy et al. 2004; Sheppard et al. 2011), which range between 0 (no coherence) and 1 (perfect coherence). Application of wavelet analysis, including cross-spectra and coherence, to study of time series, is well-described by Torrence & Compo (1998), and Grinsted et al. (2004) and Shiogai et al. (2010).

To investigate the effect of heating on the interactions between pairs of signals, the phase coherence was calculated for 1000 s segments before heating, and the last 1000 s segments during heating.

Statistical analysis

Since many data sets were not distributed normally (Kolmogorov–Smirnov test), we report medians, ranges, and individual values, and we use a non-parametric statistical test to identify significant coherences and significant changes with heating. With wavelet transforms, each signal is decomposed into specific oscillations by using different window lengths. With each window a specific part of the signal is targeted and the strength of a particular oscillation is extracted. Therefore, wavelet decomposition yields observations which are independent, even though they are extracted from the same time series.

We used the paired signed rank test to compare group data over two types of frequency ranges. First, we divided the logarithmic frequency range, 0.0095–2 Hz, into 115 segments for statistical analysis. These 115 comparisons were made to determine if phase coherences from the original data are significantly higher than their corresponding surrogate values (see below). In the graphs, a red vertical line is drawn at each of the 115 frequency ranges where the paired test showed a significant difference from surrogate values; where many contiguous frequencies show significant effects, these lines are confluent, and appear as a continuous red colour.

Second, we evaluated different, fixed frequency ranges to obtain results that could be compared with data published by others. These frequency ranges were 0.0095–0.021, 0.021–0.052, 0.052–0.145, 0.145–0.6 and 0.6–2 Hz (Stefanovska & Bračič, 1999; Shiogai et al. 2010).

The method used to determine the significance of wavelet phase coherences represents a special case. Obviously, over finite-length, non-stationary cardiovascular time series, low-frequency components are represented by fewer periods than high-frequency components. Consequentially, less variation of phase differences occurs at low frequencies, and this is reflected in higher coherence values for low than high frequencies. To identify a floor which demarcates truly significant coherence for all the frequencies, we employed surrogate analysis (Schreiber & Schmitz, 1996). Amplitude-adjusted Fourier transform (AAFT) surrogate signals were generated by shuffling the phases of the original time series to create new time series with the same means, variances, autocorrelation functions (and therefore, the same power spectra) as the original sequences, but without their phase relations. We averaged 100 wavelet phase coherences calculated from surrogate signals, and considered that wavelet coherences from the original recordings were statistically significant when they were 2 standard deviations above the mean surrogate coherence values.

In all statistical tests, P < 0.05 was considered significant.

Results

Before heating

Figure 1 shows recordings made from Subject 3 at a room temperature of 26.7°C. This subject, and all others controlled respiratory rates well, at 0.25 Hz (one breath every four s, Fig. 1C). Skin sympathetic nerve activity (Fig. 1E) occurred as irregular bursts whose durations, amplitudes, and appearances varied widely. Skin sympathetic nerve activity bore no obvious relation to either cardiac or respiratory activities. Muscle sympathetic nerve activity (Fig. 1F) occurred as volleys of narrow-waisted bursts, which appeared to fluctuate systematically, at low (∼0.1 Hz) and cardiac (∼1 Hz) frequencies.

Figure 1. Recording at room temperature from Subject 3.

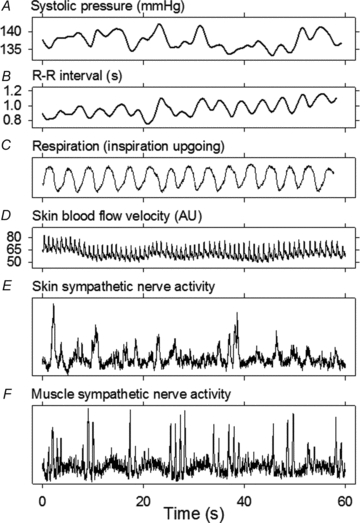
Figure 1

Open in a new tab

Respiration was controlled well by this and other subjects, who breathed with a metronome at 0.25 Hz.

Figure 2 shows a wavelet transform of skin sympathetic nerve activity from the same subject whose data are depicted in Fig. 1. Figure 2A shows the average wavelet transform, and indicates that the skin sympathetic nerve activity signal comprises spectral components which extend over a wide frequency range, from 0.01 Hz to the cardiac frequency. The most prominent periodicity in this subject (Fig. 2A) is at the respiratory frequency (0.25 Hz). The contour and three-dimensional plots shown in Fig. 2B and C indicate that the spectrum, depicted by the average wavelet transform in Fig. 2A, vastly obscures the richness of the frequency and power variability occurring over time.

Figure 2. Wavelet transform of skin sympathetic nerve activity from Subject 3.

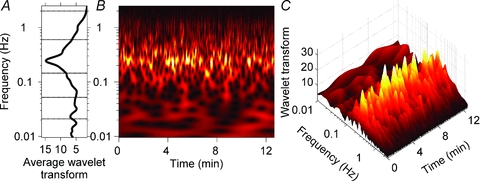
Figure 2

Open in a new tab

A, the average wavelet transform of skin sympathetic nerve activity for the recording period. B and C, a contour plot (B) and a three-dimensional plot (C) of the wavelet transform. The strongest periodicity, shown in yellow, is at the respiratory frequency (0.25 Hz). B and C illustrate the complexity of this subject's skin sympathetic rhythms, whose occurrence, frequency and strength were highly variable. The average data shown in A mask the major ongoing fluctuations present in the time series.

Figure 3 depicts a wavelet transform of muscle sympathetic nerve activity from Subject 2. The average wavelet transform in Fig. 3A indicates that the muscle sympathetic nerve activity signal contains oscillations at cardiac (∼1 Hz), respiratory (0.25 Hz), ∼0.1 Hz, and lower frequencies. As in Fig. 2, the contour (Fig. 3B) and three-dimensional (Fig. 3C) plots dramatically illustrate the complexity of human sympathetic neural oscillations. In this ostensibly ‘steady-state’ resting subject, the occurrence, level and frequency of wavelet aggregations varied widely over time (this variability is seen most convincingly at frequencies below the breathing frequency, lower two-thirds of Fig. 3B). The wavelet plots shown in Figs 2 and 3 make a compelling case that average power (however measured) in time series (whatever signal) provides a poor indication of the ongoing physiological oscillations that are present in healthy resting humans (Eckberg & Kuusela, 2005; Westerhof et al. 2006). Note that wavelet transforms are presented, rather than wavelet powers, to illustrate lower frequency components in both signals.

Figure 3. Wavelet transform of muscle sympathetic nerve activity from Subject 2.

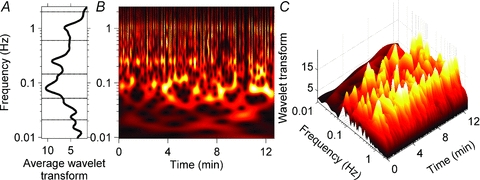
Figure 3

Open in a new tab

A, the average wavelet transform of the muscle sympathetic nerve activity. B and C, contour and three-dimensional plots of the same data. As with the analysis of skin sympathetic nerve activity (Fig. 2), the occurrence, frequency and strength of oscillations varied in major ways during the recording. This is particularly evident in the ∼0.1 Hz rhythm, which appeared and disappeared at highly variable rates. The average data shown in A do not accurately represent these ongoing fluctuations.

Figure 4 shows median (red) and individual (grey) skin and muscle sympathetic wavelet power spectra for all subjects. Skin sympathetic nerve power was strongest at the breathing frequency (0.25 Hz), but was also well represented at the cardiac frequency (∼1 Hz). (The peak at 0.5 Hz (arrow) is the second harmonic of the breathing frequency, which resulted from the regular, non-sinusoidal modulation introduced by paced breathing.) Muscle sympathetic nerve power was strongest at cardiac frequencies, but was also distinct at respiratory and ∼0.1 Hz frequencies. Median power in the lowest frequency ranges (components seen in the wavelet transform in Fig. 3) was very low.

Figure 4. Median (red) and individual (grey) wavelet power spectra of skin and muscle sympathetic neurograms before heating.

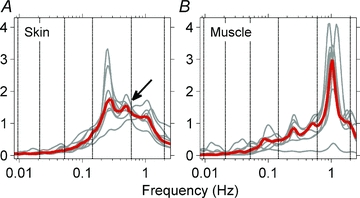
Figure 4

Open in a new tab

The strongest periodicity in skin sympathetic nerve activity (A) was at the respiratory frequency. A rhythm at the cardiac frequency was present, but was not prepossessing. The arrow points to the second harmonic of the respiratory frequency. The strongest periodicity in muscle sympathetic activity (B) was at the cardiac frequency. These median data also show oscillations at the respiratory frequency and ∼0.1 Hz.

We used wavelet phase coherence to identify interactions between skin and muscle sympathetic nerve activities, and to determine the frequency regions where such interactions occur. Figure 5A shows median wavelet phase coherence between skin and muscle sympathetic recordings at normal room temperature for all subjects. In this panel, the leftmost line (black) indicates median coherence (that is, the median value of the nine black relations shown in Fig. 5B), and the rightmost line in Fig. 5A (grey) indicates median surrogate values. Significant differences in the median and individual relations among the 115 frequency regions (see Methods) are denoted by the confluent red coloured areas beneath the median lines, and significant differences within the five fixed frequency ranges are denoted by the asterisks.

Figure 5. Median (A) and individual phase coherences (B) between skin and muscle sympathetic nerve activities for all subjects.

Figure 5

Open in a new tab

The heavy black lines indicate median (A) and individual (B) phase coherences; the grey lines indicate average surrogate values (see Methods), and the red areas indicate coherence which was significantly different (greater than 2 standard deviations above) from the surrogate values. The asterisks indicate frequency ranges within which skin and muscle coherences were significant. In all subjects, skin and muscle sympathetic nerve activities were significantly coherent over a broad range, including cardiac frequencies (extreme right of individual data panels). The group median data (A) obscure the significant narrow frequency ranges over which skin and muscle sympathetic nerve activities are coherent in individuals.

Figure 5B shows that skin and muscle sympathetic nerve phase coherences for all nine subjects were significant over a wide range of low frequencies, as well as respiratory and cardiac frequencies. These analyses indicate that, just as the average sympathetic nerve wavelet transform spectra from individual subjects (Figs 2A and 3A) obscure ongoing, time-varying frequencies and spectral powers over time, the average coherence from a group of subjects obscures the variability that is present in individual subjects.

During heating

Table 1 lists median and inter-quartile (25th and 75th percentiles) temperatures and haemodynamic data before and during heating, and the statistical significance of the changes. Systolic and diastolic pressures and R-R intervals did not change significantly during heating.

Table 1.

Median responses to heating

Before heating During heating P
Room temperature (°C) 27.2 (26.4, 28.4) 37.7 (37.3, 38.1) 0.01
Skin temperature (°C) 31.5 (30.7, 32.8) 33.1 (34.8, 37.0) 0.01
Tympanic membrane temperature (°C) 38.4 (37.1, 38.6) 38.6 (38.1, 38.8) 0.01
Sweating (AU) 0.043 (0.004, 0.097) 0.155 (0.060, 0.284) 0.01
Systolic pressure (mmHg) 135 (130, 138) 138 (127, 142) 0.95
Diastolic pressure (mmHg) 81 (72, 86) 80 (69, 86) 0.64
R-R interval (s) 0.96 (0.93, 1.01) 0.89 (0.87, 0.92) 0.25
Open in a new tab

Median values and their inter-quartile range (25th and 75th percentiles). P values were derived with the paired signed rank test.

Figure 6 shows median group coherences between skin and muscle sympathetic nerve activities before (Fig. 6A) and during heating (Fig. 6B), and their comparison (Fig. 6C). Red areas and asterisks in Fig. 6A and B indicate frequencies and frequency ranges at which coherences between the neural oscillations were significantly greater than surrogate values (P ≤ 0.05). Before heating (Fig. 6A) skin and muscle nerve activities were coherent over a broad range, from ∼0.05 to >1.0 Hz. During heating (Fig. 6B), significant coherence persisted over this range, and extended also to the next lower frequency range. (In this range, the differences were very small, but significant.) Figure 6C shows a comparison of coherences before and during heating. Heating modestly, but significantly, reduced coherence between skin and muscle sympathetic wavelet powers in the 115 individual frequencies, and in the highest (cardiac) frequency range (asterisk).

Figure 6. Median skin and muscle sympathetic activity wavelet phase coherence before and during heating.

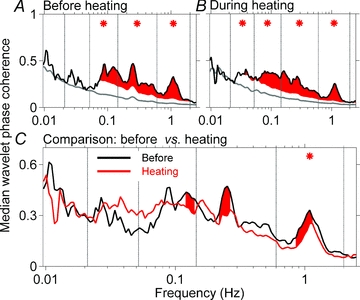
Figure 6

Open in a new tab

The black lines in A and B indicate median group coherences, the grey lines indicate average surrogate values, and the red shaded areas indicate coherences in 115 frequency ranges which are greater than 2 standard deviations above the surrogate values. Asterisks indicate conventional frequency ranges, in which the mean coherences are significantly above the mean surrogate values. C compares coherences before and during heating. Note that in C, the scale is narrower than in A and B. The only frequency range over which this reduction is significant is the cardiac frequency (*).

Figure 7 depicts room and skin temperatures, skin blood flow, and the wavelet transform of blood flow at the cardiac, ∼1.1 Hz, and respiratory (0.25 Hz) frequencies, from Subject 4 during heating. Note that the subject's skin temperature reflects his response to heating, not the temperature stimulus that provoked the response. The blood flow signal in the time domain (middle panel) does not show obvious changes with heating. The wavelet transform, however, which allows for a decomposition of the signal into specific frequency components and an independent tracing of their changes in time, identifies a steady increase of respiratory and cardiac frequency fluctuations during heating (lower panel).

Figure 7. Skin blood flow responses of Subject 4 to heating.

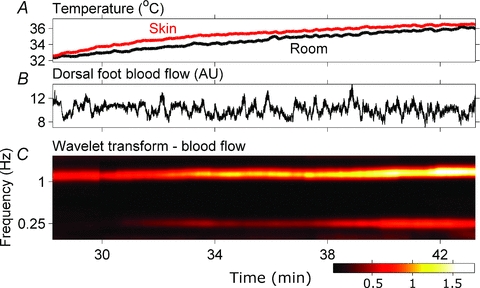
Figure 7

Open in a new tab

The blood flow signal (B) does not show obvious changes with heating in the time domain. The wavelet transform, which decomposes the signal into several oscillatory components and their variation in time documents a steady increase of the amplitudes of oscillatory components at cardiac and respiratory frequencies with heating (C).

Figure 8 shows the influence of heating on wavelet power spectra of neural and haemodynamic signals. Median wavelet powers for the group are shown as a black line, before heating and as a red line, during heating. Red shaded areas indicate specific frequencies at which the effect of heating is significant (as indicated, a paired signed rank test was applied to wavelet power values at each of the 115 frequencies within the entire frequency range). Asterisks indicate frequency ranges at which the effect of heating was significant.

Figure 8. Influence of heating on wavelet power spectra of neural and haemodynamic signals.

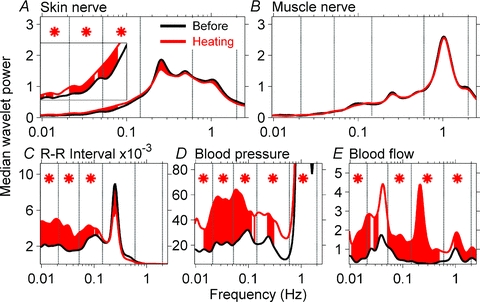
Figure 8

Open in a new tab

Wavelet power spectra of signals are compared before and during heating. Red shaded areas indicate significant effect of heating at specific frequencies and asterisks indicate significances within the frequency ranges. Skin sympathetic nerve wavelet power increased significantly during heating at low frequencies (A, inset), but muscle sympathetic nerve wavelet power (B) was not affected by heating. R-R interval, blood pressure, and skin blood flow wavelet powers were significantly increased by heating, primarily at low frequencies.

Heating significantly increased skin sympathetic nerve wavelet power at ∼0.1 Hz and lower frequencies (Fig. 8A, inset), and decreased the power of oscillations at the breathing frequency (Fig. 8A, red shaded area); however, the difference was not significant for the entire breathing frequency range. Heating did not alter muscle sympathetic nerve wavelet power (Fig. 8B), but significantly augmented R-R interval, blood pressure, and skin blood flow wavelet powers, predominantly at low frequencies (Fig. 8C–E, shaded areas and asterisks). R-R interval power at the respiratory frequency (0.25 Hz, Fig. 8C) declined significantly; however, the decline was not significant for the entire respiratory frequency range.

Discussion

We made simultaneous recordings of skin and muscle sympathetic nerve activities in healthy supine young men before and during whole body heating, and analysed results with wavelet phase coherence. Our findings treat the fundamental nature of human sympathetic rhythmicity: both skin and muscle sympathetic outflows (which travel in different nerve fascicles to different target organs) oscillate in a coordinated fashion over a wide range of frequencies. Our study provides strong support for the existence of multiple, time-varying central sympathetic neural oscillators in human subjects.

Strengths of our study

Our study may have several unique features. First, the number of subjects, nine, may be the largest group studied with simultaneous skin and muscle sympathetic nerve recordings. Second, we analysed long data segments, ranging from 17 to 35 min; such long analysis periods allow us to deal confidently with rhythms as slow as 0.01 Hz. Moreover, we carried our analyses to frequencies above the cardiac frequency; this enabled us to define frequencies higher than those considered in most human research. Third, we used wavelet phase coherence – the first use of this approach with dual human sympathetic microneurographic signals. As we indicate in the Introduction, this analytical method is particularly well-suited to study of very low frequency rhythms. Fourth, we compared our measurements with surrogate values; this permitted us to move beyond simple descriptions and determine actual statistical probability. Fifth, our experimental preparation, conscious, minimally invaded cooperative human subjects, may be simpler than those used in animal research, with potential confounds introduced by anaesthesia and surgical manipulation.

The nature of human sympathetic rhythmicity

We found that both skin and muscle sympathetic nerve activities oscillate over broad, generally similar frequency ranges, from 1 cycle per 100 s to the cardiac frequency, ∼1 Hz (Fig. 4). The earliest frequency-domain analysis of human muscle sympathetic neurograms (Eckberg et al. 1985) also documented a similar broad frequency range. Our time–frequency analyses with their logarithmic frequency resolution yield new insights into the breadth of human sympathetic spectra: the broad, not well-differentiated frequency ranges in individual subjects (Figs 2A and 3A) are broad because the discrete frequencies that go into their making fluctuate. As in experimental animals (Chang et al. 1999), the frequencies of sympathetic oscillations, skin and muscle, drift. Moreover, the average wavelet spectrum of the group of subjects we studied is broad because the discrete frequencies from individual subjects that go into its making differ greatly (Fig. 5).

Simultaneous recordings of human skin sympathetic nerve traffic travelling to the right and left sides of the body are remarkably similar, both in the timing and appearance of bursts (Bini et al. 1980). This indicates that bilateral skin outflows are driven by a common central oscillator. The same conclusion holds true for muscle sympathetic outflows (Sundlöf & Wallin, 1977). Our study extends understanding of these central mechanisms by showing that the two disparate, anatomically distinguishable (Dampney & McAllen, 1988) motoneurone pools, whose outflows travel in different nerve fascicles to different target organs, skin and muscle, also are influenced by the same central generator(s). Coordination between skin and muscle sympathetic oscillations is not limited to a small number of frequency ranges, but covers a broad range of frequencies, which differ from subject to subject (Fig. 5B).

In early human microneurographic studies, one feature used to distinguish skin from muscle sympathetic nerve outflows was that skin sympathetic activity lacks cardiac periodicity (Hagbarth et al. 1972; Wallin et al. 1974). Subsequent research, however, showed that a cardiac rhythm can be detected in skin sympathetic neurograms, with no intervention (Macefield & Wallin, 1999; Cui et al. 2006) or with heating (Bini et al. 1981; Jänig et al. 1983). Our results confirm and extend these earlier observations; we document unmistakable coordination between skin and muscle sympathetic nerve activities at cardiac frequencies, in all subjects under baseline conditions, with no intervention (Fig. 5). Our data (Figs 2, 4 and 5) also confirm the presence of respiratory periodicity in skin sympathetic recordings, a finding that has been remarked since the earliest human neurograms were published (Hagbarth et al. 1972; Wallin et al. 1974; Bini et al. 1980). Our study is new in its documentation (Fig. 5B) of significant skin and muscle sympathetic coordination over a wide range of low frequencies, below 0.1 Hz.

These results are not consistent with a model based upon a single central sympathetic oscillator, since we identified not one, but many frequencies of neuronal oscillation (Figs 2, 3 and 5). By the same token, our results are not consistent with a model based upon two fixed sympathetic oscillators, since skin and muscle oscillations are broadly coherent (Fig. 5). The firing patterns we identified point towards the existence of multiple oscillators with time-varying frequencies that influence and modulate skin and muscle motor neurones in a coordinated fashion.

Responses to heating

We used one intervention, strictly controlled whole-body heating in an artificial climate chamber, as a means to distinguish skin from muscle sympathetic nerve oscillatory behaviour. Heating had no effect on muscle sympathetic nerve rhythms (Fig. 8B). This stands in contrast to the effect heating had on skin sympathetic rhythms: heating increased low-frequency skin sympathetic rhythms significantly (Fig. 8A). The differential effect that heating exerts on skin and muscle sympathetic nerve rhythms suggests that skin sympathetic motoneurones have central inputs that are not shared by muscle sympathetic motoneurones. Heating reduced coordination between skin and muscle sympathetic firing, but only at higher frequencies, and only to a small extent (Fig. 6C).

R-R interval responses to heating deserve special mention. In her seminal study of conscious dogs, Solange Axelrod and her colleagues discussed mechanisms responsible for heart rate fluctuations in three frequency ranges (Akselrod et al. 1981). She reported that renin–angiotensin blockade increases spectral power in the very low-frequency range (below ∼0.05 Hz). We confirmed this observation in an earlier study of healthy human subjects (Taylor et al. 1998); however, we failed to define a discrete frequency; rather, renin–angiotensin blockade increased R-R interval spectral power over a broad low-frequency range. Axelrod also cited speculation (Sayers, 1973) regarding a thermoregulatory role for very low-frequency rhythms. Our study (Fig. 8C) may provide the most convincing evidence to date for this possibility. However, as with the renin–angiotensin blocking study (Taylor et al. 1998), heating increased low-frequency R-R interval rhythms broadly; the effect was not restricted to a discrete low-frequency range. A third mechanism involved in very low-frequency haemodynamic oscillations is endothelial reactivity (Kvandal et al. 2003; Shiogai et al. 2010; Sheppard et al. 2011), whose influence on R-R interval oscillations might profitably be explored.

Mutability of human sympathetic rhythms

We found great variability in the occurrence, frequency, and strength of human skin and muscle sympathetic rhythms. Although many discrete areas of the brain subserve specific functions, the connections among brain areas are myriad, and this anatomical organization provides a rich substrate for ongoing, ever-changing, long-recognized (Sherrington, 1913) functional organization and reorganization. The most prominent periodicity in human muscle sympathetic neurograms is at the cardiac frequency (Eckberg et al. 1985; this study, Fig. 4). Cardiac rhythmicity is not a fixed feature of human sympathetic rhythms, however: cardiac periodicity in muscle sympathetic outflow is abolished by anaesthesia of baroreceptor (and other) nerves in the neck (Fagius et al. 1985); by non-REM sleep (Takeuchi et al. 1994; Kodama et al. 1998) and syncope (Iwase et al. 2002); and by reduction of baroreceptor input by intense lower body suction (Cooke et al. 2009). Similarly, respiratory periodicity in muscle sympathetic neurograms also is not fixed: muscle sympathetic rhythms follow breathing frequency (Stankovski et al. unpublished), and are absent during apnoea (Badra et al. 2001) and during upright tilt, when the level of arterial baroreceptor stimulation is diminished (Cooke et al. 1999).

In animal studies, brainstem rhythms can be changed by altering blood pressure (Barman et al. 1994; Barman & Gebber, 1997); denervating arterial baroreceptors (Taylor & Gebber, 1975); changing heart (Morrison & Gebber, 1982; 1984) or breathing (Chang et al. 1999) rate; and blocking neurotransmitters in areas anatomically remote from known sympathetic premotor areas (Orer et al. 1999; Kenney et al. 2001). These and the present results underscore the richness and complexity of the dynamic control of central rhythm-generating mechanisms. Although whole-body heating increases brain temperature (Baldwin & Ingram, 1998), to our knowledge, the possibility that isolated brain heating (not associated with whole-body heating) alters sympathetic rhythms directly has not been studied.

Limitations

Our study may have real or potential limitations. First, although we report what we believe to be the largest series of simultaneous human skin and muscle sympathetic nerve recordings (n = 9), we cannot exclude the possibility that negative results reflect a beta-statistical error. Second, although the instrumentation of our volunteers was comprehensive (see Methods), we did not measure respiratory carbon dioxide concentrations. We can say, however, that if control of breathing led to hypocapnia, the effects on our measurements were likely to be small (Trzebski et al. 1995; Henry et al. 1998). We make no claim that the data we analysed were stationary; as we argue elsewhere (Eckberg & Kuusela, 2005), stationarity is a construct that enjoys no meaningful existence in healthy, conscious human subjects.

Our study involved only one intervention, whole-body heating; therefore, we cannot speculate about how other interventions which raise or lower sympathetic nerve activity might have influenced the rhythms we studied. Similarly, since our volunteers were all healthy young men, we cannot speculate about how other populations might have responded. We can say, however, that although levels of muscle sympathetic nerve activity are high in patients with heart failure, hypertension, obesity and renal failure, levels of skin sympathetic nerve activity in these patients are not different from those in healthy populations (Grassi et al. 1998, 2003; Park et al. 2008).

We followed established precedent (Wallin & Charkoudian, 2007) and analysed integrated, rather than raw, sympathetic nerve activity, and used the same time constant, 0.1 s, to integrate both skin and muscle sympathetic activities. Since single unit studies show that both skin and muscle nerve firings occur within bursts (Macefield et al. 1994; Macefield & Wallin, 1996), our studies of integrated neurograms should be appropriate to identify rhythms and their coordination. Moreover, our signal-to-noise ratios were high in all recordings (Fig. 1), and since we used the entire integrated nerve signal (we did not attempt to identify individual bursts), oscillations involving very small numbers of firings and small bursts were included in the analyses. Moreover, wavelet phase coherence is calculated from phase rather than amplitude dynamics. As phase dynamics are less affected by integration than amplitude dynamics, the phase coherences probably would differ minimally if signals were integrated with slightly longer, or shorter, time constants (such as 0.2 or 0.05 s). We cannot exclude the possibility that the 0.1 s time constant we used excluded oscillations above the cardiac frequency, if such exist.

In conclusion, we recorded skin and muscle sympathetic nerve activities simultaneously in young men before and during whole-body heating, and analysed results with wavelet transform and wavelet phase coherence methods. We tested two null hypotheses: that human skin and muscle sympathetic nerve activities oscillate congruently, and that whole-body heating affects these neural outflows, their coordination, and consequences, in similar ways. We validated the first hypothesis and showed that skin and muscle sympathetic neural outflows oscillate coherently over a 100-fold range of frequencies. Importantly, we show that human sympathetic rhythms drift – they are unstable and mutable. We rejected the second hypothesis and showed that the intervention we used, whole-body heating, differentially affects skin and muscle sympathetic nerve rhythms. Skin sympathetic oscillations (and R-R intervals) increased over a wide low-frequency range, but muscle sympathetic oscillations were not affected by heating. Our study provides strong support for the existence of multiple, time-varying central sympathetic neural oscillators in human subjects.

Acknowledgments

We thank the subjects who volunteered for and participated in this research. The research was supported by a Royal Society International Short Visit Grant, and in part by the ESRC, UK ‘New dynamics of ageing’ programme.

Appendix

Wavelet transform

Wavelet transforms analyse signals with windows of variable length. The procedure begins with a window function, the mother wavelet ψ (u). This function introduces a scale (the width of a window function) into the analysis. Commitment to any particular scale is avoided by using not only ψ (u) but also different scalings of ψ (u). The mother wavelet is also translated within the signal to achieve time localisation. Thus, a family of non-orthogonal basis functions is obtained:

graphic file with name tjp0590-0363-m1.jpg

where s is the scaling parameter, determining the factor by which the mother wavelet is stretched (s > 1) or compressed (s < 1). Changing the scale (lengths of the wavelets) selects the frequency components of the signal to be analysed. Parameter t shifts the wavelet within the original signal and allows tracing the spectral properties of the signal in time. Parameter p is an arbitrary non-negative number. The prevailing choice in the literature is p = 0.5, and in this case the norm of the wavelet and its energy are unaffected by the scaling operator.

The continuous wavelet transform of a signal g(u) is defined as:

graphic file with name tjp0590-0363-m2.jpg

The wavelet transform 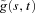Inline graphic is a mapping of the function g(u) onto the time-scale plane; its interpretation depends on the mother wavelet being used. Choice of a wavelet well concentrated in both time and frequency allows detection of the precise frequency content in a given time interval. For our analyses, we used the Morlet mother wavelet, a Gaussian function modulated by the sine (cosine) wave:

graphic file with name tjp0590-0363-m3.jpg

The shape of the Morlet wavelet in the frequency domain is also a Gaussian function and thus this wavelet provides good localisation in both time and frequency. The choice of f0 is a compromise between resolution in time and frequency and by selecting f0= 1 we require that at least six periods of each oscillation are considered in determination of their strength. This is a reasonable compromise, since it emphasizes detection of the frequency content of the signal over isolated time events. Further, by choosing f0= 1, a simple relation between the scale and frequency is obtained: f = 1/s. In practice this means that with s = 1, we analyse the 1 Hz component of the signal. Using scale s = 2, the wavelet length is stretched by the factor 2 and the frequency to be analysed becomes 0.5 Hz. Scales smaller than 1 compress the wavelet length for analysis of frequencies higher than 1 Hz.

The relatively wide frequency range from 0.0095 Hz to 2 Hz is analysed by using a logarithmic frequency resolution. This is achieved by exponentially increasing the scaling factor, and with it, the length of the wavelet. The first scaling factor was set at 0.5 (corresponding to 2 Hz), and all the succeeding factors were calculated from the previous ones by multiplying them by 1.05: sm+1= sm × 1.05, until the final scaling factor reached 105 (corresponding to 0.0095 Hz). The time resolution of the wavelet transform is set at 1 s.

From the wavelet transform the energy density of the signal in the time-scale plane is obtained, and the wavelet power within the f1:f2 frequency range can be calculated:

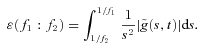graphic file with name tjp0590-0363-m4.jpg

Wavelet phase coherence

The complex nature of the Morlet wavelet (its real part is a sine function and its imaginary part is a cosine function) makes the wavelet transform a complex function with complex values:

graphic file with name tjp0590-0363-m5.jpg

For each time tn and scale sk the wavelet amplitude is calculated as the absolute value of the wavelet coefficient 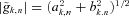Inline graphic and its phase 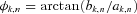Inline graphic is the instantaneous frequency at (k,n).

To calculate the wavelet phase coherence between two signals, the instantaneous phases of both signals, ϕ1k,n and ϕ2k,n, are obtained from their wavelet transforms and their relative phase difference is calculated: Δϕk,n=ϕ2k,n−ϕ1k,n. Then the sine and cosine components of the phase difference are calculated and averaged in time for the whole length of the signal. Finally, the phase coherence function is defined as:

graphic file with name tjp0590-0363-m6.jpg

The phase coherence function, Cϕ(fk), has a value between 0 and 1. For values around 0 there is no phase coherence between the two signals while for values close to 1 the signals are coherent at the selected frequency.

Author contributions

A.B. analysed the data, prepared the graphs, and contributed to the writing of the article. J.C. contributed to the design of the experiment, its execution, and early analysis of data, and wrote the first draft of the article. S.I. and T.M. contributed to the design of the experiment and the collection of data. A.S. developed the mathematical algorithms used to analyse the data, and contributed to the analysis of the results and the writing of the manuscript. D.L.E. contributed to the design of the experiment, the collection of data, the analysis of the results, and the writing of the article. All authors reviewed and contributed to the final manuscript.

References

  1. Akselrod S, Gordon D, Ubel FA, Shannon DC, Barger AC, Cohen RJ. Power spectrum analysis of heart rate fluctuation: a quantitative probe of beat-to-beat cardiovascular control. Science. 1981;213:220–222. doi: 10.1126/science.6166045. [DOI] [PubMed] [Google Scholar]
  2. Badra LJ, Cooke WH, Hoag JB, Crossman AA, Kuusela TA, Tahvanainen KUO, Eckberg DL. Respiratory modulation of human autonomic rhythms. Am J Physiol Heart Circ Physiol. 2001;280:H2674–H2688. doi: 10.1152/ajpheart.2001.280.6.H2674. [DOI] [PubMed] [Google Scholar]
  3. Baldwin BA, Ingram DL. The influence of hypothalamic temperature and ambient temperature on thermoregulatory mechanisms in the pig. J Physiol. 1998;198:517–529. doi: 10.1113/jphysiol.1968.sp008622. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bandrivskyy A, Bernjak A, McClintock P, Stefanovska A. Wavelet phase coherence analysis: application to skin temperature and blood flow. Cardiovasc Eng. 2004;4:89–93. [Google Scholar]
  5. Barman SM, Gebber GL. Subgroups of rostral ventrolateral medullary and caudal medullary raphe neurons based on patterns of relationship to sympathetic nerve discharge and axonal projections. J Neurophysiol. 1997;77:65–75. doi: 10.1152/jn.1997.77.1.65. [DOI] [PubMed] [Google Scholar]
  6. Barman SM, Orer HS, Gebber GL. Caudal ventrolateral medullary neurons are elements of the network responsible for the 10-Hz rhythm in sympathetic nerve discharge. J Neurophysiol. 1994;72:106–120. doi: 10.1152/jn.1994.72.1.106. [DOI] [PubMed] [Google Scholar]
  7. Bini G, Hagbarth K-E, Hynninen P, Wallin BG. Regional similarities and differences in thermoregulatory vaso- and sudomotor tone. J Physiol. 1980;306:553–565. doi: 10.1113/jphysiol.1980.sp013414. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Bini G, Hagbarth K-E, Wallin BG. Cardiac rhythmicity of skin sympathetic activity recorded from peripheral nerves in man. J Autonom Nerv Syst. 1981;4:17–24. doi: 10.1016/0165-1838(81)90003-5. [DOI] [PubMed] [Google Scholar]
  9. Boczek-Funcke A, Häbler H-J, Jänig W, Michaelis M. Respiratory modulation of the activity in sympathetic neurones supplying muscle, skin and pelvic organs in the cat. J Physiol. 1992;449:333–361. doi: 10.1113/jphysiol.1992.sp019089. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Chang H-S, Staras K, Smith JE, Gilbey MP. Sympathetic neuronal oscillators are capable of dynamic synchronization. J Neurosci. 1999;19:3183–3197. doi: 10.1523/JNEUROSCI.19-08-03183.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Cooke WH, Hoag JB, Crossman AA, Kuusela TA, Tahvanainen KUO, Eckberg DL. Human responses to upright tilt: a window on central autonomic integration. J Physiol. 1999;517:617–628. doi: 10.1111/j.1469-7793.1999.0617t.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Cooke WH, Rickards CA, Ryan KL, Kuusela TA, Convertino VA. Muscle sympathetic nerve activity during intense lower body negative pressure to presyncope in humans. J Physiol. 2009;587:4987–4999. doi: 10.1113/jphysiol.2009.177352. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Cui J, Sathishkumar M, Wilson TE, Shibasaki M, Davis SL, Crandall CG. Spectral characteristics of skin sympathetic nerve activity in heat-stressed humans. Am J Physiol Heart Circ Physiol. 2006;290:H1601–H1609. doi: 10.1152/ajpheart.00025.2005. [DOI] [PubMed] [Google Scholar]
  14. Dampney RAL, McAllen RM. Differential control of sympathetic fibres supplying hindlimb skin and muscle by subretrofacial neurones in the cat. J Physiol. 1988;395:41–56. doi: 10.1113/jphysiol.1988.sp016907. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Delius W, Wallin G, Hagbarth K-E. Role of sympathetic nerve impulses in regulation of peripheral circulation. Scand J Clin Lab Invest. 1973;128:47–50. [PubMed] [Google Scholar]
  16. Eckberg DL, Kuusela TA. Human vagal baroreflex sensitivity fluctuates widely and rhythmically at very low frequencies. J Physiol. 2005;567:1011–1019. doi: 10.1113/jphysiol.2005.091090. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Eckberg DL, Nerhed C, Wallin BG. Respiratory modulation of muscle sympathetic and vagal cardiac outflow in man. J Physiol. 1985;365:181–196. doi: 10.1113/jphysiol.1985.sp015766. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Fagius J, Wallin BG, Sundlöf G, Nerhed C, Englesson S. Sympathetic outflow in man after anaesthesia of the glossopharyngeal and vagus nerves. Brain. 1985;108:423–438. doi: 10.1093/brain/108.2.423. [DOI] [PubMed] [Google Scholar]
  19. Grassi G, Colombo M, Seravalle G, Spaziani D, Mancia G. Dissociation between muscle and skin sympathetic nerve activity in essential hypertension, obesity, and congestive heart failure. Hypertension. 1998;31:64–67. doi: 10.1161/01.hyp.31.1.64. [DOI] [PubMed] [Google Scholar]
  20. Grassi G, Seravalle G, Turri C, Bertinieri G, Dell’Oro R, Mancia G. Impairment of thermoregulatory control of skin sympathetic nerve traffic in the elderly. Circulation. 2003;108:729–735. doi: 10.1161/01.CIR.0000081769.02847.A1. [DOI] [PubMed] [Google Scholar]
  21. Grinsted A, Moore JC, Jevrejeva S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlin Proc Geophys. 2004;11:561–566. [Google Scholar]
  22. Hagbarth K-E, Hallin RG, Hongell A, Torebjörk HE, Wallin BG. General characteristics of sympathetic activity in human skin nerves. Acta Physiol Scand. 1972;84:164–176. doi: 10.1111/j.1748-1716.1972.tb05167.x. [DOI] [PubMed] [Google Scholar]
  23. Henry RA, Lu I-L, Beightol LA, Eckberg DL. Interactions between human CO2 chemoreflexes and arterial baroreflexes. Am J Physiol Heart Circ Physiol. 1998;274:H2177–H2187. doi: 10.1152/ajpheart.1998.274.6.h2177. [DOI] [PubMed] [Google Scholar]
  24. Iwase S, Mano T, Kamiya A, Niimi Y, Fu Q, Suzumura A. Syncopal attack alters the burst properties of muscle sympathetic nerve activity in humans. Autonom Neurosc: Basic Clin. 2002;95:141–145. doi: 10.1016/s1566-0702(01)00362-9. [DOI] [PubMed] [Google Scholar]
  25. Jänig W, Sundlöf G, Wallin BG. Discharge patterns of sympathetic neurons supplying skeletal muscle and skin in man and cat. J Auton Nerv Syst. 1983;7:239–256. doi: 10.1016/0165-1838(83)90077-2. [DOI] [PubMed] [Google Scholar]
  26. Kenney MJ, Weiss ML, Patel KP, Wang Y, Fels RJ. Paraventricular nucleus bicuculline alters frequency components of sympathetic nerve discharge bursts. Am J Physiol Heart Circ Physiol. 2001;281:H1233–H1241. doi: 10.1152/ajpheart.2001.281.3.H1233. [DOI] [PubMed] [Google Scholar]
  27. Kodama Y, Iwase S, Mano T, Cui J, Kitazawa H, Okada H, Takeuchi S, Sobue G. Attenuation of regional differentiation of sympathetic nerve activity during sleep in humans. J Autonom Nerv Sys. 1998;74:126–133. doi: 10.1016/s0165-1838(98)00150-7. [DOI] [PubMed] [Google Scholar]
  28. Kvandal P, Stefanovska A, Veber M, Kvermmo HD, Kirkebøen KA. Regulation of human cutaneous circulation evaluated by laser Doppler flowmetry, iontophoresis, and spectral analysis: importance of nitric oxide and prostaglandines. Microvasc Res. 2003;65:160–171. doi: 10.1016/s0026-2862(03)00006-2. [DOI] [PubMed] [Google Scholar]
  29. Macefield VG, Wallin BG. The discharge behaviour of single sympathetic neurones supplying human sweat glands. J Autonom Nerv Syst. 1996;61:277–286. doi: 10.1016/s0165-1838(96)00095-1. [DOI] [PubMed] [Google Scholar]
  30. Macefield VG, Wallin BG, Vallbo ÅB. The discharge behaviour of single vasoconstrictor motoneurones in human muscle nerves. J Physiol. 1994;481:799–809. doi: 10.1113/jphysiol.1994.sp020482. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Macefield VG, Wallin BG. Respiratory and cardiac modulation of single sympathetic vasoconstrictor and sudomotor neurones to human skin. J Physiol. 1999;516:303–314. doi: 10.1111/j.1469-7793.1999.303aa.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Morrison SF, Gebber GL. Classification of raphe neurons with cardiac-related activity. Am J Physiol Regul Integr Comp Physiol. 1982;243:R49–R59. doi: 10.1152/ajpregu.1982.243.1.R49. [DOI] [PubMed] [Google Scholar]
  33. Morrison SF, Gebber GL. Raphe neurons with sympathetic-related activity – baroreceptor responses and spinal connections. Am J Physiol Regul Integr Comp Physiol. 1984;246:R338–R348. doi: 10.1152/ajpregu.1984.246.3.R338. [DOI] [PubMed] [Google Scholar]
  34. Orer HS, Barman SM, Gebber GL, Sykes SM. Medullary lateral tegmental field: an important synaptic relay in the baroreceptor reflex pathway of the cat. Am J Physiol Regul Integr Comp Physiol. 1999;277:R1462–R1475. doi: 10.1152/ajpregu.1999.277.5.R1462. [DOI] [PubMed] [Google Scholar]
  35. Park J, Campese VM, Nobakht N, Middlekauff HR. Differential distribution of muscle and skin sympathetic nerve activity in patients with end-stage renal disease. J Appl Physiol. 2008;105:1873–1876. doi: 10.1152/japplphysiol.90849.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Saito M, Naito M, Mano T. Different responses in skin and muscle sympathetic nerve activity to static muscle contraction. J Appl Physiol. 1990;69:2085–2090. doi: 10.1152/jappl.1990.69.6.2085. [DOI] [PubMed] [Google Scholar]
  37. Sayers BMcA. Analysis of heart rate variability. Ergonomics. 1973;16:17–32. doi: 10.1080/00140137308924479. [DOI] [PubMed] [Google Scholar]
  38. Schreiber T, Schmitz A. Improved surrogate data for nonlinearity tests. Physical Rev Let. 1996;77:635–638. doi: 10.1103/PhysRevLett.77.635. [DOI] [PubMed] [Google Scholar]
  39. Sheppard LW, Vuksanović V, McClintock PVE, Stefanovska A. Oscillatory dynamics of vasoconstriction and vasodilation identified by time-localized phase coherence. Phys Med Biol. 2011;56:3583–3601. doi: 10.1088/0031-9155/56/12/009. [DOI] [PubMed] [Google Scholar]
  40. Sherrington CS. Further observations on the production of reflex stepping by combination of reflex excitation with reflex inhibition. J Physiol. 1913;47:196–214. doi: 10.1113/jphysiol.1913.sp001620. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Shiogai Y, Stefanovska A, McClintock PVE. Nonlinear dynamics of cardiovascular ageing. Physics Rep. 2010;488:51–110. doi: 10.1016/j.physrep.2009.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Smith ML, Beightol LA, Fritsch-Yelle JM, Ellenbogen KA, Porter TR, Eckberg DL. Valsalva's maneuver revisited: a quantitative method yielding insights into human autonomic control. Am J Physiol Heart Circ Physiol. 1996;271:H1240–H1249. doi: 10.1152/ajpheart.1996.271.3.H1240. [DOI] [PubMed] [Google Scholar]
  43. Stefanovska A, Bračič M. Physics of the human cardiovascular system. Contemp Phys. 1999;40:31–55. [Google Scholar]
  44. Stefanovska A, Bračič M, Kvernmo HD. Wavelet analysis of oscillations in the peripheral blood circulation measured by laser Doppler technique. IEEE Trans Biomed Eng. 1999;46:1230–1239. doi: 10.1109/10.790500. [DOI] [PubMed] [Google Scholar]
  45. Sundlöf G, Wallin BG. The variability of muscle nerve sympathetic activity in resting recumbent man. J Physiol. 1977;272:383–397. doi: 10.1113/jphysiol.1977.sp012050. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Takeuchi S, Iwase S, Mano T, Okada H, Sugiyama Y, Watanabe T. Sleep-related changes in human muscle and skin sympathetic nerve activities. J Auton Nerv Sys. 1994;47:121–129. doi: 10.1016/0165-1838(94)90073-6. [DOI] [PubMed] [Google Scholar]
  47. Taylor DG, Gebber GL. Baroreceptor mechanisms controlling sympathetic nervous rhythms of central origin. Am J Physiol. 1975;228:1002–1013. doi: 10.1152/ajplegacy.1975.228.4.1002. [DOI] [PubMed] [Google Scholar]
  48. Taylor JA, Carr DL, Myers CW, Eckberg DL. Mechanisms underlying very-low-frequency RR-interval oscillations in humans. Circulation. 1998;98:547–555. doi: 10.1161/01.cir.98.6.547. [DOI] [PubMed] [Google Scholar]
  49. Torrence C, Compo GP. A practical guide to wavelet analysis. Bull Amer Meteor Soc. 1998;79:61–78. [Google Scholar]
  50. Trzebski A, Smith ML, Beightol LA, Fritsch-Yelle JM, Rea RF, Eckberg DL. Modulation of human sympathetic periodicity by mild, brief hypoxia and hypercapnia. J Physiol Pharmacol. 1995;46:17–35. [PubMed] [Google Scholar]
  51. Vissing SF, Scherrer U, Victor RG. Stimulation of skin sympathetic nerve discharge by central command. Differential control of sympathetic outflow to skin and skeletal muscle during static exercise. Circ Res. 1991;69:228–238. doi: 10.1161/01.res.69.1.228. [DOI] [PubMed] [Google Scholar]
  52. Wallin BG, Charkoudian N. Sympathetic neural control of integrated cardiovascular function: insights from measurement of human sympathetic nerve activity. Muscle Nerve. 2007;36:595–614. doi: 10.1002/mus.20831. [DOI] [PubMed] [Google Scholar]
  53. Wallin BG, Delius W, Hagbarth K-E. Comparison of sympathetic nerve activity in normotensive and hypertensive subjects. Circ Res. 1973;33:9–21. doi: 10.1161/01.res.33.1.9. [DOI] [PubMed] [Google Scholar]
  54. Wallin G, Delius W, Hagbarth K-E. Regional control of sympathetic outflow in human skin and muscle nerves. In: Umbach W, Koepchen HP, editors. Central Rhythmic and Regulation. Stuttgart: Hippokrates Verlag; 1974. pp. 190–195. [Google Scholar]
  55. Westerhof BE, Gisolf J, Karemaker JM, Wesseling KH, Secher NH, van Lieshout JJ. Time course analysis of baroreflex sensitivity during postural stress. Am J Physiol Heart Circ Physiol. 2006;291:H2864–H2874. doi: 10.1152/ajpheart.01024.2005. [DOI] [PubMed] [Google Scholar]

Articles from The Journal of Physiology are provided here courtesy of The Physiological Society

RESOURCES