Conformational Transitions and Convergence of Absolute Binding Free Energy Calculations

Abstract

The Binding Energy Distribution Analysis Method (BEDAM) is employed to compute the standard binding free energies of a series of ligands to a FK506 binding protein (FKBP12) with implicit solvation. Binding free energy estimates are in reasonably good agreement with experimental affinities. The conformations of the complexes identified by the simulations are in good agreement with crystallographic data, which was not used to restrain ligand orientations. The BEDAM method is based on λ -hopping Hamiltonian parallel Replica Exchange (HREM) molecular dynamics conformational sampling, the OPLS-AA/AGBNP2 effective potential, and multi-state free energy estimators (MBAR). Achieving converged and accurate results depends on all of these elements of the calculation. Convergence of the binding free energy is tied to the level of convergence of binding energy distributions at critical intermediate states where bound and unbound states are at equilibrium, and where the rate of binding/unbinding conformational transitions is maximal. This finding mirrors similar observations in the context of order/disorder transitions as for example in protein folding. Insights concerning the physical mechanism of ligand binding and unbinding are obtained. Convergence for the largest FK506 ligand is achieved only after imposing strict conformational restraints, which however require accurate prior structural knowledge of the structure of the complex. The analytical AGBNP2 model is found to underestimate the magnitude of the hydrophobic driving force towards binding in these systems characterized by loosely packed protein-ligand binding interfaces. Rescoring of the binding energies using a numerical surface area model corrects this deficiency. This study illustrates the complex interplay between energy models, exploration of conformational space, and free energy estimators needed to obtain robust estimates from binding free energy calculations.

Introduction

Molecular recognition is essential for virtually all biological processes. By binding to specific sites, medicinal compounds modulate the specific activity of protein targets; the main aim of structure-based drug design is to select compounds with both specific and strong affinity for their target receptors. Accurate computational prediction of the affinity of small molecules to proteins remains a very difficult task.^1–3 Docking programs that predict the orientation of a small molecule in the three-dimensional structure of the receptor have become a widely used tool for structure-based rational drug design.^4–7 Docking and scoring approaches are useful to screen large databases of ligand candidates, but are not considered sufficiently accurate for quantitative estimation of the binding free energies.⁸ One reason is that docking-based methods do not generally treat entropic effects and receptor flexibility, which have a significant effect on binding affinities. Physics based-models for binding,^9,10 which use realistic representations of molecular interactions and atomic motion, have the potential to include these important effects.

Statistical mechanics provides the framework to derive a comprehensive theory for the binding free energy of ligands to a protein.¹¹ Simplified formulations of this theory, such as the Linear Interaction Energy (LIE)^12–14 models, have been proposed. Other so-called end point methods such as MM/PBSA and Mining Minima (MM)^15,16 include explicit or implicit approximations and simplifications. Even the most advanced free energy models available based on molecular dynamics (MD) multi-state sampling and state of the art atomistic force fields, are affected by inaccuracies due to limitations of potential models and conformational sampling, as well as uncertainties regarding the relevant physiochemical states of the system (solution conditions, protonation state and tautomeric state assignments, etc.).¹⁷ Despite these challenges, MD-based free energy models remain a key topic of development given their potential to achieve sufficient realism to tackle detailed aspects of ligand optimization, and to address questions such as drug specificity and resistance.

Applications of free energy methods to pharmaceutical design have historically focused on computing the relative binding free energy between two related compounds to the same receptor. These models, commonly based on Free Energy Perturbation (FEP) or Thermodynamic Integration free energy estimators,^18–21 are most suitable for sets of very similar ligands sharing the same binding mode. There are, however, many instances where one is interested in estimating binding affinities of sets of structurally diverse molecules such as when searching for novel scaffolds or comparing binding to different mutant forms of the receptor. In recent years, double decoupling free energy methodologies that allow the computation of absolute, rather than relative, binding free energies have been reported.^22–25 Early studies in this area have often been proofs of principle,^26,27 and recent applied work has focused on simple model systems.^28,29 A critical aspect of these methods is the level of conformational sampling, which needs to be capable of generating a sufficiently comprehensive representation of protein-ligand conformations, including possibly rearrangements of the receptor.^2,22,30,31

In this paper, we analyze the performance of the Binding Energy Distribution Analysis Method (BEDAM), an absolute binding free energy method we recently proposed,²⁹ on the calculation of the standard binding free energies of a series of inhibitors of the FKBP receptor.³² BEDAM is based on the statistical analysis of probability distributions of the effective binding energy of the complex as a function of a thermodynamic progress variable, λ, connecting the coupled and decoupled states of the complex. The methodology is aimed at not only providing reasonable affinity estimates but also at providing physical insights concerning the driving forces for or against binding. The method makes use of parallel Hamiltonian replica exchange (HREMD) to enhance conformational sampling efficiency to search for the most effective binding mode as well as to explore multiple binding modes as a function of λ. Advanced statistical reweighting techniques^33–35 are used to optimally merge data obtained along the binding thermodynamic path. In BEDAM solvation effects are treated using the analytical generalized Born plus non-polar (AGBNP) implicit solvent model,^36,37 which is particularly suitable for binding applications.

One aim of this study is to validate the BEDAM computational protocol, previously tested on fragment binding to a model binding site,²⁹ to more complex systems closer to actual pharmaceutical design. We selected a validation system composed of a series of inhibitors of a FK506 binding protein (FKBP12). FKBP12 is a 12-kD immunophilin enzyme which catalyzes the cis-trans isomerization of peptide bonds. Inhibitors bind in the relatively shallow and solvent-exposed hydrophobic pocket.³⁸ The FKBP system is a suitable target for this purpose as it is relatively well understood and has been studied before by double decoupling free energy methods.^39,40 The larger size of the ligands is one obvious difference between this system and the mutant T4 lysozyme system we studied previously.²⁹ As it involves alchemically creating protein-ligand interactions at the expense of hydration interactions, the magnitude of the perturbation to the system increases with ligand size. The mixed hydrophobic and polar composition of the ligands and of the receptor binding pocket, and their partial exposure to solvent also contribute to the added complexity of this system relative to earlier tests.

We evaluate on this system a loose restraining scheme of the kind that would be employed when structural information regarding the complexes is either lacking or uncertain. The protocol employed here does not restrain the complex to the crystallographic conformation; the ligand is free to explore all orientations and a wide variety of positions in the binding site, and both the ligand and the receptor are modeled flexibly. This choice, although a source of added complexity, reflects our interest in evaluating the ability of the BEDAM method to predict the main binding mode, together with other binding modes if present, and in studying the physical mechanisms of ligand binding and unbinding. An approach which does not rely as much on crystallographic information is conceivably better suited for cases when information about the structure of the complex is uncertain or not available, or when, such as in fragment screening,^41–43 multiple binding poses contribute to binding. On the other hand it has been shown that including available structural information, implemented in terms of configurational restraints, leads to better convergence of binding free energies.^17,44 Previous binding free energy studies of the FKBP12 target,^39,40 in particular, employed a conservative restraining approach, using the knowledge of the structures of the complexes to restrain sampling near the bound structures of the protein-ligand complexes. In this study we address the relationship between the level of restraining used to define the binding site volume and the ease of convergence of absolute binding free energy calculations. The ability to follow the mechanism of association is one benefit of conducting this kind of binding free energy calculations in a less restrained fashion. We illustrate examples of association events that could be relevant to the physical mechanism of binding.

The study of the role of the binding reorganization free energy effects is also facilitated by a wider exploration of conformational space. It is often the case that both binding partners undergo substantial conformational changes upon binding. The corresponding reorganization free energy is recognized as an important component of the binding free energy⁴⁵ and a key factor needed to understand ligand affinity and specificity.⁴⁶ We have previously shown that conformational reorganization upon binding plays a pivotal role in cases, such as epitope-antibody binding,^47,48 in which there are small variations in the binding interface and most of the variations in binding affinities are due to differences in reorganization of the binding partners. Binding reorganization effects have been shown to be important in the FKBP12 system as well.^49,50 One question we would like to answer is to what extent the λ -hopping HREMD conformational sampling algorithm in BEDAM is capable of capturing binding reorganization effects, particularly those involving internal degrees of freedom of the receptor and the ligand which are not directly accelerated by the method.

We find that in this regime the convergence of the binding free energy is dominated by the rate of conformational transitions between bound and unbound macrostates of the complex, and that these transitions have the features of pseudo order/disorder phase transition analogous to protein folding equilibria. The rate of conformational transitions depends mainly on the conformational sampling algorithm and, conversely, optimization of the λ schedule does not necessarily lead to an improvement of the convergence rate of the binding free energy. We believe that these are general issues applicable to many alchemical binding free energy methods.

Theory and Methods

The Binding Energy Distribution Analysis Method (BEDAM)

The BEDAM method²⁹ computes the binding free energy $\mathrm{\Delta }{F}_{AB}^{\circ }$ for the monovalent association of a receptor A and a ligand B by means of the expression

$$\mathrm{\Delta }{F}_{AB}^{\circ }=-\mathit{kT}ln\left[C^{\circ }{V}_{\text{site}}\int du{p}_0(u)e^{-\beta u}\right]=-\mathit{kT}ln{C}^{\circ }{V}_{\text{site}}+\mathrm{\Delta }{F}_{AB},$$ (1)

which follows, without approximations, from a well-established statistical mechanics theory of molecular association,¹¹ where β = 1/kT, C∘ is the standard concentration of ligand molecules (set to C∘ = 1 M, or equivalently 1,668 Å⁻³), V_site is the volume of the binding site, and p₀(u) is the probability distribution of binding energies collected in an appropriate decoupled ensemble of conformations in which the ligand is confined in the binding site while the receptor and the ligand are both interacting only with the solvent continuum and not with each other. The binding energy

$$u({\mathbf{r}}_B,{\mathbf{r}}_A)=V({\mathbf{r}}_B,{\mathbf{r}}_A)-V({\mathbf{r}}_B)-V({\mathbf{r}}_A)$$ (2)

is defined for each conformation r = (r_B, r_A) of the complex as the difference between the effective potential energies V (r) of the associated and separated conformations of the complex without conformational rearrangements. In our implementation BEDAM employs an effective potential in which the solvent is represented implicitly by means of the AGBNP2 implicit solvent model³⁷ together with the OPLS-AA^51,52 force field for covalent and non-bonded interatomic interactions.

Eq. (1) explicitly indicates that the standard binding free energy is the sum of two terms. The first term, −kT lnC∘V_site, represents the entropic work to transfer the ligand from the solution environment at concentration C∘ into the binding site of the complex. This term depends only on the standard state and the definition of the complex macrostate. The second term, ΔF_AB, involving the Boltzmann-weighted integral of p₀(u), corresponds to the work for turning on the interactions between the receptor and the ligand when the ligand is confined in the binding site region.²⁹ Eq. (1) also naturally leads to the the definition of a binding affinity density function k(u) = C∘V_site p₀(u) exp(−βu) in terms of which the binding constant is written as

$$K_{AB}=e^{-\beta \mathrm{\Delta }{F}_{AB}^{\circ }}=\int k(u)du.$$ (3)

Based on Eq. (3) the binding affinity density k(u) can be interpreted as a measure of the contribution of the conformations of the complex with the binding energy, u, to the binding constant.²⁹ We have shown that k(u) is proportional to p₁(u), the binding affinity density in the coupled ensemble of the complex, with a proportionality constant related to the binding free energy.²⁹

The larger the value of the integral in Eq. (1), the more favorable is the binding free energy. The magnitude of the p₀(u) distribution at positive, unfavorable, values of the binding energy u reflects the entropic thermodynamic driving force which opposes binding, whereas the tail at negative, favorable, binding energies measures the energetic gain for binding due to the formation of ligand-receptor interactions. The interplay between these two opposing forces ultimately determines the strength of binding. We found that the ability of BEDAM to explicitly include both favorable energetic gains and unfavorable entropic losses to be essential to properly reproduce experimental binding affinities in a challenging set of candidate ligands to T4 lysozyme receptors whose estimates of binding affinity failed by simplified docking & scoring approaches.⁵³

The accurate calculation of the important low energy tail of p₀(u) can not be accomplished by a brute-force collection of binding energy values from a simulation of the complex in the decoupled state because these are rarely sampled when the ligand is not guided by the interactions with the receptor. Instead we use biased sampling and parallel Hamiltonian Replica Exchange (HREM) in which swarms of coupled replicas of the system, differing in the value of an interaction parameter 0 ≤ λ ≤ 1 controlling the strength of ligand-receptor interactions, are simulated simultaneously. The replicas collectively sample a wide range of unfavorable, intermediate and favorable binding energies which are then unbiased and combined together by means of reweighting techniques.^34,35

BEDAM is based on biasing potentials of the form λ u(r) yielding a family of λ -dependent hybrid potentials of the form

$$V_{\lambda }(\mathbf{r})=V_0(\mathbf{r})+\lambda u(\mathbf{r}),$$ (4)

where

$$V_0(\mathbf{r})=V({\mathbf{r}}_B)+V({\mathbf{r}}_A),$$ (5)

is the potential energy function of the decoupled state. It is easy to see from Eqs. (2), (4), and (5) that V_{λ =1} corresponds to the effective potential energy of the coupled complex and V_{λ =0} corresponds to the state in which the receptor and ligand are not interacting (decoupled state). Intermediate values of λ trace an alchemical thermodynamic path connecting these two states. The binding free energy ΔF_AB is by definition the difference in free energy between these two states.

For later use we introduce here the reorganization free energy for binding $\mathrm{\Delta }{G}_{\mathit{reorg}}^{\circ }$ defined by the expression¹⁰

$$\mathrm{\Delta }{F}_{AB}^{\circ }={\langle u\rangle }_1+\mathrm{\Delta }{G}_{\mathit{reorg}}^{\circ }$$ (6)

where 〈u〉₁ is the average binding energy at λ = 1 and $\mathrm{\Delta }{F}_{AB}^{\circ }$ is the standard binding free energy.

Soft core implementation

To improve convergence of the free energy near λ = 0, in this work we employ a modified “soft-core” binding energy function,¹⁰ similar in spirit to a recently proposed approach,⁵⁴ of the form

$$u^{\prime }(\mathbf{r})=\{\begin{array}{ll}{u}_{max}tanh[u(\mathbf{r})/u_{max}],\hfill & u(\mathbf{r})>0\hfill \\ u(\mathbf{r})\hfill & u(\mathbf{r})\le 0\hfill \end{array},$$ (7)

where u_max is some large positive value (set in this work as 1, 000 kcal/mol). This modified binding energy function, which is used in place of the actual binding energy function [Eq. (2)] wherever it appears, caps the maximum value of the binding energy while leaving unchanged the value of favorable binding energies. This serves two purposes. One purpose is to improve sampling at small λ’s by letting atoms to pass through each other without clashing. This is possible because for values of λ around 1/u_max or smaller λu′(r) in Eq. (4) is guaranteed to be comparable to thermal energy even for conformations with atomic overlaps and large and unfavorable binding energies. In contrast, with the original definition of the binding energy, only at λ = 0 can atoms pass through each other without clashing. In addition, the soft-core binding energy function simplifies the choice of the λ schedule near λ = 0. As discussed below, overlaps between neighboring binding energy distributions are necessary for free energy estimation. The large range of binding energies sampled in the positive range and the rate of change of the binding energy distributions as a function of λ for small λ, make it difficult to select a λ schedule near λ = 0 to ensure sufficient overlaps between binding energy distributions. The distributions p_λ (u′) of the soft core binding energy are instead much better behaved because the range of soft core binding energies has a finite upper limit (u′ = u_max) for any conformation of the complex. Moreover, because the corresponding replicas can sample equally well conformations with atomic overlaps, it is guaranteed that distributions p_λ (u′) for values of λ on the order of 1/u_max or smaller will overlap with the distribution at λ = 0. In this work we set the minimum non-zero value of λ as 1/u_max and confirmed numerically that the corresponding binding energy distribution overlaps significantly with p₀(u).

It is evident from Eqs. (4) that λ = 0 identifies the decoupled state regardless of the definition of the binding energy. However the potential energy function of the coupled state V₁ = V₀ + u is in principle affected by whether we employ Eq. (2) or Eq. (7) to represent the binding energy. Therefore we must consider as to what degree the binding free energy, which measures the free energy difference between these two states, is affected by the introduction of the soft core binding energy function. Intuitively the binding free energy can not significantly be affected by the soft core function if u_max is very large compared to thermal energy (we set u_max = 1, 000 kcal/mol). The alternative would imply that the binding affinity depends on the details of the interatomic potentials at high energies which are not known accurately and much less modeled correctly by classical force fields. Indeed, the λ = 1 ensemble with the soft core function is virtually indistinguishable from the original λ = 1 ensemble because the probability of sampling large positive binding energies, which are the only cases in which the original and soft core binding energy functions differ substantially, is infinitesimally small at λ = 1. A study including theoretical considerations and numerical tests of hard-core versus soft-core functions will be reported in a separate publication.

Free Energy Estimation

In this work we employ the multistate Bennett acceptance ratio estimator (MBAR)^35,55 to estimate binding energy distributions and standard binding free energies from binding energy samples obtained from the HREM simulations. Based on Eq. (4) the binding free energy ΔF_AB, that is the standard binding free energy minus that standard state term −kT lnC∘V_site, is given by the free energy difference between the λ = 1 and λ = 0 states with potential energy functions defined by Eq. (4). This is a consequence of having selected biasing potentials, aimed at properly sampling the p₀(u) distribution at low binding energies, of the form λ u – noting, however, that in general BEDAM computes the binding free energy based on Eq. (1) where p₀(u) is estimated by the application of any suitable series of biasing potentials not necessarily connecting the decoupled and coupled states. With the present setup it is nevertheless convenient to compute the binding free energy directly from the MBAR dimensionless free energies f̂_λ using the relationship

$$\mathrm{\Delta }{F}_{AB}=kT({\widehat{f}}_1-{\widehat{f}}_0).$$ (8)

The MBAR dimensionless free energies f̂_λ = −ln Z_λ are defined as the negative of the logarithm of the λ -dependent biased partition functions Z_λ. In this case the dimensionless free energies are estimated by the self-consistent solution of the set of equations³⁵

$${\widehat{f}}_i=-ln\sum _{j=1}^K\sum _{n=1}^{N_j}\frac{exp\left[-\beta {\lambda }_i{u}_{jn}\right]}{{\sum }_{k=1}^K{N}_{k}exp\left[{\widehat{f}}_k-\beta {\lambda }_k{u}_{jn}\right]}$$ (9)

where f̂_i = f̂_λi, u_jn is the n-th binding energy sample from replica j sampled with biasing potential λ_j, K is the number of replicas and N _j is the total number of binding energy samples from replica j. For the MBAR analysis we employed the code provided by John Chodera and Michael Shirts.³⁵ Block bootstrap analysis⁵⁶ with 10 blocks and 8 resampling trials was used to estimate statistical uncertainties.

Computational Details

BEDAM calculations were performed for 7 ligands of FKBP (Figure 1). This is the same ligand series investigated in prior binding free energy studies.^39,40 The initial structure of the complexes with ligand 8, 9, and 20 were retrieved from the PDB (PDB ID 1FKG, 1FKH, and 1FKJ respectively). The starting structures for the receptor of the other complexes were built based upon the existing crystal structure of 1FKG. The crystallographic water molecules and ions were removed. Ionization states were assigned considering neutral pH, histidines were not protonated and hydrogen atoms were added. Cα-atoms of the FKBP receptor were restrained around the X-ray original coordinates using an isotropic quadratic function with force constant k _f = 0.6 kcal/mol/Ų, which allows a motion of 4 Å around the original positions at the temperature used in the simulations. Free motion of all the remaining atoms was allowed. This restraining scheme leads to convergence of the binding free energies while it is sufficiently relaxed to encompass all likely conformations of the complex. All the simulations were carried out using the IMPACT program.⁵⁷ The RMSD’s of the ligand conformations were calculated including the atoms of the core (C1-C2-C3-C4-C5-C6-N7-C8) only.

Figure 1.

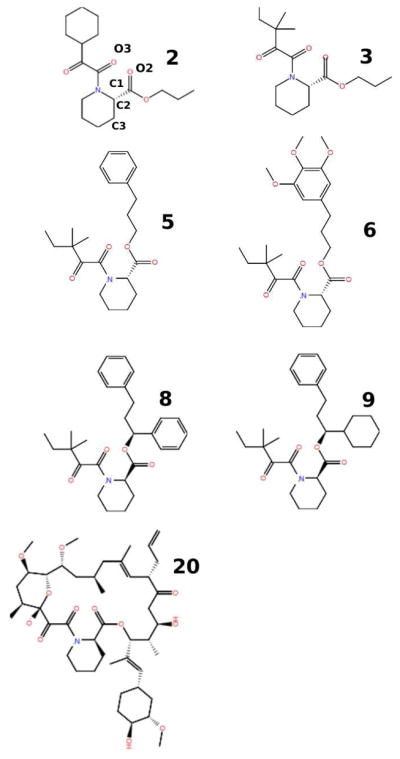
Structural formulas of the seven ligands of FKBP12 investigated in this work. Ligand 20 (bottom right) also known as Tacrolimus or FK506 is an immunosuppressive drug. Atom labels are shown for ligand 2.

All the complexes were minimized and thermalized at 300 K using the same procedure. λ -biased molecular dynamics simulations were performed for 2 ns per replica (~280 ns of total computation time for all complexes) with a time step of 1.5 fs at 300 K. Fifteen replicas at λ = 0, 10⁻³, 2 ×10⁻³, 4 ×10⁻³, 6 ×10⁻³, 8 ×10⁻³, 10⁻², 2 ×10⁻², 6 ×10⁻²,0.1, 0.25, 0.5, 0.75, 0.9 and 1 were used for all ligands. For ligand 20 we also employed 36 replicas at λ = 0, 10⁻³, 2 ×10⁻³, 4 × 10⁻³, 6 × 10⁻³, 8 × 10⁻³, 10⁻², 2 × 10⁻², 6 × 10⁻², 0.1, 0.25, 0.30, 0.45, 0.50, 0.55, 0.60, 0.62, 0.65, 0.68, 0.70, 0.72, 0.74, 0.75, 0.77, 0.80, 0.82, 0.85, 0.86, 0.87, 0.88, 0.89, 0.90, 0.92, 0.94, 0.97 and 1.0. We employed the OPLS-AA⁵¹ force field with the AGBNP2 implicit solvent model.^36,37 The AGBNP2 model includes a novel first solvation shell hydration function to improve the balance between solute-solute and solute-solvent interactions that makes it more suitable for free energy calculations. Bond lengths with hydrogen atoms were constrained using SHAKE. A 12 Å residue-based cutoff was imposed both on direct and generalized Born pair interactions. Binding energies for protein-ligand binding were calculated every 1 ps during the second nanosecond of the simulation. The dataset for each complex consisted of 15,000 binding energy values corresponding to 1,000 samples for each of 15 HREMD replicas.

The replicas were coupled using an Hamiltonian Replica Exchange Method (HREMD) previously described, which was shown to significantly improve conformational sampling efficiency.²⁹ As further discussed below the λ schedule was determined so as to insure overlaps between neighboring binding energy distributions and frequent accepted λ exchanges (acceptance ratio of at least 50%).

The binding site volume^11,58 was defined in terms of flat-bottom harmonic potentials as previously described.²⁹ Briefly, an indicator function is introduced of the form I(r, cosθ,φ) = exp[−β ω(r, cosθ,φ)] where ω(r, cosθ,φ) is a product of flat-harmonic potentials acting on the position, expressed in polar coordinates, of a reference atom of the ligand with respect to the position of the Cα atoms of three reference residues of the receptor.⁵⁹ The distance restraint potential between atom C2 of the ligand (see Figure 1) and the Cα atom of residue 55 was centered at 5 Å distance with a 5 Å tolerance on either side, beyond these limits a quadratic function penalizes the distances with a force constant of 3 kcal/mol/Ų. The flat-bottom harmonic restraint potential for the cosine of the angle θ between the reference ligand atom, the Cα atom of residue 55, and the Cα atom of residue 46 was centered at cosθ = 0.67 with a 0.3 tolerance on both sides and a force constant of 100 kcal/mol beyond that. The restraint potential for the dihedral angle defined by the three atoms described above plus the Cα atom of residue 44 was centered at φ = 32° with a tolerance of 50° on either side and a force constant of 0.1 kcal/mol/deg beyond that. The volume of the binding site (V_site = 504 ų) given by the integral of the indicator function as defined was computed analytically. The resulting standard state term is computed as −kT lnC∘V_site = 0.71 kcal/mol. For ligand 20 we also employed a stricter definition of the complex by imposing additional limits on the orientation of the ligand in the binding site. These were implemented in terms of flat-bottom harmonic potentials similar to the those given above based on one bond angle and two dihedral angles involving two additional reference atoms (C1 and C3, see Figure 1) of the ligand as described⁵⁹ centered on the crystallographic orientation (1FKJ). The volume of this more restrictive binding site volume and the corresponding standard state free energy term were computed as 43 ų and 2.71 kcal/mol, respectively.

A rescoring procedure was conducted to overcome a deficiency of the AGBNP2 surface area model. In AGBNP2 the free energy of cavity formation is modeled in terms of the solute surface area, which is calculated taking the analytical derivative of the solute volume. This analytical model is fast and yields stable MD trajectories but is not particularly accurate for these systems relative to numerical molecular surface or solvent accessible surface area evaluations.³⁷ As sufficiently accurate surface area models with the desired characteristics are currently lacking, in this work we sought to replace in postproccessing the cavity term, denoted here as G_cav(1), of the AGBNP2 model³⁷ with a more accurate model G_cav(2) = γ₂A_SASA where A_SASA is the solvent accessible surface area of the solute evaluated numerically (we used the SURFV⁶⁰ program) and γ₍₂₎ is an adjustable surface tension parameter. We estimated the change in binding free energy, ΔΔF_AB, in going from the original cavity free energy model to the numerical SASA cavity free energy model assuming first order perturbation theory, by rescoring the binding energies of the conformations of the complex collected at λ = 1:

$$\mathrm{\Delta }\mathrm{\Delta }{F}_{AB}\cong {\langle u_{(2)}-u_{(1)}\rangle }_1={\gamma }_{(2)}{\langle \mathrm{\Delta }{A}_{\text{SASA}}\rangle }_1-{\langle \mathrm{\Delta }{G}_{\text{cav}}(1)\rangle }_1,$$ (10)

where u₍₁₎ and u₍₂₎ represent, respectively, the binding energies of each complex conformation evaluated with the original and numerical cavity free energy models, ΔA_SASA = A_SASA(AB) − A_SASA(A) −A_SASA(B) is the change in surface area in going from the separated ligand and receptor to the complexed conformation, and ΔG_cav(1) is the corresponding change in cavity free energy as computed using the original model. To assign a value for the surface tension coefficient γ₍₂₎, Eq. (10) was fitted to the residuals between the binding free energies computed with the original energy model and the experimental affinities. We obtained γ₍₂₎ = 0.051 kcal/mol/Ų, a value in good agreement with an earlier independent analysis of cavity hydration free energies.⁶¹

Results

FKBP ligands

This study covers a ligand set composed of seven related inhibitors (Figure 1) of FKBP12 (Figure 2) with known experimental binding free energies.³² These ligands were originally developed by stepwise addition of hydrophobic rings to a central core in an attempt to increase potency. The compounds contain from one to three rings and several different functional groups commonly encountered in drug-like molecules. The inhibitors have moderate molecular weight (~450–500 u), with the exception of FK506 (ligand 20 in Figure 1), a natural inhibitor of FKBP12 with an unusually large molecular weight (804 u) compared to most drug-like molecules. The measured binding free energies of the compounds range from low nanomolar to micromolar (Table 1). Crystal structures are available for three of the inhibitors (1FKG for ligand 8, 1FKH for ligand 9, and 1FKJ for ligand 20).³² These show close similarity between the binding modes of the core of the ligands, as represented in Figure 2 for ligand 9. Two carbonyl oxygen atoms O2 and O3 (see Figure 1 ligand 2, for atom labeling), of the ligand core form two hydrogen bonds with Tyr82 and Ile56, hydrophobic moieties form π-π contacts with Tyr82 and Phe46, and other generally hydrophobic contacts with Gln53, Glu54, Val55, Ile56, His87, and Ile90 of the receptor.

Figure 2.

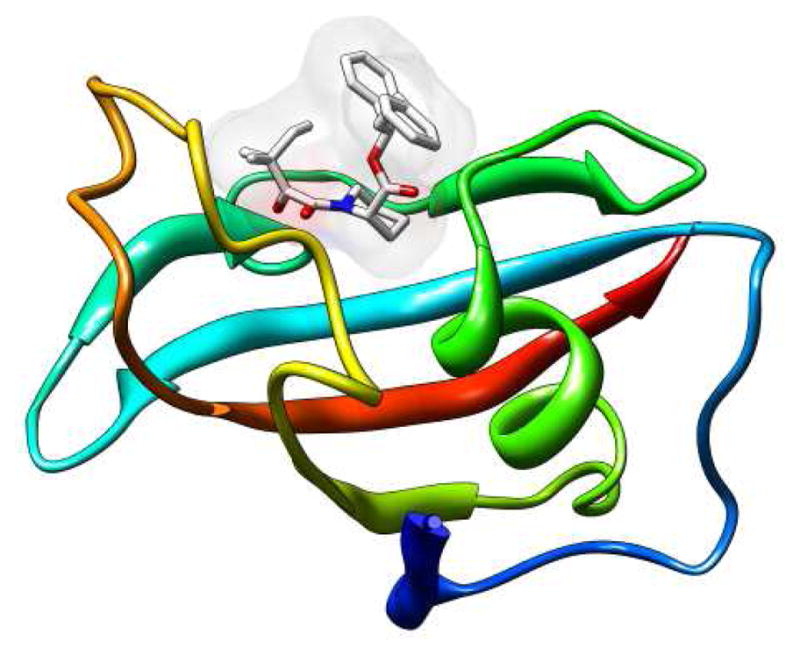
Representation of the crystal structure (PDB ID 1FKJ) of the complex of FKBP12 with ligand 9. The receptor is shown in cartoon representation and the ligand in wire representation.

Table 1.

Experimental and calculated standard binding free energies of the complexes of FKBP12 with the ligands investigated. The “S-Calc” column lists the surface area-corrected binding free energies (see text). The last two columns report the decomposition of the S-Calc estimates into the average binding energy and reorganization free energy, respectively.

Ligand	Expta	Calca	S-Calca	〈u〉1a	$\mathrm{\Delta }{G}_{\text{reorg}}^{\circ }$ a
2	−7.80±0.1	−2.54±0.05	−7.61±0.05	−28.14	20.53
3	−8.40±0.1	−3.97±0.03	−7.83±0.04	−28.40	20.57
5	−9.50.±0.1	−3.95±0.04	−7.91±0.04	−30.44	22.53
6	−10.80±0.3	−3.82±0.05	−10.95±0.05	−34.47	23.52
8	−10.90 ±0.1	−4.80±0.01	−10.66±0.02	−35.97	25.31
9	−11.10±0.2	−6.25±0.02	−12.55±0.03	−36.05	23.50
20b	−12.70±0.2	−0.93±0.05	−13.43±0.03	−42.05	28.62

^ain kcal/mol.

^bObtained with a stricter binding site definition (see text)

Binding free energy estimates

The computed binding free energies obtained from BEDAM (see Methods) are shown in the second column of Table 1 compared to the available measurements.³² As further discussed below, because convergence could not be achieved with the standard settings, the calculated binding free energy for ligand 20 reported in Table 1 was obtained using a different, stricter, binding site definition than for the other ligands. The computed affinities achieve good discrimination between good binders and weak binders. The confidence ranges reported in Table 1, estimated using the bootstrap method, indicate robustness of the free energy estimates with respect to variations in the binding energy data. However these probably underestimate the actual statistical uncertainties due to the difficulty of reliably infering them from a finite set of samples.

The calculated standard binding free energies are reasonably correlated with the experimental values (R² = 0.59, not including ligand 20). However, it is clear that the magnitude of the binding free energies are underestimated by the BEDAM model. A likely cause of the discrepancy is the inaccurate representation of changes in non-polar solvation upon binding. To test this we have computed the surface area loss upon binding using an accurate numerical method (see Methods) for all of the trajectory frames corresponding to the coupled state (λ = 1) and compared these to the surface area loss estimates produced by AGBNP2. We found that on average the AGBNP2 surface area model captures only about half of the surface area loss. This result is consistent with the nature of the analytical surface area model implemented in AGBNP2, which is based on an atomic radius offset of 0.5 Å, significantly smaller than the conventional value of 1.4 Å commonly used for the solvent accessible surface. Because the surfaces of each of the binding partners do not sufficiently extend over the region in between the two molecules, the AGBNP2 analytical surface model incorrectly represents as solvent exposed some of the atoms facing voids within the binding interface too small to contain water molecules. This results in the underestimation of the surface area loss of these atoms as they go from solvent-exposed in the conformation to buried in the bound conformation. Using the procedure described in the Methods section we have rescored the binding free energies using a more accurate surface area model and determined an optimal value of γ = 0.051 kcal/mol/Ų for the surface tension coefficient. This value is in good agreement with the surface tension coefficient to γ = 0.058 kcal/mol/Ų obtained from the cavity hydration free energies of a series of alkanes.⁶¹ This observation further supports the hypothesis that the discrepancies between the measured and computed affinities of the FKBP inhibitors is physically related to the inaccurate representation of hydrophobic driving forces, and that a more accurate geometrical description of the surface area loss upon binding leads to better quantitative predictions.

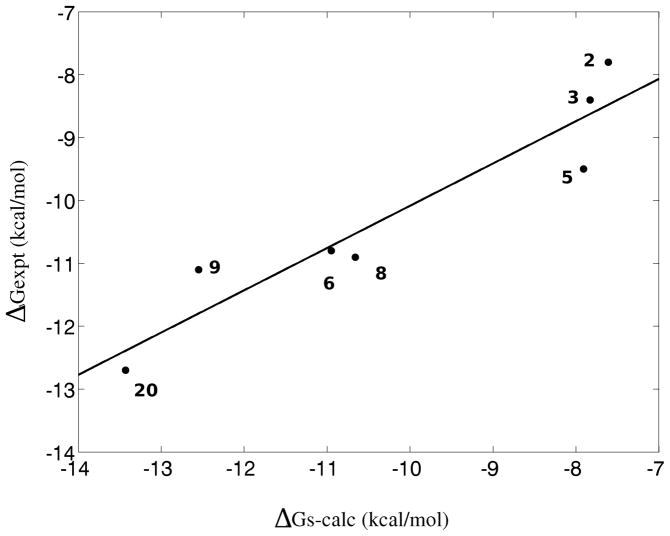
Indeed the surface-rescored binding free energies, shown in Table 1, are in overall good agreement with the experimentally measured affinities and the correlation with the experiments is high (R² = 0.88) as shown in Figure 3. Very good agreement is obtained for ligand 2 with a computed binding free energy of −7.84 kcal/mol compared to the experimental value of −7.80 kcal/mol (Table 1). This ligand resulted as an outlier in earlier work.³⁹ The binding free energy of ligands 3 and 4 follow the same trend towards stronger affinities as in the experiments but with significantly smaller variations. Indeed ligands 2, 3, and 5 are estimated as having nearly equivalent affinities compared to an experimental spread of approximately 1.7 kcal/mol. The higher affinities of the second set of ligands (6, 8, and 9) are well reproduced with the exception of the strongest binder, ligand 9, whose computational estimate (−12.7 kcal/mol) is off by 1.6 kcal/mol relative to the experimental binding free energy (−11.1 kcal/mol). The agreement for ligand 20 is very good; a large surface area correction is obtained for this ligand consistent with its much larger surface area relative to the other ligands. The trend observed experimentally towards higher affinities in relation to increase in size and number of cycles on the ester functionality of the inhibitors is reproduced by the calculations. The predicted rank order is in very good agreement with the measurements, with the exception of the inversion of ligands 6 and 8 which have very similar predicted binding free energies but the experimental values differ by ~1 kcal/mol. Overall, the quality of the agreement between calculations and experimental measurements is sufficiently good to give us confidence that the computational model appropriately includes the main physical driving forces and that it can be used to extract useful insights into the thermodynamics and mechanism of the binding process.

Figure 3.

Correlation plot between calculated and experimental standard binding free energies of the seven FKBP complexes studied. The line represents a least-squared fit to the data.

Thermodynamic Decomposition

Thermodynamic decomposition¹⁰ (see Methods) of the computed binding free energies into the average binding energy in the coupled state (〈u〉₁) and the reorganization free energy ( $\mathrm{\Delta }{G}_{\text{reorg}}^{\circ }$) (Table 1), reveals that the trend towards greater affinities in going from ligand 2 to ligand 20 is primarily driven by stronger ligand-receptor interactions. For example the computed average binding energy 〈u〉₁ of ligand 2 is approximately −28 kcal/mol compared to −42 kcal/mol for ligand 20. This trend is consistent with the increased number of mainly hydrophobic contacts between the ester sidechain of the larger ligands and the receptor.

This favorable energetic driving force towards binding is opposed by a reorganization free energy loss (Table 1), which increases in magnitude with increasing ligand size. The reorganization free energy term measures the unfavorable work necessary to remodel the unbound conformational ensembles of the ligand and the receptor in order to form favorable interactions in the bound state, and it necessarily opposes binding because in the absence of receptor-ligand interactions the lig-and and the receptor would spontaneously return to their unbound states at lower free energy. The reorganization free energy cost can in turn be thought of as originating from both configurational entropy losses and energetic strain of the ligand and receptor in solution, while thermodynamic effects due to the solvent are implicitly included by the implicit free energy model of solvation.^10,62 In the context of an implicit solvent model the entropic cost is in part due to the loss of translational and orientational freedom of the ligand as it is being localized into the binding site of the receptor. The receptor and especially the larger and more flexible ligands undergo additional conformational entropy losses to mutually adapt their conformations in order to form favorable interactions. Bound conformations can also be disfavored energetically relative to their more relaxed unbound conformations in solution. This energetic strain opposes binding and further reduces the effect of favorable receptor-ligand interactions. As the data in Table 1 shows, the reorganization free energy grows nearly monotonically from ligand 2 to ligand 20 consistent with increasing ligand size and flexibility.

Choice of λ -schedule

The choice of the number of replicas and their λ assignments affects BEDAM calculations in two related ways. To estimate the binding free energy it is believed to be necessary that an unbroken sequence of overlaps between the binding energy distributions p_λ (u) be constructed between λ = 0 (the decoupled state) and λ = 1 (the coupled state). So the choice of the λ -schedule must meet this minimum requirement.⁶³ A larger density of replicas however is beneficial because it increases the amount of overlap between the distributions and allows us to obtain reliable free energy estimates with fewer samples especially when using multi-state approaches such as MBAR.³⁵ The choice of the λ schedule also affects the acceptance ratio of λ -exchanges in the HREM conformational sampling scheme. λ -exchanges are accepted with probability min[1, exp(−β Δλ Δu)]²⁹ where Δλ is the difference in λ’s being exchanged and Δu is the difference in binding energies between the replicas exchanging them. Statistically, the magnitude of both of these quantities tends to decrease as overlaps between binding energy distributions increase thereby making exchanges more likely. It follows that monitoring the extent of diffusion in λ -space of HREM replicas is also equivalent to monitoring the level of overlaps between binding energy distributions and ultimately the quality of the selected λ schedule.

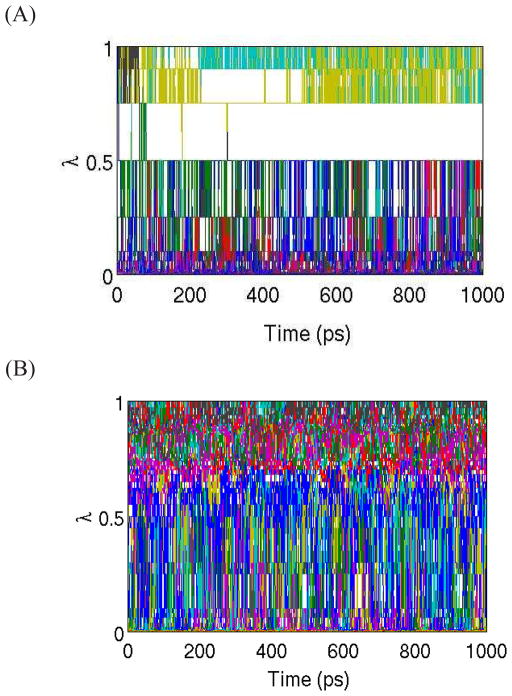
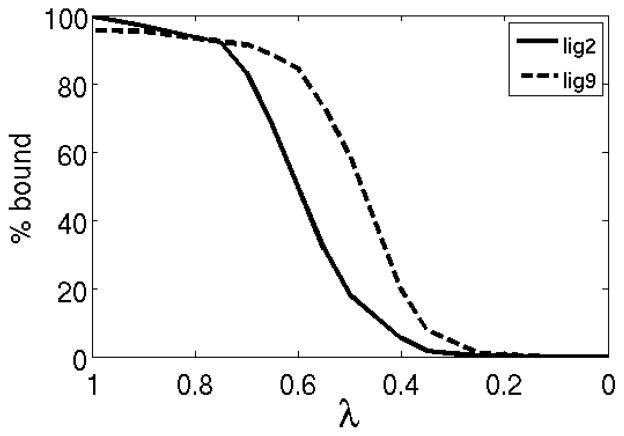
Analysis of the HREMD data shows that λ space is well explored by most of the 15 replicas of ligands 2 to 9, although exchange bottlenecks can be seen at specific λ’s as for example with ligand 2 between λ = 0.5 and 0.75 consistent with the relatively small overlap between the corresponding binding energy distributions (Figure 4). In contrast, the diffusion in λ space of the complex with ligand 20 is very limited. As shown in Figure 5A, replicas very rarely cross the large gap in λ space between λ = 0.5 and λ = 0.75. The reason for this is that the corresponding distributions do not overlap to any significant extent. This is expected because the complex with ligand 20 explores a wider range of binding energies requiring more intermediate λ’s to cover it appropriately. We found that 36 replicas were sufficient to remove gaps in λ exchanges (Figure 5B) for this complex. Nevertheless, it is clear from the patterns of color mixing in Figure 5B that, unlike those for ligands 2–9, replicas for ligand 20 are divided into two disjoint groups; those that tend to visit only lower values of λ and those that tend to visit only high values of λ. This is because, even though local λ exchanges are promoted by a larger distribution of overlaps, global diffusion of replicas in λ space also depends on the ability of replicas to undergo conformational transitions.

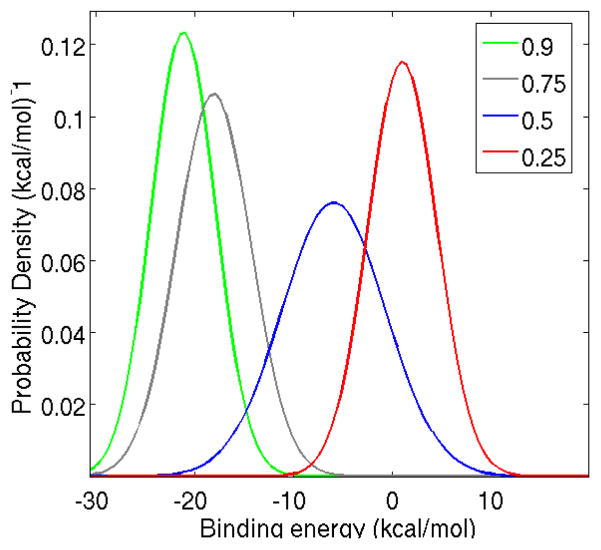
Figure 4.

Binding energy probability densities for the complex with ligand 2 at λ = 0.25, 0.5, 0.75, and 0.9. The amount of overlap between these distributions, which is important for accurate binding free energy estimation, is reasonably good with the distribution at the critical value λ_1/2 = 0.5 being wider than the others and acting as a bridge between the other distributions.

Figure 5.

Time evolution of λ for each of the HREM replicas of ligand 20 with 15 replicas (A) and with 36 replicas (B). Each color corresponds to a different replica.

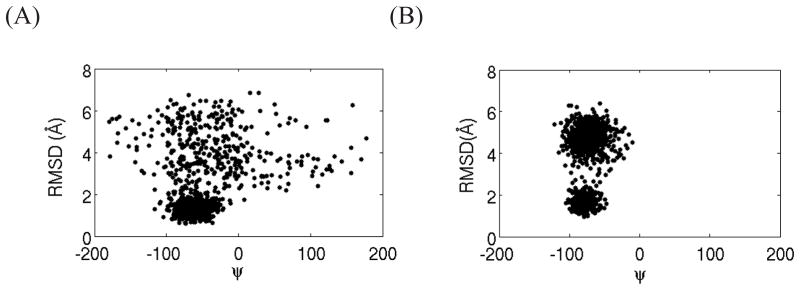
The binding site indicator function as defined (see Methods) does not restrict configurational and rotational degrees of freedom of the ligand, and the binding site volume is sufficiently wide for the occurrence of conformations of the complex distinct from the bound crystallographic binding mode, as for example shown in Figure 7 in terms of RMS deviation. Examples of these conformations, which we refer to as unbound, are shown in Figure 6A and B. (The bound/unbound macrostates of the complex should not be confused with the coupled, λ = 1, and uncoupled, λ = 0, thermodynamic states of the complex.) Replicas in unbound conformations with unfavorable binding energies tend to remain at small values of λ whereas replicas in bound conformations with favorable binding energies tend to remain at large values of λ. To explore the whole range of λ’s a replica needs to undergo conformational transitions from bound to unbound conformations or vice versa.⁶⁴ This issue, which strongly affects the convergence of binding free energy estimates, is further discussed below. We note here that, because it is mainly tied to the occurrence of conformational transitions, this type of convergence behavior is not directly addressable by simply increasing the density of λ replicas. It must be concluded therefore that an appropriate choice of the λ schedule is a necessary but not sufficient condition for obtaining converged binding free energy estimates.

Figure 7.

The binding energies vs. RMSD of the core region of the ligands relative to the corresponding crystal structures for the conformations of the complex with ligand 2 at λ = 0.5 (A) and with ligand 20 at λ = 0.65 (B).

Figure 6.

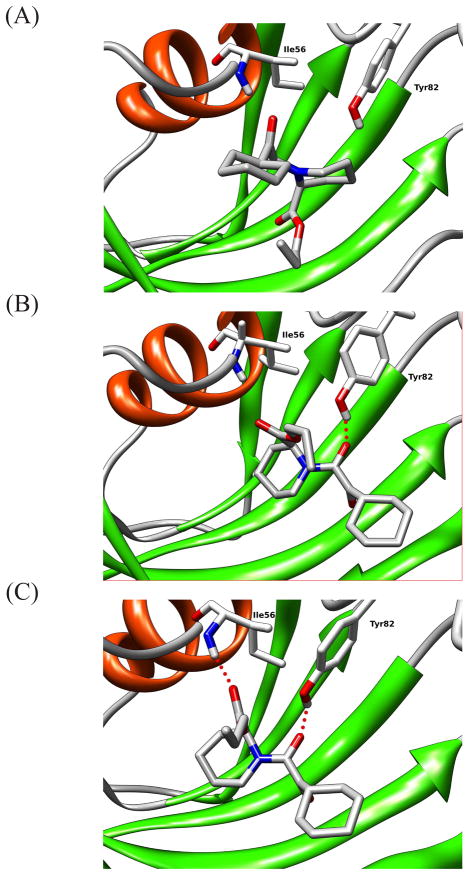
Transition mechanism from unbound conformations with no hydrogen bond (A) to the bound conformation with 2 hydrogen bonds in ligand 2 (C). The intermediate state has one hydrogen bond (B).

Discussion

The complexes of FKBP12 we investigated in this work provide very useful data to better understand the features and behavior of the BEDAM computational protocol and alchemical binding free energy calculations in general. One of the aims has been to explore the application of the method to pharmaceutical targets involving larger and more flexible ligands than the T4 Lysozyme system we have previously studied.²⁹ In this respect, the FKBP12 system is relatively well understood and has served as a useful validation target for absolute binding free energy methods.^39,40 The size and diversity of this ligand series (Figure 1), makes it unsuitable for relative binding free energy methods, which are more commonly employed than absolute binding free energy methods in applied research.¹ Although they are recognized as being more challenging, absolute binding free energy models are considered more suitable to study the fundamental thermodynamic components of the binding equilibrium.³ In particular, BEDAM emphasizes effects such as conformational entropy and reorganization, and the contribution of multiple binding modes,²⁹ issues that are not easily tackled with methods based on relative free energy perturbation approaches.

As it is often recognized, the performance of atomistic computational models primarily hinges on the quality of the energy function and the extent of conformational sampling. We have con-firmed a weakness of the AGBNP2 surface-based cavity free energy model, which underestimates the favorable hydrophobic component of binding. This limitation, which also affected our previous binding free energy estimates for the T4 lysozyme system,²⁹ is more noticeable in the present application given the larger amount of buried surface area involved. We were able to show that in this case a simple rescoring scheme of the binding energies in the coupled ensemble with a more accurate surface model is sufficient to recover binding free energies in good agreement with the experimental affinities. The validity of the surface area rescoring approach is further supported by the fact that it leads to an estimated value of the effective surface tension coefficient in agreement with independent estimates of the same quantity based on computed cavity free energies of alkanes.⁶¹ The general applicability of the surface rescoring scheme we employed here is uncertain. The method is implicitly based on first order perturbation theory, which assumes that changes in the surface area model affect binding energies without significantly altering conformational ensembles. It is conceivable therefore that these assumptions are not as valid for marginally stable complexes, or complexes characterized by multiple binding poses, whose conformational distributions are easily perturbed by changes in the potential energy model.

The BEDAM method employs advanced conformational sampling based on Hamiltonian replica exchange (HREM), a well established strategy to improve sampling in a variety of applications,^65–67 including binding free energy calculations.^2,68 We have shown²⁹ that HREM λ -hopping is in general quite efficient at exploring intermolecular degrees of freedom, and specifically the position and orientation of the ligand relative to the receptor. This is understandable since the λ perturbation parameter directly controls the magnitude of the interaction between the ligand and the receptor. At λ ≃ 0, where protein-ligand interactions are very weak, the ligand is free to explore a wide variety of positions and orientations, some of which, by means of λ -exchanges, anneal to low energy conformations at λ ≃ 1. Conversely, stable conformations of the complex that would normally remain trapped using conventional molecular dynamics, have the opportunity to escape by migrating to smaller λ values. Overall we have confirmed on this system the critical advantages afforded by the λ -hopping strategy at aiding conformational transitions and speeding up the convergence of free energy estimates. On the other hand, we found that binding/unbinding conformational transitions were hampered by slow conformational rearrangements not directly accelerated by λ -hopping. As discussed in detail below, we found that this effect slows convergence and it turned out to be sufficiently severe for FK506 (ligand 20) to prevent reaching convergence for this ligand using the same protocol used for the smaller ligands.

Binding/unbinding transitions

As discussed,²⁹ BEDAM binding free energies rely on the probability distributions, p_λ (u), of the binding energy as a function of λ (see Figure 4), and, consequently, convergence of binding free energies is necessarily tied to the level of convergence of binding energy distributions. In principle, all of the distributions along λ are required to reach a sufficient level of convergence to achieve convergence of the binding free energy. In practice we found that it is more difficult to converge a p_λ (u) distribution which contains components from both bound and unbound conformations. In these cases it is necessary to sample both macrostates with the correct probability in order to reach convergence. So, in other words, convergence of binding energy distributions depends on the quality of sampling along conformational degrees of freedom that can be considered orthogonal to the progress parameter λ.^64,69

We have found little evidence of multiple binding modes at λ = 1 for the FKBP12 complexes we have investigated in this study. The conformations of the coupled state we have obtained are all characterized by the dual hydrogen bonding pattern seen in the available crystal structures as discussed above. Furthermore we observed little variation of the distributions near λ = 1 as a function of simulation length. We conclude therefore that the distributions at λ near 1 correspond to a single, well sampled conformational macrostate and are appropriately converged. The distributions at the other end of the spectrum near λ = 0 are similarly converged. Obviously these result from a large variety of conformations which, however, are rapidly interconverting due to weak protein-ligand interactions as λ → 0. We find that slow convergence is instead caused by sluggish binding/unbinding conformational interconversions at intermediate critical values of λ. At these λ states conformations of the ligand bound to the receptor in the crystallographic binding mode are in equilibrium with unbound conformations in which the ligand is either displaced from the binding site or oriented so that it is unable to form the proper interactions with the receptor. See Figure 6 for representative bound and unbound conformations.

An illustration of the conformational landscape characterizing the binding/unbinding equilibrium is presented in Figure 7 for ligand 2 at λ = 0.5. Points in the upper right of the plot with high RMSD and less favorable binding energies correspond to unbound conformations while the tight cluster of points at low RMSD and more favorable binding energies correspond to bound conformations. At this particular λ the populations of the bound and unbound conformational macrostates are approximately equal (see Figure 8). As Figure 7A illustrates, the unbound macrostate is characterized by a wider variety of conformations spanning many units of RMSD from the reference crystallographic conformation. The interpretation is therefore that the unbound macrostate, while energetically disfavored, is entropically stabilized relatively to the bound macrostates leading to approximately equal populations at this λ value.

Figure 8.

Fractional population of the bound macrostate as a function of λ for the complexes with ligand 2 and ligand 9.

As shown in Figure 8 for ligand 2, the relatively sharp population switch from the unbound macrostate to the bound macrostate as a function of λ is indeed characteristic of thermodynamic transitions involving large energy/entropy compensation. The equilibrium between unbound and bound macrostates can be described as a pseudo order/disorder phase transition similar to those observed in protein folding, in which the the ordered phase (the bound state) is increasingly destabilized relative to the disordered phase (the unbound state) as λ is decreased and receptor-ligand interactions are turned off. Using a formalism from the protein folding realm, the free energy difference between the unbound and bound macrostate at the half point of the transition λ = λ _1/2 (corresponding to the “melting temperature” of protein folding equilibria) is zero and the steepness of the “melting curve”, shown in Figure 8 for ligands 2 and 9, is proportional to the average binding energy difference between the bound and unbound states. Specifically, as shown in the Appendix, at the half point λ = λ _1/2 we have

$${\left(\frac{{dP}_{\lambda }(B)}{d\lambda }\right)}_{{\lambda }_{1/2}}=\frac{\mathrm{\Delta }{u}_{1/2}}{4k_{B}T},$$ (11)

where P_λ (B) is the λ -dependent population of the bound state and Δu_1/2 = 〈u〉_λ1/2B −〈u〉_λ1/2U is the difference of the average binding energies of the bound and unbound states at the half point. A very similar relationship exists for folding/unfolding equilibrium as a function of temperature.⁷⁰ Consequently, the steepness of the unbinding curve at the half point, is related to the magnitude of the entropic and energetic changes during the transition, which are exactly equal in magnitude and of opposite sign given that at the half point the binding free energy is zero. The larger these changes, the sharper is the transition from the bound state to the unbound state. Therefore for ligands that incur large energetic (and entropic) changes in going from the bound to the unbound conformations there is a small range of λ values at which the bound and unbound states are in equilibrium. As further discussed below, this is a crucial aspect to understand the rate of convergence of binding free energy calculations of this kind as critical interconversions between bound and unbound states occur only in the narrow range of λ in which bound and unbound states are in equilibrium.

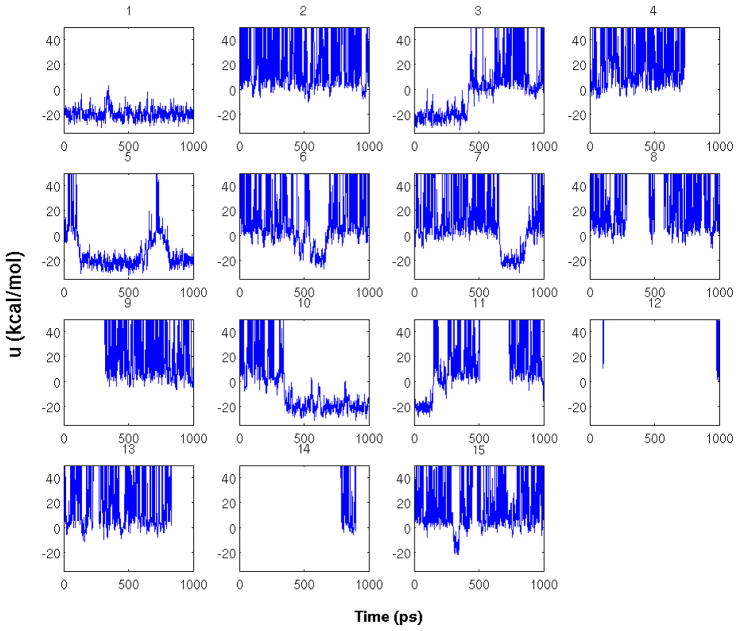
From the spread along the y-axis of Figure 7 we can see that the distribution of binding energies for ligand 2 at λ = 0.5 is composed of two distinct and equally important contributions, one from the bound macrostate at low binding energies and the other from the unbound macrostate at less favorable binding energies. To achieve the correct proportions of these two contributions and ultimately reach convergence of the corresponding binding energy distributions, it is necessary to converge the relative populations of the bound and unbound macrostates. Our results show that difficulties of achieving equilibration of this binding/unbinding process is the cause for the overall slow convergence of the BEDAM binding free energy. To see why this is the case it is useful to analyze the conformational trajectories of HREM replicas. Figure 9 shows the time evolution of the binding energy for the 15 replicas of ligand 2 in a 1 ns section of the BEDAM simulation. Note that in these trajectories λ is not constant as this is the quantity that is being periodically exchanged with other replicas. We see that during this time replica 1 is trapped at low binding energies at or near the bound state, while other replicas (replicas 2 and 4 for example) remain in the unbound state at high binding energies. Infrequently some replicas transition from the bound state to the unbound state or vice versa. For example replica 3 does so at 0.5 ns and replica 5 exhibits two short excursions to the unbound state at 0.1 and 0.75 ns. These transitions occur only in a relatively narrow range of λ centered at 0.5, which is the range in which both states have significant populations (see Figure 7). It is the rate of binding/unbinding transitions that determines the convergence of the relative populations of the bound and unbound states and, as discussed above, the convergence of the intermediate binding energy distributions and, ultimately, of the BEDAM binding free energy.

Figure 9.

Time evolution of the binding energies of the 15 replicas of the HREMD simulation of the complex with ligand 2. Each panel corresponds to a different replica.

Based on these insights it becomes clear why we were unable to reach convergence for ligand 20 using the same definition of the binding site volume employed for the other ligands. Unlike ligand 2 and the other smaller ligands, none of the replicas of this ligand exhibit binding/unbinding transitions during the BEDAM simulation. Some of the replicas of ligand 20 are trapped in the bound state like replica 1 for ligand 2, and others are confined to the unbound state similarly to replica 2 of ligand 2 (see Figure 9). None of the replicas of ligand 20 exhibited binding/unbinding transitions as, for example, replica 3 of ligand 2. As discussed above, it is not possible to arrive at a converged estimate of the binding free energy without proper equilibration between the bound and unbound states. One likely cause for the lack of transitions is the large binding energy difference between bound and unbound states of ligand 20. See for example the spread in binding energies in Figure 7B. The data shown in Figure 7B for ligand 20 corresponds to λ_1/2 = 0.65, the value at which we measure equal populations of bound and unbound conformations. However note that this is only a rough estimate of λ _1/2 for ligand 20 because, lacking binding/unbinding transitions, the bound and unbound states have not reached equilibrium. Nevertheless, this data strongly suggests that the transition binding energy Δu_1/2 for ligand 20 is much larger than the other ligands. Based on Eq. (11) we conclude that ligand 20 undergoes binding/unbinding transitions in a much narrower range of λ ’s than the other ligands and that, therefore, there is a smaller likelihood that a sufficient number of replicas visit this narrow range for a sufficient length of time to observe transitions.

In addition to the larger binding energy difference between the bound and unbound states, the data in Figure 7 also clearly shows that, unlike ligand 2, ligand 20 never visits the conformational space in between the bound and unbound states. (Compare the lack of dots in between the clouds corresponding to the bound and unbound states of ligand 20 in Figure 7B, to the nearly continuous density of dots connecting the same states of ligand 2 in Figure 7A.) It must be concluded therefore that a large free energy barrier separates bound and unbound conformations of ligand 20 and that an additional cause of the lack of observed transitions is the slow rate of binding/unbinding transitions even at those value of λ ’s where the rate of transitions is maximal. What is the molecular nature of these slow transitions? A recent computational study by Olivieri et al.⁷¹ has confirmed the hypothesis that large conformational change of the so called 80’s loop facilitates the entry and exit of ligands from the FKBP12 binding site.^72,73 Without this rearrangement the entryway to the binding site is too constricted to allow a rigid docking binding mechanism. Given that the backbone conformation FKBP12 is harmonically restrained (see Methods), in our calculations this gating movement of the 80’s loop can not occur thereby hampering binding/unbinding transitions. We were able to observe a significant number of transitions for the smaller ligands 2–9 because the λ -based alchemical path employed in BEDAM accelerates binding/unbinding transitions beyond what is achievable under physical conditions. However, evidently, this strategy is insufficient for ligand 20, which, given its size and rigidity, has greater difficulty to bind and unbind without receptor rearrangements.

The role of ligand conformational flexibility in the binding mechanism is illustrated in Figure 6 which shows a typical pathway for binding for ligands 2–9. This pathway goes through an intermediate state (panel B) in which only one of the two key receptor-ligand hydrogen bonds is formed (the one between O1 and the sidechain of Tyr82), whereas the second hydrogen bond between the ester carbonyl of the ligand and the backbone of Ala56 is not formed because the relevant ligand sidechain is rotated away from the donating receptor group (Figure 6, panel B). The last step in the binding transitions consists in the rotation of the ester ligand sidechain and the formation of the second hydrogen bond (Figure 6, panel C). Figure 10 indeed shows that rotation of the ligand ester sidechain is highly correlated to achieving the crystallographic bound conformation. The majority of the recorded binding events involve this ligand sidechain rotation, indicating its likely role in helping the ligand cross the constriction for entering the binding site and, subsequently, form the second receptor-ligand hydrogen bond. Conversely, and unlike the smaller ligands, ligand 20, likely due to its cyclic structure, does not undergo rotation of the ester sidechain (Figure 10) and it is forced to follow a less favorable pathway involving the simultaneous formation of both receptor-ligand hydrogen bonds. We believe that the combination of all these factors – lack of receptor rearrangement and ligand size and rigidity – is the cause of the lack of observed binding/unbinding transitions for ligand 20 and the failure to converge its binding free energy using the same protocol used for the other ligands.

Figure 10.

Representation of the reduction in intramolecular conformational freedom of the ligands (ligand 2 in panel A and ligand 20 in panel B) as they bind the receptor. The x-axis reports the dihedral angle formed by the C1-C2-C3-O2 atoms of the ligand corresponding to the orientation of one of the two carbonyl groups of the ligand (see text). The y-axis report the RMSD of the core of the ligand relative to the bound crystal structure which serves here as a binding progress coordinate

To further confirm this hypothesis we have conducted a BEDAM calculation of ligand 20 using a stricter definition of the complexed state (see Methods) which limits not only the position of the ligand relative to the receptor but also its orientation. This is in principle a valid approach as long as the stricter definition includes all significantly populated conformations of the complex.^10,58 We have confirmed that this is the case based on the λ = 1 ensembles of the complexes obtained with the larger binding site definition, which however, as discussed above, resulted in lack of convergence for ligand 20. The purpose of this calculation was to confirm whether circumventing the need to go through the free energy barrier between bound and unbound conformations of the complex with ligand 20 (see Figure 7B), would lead to better convergence of the BEDAM binding free energy estimate. Indeed, with the stricter binding site definition we observed several transitions between high to low binding energy for ligand 20 and vice versa similar to those observed for ligand 2 with the larger binding site definition (Figure 9). λ trajectories (Figure 5) also showed more thorough mixing. The larger number of observed binding/unbinding transitions is a consequence of the fact that with the stricter binding site definition unbound conformations of the complex (those with unfavorable binding energies) are conformationally similar to the bound conformations. Because ligand orientations are restrained around the crystallographic pose, the cluster of conformations at high RMSD in Figure 7B are no longer present and both bound and unbound conformations are found at low RMSD’s in such a way that their interconversion no longer requires crossing the free energy barrier. These observations indicate that the binding free energy estimate for ligand 20 reached reasonable convergence with the stricter binding site definition. Based on the conformational analysis of the λ = 1 trajectories with the original and orientationally restricted binding site definitions (see above), we also expect that this new estimate also retains good accuracy. Although full confirmation of this hypothesis would require further calculations with a range of binding sites definitions, it is reassuring that the resulting binding free energy estimate for ligand 20 is in relatively good agreement with the experimental affinity (Table 1).

Conclusions

In this work we have presented the results of BEDAM binding free energy calculations for a series of complexes of the FKBP12 receptor. Analysis of the data generated by parallel HREM simulations have provided valuable insights into the factors that affect convergence of BEDAM binding free energy calculations and, importantly, how to detect and analyze these factors. We have shown that the BEDAM protocol is applicable to protein-ligand systems of the size and complexity often found in pharmaceutical applications. We found that reasonable convergence of the calculations can be achieved for these systems if the λ schedule is adjusted appropriately to ensure sufficient overlaps between neighboring binding energy distributions and if a sufficient number of conformational transitions occur so as to achieve equilibration between the bound and unbound macrostates of the complex. Because of the latter, often under appreciated, requirement, increasing the number of replicas improves the binding energy distributions overlap, but it does not necessarily lead to an improvement of the convergence rate of the binding free energy.

The BEDAM protocol employed here does not rely on the exact structural knowledge of the binding mode; it employs a minimally restrained conformational sampling protocol which is capable of identifying potential multiple bound poses of the complex. The good correspondence between the bound ensemble and the crystallographic bound structure in our simulation is solely due to the ability of the HREM sampling protocol to explore many conformations and the ability of the energy function to recognize conformations similar to the crystallographic structure as more favorable. By performing binding free energy calculations in an unrestrained fashion, we were able to resolve a common binding pathway which involved the stepwise formation of two hydrogen bonds between the ligand and receptor (see Figure 6). We are also exploring the possibility to use BEDAM HREM data as input for the construction of network models of binding similar to the use of temperature replica exchange data to construct network models for protein folding and dynamics.^74,75

However, as we have shown, our model, which allows replicas to visit both bound and unbound conformations of the complex, also requires that independent transitions are observed between these two states in order to reach convergence of the binding free energy. We showed that these transitions have the features of pseudo order/disorder phase transition analogous to protein folding equilibria. The lack of sufficient number of transitions prevented convergence for ligand 20 unless a more restrained setup was used. We are currently evaluating ways to increase the occurrence of binding/unbinding transitions with the aim of improving convergence even in cases when the model of the complex explores a large variety of conformations and exhibits phase change characteristics.⁷⁶

Even though they are difficult to model, we have shown that to achieve a realistic representation of the binding equilibrium it is necessary to include the role of conformational entropy loss and intramolecular energetic strain. Although in this system increased affinity qualitatively tracks more favorable receptor-ligand interactions (Table 1), neglecting reorganization free energies grossly overestimates variations of binding affinities from one ligand to another.

Having included in the model the main thermodynamic driving forces and having achieved a good quality of conformational sampling and convergence in the numerical calculations, we believe that the level of agreement of the binding free energy estimates with the experimental affinities primarily reflects the accuracy of the potential energy model (here OPLS-AA with AGBNP2 implicit solvation). The model reproduces ligand ranking reasonably well and we have shown that quantitative agreement can be achieved by adopting a more realistic geometrical model of the solvent accessible surface area of the complex. These promising results indicate that the foundations of the OPLS-AA/AGBNP2 effective potential are solid but that further development and parametrization is required to achieve improved accuracy and transferability in binding free energy applications.

Appendix

In this Appendix we derive Eq. (11). The population P_λ (B) of the bound state B at λ is given by

$$P_{\lambda }(B)=\frac{1}{Z_{\lambda }}\int e^{-\beta [V_0(\mathbf{r})+\lambda u(\mathbf{r})]}{\mathrm{\Theta }}_B(\mathbf{r})d\mathbf{r}=\frac{Z_{\lambda }(B)}{Z_{\lambda }},$$ (12)

where integration is over all the possible conformations of the complex, the λ -dependent potential energy is from Eq. (4), Θ_B(r) is an indicator function equal to 1 if conformation r belongs to the bound macrostate and 0 otherwise, Z_λ is the configurational partition function of the complex at λ and Z_λ (B) is the configurational partition function of only the bound macrostate. Differentiation of Eq. (12) leads to the expression

$$\frac{{dP}_{\lambda }(B)}{d\lambda }=-\beta P_{\lambda }(B)({\langle u\rangle }_{\lambda ,B}-{\langle u\rangle }_{\lambda }),$$ (13)

where the first term in parenthesis comes from the differentiation of Z_λ (B) and the second from the differentiation of Z_λ at the denominator of Eq. (12),

$${\langle u\rangle }_{\lambda }=\frac{1}{Z_{\lambda }}\int u(\mathbf{r})e^{-\beta [V_0(\mathbf{r})+\lambda u(\mathbf{r})]}d\mathbf{r}$$ (14)

is the average binding energy at λ, and

$${\langle u\rangle }_{\lambda ,B}=\frac{1}{Z_{\lambda }}\int u(\mathbf{r})e^{-\beta [V_0(\mathbf{r})+\lambda u(\mathbf{r})]}{\mathrm{\Theta }}_B(\mathbf{r})d\mathbf{r}$$ (15)

is the average binding energy of the bound macrostate at λ. The average binding energy 〈u〉_λ is the weighted sum of the average binding energies 〈u〉_λ,_B and 〈u〉_λ, _U, respectively, in the bound (B) and unbound (U) macrostates (which together are assumed to comprise all of the conformations of the complex)

$${\langle u\rangle }_{\lambda }=P_{\lambda }(B){\langle u\rangle }_{\lambda ,B}+P_{\lambda }(U){\langle u\rangle }_{\lambda ,U}.$$ (16)

At λ = λ_1/2 where P_λ (B) = P_λ (U) = 1/2 we have

$${\langle u\rangle }_{{\lambda }_{1/2}}=\frac{1}{2}({\langle u\rangle }_{{\lambda }_{1/2},B}+{\langle u\rangle }_{{\lambda }_{1/2},U}),$$ (17)

which, when substituted into Eq. (13), yields

$${\left(\frac{{dP}_{\lambda }(B)}{d\lambda }\right)}_{\lambda ={\lambda }_{1/2}}=-\frac{\beta }{4}({\langle u\rangle }_{{\lambda }_{1/2},B}-{\langle u\rangle }_{{\lambda }_{1/2},U})=-\frac{1}{k_{B}T}\mathrm{\Delta }{u}_{1/2}.$$ (18)

which is Eq. (11).