Model Selection and Estimation in the Matrix Normal Graphical Model

Abstract

Motivated by analysis of gene expression data measured over different tissues or over time, we consider matrix-valued random variable and matrix-normal distribution, where the precision matrices have a graphical interpretation for genes and tissues, respectively. We present a l₁ penalized likelihood method and an efficient coordinate descent-based computational algorithm for model selection and estimation in such matrix normal graphical models (MNGMs). We provide theoretical results on the asymptotic distributions, the rates of convergence of the estimates and the sparsistency, allowing both the numbers of genes and tissues to diverge as the sample size goes to infinity. Simulation results demonstrate that the MNGMs can lead to better estimate of the precision matrices and better identifications of the graph structures than the standard Gaussian graphical models. We illustrate the methods with an analysis of mouse gene expression data measured over ten different tissues.

1. Introduction

Gaussian graphical models (GGMs) provide natural tools for modeling the conditional independence relationships among a set of random variables [1, 2]. Many methods of estimating the standard GGMs have been developed in recent years, especially in high-dimensional settings. Meinshausen and Bühlmann [3] took a neighborhood selection approach to this problem by fitting a l₁ penalized regression or Lasso [4] to each variable using the other variables as predictors. They show that this neighborhood selection procedure consistently estimates the set of non-zero elements of the precision matrix. Other authors have proposed algorithms for the exact maximization of the l₁-penalized log-likelihood. Yuan and Lin [5], Banerjee et al. [6] and Dahl et al. [7] adapted interior point optimization method for the solution to this problem. Based on the work of Banerjee et al. [6] and a block-wise coordinate descent algorithm, Friedman et al. [8] developed the graphical Lasso (glasso) for sparse inverse covariance estimation, which is computationally very efficient even when the dimension is greater than the sample size. Yuan [9] developed a linear programming procedure for high dimensional inverse covariance matrix estimation and obtained oracle inequalities for the estimation error in terms of several matrix norms. Some theoretical properties of this type of methods have also been developed by Yuan and Lin [5], Ravikumar et al. [10], Rothman et al. [11] and Lam and Fan [12]. Cai et al. [13] developed a constrained l₁ minimization approach to sparse precision matrix estimation, extending the idea of Dantzig selector [14] developed for sparse high dimensional regressions.

The standard likelihood framework for building Gaussian graphical models assumes that samples are independent and identically distributed from a multivariate Gaussian distribution. This assumption is often limited in certain applications. For example, in genomics, gene expression data of p genes collected over q different tissues from the same subject are often correlated. For a given sample, let Y be the p × q matrix of the expression data, where the jth column corresponds to the expression data of p genes measured in the jth tissue, and the ith row corresponds to gene expressions of the ith gene over q different tissues. Instead of assuming that the columns or rows are independent, we assume that the matrix variate random variable Y follows a matrix normal distribution [15, 1, 16], where both row and column precision matrices can be specified. The matrix-variate normal distribution has been studied in analysis of multivariate linear model under the assumption of independence and homoscedasticity for the structure of the among-row and among-column covariance matrices of the observation matrix [17, 18]. Such a model has also be applied to spatio-temporal data [19, 20]. In genomics, Teng and Huang [21] proposed to use the Kronecker product matrix to model gene-experiment interactions, which leads to gene expression matrix following a matrix-normal distribution. The gene expression matrix measured over multiple tissues is transposable, meaning that potentially both the rows and/or columns are correlated. Such matrix-valued normal distribution was also used in Allen and Tibshirani [22] and Efron [23] for modeling gene expression data in order to account for gene expression dependency across different experiments. Dutilleul [24] developed the maximum likelihood estimation(MLE) algorithm for the matrix normal distribution. Mitchell et al [25] developed a likelihood ratio test for separability of the covariances. Muralidharan [26] used a matrix normal framework for detecting column dependence when rows are correlated and estimating the strength of the row correlation.

The precision matrices of the matrix normal distribution provide the conditional independence structures of the row and column variables [1], where the non-zero off-diagonal elements of the precision matrices correspond to conditional dependencies among the elements in row or column of the matrix normal distribution. The matrix normal models with specified non-zero elements of the precision matrices define the matrix normal graphical models (MNGMs). This is analogous to the relationship between the Gaussian graphical model and the precision matrix of a multivariate normal distribution. Despite the flexibility of the matrix normal distribution and the MNGMs in modeling the transposable data, methods for model selection and estimation of such models have not been developed fully, especially in high dimensional settings. Wang and West [27] developed a Bayesian approach for the MNGMs using Markov Chain Monte Carlo sampling scheme that employs an efficient method for simulating hyper-inverse Wishart variates for both decomposable and nondecomposable graphs. Allen and Tibshirani [22, 28] proposed penalized likelihood approaches for such the matrix normal models, where both l₁-norm and l₂-norm penalty functions are used on the precision matrices.

The focus of this paper is to develop a model selection and estimation method for the MNGMs based on a l₁ penalized likelihood approach under the assumption of both row and column precision matrices being sparse. Our penalized estimation method is the same as that proposed in [22, 29, 28] when l₁ penalty is used. Allen and Tibshirani [22, 28] only considered the setting when there is one observed matrix-variate normal data and used the estimated covariance matrices for imputing the missing data and for de-correlating the noise in the underlying data. We focus on evaluating how well such a l₁ penalized estimation method recovers the underlying graphical structures that correspond to the row and column precision matrices when we have n i.i.d samples from a matrix normal distribution. In addition, we provide asymptotic justification of the estimates and show that the estimates enjoy similar asymptotic and oracle properties as the penalized estimates for the standard GGMs [30, 12, 5] even when the dimensions p = p_n and q = q_n diverge as the number of observations n → ∞. In addition, if consistent estimates of the precision matrices are available are used in the adaptive l₁ penalty functions, the resulting estimates have the property of sparsistency.

The rest of the paper is organized as follows. We introduce the MNGMs as motivated by analysis of gene expression data across multiple tissues in Section 2. In Section 3 we present an l₁ penalized likelihood estimate of such a MNGM and an iterative coordinate descent procedure for the optimization. We present the asymptotic properties of the estimates in Section 4 in both the classic setting when the dimensions are fixed and the setting allowing the dimensions to diverge as the sample size goes to infinity. In Section 5 we present simulation results and comparisons with the standard Gaussian graphical model. We present an application of the MNGM in Section 6 to an analysis of mouse gene expression data measured over 10 different tissues. Finally, in Section 7 we give a brief discussion. The proofs of all the theorems are given in the Appendix.

2. Matrix Normal Graphical Model for Multi-tissue Gene Expression Data

We consider the gene expression data measured over different tissues. Let Y be the random p × q matrix of the gene expression levels of p genes over q tissues. Let vec(A) be the vectorization of a matrix A obtained by stacking the columns of the matrix A on top of one another. Instead of assuming that the expression levels are independent over different tissues, following [21], we can model this gene expression matrix as

$$\mathbf{Y}=\mathbf{G}+\mathbf{T}+{\mathbf{I}}_{GT}+∊,$$ (1)

where G and T are expected (constant) effects from the genes and tissues respectively, I_GT are the interaction effects that are assumed to be random with vec(I_GT ) following a multivariate normal distribution with zero means and a covariance matrix $\mathbf{V}\otimes \mathbf{U}$, where the covariance matrices U and V respectively represent the gene and tissue dependencies, and ε represents small random normal noises with zero means arising from all nuisance sources. With negligible nuisance effects, vec(Y) follows a multivariate normal distribution with means vec(M) = vec(G + T) and a covariance matrix $\mathbf{V}\otimes \mathbf{U}$ [21].

Treating the data Y as a matrix-valued random variable, we say Y follows a matrix normal distribution, if Y has a density function

$$p(\mathbf{Y}\mid \mathbf{M},\mathbf{U},\mathbf{V})=k(\mathbf{U},\mathbf{V})\text{exp}(-\mathrm{tr}\{{(\mathbf{Y}-\mathbf{M})}^T{\mathbf{U}}^{-1}(\mathbf{Y}-\mathbf{M}){\mathbf{V}}^{-1}∕2\}),$$ (2)

where k(U, V) = (2π)^−pq/2|U|^−q/2|V|^−p/2 is the normalizing constant, M is the mean matrix, U is row covariance matrix and V is column covariance matrix. This definition is equivalent to the definition via the Kronecker product [31, Section 8.8 and 9.2]. Specifically,

$$\mathbf{Y}\sim M{N}_{p,q}(\mathbf{M};\mathbf{U},\mathbf{V})\text{if and only if}\text{vec}\left(\mathbf{Y}\right)\sim N_{pq}(\text{vec}\left(\mathbf{M}\right),\mathbf{V}\otimes \mathbf{U}).$$ (3)

We denote the corresponding precision matrices as A = U⁻¹, B = V⁻¹ for U and V, respectively. This model assumes a particular decomposable covariance matrix for vec(Y) that is separable in the geostatistics context [32]. The parameters U and V are defined up to a positive multiplicative constant. We can set B₁₁ to any positive constant to make the parameters identifiable.

The following proposition shows that there is a graphical model interpretation for the two precision matrices A and B in the matrix normal model (2).

Proposition 2.1. Assume that Y ~ MN_p,q(M; U, V). If we partition the columns of Y as Y = (y₁, ···, y_q), then it holds for γ, μ ∈ = Γ = {1, ···, q} with γ ≠ μ that

$${\mathbf{y}}_{\gamma }⫫{\mathbf{y}}_{\mu }\mid {\mathbf{y}}_{\Gamma \setminus \{\gamma ,\mu \}}ifandonlyif{b}_{\gamma \mu }=0,$$ (4)

where B = {b_αβ]_α,β∈Γ = V^–1 is the column precision matrix of the distribution; similarly, if we partition the rows of Y as Y = (y¹, ···, y^p)^T, then it holds for δ, β ∈ Ξ = (1, ..., p} with δ ≠ η that

$${\mathbf{y}}^{\delta }⫫{\mathbf{y}}^{\eta }\mid {\mathbf{y}}^{\Delta \setminus \{\delta ,\eta \}}ifandonlyif{a}_{\delta \eta }=0$$ (5)

where A = {a_δη}_δ,η∈Ξ = U⁻¹ is the row precision matrix of the distribution.

This proposition is based on a proposition in Lauritzen [1]. Detailed proof can be found in the Appendix. Without loss of generality, we assume M = 0 in this paper since it can be easily estimated.

3. l₁-Penalized Maximum Likelihood Estimation of the Precision Matrices

We propose to estimate the precision matrices A = U⁻¹, B = V⁻¹ in model (2) by maximizing a penalized likelihood function. Since for any c > 0, p(Y | A, B) = p(Y | cA, B/c), A and B are not uniquely identified. We set b₁₁ = 1 for the purpose of parameter identification. We propose to estimate A and B by minimizing the following penalized negative log-likelihood function

$$\varphi (\mathbf{A},\mathbf{B})=-q\text{log}\left(\mid \mathbf{A}\mid \right)-p\text{log}\left(\mid \mathbf{B}\mid \right)+\frac{1}{n}\sum _{k=1}^n\mathrm{tr}\left\{{\mathbf{Ay}}_k{\mathbf{By}}_k^T\right\}+\sum _{i\ne j}{p}_{{\lambda }_{ij}}\left(a_{ij}\right)+\sum _{i\ne j}{p}_{{\rho }_{ij}}\left(b_{ij}\right),$$ (6)

where p_λij (·) is the penalty function for the element a_ij of A with tuning parameter λ_ij, while p_ρij (·) is the corresponding penalty function for b_ij with tuning parameter ρ_ij. We consider both l₁-penalty with p_λij (a_ij) = λ|a_ij| and p_ρij (b_ij) = ρ|b_ij| and adaptive l₁ penalty with p_λij (a_ij) = λ|ã_ij|^−γ1|a_ij| and p_ρij(b) = ρ|b̃_ij|^−γ2|b_ij|, where à = {ã_ij} and B̃ = {b̃_ij} are some consistent estimate of A and B and γ₁ > 0 and γ₂ > 0 are two constants.

It is easy to check that the objective function (6) is a bi-convex function in A and B. We propose the following iterative procedure to minimize this function:

1. Initialization: B̂⁽⁰⁾ = I_q.

2. In ith step, given the current estimate of B, B̂⁽ⁱ⁾, we update A by

   $${\widehat{\mathbf{A}}}^{(i+1)}=\text{arg}\underset{\mathbf{A}}{\text{min}}\left\{-\text{log}\left(\mid \mathbf{A}\mid \right)+\mathrm{tr}\left({\widehat{\mathbf{S}}}_{\mathbf{A}}^{\left(i\right)}\mathbf{A}\right)+\sum _{i\ne j}{p}_{{\lambda }_{ij}^{\ast }}\left(a_{ij}\right)\right\},$$ (7)

   where ${\widehat{\mathbf{S}}}_{\mathbf{A}}^{\left(i\right)}=1∕\left(nq\right){\sum }_{k=1}^n{\mathbf{y}}_k{\widehat{B}}^{\left(i\right)}{\mathbf{y}}_k^T,{\lambda }_{ij}^{\ast }={\lambda }_{ij}∕q$.
3. In (i+1)th step, given the current estimate of A, Â⁽ⁱ⁺¹⁾, we update B by

   $${\widehat{\mathbf{B}}}^{(i+1)}=\text{arg}\underset{\mathbf{B}}{\text{min}}\left\{-\text{log}\left(\mid \mathbf{B}\mid \right)+\mathrm{tr}\left({\widehat{\mathbf{S}}}_{\mathbf{B}}^{(i+1)}\mathbf{B}\right)+\sum _{i\ne j}{p}_{{\rho }_{ij}^{\ast }}\left(b_{ij}\right)\right\},$$ (8)

   when ${\widehat{\mathbf{S}}}_{\mathbf{B}}^{(i+1)}=1∕\left(np\right){\sum }_{k=1}^n{\mathbf{y}}_k^T{\widehat{\mathbf{A}}}^{(i+1)}{\mathbf{y}}_k$, ${\rho }_{ij}^{\ast }={\rho }_{ij}∕p$.

4. Iterate step 2 and 3 until convergence.

5. Scale (Â, B̂) = (Â/c, cB̂) such that b̂₁₁ = 1.

Optimizations (7) and (8) can be solved using the block coordinate descent algorithm in the same way as that developed for estimating the precision matrix in standard Gaussian graphical models [8]. We use the program glasso [8] in this paper for these optimizations when the l₁ or the adaptive l₁ penalty functions are used. The glasso algorithm guarantees that the estimates  and B̂ are positive definite.

Note that in Step 5 of the algorithm, we rescale the A and B matrices to ensure that b̂₁₁ = 1. However, when l₁ or the adaptive l₁ penalty functions are used, the solution to (6) is always unique in the sense that for a given λ and ρ, there is a unique scaling factor c*,

$$c^{\ast }=\sqrt{\rho {\Vert {\mathbf{B}}_0\Vert }_1∕\left(\lambda {\Vert {\mathbf{A}}_0\Vert }_1\right)}$$

in the equivalent class ${\mathcal{C}}_{{\mathbf{A}}_0,{\mathbf{B}}_0}:=\{(\mathbf{A},\mathbf{B})\mid \mathbf{A}=c{\mathbf{A}}_0,\mathbf{B}=c^{-1}{\mathbf{B}}_0,\text{for some}0<\mathrm{c}<\infty \}$ that minimizes Φ(A, B), where ${\Vert {\mathbf{A}}_0\Vert }_1={\sum }_{i=1}^p{\sum }_{j=1}^p\mid {\mathbf{A}}_0(i,j)\mid$ is matrix l₁ norm. This can be seen by

$${\lambda }_1{\Vert {\mathbf{A}}_0\Vert }_{1}c+{\lambda }_2{\Vert {\mathbf{B}}_0\Vert }_1\frac{1}{c}\ge 2\sqrt{{\lambda }_1{\lambda }_2{\Vert {\mathbf{A}}_0\Vert }_1{\Vert {\mathbf{B}}_0\Vert }_1},$$

based on the algebra-geometry inequality. Equality holds and hence the minimum is attained when $c^{\ast }=\sqrt{{\lambda }_2{\Vert {\mathbf{B}}_0\Vert }_1∕\left({\lambda }_1{\Vert {\mathbf{A}}_0\Vert }_1\right)}$. Hence A = c* A₀, B = B₀/c* are uniquely determined.

Finally, the tuning parameters λ and ρ in the l₁ penalty functions are chosen using the cross-validated likelihood function.

4. Asymptotic Theorems

Throughout this paper, for a given p × q matrix A = (a_ij), we denote $\Vert \mathbf{A}\Vert =\text{max}\{\Vert \mathbf{Ax}\Vert ∕\Vert \mathbf{x}\Vert ,\mathbf{x}\in {\mathfrak{R}}^q,\mathbf{x}\ne 0\}$ as operator or spectral norm of A, ||A||_∞ = max|a_ij| as the element-wise l_∞ norm of A, and ${\mid \Vert \mathbf{A}\Vert \mid }_{\infty }={\text{max}}_{1\le i\le p}{\sum }_{j=1}^q\mid a_{ij}\mid$ as the matrix l_∞ norm of A. Furthermore, we use ${\Vert \mathbf{A}\Vert }_F=\sqrt{{\sum }_{ij}{a}_{ij}^2}$ as the Frobenius norm of A. Denote λ_min(A) and λ_max(A) the smallest and largest eigenvalues of the matrix A.

4.1. Asymptotic theorems when p and q are fixed

We first consider the asymptotic distributions of the penalized maximum like lihood estimates in the setting when p and q are fixed as n → ∞. The following theorem provides the asymptotic distribution of the estimate (Â, B̂).

Theorem 1. For n independent identically distributed observations Y₁, ··· Y_n from a matrix normal distribution MN (0; A⁻¹, B⁻¹), the optimizer (Â, B̂) of the penalized negative log-likelihood function (6) with the l₁ penalty functions has the following property:

If n^1/2 λ → λ₀ ≥ 0, n^1/2 ρ → ρ₀ ≥ 0, as n → ∞, then

$$n^{1∕2}\{(\widehat{\mathbf{A}},\widehat{\mathbf{B}})-(\mathbf{A},\mathbf{B})\}\to {\text{argmin}}_{\mathbf{M}={\mathbf{M}}^T,\mathbf{N}={\mathbf{N}}^T}f(\mathbf{M},\mathbf{N})$$

in distribution, where

$$f(\mathbf{M},\mathbf{N})=q\mathrm{tr}\left(\mathbf{MUMU}\right)+p\mathrm{tr}\left(\mathbf{NVNV}\right)+\mathrm{tr}\left(\mathbf{MU}\right)\mathrm{tr}\left(\mathbf{NV}\right)+W+{\lambda }_0\sum _{i\ne j}\{m_{ij}\mathrm{sgn}\left(a_{ij}\right)I(a_{ij}\ne 0)+\mid m_{ij}\mid I(a_{ij}=0)\}+{\rho }_0\sum _{i\ne j}\{n_{ij}\mathrm{sgn}\left(b_{ij}\right)I(b_{ij}\ne 0)+\mid n_{ij}\mid I(b_{ij}=0)\},$$

in which W is a random variable such that W ~ N (0, σ²), where

$${\sigma }^2=2\{q\mathrm{tr}\left(\mathbf{MUMU}\right)+p\mathrm{tr}\left(\mathbf{NVNV}\right)+2\mathrm{tr}\left(\mathbf{MU}\right)\mathrm{tr}\left(\mathbf{NV}\right)\}.$$

This result parallels to that of Yuan and Lin [5] for the l₁ penalized likelihood estimate of the precision matrix in the standard Gaussian graphical model.

Suppose that we have c_n-consistent estimators of A and B, denoted by à = (ã_ij)_1≤i,j≤p and B̃ = (b̃_ij)_1≤i,j≤q, that is c_n(à – A) = O_p(1), c_n(B̃ – B) = O_p(1), we consider the penalized likelihood estimates using the adaptive l₁ penalty function

$$\sum _{i\ne j}{p}_{{\lambda }_{ij}}\left(a_{ij}\right)=\lambda \sum _{i\ne j}{\mid {\tilde{a}}_{ij}\mid }^{-{\gamma }_1}\mid a_{ij}\mid ,\sum _{i\ne j}{p}_{{\rho }_{ij}}\left(b_{ij}\right)=\rho \sum _{i\ne j}{\mid {\tilde{b}}_{ij}\mid }^{-{\gamma }_2}\mid b_{ij}\mid$$

in the objective function (6), where γ₁ and γ₂ are two constants. The following theorem shows that the resulting estimates of the precision matrices have the oracle property that parallels to that of Fan et al. [30] for the standard Gaussian graphical model.

Theorem 2. For n independent identically distributed observations Y₁, ···, Y_n from a matrix normal distribution MN(0; A⁻¹, B⁻¹), the optimizer (Â, B̂) of the object function (6) with adaptive l₁ penalty functions has the oracle property in the sense of Fan and Li [33]. That is, when n^1/2λ = O_p(1), n^1/2ρ = O_p(1), $n^{1∕2}\lambda c_n^{\gamma }\to \infty$ and $n^{1∕2}\rho c_n^{\gamma }\to \infty$ as n → for some λ₁ > 0 and γ₂ > 0, then (1). asymptotically, the estimates  and B̂ have the same sparsity pattern as the true precision matrix A and B.

(2). the non-zero entries of  and B̂ are c_n-consistent and asymptotically normal.

4.2. Asymptotic theorems when p = p_n and q = q_n diverge

The next two theorems provide the convergence rates and sparsistency properties of the estimates allowing p = p_n, q = q_n to diverge as n → ∞. We use ${\mathbf{A}}_0=\left(a_{ij}^{\left(0\right)}\right)$ and ${\mathbf{B}}_0=\left(b_{kl}^{\left(0\right)}\right)$ to denote the true precision matrices and $S_{\mathbf{A}}=\{(i,j):a_{ij}^{\left(0\right)}\ne 0\}$ and $S_{\mathbf{B}}=\{(k,l):b_{kl}^{\left(0\right)}\ne 0\}$ to denote the support of the true matrices, respectively. Let s_n1 = card(S_A) – p_n and s_n2 = card(S_B) – q_n be the number of nonzero elements in the off-diagonal entries of A₀ and B₀, respectively. We assume the following regularity conditions:

1. There exist constants ε₁ and ε₂ such that

   $$0<{\epsilon }_1\le {\lambda }_{\text{min}}\left({\mathbf{A}}_0\right)\le {\lambda }_{\text{max}}\left({\mathbf{A}}_0\right)\le {\epsilon }_2<\infty ,\text{for all}n.$$
2. There exist constants ε₃ and ε₄ such that

   $$0<{\epsilon }_3\le {\lambda }_{\text{min}}\left({\mathbf{B}}_0\right)\le {\lambda }_{\text{max}}\left({\mathbf{B}}_0\right)\le {\epsilon }_4<\infty ,\text{for all}n.$$
3. The tuning parameter λ_n satisfies

   $${\lambda }_n=O\left\{\left(1+\frac{\sqrt{p_n}}{\sqrt{s_{n1}}+1}\right)q_n\sqrt{\frac{q_n(\text{log}{p}_n+\text{log}{q}_n)}{n}}\right\}.$$
4. The tuning parameter ρ_n satisfies

   $${\rho }_n=O\left\{\left(1+\frac{\sqrt{q_n}}{\sqrt{s_{n2}}+1}\right)p_n\sqrt{\frac{p_n(\text{log}{p}_n+\text{log}{q}_n)}{n}}\right\}.$$

Conditions (A) and (B) bound uniformly the eigenvalues of A₀ and B₀, which facilitates the proof of consistency. These conditions are also assumed for the penalized likelihood estimation for the standard Gaussian graphical models [34, 12]. The upper bounds on λ_n and ρ_n in condition (C) and (D) are related to the control of bias due to the l₁ penalty terms in the objective function [33, 35, 12].

Denote ${\mathbf{S}}_n=1∕n{\sum }_{k=1}^n{\mathbf{Y}}_k\otimes {\mathbf{Y}}_k$. It is easy to check that Σ₀ = (vec(U))(vec(V))^T = ES_n. We use the double indices (i, j) and (k, l) to refer to a row or a column in S_n or Σ₀. The following Lemma provides the tail probability bound of (S_n – Σ₀).

Lemma 4.1. Suppose the matrix observations Y_k's are i.i.d. from a matrix normal distribution, Y_k ~ MN(0; U, V), and ${\lambda }_{\text{max}}\left(\mathbf{U}\right)\le {\epsilon }_1^{-1}$, ${\lambda }_{\text{max}}\left(\mathbf{V}\right)\le {\epsilon }_3^{-1}$. Then we have the tail bound:

$$Pr\left(\underset{1\le i,j\le p_n,1\le k,l\le q_n}{\text{max}}\mid {({\mathbf{S}}_n-{\Sigma }_0)}_{(i,j)(k,l)}\mid \ge t\right)\le C_1{p}_n^2{q}_n^2\text{exp}(-C_{2}n{t}^2),\text{for}\mid t\mid \le \delta ,$$ (9)

for some constants C₁, C₂ and δ that depend on ε₁, ε₃ only.

In this lemma, if we choose $t=\sqrt{\text{log}\left(p_n^2{q}_n^2\right)∕\left(n{C}_2\right)}M$ for some M such that |t| ≤ δ, then

$${\Vert {\mathbf{S}}_n-{\Sigma }_0\Vert }_{\infty }=O_P\left(\sqrt{(\text{log}{p}_n+\text{log}{q}_n)∕n}\right).$$

The next theorem provides the rates of convergence of the penalized likelihood estimates  and B̂ in terms of the Frobenius norms.

Theorem 3 (Rate of convergence). Under the regularity conditions (A)-(D), if $q_n^3(\text{log}{p}_n+\text{log}{q}_n)∕n=O\left({\lambda }_n^2\right)$ and q_n(p_n + s_n1) (log p_n + log q_n)^k/n = O(1) for some k > 1; $p_n^3(\text{log}{p}_n+\text{log}{q}_n)∕n=O\left({\rho }_n^2\right)$ and p_n (q_n + s_n2) (log p_n + log q_n)^l/n = O(1) for some l > 1. Then when the l₁ penalty functions are used, there exists a local minimizer (Â, B̂) of (6) such that ${\Vert \widehat{\mathbf{A}}-{\mathbf{A}}_0\Vert }_F^2=O_P\{q_n(p_n+s_{n1})(\text{log}{p}_n+\text{log}{q}_n)∕n\}$ and ${\Vert \widehat{\mathbf{B}}-{\mathbf{B}}_0\Vert }_F^2=O_P\{p_n(q_n+s_{n2})(\text{log}{p}_n+\text{log}{q}_n)∕n\}$.

Theorem 3 states explicitly how the number of nonzero elements and dimensionality of both precision matrices affect the rates of convergence of the estimates. Since there are (q_n + s_n2)(p_n + s_n1) nonzero elements in the Kronecker product $\mathbf{A}\otimes \mathbf{B}$ and $\mathbf{B}\otimes \mathbf{A}$ and each of them can be estimated at best with rate n^−1/2, the total square errors are at least of rate q_n(p_n + s_n1)/n for estimating A and p_n(q_n + s_n2) for estimating B. The price that we pay for high dimensionality is a logarithmic factor (log p_n + log q_n). The estimates  and B̂ converge to their true values in Frobenius norm as long as q_n(p_n + s_n1) and p_n(q_n + s_n2) are at a rate O((log p_n + log q_n)^−l) for some l > 1, which decays to zero slowly. This means that in practice p_nq_n can be comparable to n without violating the results. Compared to the rates of convergence of the l₁ penalized likelihood estimates of the precision matrix in the standard GGM [12], the convergence rates for  and B̂ are increased by a factor q_n and p_n. If q_n (or p_n) is fixed as n → ∞, then the rate for  (or B̂) is exactly the same as that given in [12] for the standard Gaussian graphical models.

When an adaptive l₁ penalty function is used, we have the following sparsistency of the penalized estimates. Here sparsistency refers to the property that all parameters in A₀ and B₀ that are zero are actually estimated as zero with probability tending to one. We use S^c to denote the complement of a set S.

Theorem 4 (Sparsistency). Under the conditions given in Theorem 3, when the penalty functions in (6) are adaptive l₁ penalty, p_λij (a_ij) = |a_ij|/|ã_ij|^γ1, p_ρkl (b_kl) =|b_kl|/|b̃_kl|^γ2 for some γ₁ > 0, γ₂ > 0, where à = (ã_ij) and B̃ = (b̃_kl) are any two e_n- and f_n- consistent estimator, i.e. e_n ||à – A₀||_∞ = O_p(1), f_n||B̃ – B₀||_∞ = O_P(1). For any local minimizer (Â, B̂) of (6) satisfying

$$\begin{array}{cc}\hfill {\Vert \widehat{\mathbf{A}}-{\mathbf{A}}_0\Vert }_F^2& =O_P\left(q_n(p_n+s_{n1})(\text{log}{p}_n+\text{log}{q}_n)∕n\right),\hfill \\ \hfill {\Vert \widehat{\mathbf{B}}-{\mathbf{B}}_0\Vert }_F^2& =O_P\left(p_n(q_n+s_{n2})(\text{log}{p}_n+\text{log}{q}_n)∕n\right),\hfill \end{array}$$

and ||Â – A₀||² = O_P(c_n,), ||B̂ – B₀||² = O_P(d_n) for sequences c_n → 0 and d_n → 0, If

$$e_n^{-2\gamma 1}{q}_n\left(\frac{p_n(q_n+s_{n2})(\text{log}{p}_n+\text{log}{q}_n)}{n}+c_n{q}_n\right)=O\left({\lambda }_n^2\right),$$ (10)

and

$$f_n^{-2{\gamma }_2}{p}_n\left(\frac{q_n(p_n+s_{n2})(\text{log}{p}_n+\text{log}{q}_n)}{n}+d_n{p}_n\right)=O\left({\rho }_n^2\right),$$ (11)

then with probability tending to 1, â_ij = 0 for all $(i,j)\in S_{\mathbf{A}}^c$ and b̂_kl = 0 for all $(k,l)\in S_{\mathbf{B}}^c$.

The sparsistency results requires a lower bound on the rates of the regularization parameters λ_n and ρ_n. On the other hand, the regularity conditions (C)(and (D) impose an upper bound on λ_n and ρ_n in order to control the estimation biases. These requirements on the tuning parameters are similar to those for the GGMs. However, in the case of the matrix normal estimation, the conditions for λ_n depend not only on the dimension p_n of A, the rate of the consistent estimator à and the rate of error for  in l₂ norm, but also depend on the dimension q_n and its sparsity s_n2 of the matrix B₀. Similarly, the conditions for ρ_n depend not only on the rate of B̃ and rate of error for B̂ in l₂ norm, but also on the dimension and sparsity of A₀. In addition, the condition (10) in the theorem, combined with the regularity Condition (C), implies that

$$e_n^{-{\gamma }_1}\le \left(1+\frac{\sqrt{p_n}}{\sqrt{s_{n1}}+1}\right)\frac{q_n}{\sqrt{p_n(q_n+s_{n2})}}<\sqrt{q_n}\left(\frac{1}{\sqrt{p_n}}+\frac{1}{\sqrt{s_{n1}}+1}\right),$$

and

$$e_n^{-{\gamma }_1}\sqrt{c_n}\le \sqrt{\frac{p_n{q}_n(\text{log}{p}_n+\text{log}{q}_n)}{n}}\left(\frac{1}{\sqrt{p_n}}+\frac{1}{\sqrt{s_{n1}}+1}\right).$$

These are the requirements for both the rate of the consistent estimator à in its element-wise l_∞ norm and rate of the operator norm of Â. Similarly, condition (11) and regularity Condition (D) imply that

$$f_n^{-{\gamma }_2}<\sqrt{p_n}\left(\frac{1}{\sqrt{q_n}}+\frac{1}{\sqrt{s_{n2}}+1}\right),$$

and

$$f_n^{-{\gamma }_2}\sqrt{d_n}\le \sqrt{\frac{p_n{q}_n(\text{log}{p}_n+\text{log}{q}_n)}{n}}\left(\frac{1}{\sqrt{q_n}}+\frac{1}{\sqrt{s_{n2}}+1}\right).$$

5. Monte Carlo Simulations

5.1. Comparison candidates and measurements

In this section we present results form Monte Carlo simulations to examine the performances of the penalized likelihood method and to compare them to several naive methods for estimating the two precision matrices. The first method uses only data from one row or column in order to ensure that the observations are independent. Specifically, to estimate the precision matrix A, we choose the ith column from every observation matrix Y_k (k = 1, ···, n), denoted by y_k·i the ith column of Y_k, to estimate the row precision matrix A. Since y_k·i ~ N(M_·i, v_iiU), we can estimate the precision matrix A up to a multiplier by fitting a standard GGM. Without loss of generality, we choose the first column y_k·1 in our simulations. We call this procedure the Gaussian graphical model using the column data (GGM-C). Similarly, we can estimate the precision matrix B by choosing the first row y_k1· from every Y_k (k = 1, ···, n). We call this procedure the Gaussian graphical model using the row data (GGM-R). The second approach simply ignores the dependency of the data across the columns or rows and estimates A by treating the q columns as independent observations and estimates B by treating the p rows as independent observations using the Gaussian graphical model. We call this procedure the Gaussian graphical model assuming independence of row variables or column variables (GGM-I). For all three procedures (GGM-C, GGMC and GGM-I), we use glasso algorithm to estimate these two matrices. When p, q < n, we also consider the adaptive version of the glasso, where the maximum likelihood estimates are used as the initial consistent estimates of the precision matrices.

We compare the performance of different estimators of the precision matrices A and B by calculating different matrix norms of the estimation errors. Let Δ_A = A –  and Δ_B = B – B̂ be the estimation errors of the estimators  and B̂, respectively. We compare ||Δ_A||_∞, |||Δ_A|||_∞, ||Δ_A|| and ||Δ_A||_F for Â, and ||Δ_B||_∞, |||Δ_B|||_∞, ||Δ_B|| and ||Δ_B||_F for B̂.

In order to evaluate how well different procedures recover the graphical structures defined by the precision matrices, we define the non-zero entry in a sparse precision matrix as “positive” and define the specificity (SPE), sensitivity (SEN) and Matthews correlation coefficient (MCC) scores as following:

$$\mathrm{SPE}=\frac{TN}{TN+FP},\mathrm{SEN}=\frac{TP}{TP+FN},\mathrm{MCC}=\frac{TP\times TN-FP\times FN}{{\left\{(TP+FP)(TP+FN)(TN+FP)(TN+FN)\right\}}^{1∕2}},$$

where TP, TN, FP and FN are the numbers of true positives, true negatives, false positives and false negatives.

5.2. Models and data generation

We generate sparse precision matrices A and B using a similar scheme as in [36] and [30]. To be specific, our generating procedure can be described as:

$$\begin{array}{cc}\hfill & a_{ii}\equiv 1\hfill \\ \hfill & a_{ij}\mid ({\delta }_{ij}=0)\equiv 0\hfill \\ \hfill & a_{ij}\mid ({\delta }_{ij}=1)\sim \text{Unif}([-1,-0.5]\cup [0.5,1]),\hfill \end{array}$$

where i ≠ j and δ_ij is a Bernoulli random variable with a success probability of p₊. Then the off-diagonal elements of each row a_ij (j = 1, ···, p and j ≠ i) are divided by 1.5Σ|a_i·|₁ (off-diagonal elements only). A is then symmetrized and U = A⁻¹ is obtained. Note that the diagonal elements in U generated in this way are heterozygous. We further modify A by WA where W is a diagonal matrix. Since A generated as above is diagonal dominant, W = diag(w₁, ···, w_p) is generated as the follows: first we choose the upper bound w_max for w_i's, here we use w_max = 1.2. Then for each j, we generate a uniformly distributed random variable r in the interval (Σ_i,i≠j|a_ij|/|a_jj|, 1) and let w_j = rw_max. Thus we can guarantee the diagonal dominance of the matrix WA and hence the positive definiteness. We further define U = (WA)⁻¹. Matrices B and V are generated in a similar way.

After we generate the parameter (A, B) and (U, V), we generate the matrix normal data by first generating a pq-dimensional normal vectors z_k from $N(0,\mathbf{V}\otimes \mathbf{U})$ and then rearranging them into a matrix Y_k such that vec(y_k) = z_k for k = 1, ···, n.

In the following, let p_A+ (or p_B+) be the probability that an off-diagonal element of matrix A (or B) is non-zero, which measures the degree of the sparsity of the matrix. We consider five different models of different dimensions and different degrees of sparsity:

$$\begin{array}{cc}\hfill & \text{Model}1:n=100,p=30,q=30,p_{A+}=1∕10\text{and}{p}_{B+}=1∕10;\hfill \\ \hfill & \text{Model}2:n=100,p=80,q=80,p_{A+}=1∕20\text{and}{p}_{B+}=1∕20.\hfill \\ \hfill & \text{Model}3:n=100,p=150,q=150,p_{A+}=1∕40\text{and}{p}_{B+}=1∕40.\hfill \\ \hfill & \text{Model}4:n=100,p=500,q=500,p_{A+}=1∕200\text{and}{p}_{B+}=1∕200.\hfill \\ \hfill & \text{Model}5:n=20,p=600,q=600,p_{A+}=1∕200\text{and}{p}_{B+}=1∕200.\hfill \end{array}$$

We use a 5-fold cross validation to tune the regularization parameters for Models 1-4 and 3-fold cross validation for Model 5 due to its small sample size. The simulations are repeated 50 times.

5.3. Simulation results

We present in Tables 1 and 2 the results of the three different procedures in terms of estimating the precision matrix and recovering the corresponding graphical structures when the l₁ penalty functions are used. For all four models considered, we observe that the MNGM results in smaller estimation errors and better performances in identifying graphical structures defined by the precision matrices than the naive applications of the Gaussian graphical models. This is true both for the settings when p, q < n (Models 1 and 2) and when p, q > n (Models 3 and 4). We observe that when only one row or one column is chosen from each observation and the standard GGM is used (GGM-R or GGM-C), the estimation errors are much higher than the MNGM or the GGM when the rows or columns are treated as independent. Similarly, both sensitivities and specificities are also lower if only data from one row or one columns are used. This can be explained by the relatively small sample sizes. On the other hand, if the dependency of the columns or rows is ignored and the data of the columns or rows are treated as independent, direct application of the Gaussian graphical model (GGM-I) results in smaller specificities and higher false positives. As a benchmark comparison, for Models 1 and 2, we also present in Table 1 the errors of the MLEs of A and B. It is clear that the MNGM gives better estimates than the MLEs. MLEs for Models 3 and 4 do not exist.

Table 1.

Comparison of the performance for simulated data sets of different dimensions when l₁ penalty functions are used.

Precision Matrix	Measure	MNGM	GGM-I	GGM-C GGM-R	MLE
	Model 1, n = 100, p = 30, q = 30
A	||ΔA||	0.17(0.026)	0.27(0.015)	0.62(0.057)	0.25(0.037)
	|||ΔA|||∞	0.35(0.042)	0.53(0.064)	1.23(0.133)	0.64(0.059)
	||ΔA||∞	0.08(0.019)	0.15(0.013)	0.34(0.066)	0.09(0.021)
	||ΔA||F	0.43(0.051)	0.73(0.025)	1.73(0.130)	0.60(0.044)
	SPEA	0.68(0.025)	0.32(0.156)	0.82(0.147)
	SENA	1.00(0.000)	1.00(0.000)	0.36(0.298)
	MCCA	0.54(0.022)	0.28(0.108)	0.23(0.068)
B	||ΔB||	0.15(0.026)	0.25(0.013)	0.61(0.052)	0.22(0.027)
	|||ΔB|||∞	0.32(0.044)	0.48(0.040)	1.28(0.100)	0.60(0.051)
	||ΔB||∞	0.08(0.018)	0.14(0.013)	0.31(0.056)	0.07(0.016)
	||ΔB||F	0.38(0.049)	0.68(0.026)	1.64(0.099)	0.57(0.033)
	SPEB	0.68(0.031)	0.40(0.060)	0.70(0.067)
	SENB	0.99(0.009)	1.00(0.006)	0.63(0.142)
	MCCB	0.47(0.027)	0.29(0.037)	0.25(0.055)
	Model 2, n = 100, p = 80, q = 80
A	||ΔA||	0.17(0.022)	0.31(0.020)	0.75(0.089)	0.25(0.021)
	|||ΔA|||∞	0.37(0.030)	0.58(0.030)	1.26(0.089)	0.93(0.045)
	||ΔA||∞	0.07(0.015)	0.19(0.015)	0.47(0.079)	0.06(0.014)
	||ΔA||F	0.67(0.082)	1.56(0.122)	3.30(0.515)	0.96(0.038)
	SPEA	0.89(0.080)	0.69(0.009)	1.00(0.000)
	SENA	1.00(0.000)	1.00(0.000)	0.00(0.000)
	MCCA	0.68(0.100)	0.43(0.008)	-
B	||ΔB||	0.14(0.013)	0.13(0.012)	0.72(0.147)	0.22(0.020)
	|||ΔB|||∞	0.45(0.047)	0.42(0.049)	1.45(0.117)	0.88(0.040)
	||ΔB||∞	0.06(0.008)	0.06(0.010)	0.53(0.180)	0.05(0.011)
	||ΔB||F	0.56(0.023)	0.54(0.025)	2.97(0.499)	0.91(0.023)
	SPEB	0.86(0.102)	0.69(0.010)	1.00(0.000)
	SENB	1.00(0.000)	1.00(0.000)	0.00(0.000)
	MCCB	0.64(0.124)	0.42(0.008)	0.06(0.000)

MNGM: the matrix normal graphical model with l₁ penalties; GGM-I: Gaussian graphical model treating rows or columns as independent; GGM-R/GGM-C: Gaussian graphical model that uses only data from the first column or the first row; MLE: maximum likelihood estimates. For each measurement, mean and standard deviation are calculated over 50 replications.

Table 2.

Comparison of the performance for simulated data sets of different dimensions when l₁ penalty functions are used.

Precision Matrix	Measure	MNGM	GGM-I	GGM-C GGM-R
	Model 3, n = 100, p = 150, q = 150
A	||ΔA||	0.12(0.014)	0.31(0.013)	0.78(0.094)
	|||ΔA|||∞	0.32(0.028)	0.59(0.027)	1.45(0.092)
	||ΔA||∞	0.05(0.011)	0.20(0.010)	0.49(0.074)
	||ΔA||F	0.61(0.069)	2.26(0.120)	4.72(0.802)
	SPEA	0.84(0.005)	0.80(0.004)	1.00(0.000)
	SENA	1.00(0.000)	1.00(0.000)	0.00(0.000)
	MCCA	0.45(0.006)	0.40(0.004)	0.05(0.022)
B	||ΔB||	0.10(0.009)	0.10(0.009)	0.77(0.186)
	|||ΔB|||	0.29(0.022)	0.32(0.025)	1.38(0.208)
	||ΔB||∞	0.04(0.007)	0.04(0.007)	0.58(0.236)
	||ΔB||F	0.53(0.025)	0.56(0.024)	4.25(0.856)
	SPEB	0.83(0.005)	0.80(0.003)	1.00(0.000)
	SENB	1.00(0.000)	1.00(0.000)	0.01(0.000)
	MCCB	0.43(0.007)	0.40(0.004)	0.07(0.021)
	Model 4, n = 100, p = 500, q = 500
A	||ΔA||	0.10(0.008)	0.22(0.008)	3.69(0.521)
	|||ΔA|||∞	0.27(0.018)	0.45(0.019)	4.23(0.502)
	||ΔA||∞	0.04(0.007)	0.14(0.006)	3.63(0.581)
	||ΔA||F	0.95(0.078)	2.94(0.131)	43.68(6.153)
	SPEA	0.99(0.001)	0.95(0.001)	1.00(0.002)
	SENA	1.00(0.00)	1.00(0.00)	0.01(0.038)
	MCCA	0.76(0.008)	0.52(0.003)	0.13(0.030)
B	||ΔB||	0.08(0.006)	0.08(0.006)	1.17(0.026)
	|||ΔB|||∞	0.26(0.019)	0.26(0.019)	6.88(0.809)
	||ΔB||∞	0.03(0.003)	0.03(0.004)	0.34(0.088)
	||ΔB||F	0.79(0.028)	0.76(0.031)	13.07(0.773)
	SPEB	0.98(0.001)	0.97(0.001)	0.64(0.055)
	SENB	1.00(0.000)	1.00(0.000)	0.65(0.095)
	MCCB	0.75(0.007)	0.62(0.003)	0.06(0.015)

MNGM: the matrix normal graphical model with l₁ penalties; GGM-I: Gaussian graphical model treating rows or columns as independent; GGM-R/GGM-C: Gaussian graphical model that uses only data from the first column or the first row. For each measurement, mean and standard deviation are calculated over 50 replications.

When p, q < n, as in Models 1 and 2, we have also implemented the penalized likelihood estimation with adaptive l₁ loss functions and performed simulation comparisons with the standard l₁ loss functions, where the maximum likelihood estimates of A and B are obtained and used as weights in the adaptive l₁ penalty functions. We present the results in Table 3. Comparing to the results in Table 1, we observe that using the adaptive penalties in the MNGM and the GGM-I can lead to better estimates of the precision matrixes and better recovery of the graphical structures defined by these precision matrices. However, if we only select one row or column and estimate the precision matrices using the GGM (GGM-R/GGM-C), the estimates based on the adaptive l₁ penalty functions are in general not as good as those based on the l₁ penalty functions. This is due to the fact that when only one row or one column is used, the sample size is small and the MLEs of the precision matrices may not provide sensible estimates of the weights in the adaptive penalty functions, which can lead to poor performance of the resulting estimates.

Table 3.

Comparison of the performance for simulated data sets of different dimensions when adaptive penalty functions are used.

Precision Matrix	Measure	MNGM	GGM-I	GGM-C GGM-R
	Model 1, n = 100, p = 30, q = 30
A	||ΔA||	0.15(0.024)	0.26(0.014)	0.64(0.033)
	|||ΔA|||∞	0.30(0.037)	0.51(0.037)	1.10(0.079)
	||ΔA||∞	0.08(0.021)	0.14(0.010)	0.35(0.061)
	||ΔA||F	0.37(0.046)	0.69(0.025)	1.74(0.059)
	SPEA	0.81(0.018)	0.41(0.028)	0.95(0.016)
	SENA	1.00(0.000)	1.00(0.000)	0.24(0.069)
	MCCA	0.67(0.022)	0.34(0.018)	0.27(0.059)
B	||ΔB||	0.14(0.024)	0.24(0.012)	0.66(0.040)
	|||ΔB|||∞	0.28(0.047)	0.48(0.037)	1.14(0.091)
	||ΔB||∞	0.08(0.019)	0.13(0.012)	0.35(0.043)
	||ΔB||F	0.35(0.052)	0.65(0.025)	1.70(0.078)
	SPEB	0.81(0.023)	0.42(0.023)	0.94(0.012)
	SENB	0.99(0.011)	1.00(0.006)	0.32(0.055)
	MCCB	0.60(0.029)	0.30(0.015)	0.32(0.056)
	Model 2, n = 100, p = 80, q = 80
A	||ΔA||	0.12(0.019)	0.28(0.020)	2.36(0.756)
	|||ΔA|||∞	0.28(0.034)	0.49(0.034)	2.94(0.792)
	||ΔA||∞	0.06(0.013)	0.18(0.015)	2.28(0.773)
	||ΔA||F	0.48(0.064)	1.44(0.123)	12.19(4.586)
	SPEA	0.92(0.005)	0.85(0.005)	1.00(0.000)
	SENA	1.00(0.000)	1.00(0.000)	0.00(0.000)
	MCCA	0.73(0.012)	0.59(0.008)	-
B	||ΔB||	0.12(0.011)	0.12(0.012)	4.78(1.206)
	|||ΔB|||∞	0.33(0.045)	0.34(0.049)	12.91(3.251)
	||ΔA||∞	0.06(0.009)	0.06(0.011)	0.74(0.320)
	||ΔA||F	0.44(0.027)	0.47(0.030)	10.48(2.145)
	SPEB	0.92(0.005)	0.85(0.008)	0.12(0.010)
	SENB	1.00(0.000)	1.00(0.000)	0.90(0.019)
	MCCB	0.73(0.013)	0.59(0.012)	0.02(0.018)

MNGM: the matrix normal graphical model with adaptive l₁ penalties; GGM-I: Gaussian graphical model treating rows or columns as independent; GGM-R/GGM-C: Gaussian graphical model that uses only data from the first column or the first row. For each measurement, mean and standard deviation are calculated over 50 replications.

As expected, since the precision matrices A and B are generated similarly and both are of the same dimensions, the estimates of these two precision matrices based on the MNGM are very comparable for all four models considered. Some differences in performances for estimating A and B in Model 4 are observed when the GGM-I or GGM-R/GGM-C is used. This is largely due to the large variability in selecting the tuning parameters when the dependence of the data is ignored as in GGM-I or when only partial data are used as in GGM-R/GGM-C.

Finally, Model 5 with n = 20, p = q = 600 mimics the scenario when n << min(p, q). The performances of the MNGM as shown in Table 4 are still quite comparable to the previous four models. However, estimates from the GGM-I or GGM-R/RRM-C are significantly worse, resulting much lower sensitivities and larger estimation errors.

Table 4.

Comparison of the performance for simulated data sets when n << min(p, q) and l₁ penalty functions are used (Model 5).

Precision Matrix	Measure	MNGM	GGM-I	GGM-C GGM-R
	Model 5, n = 20, p = 600, q = 600
A	||ΔA||	0.14(0.013)	0.85(0.012)	6.85(1.532)
	|||ΔA|||	0.67(0.041)	1.52(0.015)	10.9(3.799)
	||ΔA||∞	0.05(0.009)	0.43(0.01)	6.78(1.563)
	||ΔA||F	1.58(0.091)	10.17(0.188)	56.92(14.796)
	SPEA	0.84(0.005)	1(0)	0.98(0.025)
	SENA	1(0)	0.03(0.001)	0.04(0.042)
	MCCA	0.22(0.004)	0.18(0.004)	0.02(0.003)
B	||ΔB||	0.15(0.01)	0.54(0.015)	1.12(0.069)
	|||ΔB|||	0.75(0.037)	1.32(0.024)	4.06(0.344)
	||ΔB||∞	0.05(0.009)	0.23(0.005)	0.74(0.191)
	||ΔB||F	1.68(0.06)	6.84(0.023)	11.96(0.807)
	SPEB	0.81(0.006)	1(0)	0.93(0.001)
	SENB	1(0)	0.03(0.001)	0.11(0.008)
	MCCB	0.21(0.004)	0.16(0.004)	0.01(0.003)

MNGM: the matrix normal graphical model with l₁ penalties; GGM-I: Gaussian graphical model treating rows or columns as independent; GGM-R/GGM-C: Gaussian graphical model that uses only data from the first column or the first row. For each measurement, mean and standard deviation are calculated over 50 replications.

6. Real Data Analysis

We applied the MNGM to an analysis of the mouse gene expression data measured over different tissues from the Atlas of Gene Expression in Mouse Aging (AGEMAP) database [37]. In this study, the authors profiled the effects of aging on gene expressions in different mouse tissues dissected from C57BL/6 mice. Mice were of ages 1, 6, 16, and 24 months, with ten mice per age cohort and five mice of each sex. Sixteen tissues, the cerebellum, cerebrum, striatum, hippocampus, spinal cord, adrenal glands, heart, lung, liver, kidney, muscle, spleen, thymus, bone marrow, eye, and gonads, were dissected from each mouse. For each issue, mRNA was isolated and hybridized to two filter membranes containing a total of 16,896 cDNA clones corresponding to 8,932 genes. In our analysis, we leave out the data from six tissues, including cerebellum, bone-marrows, heart, gonads, striatum and liver, from our analysis due to the fact that some mice did not have data on these tissues. Due to the small sample size n = 40, we consider a set of 40 genes that belong to the mouse vascular endothelial growth factor (VEGF) signaling pathway and have measured gene expression levels over all 10 tissues.

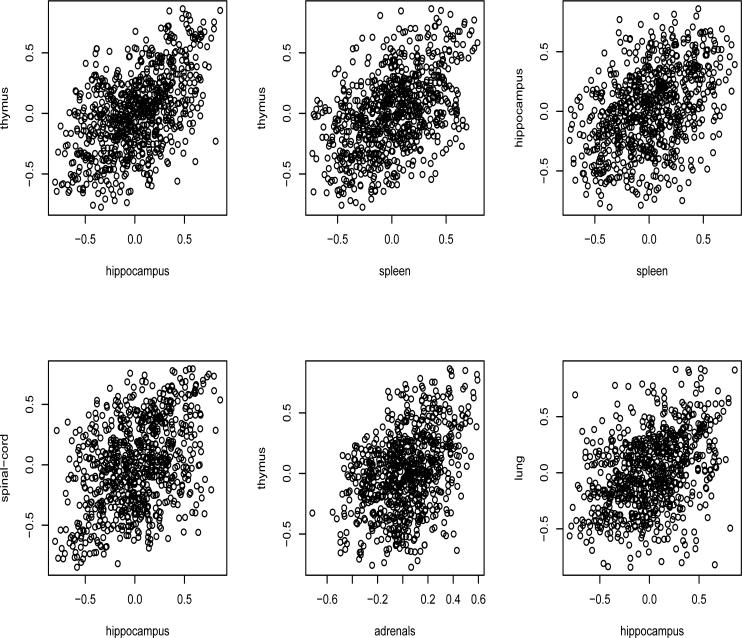
Figure 1 shows the scatter plots of the pair-wise correlations of expression levels of these 40 genes in different tissues, clearly indicating that many gene pairs have similar correlations across different tissues and also the gene expression levels are clearly not independent across multiple tissues. The plots indicate that the assumption of the Kronecker covariance structure for the gene-tissue matrix normal data would be helpful in studying the covariance structure of the genes across different tissues.

Figure 1.

Mouse gene expression data: scatter plots of pair-wise correlations of 40 genes across different tissues, showing that the expression levels in different issues are dependent.

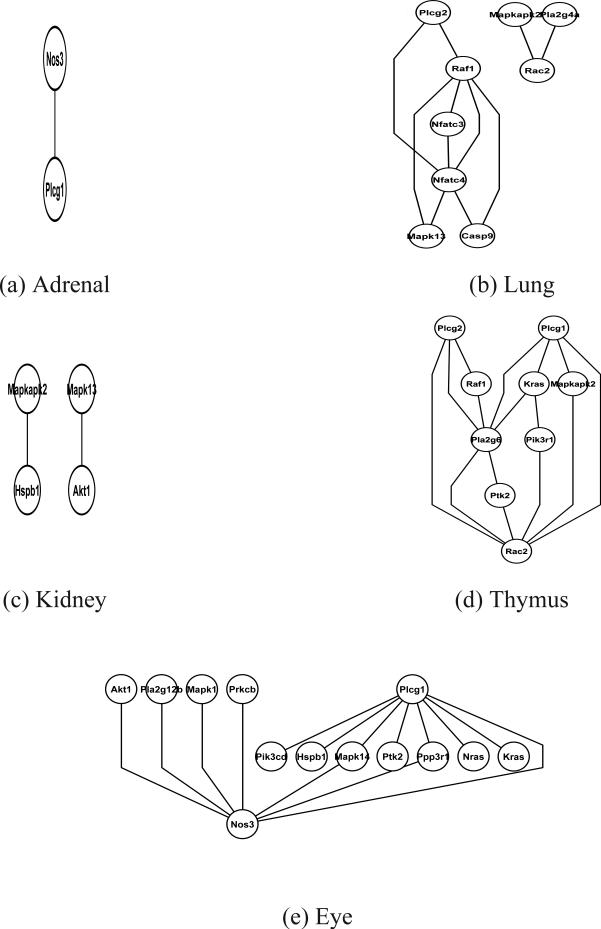
Our goal is to study the dependency structure of these 40 genes of the VEGF pathway using the expression data across all 10 tissues. When the standard GGM is used to the data of each of the tissues separately, gene networks are identified from five out of 10 tissues, including andrenal, kidney, lung, thymus and eye. However, no gene links are identified for the other five tissues. The corresponding gene network graphs are shown in Figure 2 for each of the five tissues. The networks identified based on the tissue-specific data only include a few VEGF genes, indicating lack of the power of the recovering biologically meaningful links based on data from single tissue. The differences of the identified networks from difference tissues might also be due to the fact that genes of the VEGF pathways are not perturbed enough in some tissues to make inferences on the conditional independence structures among the genes. On the other hand, if all the data are pooled together and the dependency of gene expression across issues is ignored, the GGM results in a very dense network with 373 links, which is biologically difficult to interpret given that the biological networks are expected to be sparse.

Figure 2.

Analysis of mouse gene expression data: networks identified by the GGM for each of the five tissues, including adrenal, lung, kidney, thymus and eye. The genes that belong to the mouse VEGF pathway are labeled on each of these network graphs. No networks are identified for other five tissues, including hippocampus, cerebral-cortex, spinal-cord, spleen and skeletal-muscle.

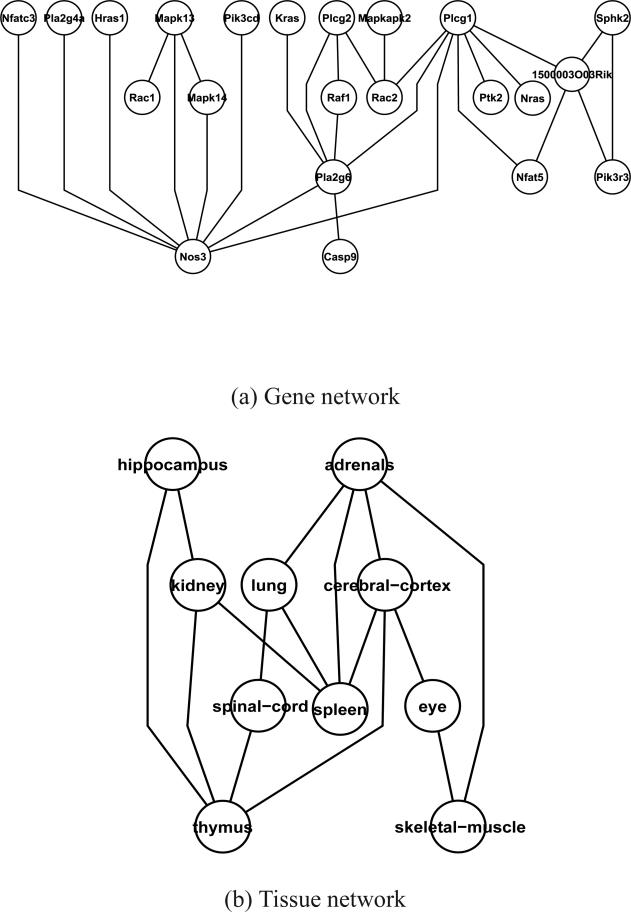
Figure 3 shows the gene and the tissue networks estimated by the proposed MNGM, including a gene network of 27 links among 22 VEGF genes and a tissue network with 15 edges among the 10 tissues. Compared to the networks estimated based on data from single tissue (see plots of Figure 2), we observe that more links are identified among these genes and many links identified by the MNGM appear in one of the graphs identified based on the issue-specific data. The difference between the overall network identified by the MNGM and the tissue-specific networks can also be due to the dependence structures of the VEGF genes are different in different tissues. It is interesting to note that many links identified by the MNGM may reflect the underlying VEGF signaling pathway [38]. For example, the binding of VEGF to VEGFR-2 leads to dimerization of the receptor, followed by intracellular activation of the PLCgamma (Plcg). It is interesting that several forms of the PLgamma gene such as Plcg1, Plcg2 and their downstream genes Nfat5 and Pla2g6 are part of network. Several genes on the PKC-Raf kinase-MEK-mitogen-activated protein kinase (MAPK) pathway such as Mapk13, Mapk14 and Mapkapk2 are interconnected.

Figure 3.

Analysis of mouse multi-tissue gene expression data using the MNGM: (a) Gene network, where the genes that belong to the mouse VEGF pathway are labeled on the network graph; (b) Tissue network based on gene expression data.

The tissue network as shown in Figure 3 (b) should be interpreted as the conditional dependency structure among the tissues with respect to the gene expression patterns observed among the genes on the VEGF pathway. It is interesting to observe links among lung, spleen and kidney in the vascular tissue group and links between eye and cerebral-cortex and between thymus and hippocampus in the neural tissue group. It is also interesting to observe that the adrenal tissue in the steroid responsive group is linked to both vascular and neural tissue groups. Similar clustering of tissue groups based on their gene expression data are also observed in [37].

7. Discussion

Motivated by analysis of gene expression data measured over different tissues on the same set of samples, we have proposed to apply the matrix normal distribution to model the data jointly and have developed a penalized likelihood method to estimate the row and column precision matrices assuming that both matrices are sparse. Our simulation results have clearly demonstrated such models can result in better estimates of the precision matrices and better identification of the corresponding graphical structures than naive application of the Gaussian graphical models. Our analysis of the mouse gene expression data demonstrated that by effectively combining the expression data from multiple tissues from the same subjects, the matrix normal graphical model can lead to conditional independence graph with meaningful biological interpretations. We also demonstrated that ignoring the dependency of gene expression across different tissues can lead to higher false positive links and dense graphs, which are difficult to interpret biologically.

The matrix normal distribution provides a nature way of modeling the dependency of data measured over different conditions. If the underlying precision matrices are sparse, the proposed penalized likelihood estimation can lead to identification of the non-zero elements in these precision matrix. We observe that the proposed l₁ regularized estimation can lead to better estimates of these sparse precision matrices than the MLEs. Such estimated precision matrices can in turn be applied to the problem of co-expression analysis [21], differential expression analysis [22] and the problem of estimating missing gene expression data. Other applications of the proposed methods include face recognition [39].

The methods proposed in this paper and the related theorems can also be extended to array normal distribution by extending the matrix-variate normal to the tensor array setting using the Tucker product [40]. Such array normal distributions were recently studied by Hoff [41]. Allen [29] proposed an l₁ penalized estimation for such an array normal distribution by regularizing separable tensor precision matrices. Similar techniques can be applied to derive the estimation error bounds and to prove the sparsistency when the adaptive l₁ penalties are used. As multi-dimensional data with possible correlations among the variables of each dimension is becoming more prevalent, further development of estimation methods and relevant theorems are important.

Appendix

Proof of Proposition 1

Before we state the proof of Proposition 1, we need the following lemma [1]:

Lemma Appendix .1. Using the same notation as in the main text, if we partition the columns of Y as Y = (Y₁, Y₂), where Y₁ is p × r, Y₂ is p × s random matrix respectively, with r + s = q. Then the conditional distribution of Y₁ given Y₂ = y₂ is $M{N}_{p\times r}({\mathbf{M}}_1+(y_2-{\mathbf{M}}_2){\mathbf{V}}_{22}^{-}{\mathbf{V}}_{21};\mathbf{U},{\mathbf{V}}_{1\mid 2})$, where M = (M₁, M₂) and ${\mathbf{V}}_{1\mid 2}={\mathbf{V}}_{11}-{\mathbf{V}}_{12}{\mathbf{V}}_{22}^{-}{\mathbf{V}}_{21}$.

Proof of Lemma Appendix .1. See Proposition C.8 in [1, Appendix C].

Proof of Proposition 2.1. From Lemma Appendix .1, we know Y_{γ,μ} given Y_Γ{γ,μ} is distributed as matrix normal $MN({\mathbf{M}}_1+(y_2-{\mathbf{M}}_2){\mathbf{V}}_{22}^{-}{\mathbf{V}}_{21};\mathbf{U},{\mathbf{V}}_{1\mid 2})$. From Proposition C.5 of [1, Appendix C], we have

$${\mathbf{B}}_{\{\gamma ,\mu \}}=\left(\begin{array}{cc}\hfill b_{\gamma \gamma }\hfill & \hfill b_{\gamma \mu }\hfill \\ \hfill b_{\mu \gamma }\hfill & \hfill b_{\mu \mu }\hfill \end{array}\right)={\mathbf{V}}_{1\mid 2}^{-1}.$$

So

$${\mathbf{V}}_{1\mid 2}={\mathbf{V}}_{\{\gamma ,\mu \}\mid \Gamma \setminus \{\gamma ,\mu \}}=\frac{1}{\text{det}{\mathbf{B}}_{\{\gamma ,\mu \}}}\left(\begin{array}{cc}\hfill b_{\mu \mu }\hfill & \hfill -b_{\gamma \mu }\hfill \\ \hfill -b_{\mu \gamma }\hfill & \hfill b_{\gamma \gamma }\hfill \end{array}\right).$$

From Proposition C.6 of [1, Appendix C] we know ${\mathbf{Y}}_{\gamma }⫫{\mathbf{Y}}_{\mu }\mid {\mathbf{Y}}_{\Gamma \setminus \{\gamma ,\mu \}}$ if and only if b_γμ = 0. Similar argument can be applied to the rows.

Proof of Theorem 1

Proof. Let M = M^T be p × p, N = N^T be q × q symmetric random matrices. Denote

$$f_n(\mathbf{M},\mathbf{N})=-q\text{log}\mid \mathbf{A}+\frac{\mathbf{M}}{n^{1∕2}}\mid -p\text{log}\mid \mathbf{B}+\frac{\mathbf{N}}{n^{1∕2}}\mid +\frac{1}{n}\sum _{k=1}^n\mathrm{tr}\left\{(\mathbf{A}+\frac{\mathbf{M}}{n^{1∕2}}){\mathbf{Y}}_k(\mathbf{B}+\frac{\mathbf{N}}{n^{1∕2}}){\mathbf{Y}}_k^T\right\}+\lambda \sum _{i\ne j}\mid a_{ij}+\frac{m_{ij}}{n^{1∕2}}\mid +\rho \sum _{i\ne j}\mid b_{ij}+\frac{n_{ij}}{n^{1∕2}}\mid +q\text{log}\mid \mathbf{A}\mid +p\text{log}\mid \mathbf{B}\mid -\frac{1}{n}\sum _{k=1}^n\mathrm{tr}\left\{{\mathbf{AY}}_k{\mathbf{BY}}_k^T\right\}-\lambda \sum _{i\ne j}\mid a_{ij}\mid -\rho \sum _{i\ne j}\mid b_{ij}\mid .$$

Using the same argument as in [5], we have

$$\begin{array}{cc}\hfill \text{log}\mid \mathbf{A}+\frac{\mathbf{M}}{n^{1∕2}}\mid -\text{log}\mid \mathbf{A}\mid & =\frac{\mathrm{tr}\left(\mathbf{MU}\right)}{n^{1∕2}}-\frac{\mathrm{tr}\left(\mathbf{MUMU}\right)}{n}+o\left(n^{-1}\right),\hfill \\ \hfill \text{log}\mid \mathbf{B}+\frac{N}{n^{1∕2}}\mid -\text{log}\mid \mathbf{B}\mid & =\frac{\mathrm{tr}\left(\mathbf{NV}\right)}{n^{1∕2}}-\frac{\mathrm{tr}\left(\mathbf{NVNV}\right)}{n}+o\left(n^{-1}\right).\hfill \end{array}$$

Let $T_k=\mathrm{tr}\left\{(\mathbf{A}+n^{-1∕2}\mathbf{M}){\mathbf{Y}}_k(\mathbf{B}+n^{-1∕2}\mathbf{N}){\mathbf{Y}}_k^T\right\}-\mathrm{tr}\left\{{\mathbf{AY}}_k{\mathbf{BY}}_k^T\right\}$, then

$$\begin{array}{cc}\hfill T_k& =n^{-1∕2}\mathrm{tr}\left({\mathbf{MY}}_k{\mathbf{BY}}_k^T\right)+n^{-1∕2}\mathrm{tr}\left({\mathbf{AY}}_k{\mathbf{NY}}_k^T\right)+n^{-1}\mathrm{tr}\left({\mathbf{MY}}_k{\mathbf{NY}}_k^T\right)\hfill \\ \hfill & =n^{-1∕2}{\left(\text{vec}{\mathbf{Y}}_k\right)}^T(\mathbf{B}\otimes \mathbf{M})\text{vec}{\mathbf{Y}}_k+n^{-1∕2}{\left(\text{vec}{\mathbf{Y}}_k\right)}^T(\mathbf{N}\otimes \mathbf{A})\text{vec}{\mathbf{Y}}_k+n^{-1}{\left(\text{vec}{\mathbf{Y}}_k\right)}^T(\mathbf{N}\otimes \mathbf{M})\text{vec}{\mathbf{Y}}_k.\hfill \end{array}$$

Denote Z_k = vecY_k, then $Z_k\sim N(0,\mathbf{V}\otimes \mathbf{U})$, $T_k=n^{-1∕2}{Z}_k^T(\mathbf{B}\otimes \mathbf{M}+\mathbf{N}\otimes \mathbf{A}+n^{-1∕2}\mathbf{N}\otimes \mathbf{M})Z_k$. Next we compute E(T_k) and var(T_k). First, $E\left(T_k\right)=n^{-1∕2}\mathrm{tr}\{(\mathbf{B}\otimes M)(\mathbf{V}\otimes \mathbf{U})+(\mathbf{N}\otimes \mathbf{A})(\mathbf{V}\otimes \mathbf{U})+n^{-1∕2}(\mathbf{N}\otimes \mathbf{M})(V\otimes \mathbf{U})\}$, so E(T_k) = n^−1/2[qtr(MU) + ptr(NV) + n^−1/2tr(NV)tr(MU)]. Next, $\text{var}\left(T_k\right)=E\left(T_k^2\right)-{\left\{E\left(T_k\right)\right\}}^2$ and $E\left(T_k^2\right)=n^{-1}E\left[Z_k^T\mathbf{L}{Z}_k{Z}_k^T\mathbf{L}{Z}_k\right]$, where $\mathbf{L}=\mathbf{B}\otimes \mathbf{M}+\mathbf{N}\otimes \mathbf{A}+n^{-1∕2}\mathbf{N}\otimes \mathbf{M}$. If Z ~ N(0, Σ), then

$$E\left(Z^T\mathbf{A}Z{Z}^T\mathbf{B}Z\right)=\mathrm{tr}\left\{\mathbf{A}\Sigma (\mathbf{B}+{\mathbf{B}}^T)\Sigma \right\}+\mathrm{tr}\left(\mathbf{A}\Sigma \right)\mathrm{tr}\left(\mathbf{B}\Sigma \right).$$ (.1)

Using (.1), we obtain

$$\begin{gathered} E\left(T_k^2\right)=2n^{-1}\{q\mathrm{tr}\left(\mathbf{MUMU}\right)+2\mathrm{tr}\left(\mathbf{NV}\right)\mathrm{tr}\left(\mathbf{MU}\right)+p\mathrm{tr}\left(\mathbf{NVNV}\right)+2n^{ \\ -1∕2}\mathrm{tr}\left(\mathbf{NV}\right)\mathrm{tr}\left(\mathbf{MUMU}\right)+2n^{-1∕2}\mathrm{tr}\left(\mathbf{MU}\right)\mathrm{tr}\left(\mathbf{NVNV}\right)+O\left(n^{-1}\right)\}+{\left\{E\left(T_k\right)\right\}}^2, \end{gathered}$$

and

$$\text{var}\left(T_k\right)=2n^{-1}\{q\mathrm{tr}\left(\mathbf{MUMU}\right)+p\mathrm{tr}\left(\mathbf{NVNV}\right)+2\mathrm{tr}\left(\mathbf{MU}\right)\mathrm{tr}\left(\mathbf{NV}\right)+2n^{-1∕2}\mathrm{tr}\left(\mathbf{NV}\right)\mathrm{tr}\left(\mathbf{MUMU}\right)+2n^{-1∕2}\mathrm{tr}\left(\mathbf{MU}\right)\mathrm{tr}\left(\mathbf{NVNV}\right)+O\left(n^{-1}\right)\}.$$

Let $\stackrel{‒}{T}=n^{-1}{\sum }_{k=1}^n{T}_k$, by the central limited theorem, W_n = n(T̄ – ET_k) → N(0, σ²), where σ² = 2[qtr(MUMU) + ptr(NVNV) + 2tr(MU)tr(NV)]. Finally,

$$n{f}_n(\mathbf{M},\mathbf{N})=-nq[\frac{\mathrm{tr}\left(\mathbf{MU}\right)}{n^{1∕2}}-\frac{\mathrm{tr}\left(\mathbf{MUMU}\right)}{n}+o\left(n^{-1}\right)]-np[\frac{\mathrm{tr}\left(\mathbf{NV}\right)}{n^{1∕2}}-\frac{\mathrm{tr}\left(\mathbf{NVNV}\right)}{n}+o\left(n^{-1}\right)]+n[\stackrel{‒}{T}-E\left(T_k\right)]+nE\left(T_k\right)+n^{1∕2}\lambda \sum _{i\ne j}\{m_{ij}\mathrm{sgn}\left(a_{ij}\right)I(a_{ij}\ne 0)+\mid m_{ij}\mid I(a_{ij}=0)\}+n^{1∕2}\rho \sum _{i\ne j}\{n_{ij}\mathrm{sgn}\left(b_{ij}\right)I(b_{ij}\ne 0)+\mid n_{ij}\mid I(b_{ij}=0)\}=p\mathrm{tr}\left(\mathbf{NVNV}\right)+q\mathrm{tr}\left(\mathbf{MUMU}\right)+\mathrm{tr}\left(\mathbf{MU}\right)\mathrm{tr}\left(\mathbf{NV}\right)+W_n+n^{1∕2}\lambda \sum _{i\ne j}\{m_{ij}\mathrm{sgn}\left(a_{ij}\right)I(a_{ij}\ne 0)+\mid m_{ij}\mid I(a_{ij}=0)\}+n^{1∕2}\rho \sum _{i\ne j}\{n_{ij}\mathrm{sgn}\left(b_{ij}\right)I(b_{ij}\ne 0)+\mid n_{ij}\mid I(b_{ij}=0)\},$$

so nf_n(M, N) → f(M, N).

Proof of Theorem 2

Proof. We prove this theorem by verifying the regularity conditions (A), (B) and (C) of [33] [42, also]. We use (A)_ij to denote the (i, j)th element of the matrix, a_ij. The log-likelihood function is

$$l=-npq∕2\text{log}\left(2\pi \right)+nq∕2\text{log}\left(\mid \mathbf{A}\mid \right)+np∕2\text{log}\left(\mid \mathbf{B}\mid \right)-1∕2\sum _{k=1}^n\mathrm{tr}\left({\mathbf{AY}}_k{\mathbf{BY}}_k^T\right).$$

So

$$\frac{\partial l}{\partial a_{ij}}=\frac{nq}{2}\frac{1}{\mid \mathbf{A}\mid }\mid \mathbf{A}\mid u_{ij}-\frac{1}{2}\sum _{k=1}^n{\left({\mathbf{Y}}_k{\mathbf{BY}}_k^T\right)}_{ij}.$$

On the other hand, $n^{-1}{\sum }_{k=1}^n{\mathbf{Y}}_k{\mathbf{BY}}_k^T$ is Wishart-distributed, so

$$E\{1∕\left(nq\right)\sum _{k=1}^n{\left({\mathbf{Y}}_k{\mathbf{BY}}_k^T\right)}_{ij}\}=u_{ij},$$

and E(∂l/∂a_ij) = 0. Similarly, one can verify E(∂l/∂b_ij) = 0, so the first part of condition (A) is verified. For the second part, we need to check

$$\begin{array}{cc}\hfill E(\partial l∕\partial a_{ij}\partial l∕\partial a_{kl})& =E(-{\partial }^{2}l∕(\partial a_{ij}\partial a_{kl})),\hfill \\ \hfill E(\partial l∕\partial b_{ij}\partial l∕\partial b_{kl})& =E(-{\partial }^{2}l∕(\partial b_{ij}\partial b_{kl})),\hfill \\ \hfill E(\partial l∕\partial b_{kl}\partial l∕\partial a_{ij})& =E(-{\partial }^{2}l∕(\partial b_{kl}\partial a_{ij})).\hfill \end{array}$$

From the property of the Wishart distribution,

$$E\left(\frac{\partial l}{\partial a_{ij}}\frac{\partial l}{\partial a_{kl}}\right)=\frac{1}{4}E\left[\sum _{k=1}^n\{{\left({\mathbf{Y}}_k{\mathbf{BY}}_k^T\right)}_{ij}-q{u}_{ij}\}\{{\left({\mathbf{Y}}_k{\mathbf{BY}}_k^T\right)}_{kl}-q{u}_{kl}\}\right]=\frac{nq}{2}{u}_{ij}{u}_{kl},$$

On the other hand, dA⁻¹ = −A⁻¹dAA⁻¹, so

$$\frac{{\partial }^{2}l}{\partial a_{ij}\partial a_{kl}}=\frac{\partial }{\partial a_{ij}}\left[\frac{nq}{2}\{u_{kl}-\frac{1}{nq}\sum _{m=1}^n{\left({\mathbf{Y}}_m{\mathbf{BY}}_m^T\right)}_{ij}\}\right]=-\frac{nq}{2}\frac{\partial u_{kl}}{\partial a_{ij}}=-\frac{nq}{2}{u}_{ij}{u}_{kl},$$

So E(∂l/∂a_ij∂l/∂a_kl) = E(−∂²l/(∂a_ij∂a_kl)) holds. We can similarly verify that E(∂l/∂b_ij∂l/∂b_kl) = E(−∂²l/(∂b_ij∂b_kl)). Denote the orthogonal bases e_i = (0, ···, 1, ··· 0), which is a vector of all zero except the ith element. We have

$$\begin{array}{cc}\hfill -\frac{{\partial }^{2}l}{\partial b_{kl}\partial a_{ij}}& =\frac{1}{2}\sum _{s=1}^n\frac{\partial }{\partial b_{kl}}\{{\left({\mathbf{Y}}_s{\mathbf{BY}}_s^T\right)}_{ij}-q{u}_{ij}\}=\frac{1}{2}\sum _{s=1}^n\frac{\partial }{\partial b_{kl}}\mathrm{tr}\left({\mathbf{BY}}_s^T{e}_j{e}_i^T{\mathbf{Y}}_s\right)\hfill \\ \hfill & =\frac{1}{2}\sum _{s=1}^n{\left({\mathbf{Y}}_s^T{e}_i{e}_j^T{\mathbf{Y}}_s\right)}_{kl}=\frac{1}{2}\sum _{s=1}^n\mathrm{tr}\left({\mathbf{Y}}_s^T{e}_i{e}_j^T{\mathbf{Y}}_s{e}_l{e}_k^T\right)\hfill \\ \hfill & =\frac{1}{2}\sum _{s=1}^n{\left(\text{vec}{\mathbf{Y}}_s\right)}^T(e_l{e}_k^T\otimes e_j{e}_i^T)\text{vec}{\mathbf{Y}}_s,\hfill \\ \hfill E(-\frac{{\partial }^{2}l}{\partial b_{kl}\partial a_{ij}})& =\frac{1}{2}\sum _{s=1}^n\mathrm{tr}\left\{(e_l{e}_k^T\otimes e_j{e}_i^T)(\mathbf{V}\otimes \mathbf{U})\right\}=\frac{1}{2}\sum _{s=1}^n\mathrm{tr}\left(e_l{e}_k^T\mathbf{V}\right)\mathrm{tr}\left(e_j{e}_i^T\mathbf{U}\right)\hfill \\ \hfill & =\frac{n}{2}{u}_{ij}{v}_{kl}.\hfill \end{array}$$

Using the same notation as in the proof of Theorem 1, let Z_k = vecY_k, then $Z_k\sim N(0,\mathbf{V}\otimes \mathbf{U})$. We then have

$$\begin{array}{cc}\hfill E\left(\frac{\partial l}{\partial b_{kl}}\frac{\partial l}{\partial a_{ij}}\right)& =\frac{1}{4}\sum _{s=1}^{n}E\left[\{{\left({\mathbf{Y}}_s^T{\mathbf{AY}}_s\right)}_{kl}-p{v}_{kl}\}\{{\left({\mathbf{Y}}_s{\mathbf{BY}}_s^T\right)}_{ij}-q{u}_{ij}\}\right]\hfill \\ \hfill & =\frac{1}{4}\sum _{s=1}^{n}E\{\left(e_i^T{\mathbf{Y}}_s{\mathbf{BY}}_s^T{e}_j\right)\left(e_k^T{\mathbf{Y}}_s^T{\mathbf{AY}}_s{e}_l\right)-pq{u}_{ij}{v}_{kl}\},\hfill \end{array}$$

and $e_i^T{\mathbf{Y}}_s{\mathbf{BY}}_s^T{e}_j=\mathrm{tr}\left(e_j{e}_i^T{\mathbf{Y}}_s{\mathbf{BY}}_s^T\right)={\left(\text{vec}{\mathbf{Y}}_s\right)}^T\{\mathbf{B}\otimes \left(e_j{e}_i^T\right)\}\text{vec}{\mathbf{Y}}_s=Z_s^T\{\mathbf{B}\otimes \left(e_j{e}_i^T\right)\}{Z}_s$, and $e_k^T{\mathbf{Y}}_s^T{\mathbf{AY}}_s{e}_l=Z_s^T\{\left(e_k{e}_l^T\right)\otimes \mathbf{A}\}{Z}_s$. Denote $\mathbf{K}=\mathbf{B}\otimes \left(e_j{e}_i^T\right)$, $\mathbf{L}=\left(e_k{e}_l^T\right)\otimes \mathbf{A}$, so $E\left\{\left(e_i^T{\mathbf{Y}}_s{\mathbf{BY}}_s^T{e}_j\right)\left(e_k^T{\mathbf{Y}}_s^T{\mathbf{AY}}_s{e}_l\right)\right\}=E\left(Z_s^T\mathbf{K}{Z}_s{Z}_s^T\mathbf{L}{Z}_s\right)$. Using (.1), we have

$$\begin{array}{cc}\hfill E\left({\mathbf{Y}}_s^T\mathbf{K}{Z}_s{Z}_s^T\mathbf{L}{Z}_s\right)& =\mathrm{tr}\left[\{\mathbf{B}\otimes \left(e_j{e}_i^T\right)\}(\mathbf{V}\otimes \mathbf{U})\{\left(e_k{e}_l^T\right)\otimes \mathbf{A}+\left(e_l{e}_k^T\right)\otimes \mathbf{A}\}(\mathbf{V}\otimes \mathbf{U})\right]+\mathrm{tr}\{I_q\otimes \left(e_j{e}_i^T\mathbf{U}\right)\}\mathrm{tr}\{\left(e_k{e}_l^T\mathbf{V}\right)\otimes I_p\}\hfill \\ \hfill & =v_{lk}{u}_{ij}+v_{kl}{u}_{ij}+pq{u}_{ij}{v}_{kl}=2v_{kl}{u}_{ij}+pq{u}_{ij}{v}_{kl}.\hfill \end{array}$$

So E(∂l/∂b_kl∂l/∂a_ij) = n/2u_ijv_kl, and E{−∂²l/(∂b_kl∂a_ij)} = E(∂l/∂b_kl∂l/∂a_ij). The condition (A) is verified.

Next, we verify condition (B). We have

$$\begin{array}{c}\hfill -2dl=-nq\mathrm{tr}\left(\mathbf{U}d\mathbf{A}\right)-np\mathrm{tr}\left(\mathbf{V}d\mathbf{B}\right)+\sum _{k=1}^n\{\mathrm{tr}\left({\mathbf{Y}}_k{\mathbf{BY}}_k^{T}d\mathbf{A}\right)+\mathrm{tr}\left({\mathbf{Y}}_k^T{\mathbf{AY}}_{k}d\mathbf{B}\right)\},\hfill \\ \hfill -2d^{2}l=nq\mathrm{tr}\left(\mathbf{U}d\mathbf{AU}d\mathbf{A}\right)+np\mathrm{tr}\left(\mathbf{V}d\mathbf{BV}d\mathbf{B}\right)+2\sum _{k=1}^n\mathrm{tr}\left({\mathbf{Y}}_{k}d{\mathbf{BY}}_k^{T}d\mathbf{A}\right)\hfill \\ \hfill =[{\left(d\text{vec}\mathbf{A}\right)}^T,{\left(d\text{vec}\mathbf{B}\right)}^T]\left(\begin{array}{cc}nq(\mathbf{U}\otimes \mathbf{U})\hfill & \hfill \sum _{k=1}^n{\mathbf{Y}}_k\otimes {\mathbf{Y}}_k\\ \sum _{k=1}^n{\mathbf{Y}}_k^T\otimes {\mathbf{Y}}_k^T\hfill & \hfill np(\mathbf{V}\otimes \mathbf{V})\end{array}\right)\left(\begin{array}{c}\hfill d\text{vec}\mathbf{A}\hfill \\ \hfill d\text{vec}\mathbf{B}\hfill \end{array}\right).\hfill \end{array}$$

One can verify that $E\left({\mathbf{Y}}_{ij}^{\left(k\right)}{\mathbf{Y}}_{pq}^{\left(k\right)}\right)=u_{ip}{v}_{jq}$, where ${\mathbf{Y}}_{ij}^{\left(k\right)}$ is the (i, j)th entry of Y_k's. So $E({\mathbf{Y}}_k\otimes {\mathbf{Y}}_k)=\left(\text{vec}\mathbf{U}\right){\left(\text{vec}\mathbf{V}\right)}^T$. Denote I(A, B) as the Fisher information matrix, then

$$2I(\mathbf{A},\mathbf{B})=\left(\begin{array}{cc}nq(\mathbf{U}\otimes \mathbf{U})\hfill & \hfill n\left(\text{vec}\mathbf{U}\right){\left(\text{vec}\mathbf{V}\right)}^T\\ n\left(\text{vec}\mathbf{V}\right){\left(\text{vec}\mathbf{U}\right)}^T\hfill & \hfill np(\mathbf{V}\otimes \mathbf{V})\end{array}\right).$$ (.2)

To see I(A, B) is non-negative definite, one only needs to check $np(\mathbf{V}\otimes \mathbf{V})-n∕q\left(\text{vec}\mathbf{V}\right){\left(\text{vec}\mathbf{U}\right)}^T(\mathbf{A}\otimes \mathbf{A})\left(\text{vec}\mathbf{U}\right){\left(\text{vec}\mathbf{V}\right)}^T=np\{\mathbf{V}\otimes \mathbf{V}-1∕q\left(\text{vec}\mathbf{V}\right){\left(\text{vec}\mathbf{V}\right)}^T\}$ is so. This is equivalent to check that for any vector t ≠ 0 in $R^{q^2}$,

$$t^T\{\mathbf{V}\otimes \mathbf{V}-1∕q\left(\text{vec}\mathbf{V}\right){\left(\text{vec}\mathbf{V}\right)}^T\}t\ge 0.$$

Denote q × q matrix D such that vecD = t, then

$$t^T\{V\otimes V-1∕q\left(\text{vec}V\right){\left(\text{vec}V\right)}^T\}t=\mathrm{tr}\left(V{D}^{T}VD\right)-\frac{1}{q}{\left\{\mathrm{tr}\left(VD\right)\right\}}^2$$ (.3)

Since V is non-negative definite, V^1/2 is well defined, denote V^1/2DV^1/2 = A, then A^T = V^1/2D^TV^1/2 and (.3) = tr(A^TA) – 1/q[tr(A)]². But in general, one has the inequality [tr(A^TB)]² ≤ tr(A^TA)tr(B^TB), so ${\left[\mathrm{tr}\left(\mathbf{A}\right)\right]}^2={\left[\mathrm{tr}\left({\mathbf{A}}^T{I}_q\right)\right]}^2\le \mathrm{tr}\left({\mathbf{A}}^T\mathbf{A}\right)\mathrm{tr}\left(I_q^2\right)=q\mathrm{tr}\left({\mathbf{A}}^T\mathbf{A}\right)$, thus we proved the condition (B).

Since the third derivative of the log-likelihood function doesn't involve any random variable, condition (C) is easy to satisfy. Theorem 2 thus holds.

Proof of Lemma 4.1

Proof. We use the notation Y^(k) to refer to Y_k for convenience. We then have

$${({\mathbf{S}}_n-{\Sigma }_0)}_{(i,j)(k,l)}=1∕n\sum _{s=1}^n({\mathbf{Y}}_{ik}^{\left(s\right)}{\mathbf{Y}}_{jl}^{\left(s\right)}-u_{ij}{v}_{kl}).$$

Since vec(Y^(s)) is normally distributed, Lemma A.3 of [34] leads to the fact that there exist some constants δ, C₁ and C₂ depending on ε₁ and ε₃ only such that

$$Pr\left(\mid \sum _{s=1}^n({\mathbf{Y}}_{ik}^{\left(s\right)}{\mathbf{Y}}_{jl}^{\left(s\right)}-u_{ij}{u}_{kl})\mid \ge nt\right)\le C_1\text{exp}\{-C_{2}n{t}^2\},\text{for}\mid \mathrm{t}\mid \le \delta .$$

Hence we have

$$Pr\left(\underset{\begin{array}{c}\hfill (i,j)\hfill \\ \hfill (k,l)\hfill \end{array}}{\text{max}}\mid {({\mathbf{S}}_n-{\Sigma }_0)}_{(i,j)(k,l)}\mid \ge t\right)\le C_1{p}_n^2{q}_n^2\text{exp}\{-C_{2}n{t}^2\},\text{for}\mid \mathrm{t}\mid \le \delta ,$$

which proves the lemma.

Proof of Theorem 3

Proof. Let W₁ be a symmetric matrix of dimension p_n and W₂ be a symmetric matrix of dimension q_n. Let D_W1, D_W2 be their diagonal matrices, and R_W1 = W₁ – D_W1, R_W2 = W₂ – D_W2 be their off-diagonal matrices, respectively. Set Δ_W1 = α_nR_W1 + β_nD_W1 and Δ_W2 = δ_nR_W2 + β_nD_W2. We show that, for ${\alpha }_n=\sqrt{q_n{s}_{n1}(\text{log}{p}_n+\text{log}{q}_n)∕n}$, ${\beta }_n=\sqrt{q_n{p}_n(\text{log}{p}_n+\text{log}{q}_n)∕n}$ and ${\delta }_n=\sqrt{p_n{s}_{n2}(\text{log}{p}_n+\text{log}{q}_n)∕n}$, for a set $\mathcal{A}$ defined as

$$\mathcal{A}=\left\{({\mathbf{W}}_1,{\mathbf{W}}_2):{\Vert {\Delta }_{{\mathbf{W}}_1}\Vert }_F^2=C_1^2{\alpha }_n^2+C_2^2{\beta }_n^{2}and{\Vert {\Delta }_{{\mathbf{W}}_2}\Vert }_F^2=C_3^2{\delta }_n^2+C_4^2{\beta }_n^2\right\},Pr(\underset{({\mathbf{W}}_1,{\mathbf{W}}_2)\in \mathcal{A}}{\text{inf}}\varphi ({\mathbf{A}}_0+{\Delta }_{{\mathbf{W}}_1},{\mathbf{B}}_0+{\Delta }_{{\mathbf{W}}_2})>\varphi ({\mathbf{A}}_0,{\mathbf{B}}_0))\to 1,$$

for sufficiently large constants C₁, C₂, C₃ and C₄. Denote ${\mathbf{A}}_1={\mathbf{A}}_0+{\Delta }_{{\mathbf{W}}_1}=\left(a_{ij}^{\left(1\right)}\right)$, ${\mathbf{B}}_1={\mathbf{B}}_0+{\Delta }_{{\mathbf{W}}_2}=\left(b_{ij}^{\left(1\right)}\right)$, then

$$\varphi ({\mathbf{A}}_1,{\mathbf{B}}_1)-\varphi ({\mathbf{A}}_0,{\mathbf{B}}_0)=-q_n[\text{log}\left(\mid {\mathbf{A}}_1\mid \right)-\text{log}\left(\mid {\mathbf{A}}_0\mid \right)]-p_n[\text{log}\left(\mid {\mathbf{B}}_1\mid \right)-\text{log}\left(\mid {\mathbf{B}}_0\mid \right)]+\frac{1}{n}\sum _{s=1}^n\mathrm{tr}\left\{{\mathbf{A}}_1{\mathbf{Y}}^{\left(s\right)}{\mathbf{B}}_1{\mathbf{Y}}^{\left(s\right)T}\right\}-\frac{1}{n}\sum _{s=1}^n\mathrm{tr}\left\{{\mathbf{A}}_0{\mathbf{Y}}^{\left(s\right)}{\mathbf{B}}_0{\mathbf{Y}}^{\left(s\right)T}\right\}+{\lambda }_n\sum _{i\ne j}\{\mid a_{ij}^{\left(1\right)}\mid -\mid a_{ij}^{\left(0\right)}\mid \}+{\rho }_n\sum _{k\ne l}\{\mid b_{ij}^{\left(1\right)}\mid -\mid b_{ij}^{\left(0\right)}\mid \}.$$ (.4)

So ϕ(A₁, B₁) − ϕ(A₀, B₀) = I₁ + I₂ + I₃ + I₄ + I₅, where

$$\begin{array}{cc}\hfill I_1& =\frac{1}{n}\sum _{s=1}^n[\mathrm{tr}\left\{{\mathbf{A}}_1{\mathbf{Y}}^{\left(s\right)}{\mathbf{B}}_1{\mathbf{Y}}^{\left(s\right)}{\mathbf{B}}_1{\mathbf{Y}}^{\left(s\right)T}\right\}-\mathrm{tr}\left\{{\mathbf{A}}_0{\mathbf{Y}}^{\left(s\right)}{\mathbf{B}}_0{\mathbf{Y}}^{\left(s\right)T}\right\}]-q_n[\text{log}\left(\mid {\mathbf{A}}_1\mid \right)-\text{log}\left(\mid {\mathbf{A}}_0\mid \right)]-p_n[\text{log}\left(\mid {\mathbf{B}}_1\mid \right)-\text{log}\left(\mid {\mathbf{B}}_0\mid \right)],\hfill \\ \hfill I_2& ={\lambda }_n\sum _{(i,j)\in S_A^c}\{\mid a_{ij}^{\left(1\right)}\mid -\mid a_{ij}^{\left(0\right)}\mid \},\hfill \\ \hfill I_3& ={\lambda }_n\sum _{\begin{array}{c}\hfill i\ne j\hfill \\ \hfill (i,j)\in S_A\hfill \end{array}}\{\mid a_{ij}^{\left(1\right)}\mid -\mid a_{ij}^{\left(0\right)}\mid \},\hfill \\ \hfill I_4& ={\rho }_n\sum _{(k,l)\in S_B^c}\{\mid b_{kl}^{\left(1\right)}\mid -\mid b_{kl}^{\left(0\right)}\mid \},\hfill \\ \hfill I_5& ={\rho }_n\sum _{\begin{array}{c}\hfill k\ne l\hfill \\ \hfill (k,l)\in S_B\hfill \end{array}}\{\mid b_{kl}^{\left(1\right)}\mid -\mid b_{kl}^{\left(0\right)}\mid \}.\hfill \end{array}$$

Denote Δ_A = Δ_W1, Δ_B = Δ_W2 and recall the definitions of ${\mathbf{S}}_n=1∕n{\sum }_{s=1}^n{\mathbf{Y}}^{\left(s\right)}\otimes {\mathbf{Y}}^{\left(s\right)}\text{and}{\Sigma }_0=\left(\text{vec}{\mathbf{U}}_0\right){\left(\text{vec}{\mathbf{V}}_0\right)}^T=E{\mathbf{S}}_n$. Using Taylor's expansion with integral residues, we have

$$I_1=-q_n\mathrm{tr}\left\{{\mathbf{A}}_0^{-1}{\Delta }_A\right\}-p_n\mathrm{tr}\left\{{\mathbf{B}}_0^{-1}{\Delta }_B\right\}+{\left(\text{vec}{\Delta }_A\right)}^T({\mathbf{S}}_n-{\Sigma }_0+{\Sigma }_0)\left(\text{vec}{\mathbf{B}}_0\right)+{\left(\text{vec}{\mathbf{A}}_0\right)}^T({\mathbf{S}}_n-{\Sigma }_0+{\Sigma }_0)\left(\text{vec}{\Delta }_B\right)+q_n{\int }_0^1(1-v)dv{\left(\text{vec}{\Delta }_A\right)}^T({\mathbf{A}}_v^{-1}\otimes {\mathbf{A}}_v^{-1})\left(\text{vec}{\Delta }_A\right)+p_n{\int }_0^1(1-v)dv{\left(\text{vec}{\Delta }_B\right)}^T({\mathbf{B}}_v^{-1}\otimes {\mathbf{B}}_v^{-1})\left(\text{vec}{\Delta }_B\right)+{\left(\text{vec}{\Delta }_A\right)}^T({\mathbf{S}}_n-{\Sigma }_0+{\Sigma }_0)\left(\text{vec}{\Delta }_B\right),$$ (.5)

where A_v = A₀ + vΔ_A, B_v = B₀ + vΔ_B. One can easily check that

$${\left(\text{vec}{\Delta }_A\right)}^T{\Sigma }_0\left(\text{vec}{\mathbf{B}}_0\right)={\left(\text{vec}{\Delta }_A\right)}^T\left(\text{vec}{\mathbf{U}}_0\right){\left(\text{vec}{\mathbf{V}}_0\right)}^T\left(\text{vec}{\mathbf{B}}_0\right)=\mathrm{tr}\left({\mathbf{U}}_0^T{\Delta }_A\right)\mathrm{tr}\left({\mathbf{V}}_0^T{\mathbf{B}}_0\right)=q_n\mathrm{tr}\left({\mathbf{U}}_0{\Delta }_A\right),$$

and similarly, (vecA₀)^TΣ₀(vecΔ_B) = p_ntr(V₀Δ_B). Then I₁ can be further simplified as I₁ = K₁ + K₂ + K₃ + K₄ + K₅ + K₆, where

$$\begin{array}{cc}\hfill K_1& =q_n{\int }_0^1(1-v)dv{\left(\text{vec}{\Delta }_A\right)}^T({\mathbf{A}}_v^{-1}\otimes {\mathbf{A}}_v^{-1})\left(\text{vec}{\Delta }_A\right),\hfill \\ \hfill K_2& =p_n{\int }_0^1(1-v)dv{\left(\text{vec}{\Delta }_B\right)}^T({\mathbf{B}}_v^{-1}\otimes {\mathbf{B}}_v^{-1})\left(\text{vec}{\Delta }_B\right),\hfill \\ \hfill K_3& ={\left(\text{vec}{\Delta }_A\right)}^T({\mathbf{S}}_n-{\Sigma }_0)\left(\text{vec}{\mathbf{B}}_0\right),\hfill \\ \hfill K_4& ={\left(\text{vec}{\mathbf{A}}_0\right)}^T({\mathbf{S}}_n-{\Sigma }_0)\left(\text{vec}{\Delta }_B\right),\hfill \\ \hfill K_5& =\mathrm{tr}\left({\mathbf{U}}_0{\Delta }_A\right)\mathrm{tr}\left({\mathbf{V}}_0{\Delta }_B\right),\hfill \\ \hfill K_6& ={\left(\text{vec}{\Delta }_A\right)}^T({\mathbf{S}}_n-{\Sigma }_0)\left(\text{vec}{\Delta }_B\right).\hfill \end{array}$$

Note that

$$\begin{array}{cc}\hfill K_1& \ge q_n{\Vert {\Delta }_A\Vert }_F^2∕2\underset{0\le v\le 1}{\text{min}}{\lambda }_{\text{max}}^{-2}\left({\mathbf{A}}_v\right)\hfill \\ \hfill & \ge q_n{\Vert {\Delta }_A\Vert }_F^2∕2{(\Vert {\mathbf{A}}_0\Vert +\Vert {\Delta }_A\Vert )}^{-2}\hfill \\ \hfill & \ge q_n∕2{\Vert {\Delta }_A\Vert }_F^2{({\epsilon }_2+o\left(1\right))}^{-2}=q_n∕2(C_1^2{\alpha }_n^2+C_2^2{\beta }_n^2){({\epsilon }_2+o\left(1\right))}^{-2},\hfill \end{array}$$ (.6)

$$K_2\ge p_n∕2{\Vert {\Delta }_B\Vert }_F^2{({\epsilon }_4+o\left(1\right))}^{-2}=p_n∕2(C_3^2{\delta }_n^2+C_4^2{\beta }_n^2){({\epsilon }_4+o\left(1\right))}^{-2}.$$ (.7)

Since

$${\mathbf{A}}_v^{-1}=(I_p-v{\mathbf{U}}_0{\Delta }_A+v^2{\mathbf{U}}_0{\Delta }_A{\mathbf{U}}_0{\Delta }_A+\cdots ){\mathbf{A}}_0^{-1},$$

hence

$$\mathrm{tr}\left({\mathbf{A}}_v^{-1}{\Delta }_A^T{\mathbf{A}}_v^{-1}{\Delta }_A\right)=\mathrm{tr}\left({\mathbf{A}}_0^{-1}{\Delta }_A^T{\mathbf{A}}_0^{-1}{\Delta }_A\right)(1+o\left(1\right)),$$

then

$$K_1\ge q_n∕2\underset{0\le v\le 1}{\text{min}}\mathrm{tr}\left({\mathbf{A}}_v^{-1}{\Delta }_A^T{\mathbf{A}}_v^{-1}{\Delta }_A\right),$$

so

$$K_1\ge q_n∕2\mathrm{tr}\left({\mathbf{U}}_0{\Delta }_A^T{\mathbf{U}}_0{\Delta }_A\right)(1+o\left(1\right)),$$ (.8)

and similarly

$$K_2\ge p_n∕2\mathrm{tr}\left({\mathbf{V}}_0{\Delta }_B^T{\mathbf{V}}_0{\Delta }_B\right)(1+o\left(1\right)).$$ (.9)

Generally, for two squared p × p matrix M and q × q matrix N, we have $\mathrm{tr}\left(\mathbf{M}\right)\le \sqrt{p\mathrm{tr}\left({\mathbf{M}}^T\mathbf{M}\right)},\mathrm{tr}\left(\mathbf{N}\right)\le \sqrt{q\mathrm{tr}\left({\mathbf{N}}^T\mathbf{N}\right)}$ and then

$$\mid \mathrm{tr}\left(\mathbf{M}\right)\mathrm{tr}\left(\mathbf{N}\right)\mid \le \sqrt{pq\mathrm{tr}\left({\mathbf{M}}^T\mathbf{M}\right)\mathrm{tr}\left({\mathbf{N}}^T\mathbf{N}\right)}\le \frac{1}{2}q\mathrm{tr}\left({\mathbf{M}}^T\mathbf{M}\right)+\frac{1}{2}p\mathrm{tr}\left({\mathbf{N}}^T\mathbf{N}\right).$$

Let $\mathbf{M}={\mathbf{U}}_0^{1∕2}{\Delta }_{\mathbf{A}}{\mathbf{U}}_0^{1∕2}$, $\mathbf{N}={\mathbf{V}}_0^{1∕2}{\Delta }_{\mathbf{B}}{\mathbf{V}}_0^{1∕2}$, we have

$$\mid K_5\mid =\mid \mathrm{tr}\left({\mathbf{U}}_0{\Delta }_{\mathbf{A}}\right)\mathrm{tr}\left({\mathbf{V}}_0{\Delta }_{\mathbf{B}}\right)\mid =\mid \mathrm{tr}\left(\mathbf{M}\right)\mathrm{tr}\left(\mathbf{N}\right)\mid \le \frac{1}{2}{q}_n\mathrm{tr}\left({\mathbf{M}}^T\mathbf{M}\right)+\frac{1}{2}{p}_n\mathrm{tr}\left(N^T\mathbf{N}\right)=\frac{1}{2}{q}_n\mathrm{tr}\left({\mathbf{U}}_0{\Delta }_{\mathbf{A}}^T{\mathbf{U}}_0{\Delta }_{\mathbf{A}}\right)+\frac{1}{2}{p}_n\mathrm{tr}\left({\mathbf{V}}_0{\Delta }_{\mathbf{B}}^T{\mathbf{V}}_0{\Delta }_{\mathbf{B}}\right).$$

Combining with (.8) and (.9) we know that |K₅| is dominated by K₁ + K₂ with a large probability.

Next we bound |K₃| and |K₄|. We have

$$\begin{array}{cc}\hfill \mid K_3\mid & =\mid {\left(\text{vec}{\Delta }_A\right)}^T({\mathbf{S}}_n-{\Sigma }_0)\left(\text{vec}{\mathbf{B}}_0\right)\mid \le L_1+L_2,\hfill \\ \hfill \mid K_4\mid & =\mid {\left(\text{vec}{\mathbf{A}}_0\right)}^T({\mathbf{S}}_n-{\Sigma }_0)\left(\text{vec}{\Delta }_B\right)\mid \le L_3+L_4,\hfill \end{array}$$

where if we use double index to indicate a row or column in S_n, Σ₀ or a position in vecΔ_A, vecB₀, vecA₀ and vecΔ_B, we have

$$L_1=\sum _{\begin{array}{c}\hfill i\ne j,(i,j)\in S_A\hfill \\ \hfill (k,l)\hfill \end{array}}\mid {\left({\Delta }_A\right)}_{(i,j)}{({\mathbf{S}}_n-{\Sigma }_0)}_{(i,j)(k,l)}{\left({\mathbf{B}}_0\right)}_{(k,l)}\mid ,$$

$$L_2=\sum _{\begin{array}{c}\hfill (i,j)\in S_A^c\hfill \\ \hfill (k,l)\hfill \end{array}}\mid {\left({\Delta }_A\right)}_{(i,j)}{({\mathbf{S}}_n-{\Sigma }_0)}_{(i,j)(k,l)}{\left({\mathbf{B}}_0\right)}_{(k,l)}\mid ,$$

$$L_3=\sum _{\begin{array}{c}\hfill k\ne l,(k,l)\in S_B\hfill \\ \hfill (i,j)\hfill \end{array}}\mid {\left({\mathbf{A}}_0\right)}_{(i,j)}{({\mathbf{S}}_n-{\Sigma }_0)}_{(i,j)(k,l)}{\left({\Delta }_B\right)}_{(k,l)}\mid ,$$

and

$$L_4=\sum _{\begin{array}{c}\hfill (k,l)\in S_B^c\hfill \\ \hfill (i,j)\hfill \end{array}}\mid {\left({\mathbf{A}}_0\right)}_{(i,j)}{({\mathbf{S}}_n-{\Sigma }_0)}_{(i,j)(k,l)}{\left({\Delta }_B\right)}_{(k,l)}\mid .$$

From Lemma 4.1 we know that

$$\underset{(i,j)(k,l)}{\text{max}}{({\mathbf{S}}_n-{\Sigma }_0)}_{(i,j)(k,l)}=O_P\left(\sqrt{(\text{log}{p}_n+\text{log}{q}_n)∕n}\right).$$

Then

$$\begin{array}{cc}\hfill L_1& \le \sqrt{s_{n1}}{\Vert {\Delta }_A\Vert }_F{O}_P\left(\sqrt{\frac{\text{log}{p}_n+\text{log}{q}_n}{n}}\right)q_n\sqrt{\mathrm{tr}\left({\mathbf{B}}_0^T{\mathbf{B}}_0\right)}\hfill \\ \hfill & \le q_n\sqrt{q_n{s}_{n1}}{\lambda }_{\text{max}}\left({\mathbf{B}}_0\right){\Vert {\Delta }_A\Vert }_F{O}_P\left(\sqrt{\frac{\text{log}{p}_n+\text{log}{q}_n}{n}}\right)\hfill \\ \hfill & \le q_n{O}_P\left({\alpha }_n\right){\Vert {\Delta }_A\Vert }_F\hfill \\ \hfill & \le q_n{O}_P(C_1{\alpha }_n^2+C_2{\beta }_n^2),\hfill \end{array}$$ (.10)

This together with (.6) shows that L₁ is dominated by K₁ by choosing sufficiently large C₁ and C₂. Symmetrically,

$$\begin{array}{cc}\hfill L_3& \le p_n\sqrt{\mathrm{tr}\left({\mathbf{A}}_0^T{\mathbf{A}}_0\right)}{O}_P\left(\sqrt{\frac{\text{log}{p}_n+\text{log}{q}_n}{n}}\right)\sqrt{s_{n2}}{\Vert {\Delta }_B\Vert }_F\hfill \\ \hfill & \le p_n\sqrt{p_n{s}_{n2}}{\lambda }_{\text{max}}\left({\mathbf{A}}_0\right)O_P\left(\sqrt{\frac{\text{log}{p}_n+\text{log}{q}_n}{n}}\right){\Vert {\Delta }_B\Vert }_F\hfill \\ \hfill & \le p_n{O}_P(C_3{\delta }_n^2+C_4{\beta }_n^2).\hfill \end{array}$$

By choosing sufficiently large C₃ and C₄, this together with (.7) shows L₃ can be dominated by K₂. Also

$$\begin{array}{cc}\hfill L_2& \le \sum _{(i,j)\in S_A^c}\mid a_{ij}^{\left(1\right)}\mid O_P\left(\sqrt{\frac{\text{log}{p}_n+\text{log}{q}_n}{n}}\right)\sum _{k,l}\mid {\left({\mathbf{B}}_0\right)}_{k,l}\mid \hfill \\ \hfill & \le \sum _{(i,j)\in S_A^c}\mid a_{ij}^{\left(1\right)}\mid O_P\left(\sqrt{\frac{\text{log}{p}_n+\text{log}{q}_n}{n}}\right)q_n\sqrt{q_n}{\lambda }_{\text{max}}\left({\mathbf{B}}_0\right)\hfill \\ \hfill & \le \sum _{(i,j)\in S_A^c}\mid a_{ij}^{\left(1\right)}\mid O_P\left(q_n\sqrt{\frac{q_n(\text{log}{p}_n+\text{log}{q}_n)}{n}}\right)\hfill \end{array}$$ (.11)

from the condition of λ_n in theorem, and using the similar technique in [12], it can be shown that L₂ is dominated by I₂. Similarly, L₄ is dominated by I₄. Thus we proved |K₃| + |K₄| can be dominated by K₁ + K₂ + I₂ + I₄. It is easy to show that |K₆| is of smaller order of K₃ and K₄, hence is also dominated by K₁ + K₂ + I₂ + I₄. We next show that

$$\begin{array}{cc}\hfill \mid I_3\mid & ={\lambda }_n\sum _{\begin{array}{c}\hfill i\ne j,\hfill \\ \hfill (i,j)\in S_A\hfill \end{array}}\mid \{\mid a_{ij}^{\left(1\right)}\mid -\mid a_{ij}^{\left(0\right)}\mid \}\mid \hfill \\ \hfill & \le {\lambda }_n\sum _{\begin{array}{c}\hfill i\ne j,\hfill \\ \hfill (i,j)\in S_A\hfill \end{array}}\mid a_{ij}^{\left(1\right)}-a_{ij}^{\left(0\right)}\mid \le {\lambda }_n\sqrt{s_{n1}}{\Vert {\Delta }_A\Vert }_F\hfill \\ \hfill & \le \sqrt{s_{n1}}O\left((1+\frac{\sqrt{p_n}}{\sqrt{s_{n1}}+1})q_n\sqrt{\frac{q_n(\text{log}{p}_n+\text{log}{q}_n)}{n}}\right)\times O(C_1{\alpha }_n+C_2{\beta }_n)\hfill \\ \hfill & =q_{n}O(C_1{\alpha }_n^2+C_2{\beta }_n^2),\hfill \end{array}$$ (.12)

where the middle term in (.12) is from regularity condition (C), thus I₃ is dominated by K₁ if we choose sufficiently large constants C₁ and C₂. Similarly, we get $\mid I_5\mid \le p_{n}O(C_3{\delta }_n^2+C_4{\beta }_n^2)$ and is dominated by K₂ when C₃ and C₄ are large. Hence the proof.

Proof of Theorem 4

Proof. For (Â, B̂), a minimizer of (6), where  = (a_ij), B̂ = (b_kl), the derivative of ϕ(A, B) with respect to a_ij for $(i,j)\in S_A^c$ evaluated at  is

$$\begin{array}{cc}\hfill \frac{\partial \varphi (\widehat{\mathbf{A}},\widehat{\mathbf{B}})}{\partial a_{ij}}& =q_n{u}_{ij}+\frac{1}{n}\sum _{s=1}^n{\left\{{\mathbf{Y}}^{\left(s\right)}\widehat{\mathbf{B}}{\mathbf{Y}}^{\left(s\right)T}\right\}}_{ij}+\frac{{\lambda }_n}{{\mid {\tilde{a}}_{ij}\mid }^{{\gamma }_1}}\mathrm{sgn}\left(a_{ij}\right)\hfill \\ \hfill & =-q_n{u}_{ij}^{\left(0\right)}-q_n(u_{ij}-u_{ij}^{\left(0\right)})+\frac{1}{n}\sum _{s=1}^n{\left\{{\mathbf{Y}}^{\left(s\right)}{\mathbf{B}}_0{\mathbf{Y}}^{\left(s\right)T}\right\}}_{ij}+\frac{1}{n}\sum _{s=1}^n{\left\{{\mathbf{Y}}^{\left(s\right)}(\widehat{B}-{\mathbf{B}}_0){\mathbf{Y}}^{\left(s\right)T}\right\}}_{ij}+\frac{{\lambda }_n}{{\mid {\tilde{a}}_{ij}\mid }^{{\gamma }_1}}\mathrm{sgn}\left(a_{ij}\right),\hfill \end{array}$$

where Û = (u_ij) = Â^–1 and ${\mathbf{U}}_0=\left(u_{ij}^{\left(0\right)}\right)$ and B₀ are the true parameters. If we can show that the sign of ∂ϕ(Â, B̂)/∂a_ij depends on sgn(a_ij) only with probability tending to 1, the optimum is then at 0, so that a_ij = 0 for $(i,j)\in S_A^c$ with probability tending to 1. Let

$$\begin{array}{cc}\hfill I_1& =\frac{1}{n}\sum _{s=1}^n{\left\{{\mathbf{Y}}^{\left(s\right)}{\mathbf{B}}_0{\mathbf{Y}}^{\left(s\right)T}\right\}}_{ij}-q_n{u}_{ij}^{\left(0\right)},\hfill \\ \hfill I_2& =-q_n(u_{ij}-u_{ij}^{\left(0\right)}),\hfill \\ \hfill I_3& =\frac{1}{n}\sum _{s=1}^n{\left\{{\mathbf{Y}}^{\left(s\right)}(\widehat{\mathbf{B}}-{\mathbf{B}}_0){\mathbf{Y}}^{\left(s\right)T}\right\}}_{ij},\hfill \end{array}$$ (.13)

we then have

$$\frac{\partial \varphi (\widehat{\mathbf{A}},\widehat{\mathbf{B}})}{\partial a_{ij}}=I_1+I_2+I_3+\frac{{\lambda }_n}{{\mid {\tilde{a}}_{ij}\mid }^{{\gamma }_1}}\mathrm{sgn}\left(a_{ij}\right).$$

Using the same argument as in [12],

$$\underset{ij}{\text{max}}\mid u_{ij}-u_{ij}^{\left(0\right)}\mid \le \Vert \widehat{\mathbf{U}}-{\mathbf{U}}_0\Vert =\Vert \widehat{\mathbf{U}}(\widehat{\mathbf{A}}-{\mathbf{A}}_0){\mathbf{U}}_0\Vert \le \Vert \widehat{\mathbf{U}}\Vert \Vert \widehat{\mathbf{A}}-{\mathbf{A}}_0\Vert \Vert {\mathbf{U}}_0\Vert =O\left(\Vert \widehat{\mathbf{A}}-{\mathbf{A}}_0\Vert \right),$$

and then ${\text{max}}_{ij}\mid I_2\mid =O_P\left(q_n{\sqrt{c}}_n\right)$.

Since Y^(s) ~ MN(0; U₀, V₀), the Y^(s)T ~ MN(0, V₀, U₀) and $\text{vec}\left({\mathbf{Y}}^{\left(s\right)T}\right)\sim N(0,{\mathbf{U}}_0\otimes {\mathbf{V}}_0)$. Let ${\mathbf{Y}}^{\left(s\right)T}=({\mathbf{Y}}_1^{\left(s\right)},\cdots ,{\mathbf{Y}}_{p_n}^{\left(s\right)})$, where ${\mathbf{Y}}_i^{\left(s\right)}$ is a q_n × 1 vector,for i = 1, ···, p_n. We have

$${\left\{{\mathbf{Y}}^{\left(s\right)}(\widehat{\mathbf{B}}-{\mathbf{B}}_0){\mathbf{Y}}^{\left(s\right)T}\right\}}_{ij}={\mathbf{Y}}_i^{\left(s\right)T}(\widehat{B}-{\mathbf{B}}_0){\mathbf{Y}}_j^{\left(s\right)},$$ (.14)

$${\left\{{\mathbf{Y}}^{\left(s\right)}{\mathbf{B}}_0{\mathbf{Y}}^{\left(s\right)T}\right\}}_{ij}={\mathbf{Y}}_i^{\left(s\right)T}{\mathbf{B}}_0{\mathbf{Y}}_j^{\left(s\right)},$$ (.15)

and

$$\left(\begin{array}{c}\hfill {\mathbf{Y}}_i^{\left(s\right)}\hfill \\ \hfill {\mathbf{Y}}_j^{\left(s\right)}\hfill \end{array}\right)\sim N\left(0,\left(\begin{array}{cc}\hfill u_{ii}^{\ast }{\mathbf{V}}_0,\hfill & \hfill u_{ij}^{\ast }{\mathbf{V}}_0\hfill \\ \hfill u_{ij}^{\ast }{\mathbf{V}}_0,\hfill & \hfill u_{jj}^{\ast }{\mathbf{V}}_0\hfill \end{array}\right)\right),$$ (.16)

$$\left(\begin{array}{c}\hfill {\mathbf{B}}_0^{1∕2}{\mathbf{Y}}_i^{\left(s\right)}\hfill \\ \hfill {\mathbf{B}}_0^{1∕2}{\mathbf{Y}}_j^{\left(s\right)}\hfill \end{array}\right)\sim N\left(0,\left(\begin{array}{cc}\hfill u_{ii}^{\ast }{I}_{q_n},\hfill & \hfill u_{ij}^{\ast }{I}_{q_n}\hfill \\ \hfill u_{ij}^{\ast }{I}_{q_n},\hfill & \hfill u_{jj}^{\ast }{I}_{q_n}\hfill \end{array}\right)\right).$$ (.17)

I₁ can be simplified as $I_1=1∕n{\sum }_{s=1}^n{\mathbf{Y}}_i^{\left(s\right)T}{\mathbf{B}}_0{\mathbf{Y}}_j^{\left(s\right)}-q_n{u}_{ij}^{\ast }$. We have the following proposition:

Proposition Appendix .1. Under the notations above, we have

$$\underset{i,j\in \{1,\cdots ,p_n\}}{\text{max}}\mid \frac{1}{n}\sum _{s=1}^n{\mathbf{Y}}_i^{\left(s\right)T}{\mathbf{B}}_0{\mathbf{Y}}_j^{\left(s\right)}-q_n{u}_{ij}^{\ast }\mid =O_P\left(q_n\sqrt{\frac{\text{log}{p}_n}{n{q}_n}}\right).$$

Proof of Proposition Appendix .1. To save notation, we use q for q_n here or there. Denote ${\mathbf{B}}_0^{1∕2}{\mathbf{Y}}_i^{\left(s\right)}={(z_1,\cdots ,z_q)}^T$ and ${\mathbf{B}}_0^{1∕2}{\mathbf{Y}}_j^{\left(s\right)}={(w_1,\cdots ,w_q)}^T$. From (.17) we have

$$\begin{array}{c}\hfill (z_k,w_k){\sim }_{i.i.d.}N\left(0,\left(\begin{array}{cc}\hfill u_{ii}^{\ast }\hfill & \hfill u_{ij}^{\ast }\hfill \\ \hfill u_{ij}^{\ast }\hfill & \hfill u_{jj}^{\ast }\hfill \end{array}\right)\right),\hfill \\ \hfill {\mathbf{Y}}_i^{\left(s\right)T}{\mathbf{B}}_0{\mathbf{Y}}_j^{\left(s\right)}={\left({\mathbf{B}}_0^{1∕2}{\mathbf{Y}}_i^{\left(s\right)}\right)}^T\left({\mathbf{B}}_0^{1∕2}{\mathbf{Y}}_j^{\left(s\right)}\right)=z_1{w}_1+\cdots +z_q{w}_q.\hfill \end{array}$$ (.18)

Note that (.18) does not depends on the sample index s, and the sum in I₁ is equivalent to nq_n normal observations. By Lemma A.3 of [34], we have

$$\underset{i,j\in \{1,\cdots ,p_n\}}{\text{max}}\mid \frac{q_n}{n{q}_n}\sum _{s=1}^n{\mathbf{Y}}_i^{\left(s\right)T}{\mathbf{B}}_0{\mathbf{Y}}_j^{\left(s\right)}-q_n{u}_{ij}^{\ast }\mid =q_n{O}_P\left(\sqrt{\frac{\text{log}{p}_n}{n{q}_n}}\right)=O_P\left(\sqrt{\frac{q_n\text{log}{p}_n}{n}}\right).$$

Hence the Proposition Appendix .1 is proved.

From Proposition Appendix .1, we know ${\text{max}}_{i,j}\mid I_1\mid =O_P\left(\sqrt{q_n\text{log}{p}_n∕n}\right)$. Next we bound |I₃|. From (.14) we know that $I_3=1∕n{\sum }_{s=1}^n{\mathbf{Y}}_i^{\left(s\right)T}(\widehat{\mathbf{B}}-{\mathbf{B}}_0){\mathbf{Y}}_j^{\left(s\right)}$, and since

$${\mathbf{Y}}_i^{\left(s\right)T}(\widehat{\mathbf{B}}-{\mathbf{B}}_0){\mathbf{Y}}_j^{\left(s\right)}=\mathrm{tr}\left((\widehat{B}-{\mathbf{B}}_0){\mathbf{Y}}_j^{\left(s\right)}{\mathbf{Y}}_i^{\left(s\right)T}\right)=\mathrm{tr}\left[(\widehat{B}-{\mathbf{B}}_0)({\mathbf{Y}}_j^{\left(s\right)}{\mathbf{Y}}_i^{\left(s\right)T}-u_{ij}^{\ast }{\mathbf{V}}_0+u_{ij}^{\ast }{\mathbf{V}}_0)\right],$$

we have

$$I_3=\mathrm{tr}\left[u_{ij}^{\ast }{\mathbf{V}}_0(\widehat{\mathbf{B}}-{\mathbf{B}}_0)\right]+\mathrm{tr}\left[(\widehat{B}-{\mathbf{B}}_0)\frac{1}{n}\sum _{s=1}^n({\mathbf{Y}}_j^{\left(s\right)}{\mathbf{Y}}_i^{\left(s\right)T}-u_{ij}^{\ast }{\mathbf{V}}_0)\right].$$

Then we have |I₃| ≤ L₁ + L₂, where

$$\begin{array}{cc}\hfill L_1& =\mid \mathrm{tr}\left(u_{ij}^{\ast }{\mathbf{V}}_0(\widehat{\mathbf{B}}-{\mathbf{B}}_0)\right)\mid ,\hfill \\ \hfill L_2& =\mid \mathrm{tr}\left[(\widehat{\mathbf{B}}-{\mathbf{B}}_0)\frac{1}{n}\sum _{s=1}^n({\mathbf{Y}}_j^{\left(s\right)}{\mathbf{Y}}_i^{\left(s\right)T}-u_{ij}^{\ast }{\mathbf{V}}_0)\right]\mid .\hfill \end{array}$$

Since ${\text{max}}_{i,j}\mid u_{ij}^{\ast }\mid \le \Vert {\mathbf{U}}_0\Vert \le {\epsilon }_1^{-1}$ and $\Vert {\mathbf{V}}_0\Vert \le {\epsilon }_3^{-1}$, then

$$\begin{array}{cc}\hfill L_1& \le \underset{i,j}{\text{max}}\mid u_{ij}^{\ast }\mid \sqrt{\mathrm{tr}\left({\mathbf{V}}_0^T{\mathbf{V}}_0\right)}\sqrt{\mathrm{tr}\left({(\widehat{B}-{\mathbf{B}}_0)}^T(\widehat{\mathbf{B}}-{\mathbf{B}}_0)\right)}\hfill \\ \hfill & \le \sqrt{q_n}\Vert {\mathbf{U}}_0\Vert \Vert {\mathbf{V}}_0\Vert {\Vert \widehat{\mathbf{B}}-{\mathbf{B}}_0\Vert }_F\le {\epsilon }_1^{-1}{\epsilon }_3^{-1}\sqrt{q_n}{\Vert \widehat{B}-{\mathbf{B}}_0\Vert }_F.\hfill \end{array}$$

On the other hand, by (.16) and Lemma A.3 of [34],

$$\underset{k,l\in \{1,\cdots ,q_n\}}{\text{max}}\mid {(\frac{1}{n}\sum _{s=1}^n{\mathbf{Y}}_j^{\left(s\right)}{\mathbf{Y}}_i^{\left(s\right)T}-u_{ij}^{\ast }{\mathbf{V}}_0)}_{(k,l)}\mid =O_P\left(\sqrt{\frac{\text{log}{q}_n}{n}}\right).$$

Denoting $1_q\mathrm{a}{q}_n\times 1$ vector of 1's, then

$${\Vert \frac{1}{n}\sum _{s=1}^n{\mathbf{Y}}_j^{\left(s\right)}{\mathbf{Y}}_i^{\left(s\right)T}-u_{ij}^{\ast }{\mathbf{V}}_0\Vert }_F^2=\mathrm{tr}\left[{\left(\frac{1}{n}\sum _{s=1}^n{\mathbf{Y}}_j^{\left(s\right)}{\mathbf{Y}}_i^{\left(s\right)T}-u_{ij}^{\ast }{\mathbf{V}}_0\right)}^T,\left(\frac{1}{n}\sum _{s=1}^n{\mathbf{Y}}_j^{\left(s\right)}{\mathbf{Y}}_i^{\left(s\right)T}-u_{ij}^{\ast }{\mathbf{V}}_0\right)\right]=O_P\left(\frac{\text{log}{q}_n}{n}\mathrm{tr}\left(1_q{1}_q^T{1}_q{1}_q^T\right)\right)=O_P\left(q_n^2\frac{\text{log}{q}_n}{n}\right).$$

Therefore,

$$L_2\le {\Vert \widehat{\mathbf{B}}-{\mathbf{B}}_0\Vert }_F{\Vert \frac{1}{n}\sum _{s=1}^n{\mathbf{Y}}_j^{\left(s\right)}{\mathbf{Y}}_i^{\left(s\right)T}-u_{ij}^{\ast }{\mathbf{V}}_0\Vert }_F=O_P\left(\sqrt{\frac{q_n\text{log}{q}_n}{n}}\sqrt{q_n}{\Vert \widehat{\mathbf{B}}-{\mathbf{B}}_0\Vert }_F\right).$$

Then $L_1+L_2=O_P\left(\sqrt{q_n}{\Vert \widehat{\mathbf{B}}-{\mathbf{B}}_0\Vert }_F(1+\sqrt{q_n\text{log}{q}_n∕n})\right)$. Since the theorem requires the condition q_n(p_n + s_n1)(log p_n + log q_n)^k/n = O(1) for some k > 1, we know that $\sqrt{q_n\text{log}{q}_n∕n}=o\left(1\right)$. So

$$\mid I_3\mid \le L_1+L_2=O_P\left(\sqrt{q_n}{\Vert \widehat{\mathbf{B}}-{\mathbf{B}}_0\Vert }_F\right)=O_P\left(\sqrt{\frac{p_n{q}_n(q_n+s_{n2})(\text{log}{p}_n+\text{log}{q}_n)}{n}}\right).$$

Concluding from above, we have

$$\mid I_1\mid +\mid I_2\mid +\mid I_3\mid \le O_P\left(\sqrt{\frac{q_n\text{log}{p}_n}{n}}\right)+O_P\left(q_n\sqrt{c_n}\right)+O_P\left(\sqrt{\frac{p_n{q}_n(q_n+s_{n2})(\text{log}{p}_n+\text{log}{q}_n)}{n}}\right)=\sqrt{q_n}{O}_P\left(\sqrt{\frac{p_n(q_n+s_{n2})(\text{log}{p}_n+\text{log}{q}_n)}{n}}+\sqrt{q_n{c}_n}\right).$$

On the other hand, for $(i,j)\in S_A^c,{\lambda }_n∕{\mid {\tilde{a}}_{ij}\mid }^{{\gamma }_1}\ge c{\lambda }_n{e}_n^{{\gamma }_1}$ for some constant c From the condition in the Theorem, we have

$$e_n^{-{\gamma }_1}\sqrt{q_n}\left\{\sqrt{\frac{p_n(q_n+s_{n2})(\text{log}{p}_n+\text{log}{q}_n)}{n}}+\sqrt{c_n{q}_n}\right\}=O\left({\lambda }_n\right)$$

So the sign of ∂ϕ(Â, B̂)/∂a_ij is dominated by sgn(a_ij), and thus we proved the sparsistency for Â. Similar proof can be applied to B̂.