Optimization of the CHARMM additive force field for DNA: Improved treatment of the BI/BII conformational equilibrium

Abstract

The B-form of DNA can populate two different backbone conformations: BI and BII, defined by the difference between the torsion angles ε and ζ (BI = ε-ζ < 0 and BII = ε-ζ > 0). BI is the most populated state, but the population of the BII state, which is sequence dependent, is significant and accumulating evidence shows that BII affects the overall structure of DNA, and thus influences protein-DNA recognition. This work presents a reparametrization of the CHARMM27 additive nucleic acid force field to increase the sampling of the BII form in MD simulations of DNA. In addition, minor modifications of sugar puckering were introduced to facilitate sampling of the A form of DNA under the appropriate environmental conditions. Parameter optimization was guided by quantum mechanical data on model compounds, followed by calculations on several DNA duplexes in the condensed phase. The selected optimized parameters were then validated against a number of DNA duplexes, with the most extensive tests performed on the EcoRI dodecamer, including comparative calculations using the Amber Parm99bsc0 force field. The new CHARMM model better reproduces experimentally observed sampling of the BII conformation, including sampling as a function of sequence. In addition, the model reproduces the A form of the 1ZF1 duplex in 75 % ethanol, and yields a stable Z-DNA conformation of duplex (GTACGTAC) in its crystal environment. The resulting model, in combination with a recent reoptimization of the CHARMM27 force field for RNA, will be referred to as CHARMM36.

INTRODUCTION

Empirical force field based computational studies of DNA and DNA-protein complexes are of ever greater value to understand the relationship of structure and dynamics to function in these biologically essential molecules.^1,2 This growing role for force field-based investigations reflects increases in computational power and improvements in molecular dynamics (MD) simulation programs, allowing for longer and more relevant MD simulations of large DNA-containing systems. In this context, improvements in the force fields (FF) used to calculate the energies and forces acting on DNA are critical.³ Several different additive all-atom force fields are available for DNA including CHARMM27,⁴ AMBER,^5,6 Bristol-Myers Squibb,⁷ and GROMOS,⁸ where AMBER and CHARMM are the most commonly used in studies involving DNA.

While these force fields have acted as the basis for a range of successful investigations of DNA,^9,10 and its components,¹¹ limitations in the models have surfaced. These limitations have become evident due to the ability to perform longer MD simulations on a wider variety of DNAs and new experimental data that can be used to test force fields.^12,13 For example, a problem was identified in simulations > 10 ns involving treatment of the α and γ dihedrals in the phosphodiester backbone with AMBER.^14,15 This problem was solved based on quantum mechanical (QM) calculations on model compounds representative of the phosphodiester backbone used to direct parameter optimization, followed by extensive MD simulations. Other improvements in the AMBER force field important for DNA simulations have involved the ions¹⁶ and various adjustments in the AMBER χ parameters have also been presented.^17-19

With the CHARMM DNA force field, limitations in the treatment of the relative populations of the BI and BII substates of the canonical B form of DNA have been noted, where the BII state is significantly underestimated relative to the BI state.^13,20,21 The BI and BII states are defined based on the phosphodiester torsions ε and ζ. BI is characterized by ε-ζ around −90° and BII by ε-ζ > 0. The BII conformation was first characterized in a crystal structure²² and subsequently observed using ³¹P NMR chemical shifts and scalar coupling constants.^20,23,24 NMR data led to quantification of the intrinsic sequence-specific propensities to populate BII in solution for every DNA base-step.²⁵ Crucially, the BI/BII equilibrium affects the DNA helicoidal parameters, especially the twist, roll and base-pair displacement from the main helicoidal axis. This influences the DNA overall structure. For instance, it explains to a large extent the sequence-specific variations in B-DNA groove dimensions.²⁶ Approximately 20% of the base steps in free DNA significantly populate BII and somewhat less in protein bound DNA.²⁷ The BI/BII equilibrium has consequences for DNA recognition by proteins involved in sequence specific binding^21,28 as well as when the binding is non-specific or uses an indirect readout mechanism.²⁵ The sequence-dependent propensity to adopt the BII state has been suggested to contribute to the ability of DNA sequences to form nucleosomes.²⁵ Changes upon going from the BI to BII state alter the solvent accessibility of backbone atoms; for instance in BI the O3′ is accessible, but not in the BII conformation. Furthermore, the BI/BII equilibrium is also sensitive to the composition (Na⁺ or K⁺) of the ionic environment at physiological concentrations,²⁹ which might provide another mechanism to tune protein-DNA recognition. The energy barrier between the BI and BII states is of interest, although the current estimates strongly depend on the model used.^24,30,31

Underestimation of the BII state by the CHARMM27 FF has been observed in a number of studies. MD simulations of transcription factor Ndt80 in complex with DNA²¹ showed the FF to not reproduce details of the crystallographic conformation of the DNA, in particular the BII state around the crucial base step T6′-G5′.^28,32 Notably, the inability to sample the BII conformation led to the simulated protein sidechains forming different interactions with the DNA, compared to the X-ray structure. Another system is the JunFos DNA oligomer, which has distinct BII populations.²⁰ JunFos has been used to develop an NMR-based method to quantify the BII populations at every phosphodiester linkage.²⁰ Subsequently, MD simulations with CHARMM27 and the Parm99bsc0¹⁵ and Parm98⁶ versions of the AMBER FF showed that none of the FFs could reproduce the experimental BI/BII populations in the absence of NMR restraints.¹³ These observations, and the fact that sampling of BII states is significant in a range of sequences,^25,33 motivated the present fine tuning of the CHARMM27 DNA FF. As presented below, this involved the systematic optimization of the dihedral parameters associated with the ε and ζ torsions as well as the C2′-C3′-C4′-O4′ torsion that influences the relative energies of the north and south sugar ring puckers. The resulting modified CHARMM DNA force field yields significant improvement in the treatment of the BI/BII equilibrium. In addition, the modified force field has improved sensitivity of the DNA to its environment, better reproducing the change from the A form of DNA to the B form as a function of water activity due to the presence of ethanol. The FF is also shown to satisfactorily reproduce the structure of a Z-form duplex in its crystal environment. The modified parameters, which are not applicable to RNA, will be included in the new CHARMM36 force field for oligonucleotides, alongside a recent enhancement in the treatment of RNA.³⁴

METHODS

Quantum mechanical calculations

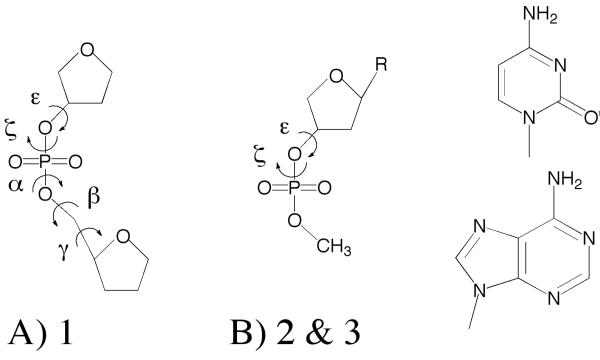
QM calculations were performed with the programs Gaussian09³⁵ and QChem³⁶ on the model compounds shown in Figure 1. As previously presented for model 1,³⁷ structures were optimized at MP2/6-31(+)G(d) to default tolerances in Gaussian and single-point energies were calculated at RI-MP2/cc-pVTZ level with QChem. Optimizations were initiated with selected dihedral angles in the sugar and phosphate moieties, constrained to values obtained from statistical surveys of DNA crystal structures in the protein³⁸ and nucleic acid databases,³⁹ as previously described.⁴⁰ For model compound 1, following the initial constrained optimizations, additional optimization of sugar pucker with the backbone dihedral constraints maintained was performed at the MP2/6-31(+)G(d) level followed by the RIMP2 single point calculations. Model compounds 2 and 3 were optimized with only a single sugar ring dihedral constrained following which the value of the sugar pucker was extracted as described by Foloppe and MacKerell.⁴ For the ε versus ζ BI/BII 2D surface on the analog of model compound 2 lacking a base, optimizations were performed at the MP2/6-31(+)G(d) level with the single sugar dihedral and α dihedral restraints corresponding to B form DNA, with ε and ζ sampled in 15° increments; no single point RIMP2 energies were obtained for this system.

Figure 1.

Model compounds used for parameter optimization. In B, the base, R, is either cytidine for model 2 or adenine for model 3, as shown.

Crystallographic Survey

Target data for FF validation were obtained, in part, from a survey of the crystal structures in the protein databank.³⁸ Included in the survey were only double helical DNA duplexes with unmodified DNA bases or backbones, no protein or RNA in the structure, and with a resolution ≤ 2.5 Å. Terminal nucleotides were excluded from the analysis unless noted.

Molecular mechanical calculations

MM calculations were performed with the programs CHARMM⁴¹ and NAMD⁴² using the CHARMM27 all-atom nucleic acid force field^4,43 with the modifications discussed below. All systems were solvated with the TIP3P water model⁴⁴, a minimum of 8 Å beyond the solute non-hydrogen atoms, and made electrically neutral by the addition of Na⁺ ions (1axp, EcoRI and JunFos) or Mg²⁺ ions (BDJ025 and GTAC2). With the EcoRI excess salt simulation, additional Na⁺ and Cl^- ions (5 Na⁺ and 5 Cl^-) yielded a concentration of 100 mM NaCl. Subsequent calculations were performed with periodic boundary conditions. Crystals were solvated and pre-equilibrated as previously described.⁴ Systems were first energy minimized for 500 adopted-basis Newton Raphson (ANBR) steps in the presence of harmonic restraints of 5 kcal/mol/Ų on the solute non-hydrogen atoms, followed by 20 ps NPT simulations in the presence of those restraints. Then an additional 500 ABNR step minimization in the absence of harmonic restraints was performed, after which the production MD simulations were initiated. Unless noted, MD simulations were performed for 100 ns (Table 1) at 298 K and pressure of 1 atm, using Hoover temperature control⁴⁵ and the Langevin piston to maintain the pressure.⁴⁶ The integration time step was 2 fs and SHAKE⁴⁷ was used to constrain X-H bonds during the simulations. For selected systems (Table 1) a lookup table was used in the evaluation of non-bonded interactions in order to speed up the simulations.⁴⁸ Electrostatic interactions were calculated using the particle mesh Ewald method (PME)⁴⁹ with a kappa value of 0.36 and a real space cutoff of 10 or 12 Å (Table 1). Lennard-Jones interactions were truncated at the same distance as the PME real space cutoff in the respective simulations, with smoothing over the last 2 Å using the force switch method.⁵⁰ Non-bond atom pair lists were updated heuristically whenever any atom moved more than half the distance between the list-cutoff (CUTNB) and the interaction cutoff (CTOFNB) distances.

Table 1.

DNA systems used for parameter training, tests and validation

Sequence	Comment/Reference
1) d(GTACGTAC)*	GTAC, A form crystal (ADH059)69
2) d(CGATCGATCG)*	BDJ025, B form crystal (BDJ025)70
3) d(CGCGAATTCGCG)	EcoRI dodecamer., MD to 300 ns with C27_2b, Xray/NMR71-77
4) d(GCATTCTGAGTCAG)*	JunFos, experimental BII content13,20,29
5) d(GAAGAGAAGC)*	1AXP, NMR, high purine content strand78
6) d(ACACTACAATGTTGCAAT)	3BSE, B form, X-ray 1.60 Å; disordered region 65
7) d(CCGTCGACGG)	1ZF7, B form, X-ray (1.05 Å)79
8) d(CCGGGCCCGG)	1ZF1, A form, X-ray (1.35Å)79
9) d(TGCGCA)	1LJX, Z form, X-ray (1.64 Å)80
10) d(GACTTTCCAGGG)*	NF-κB, B form, NMR 62, experimental BII content
11) d(TGCGACACAAAAACT)*	Ndt80 binding site, complex with protein, X-ray (1.4Å)28

All validation simulations were performed for 100 ns unless noted. Comment/Reference include the PDB or NDB identifiers. Starting structures for the simulations were the crystal structures except with 5) 1AXP where the NMR structure was used and 3) EcoRI and 4) JunFos, where the canonical B form was used as the starting structure.

Systems indicated with * were simulated using the non-bond lookup table in CHARMM.48

Analysis was performed on coordinates saved every 5 ps from the MD simulations unless noted. Dihedral angle distributions were analyzed using 5° bins and the following torsion definitions: α = O_3′-P-O_5′-C_5′, β = P-O_5′-C_5′-C_4′, γ = O_5′-C_5′-C_4′-C_3′, ε = C_4′-C_3′-O_3′-P, ζ = C_3′-O_3′-P-O_5′. Helicoidal analysis used the Curves^51,52 package with data placed in 5° or 0.2 Å bins. Root-mean-square (RMS) differences were calculated with respect to the canonical (A, B or Z) DNA forms of the respective sequences, unless noted, following alignment of all non-hydrogen atoms. Unless noted, the terminal nucleotides were excluded from the analyses. BI versus BII populations from the MD simulations were obtained by simple counting, i.e. BI if ε-ζ < 0 and BII if ε-ζ > 0; however, this method differs from that used to obtain BII population estimates from NMR, as discussed below.

RESULTS AND DISCUSSION

In the present work a systematic optimization of the CHARMM27 all-atom additive force field for nucleic acids^4,43 was undertaken to improve the ability of the model to represent the relative populations of the BI and BII conformers of DNA. To achieve this without significantly altering the remainder of the FF (e.g. the treatments of Watson-Crick base pair interactions, which have been shown to yield good agreement with NMR experiments with respect to base flipping^53-55), the optimization focused on the dihedral parameters associated with the ε and ζ torsions in the phosphodiester backbone. In addition, it was necessary to modify the relative energies of the north and south puckers of the deoxyribose sugar, targeting the C2′-C3′-C4′-O4′ associated dihedral parameter, to allow for sampling of A-form DNA in the appropriate conditions. In the following, results for model compounds on which QM data are available are presented for the CHARMM27 FF (C27) and for 5 modified parameters sets, which were used in preliminary simulations of three systems (Table 1, systems 1-3). The final selected set of parameters was then used to simulate additional systems (Table 1, systems 4-11) to more rigorously test the force field. Altogether 3.4μs of simulation was performed on 11 DNA duplexes of different compositions and sizes (total system sizes range from 1200 to 51000 atoms) with explicit solvent, in crystal or solution, and also bound to a protein.²¹

Model compound calculations

Model compounds representative of the backbone and nucleotide unit in DNA on which QM data is available are shown in Figure 1. The first model, 1, which contains two furanoses connected by a phosphodiester linkage, has been subjected to extensive QM calculations.³⁷ The conformational energies of compound 1 as a function of its dihedrals reflected the dihedral distributions from survey data on crystal structures of duplex DNA, thereby validating it as a model for the phosphodiester backbone. Accordingly, model compound 1 was used for optimization of the ε and ζ dihedral parameters. The other model compounds, 2 and 3, are cytosine and adenosine nucleosides, respectively, used previously in the optimization of the C27 nucleic acid FF. As the goal of the present study was to perform minimal adjustments of the C27 FF, use of two nucleosides to evaluate changes in sugar pucker energies was deemed sufficient. As shown below, the changes to the sugar parameters only had a minor impact on the relative energies of the north (C3′endo) vs. south (C2′endo) conformations while the overall energy as a function of pucker was not significantly changed.

Table 2 presents the relative energies of the BII conformation of 1 with respect to the BI conformation. As may be seen, C27 significantly overestimates the QM result. Accordingly, initial efforts aimed to alter only the BI/BII energy difference by altering just the ζ dihedral to yield parameter set C27_1, and then both ε and ζ in set C27_2; adjusted parameters for all sets are shown in Table S1 of the supporting information. Adjustments in C27_1 led to improved agreement with the QM target data, but the C27_2 modification further lowers the relative energy and further improves agreement with the QM value. A third set, C27_3, was developed in which only ζ parameters were again modified, yielding a relative energy slightly lower than that of the C27_2 set. As shown below, these initial sets yielded improvements in sampling of the BII state; however, they overly destabilized the A-form of DNA.

Table 2.

Relative energies of the BI and BII conformations of model compound 1 including the minimized values of the dihedral angles.

BI	ΔE	Puck1	ε	ζ	α+1	β+1	γ+1	Puck2
Level of theory
QM	0.00	8.3	201.1	281.6	288.5	181,6	46,6	−4.1
C27	0.00	9.0	189.3	267.0	302.2	170.4	28.2	−2.7
C27_1	0.00	9.2	191.5	267.5	302.2	170.1	28.4	−2.7
C27_2	0.00	9.3	190.0	265.2	302.9	169.9	27.8	−3.0
C27_2b	0.00	7.6	190.2	264.3	304.0	172.4	22.7	−9.6
C27_3	0.00	8.9	188.0	266.8	302.2	170.7	28.0	−2.8
C27_3b	0.00	7.0	187.7	266.0	303.1	173.0	23.5	−9.1
BII
QM	0.97	3.0	267.1	167.4	289.6	242.5	49.0	−6.6
C27	2.78	15.7	260.5	184.2	293.1	171.0	51.0	−4.9
C27_1	1.91	16.1	262.8	184.6	292.9	170.9	51.0	−4.9
C27_2	1.59	15.8	261.7	183.6	293.0	171.0	51.0	−4.9
C27_2b	1.37	16.3	262.3	183.7	293.0	170.7	51.0	−10.7
C27_3	1.49	17.4	267.6	186.5	292.4	170.8	51.0	−4.9
C27_3b	1.49	18.3	267.8	186.7	292.4	170.5	51.0	−10.8

Energies in kcal/mol and angles in degrees. QM relative energies were obtained at the MP2/6-31(+)G(d)//RIMP2/cc-pVTZ level. Pucker is represented by the C1′-O4′-C4′-C3′ dihedral angle for the first (Puck1) and second (Puck2) sugar in model compound 1.

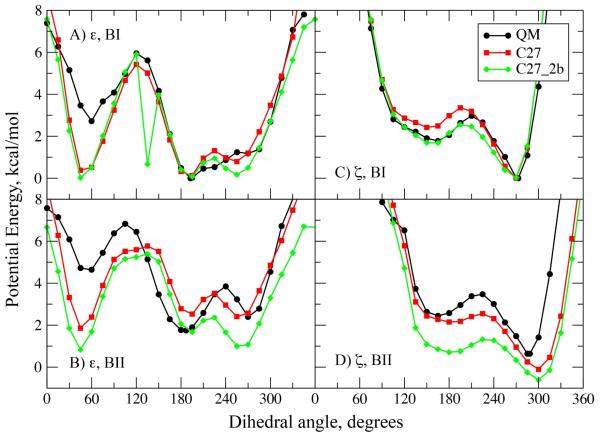
The ε and ζ potential energy surfaces for 1 are shown in Figure 2 from QM calculations as well as from C27 and from the final, selected parameter set, C27_2b (see below). The overall shape of the empirical surfaces mimics that of the QM surfaces; however, differences in the relative energies of different minima are evident. These differences are due to limitations in the ability of the MM energy function to reproduce all the details of the QM energy surfaces and, more importantly, systematic shifts in the C27 energy surface relative to the QM surfaces implemented to yield better sampling in oligonucleotide simulations as judged by the reproduction of crystal survey data⁴. Such deviations from QM energies are necessary for the FF to improve agreement with the condensed phase properties for oligonucleotides given the inherent limitations in the potential energy function as well as the challenges of parameter optimization.

Figure 2.

Potential energies as a function of the ε (A and B) and ζ (C and D) dihedrals for model compound 1 with the remainder of the rotatable bonds maintained at dihedral angles corresponding to the BI (A and C) or BII (B and D) canonical conformations. Note that in the surface in panel A with C27_2b a local minimum was present at 135°; this minimum in the potential energy surface was not observed to impact MD simulations of the DNA duplexes

To account for the inability of the first modified parameter sets to both adequately sample the BII conformation and maintain the A-form of DNA in its crystal environment (see below), modifications of the sugar dihedral parameters were undertaken. These modifications were based on the adenine and cytosine nucleosides (Figure 1b) and only involved a single dihedral (C2′-C3′-C4′-O4′) in the furanose ring (Table S1). Shown in Table 3 are the relative energies of the north pucker relative to those of the south pucker for the two nucleosides. The C27 puckers were empirically adjusted to reproduce the north versus south distributions from a crystal survey of the nucleic acid database, with QM MP2/6-31G(d) relative energies also used as a guideline. The resulting empirical model overestimates the QM values of the north pucker for both model compounds; the lower energy of the north pucker of the cytosine nucleoside is consistent with cytidine bases favoring the A form of DNA, as previously discussed.⁵⁶ Once it was observed that the ε and ζ dihedral parameter modifications led to destabilization of the A form of DNA (see below), the north pucker energy was lowered relative to that of the south by 0.7-0.8 kcal/mol. The resulting model of the sugar now underestimates the QM relative north pucker energy by 0.3 and 0.1 kcal/mol for the adenine and cytosine nucleosides, respectively (Table 3). This altered sugar energetics was combined with the C27_2 set to give the C27_2b set, which yielded satisfactory simulated sugar pucker distributions for duplex DNA in condensed phase, as shown below. The same sugar parameter modification was also applied to C27_3, yielding C27_3b.

Table 3.

Relative energies of the north and south conformations of the nucleosides of adenine and cytosine (model compound 2).

NUSA	North		South
Level of theory	Phase Angle	ΔE	Pucker	ΔE
QM	10.7	1.03	169.2	0.00
C27	9.4	1.40	167.1	0.00
C27_1	9.4	1.40	167.1	0.00
C27_2	9.4	1.40	167.1	0.00
C27_3	9.4	1.40	167.1	0.00
C27_2b	12.3	0.69	168.7	0.00
C27_3b	12.3	0.69	168.7	0.00
NUSC
QM	10.3	−0.49	164.0	0.00
C27	9.6	0.18	167.1	0.00
C27_1	9.6	0.18	167.1	0.00
C27_2	9.6	0.18	167.1	0.00
C27_3	9.6	0.18	167.1	0.00
C27 2b	12.3	−0.60	168.7	0.00
C27_3b	12.3	−0.60	168.7	0.00

Energies in kcal/mol and angles in degrees. Sugar pucker phase angle calculated based on the method of Altona and Sundaralingam⁸¹ with QM data at the RIMP2/cc-pVTZ//MP2/6-31(+)G(d) level.

Initial parameter set selection based on MD simulations

Selection from the parameter sets developed in the preceding section was based on condensed phase simulations of three DNA duplexes, GTAC2, BDJ025 and the EcoRI dodecamer (Table 1)). GTAC2 and BDJ025, which are in the A and B forms, respectively, were simulated in their crystal environments, thereby allowing for a more rigorous comparison of the experimental and simulation data. Special care was taken to maintain the A form of GTAC2. Inclusion of the EcoRI dodecamer in solution was based on the central role that duplex has played as a benchmark in computational studies of DNA^4,57-59 and on the need to include solution data to assess the behavior of the parameter sets with respect to Watson-Crick (WC) base pair interactions, sugar pucker as well as the BI/BII sampling in the phosphodiester backbone in a high water activity environment.

Populations of the BI and BII states for BDJ025 and EcoRI averaged over all the nucleotides in the duplexes for the different parameter sets are in Table 4. Such analysis did not include GTAC2 at this stage of the study as A form DNA does not populate the BII conformation. As expected from previous investigations, the BI/BII equilibrium with C27 in BDJ025 and EcoRI is dominated by the BI state. Alteration of the parameters based on model compound 1 to lower the relative energy of the BII conformation yielded the anticipated increase in sampling of that state for both systems. The C27_2 and C27_3 sets give additional sampling of BII, consistent with the lower energy of the BII conformation in model compound 1 (Table 2). Given that experimental studies indicate the overall population of the BII state to be 37% in EcoRI in solution,²⁴ the sampling of BII by sets C27_2 and C27_3 indicated that they provided a reasonable basis to develop the final model.

Table 4.

Population of the BI and BII states for the EcoR1 dodecamer and BDJ025 over the full oligonucleotides for all parameter sets tested.

Parameter Set	EcoRI		BDJ025
	BI	BII	BI	BII
C27	0.89	0.11	0.83	0.17
C27_1	0.75	0.25	0.67	0.33
C27_2	0.72	0.28	0.60	0.40
C27_2b	0.74	0.26	0.62	0.38
C27_3	0.70	0.30	0.59	0.41
C27_3b	0.79	0.21	0.65	0.35

Results obtained over 40 ns or 80 ns simulations for EcoR1 and BDJ025, respectively, with the average over all the ε,ζ, pairs for EcoRI and with BDJ025 the average populations were obtained for each nucleotide with the presented values being the average of those values .

As increasing the BII population was readily achieved, the simulations were analyzed with respect to the ability of the models to reproduce the A and B conformations of DNA. Average RMS differences versus canonical forms of DNA for all non-terminal non-hydrogen atoms are presented in Table 5. The B form conformation (BDJ025 and EcoRI duplexes) was maintained for all the parameter sets. With A form GTAC2 with sets C27_2 and C27_3 there is a tendency for the RMS difference versus the A form to increase as compared to that occurring with C27. Detailed analysis of these trajectories (not shown) indicated that the shift away from the A form was associated with the sugars switching from the typically A-form north pucker to the typically B-form south pucker. Accordingly, selected sugar dihedrals were adjusted to lower the relative energy of the north conformation, also yielding better agreement with QM data on the adenine and cytosine nucleoside model compounds (Table 2). For C27_2 an additional adjustment of the ε dihedral parameter was undertaken (Table S1) leading to a slight lowering of the energy of the BII conformation in model compound 1.

Table 5.

Average RMS differences (Å) with respect to the canonical forms of DNA for the EcoRI dodecamer, BDJ025 and GTAC2 oligonucleotides for all parameter sets tested.

Parameter Set	EcoRI		BDJ025		GTAC2
	vs A	vs B	vs A	vs B	vs A	vs B
C27	4.26 0.46	2.10 0.40	3.77 0.21	1.73 0.17	1.81 0.14	3.56 0.17
C27_1	5.66 0.45	2.33 0.39	4.24 0.24	1.53 0.13	1.56 0.11	3.37 0.20
C27_2	5.62 0.39	2.18 0.32	4.78 0.20	1.40 0.12	2.10 0.19	2.90 0.25
C27_2b	4.46 0.51	2.19 0.40	4.21 0.19	1.72 0.13	1.69 0.14	3.64 0.15
C27_3	5.80 0.47	2.29 0.49	4.65 0.24	1.47 0.13	2.21 0.12	2.40 0.23
C27_3b	4.80 0.52	2.16 0.38	4.71 0.19	1.43 0.11	1.79 0.14	3.54 0.21

Results, over all non-terminal non-hydrogen atoms, obtained over 20 to 40 ns for EcoR1 and 60 to 80 ns for BDJ025 and GTAC2. Errors represent the RMS fluctuations

The two parameter sets with the modified sugar parameters, C27_2b and C27_3b, were then tested in simulations of the three training set oligonucleotides. Both models maintained the A conformation of GTAC2 as well as the B conformations of EcoRI and BDJ025 (Table 5). Consistent with the BII conformational energies in model compound 1, C27_2b sampled the BII state more than C27_3b (Table 4), with C27_2b yielding an overall BII population closer to the 37% seen in experimental studies of EcoRI. Accordingly, parameter set C27_2b was tested further with simulations of additional DNA duplexes for a more rigorous and general validation.

Further Tests and Validation of the C27_2b parameter set

Additional testing and validation of the C27_2b parameter set was performed via extending the simulations on the EcoRI, BDJ025 and GTAC2 duplexes as well as performing simulations on additional systems (Table 1). The additional systems were selected to vary in sequence and size, to be of high crystallographic resolution, or to have been subjected to analysis of BII content in NMR studies. For example, the EcoRI (#1), JunFos (#4) and NF-κb (#10) sequences have been subjected to explicit analysis of the BII content in solution. A longer oligonucleotide (3BSE, #6) was selected in part due to unique dynamic aspects of the molecule in solution. Sequences (1ZF7 #7 and 1ZF1, #8) were of interest as they crystalize in the B and A form, respectively, despite their similar sequences. 1LJX (#9) was selected as it is in the Z form; this system along with GTAC2 and BDJ025 were simulated in their explicit crystal environments while the remaining systems were simulated in solution. The oligonucleotide targeted by NF-κB (#10) was selected due to the availability of experimental BII populations on that sequence. This system was also the first in which underestimation of the BII state in MD simulations was noted by us. The Ndt80 sequence (#11) was also of interest as its BII conformation at a specific nucleotide is important for interaction with the protein; this system was one in which the inability to properly sample the BII conformation was noted.²¹

With EcoRI and JunFos, simulations were also performed with the AMBER Parm99bsc0 force field^5,15 to allow comparison with the final parameter set developed in the present study; this will be referred to as AMBER for the remainder of the manuscript, unless noted. In this section various quantities from simulations of these systems are presented, including comparison of the C27_2b FF results with experimental data and with the C27 FF. The C27_2b results are also compared with AMBER for EcoRI and JunFos. Some results are presented in the supporting information. Given the extensive amount of literature on the EcoRI dodecamer, the majority of presented data is on that system.

The first test examined the RMS differences (RMSD) between the simulated duplexes and their corresponding canonical A and B forms. In all cases, the outcomes were consistent with the experimental data (Table 6). For EcoRI, 1AXP, 3BSE, 1ZF7, JunFos and NF-κB the conformations in solution are closer to the B form versus the A form. With EcoRI, a second simulation at higher salt (100 mM NaCl, see below) yielded an average conformation which showed no tendency to shift towards the A form; this result is consistent with experiment since the salt concentration is well below that required to stabilize the A form of DNA. The BDJ025 crystal simulation is also closer to the B form, as expected. Of note are the results for the A form structures (GTAC2 and 1ZF1). The GTAC2 crystal simulation yields a structure close to the canonical A form, as does the 1ZF1 simulation in 75% ethanol for the C27_2b FF, consistent with expectations for a GC-rich duplex in a low water-activity environment. In contrast the simulation of 1ZF1 in 75% ethanol using C27 converts to the B form (see Figure S1, supporting information). Importantly, the simulation using C27_2b converted to the B form in the water (0% ethanol) simulation, consistent with the impact of high water activity on DNA conformation⁶⁰. These results indicate that C27_2b is more sensitive than C27 to changes in the water activity environment, a critical and stringent test for DNA force fields. Additional testing of this phenomenon is warranted in future studies.

Table 6.

Average RMS differences (Å) with respect to the canonical forms of DNA for the C27_2b validation simulations.

System	C27		C27_2b		AMBER bsc0
	vsA	vsB	vsA	vsB	vsA	vsB
EcoRI1	4.21±0.46	2.14±0.43	4.09±0.56 5.05±0.53	2.42±0.45 2.31±0.45	5.27±0.49	2.37±0.35
GTAC2	1.92±0.19	3.73±0.23	1.68±0.14	3.53±0.22
BDJ025	3.92±0.25	1.66±0.17	4.13±0.22	1.72±0.14
1AXP	3.71±0.35	1.58±0.31	4.02±0.57	2.42±0.58
3BSE	4.26±0.55	2.77±0.59	5.21±0.65	3.71±0.91
1ZF7	3.62±0.42	1.52±0.31	4.23±0.57	2.07±0.51
1ZF1(H2O)	3.50±0.43	1.67±0.34	4.06±0.50	2.07±0.52
1ZF1(EtoH)	3.27±0.47	1.68±0.41	1.34±0.22	4.43±0.31
JunFos	4.24±0.40	1.58±0.26	6.06±0.69	2.61±0.57	5.38±0.56	3.20±0.65
NF-κb	5.02±0.58	2.34±0.58	5.50±0.61	2.32±0.54
Ndt80			6.47±0.26	2.28±0.21	6.09±0.39	2.40±0.29
1LJX(Zform)3	1.14±0.08		1.18±0.10

Data averaged over 20 to 100 ns except for 1AXP C27 (20 to 98 ns), Ndt80 C27_2b (10 to 50 ns) and Ndt80 Amber parm94 (1 to 10 ns). Errors represent the RMS fluctuations about the average. 1) The second row of C27_2b results for EcoRI are from the high salt simulation. 2) Trajectory from Hart et al.²¹ where the AMBER parm94 parameters⁵ were used. 3) Results for 1LJX are with respect to the crystallographic structure.

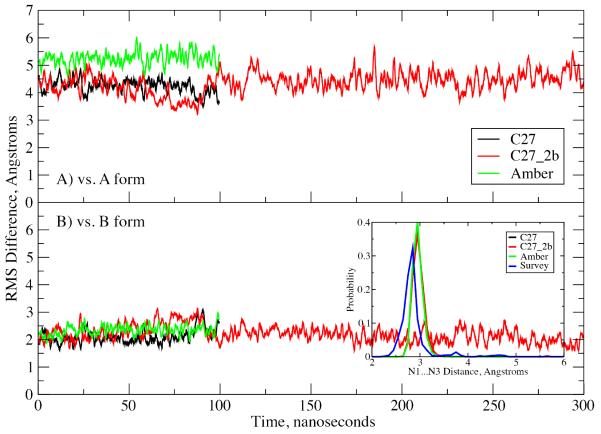
To robustly test the stability of C27_2b, the EcoRI simulation was extended to 300 ns (Figure 3) during which the duplex remained close to the B form. The Watson-Crick base pairing as defined by the N1...N3 distance is well maintained in the simulation for all the FFs (inset in Figure 3). Interestingly, the N1...N3 distance distributions from the simulations peak at a slightly longer distance (approximately 0.1Å) than the X-ray counterpart. While correcting the discrepancy would require reoptimization of the base nonbonded parameters, a far from trivial task, it should be considered in future FF development efforts. It is worth noting that the N1...N3 distance in crystal simulations using a polarizable FF of the bases developed in our laboratory has a maximum approximately 0.1 Å shorter than that of C27,⁶¹ such that this issue appears resolved in the polarizable model.

Figure 3.

RMS difference versus time for the EcoR1 dodecamer in solution. RMS differences vs. the A) canonical A form and B) canonical B form of DNA for all non-hydrogen atoms in the non-terminal residues. Results are for the C27 (black), C27_2b (red) and AMBER Parm99bsc0 (green) force fields. Inset: Watson-Crick base pair interaction based on the N1…N3 distance distributions for the three force fields and data from the survey of B form DNA crystal structures (blue).

Since the primary goal of the present effort was increased sampling of the BII state, the populations of the BI and BII states were determined over all nucleotides in the simulated systems (Table 7). In the analysis, the BI and BII states are defined as the difference between the ε and ζ dihedrals, where BI = ε - ζ ≤ 0° (peak around −90°) and BII = ε - ζ > 0° (peak around +90°). C27_2b shows an increase in sampling of the BII states over C27 in all cases, with the exception of 1ZF1 in ethanol where both FFs only sample a small amount of BII. The amount of BII in EcoRI and JunFos using AMBER is significantly less than with the C27_2b model; similar results are seen for a previously reported simulation²¹ of the sequence targeted by the Ndt80 transcription performed with the AMBER FF94.⁵

Table 7.

Populations of the BI and BII states for the C27_2b validation simulations.

DNA	C27		C27_2b		Amber
	BI	BII	BI	BII	BI	BII
EcoRI1	0.89	0.11	0.75	0.25	0.82	0.18
GTAC2	0.97	0.03	0.92	0.08
BDJ025	0.83	0.17	0.62	0.38
1AXP	0.91	0.09	0.70	0.30
1ZF1(H2O)	0.85	0.15	0.54	0.46
1ZF1(EtOH)	0.90	0.10	0.91	0.09
1ZF7	0.81	0.19	0.55	0.45
3BSE	0.87	0.13	0.70	0.30
JunFos	0.92	0.08	0.76	0.24	0.90	0.10
NF-κB	0.93	0.07	0.72	0.28
Ndt80			0.76	0.24	0.832	0.172

Results obtained over 100 ns simulations. 1) Statistical analysis for EcoRI based on 5 20 ns blocks from which the averages and standard deviations were obtained as follows (%BII, average±standard deviation) C27: 10.9±1.2, C27_2b: 24.7±3.21, and Amber; 18.2±1.9 %. A t test shows that the difference between C27 and C27_2b BII populations is statistically significant, with a P value of < 0.0001. 2) Trajectory from Hart et al.²¹ where the amber parm94 parameters⁵ were used.

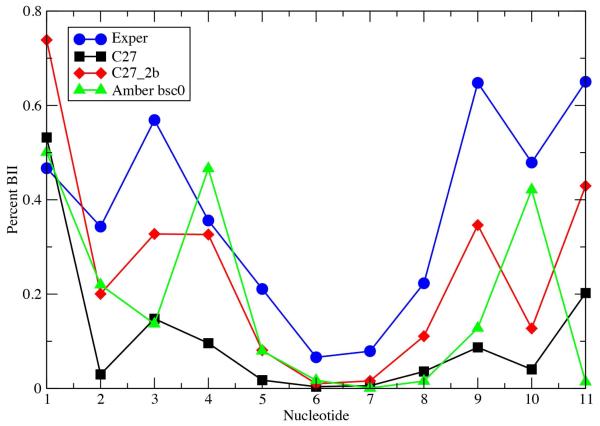
While C27_2b achieved an overall increased sampling of the BII conformation, the ability to properly treat the sampling of BII as a function of sequence is of special interest, and a more difficult objective. For three of the studied sequences, EcoRI, JunFos and NF-κb, experimental data is available on the percent BII as a function of sequence.^20,24,62 For EcoRI, consistent with the data in Table 7, C27_2b yields increased BII sampling (Figure 4 and Table 8) in better agreement with experiment as compared to both C27 and AMBER, although the amount of BII is systematically underestimated, a point addressed below. With respect to the base-step specific percent BII, C27_2b offers significant improvement over both C27 and AMBER (Figure 4 and Table 8). For the base-step specific percent BII, the correlation coefficients between simulation and experiment were 0.69 with C27_2b, 0.47 with C27 and 0.31 with AMBER. Results for JunFos and NF-κb were similar to those for EcoRI (Table S2, supporting information). For JunFos the average difference in BII population between simulation and experiment was -7 for C27_2b compared to values of -22 and -20 for C27 and AMBER, respectively. The percent BII as a function of base step in JunFos was also improved with C27_2b with a correlation coefficient of 0.49 versus 0.30 and 0.26 for C27 and AMBER, respectively. In the case of NF-κb (Table S2B) the average differences were -2 and -22 and the correlation coefficients were 0.45 and 0.29 for C27_2b and C27, respectively. Thus, the reoptimization of the selected dihedral parameters increased the sampling of BII in a sequence-specific manner that is largely consistent with experimental observations.

Figure 4.

Percent BII conformation as a function of nucleotide for EcoR1 from experiment and from the MD simulations using the C27, C27_2b and AMBER Parm99bsc0 force fields. Data for the symmetrically related basepair steps have been combined.

Table 8.

Average percent BII as a function of base-step for EcoR1, from experiments and simulations.

Base Step	Exper	C27		C27_2b		Amber bsc0
		Ave	Diff	Ave	Diff	Ave	Diff
C1pG2	46.7	53.2±4.7	6.5	73.9±8.1	27.2	50.1±13.9	3.4
G2pC3	34.3	3.0±1.3	−31.3	20.0±10.6	−14.3	22.0±5.8	−12.3
C3pG4	56.9	14.8±1.8	−42.1	32.8±7.8	−24.2	13.7±5.1	−43.2
G4pA5	35.6	9.6±0.8	−26.0	32.6±6.5	−3.0	46.6±7.1	11.0
A5pA6	21.1	1.8±0.4	−19.3	8.1±1.6	−13.0	8.0±2.1	−13.2
A6pT7	6.6	0.4±0.2	−6.2	1.0±0.3	−5.6	1.7±0.9	−4.9
T7pT8	7.9	0.6±0.2	−7.3	1.6±0.5	−6.3	0.1±0.1	−7.8
T8pC9	22.3	3.6±0.6	−18.7	11.1±1.4	−11.2	1.6±0.3	−20.8
C9pG10	64.8	8.7±0.5	−56.1	34.6±6.1	−30.2	12.8±3.8	−52.0
G10pC11	47.9	4.1±1.6	−43.9	12.7±3.8	−35.2	42.1±11.3	−5.8
C11pG12’	65.0	20.2±14.5	−44.8	42.9±5.9	−22.1	1.4±0.5	−63.6
Average Difference Correlation			−26.3±5.8 0.47		−12.5±5.1 0.69		−19.0±7.2 0.31

Results obtained over 100 ns simulations. Statistical analysis for the individual base steps accounting for the symmetry of the sequence based on 5 20 ns blocks from which the averages and standard deviations were calculated. The errors for the average differences are the standard error over all the base steps. Correlations are between the experimental and average simulation values over the base steps. Experimental data from reference²⁴ at 297.2 K.

The C27_2b FF clearly is an improvement over C27 and AMBER Parm99bsc0 with respect to sampling of the BII conformation as compared to experiment. However, for both EcoRI and JunFos, C27_2b still underestimates the extent of BII compared experiment. While this may be a limitation of the FF, the method of analysis may contribute to the difference. Analysis of the simulations was based on direct counting of the amount of BI and BII (i.e. based on BI is ε – ζ < 0) from which the relative probabilities of the two states were obtained. Alternatively, in the ³¹P NMR analysis,²⁰ the chemical shift is converted to an average ε – ζ value that is used to identify the percent BI by interpolation between ε – ζ = 90° (0% BI) and ε - ζ = −90° (100% BI). While the results are similar for the two analyses, the more approximate interpolation method tends to overestimate the amount of BII (Figure S2 of the supporting information). Accordingly, the interpolation method used to estimate the BI/BII content from ³¹P NMR chemical shifts slightly overestimates the actual BII content. For example, with JunFos, the BII content when calculated using the interpolation method for C27_2b is in excellent agreement with the experimental estimate; the average difference between calculated and experimental percent BII is 2.3 although the correlation is slightly worse (0.43 vs. 0.49).

As discussed above, in a 10 ns MD simulations of the Ndt80-DNA complex the BII conformation at specific base steps was not maintained using C27.²¹ In the crystal structure of the complex the BII conformation occurs at two important YpG base steps where arginines hydrogen-bond specifically with guanines; these were maintained with the AMBER Parm94 FF, leading to that FF being used in that study. In the crystal structure the BII conformation is less pronounced for the T6′-G5′ step (ε-ζ=38°) than for the T4′-G3′ step (ε-ζ=84°). In simulations of the Ndt80-DNA complex, Parm94 gave 49% and 55% BII for these two steps, whereas the corresponding BII populations were 10% and 85%, respectively, in a 100 ns simulation with C27_2b done as part of the present study. The arginine hydrogen bonding patterns were similar with the two force fields, with R111 and R177 forming classical arginine double hydrogen bonds to the guanine N7 and O6 atoms. Both Parm94 and C27_2b formed the R111-Gua3′ hydrogen bonds >90% of the time, and the R177-Gua5′ hydrogen bonds > 95% of the time. Thus, C27_2b has rectified the problem with C27 observed by Hart et al.²¹

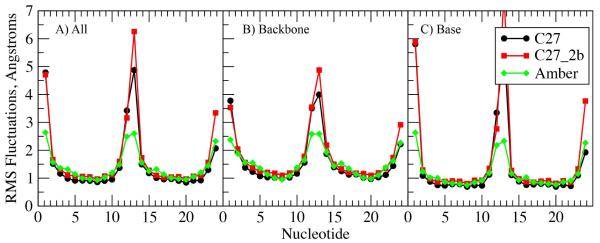
Alteration of the ε, ζ and sugar dihedral parameters may also impact the flexibility of the FF, making it necessary to test this aspect of the model in MD simulations. This was addressed by analyzing the RMS fluctuations for selected systems and comparison with the NMR order parameters for EcoRI. Figure 5 presents the RMS fluctuations as a function of nucleotide for EcoRI for C27, C27_2b and AMBER from 100 ns simulations. The overall pattern of fluctuations is similar for the three FFs, though the terminal base pairs are clearly more mobile in C27 and C27_2b as compared to AMBER. Despite more flexible termini, the fluctuations of the central nucleotides are similar for the three FFs, with slightly larger RMS fluctuations with C27_2b than with C27. The RMS fluctuations for C27 and C27_2b for 1ZF7 and 3BSE (Figure S3 of the supporting information) confirm the results from EcoRI (Figure 5), with C27_2b being more flexible than C27, a somewhat expected outcome considering the increased BII sampling with C27_2b.

Figure 5.

RMS Fluctuations of the EcoR1 dodecamer as a function of nucleotide from 100 ns MD simulations using the C27 (black), C27_2b (red) and AMBER Parm99bsc0 (green) for the non-hydrogen atoms for the A) full duplexes, B) the phosphodiester backbone or C) the bases. Structures were least-squares aligned to the starting stuctures based on all non-hydrogen atoms prior calculation of the RMS fluctuations. The sequence numbering on the X-axis covers the two strands of the oligonucleotide, with positions 12 and 13 corresponding to termini nucleotides.

Dynamics of the FFs were also tested based on the reproduction of NMR order parameters for EcoRI⁶³ for the C27, C27_2b and AMBER FFs. Results for the C1′, C3′ and C6/C8 atoms are in Table 9 for the individual palindromic strands in the duplex, to probe convergence of the results. In general, the C27_2b order parameters are lower than those for both C27 and AMBER, as seen in the average differences in Table 9, with C27 and AMBER having similar values and being in good overall agreement with experiment. Thus, the increased fluctuations observed for C27_2b appear associated with order parameters systematically lower than those experimentally derived, though it may be related to the salt concentration in the simulations, as discussed below.

Table 9.

Order parameters, S², for EcoRI from NMR experiments and MD simulations. Results from the simulations are presented individually for strand 1 (s1) and strand 2 (s2).

C1’ atom	Exper		C27		C27_2b		Amber
Base	S2	SD	s1	s2	s1	s2	s1	s2
1	0.52	0.02	0.26	0.30	0.17	0.02	0.56	0.38
2	0.78	0.03	0.80	0.80	0.78	0.59	0.70	0.78
3	0.74	0.03	0.66	0.65	0.54	0.61	0.66	0.72
4	0.88	0.03	0.85	0.86	0.79	0.82	0.67	0.70
5	0.84	0.03	0.89	0.88	0.82	0.83	0.74	0.76
6	N.A.	N.A.	0.77	0.79	0.57	0.57	0.81	0.82
7	0.92	0.02	0.74	0.76	0.66	0.66	0.85	0.85
8	0.86	0.02	0.83	0.82	0.81	0.80	0.82	0.82
9	0.68	0.03	0.64	0.61	0.56	0.54	0.71	0.69
10	0.85	0.02	0.80	0.84	0.59	0.81	0.73	0.67
11	0.71	0.02	0.66	0.78	0.62	0.64	0.78	0.77
12	N.A.	N.A.	0.30	0.69	0.23	0.57	0.50	0.67

Difference analysis
Average all	−0.06	−0.05	−0.14	−0.14	−0.05	−0.06
Correlation	0.90	0.88	0.84	0.89	0.70	0.79
Average_non_terminal	−0.04	−0.03	−0.12	−0.11	−0.06	−0.05
Correlation	0.74	0.69	0.57	0.73	0.39	0.36

C3′ atom	Exper		C27		C27_2b		Amber
Base	S2	SD	s1	s2	s1	s2	s1	s2
1	0.39	0.02	0.29	0.35	0.15	0.07	0.52	0.36
2	N.A.	N.A.	0.75	0.79	0.78	0.59	0.79	0.78
3	N.A.	N.A.	0.57	0.53	0.45	0.54	0.70	0.65
4	N.A.	N.A.	0.85	0.85	0.79	0.84	0.74	0.78
5	0.90	0.02	0.90	0.87	0.80	0.81	0.78	0.78
6	0.79	0.03	0.67	0.71	0.35	0.37	0.82	0.83
7	N.A.	N.A.	0.63	0.71	0.44	0.44	0.83	0.82
8	0.79	0.03	0.81	0.78	0.76	0.73	0.79	0.78
9	0.67	0.04	0.46	0.42	0.45	0.39	0.66	0.67
10	N.A.	N.A.	0.73	0.80	0.37	0.78	0.80	0.75
11	N.A.	N.A.	0.39	0.72	0.35	0.52	0.74	0.79
12	0.43	0.05	0.49	0.70	0.35	0.48	0.54	0.61

Difference analysis
Average all	−0.06	−0.02	−0.18	−0.18	0.03	0.01
Correlation	0.89	0.67	0.80	0.74	0.95	0.88
Average non terminal	−0.08	−0.09	−0.20	−0.21	−0.02	−0.02
Correlation	0.93	0.94	0.61	0.72	0.70	0.72

C6/C8 atoms	Exper		C27		C27_2b		Amber
Base	S2	SD	s1	s2	s1	s2	s1	s2
1_C6	0.77	0.04	0.39	0.45	0.29	0.11	0.58	0.56
2_C8	0.81	0.07	0.87	0.87	0.84	0.84	0.86	0.85
3_C6	0.92	0.04	0.86	0.86	0.84	0.85	0.85	0.86
4_C8	N.A.	N.A.	0.90	0.90	0.88	0.88	0.88	0.88
5_C8	N.A.	N.A.	0.90	0.90	0.89	0.89	0.88	0.89
6_C8	N.A.	N.A.	0.91	0.91	0.90	0.90	0.91	0.91
7_C6	0.83	0.02	0.86	0.87	0.86	0.86	0.92	0.92
8_C6	0.87	0.04	0.86	0.86	0.85	0.85	0.91	0.91
9_C6	0.79	0.06	0.87	0.86	0.83	0.84	0.87	0.87
10_C8	0.88	0.04	0.89	0.90	0.87	0.88	0.88	0.87
11_C6	0.88	0.04	0.86	0.85	0.82	0.82	0.87	0.87
12_C8	0.91	0.08	0.70	0.80	0.61	0.65	0.76	0.78

Difference analysis
Average all	−0.05	−0.04	−0.09	−0.11	−0.02	−0.02
Correlation	0.42	0.50	0.36	0.46	0.35	0.41
Average non terminal	−0.01	0.00	−0.05	−0.04	0.00	0.01
Correlation	0.09	0.06	0.12	0.18	−0.13	−0.09

Experimental data from Duchardt et al.⁶³ Analysis over the 5 to 100 ns portions of the trajectories. SD indicates the standard deviation in the experimental values. Difference and correlation coefficient calculated over nucleotides for which experimental data are available, excluding the terminal nucleotides.

Correlation coefficients between the MD-based and NMR order parameters helped analyze how the FFs reflect those values as a function of sequence (Table 9). For C1′, the C27 and C27_2b correlations range from 0.84 to 0.90 for all nucleotides (0.57 to 0.74 without terminal nucleotides). These values are higher than their AMBER counterpart. Similar levels of correlation are obtained for the C3′-H vector with all three FFs. For the C6/C8 values, the correlations are again similar for all the FFs. When the terminal nucleotides are excluded, the correlation coefficients are relatively small, possibly due to the small range of S² values. With both CHARMM FFs the values are positive, while with AMBER they are negative indicating slightly anticorrelated behavior. These results are generally consonant with the BII analysis as a function of sequence (Table 8 and Table S2) suggesting that C27_2b satisfactorily treats the analyzed properties as a function of sequence.

Due to their polyanionic nature oligonucleotides are sensitive to salt concentration.^60,64 To test the potential impact of salt on the reproduction of the NMR order parameters, a second C27_2b simulation of EcoRI was performed with the salt concentration adjusted to approximate the experimental regimen.⁶³ Interestingly, all the calculated S² values tend to be larger in that simulation (Table S3), leading to average differences that are less negative than those obtained with C27_2b in low (i.e. neutralizing) salt (Table 9). The increase in the order parameters are largest at the termini, though increases in the duplex central region are evident. Thus, even a small change in salt concentration (i.e. 5 additional Na⁺ and 5 additional Cl^- ions added to a simulation box of almost 26,000 atoms) appear to impact the calculated order parameters. These results, along with those for the method used to estimate the BI/BII ratio, indicate the difficulties and care that must be taken in performing a rigorous, quantitative comparison of computed and experimental data. Incidentally, experimentally determined BI/BII ratios have been shown to depend on the concentration of monovalent cations.²⁹

The above analyses indicate that C27_2b provides a reasonable treatment of the equilibrium between the A and B forms of DNA, and improves the representation of the equilibrium between the BI and BII states. Yet, it was necessary to check that the C27_2b FF satisfactorily treated other detailed (but crucial) aspects of DNA structure. This involved examination of the probability distributions of dihedrals in the phosphodiester backbone, of the glycosidic linkage, of the sugar puckering, and of helicoidal parameters. Those distributions may be compared to X-ray survey data of DNA structures (see Methods). In addition, time series may be analyzed to understand details of the dynamics of the systems. Comparison to crystallographic data is informative, especially for localized geometric properties. However, one must keep in mind that the sequence-specific properties of DNA in solution may depart from crystallographic averages, especially regarding helicoidal parameters. Unfortunately, accurate structures of DNA duplexes in solution are still too scarce¹³ to provide sufficient reference data for systematic evaluation of simulated structure across sequences.

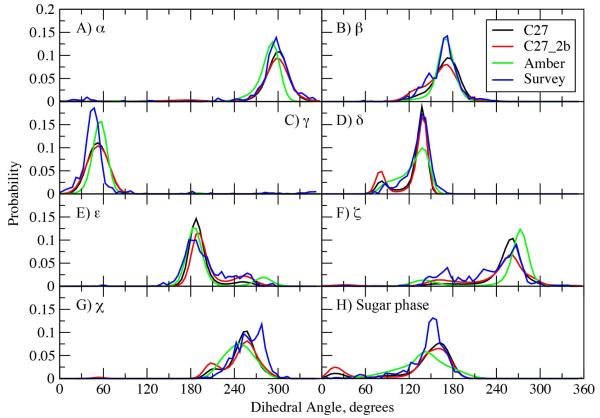
Dihedral and pucker distributions for the EcoRI dodecamer for the C27, C27_2b and AMBER FFs are shown in Figure 6 along with NDB survey data obtained as part of the present study. Similar distributions for 3BSE, 1ZF7 and 1ZF1 in ethanol are included in Figure S4 of the supporting information. In EcoRI (Figure 6) the CHARMM force fields satisfactorily reproduce the NDB distributions with respect to both the location and ranges. With all FFs, there is a slight shift in the γ distribution towards higher values. In the glycosidic χ distribution, the conventional B form range from 140 to 270 is populated as expected, but a peak at higher χ around 280° is not present in the FF results. This peak in the crystal distribution is associated with terminal nucleotides in the survey; the terminal nucleotides were not included in the analysis of the MD simulations. Also, the CHARMM FFs show a minor but distinct population for χ around 210°, representing A-like χ conformations, which is slightly more stabilized in C27_2b than C27. This is consistent with more sampling of δ around 80° (associated with north sugar puckers) in C27_2b than in C27. Importantly, this increased sampling of the A-like χ conformation and sugar pucker has not destabilized the overall B form in C27_2b. With ε and ζ, C27_2b allows increased sampling in the regions of 240° and 165°, respectively, associated with the increased BII populations. The increased BII conformation is also associated to the shoulder in the β distribution in the region of 140°, consistent with the previously reported correlation between β and the BI and BII states.²⁷

Figure 6.

Dihedral angle and pseudorotation angle probability distributions from 100 ns MD simulations of EcoRI using the C27 (black), C27_2b (red) and AMBER Parm99bsc0 (green). Included are corresponding distributions from a NDB survey of all B form structures with a resolution ≤ 2.5 Å.

Changes in sugar dihedral parameters (Table S1) altered the sugar pucker distributions while lowering of the energy of the north conformation in model compound 2 (Table 3). Both CHARMM FFs reproduce the overall distribution in the south region (~140 to 180°, ~C2′endo pucker) associated with B form DNA, although the distinct peak at around 150° in the survey distribution is not reflected in the FF distributions. The shape of the distributions reproduce the shoulder in the vicinity of 120°, followed by low sampling at lower pucker values (~ 90°, associated with the east energy barrier), followed by a peak at 15° associated with north puckering common to A form DNA (~C3′endo). Interestingly, the NDB survey shows no sampling in the north region, although sampling is observed in the vicinity of 90° for δ in the survey. Detailed analysis indicates that subtle differences in the nature of the sugar puckering (i.e. associated with differences in the 5 furanose ring dihedrals that define the pucker) in A vs. B form crystal structures when δ is ~90° are present, leading to the lack of north sampling in the sugar phase in the survey data. Studies to better elucidate this effect are ongoing.

Concerning systems 1ZF7, 3BSE and 1ZF1 in 75% ethanol (Figure S4), the results from 1ZF7 and 3BSE are similar to those for EcoRI, consistent with those structures sampling the B form in solution. With 1ZF7, increased sampling of the BII conformation, consistent with its high GC content (Table 1), is seen in the β, ε and ζ distributions for C27_2b. In the 3BSE simulation the additional peak in the ζ distribution with C27 and the additional sampling of north sugars in C27_2b are consistent with the reported disordered nature of the duplex in solution.⁶⁵ In particular, the authors note a six base A+T rich segment at the center of the strand, showing “unusually weak electron density, suggesting conformational fluctuations,” and propose that its disorder is “intrinsic to its sequence”. In this region, C27 gives an average RMS fluctuation of 1.64 Å over all residues, with C27_b giving an average RMS fluctuation of 1.87 Å. For comparison, in the B form structures EcoRI and 1ZF7, and considering all non-terminal residues, C27 gives average RMS fluctuations of 1.24 and 1.20 Å, respectively, while C27_2b gives average RMS fluctuations of 1.43 and 1.49 Å, respectively.

For 1ZF1 in ethanol, where the survey data is that from A form helices, the difference in sampling associated with C27 assuming a B conformation while C27_2b remained in the A conformation is evident. The A form conformation in the C27_2b simulation nicely reproduces all the survey distributions. Increased sampling of δ = ~80° and north puckers is evident. The model reproduces the shift in the location of the maxima in the ε and ζ distributions, versus that occurring in the B form survey data (i.e. compare survey results in Fig. S4b and S4c), further indicating the conformational properties of C27_2b to be sensitive to changes in the environment.

The dihedral and pucker distributions with AMBER for EcoRI (Figure 6) are generally similar to the CHARMM FFs, but with notable differences. The AMBER α distribution is shifted to lower values compared to the survey, though the peak height is in good agreement. The peak height is also in good agreement for β, though the shoulder in the vicinity of 140° is too small, consistent with the lower amount of sampling of the BII conformation. A shift to higher values is present in the γ distribution as compared to the survey. With δ the range covered by AMBER is similar to that from the survey while sampling of the ~90° region is more a shoulder rather than a distinct peak. This is consistent with the sugar phase distribution, which is quite broad with no sampling of the north conformation. A study by Kollman and coworkers addressed this issue,⁶ though the resulting parametrization is not included in the AMBER parm99bsc0 FF. With ε and ζ, sampling of the 240° and 165°regions, respectively, is underestimated relative to that in the survey, again consistent with the lower amount of BII sampling. The major ε peak agrees well with experiment, though the peak at higher values associated with the BII conformation is systematically shifted relative to that from the survey. The major peak for ζ in the 270° region is shifted to values higher than in the survey, while the BII associated peak extends to values lower than in the survey. Finally, with χ a broad range of values are sampled in general agreement with the survey data; a distinct peak at ~210°, associated with A-like conformations, that occurs in the CHARMM force fields, is not present. This analysis indicates AMBER to generally sample ranges of the dihedrals seen in the survey data, consistent with the B form of the dodecamer being stable in solution; however, systematic shifts with respect to the survey data are present in a number of cases.

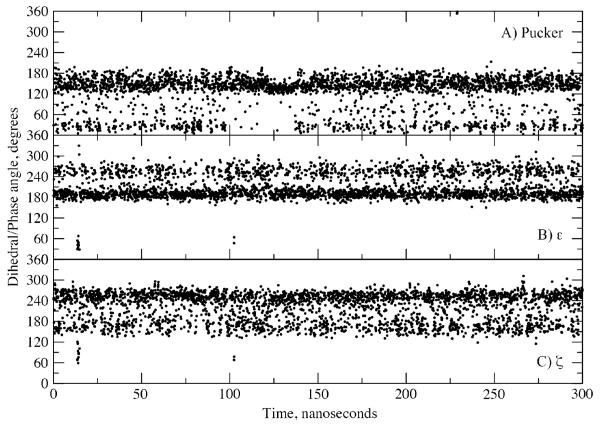
To better understand the nature of the conformational transitions giving rise to the distinct peaks in the distributions of the sugar pucker, ε and ζ (Figure 6), the corresponding time series from the C27_2b EcoRI simulation were analyzed. Selected time series are shown in Figure 7 with all of the pucker, ε and ζ time series shown in Figures S5, S6 and S7 of the supporting information, respectively. These plots show that the three degrees of freedom have undergone a large number of transitions, such that the lifetimes of the distinct conformations are on the 10 picosecond time scale. Similar results were obtained in the AMBER EcoRI simulation (not shown). The relatively short lifetimes are consistent with NMR 13C spin relaxation experiments from which relaxation times in sub 100ps range were measured for the C1′-H1′ and C3′-H3′ vectors.⁶³ Concerning ε and ζ, some ³¹P NMR experiments suggested that the free energy barrier for the BI to BII transition might be in the range of 12 to 15 kcal/mol.²⁴ This barrier height would suggest a lifetime on the order of milliseconds, significantly longer than observed with the present FFs. However, those estimates are based on the assumption of a two state model, which the present calculations indicate may not be appropriate given the significant sampling of intermediate states in both ε and ζ.

Figure 7.

Time series from EcoRI C27_2b simulation for A) sugar puckering of strand 1, nucleotide 3, B) ε of strand 1, nucleotide 4 and C) ζ of strand 1, nucleotide 4. Data points are shown for every 100 ps. See Figures S6, S7 and S8 of the supporting information for all puckering, ε and ζ time series. Note that in the BI state ε and ζ are approximately 190° and 270°, respectively, and in the BII state they are approximately 270° and 180°, respectively.

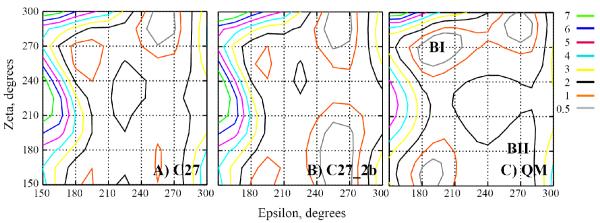
The “intrinsic” contribution to the barrier between the BI and BII states had been found to be less than 2.0 kcal/mol in QM calculations based on compound 2 without the base.³¹ Here, additional 2D ε vs. ζ energy surfaces were obtained with C27, C27_2b and QM at the MP2/6-31+G(d) level for model compound 2 in which the base had been omitted. Shown in Figure 8 are the three energy surfaces with the locations of the BI and BII conformations shown on the right-hand panel. The overall shapes of the surfaces are similar, though differences are evident. The BI minimum is not as deep in the empirical surfaces versus the QM, while the opposite is true for the BII minimum. The increased depth of the BII minimum in C27_2b versus C27 is evident, consistent with the lowering of the relative BII energy based on model compound 1 (Table 2). Concerning the barrier between the BI and BII conformations, there are two low energy paths along ε ~200 and ~270° in all three surfaces. In all of the surfaces, the highest energies are between 1 and 2 kcal/mol with the barriers being lower in the empirical surfaces. A previous study estimated the free energy barrier to be in the range of 2.6 to 3.1 kcal/mol based on potential of mean force calculations between the A and B forms of DNA.⁶⁶ These values are consistent with the 1D surfaces for 1 (Figure 2) and indicate that the experimental estimate of >12 kcal/mol is not due to the intrinsic energies of the phosphodiester backbone, suggesting that more global structural phenomena (eg. base stacking, sugar puckering etc.) may be contributing to the barrier if the model used to make the experimental estimates is appropriate. Future studies are required address this issue.

Figure 8.

2D potential energy surfaces of ε vs. ζ, for the A) C27 FF, the B) C27_2b FF and C) QM MP2/6-31+G(d) level of theory for model compound 2 with the base omitted. Energies in kcal/mol. Sugar pucker was restrained to the south pucker by constraining C1′-O4′-C4′-C3′ = 0.0 and the a dihedral was constrained to 300°.

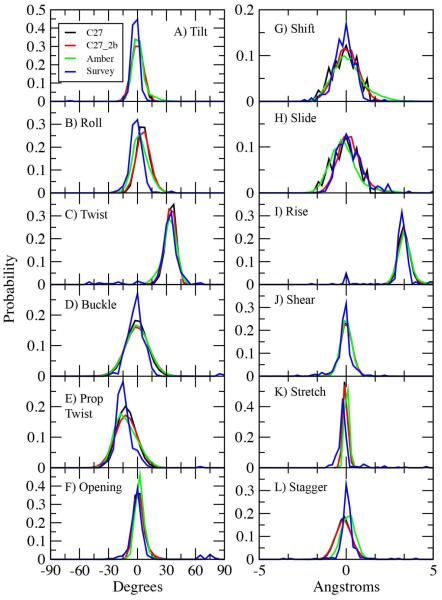
Helicoidal parameters are commonly used to define the orientations of the bases relative to the helical axis, and vary among the different forms of DNA.^51,52,67 Accordingly, the FFs should be able to reproduce experimental values for these descriptors. In the present study, the experimental data are probability distributions of selected helicoidal parameters based on the survey of crystallographic structures. Presented in Figure 9 is the survey data along with probability distributions from the EcoRI simulations using C27, C27_2b and AMBER. In general, all three forces fields adequately reproduce the survey distributions. With roll, the AMBER distribution is in slightly better agreement with the survey while C27_2b yields slightly better overlap with the survey data for slide than both C27 and AMBER. Comparison of the C27 and C27_2b distributions show them to generally be similar. This is expected as the base parameters have not changed, although some correlations between backbone conformation and helicoidal parameters are known.

Figure 9.

Helicoidal parameter probability distributions from 100 ns MD simulations using the C27 (black), C27_2b (red) and AMBER Parm99bsc0 (green). Included are corresponding distributions from a NDB survey of all B form structures with a resolution = 2.5 Å.

Analyses of selected helicoidal parameters as a function of nucleotide from the EcoRI simulations are presented in Figure S8 of the supporting information. The figures include the values from the EcoR1 crystal structure 1BNA. All three FFs do well in reproducing the trends observed in the crystal structures. Notably, none of the FFs reproduce the large value of twist at base pair 2 (the first G along the X axis) and the small values of Roll and Rise at base pair 3. Concerning the overall values of twist, the C27, C27_2b and AMBER values were 34.4±4.8, 33.8±5.4 and 32.8±6.4°, respectively, where the values are the averages and the standard deviations over the nucleotides. AMBER is in better agreement with the average value from the 1BNA crystal structure of 32.8±10.6°, though both CHARMM force fields are in better agreement with the value for canonical B form DNA, 36°, consistent with previous studies.^43,68

Finally, to further test the generality of the C27_2b FF, it was used to simulate a Z-form dodecamer in its crystal environment (1LXJ, #9 in Table 1). RMSD analysis (Table 6) showed the simulations to stay close to the initial Z-form crystal structure. Dihedral distributions were also calculated and compared to survey data of Z-DNA structures that included unmodified and base-modified duplexes to get a satisfactory sample size (Figure S4d, supporting information). The simulated distributions are in overall reasonable agreement with the survey distributions. Notably, the two peaks associated with the syn and anti conformations about the glycosidic linkage (χ) are maintained, although some systematic shifts relative to experiment are observed. Similar systematic shifts are seen in the calculated phase distributions as well as elsewhere, which is assumed to be associated with the FF being optimized to reproduce dihedral distributions of A and B forms of DNA. Despite these differences it appears that C27_2b is of utility for simulations of Z DNA in the appropriate environment. While not shown, a simulation of 1LXJ in solution was unstable, with the DNA unwinding, indicating that C27_2b does not artificially stabilize Z DNA.

Conclusions

We have presented a refinement of the CHARMM27 all-atom additive force field for nucleic acids with emphasis on improving the sampling of the BII state of B form DNA. This required adjustment of selected parameters and validation of many facets of the resulting force field in relation to its representation of various forms of DNA and the conditions in which they are stable. Parameter optimization was initially based on model compounds allowing for systematic changes in only the dihedral parameters to improve agreement with target QM data. This yielded several parameter sets that were tested in condensed phase simulations of a training set of oligonucleotides. This procedure was also applied to improve treatment of the sugar pucker with respect to north and south conformations that dominate the A and B forms of DNA, respectively. The most promising FF model (C27_2b) was then used in simulations of other DNA molecules for a duration of 100 ns, with the EcoRI simulation extended to 300 ns. Analysis of these simulations showed the C27_2b FF model to reproduce a range of experimental data in DNA, thereby providing convincing validation for C27_2b. In particular, C27_2b provides a more accurate treatment of the BI/BII equilibrium in DNA, which is a significant improvement over C27. Simulations using the AMBER parm99bsc0 FF were also undertaken on EcoRI and JunFos, yielding overall results similar to those for both CHARMM force fields, although some differences in the sampling of backbone dihedrals were observed. While general agreement of the C27_2b with a range of experimental observables was obtained, technical difficulties in obtaining rigorous quantitative comparisons of calculated and experimental results for the BII populations and NMR order parameters were noted. Also, the dearth of accurate DNA structures in solution, with experimentally characterized populations and dynamics, remains a fundamental limitation for the development and optimization of DNA force fields. The selected DNA FF will be included with a recent revision of the CHARMM RNA FF,³⁴ yielding the CHARMM36 all-atom additive force field for nucleic acids.