Time-Resolved and Spatio-Temporal Analysis of Complex Cognitive Processes and their Role in Disorders like Developmental Dyscalculia

Abstract

The aim of this article is to report on the importance and challenges of a time-resolved and spatio-temporal analysis of fMRI data from complex cognitive processes and associated disorders using a study on developmental dyscalculia (DD). Participants underwent fMRI while judging the incorrectness of multiplication results, and the data were analyzed using a sequence of methods, each of which progressively provided more a detailed picture of the spatio-temporal aspect of this disease. Healthy subjects and subjects with DD performed alike behaviorally though they exhibited parietal disparities using traditional voxel-based group analyses. Further and more detailed differences, however, surfaced with a time-resolved examination of the neural responses during the experiment. While performing inter-group comparisons, a third group of subjects with dyslexia (DL) but with no arithmetic difficulties was included to test the specificity of the analysis and strengthen the statistical base with overall fifty-eight subjects. Surprisingly, the analysis showed a functional dissimilarity during an initial reading phase for the group of dyslexic but otherwise normal subjects, with respect to controls, even though only numerical digits and no alphabetic characters were presented. Thus our results suggest that time-resolved multi-variate analysis of complex experimental paradigms has the ability to yield powerful new clinical insights about abnormal brain function. Similarly, a detailed compilation of aberrations in the functional cascade may have much greater potential to delineate the core processing problems in mental disorders.

1. Introduction

This article describes our experiences with time-resolved and spatio-temporal multivariate analysis of fMRI obtained from a complex experimental design for studying the higher-order cognitive processes in mental arithmetic and its associated deficits, namely developmental dyscalculia (DD). DD, a biologically based learning disability, specifically impairs the normal acquisition of arithmetic knowledge (Shalev and Gross-Tsur, 2001; von Aster and Shalev, 2007; Geary, 2010; Butterworth, 2010). It manifests as a marked lifelong difficulty in executing the four base arithmetic operations and affects approximately 5–6% of normal children. Estimates from numerous studies suggest that it imposes a substantial socio-econmical burden worldwide (Butterworth et al., 2011). The diagnosis of DD (WHO, 2005) is still made primarily by nonmedical methods (Shalev and Gross-Tsur, 2001), and research on its neurobiological basis is just beginning (Levy et al., 1999; Kucian et al., 2006; Rotzer et al., 2009), particularly for its neuroanatomical markers (Isaacs et al., 2001; Eliez et al., 2001; Molko et al., 2003; Rotzer et al., 2008; Kaufmann et al., 2011). The principal hypothesis of this paper, that subjects with DD are deficient in the rapid monitoring of numerical magnitudes (Stanescu-Cosson et al., 2000; Dehaene et al., 1999), is supported by their striking unawareness of absolute and relative discrepancies between numbers, irrespective of poor procedural skills, attention deficit, and hyperactivity disorders (Shalev and Gross-Tsur, 2001). A network interference model suggests that an abundant variety of solutions - some necessarily incorrect - are generated during arithmetic calculation (Campbell and Tarling, 1996). The capacity of healthy people and even primates to monitor numerical magnitudes may be rapid enough to serve as an `analog', real-time estimator of such candidate solutions (Dehaene and Cohen, 1995; McCrink and Spelke, 2010; Livingstone et al., 2010; Jones et al., 2010). A subsequent verification process (Campbell and Tarling, 1996) profits from accurate assessment of number size when evaluating the choices offered by the language-bound computation and memory unit. This evaluative last step might operate erroneously in individuals with DD because of faulty judgment about numerical magnitudes.

The aim of our study was to explore the impairment of this magnitude assessor in DD under two principally different conditions within the same arithmetic task: a) during a first period of exact calculation and b) during a second period of approximate calculation. Subjects with pure DD (Shalev and Gross-Tsur, 2001) and healthy controls were asked in an fMRI study to solve simple multiplication problems and thereafter to make a judgement about the incorrectness of subsequently presented results. The first reason for combining the two operations was to increase the number of cortical areas recruited over time and thereby to improve the likelihood of detecting aberrant responses in the neural activation cascade. The second reason was the assumption that an “algebraic mental state” - induced by the preceding multiplication step - would improve our ability to assess the performance of numerical approximation. We expected, along the neural activation cascade for arithmetic problem solving, a distinctive pattern to surface in DD, not only in the parietal lobes in line with observations reported by others, but also in brain regions known for rapid evaluation of sensory inputs of diverse modalities (Mathiak et al., 2004; Fiez, 1996; Allen et al., 1997) such as the cerebellum.

A standard voxel-based analysis of the data revealed parietal differences between controls and subjects with DD. Further differences, however, surfaced with a time-resolved examination of the neural response to a number size effect : In controls an initial right cerebellar focus was observed, then an extensive extrastriate and left angular involvement followed by a striate and left prefrontal activation. On the other hand in DD a delayed and prolonged recruitment of the entire right intraparietal sulcus was observed instead. Intrigued by the possibility of discriminating between the cognitive processes of subjects, a novel state-space model (SSM) technique was applied to comprehensively compare the spatio-temporal signatures of mental activity in terms of the mutual information of the estimated models (Janoos et al., 2011a). The method revealed functional differences between controls and DD for each of the three experimental phases (reading, computing, responding).

In order to further explore the implications of this finding, we included data of a group of subjects diagnosed with developmental dyslexia (DL) (Breznitz and Misra, 2003; Bitan et al., 2010) but with no history of dyscalculia. We expected to find no distinct signal characteristics for DL as compared with the healthy subject group, as only numerical digits were presented without any verbal material having alphabetic characters. However, the analysis showed functional dissimilarity during the initial reading phase, indicating that the disorder of DL had an impact on the digit reading process or possibly also on the rote memory recall process for multiplication products, resulting in irregular signatures within the metabolic traces of brain activity of the individuals.

Thus our results suggest that time-resolved multi-variate analysis of complex experimental paradigms has the ability to yield powerful new clinical insights of abnormal brain function (Goswami and Szűcs, 2011). Similarly, the detailed compilation of aberrations in the functional cascade may have greater potential to delineate the core processing problems in mental disorders. For example, based on the analysis of the DD study, it is hypothesized that the atypical trajectory commences in a cerebellum where incertitude in numerical judgement induces ineffective compilation of numerical knowledge into working memory further downstream. For typically developing individuals, the left frontal silent verbal rehearsal and occipital visual conception buffers enable keeping track of interim results during mental calculation. However, the time-resolved results imply that in DD this process takes place instead in the right parietum, resorting to a non-verbal non-visual representation featuring discrete spatial attributes. Furthermore, such flawed awareness of numerical magnitudes may lead to erroneous and deficient left-angular registration of language-coded multiplication facts. It is posited that because learning by rote fundamentally relies on the accurate assessment of number size, subjects with DD might benefit from strengthening their rapid magnitude-processing skills.

2. Materials

2.1. Subjects

Thirty-six control subjects (23 female; one female and one male left-handed, one male ambidextrous; age 21–34 y; mean age 25.6 y ± 3.0 y) and 13 normal-intelligent (full-scale IQ>95) individuals with pure DD (5 female; 1 male left-handed, other individuals right-handed; age 22–23 y; mean age 22.46 y ± 0.52 y) participated. These subjects were free of neurological and psychiatric illnesses, dyslexia, and attention-deficit/hyperactivity disorder. All controls denied a history of any calculation difficulties.

Individuals diagnosed with DD were selected in a two-stage screening process and were taken initially from a large pool of affected individuals starting with 3029 school-children 10 to 11 years old (Shalev and Gross-Tsur, 2001). They have been followed prospectively since 1990 and assessed frequently for various scholastic skills and neurological deficits in the framework of an epidemiological study of dyscalculia.

An additional nine subjects with DL (Bitan et al., 2010) (2 females and 2 males left-handed; age 18–32 y; mean age 24.6 y ± 3.7 y) participated and their data were included for scientific interest in the brain-states analysis phase. Except for diagnosis of dyslexia, they were subject to the same inclusion criteria as controls, and were shown the same arithmetic stimuli during the fMRI studies.

Before the experiment and after an informative introduction, we obtained written consent from every participant in compliance with the institutional guidelines of the Chaim Sheba Medical Center Helsinki Committee and the Health Ministry of the State of Israel.

2.2. Paradigm design and stimuli

A major concern in this study is the inability to cease thinking about the arithmetic exercise because such mental efforts during the resting phase detrimentally alter the quality of the baseline brain signal. Shortening the baseline condition to a negligible length remedies this problem and, combined with self-paced task cessation, produces an irregular and accelerated fMRI design with the benefit of acquiring extra events per session. Additionally, the resulting aperiodic scheme negates the effects of the many periodic artifacts of physical, biological, and neuropsychological origin and may yield a less noisy BOLD signal. We presume that most brain activation is secondary to the cognitive demand of the rapid arithmetic task, is recruited only for a fraction of the event duration. and that the BOLD signal within such areas recovers swiftly enough to provide a baseline signal. Furthermore, it is assumed that the signal is modulated by experimental parameters intrinsic to arithmetic exercises such as the number size (Stanescu-Cosson et al., 2000) which even in the absence of a proper `resting condition' produce detectable traces in the signal.

The self-paced, irregular paradigm is illustrated schematically in figure 1. Subjects were exposed visually to simple multiplication problems with single digit operands, e.g., 4 × 5, and had to decide if the incorrect solution subsequently displayed was, e.g., `close' for 23, `too small' for 12, or `too big' for 27 from the calculated, correct result of 20. All solutions were up to 50% less or more than the correct answer. Only one solution was presented at a time. The 'close' answer had to be applied for solutions that were within a ±25% proximity to the correct result, while the two remaining exceeded this threshold. Subjects answered by pressing a button with the index finger of the dominant hand for `too small', the middle finger for `close', and the ring finger for `too big'. Identical operand pairs were excluded. The simplest operand pair was 3 × 4, while the most demanding pair was 8 × 9. The order of small vs large operands was approximately counterbalanced. Presentation times were the following: multiplication problem 2.5 s, equal sign (=) 0.3 s, solution 0.8 s, judgment period (with − ~ + representing symbols for `too small', `close' and `too big') maximally 4 s, and rest condition with fixation point of 1 s until the beginning of a new cycle. Subjects were encouraged to respond as quickly as possible. Stimulus onset asynchrony (SOA) ranged from around 4 s to a maximum of 8.6 s. All subjects were exposed to two different sets of multiplication problems, with an interval of approximately 30 min between sessions 1 and 2 during which time they solved other nonnumerical tasks. Each subject underwent a training session of 10min with a separate set of stimuli on a computer laptop shortly before scanning.

Figure 1. Task design.

The paradigm flow chart depicts a single event in the upper figure part and consists of an initial multiplication (green background), a trailing estimation phase (light red), and a resting phase (light blue). The sequential order of the three parametric effects (in brown polygons) such as `product size', `distance', and task `difficulty' reflects their presumed temporal position within a paradigm event. The horizontal black axis (top) marks time in seconds. The horizontal gray bars below imply the temporal extent of FIR bins which each correspond with the scan time for one brain volume. The presentation times for visual frames are indicated in seconds (white letters) for the multiplication problem (4 × 5, for 2,5 s), the equal sign (=, for 0.3 s), an incorrect solution (only one at the time, though incorrect throughout, e.g. 23, for 0.8 s), the auxiliary frame (− ~ +, for maximally 4.0 s) for the three response choices like `too small', `close' and `too big', and the fixation point (• for 1.0 s). The choice that fits best the offered product solution (for example `too big' for the incorrect solution 27, as opposed to the correct solution 20 for 4 × 5) is indicated with a green square key, whereas the red keys correspond with the less-valid choices. The response window (red color gradient) outlines the variable time period when button presses are recorded (till time-out at 4 s). Red triangles mark button presses. The diagram at the lower figure part reflects the schedule of the FIR analysis for a first eight events (blue digits). At the onset of each event (black vertical lines) commences a new train of 10 FIR bins (boxes in black-to-gray color gradient, each 2.64 s long). It analyses the event signal time course (symbolized with a yellow `HRF' curve) over a total period of 26.4 s. The FIR trains are not time-locked with the MRI scan cycles because this is a self-paced paradigm design.

A back projection installation served for stimulus presentation and fiber-optic response pads were used for behavioral measures (Lumina LSC400, Cedrus, San Pedro, CA, USA). Scanning onset was electronically synchronized with the stimulus presenting and response recording software Noisis (see I.A.M. in (Howe et al., 2009; Livingstone et al., 2010)), written in the MATLAB programming language (Mathworks Inc., Natick, MA, USA).

2.3. Parametric variables

Each arithmetic problem in this experiment imposes a specific repertoire of cognitive demands and inherently invokes a wealth of neural processes, some of them related to numerical ratios between the event-specific operands, products and differences which renders them permutable:

$$a\times b=R_c\iff R_d$$ (1)

where in our study R_c is the correct product and R_d is the displayed though incorrect result. The following three parametric vectors were included as stimuli / regressors in the analysis described in the Methods Section: i) the multiplication product size (Nieder and Dehaene, 2009) or product size effect (PSE):

$$P_{\mathit{pse}}=\log \left(R_c\right)$$ (2)

ii) the relative numerical disparity or distance effect (DE) (Pinel et al., 2001; Nieder, 2005) between the mental (correct) product and the offered incorrect (displayed) result:

$$P_{de}=-\log \left(\frac{\mid R_c-R_d\mid }{R_c}\right)$$ (3)

and iii) the task difficulty effect (TDE) based on the relative numerical distance from the incorrect (displayed) result to the ±25 % threshold (T_h = ±0.25):

$$P_{\mathit{tde}}=-\log \left(\frac{\mid R_c\times (1+T_h)-(R_c+\mid R_d-R_c\mid )\mid }{R_c\times (1\pm T_h)}\right)$$ (4)

Maximum difficulty was numerically defined as 6 for incorrect results that fell exactly on this threshold. Empirically, a logarithmic correction of both effects appeared appropriate, an observation in agreement with that of others (Stanescu-Cosson et al., 2000; Pinel et al., 2001; Nieder, 2005).

2.4. Imaging

Data were acquired on a General Electric 3-Tesla MRI scanner (vh3) with quadrature head coil. After localizer scans, a first anatomical, axial-oblique 3D-SPGR volume was acquired. Slab coordinates and matrix size corresponded to those applied during the subsequent fMRI runs using the 3D PRESTO BOLD pulse sequence with phase navigator correction (van Gelderen et al., 1995; Ramsey et al., 1998) and the following specifications: echo time 40ms, repetition time 26.4ms, echo train length 17, flip angle 17°, volume scan time 2.64 s, number of scans 280, session scan time 12:19min, 3D matrix size 51 × 64 × 32, and isomorph voxel size 3.75mm. At the end of the study, a sagittal 3D-SPGR scan was acquired with a slice-thickness of 1.2mm and in-plane resolution of 0.94mm. Raw data were reconstructed off-line using MATLAB scripts. The first four fMRI scans were discarded leaving 276 scans for analysis.

2.5. Preprocessing

Data preprocessing including spatial realignment for motion correction, spatial normalization to an atlas brain space with isometric voxel size of 2 mm, and spatial smoothing with a 12mm Gaussian filter were applied to the data of all subjects using standard routines provided in the Statistical Parametric Mapping (SPM)¹ software (Friston et al., 2007).

3. Methods

Three distinct methods were applied for data analysis, in addition to a chronometric visualization of the data (see fig. 2). The first two analysis were performed with General Linear Model (GLM) regression in SPM, using the canonical hemodynamic response function (HRF) basis and the time-sensitive Finite Impulse Response (FIR) basis respectively. Thirdly, a recently published novel spatio-temporal “brain-state” analysis technique (Janoos et al., 2011a,b) was also applied to the data.

Figure 2. Flow model of mental chronometry.

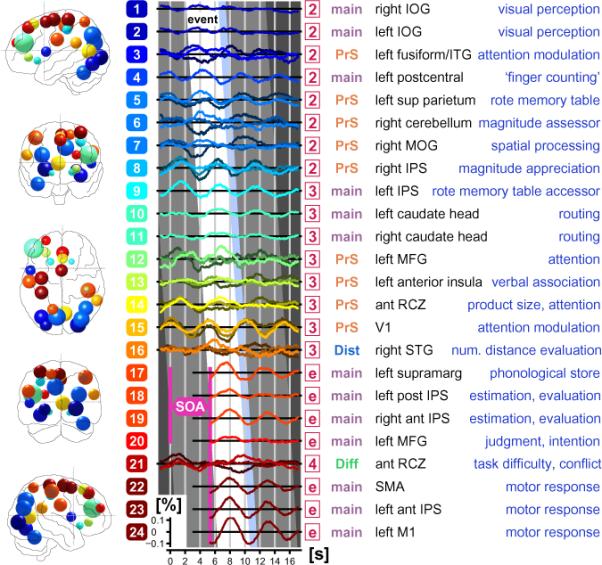
A hypothetical roadmap about focal neural recruitment following mental arithmetic is shown for the healthy subjects. The cascade of 24 selected signal time courses (for criteria see text) reflect the putative hierarchic order of the following cognitive subprocesses invoked with the current paradigm : i) multiplication, ii) estimation, iii) decision making, and iv) execution of a motor response. The inclination of the canted white band called `event' implies the evolution of neural involvement over the time span of one single event. The temporal width (4.345 s) of this skewed white `event window' covers the duration of the mean SOA (5.345 s) minus the rest condition (ISI, light blue band, 1.0 s). The time-locked 100-fold expanded fMRI BOLD signal time courses are averaged across events, sessions and subjects. This adds up for each of the 24 ROIs to approximately 9,100 averages / voxel in 27 voxels (≅ 216 mm³) at the position of the peak t-score in the FIR RFX analysis. The curves either represent averaged data (single line per ROI), or are split into three averaged lines if parametric data was available. An example for such a parametric triad are the low (dark colored lines), intermediate (medium intensity lines), and high scores (bright lines) from the multiplication product size. The abscissa denotes time in seconds, while the ordinate for each ROI signifies BOLD signal change in percent. The color-coded rectangles (with white digits for each ROI 1–24) to the left of the signal curves correspond to the blobs in the brain diagrams (left, front, top, back and right view). The location and diameter of each blob is defined by the center and the size of the voxel cluster of the given ROI (Supplementary Table). The numbering scheme implies a hierarchic order among the 24 ROIs, while the coloring scheme seeks to group the ROIs into 16 logical subsets. A red square (numbered 2, 3, 4 or e) in the fourth column codes for the FIR bin an ROI in question was detected in (see Supplement Table and figg. 3–5). The signal time course excerpts for FIR bin `e' (`e' for end) were collected from the previous event (time moved forward by one mean SOA of 5.345 s in pink SOA diamond; for explanation, see Methods and fig. 5). The term main (in gray) in the fifth column signifies linear GLM effect in the given ROI, the term PrS (red) the parametric product size effect (eq. 2), the term Dist (blue) the distance effect (eq. 3), and the term Diff (green) the task difficulty effect (eq. 4). The sixth column names the anatomical structure the ROIs resides in, while the last column (blue text) explains the presumed neuropsychological function at those regions and time courses.

3.1. Exploratory Chronometry of Mental Arithmetic in Controls

In order to get an initial summarization of the timing of the mental processing pipeline from the fMRI data, a movie-like chronometric impression (see fig. 2) of the signal alterations at salient foci was generated (see Supplement Table). A simple time-shifted averaging using event-related signal excerpts (9,100 events phase-locked with task onset) was able to successfully detect many focal time course patterns in the fMRI data of the control group. Twenty-four (24) regions of interest (ROIs) corresponding with significant FIR ROIs (see Section 3.3) were selected. Many of these ROIs have also been reported in literature in the context of mental arithmetic and related disabilities. The display of these time-courses clearly shows the temporal hierarchy and cascade-like character of signal modulations in these 24 ROIs. Furthermore, this activation flow-chart tightly corresponds to the hypothesized functional recruitment pattern of a healthy brain as it processes the arithmetical task. For example, the visual occipital area (dark blue fields at top) is invoked first and is locked to the beginning of the event, while the primary motor hand area (bottom in dark red fields) is recruited in the final moments of the exercise, time locked to the button press (for further explanations see comprehensive caption in fig. 2).

3.2. HRF based analysis

First, a GLM regression analysis of SPM2 was used with regressors obtained by convolving the paradigm stimulus onset vector with the canonical HRF. This provided a well-conditioned statistical approach for evaluating the parametric numerical (magnitude) product size effect. The principle drawback of this univariate method, however, was that it insufficiently accounted for the subtle dynamic, time-varying and spatially integrative traces of a complex cognitive process like mental arithmetic and no significant group-wise differences were identified.

3.3. FIR analysis

Due to concerns with the temporal resolution of the HRF method, the more flexible FIR method was used for the following three interrelated reasons: i) to enhance the temporal sensitivity of our analysis, ii) to tease out the cascadic (serial) nature of activations, and iii) to account for the irregular paradigm design and briefness of the base line condition. Linear effects of mental multiplication and estimation were identified with FIR trains of 10 bins (bottom of fig. 1), each bin was 2.64 s long and represented by its own regressor column in the design matrix of the GLM. Additionally, the three parametric variables of 10 FIR bins each were added (resulting in a design matrix of 40 regressors). Contrasts resulting from the “first-level” fixed effect analysis were pooled to the “second-level”, random-effect analysis (RFX) for one-sample and two-sample t-tests. The 40 FIR contrasts were processed separately on a bin-by-bin basis. Family-wise error (FWE) corrected p-value were computed on the entire search volume of the smoothed (FWHM=8mm) mean image (a mean of all normalized, subject-specific mean images covering the entire brain, including the cerebellum).

3.4. State Space Analysis

Traditional analysis methods tend to emphasize the spatial features of the brain phenomena while disregarding information about the neural dynamics and spatial integration contained in the data. In order to address this constraint, we recently developed a multivariate spatio-temporal analysis method (Janoos et al., 2011a,b), which models the concept of the functional brain transitioning through a mental state-space, as depicted in figure 3.

Figure 3. The State-Space Model (SSM).

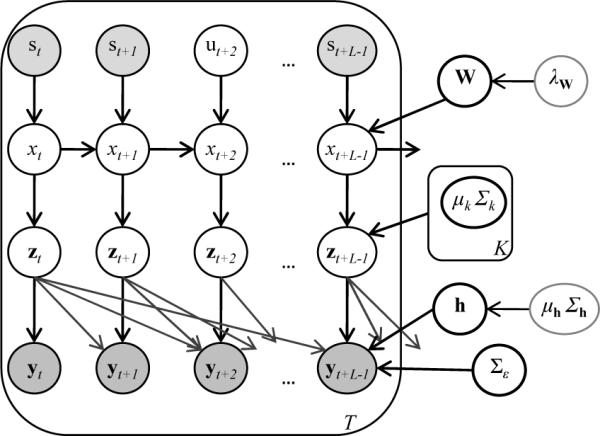
The experimental parameters are represented by st, while the corresponding brain-state is x_t, and the instantaneous activation pattern is z_t. The activation pattern is observed in the fMRI data y_t…y_t+L−1 after convolution with the HRF h.

The probability that the brain at time t = 1 … T (in TR units) is in state x_t = k where k = 1 …K depends on not only on the previous state of the brain but also on the current experimental stimulus described by the vector s_t. Given the goal-oriented and directed nature of human thought these brain-states not only exhibit a temporal ordering but also respond to external stimuli. At each time-point, facts about the experimental task such as the multiplication product size (PSE), the task difficulty score (TDE) and the current phase of the current trial (viz. 1: “reading”, 2: “computing” or 3: “responding”) are included in the stimulus vector.

In addition to observed experimental stimuli s_t, it is possible to model epochs of unobserved (hidden) stimuli u_t whose values are in turn estimated from the fMRI data, which enables prediction of the perceptual or cognitive state of the subject, as proxied by the recorded stimuli, from the spatio-temporal patterns in the measured signal. In most neuroscientific investigations, prediction of stimulus from fMRI data is not of direct interest, but rather the generalization error-rate (i.e. the error-rate in predicting new samples, typically estimated by cross-validation) is used to assess the fit of the model to the data and to detect the presence of an effect of an experimental manipulation (Friston et al., 2008). For the SSM, prediction error is used to test how well the spatio-temporal patterns discovered by the model relate to the mental states of the subject, as proxied by behavioral indicators. Furthermore, the predictability indicates the degree to which the neural patterns evoked by a specific experimental condition match those evoked by other occurrences of the same condition. The differences in the prediction accuracy of the DD group, with the control group as a baseline, therefore provides a quantification of the differential organization or regularity in the neural representation of their mental processes.

Each abstract brain-state k = 1 …K is associated with a characteristic spatial distribution of neural² activity in the cortex μ_k, and for each occurrence x_t of the brain-state k at time t, the neural activation z_t is a realization from the probability model ${\mathbf{Z}}_t~\mathcal{N}({\mu }_k,{\sum }_k)$, where ${\sum }_k$ is a covariance matrix describing the possible modes of variation in the realization z_t from the idealized activation μ_k. The transformation of the activation pattern z_t into the observed fMRI signal y_t is modeled by a element-wise linear convolution ${\mathbf{y}}_t={\sum }_l{\mathbf{h}}_l{\mathbf{z}}_{t-l}+{∊}_t$. Here $\mathbf{h}\triangleq \left({\mathbf{h}}_0\dots {\mathbf{h}}_L\right)$ is an unknown and spatially-varying FIR filter of length L+1, typically set to correspond to an HRF of 32s.

The estimation of the model parameters, namely the state-transition probabilities, the state-wise neural activation patterns, the spatially varying HRF and the unobserved (latent) stimuli u_t are done using expectation-maximization (EM) under a mean-field approximation. The optimal number of states K for the model of a subject is selected such that the error in predicting the latent stimuli u_t, with respect to their ground-truth (observed) values, is minimized. The advantage of this procedure is that it selects, from alternatives, the model most relevant to the experiment being conducted.

The representation of mental processes as a sequence of abstract brain-states by the SSM can be used to compare the spatio-temporal patterns, in their entirety, between subjects. To measure the similarity between the SSMs of two subjects, the mutual information (MI) between the state-sequences of the two subjects is used. Specifically, the MI is measured from the joint histogram of the sequences of state-labels assigned to the same fMRI data by the SSMs of the two subjects. The relationship between the state labels of two different SSMs is unknown and by comparing the state-sequences assigned to the same data, a mapping is enforced. A higher MI indicates a higher level of correspondence between the two state-sequences, while an MI of zero indicates no agreement.

This procedure when applied to all pairs of subjects yields a similarity matrix of pairwise MI, which can be thought of as assigning a position to each subject relative to all other subjects. Using the technique of multidimensional scaling (MDS), the subjects are embedded in a low (typically 2) dimensional Euclidean space which tries to preserve the distances implied by this similarity matrix. Although the accuracy of the embedding increases with number of dimensions retained, for this data-set reducing the dimensionality to 2 preserved the original distances with less than 15% error.

This layered state-space model of a mental process serves three important purposes: a) To enforce a temporal structure on the ordering of the states; b) To model higher order interactions between stimuli and mental states, by aggregating the history of the experiment into the current state; and c) To decouple the stimulus from the fMRI signal through the latent neural activation layer, thereby obviating specification of the exact mathematical relationship between the two. This is in contrast to alternative methods, such as GLM (Worsley et al., 2002), multivariate linear models (Friston et al., 2008) and even non-linear models (Kruggel et al., 2000), which assume a direct relationship between the value of the stimulus and the signal, and which have only a limited ability to capture the modulatory effects of past stimuli on the current mental state. Moreover, by comparing the MI of the models of the subjects (as compared to spatial maps), differences in spatio-temporal patterns of mental processes are revealed (Janoos and et al., 2011).

4. Results

This section begins with the analysis of the behavioral data, followed by the results of the HRF and FIR analysis. Next, the results of the SSM analysis method are presented.

4.1. Behavioral evidence

Behavioral measurements (fig. 4a and table 1) revealed significant, although subtle, performance differences (p < 0.05 between the groups in all four measures). Subjects with DD answered fewer problems, missed more responses, were less accurate, and were slower than their peers. This difference between the groups decreased during the second study exposure slightly and overall scores improved. Separate plots (fig. 4b) of correct and incorrect responses show that for both groups the reaction time (RT) for correct answers are shorter than those for incorrect answers and accumulate in three clusters for `too small', `close', and `too big' solutions (−50%, 0%, and +50% numerical distance). Incorrect responses pile up along the ±25% numerical distance thresholds, and missed button presses aggregate around the same distance thresholds (at 4.8 s). Last, problems with low difficulty scores (TDE in eq. 4, or LogDiff in fig. 4c) are answered rapidly, whereas incorrect answers are associated with higher difficulty scores and slower RT.

Figure 4. Behavioral results.

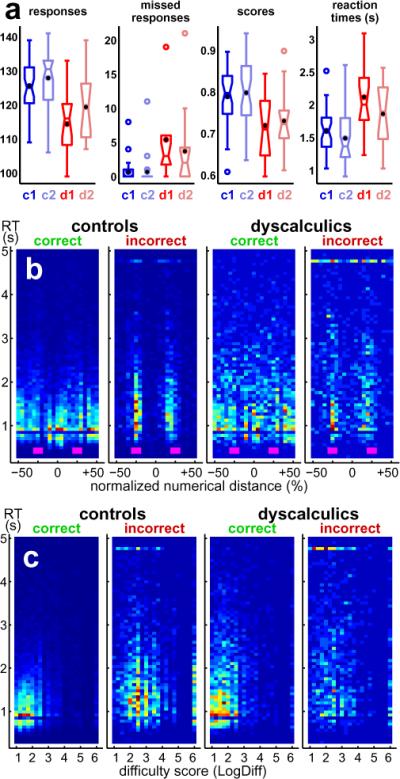
Box and whisker plots (a) summarize the psychophysical measures obtained from control subjects (blue, c1 for first MRI session, c2 for second exposure) and from subjects with DD (red, d1 and d2) for the following evaluations : i) number of responses, ii) number of missed button presses, iii) scores for correctness of answers, and iv) reaction times in seconds. Sample median is marked as horizontal tick within each box; black dot is arithmetic mean. Upper and lower box ticks denote sample quartiles (25th and 75th percentile of distribution). Whiskers (ticks) above and below boxes represent the extremes (10th and 90th percentile), and circles are outliers. Notches in the boxes indicate 95% confidence interval. Scatter plots (b and c) visualize behavioral performance with respect to task difficulty : The abscissa in (b) stands for the normalized numerical distance (in %) between the mental (presumably correct) and the offered (incorrect) solution. The abscissa in (c) stands for the event difficulty score (eq. 4). Both ordinates represent reaction time throughout. Plot pairs represent data for controls (left pair) and subjects with DD (right pair), respectively. Correct and incorrect responses are separated into a left and a right plot, respectively. Color maps are rescaled in each plot and indicate with a blue-yellow-red gradient the relative number of hits. The small boxes in magenta (plot b) mark the ±25% thresholds that separate the response ranges `too small', `close', and `too big' the subjects adhered to while choosing the best among the three possible answers.

Table 1. Behavioural measures.

	session 1*		session 2*
	controls	dyscalculia	controls	dyscalculia
subjects	36	13	36	13
responses	125.5 ±7.0	114.4 ±9.4	127.9 ±8.3	119.4 ±9.7
missed responses	0.7 ±1.5	5.4 ±6.3	0.7 ±2.0	3.7 ±5.9
score (% correct)	78.2 ±8.3	71.9 ±8.5	79.8 ±8.2	73.0 ±8.0
reaction time (s)	1.60±0.33	2.12±0.51	1.49±0.41	1.86±0.44

Statistical evaluation is shown for both exposures, session 1 and session 2, for the control and the dyscalculia (DD) group (see also fig. 4). The comparison of the means between the groups is computed for number of responses per session, number of missed responses, the average correctness (score in %) and the average reaction time.

^*The asterisk character stands for statistical significance (at p < 0.05) for the comparison of each of the four measures between the two subject groups, separately for both, the first and the second session.

4.2. HRF Analysis

The traditional voxel-based HRF analysis method failed to detect a significant main effect for mental arithmetic in the control group and in DD, and importantly also when comparing between the two groups. This is not surprising and even anticipated given how the HRF method crucially depends on signal baseline. The rest condition in the current paradigm design was indeed extraordinarily short which on the other hand allowed to collect a particularly large amount of experimental events. The parametric design, in contrast, with its uniquely shaped regressor was more successful in unearthing focal findings with the HRF method. The parametric PSE exhibited the strongest metabolic signature in the fMRI data, with a response in the entire bank of the right intraparietal sulcus (IPS) distinctively stronger in DD than in control subjects (see upper panel in fig. 6, [54–50 58mm], two-sample t-test, t_HRF=4.96, p < 0.001 uncorrected, k=1052 voxels ≈ 8.4 cm³). Control subjects showed for the PSE comparison only one small focus of stronger modulation in the left middle frontal gyrus (MFG) ([−52 10 26mm], t_HRF =2.51, p < 0.01, k=9 voxels).

Figure 6. Comparison of product size effect (PSE) between the two subject groups.

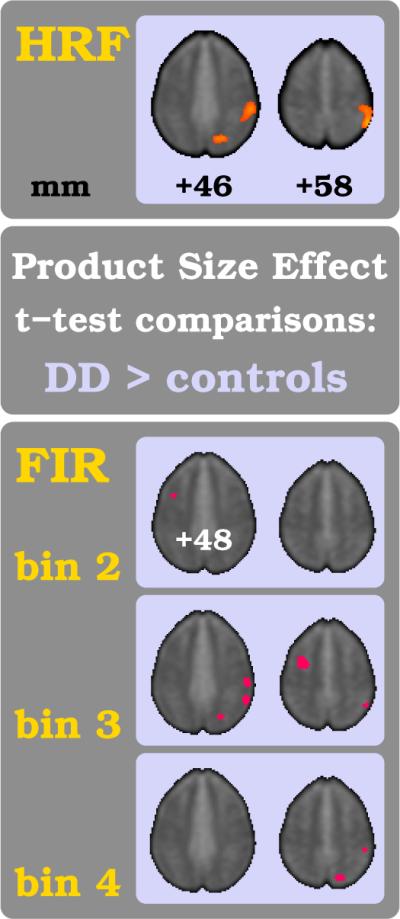
In the upper figure part the traditional HRF-based analysis results are shown for the comparison of healthy subjects versus individuals with DD. The lower figure part shows the results of the equivalent analysis in the FIR bin space for the three time bins 2–4. For each comparison a two-sample t-test was computed and threshold set at p < 0.01. The color-coding of t_FIR-scores and other figure parameters are the same as in fig. 5.

4.3. FIR Analysis

Numerous non-parametric and parametric effects were detected with the FIR analysis (see exhaustive list of distinct foci in Supplementary Table). The time-sensitive technique revealed a wealth of activation foci distinctly separated in time and space. This was the case for both the main and the three parametric effects. In controls many more such foci were captured throughout the task, whereas for subjects with DD, the activity pattern remained sparse at the group analysis level (voxel-based RFX). For the sake of brevity and intelligibility, we refrain from reporting the vast cascade of FIR activations but will concentrate primarily on brain areas which distinguish the two subject groups.

4.3.1. Main Effects using FIR

The main effect spatial maps with the one-sample t-test are far richer for each subject group separately, but do not translate well for group comparisons due to reasons discussed further below. The group-level comparison (two-sample t-test) reveals only the right basal ganglia (bin: 4, [14 16 2 mm], t_FIR = 3.69, p < 0.001, k = 60 voxels) and the left MFG (bin: end, [−28 50 24 mm], t_FIR = 3.59, p < 0.001, k = 33 voxels) in favor for the control group. However, it should be noted that the parametric responses, discussed in the next section, were more informative and more robust in distinguishing control from DD data (see Supplementary Table for statistical evidence).

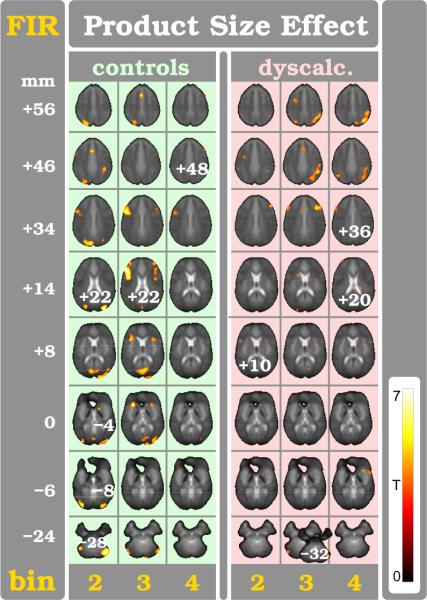
4.3.2. Product Size Effect in Controls using FIR

The FIR method confirmed, for the PSE (eq. 2), the findings of the HRF analysis, revealing consistently more activation foci distributed over time (see Supplementary Table). The PSE is experienced at the initial phase of the calculation (diagram in fig. 1). Correspondingly, the bulk of the PSE related modulation occurs in controls right after event beginning (bins: 2–3 in fig. 5). Specifically, first the posterior parieto-occipital lobe is extensively recruited (bin:2); then the bilateral occipital gyri including the primary visual cortex and cuneus, the right rostral IPS, both lingual gyri (although more on the left), the left inferior temporal gyrus, the right putamen, and the right upper cerebellum (where the PSE related modulation is remarkably strong, t_FIR=6.11) are recruited; and finally several foci in the frontal lobes enclosing the anterior rostral cingulate zone (aRCZ) are activated. Thereafter (bin: 3), the posterior parieto-occipital and cerebellar activations become weaker, while both anterior insulae (aIn), caudate head (CdH), and putamina activate. The bilateral MFG and inferior frontal gyri (IFG) are recruited even more prominently, especially on the left, together with the aRCZ. Eventually (bin: 4), small foci persist in both IFG and MFG and both aIn.

Figure 5. Multiplication product size effect (PSE).

Brain regions modulated through PSE (see eq. 2) are shown for the three FIR bin periods 2–4 (yellow digits). Each FIR bin covers the length of one brain volume scan period (TR of 2.64 s). Statistical maps (one-sample t-test at p < 0.001) are superimposed on axial slices for control subjects (light green columns, left) and for subjects with DD (light red columns, right). The color-bar indicates t_FIR-scores. Slice height is indicated in millimeters (white digits). The axial slices were taken from the grand-mean BOLD PRESTO data of this study (normalized in the MNI-152 brain space). All pictures follow neurological convention (left hemisphere is left). A comprehensive list of areas with significant signal changes can be found in the Supplementary Table.

4.3.3. Product Size Effect in Dyscalculia using FIR

In striking contrast, the response pattern in DD appears delayed and prolonged (bins: 3–4 in fig. 5) as compared to controls. Subjects with DD initially involve just a few small areas in the left IFG, the right MFG, the left precentral gyrus, and both IPS (bin: 2). Thereafter, a strong and long-lasting recruitment (bins: 3–4) is seen in the entire extent of the right IPS. Moreover, additional foci are seen (bin: 3) bilaterally in the MFG, aRCZ, posterior inferior parietum, upper cerebellar lobules, CdH, and right aIn. Smaller activations persist (bin: 4) in both frontal lobes and the aRCZ, right aIn, and posterior caudate body.

4.3.4. Product Size Effect in Group Comparison using FIR

The FIR group comparison for the PSE between controls and DD confirms the previous HRF analysis results regarding its spatial location in the right IPS for DD (upper and lower parts of fig. 6). Importantly however, the time-sensitive FIR method is able to demonstrate that the aberrant activation pattern in the right parietum and IPS and, to a lesser degree, in the cuneus (bins: 3–4 in lower part of 6)) is delayed in the case of DD.

4.3.5. Numerical distance effect using FIR

The intermediate phase in the arithmetic exercise (diagram in fig. 1) addresses the numerical distance (DE in eq. 3) between the correct (mental) and incorrect (presented) solution. The associated mental computation generates an interim result stored in working memory. The corresponding parametric values are highly specific and leave unique traces in the BOLD signal at defined spatial and temporal locations. FIR analysis revealed various brain regions (see Supplement Table) though for clarity and brevity only two foci for the control subjects are listed: (a) one focus in the aRCZ (FIR bins 3–4, t_FIR=4.12); and (b) another focus in the right STG (bin: 3, t_FIR=4.65). The latter maintained significance in the group comparison albeit weakly (RFX, t_FIR=3.42).

4.3.6. Task difficulty effect using FIR

The final phase in the arithmetic exercises is dominated by the effect of `task difficulty' (TDE in eq. 4). The high temporal specificity of the parametric TDE vector, phase-locked with the task paradigm (diagram in fig. 1), discovered a strong focus with high certainty in time bin #4 (left panel in fig. 7). In terms of spatial attributes there is a strongest BOLD signal trace at the aRCZ (t_FIR=5.94, see also Supplement Table), although importantly only for the control group but not in subjects with DD. The group comparison (RFX) confirms this impression in favor of the control subjects (right panel in fig. 7).

Figure 7. Task diffculty effect (TDE).

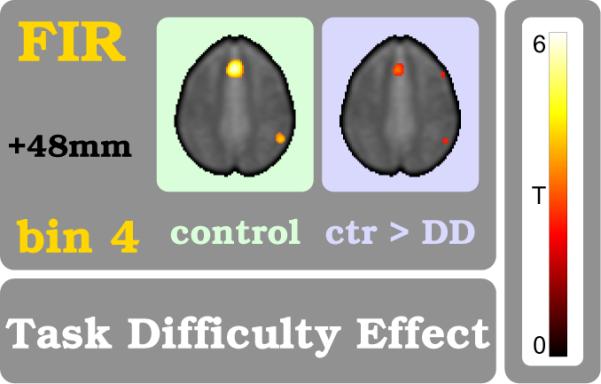
Brain regions that respond to the TDE are shown. This parametric measure is related to mental efforts like conflict resolution, attention, decision making and more. It reflects the sum of cognitive demands for estimating the likelihoods for the correct button choice among `too small', `close', and `too large'. The TDE modulation appears with the begin of FIR bin:4 which corresponds to the final phase of the exercise. The left plot shows the TDE in control subjects (one-sample t-test, p < 0.001) while the right plot shows the comparison between controls and subjects with DD (two-sample t-test, p < 0.01). Procedures and color coding are the same as in fig. 5.

4.4. State-Space Analysis

The ability of the SSM to capture and explain the spatio-temporal patterns of a subject is measured by the error in predicting the presented stimulus from the fMRI data. The average number of brain-states K required for a subject and the error in predicting the stimuli, along with ±1 standard error of the mean (SEM), are shown in Table 2. It can be seen that, although the DD group is much smaller than the control group, there is a much larger variation in the optimal number of states for subjects of this group. This indicates a greater degree of heterogeneity in the mental patterns of the DD group necessitating models with different levels of complexity. Also, the consistently higher error-rate of the DD population indicates the relative inability of the SSM to explain their mental processes, as compared to the controls, which may point to a greater degree of uncertainty or irregularity in their mental processes preventing the SSM from accurately encoding the spatio-temporal regularities of the data.

Table 2. Overall Results.

	Control	DD
Number of States	22.57±2.19	26.23±3.95
Overall Error (%)	31.0±5.2	40.1±8.9

The mean optimal model size and prediction error (± 1 SEM) for the control and dyscalculic (DD) subjects. The chance-level error-rate is ≈ 83%, computed by permuting the stimuli with respect to the scans.

Table 3 shows the breakdown of the error-rate of the SSM with respect to the “reading”, “computing” and “responding” phase of an experimental trial. The change in SSM prediction error with respect to product size and task difficulty modulations³ is compiled in table 4.

Table 3. Phase-wise Prediction Error.

	Control	DD
Reading	21.15±3.9	23.63±3.5
Computing	26.48±3.5	38.15±6.2
Responding	43.11±6.2	56.79±6.8

The breakdown of prediction error (%) during the reading, computing and responding phase of a trial of the experiment is tabulated for both groups.

Table 4. Parametric Effect on Prediction Error.

	Product Size Effect		Task Difficulty Effect
	Control	DD	Control	DD
Reading	−4.0±0.6	−4.9±0.5	−0.1±0.01	0.3±0.04
Computing	−2.1±0.3	−1.3±0.1	−0.3±0.05	0.4±0.05
Responding	−0.8±0.1	0.9±0.1	−0.2±0.02	−0.1±0.03

The effect of the parametric product-size and task difficulty variables on prediction error (%) during the reading, computing and responding phase of a trial of the experiment is tabulated for both groups.

The differences between the overall predictability of the two groups is significant at p < 0.01, assessed using permutation testing. During the reading phase, the error rate for the DD group is slightly but significantly higher (p=0.05, permutation testing) than that for the controls, while an increase in product-size causes a large (p=0.01) drop in the prediction error for both groups. In the computing phase, however, the prediction error for the DD group increases drastically as compared to controls, with the difference between the two groups significant at p < 0.001. Product-size reduces the error rate for both groups, with a significantly stronger modulatory effect on the controls (p < 0.005). During the responding phase, again the DD group exhibits significantly higher error (p < 0.001), while product-size elicits a negligible response. In all three phases, task difficulty has a very small effect on the the error rate. However, the direction of its modulation on the two groups is significantly different with a downward effect on the controls in the reading and computing phases as compared to an upward effect on the error of the DD group.

As described in the Methods Section, subjects can be represented in a low dimensional space through MDS of the matrix giving the pair wise MI between their SSMs. During this computation, we included the data of the 9 subjects with DL in order to highlight the ability of this method to discriminate between subjects with fundamentally different mental processing templates.

Figure 9 shows a clustering of subjects in the MDS space with respect to their group (control, DD and DL). Again, it should be noted that this representation is obtained by first projecting the pairwise 58 × 58 MI matrix of all 58 subjects together, and then labeling them, post hoc, according to group type. Therefore, the clustering of subjects has been discovered intrinsically from their spatio-temporal patterns without any input or cues from the investigators. Interestingly, there are a few DD subjects that cluster along with the DL group (at the top of phase 1 in fig. 9c). This is not surprising, given that oftentimes dyscalculia is comorbid with dyslexia (Molko et al., 2003) and these DD subjects may exhibit dyslexic deficits during this task. We elaborate on this further during the Discussion.

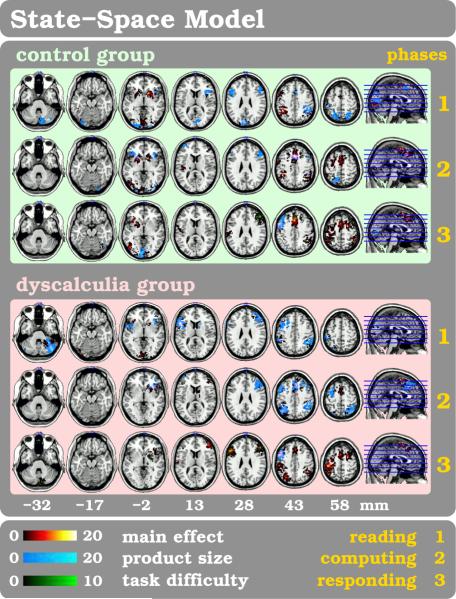
Figure 9. State-Space Model - MDS plots.

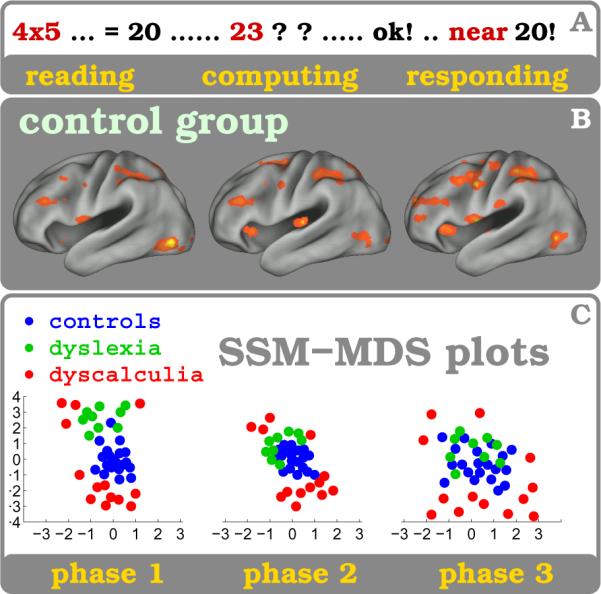
Participants from three subject groups, 20 healthy controls, 13 subjects with DD and 9 subject with DL, are compared with the SSM analysis method while solving arithmetic exercises. A : illustrates the time course of the arithmetic task (event) which usually is terminated by a button press. B : shows brain states cluster related activation maps for healthy subjects for the three experimental phases (1: reading and multiplication, 2: computing and estimating, 3: decision making and responding). C : Functional similarity using mutual information (MI) is shown for all three subject groups for the three experimental phases. The multidimensional scaling (MDS) plots show MI between all pairs of subjects and reveal for each phase the relative arrangement of the subjects based on their MI. Psychological attributes utilized as covariables like the Multiplication Product Size (PSE in phases 1&2) or the Task Difficulty Score (TDE in phase 3) facilitate separability between subjects. Dyscalculic subjects (red) seclude throughout all phases from the control group (blue) while the Dyslexic subjects (green) deviate solely during the reading phase #1 - even though digits are shown, and not words or letters. For methodological details including data analysis be referred elsewhere (Janoos et al., 2011b,a).

To study the separation between the groups in this low-dimensional representation space, an SVM classifier was trained (Gaussian kernel; feature-vector: subject's 2-d MDS coordinates; label: group, i.e. Control, DD or DL). The quality of the separation between the groups was assessed using a non-parametric test for the significance of the generalization error (measured using leave-one-out cross validation), with the null distribution estimated by permuting group labels (see table 5). Also, the effect of the parametric variables (i.e. product-size and task-difficulty) on the separation between the groups was measured.⁴ A clear separation between all three groups in this representation space can be observed, with a significant effect of the product-size and task-difficulty parameters between control vs. DD and between DL vs. DD groups. Interestingly, the parameters do not have a strong and consistent effect on the separation between the control and dyslexic subjects. During the reading phase, there is a strong segregation between the DL and control groups, while both parametric variables cause a marked change in the separation of the DD with the other two. During the computing phase, in contrast, the separation between the controls and DL subjects becomes less distinct, and both parametric variables again strongly affect the DD group separability.

Table 5. Phase-wise Group Separation.

	Control vs. DD	Control vs. DL	DD vs. DL
Overall	0.01 (0.005,0.01)	0.01 (0.05,–)	0.01 (0.05,0.1)
Reading	0.005 (0.001, 0.005)	0.001 (0.01,–)	0.001 (0.01, 0.005)
Computing	0.001 (0.005, 0.001)	0.05 (–,–)	0.001 (0.005, 0.001)
Responding	0.05 (–, –)	− (–,–)	0.001 (–, –)

Tabulated is the p–value of the separation between the three groups (Controls, DD, and DL) assessed through permutation testing of the class labels assigned by a non-linear SVM classifier. The values in brackets are the p–value of the change in SVM classification accuracy due to product-size and task-difficulty parametric modulations, respectively. Dashes indicate “not significant at any p < 0.1.”

5. Discussion

In this study, three analysis methods were used to localize in space and time, with varying levels of efficacy, the functional substrates and processing cascades differentially associated with deficits in mental arithmetic. The ensuing discussion first addresses the neurobiological relevance of these findings and interprets the brain recruitment patterns that differentiated the participating subjects. Thereafter we summarize our impressions and experiences with functional imaging of complex cognition and compare the way traditional and novel analysis techniques influenced our understanding of mental processes in the case of developmental dyscalculia (DD), with an emphasis on the crucial importance of both the spatial and temporal dimension of brain function. Finally we explore methodological nuances in paradigm design, imaging technology and analysis that may affect the validity of a brain mapping study.

The emphasis in this discussion is on signal acquisition and analysis, where we hope that improvement in the spatio-temporal qualities of both would eventually elaborate disease characteristics at greater detail. Alternatively, by merging all the time-resolved FIR activations of healthy subjects (time bins in fig. 5) along the temporal direction a new synthetic `activation pattern' is created that resembles the outcome of a PET (Positron Emission Tomography) study for mental calculation (Zago et al., 2001). This simplified spatial pattern certainly eases interpretation but the highly valuable and discriminative temporal information is lost. We feel that this gedanken exercise mirrors what happens during an HRF-analysis where temporal resolution does not receive the attention it deserves - especially in the case of a fast event-related paradigm design.

5.1. HRF Analysis and Right Parietum

The results obtained with the HRF analysis method indicate that the processing of numerical magnitudes during mental multiplication and estimation occur mainly in the parietal lobes and in the right cerebellum in both subject groups. However, the principle difference between controls and subjects with dyscalculia appears in the right IPS with significantly more task-related signal increase in DD. This difference pattern replicates results of others and suggests - given the specifics of the experiment - an elementary role of the parietal lobes in processing mental arithmetic (Piazza, 2010; Rotzer et al., 2009; Kucian et al., 2008; Cho et al., 2011; Dehaene and Cohen, 1995; Molko et al., 2003; Zago et al., 2001). This viewpoint was recently affirmed from a different perspective when it was demonstrated that therapeutic intervention using transcranial direct current stimulation is most effective if applied parietally (Cohen-Kadosh et al., 2010). It should be noted that all subjects with DD had normal intelligence, performed behaviorally almost on par with their peers and solved the simple multiplication exercises without major effort or delay. No feeling of failure, frustration or related distress was expressed upon inquiry after scanning and therefore we assume that the brain patterns differ for pathophysiological reasons related to DD.

5.2. The FIR Cascade

The main observation from the FIR analysis is the pattern diversity which, in contrast to the HRF method, turns out to be immeasurably richer. In fact, the number of distinct foci are so overwhelming that we decided to eschew a comprehensive discussion thereof, in favor of a Supplementary Table. Instead, a chronometric summary (fig. 2) was created to provide a more comprehensible presentation of the dynamics in brain activation (Buzsáki, 2005) by visualizing the averaged signal time courses in 24 ROIs that emerged through the FIR analysis. The following few paragraphs provide a salient interpretation of the spatial and temporal character of these foci within the task diagram and their respective neurocognitive function in the context of mental arithmetic and DD. We begin by discussing the evidence in the healthy population.

5.2.1. FIR Cascade in Controls

Here, a condensed and summarized flow-chart of the recruitment sequence in the 24 functional ROIs identified through FIR analysis (see third column in Supplementary Table) is developed. We aim to create a logical hierarchy of task phases by grouping the activation foci into a hypothesized cascade, synthesizing work of others on arithmetic processing (Dehaene and Cohen, 1995; Dehaene et al., 2003; Molko et al., 2003; Delazer and Butterworth, 1997; Zago et al., 2001; Nieder, 2005; Feigenson et al., 2004; Nieder and Miller, 2004).

Early Multiplication Phase

The visual exposure to the multiplication stimulus elicits a linear BOLD response in the first two ROIs (subsequently called r:1, r:2, etc., see third column in Supplementary Table) within the occipital visual areas (Zago et al., 2001; Rickard et al., 2000). Simultaneously, the parametric PSE (product size) becomes manifest in the striates and extras-triates, in the left fusiform gyrus (r:3) (Rickard et al., 2000; Zago et al., 2001) possibly as an expert number reader (Dehaene and Cohen, 1995; McCandliss et al., 2003), in the left inferior precentral focus (r:4) as a potential relict of finger counting and related learning strategies (Stanescu-Cosson et al., 2000; Zago et al., 2001; Fiez and Petersen, 1998; Wilson et al., 2004), and in the primary visual cortex for a prolonged phase (r:15), probably as an attention related top-down effect (Murray and Wojciulik, 2004; Somers et al., 1999; Chawla et al., 1999; Corbetta and Shulman, 2002; Kanwisher and Wojciulik, 2000).

Intermediate Multiplication Phase

Four seconds later, the PSE becomes apparent in the left posterior superior parietum (r:5) and left angular gyrus where multiplication facts are stored with verbal and spatial attributes (Simon et al., 2002; Roux et al., 2003; Nieder, 2005; Sawamura et al., 2002), with an adjacent non-parametric focus in the left IPS (r:9) (Chochon et al., 1999; Simon et al., 2002; Eger et al., 2003; Shuman and Kanwisher, 2004) which may control access to rote memory multiplication tables (Dehaene and Cohen, 1995; Chochon et al., 1999; Stanescu-Cosson et al., 2000; Zago et al., 2001). A more distinct focus in the right superior semilunar cerebellar lobule (r:6) suggests a pivotal role for processing numerical magnitude and related cognitive functions (Pinel et al., 2001; Nieder, 2005; Mathiak et al., 2004; Fiez, 1996; Allen et al., 1997). The role of the intense focus in the right middle and superior occipital gyrus (r:7) is less clear, though the proximity to occipito-parietal networks that process spatial scenes and body layouts suggests processing of arithmetic dimensions (Rickard et al., 2000). The right IPS (r:8) reveals a bi-phasic property where the first occurrence may assess numerical magnitudes (Stanescu-Cosson et al., 2000; Chochon et al., 1999; Eger et al., 2003) or arithmetic computation (Dehaene et al., 2003; Zago et al., 2001), while the second peak in the left IPS and both CdH (r:9–11) may reflect computational efforts for comparing correct vs incorrect solutions (Chochon et al., 1999) and for routing information between the parieto-occipital and frontal lobes (Dehaene and Cohen, 1995; Delazer and Butterworth, 1997).

Late Multiplication Phase

Four regions in synchrony (r:12–15) elicit a late signal response to PSE suggestive of a common functionality. The left MFG (r:12) may serve verbal working memory (Stanescu-Cosson et al., 2000; Nieder, 2005; Zago et al., 2001; Manoach et al., 2004), while others proposed a memory loop with the right cerebellum (Mathiak et al., 2004) which we consider less likely due to temporal difference of more than 2 s between their peaks. The recruitment of both aIn (r:13) (stronger on the left) was interpreted by others as verbal rehearsal and phonological storage (Dehaene and Cohen, 1995), while language-based fact retrieval (Zago et al., 2001) or processing of automated arithmetic routines (Bush et al., 2000) appear unlikely at this late stage into the event time course. The striking resemblance of the parametric signal in the MFG (r:12) and the strong focus in the aRCZ (r:14) suggest temporary functional connectivity of the attention networks, while conflict monitoring (Ridderinkhof et al., 2004; Kerns et al., 2004; Walton et al., 2004) may be evident in these structures at a later event phase (see below). As mentioned earlier, the impressive PSE response in the primary visual cortex (r:15) at this phase may be invoked by visual working memory to temporarily store multiplication facts, perhaps even as imagery of the multiplicand numerals.

Numerical Distance Phase

Several brain areas show response to the DE, a parametric measure of the disparity between the expected and presented numerical product, namely the posterior right STG (r:16) and to a lesser degree bilateral superior frontal gyri, a location which has not been identified in extant literature. Additional foci may correspond to findings by others with fMRI and event-related potential (ERP) (Pinel et al., 2001). However, absence of involvement of the IPS, in contrast to numerous reports by others, may be explained by significant technical and paradigm related differences, while activations within that area may have been confounds with motor or numerical magnitude responses (Pinel et al., 2001; Thioux et al., 2005; Lau et al., 2004; Toni et al., 2002).

Decision Making and Response Phases

This phase encompasses thinking about the various response options, the button press and the subsequent motor action, where the temporal succession of the related functional stations is tightly orchestrated in ordering but variable in timing, due to the fast self-paced paradigm design. The left supramarginal gyrus (r:17) may reflect covert speech production (Dehaene and Cohen, 1995), perhaps jointly with the left MFG. They are followed by foci in the caudal (r:18) and rostral (r:19) IPS, probably related to mental calculation (Simon et al., 2002; Stanescu-Cosson et al., 2000; Chochon et al., 1999; Shuman and Kanwisher, 2004) or numerical comparison (Chochon et al., 1999; Dehaene et al., 2003, 1999), while the late left MFG focus (r:20) may be a result of other cognitive demands such as attention, thought coordination, and planning and execution of motor action (Bush et al., 2000; Simon et al., 2002).

The phase, when the subject decides which of the three buttons (response options) to press, corresponds to the `task difficulty effect' (TDE) although other terms such as `attention, conflict resolution, task uncertainty, decision making, error prediction or detection, motor planning' may serve equally well (Carter et al., 1998; Kerns et al., 2004; Botvinick et al., 1999; Holroyd et al., 2004; Bush et al., 2000; Ru et al., 2001; Ridderinkhof et al., 2004; Carter et al., 1998; Kerns et al., 2004; Walton et al., 2004; Brown and Braver, 2005; Holroyd et al., 2004; van Schie et al., 2004; Ridderinkhof et al., 2004). A robust parametrically time-locked focus in the aRCZ (r:21) is predominant and so are bilateral MFG foci suggestive of a frontal network for decision making and related cognitive processes (Krawczyk, 2002; Kerns et al., 2004; Duncan and Owen, 2000; Walton et al., 2004; MacDonald et al., 2000; Miller and Cohen, 2001).

The final three stations in the cascade invoke motor planning and execution (Lau et al., 2004; Picard and Strick, 2001) where first the supplementary motor area (SMA) (r:22) is recruited, interestingly followed by the left anterior IPS (r:23), probably as a result of goal-directed (response) movement and visuo-spatial attention (Simon et al., 2002; Toni et al., 2002), and finally, approximately 200 ms latter, terminated with the focal activity in the primary motor hand area secondary to the response action (r:24).

5.2.2. FIR Cascade in Dyscalculia

The FIR analysis of the dyscalculic subjects turned out to be much less impressive than controls, even accounting for the unequal number of participants. While key regions like occipital visual areas or the motor area are activated as expected, not many of the regions that code for the various intermediate cognitive sub-processes show a response similar to controls. Because the behavioral results suggest otherwise, with subjects with DD performing the task at par with their peers, we assume that this discrepancy is rooted in the inter-individual differences of brain recruitment and in the established (hardwired) individual neuropsychological strategies for arithmetic problem solving (Metcalfe and Campbell, 2011; Cho et al., 2011). Such spatial incompatibilities between functional maps are not addressable through conventional voxel-based analysis methods operating in a normalized brain space. Moreover, it may well have hampered the group comparisons in the current study, where only the parametric PSE distinguished between the groups. Initially it appears as if in DD the general response to the PSE is delayed by a `lag' of one full bin length (2.64 s) which is not explained by their negligibly longer reaction times. However, the foci found in the control group simply do not surface as equivalent foci in DD, with the notable exception of the right superior parietal activation and a small cerebellar focus.

Cerebellum

Our main hypothesis regarding a pathogenesis in DD includes a cerebellar deficiency for rapid assessment of a variety of magnitude measures (Mathiak et al., 2004; Fiez, 1996). Now, while the cerebellar response in controls to the PSE is overwhelming, it has a very weak equivalent in DD. But, it is also the practically non-existent left frontal recruitment in DD that suggests an absent or a insufficiently recruited functional loop for assessing numerical magnitudes and related cognitive processes between these two brain areas, in stark contrast to the control group (Gottwald et al., 2004; Chen and Desmond, 2005; Schmahmann and Sherman, 1998; Ravizza et al., 2006). The weak cerebellar engagement in DD points to a potential source of inexact computation, in that the subsequent verification and memorization processes that rely on estimations of number size (Campbell and Tarling, 1996) do not receive the numeric magnitude information they depend on. However, currently it is unclear if the absent metabolic response to PSE reflects a globally decreased awareness to numerical magnitudes in DD, especially since their performance was just slightly worse than their healthy peers.

Left Parietum

The absence of a BOLD response to mental arithmetic and to the parametric PSE in the left IPS and practically in the entire left parietum conforms to observations by others regarding functional and anatomical irregularities in dyscalculia (Levy et al., 1999; Verstichel and Masson, 2003; Isaacs et al., 2001). It supports assumptions about abnormally developed pathways or structures in the left lower posterior parietal lobule in DD that otherwise store language-encoded multiplication facts, readily available to healthy subjects (Zago et al., 2001; Rickard et al., 2000; Dehaene et al., 1999). The left IPS indeed may act in controls as a gatekeeper for multiplication facts flowing to and from the left posterior parietum, where in both structures, as observed in the current study, the response to the PSE is almost completely absent in DD, even without any correction applied to the statistical threshold.

Right Parietum

The right hemisphere in DD responds to the PSE in the MFG (late) and perhaps even bi-phasic in the IPS, first early like controls in a small focus, and the later dominantly throughout its entire bank. We hypothesize that both subject groups assess early, at event beginning, the numerical magnitudes within the right IPS (Chochon et al., 1999), a function seemingly intact in DD. The second response in the IPS may be interpreted as an extra verification effort although we would like to propose, instead, that a short-term retention of interim multiplication solutions evokes this strong parametric response. Therefore, the multiplication procedure, per se, should be complete by this event phase (FIR bins: 3–4) - but continuing the arithmetic exercise requires a mental buffer for the computed product to be used in the subsequent comparison and decision making phase. Therefore, this working memory shows up in controls - in the left FG as a digital, verbal (Dehaene et al., 1999) or shape based (Manoach et al., 2004) representation - or in the primary visual cortex as a digital visual pattern - while in individuals with DD the same memory operation may reside in the right IPS, where spatial features are encoded (Manoach et al., 2004). This scenario hints at a further source for numerical inexactness in DD, in that numerical information, rather than being stored `digitally' in a verbal or visual system, is stored transiently in the transcoded, presumably `analog' and imprecise spatial memory system of the right IPS (Shalev and Gross-Tsur, 2001; Chochon et al., 1999; Dehaene et al., 1999; Dehaene and Cohen, 1995; Dehaene et al., 2003; Shuman and Kanwisher, 2004).

Clinical Syndromes with Developmental Dyscalculia

Patients suffering from Turner syndrome present both severe DD and impairment in estimating number sizes, with anatomical abnormalities in the right IPS (Molko et al., 2003). We hypothesize that the 'high-functioning' dyscalculic population in the current study can resort to an intact right IPS during simple arithmetic operations (Dehaene et al., 2003) which they indeed solved successfully. But this anatomical and functional option may not be available to subjects with structural abnormalities in the parietal lobes which may contribute to the severe calculation and spatial orientation deficiency observed in Turner and Velocardial syndrome (Molko et al., 2003; Barnea-Goraly et al., 2005; Eliez et al., 2001).

Effects of Numerical Distance and Task Difficulty

We refrain from a detailed discussion of the DE and TDE for the dyscalculic group because of a lack of conclusive signal changes or reliable differences with the healthy subject group. Several explanations are possible for this failure: First, the individual activation patterns in DD may, in general, be too heterogeneous for a group analysis and for a group comparison. We believe that learning disabilities like DD result in highly specific and individualized psychological strategies which render the BOLD signal activation patterns unique, a hypothesis confirmed by the higher inaccuracy in the predictability for this group during the SSM analysis. Second, it is possible that individuals with DD may not show the same signal modulations as a healthy control, for example in response to the TDE. Subjects with DD may experience the arithmetic exercises as uniformly difficult (stressful) which would flatten the BOLD response against this specific parametric variable during analysis.

5.3. Brain States Analysis

Reading Phase

The higher error of the DD subjects may be due to irregular patterns in accessing the verbally encoded rote multiplication tables usually located in the left angular gyrus. The reduction in error-rates of all subjects with increase in product-size may be due to increased organization of their mental processes as their multiplication memory is stressed, while the increased separation between the groups would indicate greater divergence of the mental patterns of the DD individuals from the controls.

Computing Phase

Prediction error for the DD group increases drastically indicating that DD subjects may experience difficulty in judging the difference between the size of the correct and incorrect results and may resort to a greater variety of mental strategies. Not surprisingly, as the reading phase of the experiment has ended, the patterns of the DL individuals begin to resemble that of the controls and the separation between these groups reduces in MDS space (see fig. 9), while the separation of the DD group increases. The PSE is in the control group (see fig. 8) consistent with strong activation of verbal (silent rehearsal) and visual working memory while in the DD group it is primarily observed in the parietal areas. Although TDE reduces the error-rate of the control and DL subjects, it has the opposite effect on the DD group as increased conflict may recruit new functional circuits.

Figure 8. State Space Model for Mental Arithmetic.

The group-wise t-score maps are shown overlaid on axial slices of a high-resolution template brain image. Values t < 3 have masked out for clarity and the color-map shows values ranging from t = 3 to t = 16. Each row shows the activation maps corresponding to three phases (seeing, computing, responding) within a single trial of the task. Also displayed are the parametric modulations due to product-size effect during the seeing and computing phase, and the product-size and task-diffculty effects during the responding phase.

Responding Phase

This phase involves decision-making and conflict-resolution and is highly variable between repetitions and subjects, causing increased inaccuracy during this phase. Also, due to the self-paced nature of the task, it very often contained the button-press and inter-trial rest interval. The spatial-maps (fig. 8) for all groups show increased activation in the supplementary and primary motor areas while the late cognitive TDE appears only in healthy subjects in the prefrontal cortex and the aRCZ.

5.4. Conclusions

The structure of this manuscript reflects our own learning curve in investigating the neurobiological mechanisms behind learning disabilities. Our search for markers to explain the neurological condition changed, over the years, from looking at focal effects (activation blobs) to locating sequential neural activation cascades to finally identifying spatio-temporal patterns or brain states. We arrived at the perhaps trivial inference that the more real-life-like the stimulus experienced by a subject the richer the collected physiological data become and the more meaningful the subsequent analysis may turn out - though at the same time perhaps also more complex. In sum, our search for stimulus related metabolic signatures underwent a reorientation from initially paying attention to traditional voxel-based univariate responses to eventually focusing on biologically plausible spatio-temporal signal patterns in form of brain state clusters.

We also encountered limitations that we like to address in future implementations of the SSM method. For example, the data pre-processing steps as well as computational algorithms require a level of manual input that makes the technique less suited for general use. Furthermore, in order to facilitate the introduction of this method as a neuroscience tool, a higher automation level and more robust algorithms would help to trace artefactual biases introduced by the technique and improve the procedural uniformity and crucially the analysis consistency of the entire pipeline. Another shortcoming of the current state of the SSM method is its dependency on stimulus-related information, albeit such input is only supportive for computational convergence and does not imply any patent correlation between signal change in the data and stimuli. The `simplest' of all experiments with no stimulus paradigm presented, the resting-state condition (Andrews-Hanna et al., 2010), is in fact the most challenging condition for disclosing hidden neural dynamics. We speculate that an initial scouting in the data for temporal structures may provide the means to initiate a successful SSM process. There is no doubt, however, that typifying resting state data for its distribution of brain state clusters will be of high clinical relevance. We believe that each mental condition or activity generates its highly characteristic cluster pattern and hence offers invaluable clinical insight into the regular and pathological unfolding of thought processes in human brains (Lehmann et al., 2010).

In the next five paragraphs, we propose approaches for functional brain mapping based on these experiences, which could further our understanding of neurological conditions like learning disabilities.

Temporal Nature

A first lesson this study offers is that an analysis strategy that is attuned to the true temporal nature of neural processes enables identification of subtle details in functional brain data. It increases the likelihood to delineate actual activation trees and to detect subject specific pathways, for example irregular trajectories in individuals with developmental dyscalculia while they solve arithmetic exercises (Ansari and Karmilo-Smith, 2002; Janoos et al., 2011a; Cho et al., 2011).

Speed of Acquisition

Second, we believe that time-sensitive analysis techniques would benefit enormously from faster sampling frequency (Lin et al., 2008) and would generate activation maps far richer temporally, than currently possible. In a separate fMRI study, we have shown that tripling the scan rate resulted in sharpening the temporal separation of activation foci in mental arithmetic in combination with the FIR analysis method (Afacan et al., 2011).

Another MR technical solution to generate a cleaner BOLD signal time course is to eliminate the signal contribution from large cortical venous vessels, restricting the signal to the cortical capillary bed located near the neuronal activity. This concept may explain why the PRESTO BOLD signal, in spite of the relatively slow acquisition rate of 2.64s, contained sufficient information for the time-sensitive analysis applied in the current study. In fact, the 3D PRESTO pulse sequence (van Gelderen et al., 1995) suppresses the signal from large vessels due to its extensive use of strong magnetic field gradients (Grandin et al., 1997).

Hypothesis and Signal Patterns

Thirdly, we posit that enhancing both scan rates for data acquisition and analysis algorithms rapidly produces an uninterpretable deluge of information (see Supplement Table) where a substantial quantum of activations may not correspond with our current understanding what constitutes a significant signal change. Nevertheless, in our opinion, it is the information contained in joint pattern of these focal occurrences (Mitchell et al., 2008) that necessitates a fundamentally new manner for reporting brain processes that : a) comprehensively captures complex data signatures ; and b) is capable of identifying the spatio-temporal traces of the parallel cognitive strategies that an individual employs.

In a similar vein, our recent results for schizophrenia (in review) (Janoos and et al., 2011) or developmental dyscalculia and dyslexia (Janoos et al., 2011a,b) imply that such multivariate spatio-temporal analysis methods have the potential to reveal biologically plausible, albeit unexpected, and statistically confirmable results.

Brain States

Fourth, we suggest that the spatio-temporal brain states analysis can successfully discriminate between subjects based on the functional similarity of their data. We observed that not only do dyscalculic subjects exhibit an atypical response as compared to controls, throughout the arithmetic exercise, but so do dyslexic subjects, who unexpectedly showed diminished functional similarity during the early reading phase of arithmetic problem solving. This is in contrast to the sparse and inconclusive findings of spatial-map based comparative analysis. These results provide a fertile ground for building new hypotheses about the pathophysiologies in question. For example, such spatio-temporal activation maps can be used to locate, in time, the turning points in an aberrant mental process where the activation cascades deviate from controls - a possibility not available when comparing spatial maps.

Deluge of Information

Fifth, there is a need to summarize the results of complex cognitive studies through simple measures of subject similarity and divergences. As seen in the Results, the FIR analysis produced an immense number of activation foci, of which we were able to discuss only a small fraction out of considerations of clarity and feasibility. It would simply go beyond the scope of this publication if the entire activation tree were listed. Importantly, it would overwhelm one's power of comprehension when comparing subjects or groups.

This stands in contrast to the SSM analysis method, which attempts to reduce the amount of information presented, by representing saliencies in the data via a temporal sequence of spatially determined brain states. In other words, the method creates a series of distinct brain state snapshots, where each snapshot represents a salient configuration of activity. Moreover, the SSM is able to e ectively summarize and highlight the spatio-temporal differences between subjects by representing them in an easily navigable low-dimensional MDS space. Both these features of the SSM method, the summarization in terms of brain states and the MDS representation of similarity between models, were used to provide new and statistically measurable perspectives on DD. Moreover, after identifying the important features and differences, we were able to explore the results of the SSM for their underlying spatio-temporal explanations (see fig. 8).

This relates to the long-debated question of whether spatially aligned focal blobs alone sufficiently explain essential neurobiological differences between two subject groups - or, if not, would a global assessment of spatio-temporal patterns help further our understanding of differential brain mechanisms.

6. Summary

In this paper, using a study on developmental dyscalculia as an example, we have demonstrated the potential of time-resolved and spatio-temporal analysis methods to provide powerful new clinical insights about abnormal brain function, in terms of four main results. First, the time sensitive FIR analysis revealed the fundamental role of the delayed response of the right IPS to number sizes in arithmetic exercises in subjects with DD. This result provides corroborative evidence that this structure serves as a working memory system using spatial attributes for interim results during calculation. Second, the spatio-temporal SSM analysis was able to show the similarities and differences between healthy individuals and those with dyscalculia and dyslexia and how the brain patterns aligned and differed during the three phases of the experiment. It revealed that DL subjects were abnormal only during a digit reading phase and appeared normal later during the mental arithmetic phases. In contrast, subjects with DD showed systematically greater deviation from healthy subjects throughout the experiment. Thirdly, the SSM showed reduced predictability for subjects with DD, especially during computationally intensive phases, which may reflect the core problem of the condition in terms of increased disorganization and irregularity in mental processing. Fourth, the time-resolved spatial activation maps produced by both the FIR method and the SSM consistently identified highly specific foci in space and time which were not seen in the static HRF analysis, for example in the right IPS and right aIn for the late phases.

The two fundamentally distinct time-resolved analysis methods used in this study arrived, with high certainty, at very similar results in both the spatial and temporal dimensions. This suggests that temporal information about sequential brain recruitment can be reliably extracted from fMRI data. Furthermore, such spatio-temporal information can be invaluable in characterizing mental activity under normal and pathological conditions.