Characterization of Tissue Structure at Varying Length Scales Using Temporal Diffusion Spectroscopy

Abstract

The concepts, theoretical behavior and experimental applications of temporal diffusion spectroscopy are reviewed and illustrated. Temporal diffusion spectra are obtained by using oscillating gradient waveforms in diffusion-weighted measurements, and represent the manner in which various spectral components of molecular velocity correlations vary in different geometrical structures that restrict or hinder free movements. Measurements made at different gradient frequencies reveal information on the scale of restrictions or hindrances to free diffusion, and the shape of a spectrum reveals the relative contributions of spatial restrictions at different distance scales. Such spectra differ from other so-called diffusion spectra which depict spatial frequencies and are defined at a fixed diffusion time. Experimentally, oscillating gradients at moderate frequency are more feasible for exploring restrictions at very short distances, which in tissues correspond to structures smaller than cells. We describe the underlying concepts of temporal diffusion spectra and provide analytical expressions for the behavior of the diffusion coefficient as a function of gradient frequency in simple geometries with different dimensions. Diffusion in more complex model media that mimic tissues has been simulated using numerical methods. Experimental measurements of diffusion spectra have been obtained in suspensions of particles and cells, as well as in vivo in intact animals. An observation of particular interest is the increased contrast and heterogeneity observed in tumors using oscillating gradients at moderate frequency compared to conventional pulse gradient methods, and the potential for detecting changes in tumors early in their response to treatment. Computer simulations suggest that diffusion spectral measurements may be sensitive to intracellular structures such as nuclear size, and that changes in tissue diffusion properties may be measured before there are changes in cell density.

Introduction

Self-diffusion describes the process by which molecules migrate from place to place within a fluid via random movements. The randomness is a consequence of frequent inter-molecular collisions that are a characteristic of Brownian motion. Even in a uniform fluid in an infinite space, the mean distance moved by a molecule in a given time interval is limited by the average speed of molecular motions (which depends strongly on temperature and molecular weight) and the likelihood of encountering another mass in a collision that may cause a change in direction. Inherently, therefore, diffusion connotes the influence of collisions that introduce hindrances to unrestricted molecular displacements. In pure water these collisions happen very frequently, and each molecular jump is very small. For water molecules in dilute solutions of other small molecules, the number and nature of such collisions may not be much different from the pure solvent, so the rate of water diffusion is little changed. However, as the concentration and size of solutes increase, the rate of water diffusion may be expected to drop. When the sizes and spacings of structures that hinder diffusion become comparable to the distance moved in the time over which movements are observed experimentally, the motion appears restricted and the measured diffusion rate reflects the number and nature of such barriers. This appears to be the case for water molecules in cellular tissues, but at present we do not possess a clear idea of what structures are responsible for affecting free diffusion at different spatial and temporal scales.

Stochastic processes can be described by various statistical properties. For water molecules undergoing self-diffusion an important parameter is the instantaneous particle velocity v, which in a pure liquid changes randomly with time at a rate that depends on the collision frequency. In a simple liquid there is little correlation between the values of v at different times (t) even when these are spaced closely together, and so the autocorrelation function of v(t) is very narrow. On the other hand, when there are spatial obstructions that hinder diffusion over multiple collisions, the velocity acquires a degree of correlation over time that depends on the dimensions and spacings of the obstructions. The shape of the autocorrelation function of v then contains information about the structure of the medium (1). Formally, this autocorrelation A can be written as

$$A(t)=\langle \mathbf{v}(\tau )\mathbf{v}(t+\tau )\rangle$$ [1]

where the average is over all values of the interval τ. The spectral density of the molecular velocity correlations is given by the Fourier Transform of A, which corresponds to a frequency-dependent diffusion tensor, D(ω) (2);

$$D_{i,j}={\int }_0^{\infty }{dt}^{\prime }exp(i\omega t^{\prime })\langle v_i(t^{\prime })v_j(0)\rangle$$ [2]

where the i and j refer to the Cartesian directions x, y, and z. For free diffusion, A is essentially infinitesimally narrow, and the spectrum of the tensor D(ω) is flat out to a very high frequency, of order of the inter-molecular collision frequency. But when diffusion is restricted, the autocorrelation function broadens and acquires a negative dip, consistent with a picture in which barriers rectify isotropic diffusion and induce negative correlations between the velocities at different times (2, 3, 4). Then, D(ω) is no longer flat but falls off at low frequencies. The manner in which D(ω) disperses with frequency can provide unique information on the structure of the medium. The characterization of materials by measurement of the diffusion spectrum we term temporal diffusion spectroscopy, as distinct from other diffusion techniques such as q-space approaches that record spectra of spatial frequencies or wavevectors (4, 5). The theory and interpretation of temporal diffusion spectra, along with experimental applications, have been discussed previously by others e.g., in (2, 3, 6).

A diffusion spectrum can be measured at single, specific frequencies, or the contributions of multiple frequencies can be simultaneously assessed by appropriate choice of diffusion gradient. In general, if a diffusion-weighting gradient g(t) is applied, its time integral is f

$$\mathbf{f}(t^{\prime })=\underset{0}{\overset{t^{\prime }}{\int }}\mathbf{g}(t)dt$$ [3]

This has a frequency spectrum F(ω)

$$\mathbf{F}(\omega )=\underset{-\infty }{\overset{\infty }{\int }}\mathit{dt}exp(i\omega t)\underset{0}{\overset{t}{\int }}{dt}^{\prime }\gamma \mathbf{g}(t^{\prime })$$ [4]

The echo amplitude following a diffusion-weighting gradient, g(t), is given (2) by

$$S=S_{0}exp\left(-\frac{1}{\pi }\underset{0}{\overset{\infty }{\int }}\mathbf{F}(\omega )\mathbf{D}(\omega )\mathbf{F}(-\omega )d\omega \right)$$ [5]

where S₀ is the signal magnitude in the absence of the diffusion-weighting gradient. F(ω) can be considered a sampling function which determines the weightings of different contributions of the spectrum D(ω) to the measurement. In practice, for a gradient in any single direction, F(ω) is a vector whose magnitude is the pulse modulation, F(ω). When it has a narrow spectral spread then only narrow ranges within D(ω) contribute to the diffusion signal losses. The use of appropriately designed oscillating gradient waveforms can be used to sample D(ω) at well defined frequencies, and by changing this frequency the shape of D(ω) can be determined. Note that conventional pulsed-gradient spin echo (PGSE) measurements of the apparent diffusion coefficient (ADC) use relatively long diffusion intervals and gradient pulses of finite width. From equations 3 – 5, these correspond to assessing the integrated contributions of a small range of values of D(ω) centered around ω=0, and do not distinguish the contributions of the high frequency part of the spectrum.

We have implemented and evaluated temporal diffusion spectra in various model, cell and animal systems by implementing oscillating-gradient spin echo (OGSE) pulse sequences, and below we summarize some of those studies and discuss the advantages of this approach compared to other methods. In particular, we emphasize that conventional MRI methods used to measure diffusion in tissues reflect the integrated effects of a variety of structural features including those arising at a relatively large spatial scale, on the order of a cell diameter, such as cell membranes. Many other factors may influence the free movement of water, including changes in intracellular organization and the presence of smaller scale restrictions, but their effects will be indistinguishable in the presence of restrictions occurring over larger dimensions if the measurement is made with conventional methods. Studies of ADC with PGSE methods record signal changes caused by diffusion over a specific interval, the diffusion time Δ. Because of technical constraints on the design of gradients and the overall sensitivity of MRI, almost all current and published measurements of ADC correspond to the regime of “long” diffusion intervals. In practice Δ is at least several milliseconds, so using the Einstein relation the ADC reflects the influence of restricting boundaries on the order >5 – 15 μm. Thus, differences between tissues detected by current PGSE methods, such as changes in cellularity in tumors, reflect alterations in the number, permeability and separation of boundaries on the whole cell scale. Such ADC measurements include the effects of restricting boundaries on at least this dimension, and are incapable of providing insights into the factors affecting diffusion at finer scales within the cells and pores within tissues unless Δ is very short. Furthermore, they cannot reveal the scale of the boundaries unless measurements are made in a regime before all nuclei encounter the restricting barrier in the time Δ. This is not usually practical using PGSE methods because extremely strong gradients are needed to produce measurable diffusion attenuation in times < 1 msec. Oscillating gradient techniques at even moderate frequencies are capable of detecting restrictions to diffusion displacements over a specific spatial scale much smaller than the diameter of a single cell, thereby resulting in a greater sensitivity specifically to the contributions of variations in sub-cellular structures to the measured ADC. In this review of recent works, we analyze the theoretical basis of temporal diffusion spectra, show how such measurements are expected to behave in various simple geometries, and illustrate the use of this method for providing greater image contrast and detecting increased structural heterogeneity in tumors. We also show how this method can be more sensitive to early changes in treatment response of tumors.

Experimental Approach

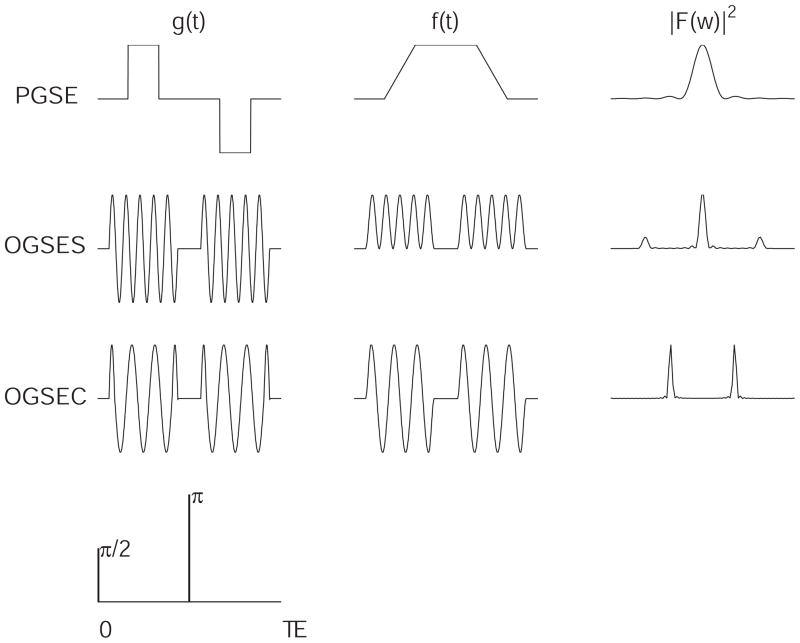
Figure 1 shows pulse sequences that may be used to acquire diffusion spectra. In our experimental work we first began with a sine-modulated gradient waveform as originally proposed by Gross and Kosfeld (7). For an ideal (infinite duration) sine-modulated gradient pulse of frequency ω_m, the spectral density of the dephasing takes the form:

$$F(\omega )\propto \mathfrak{I}\left[{\int }_0^{t}sin({\omega }_m{t}^{\prime }){dt}^{\prime }\right]\propto \delta (\omega )-\frac{\pi }{{\omega }_m}(\delta (\omega +{\omega }_m)+\delta (\omega -{\omega }_m))$$ [6]

where 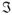denotes the Fourier Transform (equation 4). The signal amplitude produced by using such a gradient will be affected by both D(0) and D(ω_m). On the other hand, for a cosine-modulated gradient pulse, the zero-frequency component does not contribute:

$$F(\omega )\propto \mathfrak{I}\left[{\int }_0^{t}cos({\omega }_m{t}^{\prime }){dt}^{\prime }\right]\propto \frac{i\pi }{{\omega }_m}(\delta (\omega +{\omega }_m)-\delta (\omega -{\omega }_m)).$$ [7]

Figure 1.

The amplitude (g), time integral (f) and spectra (F) corresponding to sine- (OGSES) and cosine-modulated (OGSEC) oscillating gradient waveforms. At the top is that of the PGSE waveform for comparison. The PGSE spectrum is centered around zero frequency, whereas the cosine-modulated waveform isolates discrete frequencies.

We have designed and implemented pulses to approximate this cosine modulation (4, 8). For a relatively long pulse the power spectrum becomes

$${\mid F(\omega )\mid }^2=\frac{{\pi }^2{g}^2{\gamma }^2}{{\omega }_m^2}{[\delta (\omega +{\omega }_m)-\delta (\omega -{\omega }_m)]}^2.$$ [8]

where g = gradient strength, γ = the gyromagnetic ratio, and ω_m = the modulation frequency. In practice the pulses must be apodized in time in an NMR experiment, which broadens each δ function and the range of spectral components that contribute.

The cosine-OGSE poses the challenge of a sharp initial pulse edge (see Figure 1). Experimentally we smoothed this initial transient by replacing the first quarter cycle cosine with a half cycle sine-lobe at twice the base frequency, which reduces the need for a very short coil rise time. Sample pulses and their spectra are shown in Figure 1 alongside those of a conventional PGSE sequence. The separation of the diffusion gradient pulses into two halves to allow for the RF p-pulse in a spin echo results in a small broadening of the peaks (8).

The b-value represents the amount of diffusion-weighting imparted by pulsed or oscillating magnetic field gradients. It can be defined as the total power of spin dephasing over the diffusion preparation time:

$$b=\underset{o}{\overset{2\tau }{\int }}dt{\left[\gamma \underset{0}{\overset{t}{\int }}g(t^{\prime }){dt}^{\prime }\right]}^2$$ [9]

For a simple cosine-modulated waveform,

$$b=\frac{{\gamma }^2{G}^2\sigma }{4{\pi }^2{f}^2}$$ [10]

where G is the peak gradient magnitude, f is the frequency, and σ is the duration of the waveform.

The effective diffusion time Δ_eff for oscillating gradients is not trivially defined in restrictive geometries, similar to the case for time-dependent diffusion coefficients measured using other gradient pulses of finite duration (9). However, it is clear that Δ_eff decreases as f, the frequency, increases. Parsons et al. (4) adopted the formalism of Fordham et al. (9) and showed that ${\mathrm{\Delta }}_{\mathit{eff}}=\frac{1}{4f}$ for unrestricted diffusion (the zeroth order case) and how this must be modified for restricting pores. For cosine modulated gradients oscillating at 1 kHz, the effective diffusion time in free media is ≈ 250 μsec, much shorter than typically achieved with PGSE methods.

Temporal Diffusion Spectroscopy in Simple Geometries

The interpretation of temporal diffusion spectra may be helped by considering how we expect OGSE data to behave for specific simple geometries. To this end, we have evaluated analytical expressions for the behavior of D(ω) in simple geometries. The derivation of these expressions were presented in (3, 8), where their accuracy was confirmed using elaborate computer simulations. It has been previously shown that the diffusion-weighted echo signal can be described as (2)

$$E(2\tau )=exp[-\beta (2\tau )]=exp\left\{-\frac{{\gamma }^2}{2}\underset{0}{\overset{2\tau }{\int }}{dt}_1\underset{0}{\overset{2\tau }{\int }}{dt}_2\mathbf{g}(t_1)\langle {\mathbf{r}}_1(t_1){\mathbf{r}}_2(t_2)\rangle \mathbf{g}(t_2)\right\}$$ [11]

where β = the signal echo attenuation factor, τ = half of the echo time, r_i = water molecule position at time t_i, g = diffusion gradient and < > denotes the ensemble average. In the presence of diffusion restrictions, a conditional probability P, which describes the likelihood that a spin at position r₁ at time t₁ will be at position r₂ at time t₂, may be introduced, which can be expressed in a general solution as (3)

$$P({\mathbf{r}}_1,t_1\mid {\mathbf{r}}_2,t_2)=\sum _{n}exp(-{\lambda }_{n}D\mid t_1-t_2\mid )u_n({\mathbf{r}}_1)u_n^{\ast }({\mathbf{r}}_2)$$ [12]

where D is the intrinsic diffusion coefficient, and u_n(r) are orthogonal functions that describe the geometry. By substituting equation 12 into 11, Stepisnik obtained the signal echo attenuation (3)

$$\begin{array}{l}\beta (2\tau )=\frac{{\gamma }^2}{2}\underset{0}{\overset{2\tau }{\int }}{dt}_1\underset{0}{\overset{2\tau }{\int }}{dt}_2\underset{V}{\int }{d\mathbf{r}}_1\underset{V}{\int }{d\mathbf{r}}_2\rho ({\mathbf{r}}_1,t_1)P({\mathbf{r}}_1,t_1\mid {\mathbf{r}}_2,t_2){\mathbf{r}}_1\mathbf{g}(t_1){\mathbf{r}}_2\mathbf{g}(t_2)\\ =\frac{{\gamma }^2}{2}\sum _n{B}_n\underset{0}{\overset{2\tau }{\int }}{dt}_1\underset{0}{\overset{2\tau }{\int }}{dt}_{2}exp(-{\lambda }_{n}D\mid t_2-t_1\mid )g(t_1)g(t_2)\end{array}$$ [13]

where ρ is the spin density, g(t) = g(t)g̑, and g̑ is a unit vector along the gradient direction. B_n and λ_n are structure dependent coefficients. Assuming a uniform distribution of spins (set equal to unity)

$$B_n=\underset{V}{\int }{d\mathbf{r}}_1\underset{V}{\int }{d\mathbf{r}}_2\stackrel{⌢}{\mathbf{g}}{\mathbf{r}}_1\stackrel{⌢}{\mathbf{g}}{\mathbf{r}}_2{u}_n({\mathbf{r}}_1)u_n({\mathbf{r}}_2)$$ [14]

B_n and λ_n describe the specific geometrical features of any system, and once known they allow the diffusion attenuation to be computed for different times. For example, for diffusion between two impermeable planes separated by a distance d, where the gradient is perpendicular to the planes,

$$B_n=\frac{8d^2}{{(2n-1)}^4{\pi }^4}\text{and}{\lambda }_n=\frac{{\pi }^2{(2n-1)}^2}{d^2}.$$ [15]

For diffusion inside an impermeable cylindrical geometry with a radius R and gradients in the direction perpendicular to the axis of the cylinder,

$$B_n=\frac{2{(R/{\mu }_n)}^2}{{{\mu }_n}^2-1}\text{and}{\lambda }_n={\left(\frac{{\mu }_n}{R}\right)}^2.$$ [16]

where μ_n is the n^th root of $J_1^{\prime }(\mu )=0$ and J₁ is a Bessel function of the first kind. For a spherical geometry, the expression for B_n is

$$B_n=\frac{2{(R/{\mu }_n)}^2}{{{\mu }_n}^2-2}$$ [17]

and λ_n are the same as for a cylindrical geometry except μ_n becomes the n^th root of $\mu J_{3/2}^{\prime }(\mu )-\frac{1}{2}{J}_{3/2}(\mu )=0$ (3).

For diffusion inside an impermeable spherical shell (a < r < b), we derived the analytical expression for the conditional probability (10) as

$$P(\mathbf{r},t\mid {\mathbf{r}}_{\mathbf{0}},0)=\frac{3}{4\pi (b^3-a^3)}+\sum _{n=1}^{\infty }\sum _{m=1}^{\infty }{A}_{nm}{U}_n({\lambda }_{nm}r)P_n(cos\theta )U_n({\lambda }_{nm}{r}_0)P_n(cos{\theta }_0)exp(-{\lambda }_{nm}^{2}Dt)$$ [18]

where

$$A_{nm}=\frac{(2n+1){\lambda }_{nm}^6{a}^3{b}^3}{2\pi \left\{a^3\left[{\lambda }_{nm}^2{b}^2-n(n+1)\right]{\left[\frac{j_n^{\prime }({\lambda }_{nm}a)}{j_n^{\prime }({\lambda }_{nm}b)}\right]}^2-b^3\left[{\lambda }_{nm}^2{a}^2-n(n+1)\right]\right\}}$$ [19]

$$U_n({\lambda }_{nm}r)=y_n^{\prime }({\lambda }_{nm}a)j_n({\lambda }_{nm}r)-j_n^{\prime }({\lambda }_{nm}a)y_n({\lambda }_{nm}r)$$ [20]

and λ_nm is the m^th root of the equation

$$y_n^{\prime }({\lambda }_{nm}a)j_n^{\prime }({\lambda }_{nm}b)=j_n^{\prime }({\lambda }_{nm}a)y_n^{\prime }({\lambda }_{nm}b),$$ [21]

where j_n(r) = r^−1/2 J_n+1/2 (r) and y_n(r) = r^−1/2 Y_n+1/2 (r), J_n+1/2 and Y_n+1/2 are Bessel functions of the first and the second kind, respectively. Equations [18] and [21] yield the B_n coefficient for this geometry as

$$B_n=\frac{2a^3{b}^3{\left[j_1^{\prime }({\lambda }_{n}a)-j_1^{\prime }({\lambda }_{n}a)\right]}^2}{{\lambda }_n^2(b^3-a^3)\left\{a^3({\lambda }_n^2{b}^2-2)j_1^{\prime 2}({\lambda }_{n}a)-b^3({\lambda }_n^2{a}^2-2)j_1^{\prime 2}({\lambda }_{n}b)\right\}}.$$ [22]

Based on the theory introduced above, we derived analytical expressions for the diffusion-induced echo attenuation obtained with the cosine OGSE waveform in these simple situations (10). Using a gradient g at frequency σ for a duration s, analytical expressions for signal echo attenuation can be obtained. The result is

$$\beta (2\tau )=2{(\gamma g)}^2\sum _n\frac{B_n{\lambda }_n^2{D}^2}{{({\lambda }_n^2{D}^2+{\omega }^2)}^2}\{\frac{({\lambda }_n^2{D}^2+{\omega }^2)}{{\lambda }_{n}D}\left[\frac{\sigma }{2}+\frac{sin(2\omega \sigma )}{4\omega }\right]-1+exp(-{\lambda }_{n}D\sigma )+exp(-{\lambda }_{n}D\tau )(1-cosh({\lambda }_{n}D\sigma ))\}$$ [23]

where D is the intrinsic diffusion coefficient, and τ half of the echo time. We have previously reported our computational approach to simulating diffusion effects in NMR using a finite difference approach (11). These analytical expressions have been validated by comparing their predictions to those of computer simulations of diffusion in simple systems (10).

(i) Diffusion between Two Parallel Planes

The elementary case of diffusion between two infinitely-large impermeable parallel planes using the cosine OGSE waveform is shown in Figure 2 for different separations of the planes. This example illustrates the major physical effects of restricted diffusion and how these interact with the OGSE parameters. A one dimensional gradient was considered perpendicular to the planes and the distance between the planes was varied from 1 to 10μm, the latter corresponding to a typical human cell size. Figure 2 shows the behavior of D(ω) for different frequencies. At low frequencies the ADC is highly reduced (highly restricted) for all spacings of the planes but the ADC shows a very rapid increase with increasing diffusion gradient frequency that depends on the spacing. This is equivalent to the observation that ADC measured by PGSE methods tend to zero as the diffusion time Δ tends to infinity. For the larger separations, at frequencies beyond 1 kHz there is little dispersion and the ADC is close to the case of free water. For the smaller separations the ADC is still only a small fraction of the free value even at frequencies of 2 kHz. These curves illustrate an important practical point; if the gradient waveform contains very low frequencies, the ADC for all these geometries is similar, so in a PGSE diffusion-weighted image there would be very little contrast between structures with different spacings. On the other hand, if a gradient at, for example, 1 kHz is used, then there would be a large difference in the signals from each of these samples, so there would be contrast between regions of different structure. The magnitude of the contrast would depend on the specific frequency used, and this can be “tuned” to maximize the distinctions between structures of specific spatial length scales.

Figure 2.

Calculated values of the ADC as a function of frequency for diffusion between two infinite, impermeable planes, for different spacings. The dispersion with increasing frequency is initially much more rapid for larger separations.

(ii) Diffusion in Other Simple Restricted Compartments

Figure 3 depicts the behavior of the ADC as a function of frequency in other simple geometries. Figure 3a shows the result of evaluating the analytical expression for diffusion in a cylinder of infinite length with an impermeable surface for different diameters 1 – 10 microns. The gradient is applied perpendicular to the long axis of the cylinder. Figure 3b shows the results for diffusion in a sphere of different diameters. Qualitatively these graphs are similar to the case for the infinite plane. Again, tuning the gradient frequency to a specific high frequency will increase the distinction between two objects of different sizes. Using even a moderate frequency (≈ a few hundred Hz) will provide greater contrast between objects smaller than 10 microns than the use of low or zero frequency measurements, in which all sizes show restricted behaviors.

Figure 3.

Theoretical behavior of ADC as a function of frequency for restricted diffusion in a single compartment. 3(a) Left; diffusion in a cylinder of different diameters. 3(b) Right; difusion in a sphere of diferent diameters. The difference in ADC values for different sized compartments depends on the selection of the gradient frequency.

(iii) Diffusion in More Complex, Multi-Compartment Systems

Xu et al. (10) have expanded on the use of these theoretical behaviors in simple geometries and employed computer simulations to study diffusion in more realistic, tissue mimicking systems. For example, cylinders placed on a square lattice may roughly simulate white matter or other fibrous materials. Figure 4a shows an array of infinitely long cylinders, each with an impermeable surface, in which water may be either inside a cylinder or in the spaces between them. Figure 4b shows the manner in which the ADC of water would behave as a function of frequency. In this case the diffusion gradients are perpendicular to the axis of cylinders. It has been reported that water exchange between axons and extracellular space is intermediate or slow (12) and so here the interface permeability was again set equal to zero. There is restricted diffusion inside the cylinder and hindered diffusion in the extracellular space (13). The total signal echo attenuation from such a model tissue is then simply the sum of the signals arising from the two compartments

Figure 4.

Left: the array of cylindrical fibers considered a simple model of white matter. Right: the predicted behavior of ADC as a function of frequency. For this curve, the intra- and extra cellular diffusion coefficients are taken as 1.0 and 2.0 μm²/ms respectively, the cylinders have diameter 1.96 μm and the lattice pacing is 2.1 μm, so the cylinder volume frction is 75.25%. Other details of the simulation are given in (10). Note the sharp inflection of the curve at between 1 and 2 kHz for this size system.

$$E=f_{\mathit{axon}}exp(-\beta (2\tau ))+(1-f_{\mathit{axon}})exp(-b{D}_{ex}),$$ [24]

where β(2τ) is the signal echo attenuation of water inside axons, D_ex is the hindered diffusion coefficient of extracellular space, and f_axon is the volume fraction of axons. Note also that Figure 4 also implicitly shows how the fractional anisotropy of the cylinders would depend on the choice of frequency.

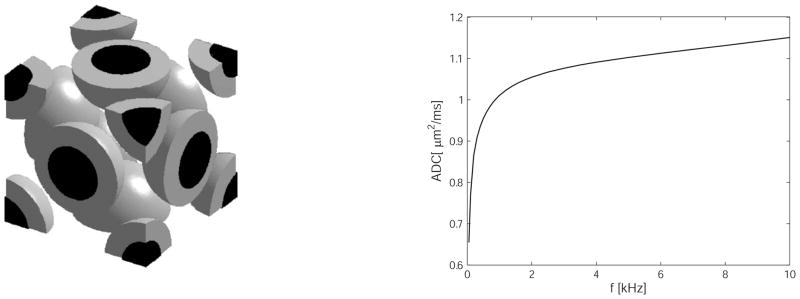
In Xu et al. (10) we reported the behavior of OGSE spectral measurements in a more realistic model consisting of close-packed spherical cells, each containing a spherical nucleus (see Figure 5). In this model system, there are three distinct compartments containing water, corresponding to intra-nuclear, cytoplasmic and extracellular spaces. Each component can be ascribed its own intrinsic parameters, including proton density, T₂ and water self-diffusion coefficient. To highlight the effects of diffusion only, proton density and T₂ values were assumed to be homogeneous. For the OGSE method, the effective diffusion time can be smaller than a few milliseconds (corresponding to gradient frequencies higher than a few hundreds of hertz). In contrast, the intracellular water exchange lifetime has been reported to be two orders of magnitude larger, e.g. the HeLa cell intracellular water lifetime was estimated to be 119±14 ms (14). Therefore, we can neglect the influence of the water exchange between intra- and extracellular spaces during the OGSE measurements. Similarly, for the nuclear envelope separating intra-nuclear and cytoplasmic compartments, water exchange across the nuclear envelope can be ignored in OGSE measurements with short diffusion times (10). Consequently, all the interfaces between the compartments in the tissue model can be effectively modeled as impermeable if the OGSE method is implemented with relatively high gradient frequencies. As a result, the total signal can be modeled as a sum of independent signals, each arising from one compartment.

Figure 5.

Left: the array of close packed spherical cells (grey) containing spherical nuclei (black) considered a simple model of tissues. Right: the predicted behavior of ADC as a function of frequency. For this curve, the intra-nuclear, cytoplasmic and extracellular diffusion coefficients are taken as 1.31, 0.48 and 1.82 μm²/ms respectively, the “cells” have diameter 10 μm, the nuclei are 7.5 μm and the lattice spacing is 10.6 μm, so the cellular volume fraction is only 39.6%. Other details of the simulation are given in (10). Note the sharp inflection of the curve at around 1 kHz for this size system.

The diffusion inside the intra-nuclear and cytoplasmic spaces is considered to be restricted, and the diffusion in the extracellular space was modeled as hindered and ascribed a constant diffusion coefficient. The total signals can then be expressed as

$$E=f_{\mathit{nuc}}exp(-{\beta }_{\mathit{nuc}})+f_{\mathit{cyto}}exp(-{\beta }_{\mathit{cyto}})+(1-f_{\mathit{nuc}}-f_{\mathit{cyto}})exp(-b{D}_{ex}),$$ [25]

where β_nuc and β_cyto represent the signal echo attenuation of intra-nuclear and cytoplasmic spaces, respectively, and f_nuc, f_cyto represent proton fractions (equal to volume fractions because proton density is assumed to be homogeneous). The signal echo attenuation was simulated and then fit to Equation 25. All cell structural parameters used in the simulation were chosen from published experimental results (15, 16): the intrinsic diffusion coefficients for nucleus = 1.31 μm²/ms, cytoplasm = 0.48 μm²/ms and the extracellular space = 1.82 μm²/ms. Spherical cells were given a diameter of 10 μm, spacing 10.6 μm for neighboring cells and each cell contained a central spherical nucleus with a diameter of 7.5 μm. Figure 5 shows the behavior of the ADC as a function of frequency for this system.

A more complex model was analyzed using computer simulations by Xu et al. (17) where the effects of finite permeabilities of the restricting membranes and the effects of cell density (cellularity) were explicitly considered. The observed relation between ADC and cellularity in conventional PGSE measurements is likely a reflection of the effects of water molecules encountering different numbers of cell membranes in the diffusion time, but no separate information can be obtained about structural variations that might occur on sub-cellular scales. In studies of cancer, although cell density may be useful as an indicator of tumor aggressiveness or metastatic capacity, it is plausible that more specific insights into tumor status may be provided by developing methods that are sensitive to intracellular changes. To assess such effects, we considered a computer model similar to the above close-packed spheres but in which each restricting membrane was assigned a finite (non-zero) permeability and the cell density and nuclear to cell size ratios were varied. Diffusion was simulated for conventional and OGSE methods. The results show that conventional measurements with the PGSE method at typical diffusion times cannot selectively probe variations within samples that occur only over short length scales and, therefore, are relatively insensitive to intracellular structure, whereas results using OGSE methods at moderate gradient frequencies may be affected by variations in cell nuclear sizes, and can distinguish tissues that differ only over sub-cellular length scales (Figure 6). In particular, using realistic values, we predicted that we should be able to distinguish tissues that have the same cell density but different ratios of the nuclear/cell volume in circumstances in which PGSE measurements would not provide significant contrast (17). Such effects may not be restricted to just the nucleus - there are other intracellular membranes with large surface areas, and changes in their properties may also affect the signals. The ability of OGSE methods to be able to detect changes within cells, without gross changes in cellularity, is a major potential advantage over conventional PGSE methods for some applications such as detecting the early response of tumors to treatment, as shown below.

Figure 6.

The ADC is calculated as a function of frequency for two tissues, each with the same cell density but with different sized nuclei, and all other parameters identical. In Tissue I the nucleus to cell volume ratio is only 6.2%, whereas in Tissue II it is 22%, so less intracellular water is confined within the faster diffusing nuclear compartment. At low frequencies the ADC values are barely different, whereas significant differences (and thus contrast in images) are expected at frequencies beyond ≈ 200 Hz. For this simulation, the intra-nuclear, cytoplasmic and extracellular diffusion coefficients are taken as 1.31, 0.48 and 1.82 μm²/ms respectively, the “cells” have diameter 10 μm, and the membrane permeabilities were 0.024 μm/ms. The cellular volume fraction was fixed and the ony the nuclear size was varied. Other details of the simulation are given in Xu et al. (17) (figure adapted from (17).

Experimental Measurements of Temporal Diffusion Spectra

Early experimental studies in model systems

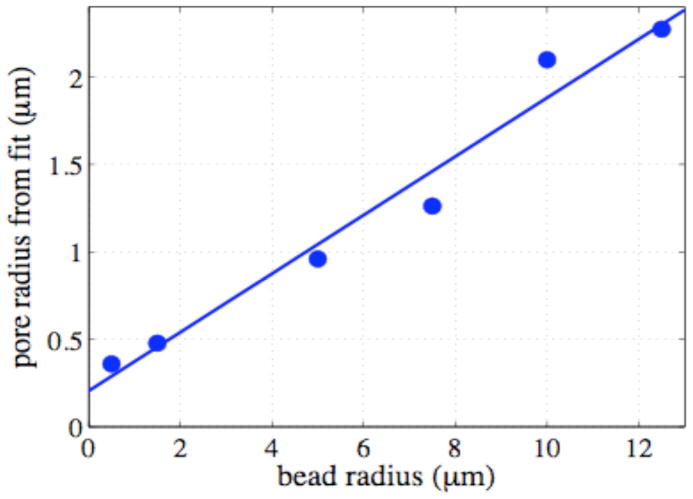
We first studied model systems that were suspensions in de-ionized water of polystyrene latex microspheres of the various diameters: (1 – 400 μm). These studies were reported in (4) and (8). The samples were centrifuged to induce close packing. Measurements were made at 200 MHz in a 30 cm bore 4.7T superconducting magnet using an imaging gradient insert with maximum gradient strength of 100 gauss/cm. Oscillating diffusion gradient waveforms were 30 ms in duration and of variable frequency. For each frequency, the gradient amplitude was adjusted so that the b-values were the same. The total width of the two pulses was 2σ = 60 ms, so the width of the frequency peak in F(ω) was in all cases 16.67 Hz. Images were collected for values of N (the number of oscillations in each gradient pulse) from 1–30, sampling the diffusion spectrum from 33.33 to 1000 Hz in 33.33 Hz increments. The measured diffusion spectra for nine packed bead samples plus a uniform gel are plotted in Figure 7. Superimposed on the data are the best fits to the data using equations derived by Stepisnik (8) for the theoretical spectra in spherical geometry. Two parameters were extracted: the pore radius and D₀. Figure 8 shows the pore sizes calculated from these fits plotted against the known bead sizes. The finite offset of the linear fit is due to an overestimation of the pore size in the smallest beads. Higher frequencies of gradient oscillation would be necessary to improve these fits. In Parsons et al. (3) we also reported the use of a simple model to extract values of S/V, the surface to volume ratio of the pores in this system.

Figure 7.

Measured ADC values for samples of close packed beads, obtained at different gradient frequencies, with fits to theoretical expressions for diffusion in spherical geometry (details reported in (8)).

Figure 8.

Fitted pore size plotted against bead size for samples with diameters from 1 μm to 25 μm. The slope of the line of best fit is 0.084, which corresponds to the ratio of pore size to bead radius (details reported in (8)).

OGSE Spectra in Packed Cells - Extending the Frequency Range

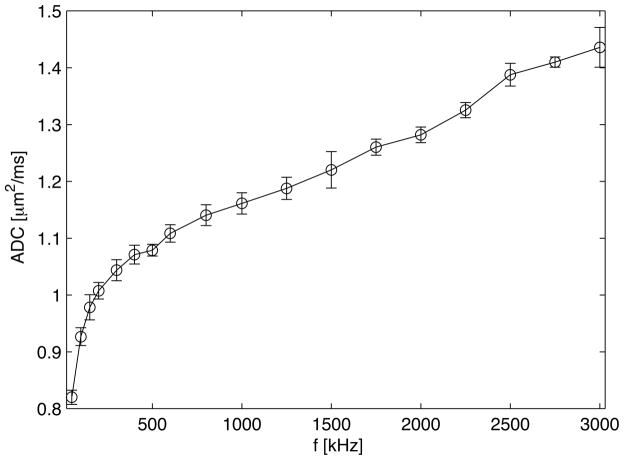
Using a special gradient system capable of gradients up to 3500 g/cm and frequencies to 3.5 kHz, we have studied the dispersion of D(ω) in samples of packed cells. Cell pellets do not usually mimic intact tissues closely, but in previous work we observed the ADC at long diffusion intervals was inversely proportional to the cell density (15). In packed human embryonic kidney cell (293-EBNA) suspensions, OGSE methods have been used to measure ADC at oscillation frequencies up to 3 kHz (effective diffusion times for uniform media down to 80 μs). These data are shown in Figure 9. Rapid increases in ADC occur over the range 0 to ≈ 300 Hz, after which there is a much more gradual and continuous increase at higher frequencies out beyond 3 kHz. These data suggest that in these cells, diffusion is reduced below the free water value by hindrances on a scale much below the dimensions of whole cells, and that even at very short diffusion times there are still hindrances that reduce the ADC significantly below that of free water. Xu et al. (10) considered how OGSE experimental spectra could be fit to theoretical expressions in order to extract structural parameters such as cell sizes using the simple two compartment model considered earlier for spherical cells. Such an approach can provide information on tissue structure not readily obtainable by other means.

Figure 9.

ADC as a function of frequency from OGSE measurements in packed cells. The error bars are the standard deviation for data obtained by averaging 10 different measurements. The ADC increases rapidly at low frequencies and more gradually at higher frequencies. Even at 3 kHz there is little evidence the curve is flattening to its asymptotic value.

OGSE Studies in Vivo

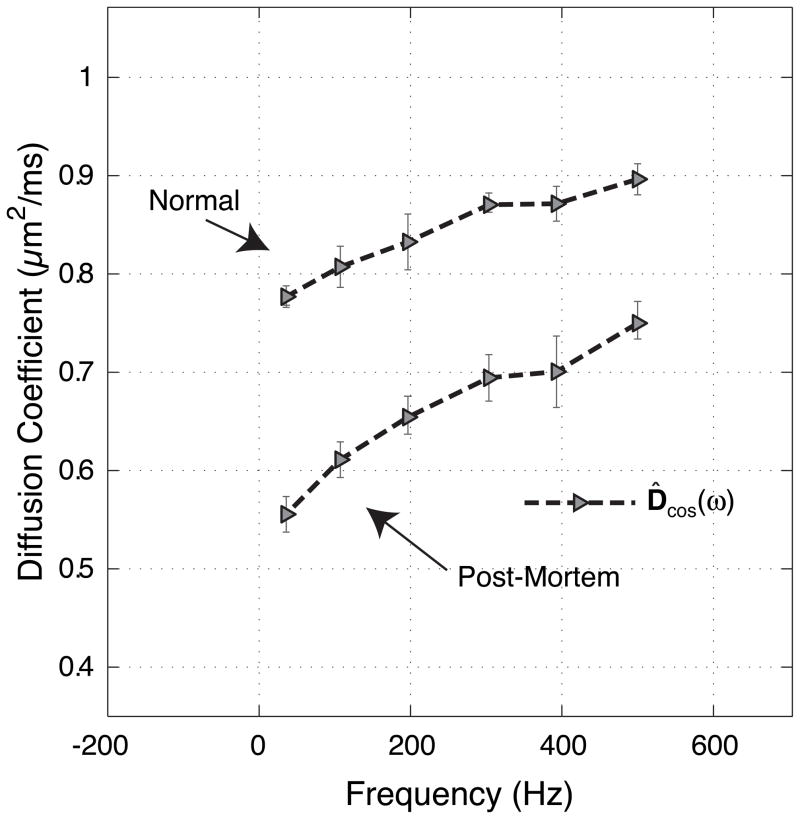
Oscillating gradient methods can be readily implemented on modern animal imaging systems equipped with typical state-of-the-art imaging gradients. In earlier work, with gradients capable of reaching 100 g/cm, oscillating gradients were used to probe the frequency dependence of water diffusion in the grey matter of normal and globally ischemic rat brain (18). These oscillating gradient measurements measured D(ω) for brain water over the range 0 – 500 Hz, corresponding to diffusion times for uniform media of between 9.75 ms and 375 μs, an order of magnitude shorter than previously studied in vivo. Over this range, D(ω) increased as much as 24 % in vivo and 50 % post-mortem (see Figure 10). The results in rat brain were found to be consistent with restricted diffusion and the known micro-anatomy of grey matter. Differences between normal and post-mortem data were consistent with an increase in water restriction, and tentatively suggest that physical changes following the onset of ischemia occur on a scale of about 2 μm, similar to a typical cellular dimension in grey matter. The diffusion studies in this paper did not fully reach the short diffusion time regime, and thus we were limited in the ability to extract other parameters.

Figure 10.

Mean ADCs from cortical grey matter of five rats (error bars are the standard deviation across rats), for OGSE cosine waveforms as a function of frequency. The upper data are from normal rats, in-vivo, and the lower are from the post-mortem images. Details of these measurements were reported in (18).

Temporal Diffusion Spectra in Tumors

Diffusion measurements have proven useful in both small animal and clinical imaging for characterizing the state and response of tumors, and reveal information on tissue characteristics such as cellularity not obtainable by other means. As emphasized earlier, conventional measurements of ADC reveal the effects of restrictions to free diffusion on a specific spatial scale determined by a diffusion time interval, which is several microns because for technical reasons the diffusion time has to be at least several milliseconds. Variations in ADC may thus be dominated by variations in the density of restricting barriers of this spacing, corresponding to variations in cell density, and no specific information is available from ADC measurements about structural changes that occur at a smaller scale. For example, if changes occur within cells before there are changes in cell density, these cannot be distinguished.

By measuring diffusion spectra using oscillating gradient waveforms. we can obtain information on diffusion in the regime in which inferences can be drawn about changes in intracellular tissue structures that modify diffusion before there are changes in cell density. We have been encouraged by our first studies looking at the effects of treatment of tumors and the use of OGSE measurements of ADC as an early biomarker of successful treatment responses.

We recently reported a preliminary assessment of tumors using OGSE methods (19). We applied OGSE methods to map the ADC at specific frequencies in rats bearing glioblastoma tumors in vivo and ex vivo to illustrate the increased contrast and structural information that is achievable using such techniques. By demonstrating an increased contrast in calculated ADC maps, at moderately high frequency (240 Hz), as well as quantitatively different ADCs measured in pathological regions, we demonstrated the benefit of OGSE techniques over currently employed techniques for evaluating microscopic variations in tumor microstructure (19).

Figure 11 shows maps of ADC obtained in one representative animal for different gradient frequencies. The ADC map obtained at the lowest frequency, 30 Hz, is similar to that obtained by the PGSE method, as expected. However, as the oscillation frequency is increased, there is increased contrast between the tumor and surrounding tissues, and new features appear within the heterogeneous tumor volume. These features correspond to regions in which the degree of restriction to diffusion varies more at shorter time and distance scales than in surrounding tissues.

Figure 11.

ADC maps of rat brain with tumor obtained using different gradient frequencies. Top row shows a T2-weighted image and ADC obtained using the conventional PGSE sequence, which is not much different from the low frequency OGSE results. At high frequency more contrast and new features emerge within the tumor in particular. Details of these experiments were reported in (19).

Plots of ADC versus oscillation frequency for two regions of interest (within tumor and normal brain) from one representative animal are shown in Figure 12. For each frequency, the corresponding mean displacement for free diffusion predicted by theory is also displayed. At the lowest frequency of 30 Hz, the effective diffusion time is approximately 8.3 ms, and the ADC is similar to that measured by PGSE methods over an interval of 15 ms. However, as the oscillation frequency increases, and the effective diffusion time decreases, there is a clear departure in ADC from that measured with PGSE methods. For example, at an oscillation frequency of 150 Hz (Δ_eff ≈ 1.7 ms) the ADC calculated using OGSE is approximately 20% larger than that calculated using PGSE, and becomes 48% larger at 240 Hz (Δ_eff ≈ 1.0 ms).

Figure 12.

Plots of ADC versus oscillation frequency for two regions of interest (within tumor and normal brain) from one representative animal. For each frequency, the corresponding mean displacement for free diffusion predicted by theory is also displayed (from (19)).

The ADC in contra-lateral grey matter was found, in general, to be smaller than that in tumor, and to increase less with frequency, with the mean value for gray matter varying from 0.60 ± 0.06 μm²/ms at 30 Hz to 0.79 ± 0.06 μm²/ms at 240 Hz (errors for values averaged across animals are reported as standard error of the mean).

In a more recent study, male rats bearing intracranial 9L glioblastoma were treated with the chemotherapeutic drug BCNU (carmustine) (20). Figure 13 shows T₂-weighted MR images (left) and ADC maps by conventional PGSE (center) and OGSE (using a gradient frequency of 240 Hz, right). The top row shows the images obtained 11 days post-inoculation: the middle and lower rows show the results 24 hrs and 72 hrs post-treatment. Note the greater contrast and heterogeneity in the OGSE data suggesting there is less restriction at finer scales. Also, changes in ADC compared to control (untreated animals) appear earlier (24 hrs), and are more marked, in OGSE images after treatment than in conventional methods. In tumors that responded to the treatment, preliminary examination of histological data suggest that these changes correspond to reductions in mean nuclear size rather than in cell density or other factors. These initial data suggest that OGSE techniques, capable of assessing diffusion effects over much shorter spatial scales, are able to reveal a greater range of spatial features within the tumor microenvironment, and may be more sensitive as early indicators of treatment response than conventional methods.

Figure 13.

T₂-weighted MR images (left) and ADC maps by PGSE (center) and OGSE (240 Hz, right) of 9L gliosarcoma in vivo. Top: 11 days post-inoculation: Middle and Lower: 24 hrs and 72 hrs post-treatment with BCNU (carmustine). Note greater contrast and heterogeneity in OGSE data suggesting less restriction at finer scales: changes in ADC appear earlier (24 hrs) and are more marked in OGSE images after treatment (20).

Conclusions

Temporal diffusion spectroscopy as described here is different from diffusion q-space imaging or other analyses of diffusion measurements. In q-space imaging, the propagator is usually defined at a given diffusion time and has spatial and directional dependences over a large range of q-space. In contrast, in temporal diffusion spectroscopy, the effective diffusion times are changed by changing diffusion gradient frequencies, and thus a spectrum of diffusion rates can be measured which describe the biological tissue microenvironment. It may be thought that the use of a high frequency gradient is merely a way to achieve short effective diffusion times, and that equivalent information may be obtained using conventional pulsed gradients with short diffusion times. Experimentally, oscillating gradients of sufficient strength and frequency are more readily implemented in small samples and animals than high-amplitude short pulsed gradients, and that alone makes the method attractive. However, it should be emphasized that different physical insights are obtained using the frequency analysis above, and there are potential practical advantages of using a discrete frequency rather than a short pulsed gradient. The latter will always correspond to sampling the diffusion spectrum at multiple frequencies around zero, whereas specific frequencies can be sampled by using cosinusoidal gradients. The contrast between tissues may be greater at a discrete, moderately high frequency than at low frequencies, as suggested by our theoretical consideration of simple geometries above and our preliminary studies in tumors.

Our efforts to extend measurements in vivo and in cells to higher frequencies have revealed interesting new insights into what scales of obstructions cause diffusion coefficients to be so small in biological samples. In packed cells, the observation that D(ω) does not appear to flatten out even at frequencies > 3 kHz suggests there are significant hindrances to diffusion over scales ≪ the cell size, even though protein solutions and simple gels of similar density show no such effects. Such data imply the existence of larger, more discrete structures than isolated macromolecules that affect diffusion.

The ability to detect early changes in tumors during a course of treatment is a potentially important application of diffusion imaging, and the ability to detect changes within tumors before there are frank reductions in cell density may be a significant advantage of OGSE methods over PGSE techniques. Simulations and theory predict that changes at subcellular levels may be discernible at high gradient frequencies, which can distinguish such effects from larger scale changes. Our preliminary findings of increased contrast and spatial heterogeneity, and earlier changes after treatment, in animal models even at moderate frequencies are encouraging and justify further studies.

Just as PGSE methods are limited in their ability to probe very short diffusion times because of limitations on gradient strength, OGSE methods are similarly constrained in practice. As frequency of gradient modulation increases, in order to keep echo times reasonable, the gradient amplitude has to increase to produce large b factors. In practice this will limit the application of OGSE methods to human scanners using currently available gradients. However, in the pre-clinical domain, gradient systems suitable for achieving quite high gradient frequencies are routinely available and in operation. We anticipate that these will find increasing application for the acquisition of temporal diffusion spectra and OGSE-weighted images in small animals.

Abbreviations used

ADC

Apparent Diffusion Coefficient

BCNU

1,3-bis(2-chloroethyl)-1-nitrosourea

DWI

Diffusion weighted imaging

OGSE

Oscillating gradient spin echo

PGSE

Pulsed gradient spin echo

BCNU

1,3-bis(2-chloroethyl)-1-nitrosourea