Abstract
Determining the functional structure of biological networks is a central goal of systems biology. One approach is to analyze gene expression data to infer a network of gene interactions on the basis of their correlated responses to environmental and genetic perturbations. The inferred network can then be analyzed to identify functional communities. However, commonly used algorithms can yield unreliable results due to experimental noise, algorithmic stochasticity, and the influence of arbitrarily chosen parameter values. Furthermore, the results obtained typically provide only a simplistic view of the network partitioned into disjoint communities and provide no information of the relationship between communities. Here, we present methods to robustly detect co-regulated and functionally enriched gene communities and demonstrate their application and validity for Escherichia coli gene expression data. Applying a recently developed community detection algorithm to the network of interactions identified with the context likelihood of relatedness (CLR) method, we show that a hierarchy of network communities can be identified. These communities significantly enrich for gene ontology (GO) terms, consistent with them representing biologically meaningful groups. Further, analysis of the most significantly enriched communities identified several candidate new regulatory interactions. The robustness of our methods is demonstrated by showing that a core set of functional communities is reliably found when artificial noise, modeling experimental noise, is added to the data. We find that noise mainly acts conservatively, increasing the relatedness required for a network link to be reliably assigned and decreasing the size of the core communities, rather than causing association of genes into new communities.
Author Summary
One of the fundamental themes in biology is the hierarchical organization of its constituents. At higher levels of a hierarchy new properties emerge due to the complex interaction of constituents at lower levels. This same organization is expected to be found in genetic regulatory networks. If so, determining this hierarchal structure would aid in understanding the properties and functional processes of the networks. With the increasing availability of genetic expression data, developing methods to infer the underlying genetic regulatory network and detect functional communities within the network is an important goal of systems biology. Unfortunately, noise in expression data creates variability in the inferred network and the stochastic nature of community detection creates variability in the functional communities detected with existing methods. Here, we present methods for exploring the hierarchical organization of genetic regulatory networks that robustly detect core functional communities. We test the methods and demonstrate their validity, by applying them to Escherichia coli genetic expression data, finding a hierarchy of functionally relevant communities and then comparing those communities to the known E. coli functional groups. We then give examples of how our methods can be used to infer regulatory interactions between genes.
Introduction
Gene regulation networks represent the set of regulatory interactions between all genes of an organism. These networks can contribute to our understanding of the development of organisms and how they integrate internal and external signals to coordinate gene expression responses [1], [2]. Moreover, knowledge of gene regulation networks allows communities of closely interacting genes to be identified. Once identified, such communities are an important resource for developing hypotheses for the function of uncharacterized genes and can provide insight into patterns of regulatory network evolution and function [3]–[8]. Examining the relationships between communities can also reveal a hierarchical set of interactions, which is thought to be a fundamental organizing principle in many biological systems [9]–[11]. For all these reasons, determining gene regulation networks and their functional organization remains a major goal of systems biology.
The increasing availability of gene expression data has spurred development of a number of approaches that aim to determine the underlying structure of the transcriptional regulatory network [2], [3], [7], [12]–[16]. Most of these techniques fall into the broad categories of correlation-based methods, information-theoretic methods, Bayesian network predictions, or methods based on dynamical models. These approaches generally infer regulatory links between the nodes (genes) of the network on the basis of the level of correlation in their transcriptional response to a series of environmental and genetic perturbations. The strength of the links is either weighted by the correlation value, or is unweighted and the links are assumed to exist only if the correlation exceeds a threshold value. Once the links are assigned, the network becomes well defined. However, variation in the application of each method can produce differences in the link weight between pairs of nodes. Additionally, if the threshold for placing links is varied even slightly there can be significant differences in the network structure inferred from a given data set [17]. Identification of groups of interacting node (gene) communities poses an additional challenge. Communities can be identified using computational methods developed in network science [18]. These methods include hierarchical clustering [19]–[21], clique based clustering [22]–[25], core-pheriphery [26]–[28], K means clustering [29], principal component analysis [30], , label propagation [32], [33], statistical mechanical approaches [34], [35], and modularity maximization methods [36]–[40]. Often these algorithms agglomerate or divide the nodes of a network into groups based on either the links of the network or the strength of the correlation value between pairs of nodes. However certain algorithm parameters, such as the number of groups, are often required as user inputs and can become increasingly difficult to predict as the size and complexity of the network grows. In addition, there can be considerable variability in the community detection process due to approximations and stochastic elements of the computational algorithms.
Here, we present methods for determining the hierarchical organization of genetic regulatory networks and for detecting functional communities of genes that are robust to variability in both gene expression data and community detection parameters. We apply a recently developed community detection method [40] to regulation networks inferred from a compendium of E. coli expression profiles using the context likelihood of relatedness (CLR) algorithm [3]. This method uses the mutual information in the data sequence for pairs of genes to construct a “Z-score matrix” that describes the relatedness of each gene pair. We then choose a threshold Z-score value and construct a network by creating links between pairs of genes whose relatedness exceeds this value. However, rather than choose one threshold value, we investigate the network using a range of threshold values. The combination of using the CLR method and varying the threshold value used to create the network captures non-linearities inherent in the network structure. We identify communities using a leading eigenvalue method with final tuning [40]. This method identifies communities by partitioning the network so as to maximize its modularity. The optimization algorithm used by this method, when applied to a series of widely studied networks, produces the partitioning with the largest modularity of any known fast algorithm for networks up to a few thousand nodes in size [40].
As mentioned above, there is variability in the community detection process. Indeed, numerous network partitions can give modularities close to the maximum and these partitions can be structurally diverse [41]. Rather than treat this property as a disadvantage, we use the stochasticity to find correlations between different runs of the community detection algorithm. We consider a core community, as those nodes that are consistently assigned to the same community over multiple partitions of the network. This ensemble analysis of partitionings to find correlations between different sets of network partitions, combined with varying the threshold value used to create a network, enables us to investigate relationships between communities at different threshold values. We define community relationships as hierarchical if communities at a higher threshold value are contained within communities at a lower threshold value. This method not only allows us to find the hierarchical organization of communities within the network, but also to determine if a network is, in fact, hierarchical – a feature that is not forced upon the network by the method.
Comparisons of independent gene expression experiments often find considerable inter- and even intra-experiment variation, which can amplify stochastic aspects of the community detection process [42]–[44]. While variation can be minimized by standardizing the platform and analysis pipeline used, the low-replication common to many gene expression studies, means that the variance of each individual gene expression estimate is typically quite high. To investigate the effects of experimental noise on our ability to assign genes to core communities, we constructed artificial data sets with various levels of experimental noise. At each noise value, multiple runs of the community detection process are performed, allowing us to determine the sensitivity of core community structure to realistic levels of expression variation. We find that increasing the value of expression noise had a similar effect to increasing the relatedness cutoff value used to create the network. Noise decreases the size of the core communities, leaving only the most strongly related genes as consistent members, but does not tend to assign genes into new core communities. To test whether the communities predicted by our methods are biologically relevant, we test whether they significantly enrich for gene ontology (GO) terms identified in E. coli. We find that, in many cases, there are statistically significant matches between a core community and GO term, indicating that communities are biologically relevant. Thus, the methods we present to investigate genetic regulatory networks and to determine the hierarchy of their functional communities appear robust to the variability in the community detection process and to the existence of experimental noise.
Results
Inferring gene interaction networks from expression data
We used the CLR algorithm to infer direct and indirect regulatory interactions between E. coli genes on the basis of the similarity of their expression response in 466 experiments in the Many Microbe Microarrays Database ( ) [45]. The resulting CLR relatedness matrix can be used to define a network with weighted links between genes. In principle this network can be analyzed to find its community structure. However, doing so would not allow an exploration of hierarchical community organization. Instead, we apply a threshold value of relatedness,
) [45]. The resulting CLR relatedness matrix can be used to define a network with weighted links between genes. In principle this network can be analyzed to find its community structure. However, doing so would not allow an exploration of hierarchical community organization. Instead, we apply a threshold value of relatedness, 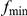 , above which a regulatory interaction is inferred. The result is an unweighted, undirected network where links between genes indicate regulatory correlations. Note that these correlations do not necessarily imply direct interactions. A link may indicate indirect interactions, as may occur between two genes if they are both regulated by a third gene. In this way the CLR network differs from annotated regulatory networks (e.g., for E. coli RegulonDB [46]) that include only direct regulatory links. The threshold value
, above which a regulatory interaction is inferred. The result is an unweighted, undirected network where links between genes indicate regulatory correlations. Note that these correlations do not necessarily imply direct interactions. A link may indicate indirect interactions, as may occur between two genes if they are both regulated by a third gene. In this way the CLR network differs from annotated regulatory networks (e.g., for E. coli RegulonDB [46]) that include only direct regulatory links. The threshold value 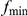 that is chosen has considerable effect on the network that is created and on its community structure. The distribution of relatedness value,
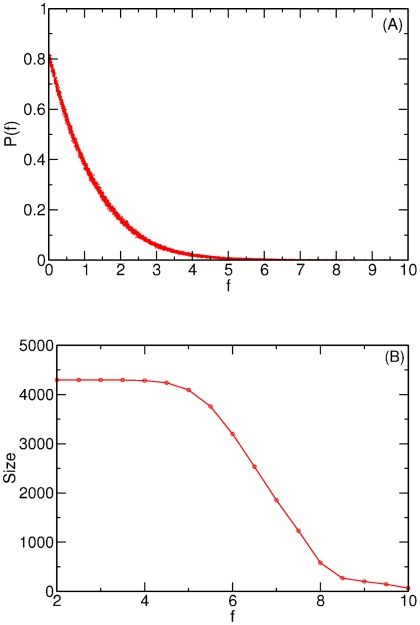
that is chosen has considerable effect on the network that is created and on its community structure. The distribution of relatedness value,  , of pairs of genes is shown in Figure 1A. Clearly, increasing the cutoff value significantly reduces the number of links in the network. At
, of pairs of genes is shown in Figure 1A. Clearly, increasing the cutoff value significantly reduces the number of links in the network. At 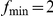 all 4,297 genes are in the largest connected component and therefore the network is fully connected (Fig. 1B). At approximately
all 4,297 genes are in the largest connected component and therefore the network is fully connected (Fig. 1B). At approximately 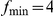 , the inferred network begins to break up and at
, the inferred network begins to break up and at 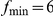 , the size of the largest connected component is substantially reduced and a number of isolated components exist. Thus,
, the size of the largest connected component is substantially reduced and a number of isolated components exist. Thus, 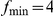 is approximately the critical value at which the network remains largely intact as one connected network. In the work below we consider networks inferred from
is approximately the critical value at which the network remains largely intact as one connected network. In the work below we consider networks inferred from 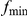 values of 2, 4 and 6. These values correspond to points on, and at either side of the critical threshold value. A list of the links in the network
values of 2, 4 and 6. These values correspond to points on, and at either side of the critical threshold value. A list of the links in the network 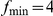 and
and 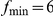 is given in Dataset S1.
is given in Dataset S1.
Figure 1. Distribution of gene relatedness and network size in the E. coli CLR network.
(A) Probability distribution of relatedness values, 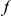 , between pairs of genes in E. coli calculated using the CLR algorithm and the full
, between pairs of genes in E. coli calculated using the CLR algorithm and the full  dataset. (B) Size of the largest connected component for relatedness value,
dataset. (B) Size of the largest connected component for relatedness value, 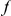 . At small values of
. At small values of  the network is fully connected but begins to break up into multiple disconnected components at a critical value of approximately
the network is fully connected but begins to break up into multiple disconnected components at a critical value of approximately 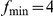 .
.
Identifying communities and their hierarchical organization
We used a recently developed extension of the leading eigenvalue method to determine the community structure of the inferred E. coli regulatory network [37]. This method aims to identify a partitioning of nodes into a disjoint set that maximizes network modularity. Modularity, 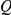 , is defined as the fraction of links that connect nodes in the same community minus the fraction expected if the partitioning and the degree sequence of the network remains fixed, but the links are randomly distributed [36]. This definition of modularity quantifies the intuitive notion that one expects there to be more links between nodes of the same community than between nodes of different communities, adding the constraint that the number of links inside a community should be larger than one would expect by chance. The definition is normalized so that the maximum possible value of
, is defined as the fraction of links that connect nodes in the same community minus the fraction expected if the partitioning and the degree sequence of the network remains fixed, but the links are randomly distributed [36]. This definition of modularity quantifies the intuitive notion that one expects there to be more links between nodes of the same community than between nodes of different communities, adding the constraint that the number of links inside a community should be larger than one would expect by chance. The definition is normalized so that the maximum possible value of 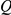 is 1. The larger the value of the modularity found by a partitioning, the more “modular” a network is. A completely nonmodular network would correspond to
is 1. The larger the value of the modularity found by a partitioning, the more “modular” a network is. A completely nonmodular network would correspond to 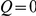 . The extension of the leading eigenvalue method that we use, known as final tuning, is an extra step in the algorithm, related to the so called Kernigan-Lin algorithm [47], that removes systematic biases and produces the best results of any known fast modularity maximizing algorithm for networks of the size considered here.
. The extension of the leading eigenvalue method that we use, known as final tuning, is an extra step in the algorithm, related to the so called Kernigan-Lin algorithm [47], that removes systematic biases and produces the best results of any known fast modularity maximizing algorithm for networks of the size considered here.
Community detection algorithms, including the one we use, contain stochastic elements that can cause different runs to give different partitionings. Indeed, partitionings of the same network can be structurally diverse, despite having similar modularity scores [41]. Here, we exploit this property, by analyzing an ensemble of partitionings and measuring their correlations. This allows us to both find the pairs of genes that are most often grouped together and examine the family of community structures that can result from a modularity maximization.
At a particular  value, which defines a unique network, we ran our community detection algorithm 10 times, generating a correlation matrix where each element represents the proportion of times gene
value, which defines a unique network, we ran our community detection algorithm 10 times, generating a correlation matrix where each element represents the proportion of times gene 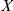 and gene
and gene 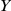 are found in the same community. We define sets of genes that are always found in the same community as a “core community”. We performed this procedure for
are found in the same community. We define sets of genes that are always found in the same community as a “core community”. We performed this procedure for 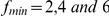 , which, as discussed above, give networks that are supercritical, critical, and subcritical, respectively. Combining the three resulting correlation matrices generates a visual representation of the overall structure of the network (Figure 2). A list of genes in each core community for
, which, as discussed above, give networks that are supercritical, critical, and subcritical, respectively. Combining the three resulting correlation matrices generates a visual representation of the overall structure of the network (Figure 2). A list of genes in each core community for 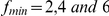 is given in Dataset S3. An alternative view of the hierarchical organization of the network, where each core community is represented as a node, is given in Figure S2.
is given in Dataset S3. An alternative view of the hierarchical organization of the network, where each core community is represented as a node, is given in Figure S2.
Figure 2. Correlation matrix showing community structure found in the E. coli network with relatedness threshold values  .
.
Genes are ordered in the same sequence along the x and y axes beginning in the upper left corner, and this ordering is the same for all three relatedness values (gene order is given in SI). The matrix element in the position 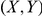 is colored blue, red, or green if genes
is colored blue, red, or green if genes 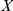 and
and 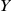 are in the same community at threshold values 2, 4 or 6, respectively. The density of the color indicates the strength of the correlation in the partitionings of the pair of genes. For example, considering the correlation between a pair of genes in the 10 replicate partitionings performed on the
are in the same community at threshold values 2, 4 or 6, respectively. The density of the color indicates the strength of the correlation in the partitionings of the pair of genes. For example, considering the correlation between a pair of genes in the 10 replicate partitionings performed on the 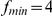 network, dark and light red indicates that the pair of genes are always and rarely found to be in the same community, respectively. The red, green and blue colors corresponding to
network, dark and light red indicates that the pair of genes are always and rarely found to be in the same community, respectively. The red, green and blue colors corresponding to 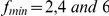 thresholds, respectively, are combined to indicate the correlations of each pair of genes at all three threshold values. Thus, the color of the matrix element in the position
thresholds, respectively, are combined to indicate the correlations of each pair of genes at all three threshold values. Thus, the color of the matrix element in the position 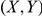 is white if genes
is white if genes 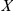 and
and 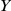 are in the same community at all three threshold values. It is purple (yellow) if the two genes are in the same community at thresholds 2 and 4 (4 and 6), but not at threshold 6 (2) and it is black if the two genes are not in the same community at any of the three threshold values. A list of the order of genes is given in Dataset S2. A full size version with each pixel representing a distinct pair of genes is given in Figure S1.
are in the same community at all three threshold values. It is purple (yellow) if the two genes are in the same community at thresholds 2 and 4 (4 and 6), but not at threshold 6 (2) and it is black if the two genes are not in the same community at any of the three threshold values. A list of the order of genes is given in Dataset S2. A full size version with each pixel representing a distinct pair of genes is given in Figure S1.
We find substantial differences in the community structure of the networks inferred at different 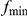 values (Figure 2). As
values (Figure 2). As 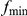 is increased, links that connect weakly related genes are removed from the network, which can cause genes to switch communities, and communities to merge or divide. Analysis of these changes lead to two conclusions. First, there is a basic community structure that is robustly determined such that many pairs of genes remain in the same community at all three
is increased, links that connect weakly related genes are removed from the network, which can cause genes to switch communities, and communities to merge or divide. Analysis of these changes lead to two conclusions. First, there is a basic community structure that is robustly determined such that many pairs of genes remain in the same community at all three 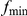 values, indicated by the block diagonal white elements. That is, there is a basic community structure that is invariant with respect to adding or subtracting links between weakly related genes. Second, community structure is hierarchical. To see this, note that at
values, indicated by the block diagonal white elements. That is, there is a basic community structure that is invariant with respect to adding or subtracting links between weakly related genes. Second, community structure is hierarchical. To see this, note that at 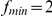 the community structure consists of six large communities, indicated by the blue blocks, while at higher values it begins to break up into smaller communities. More importantly, the relationship between communities at different
the community structure consists of six large communities, indicated by the blue blocks, while at higher values it begins to break up into smaller communities. More importantly, the relationship between communities at different 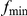 values indicates that the structure of the network is largely hierarchical. A hierarchical structure is revealed when a community breaks up into subcommunities as
values indicates that the structure of the network is largely hierarchical. A hierarchical structure is revealed when a community breaks up into subcommunities as 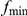 increases. If the E. coli regulatory network was completely hierarchical, we would see only block diagonal elements consisting of large blue blocks that break up into purple then white sub-blocks as
increases. If the E. coli regulatory network was completely hierarchical, we would see only block diagonal elements consisting of large blue blocks that break up into purple then white sub-blocks as 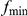 is increased. Communities at one value of
is increased. Communities at one value of 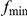 that are subcommunities of the same community at a smaller
that are subcommunities of the same community at a smaller 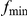 value are therefore hierarchically closer to each other than ones that remain in different communities at the smaller
value are therefore hierarchically closer to each other than ones that remain in different communities at the smaller 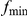 value. Figure 2 indicates that the inferred E. coli regulatory network has a largely but not completely hierarchical structure. This is apparent from the large fraction of the blue blocks (
value. Figure 2 indicates that the inferred E. coli regulatory network has a largely but not completely hierarchical structure. This is apparent from the large fraction of the blue blocks (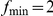 communities) that contain on diagonal purple and white blocks (
communities) that contain on diagonal purple and white blocks (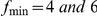 , respectively). However, there are some red off diagonal blocks that indicate a non-hierarchical ordering as
, respectively). However, there are some red off diagonal blocks that indicate a non-hierarchical ordering as 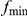 is increased from 2 to 4. Furthermore, although the purple
is increased from 2 to 4. Furthermore, although the purple 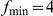 blocks largely break up into white blocks as
blocks largely break up into white blocks as 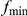 is increased to 6, there are some off diagonal cyan and green blocks that indicate non-hierarchical ordering. About 68% of the core community matrix elements at
is increased to 6, there are some off diagonal cyan and green blocks that indicate non-hierarchical ordering. About 68% of the core community matrix elements at 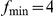 were hierarchically in core communities at
were hierarchically in core communities at 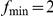 , and about 80% of the core community matrix elements at
, and about 80% of the core community matrix elements at 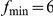 were hierarchically in core communities at
were hierarchically in core communities at 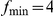 . The organization of genes shown in this plot, is given in Dataset S4, where the, blue, purple, and white module membership of each gene is listed.
. The organization of genes shown in this plot, is given in Dataset S4, where the, blue, purple, and white module membership of each gene is listed.
At 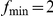 there are only six communities, while at
there are only six communities, while at 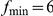 there is a mode of 965 communities with the largest consisting of 417 genes. This is consistent with the finding that at small values of
there is a mode of 965 communities with the largest consisting of 417 genes. This is consistent with the finding that at small values of 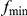 the network is fully connected, while at large values the network breaks up into a large number of small disconnected parts. At intermediate values of the threshold, where the network begins to break up, the community structure is complex, consisting of a broad distribution of different sized communities. Interestingly, as
the network is fully connected, while at large values the network breaks up into a large number of small disconnected parts. At intermediate values of the threshold, where the network begins to break up, the community structure is complex, consisting of a broad distribution of different sized communities. Interestingly, as 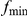 increases so does the value of the maximum modularity found,
increases so does the value of the maximum modularity found, 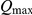 . At
. At 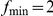 ,
, 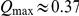 indicating that the network structure is not particularly modular, while at
indicating that the network structure is not particularly modular, while at 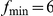 ,
, 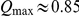 indicating that the network structure is highly modular.
indicating that the network structure is highly modular.
Community structure is robust to experimental noise
Given the relatively high experimental variation and low replication typical of gene expression measurements, it is of practical interest to determine whether inferred community structure is robust to this source of noise. To address this question, we consider a restricted set of the gene expression data comprising the 152 experiments present in the  database that were repeated at least three times. For each of these experiments, a mean value
database that were repeated at least three times. For each of these experiments, a mean value 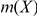 and a standard error
and a standard error 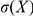 for the expression level of each gene
for the expression level of each gene  is calculated. These values are used to generate artificial datasets with a variable level of noise,
is calculated. These values are used to generate artificial datasets with a variable level of noise,  . For a value of
. For a value of 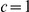 , the artificial data sets have noise levels consistent with the experimental data. For larger (smaller) values of
, the artificial data sets have noise levels consistent with the experimental data. For larger (smaller) values of  , the artificial datasets have more (less) variability in the expression of each gene, than the experimental data. For each of a number of values of
, the artificial datasets have more (less) variability in the expression of each gene, than the experimental data. For each of a number of values of  , ranging from 0 to 4, 20 artificial data sets are produced. Crucially, these data sets considered each gene and experiment independently, thereby preserving any inherent differences between different gene's expression variability.
, ranging from 0 to 4, 20 artificial data sets are produced. Crucially, these data sets considered each gene and experiment independently, thereby preserving any inherent differences between different gene's expression variability.
For each noisy data set, we used the CLR algorithm to infer a regulation network at an 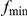 value of 2, and the community structure was determined with the methods described above. For each dataset, 10 different community partitionings were obtained, giving a total of 200 partititonings for each value of
value of 2, and the community structure was determined with the methods described above. For each dataset, 10 different community partitionings were obtained, giving a total of 200 partititonings for each value of  . Figure 3 shows a series of correlation matrix plots for the community structure found for the partitioning ensembles for
. Figure 3 shows a series of correlation matrix plots for the community structure found for the partitioning ensembles for 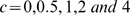 . The degree of noise clearly has a major impact on community structure. Nevertheless, except at
. The degree of noise clearly has a major impact on community structure. Nevertheless, except at 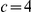 , there exist robustly determined core communities. In addition this analysis revealed two important results. First, as the noise level
, there exist robustly determined core communities. In addition this analysis revealed two important results. First, as the noise level  increased, a large proportion of the genes in a core community are partitioned into sub communities but genes rarely switch out of their
increased, a large proportion of the genes in a core community are partitioned into sub communities but genes rarely switch out of their 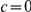 core communities. This is similar to what happens when the threshold value for creating the network was increased (Figure 2). Second, with one exception, the number of nodes included in each core community decreased as
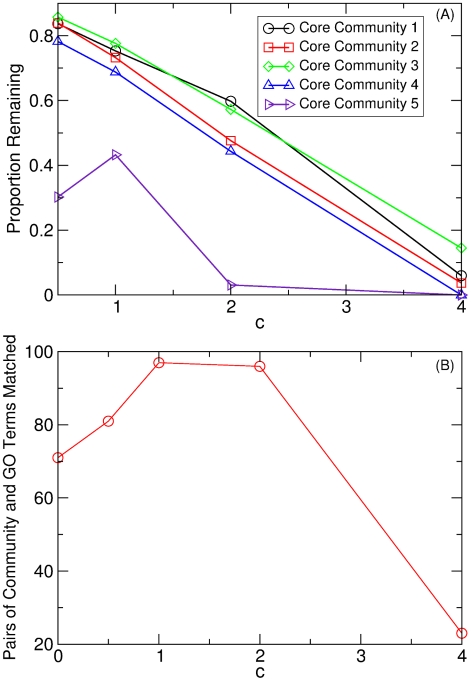
core communities. This is similar to what happens when the threshold value for creating the network was increased (Figure 2). Second, with one exception, the number of nodes included in each core community decreased as  was increased (Figure 4A). We conclude that noise acts mainly conservatively, decreasing the size of core communities, rather than causing association of genes into new communities.
was increased (Figure 4A). We conclude that noise acts mainly conservatively, decreasing the size of core communities, rather than causing association of genes into new communities.
Figure 3. Change in core community structure as noise is increased from 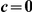 to
to 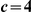 .
.
The grey scale value of each element indicates the fraction of times the two genes occurred in the same community over replicate community partitionings. If the element is white (black) the two genes were always (never) found in the same community. At each noise value there are clearly white diagonal blocks indicating sets of genes that are always found in the same community, which we refer to as core communities. Note that, the five core communities at 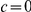 (Figure 3A) are in the same order in Figure 3:B, C, D, and E. Within each of the five core communities of Figure 3A, the node order is allowed to change in Figure 3:B, C, D, and E in order to display the largest subcommunity first. For each panel, he list of of the order of genes and the core community they belong to is given in Dataset S5 and Dataset S6, respectively. A full size version with each pixel representing a distinct pair of genes is included in Figure S3.
(Figure 3A) are in the same order in Figure 3:B, C, D, and E. Within each of the five core communities of Figure 3A, the node order is allowed to change in Figure 3:B, C, D, and E in order to display the largest subcommunity first. For each panel, he list of of the order of genes and the core community they belong to is given in Dataset S5 and Dataset S6, respectively. A full size version with each pixel representing a distinct pair of genes is included in Figure S3.
Figure 4. The effect of noise on core community structure and GO term enrichment.
(A) Proportion of 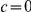 core community nodes that remain in a core community. (B) The number of significant GO term enrichments as a function of noise level
core community nodes that remain in a core community. (B) The number of significant GO term enrichments as a function of noise level  for networks constructed with
for networks constructed with 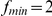 . If a GO term is enriched by more than one community, each enrichment is counted separately.
. If a GO term is enriched by more than one community, each enrichment is counted separately.
Communities enrich for functionally related genes
We have thus far demonstrated that our computational methods can robustly identify a community structure in the E. coli regulatory network. An important remaining question is whether this structure is biologically relevant. To test this, we first examined the simple expectation that genes in the same operon, and that therefore share at least one promoter control region, will tend to group together in the same community. Even using the very stringent requirement that all genes within an operon be in the same community and not accounting for the presence of secondary promoters that are internal to the operon and might act to decouple operon regulation, we find that genes within an operon are much more likely to group together that expected by chance (Permutation test, 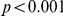 )(Figure S4). For example, given the number and size of communities found at
)(Figure S4). For example, given the number and size of communities found at 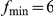 , approximately 1% of operons remain together if individual genes are assigned to communities randomly, compared to
, approximately 1% of operons remain together if individual genes are assigned to communities randomly, compared to 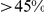 in the community assignments determined by the final tuning algorithm.
in the community assignments determined by the final tuning algorithm.
Next we asked whether the community structure inferred by our method groups genes with similar biological functions. To do this, we tested whether the identified communities significantly enrich for any of the gene ontology (GO) terms identified in E. coli
[48]–[50]. (Note only core communities larger than 10 were considered because the method we use to partition the network will not accurately identify small communities [51].) We found 147, 239 and 288 statistically significant matches between core communities and GO terms for communities identified at 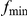 values of 2, 4 and 6, respectively. Table 1 details these results for the 25 most enriched relationships found at
values of 2, 4 and 6, respectively. Table 1 details these results for the 25 most enriched relationships found at 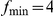 (complete tables of GO enrichments at
(complete tables of GO enrichments at 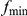 values of 2, 4 and 6, and GO terms used are given in Dataset S7 and Dataset S8, respectively). Note that many genes are described by multiple GO terms, e.g., the gene
values of 2, 4 and 6, and GO terms used are given in Dataset S7 and Dataset S8, respectively). Note that many genes are described by multiple GO terms, e.g., the gene 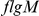 is a member of all terms in the GO hierarchy: ‘flagellin-based flagellum basal body, rod’
is a member of all terms in the GO hierarchy: ‘flagellin-based flagellum basal body, rod’ ‘flagellin-based flagellum’
‘flagellin-based flagellum’ ‘flagellum’ so not all enrichments are independent. Nevertheless, our network partitioning results in communities that significantly enrich for many GO terms, suggesting that the gene groupings are biologically meaningful.
‘flagellum’ so not all enrichments are independent. Nevertheless, our network partitioning results in communities that significantly enrich for many GO terms, suggesting that the gene groupings are biologically meaningful.
Table 1. The 25 most relevant relationships found for 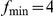 without noise.
without noise.
| P value | GO term num | Com size | GO size | In common | Description |
| 8.41e-42 | 9288 | 72 | 24 | 24 | bacterial-type flagellum |
| 9.57e-39 | 6826 | 53 | 37 | 25 | iron ion transport |
| 8.22e-38 | 1539 | 72 | 28 | 24 | ciliary or flagellar motility |
| 3.67e-35 | 6412 | 826 | 101 | 79 | translation |
| 6.51e-34 | 3735 | 826 | 56 | 54 | structural constituent of ribosome |
| 3.08e-31 | 3723 | 826 | 105 | 77 | RNA binding |
| 1.73e-29 | 6935 | 72 | 22 | 19 | chemotaxis |
| 4.30e-29 | 3774 | 72 | 17 | 17 | motor activity |
| 5.38e-29 | 9425 | 72 | 17 | 17 | bacterial-type flagellum basal body |
| 2.06e-25 | 19861 | 72 | 15 | 15 | flagellum |
| 5.61e-25 | 5506 | 53 | 210 | 31 | iron ion binding |
| 3.72e-24 | 19843 | 826 | 42 | 40 | rRNA binding |
| 6.98e-23 | 6811 | 53 | 79 | 22 | ion transport |
| 6.99e-22 | 30529 | 826 | 36 | 35 | ribonucleoprotein complex |
| 1.72e-21 | 5840 | 826 | 38 | 36 | ribosome |
| 6.62e-21 | 8652 | 247 | 62 | 32 | cellular amino acid biosynthetic process |
| 4.11e-17 | 5506 | 139 | 210 | 39 | iron ion binding |
| 6.66e-16 | 9055 | 139 | 116 | 29 | electron carrier activity |
| 7.30e-15 | 51539 | 139 | 98 | 26 | 4 iron, 4 sulfur cluster binding |
| 8.22e-15 | 15453 | 300 | 15 | 15 | oxidoreduction-driven active transmembrane transporter activity light-driven active transmembrane transporter activity |
| 1.85e-13 | 6865 | 247 | 70 | 27 | amino acid transport |
| 6.13e-13 | 45272 | 300 | 13 | 13 | plasma membrane respiratory chain complex I |
| 9.19e-13 | 30964 | 300 | 13 | 13 | NADH dehydrogenase complex |
| 1.97e-12 | 9060 | 300 | 21 | 16 | aerobic respiration |
| 2.15e-12 | 5515 | 826 | 875 | 251 | protein binding calmodulin binding |
The “P value” or random probability, calculated with a hypergeometric test with Benjamini-Hochberg correction, of the common occurrence, or overlap, of genes in an inferred community and in a GO term for the 25 most statistically relevant relationships are listed. Also listed are the “GO term num” that distinguishes the GO term and its “Description” in the GO database, the number of genes in the GO term “GO size”, the number of genes in the inferred community “Com size”, and the number of genes they have in common “In common.” The complete set of the 239 relevant relationships found for 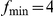 , as well as the relevant relationships found for
, as well as the relevant relationships found for 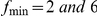 , are given in Dataset S7.
, are given in Dataset S7.
Figure 4B shows the number of statistically significant GO term enrichments as a function of noise level,  . Interestingly, enrichment peaks at a noise level of
. Interestingly, enrichment peaks at a noise level of 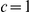 , which corresponds to the artificial data with noise level consistent with that of the experimental data. This is presumably due to the fact that the mean expression values found from the experimental data are estimates, so that a noise value of
, which corresponds to the artificial data with noise level consistent with that of the experimental data. This is presumably due to the fact that the mean expression values found from the experimental data are estimates, so that a noise value of  will give a precise, but not necessarily accurate estimate of gene expression. As discussed above, increasing the noise in the artificial datasets causes the size of the core communities to decrease. Interestingly, the
will give a precise, but not necessarily accurate estimate of gene expression. As discussed above, increasing the noise in the artificial datasets causes the size of the core communities to decrease. Interestingly, the 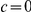 core community that dissolves the quickest, core community 5 (numbered beginning in the upper left hand corner of Figure 3A), contributes only one significant GO term enrichment at
core community that dissolves the quickest, core community 5 (numbered beginning in the upper left hand corner of Figure 3A), contributes only one significant GO term enrichment at 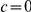 (full details in Dataset S9). Finally, we note that there are some differences in the identity of core communities when the restricted set of 152 experiments is compared to those generated using the full experimental data (at
(full details in Dataset S9). Finally, we note that there are some differences in the identity of core communities when the restricted set of 152 experiments is compared to those generated using the full experimental data (at 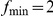 ). Nevertheless, as mentioned in Ref. [3], the CLR algorithm can produce nearly equivalent results as the full data set when a small, yet diverse set of expression profiles is chosen. This fact highlights the importance of judiciously choosing experimental conditions when the data set is small.
). Nevertheless, as mentioned in Ref. [3], the CLR algorithm can produce nearly equivalent results as the full data set when a small, yet diverse set of expression profiles is chosen. This fact highlights the importance of judiciously choosing experimental conditions when the data set is small.
Inferring candidate regulatory interactions
Partitioning of regulatory networks into communities of genes with similar responses to genetic and environmental perturbations can be used to identify candidate new regulatory interactions between genes. To this end, we consider the communities that most significantly enriched for a GO Term at 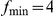 and
and 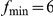 , and compare the relatedness network among the genes within each community to the subnetwork of known regulatory interactions involving these genes presented in RegulonDB. We stress, however, that what follows are simply two examples. Our results, given in the supporting information, contain a wealth of other gene communities whose interactions can be analyzed in a similar manner.
, and compare the relatedness network among the genes within each community to the subnetwork of known regulatory interactions involving these genes presented in RegulonDB. We stress, however, that what follows are simply two examples. Our results, given in the supporting information, contain a wealth of other gene communities whose interactions can be analyzed in a similar manner.
The community with the most significant GO term enrichment at 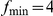 contains 72 genes, including all 24 genes in the GO term for bacterial-type flagellum (Table S1). Because of their co-regulation, the remaining 48 genes in this community are implicated as having some relevance for the development, function or control of the E. coli flagellum. Indeed, of these genes, many have recognized roles in environmental sensing and signal transduction, functions that are physiologically upstream of flagellum control. An additional 11 genes in the community do not have any annotated function, but two of them, ycgR and yhjH, contain domains that are consistent with flagellum related activity and five of them (yjdA yjdZ ynjH ycgR and yhjH) are annotated as being regulated by at least one of the two characterized regulators present in the community (flhDC and the flagellum sigma factor, fliA) [46], [52]. One further unannotated gene, ymdA, is connected to flhDC only in the CLR network, and is therefore a candidate for being connected to flagellum regulation as well as having a role in flagellum function. The pattern of connections in this community also serves to highlight the difference between the RegulonDB (direct regulatory links) and CLR (co-regulation) networks. We identify ten operons that interact with FlhDC in the CLR but not the RegulonDB network. These interactions might represent previously unknown direct interactions, but are probably best explained as indirect interactions mediated through their direct regulation by FliA, which is regulated by FlhDC (Figure S5).
contains 72 genes, including all 24 genes in the GO term for bacterial-type flagellum (Table S1). Because of their co-regulation, the remaining 48 genes in this community are implicated as having some relevance for the development, function or control of the E. coli flagellum. Indeed, of these genes, many have recognized roles in environmental sensing and signal transduction, functions that are physiologically upstream of flagellum control. An additional 11 genes in the community do not have any annotated function, but two of them, ycgR and yhjH, contain domains that are consistent with flagellum related activity and five of them (yjdA yjdZ ynjH ycgR and yhjH) are annotated as being regulated by at least one of the two characterized regulators present in the community (flhDC and the flagellum sigma factor, fliA) [46], [52]. One further unannotated gene, ymdA, is connected to flhDC only in the CLR network, and is therefore a candidate for being connected to flagellum regulation as well as having a role in flagellum function. The pattern of connections in this community also serves to highlight the difference between the RegulonDB (direct regulatory links) and CLR (co-regulation) networks. We identify ten operons that interact with FlhDC in the CLR but not the RegulonDB network. These interactions might represent previously unknown direct interactions, but are probably best explained as indirect interactions mediated through their direct regulation by FliA, which is regulated by FlhDC (Figure S5).
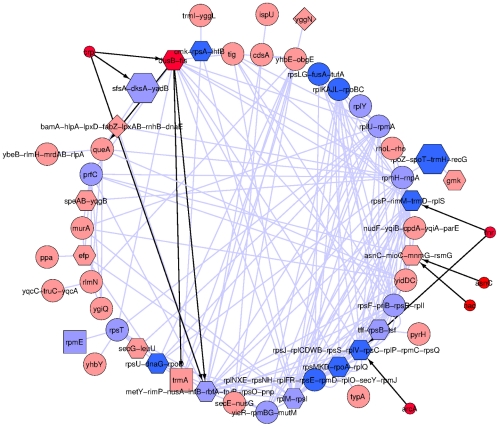
At 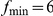 the community with the most significant functional enrichment contains 107 genes, including 51 of 56 genes annotated as being structural components of the ribosome (Table 2). This very significant enrichment suggests that the 15 genes present in the community that do not have any annotated function might also be involved in translational processes. The most striking aspect of this community, however, is that it contains only one recognized regulator, fis, which, as annotated in the regulonDB database, is involved in only a very small fraction of the inferred regulatory interactions (Figure 5). Moreover, no recognized transcription factor serves to indirectly connect regulation of more than three of the community operons and no sigma factor is unique to this community. These observations suggest the presence of some other regulatory factor that is in common to some or all of the genes in the community. One candidate for this factor is ppGpp, a small molecule which, in association with DskA, is known to affect regulation of many ribosome associated genes by decreasing the stability of the RNA polymerase open complex [53]. Indeed, a recent study directly examined the effect of ppGpp on nine of the 51 primary promoters present in the community. In all cases, ppGpp was shown to affect promoter activity in at least one of the tested conditions and a comparison of global gene expression profiles of bacteria that differed in ppGpp levels, found that a further twelve promoters in the community differed in expression by at least 2-fold in response to ppGpp [54], [55]. Together, these results suggest the remaining 30 promoters in the community as candidates to also be affected by ppGpp.
the community with the most significant functional enrichment contains 107 genes, including 51 of 56 genes annotated as being structural components of the ribosome (Table 2). This very significant enrichment suggests that the 15 genes present in the community that do not have any annotated function might also be involved in translational processes. The most striking aspect of this community, however, is that it contains only one recognized regulator, fis, which, as annotated in the regulonDB database, is involved in only a very small fraction of the inferred regulatory interactions (Figure 5). Moreover, no recognized transcription factor serves to indirectly connect regulation of more than three of the community operons and no sigma factor is unique to this community. These observations suggest the presence of some other regulatory factor that is in common to some or all of the genes in the community. One candidate for this factor is ppGpp, a small molecule which, in association with DskA, is known to affect regulation of many ribosome associated genes by decreasing the stability of the RNA polymerase open complex [53]. Indeed, a recent study directly examined the effect of ppGpp on nine of the 51 primary promoters present in the community. In all cases, ppGpp was shown to affect promoter activity in at least one of the tested conditions and a comparison of global gene expression profiles of bacteria that differed in ppGpp levels, found that a further twelve promoters in the community differed in expression by at least 2-fold in response to ppGpp [54], [55]. Together, these results suggest the remaining 30 promoters in the community as candidates to also be affected by ppGpp.
Table 2. Genes in the community at 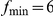 that enriches GO:3735 structural constituent of ribosome.
that enriches GO:3735 structural constituent of ribosome.
| Genes in the GO Term | Genes not in GO Term |
| rplA, rplB, rplC, rplD, rplE, rplF, rplI, rplJ, rplK, rplL, rplM, rplN, rplO, rplP, rplQ, rplR, rplS, rplU, rplV, rplW, rplX, rplY, | cdsA, cmk, dnaG, dusB, efp, fis, fusA, gidB, gmk, infB, ispU, lpxB, mnmG, mrdA, murA, nusA, nusG, obgE, parE, |
| rpmA, rpmB, rpmC, rpmD, rpmE, rpmG, rpmH, rpmJ, rpsA, rpsB, rpsC, rpsD, rpsE, rpsF, rpsG, rpsH, rpsI, rpsJ, rpsK, | ppa, prfC, priB, pyrH, queA, rbfA, rho, rimM, rlmN, rnhB, rnpA, rpoA, rpoZ, secE, secG, secY, speA, speB, tff, tig, |
| rpsL, rpsM, rpsN, rpsO, rpsP, rpsQ, rpsR, rpsS, rpsT, rpsU, | trmA, trmD, trmI, truB, truC, tsf, typA, yadB, yggN, ygiQ, yhbC, yhbE, yhbY, yidC, yidD, yqcC |
Figure 5. Links connecting operons in the 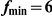 community that enriches for genes involved in ribosome structure.
community that enriches for genes involved in ribosome structure.
CLR links are in light blue, RegulonDB links are in black. Small symbols are genes that are not in the community, but are regulators of genes that are in the community and are therefore candidates for mediating indirect interactions between community genes. Symbol shape and color indicate attributes as follows: red, transcription factors; dark blue, ppGpp regulated promoter by direct assay [54]; light blue, ppGpp regulated translation related promoter by microarray [55]; pink, other; hexagon, 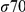 promoter; diamond,
promoter; diamond, 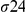 promoter; square,
promoter; square, 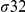 promoter; circle, unknown sigma factor. Note that very few interactions observed in the CLR network can be explained by the direct interactions annotated in RegulonDB. The high proportion of ppGpp sensitive promoters among operons contained in the community suggests this molecule as a good candidate for regulating the remaining interactions. The network layout was determined by the circular layout option in Cytoscape 2.8.1, no particular significance should be attached to operons being outside the main circle.
promoter; circle, unknown sigma factor. Note that very few interactions observed in the CLR network can be explained by the direct interactions annotated in RegulonDB. The high proportion of ppGpp sensitive promoters among operons contained in the community suggests this molecule as a good candidate for regulating the remaining interactions. The network layout was determined by the circular layout option in Cytoscape 2.8.1, no particular significance should be attached to operons being outside the main circle.
Discussion
We present unsupervised methods for determining communities of co-regulated genes and their hierarchical organization based on expression data profiles collected under a variety of environmental and genetic perturbations. Our methods combine the CLR algorithm and a tunable threshold value to infer the underlying regulatory network. We then use a statistical ensemble analysis of the network partitionings that result from a recently developed community detection algorithm to determine the network's community structure. Applying our method to E. coli expression data we obtain three key results. i). Regulatory communities in E. coli are largely hierarchical so that the effect of increasing (decreasing) the 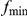 threshold is largely simply to split (combine) the communities found. ii) The structure of the inferred regulatory network is robust to relatively high experimental noise. iii) Regulatory communities significantly enrich for functionally related gene groupings. We discuss these findings in turn.
threshold is largely simply to split (combine) the communities found. ii) The structure of the inferred regulatory network is robust to relatively high experimental noise. iii) Regulatory communities significantly enrich for functionally related gene groupings. We discuss these findings in turn.
The technique we use applies a threshold to determine whether mutual information between the expression responses of two genes is sufficient to infer a connecting regulatory link. We find that the value of this threshold influences the size and unity of the inferred network. However, the network structure is relatively invariant to the addition or removal of links between more weakly related genes. We note that there at least two broad mechanisms that might cause genes to be weakly connected in our network. First, the relevant molecular interactions may exert weak expression control on the regulated gene. Second, the regulatory interactions might be environmentally dependent, being active in only a subset of the experimental conditions. Comparison of communities present in regulatory networks obtained at increasingly stringent thresholds indicates that the regulatory network is largely hierarchical such that large communities present in the low threshold network tended to split into smaller sub-groups of strongly related genes as the threshold was increased. By contrast, increasing the threshold causes relatively few genes to associate in new communities that were not subsets of the original communities.
Relatively high experimental noise is of considerable concern in analysis of gene expression data. Indeed, even small differences in preparation and sample growth conditions, or in the exact platform and analysis procedure used, can manifest as substantial differences in gene expression estimates [42]–[44], [56]. To address the influence of experimental noise on our ability identify regulatory interactions and communities, we generate datasets with different noise levels, calculated independently across experiments and genes. Comparing communities identified in networks inferred from these data sets, we find that not only are our predictions for the functional communities robust against noise up to double that seen in the original empirical dataset, but that the effects of experimental noise are mainly conservative. That is, experimental noise reduces the size of core regulatory communities but does not tend to create new communities.
For the purpose of identifying functional communities in a biological network, we find that it is useful to study the community structure of different networks constructed with a range of relatedness threshold values. At large threshold values, the nodes in each of the small disconnected pieces are highly related. These small groups provide the most statistically significant enrichments for GO terms and thus best identify biologically relevant communities. However, as the threshold value used to construct a network is reduced, the community sizes tend to increase. These enlarged communities include other nodes that may also be relevantly related to the core communities found at higher threshold values. Because of these competing considerations, if only one threshold value is to be chosen for which to make biological comparisons, we suggest that the critical threshold value should be used, which for E. coli is approximately 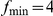 . Choosing the critical value will not only balance the above two considerations, but as discussed earlier, also gives the most statistically complex distribution of community structure.
. Choosing the critical value will not only balance the above two considerations, but as discussed earlier, also gives the most statistically complex distribution of community structure.
The usefulness of our methods are multifold. First, the functional community predictions of the methods can be used to refine existing knowledge of the functional relationships of genes in well known organisms such as E. coli. That is, the overlap of the core communities we find to the E. coli GO Terms is not exact, suggesting that the additional genes in our core communities that enrich a particular GO term may themselves be candidates for genes that should be included in that term of the gene ontology. In this way, the predictions of our method can be used to suggest new experiments to refine our understanding of the E. coli regulatory system. We have explicitly demonstrated how this can be done by analyzing two of the communities found with our methods that significantly enrich GO terms and predicting previously unknown regulatory interactions. Furthermore our methods can readily be applied to expression data for other, less well studied, organisms, and to other types of biological data, to identify functional communities in their networks. The predictions from our unsupervised methods will be particularly useful, for making initial approximate predictions for the functional communities and their organization of less well known organisms. Additionally, it should be noted that we have applied our methods to expression data based on an arbitrary variety of experimental and genetic perturbations. However, the methods could instead be applied to more targeted sets of expression data. For example, data based on particular types of environmental perturbations, particular types of genetic knockouts, with cells in a particular stage of the cell cycle, or with cells in a particular developmental stage of a multi-cellular organism. By examining more targeted data of these sorts, the dynamics of particular functional communities can be explored.
Methods
The expression data analyzed
We analyze E. coli expression data downloaded from the Many Microbe Microarrays Database ( ) version 4, build 5 [45]. This build consists of a compendium of expression profiles from 730 different experiments reporting expression of 4,298 E. coli MG1655 genes. These experiments report the effect on gene expression of 380 different perturbations, of which 152 were repeated at least three times. Experiments include environmental perturbations such as PH levels, growth phase, presence of antibiotics, temperature, growth media and oxygen concentration, as well as genetic perturbations. For each gene the data from the various experiments were normalized to account for varying detection efficiencies and differences in labeling. The values then reported are the
) version 4, build 5 [45]. This build consists of a compendium of expression profiles from 730 different experiments reporting expression of 4,298 E. coli MG1655 genes. These experiments report the effect on gene expression of 380 different perturbations, of which 152 were repeated at least three times. Experiments include environmental perturbations such as PH levels, growth phase, presence of antibiotics, temperature, growth media and oxygen concentration, as well as genetic perturbations. For each gene the data from the various experiments were normalized to account for varying detection efficiencies and differences in labeling. The values then reported are the 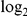 of the normalized expression intensity.
of the normalized expression intensity.
The context likelihood of relatedness method
To identify interactions between genes we apply the context likelihood of relatedness (CLR) algorithm [3]. Generally, network inference is difficult because of bias from uneven condition sampling, upstream regulation, and inter-laboratory variations in microarray results. The CLR algorithm attempts to mitigate these difficulties by increasing the contrast between the physical interactions and the indirect relationships by taking the context of each interaction and relationship into account. Links are assigned based on the mutual information in gene expression patterns, which, unlike simple correlation methods, can accommodate non-linear relationships between pair-wise gene expression patterns. Although some other algorithms offer higher precision in terms of recovering known regulatory links [57], CLR is attractive for allowing identification of indirect links that might serve to strengthen relationships between genes within co-regulated communities. We note, however, two limitations of networks derived from the underlying data set and CLR approach we use. First, the expression experiments are not considered as time series, which could give information as to the direction of regulatory interactions [58]. Second, we do not consider combinatorial regulatory interactions, for example, in which two or more regulator genes must be active to regulate a target gene.
Our implementation of the CLR algorithm begins by calculating the mutual information in the expression data for each pair of genes. This is done by treating the data for each gene as a discrete random variable, so that every pair of genes 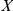 and
and 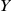 is assumed to have expression levels
is assumed to have expression levels 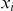 and
and 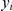 for each experiment
for each experiment 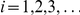 . The mutual information
. The mutual information 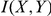 in the expression of
in the expression of 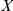 and
and 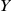 is
is
| (1) |
where 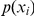 and
and 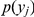 are the marginal probability distributions that the expression level of
are the marginal probability distributions that the expression level of 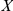 is
is 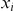 and of
and of 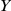 is
is 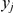 , respectively, and
, respectively, and 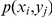 is the joint probability distribution that, simultaneously, the expression levels of
is the joint probability distribution that, simultaneously, the expression levels of 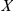 and
and 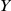 are
are 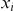 and
and 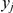 , respectively. These discrete probability distributions are calculated from the continuous expression data using B-spline smoothing and discretization. Rather than assign an expression value to one bin, as in classical binning, the B-spline functions allow an expression value to be assigned to multiple bins to account for fluctuations in biological and measurement noise. This is sometimes referred to as “fuzzy binning” [59]. For
, respectively. These discrete probability distributions are calculated from the continuous expression data using B-spline smoothing and discretization. Rather than assign an expression value to one bin, as in classical binning, the B-spline functions allow an expression value to be assigned to multiple bins to account for fluctuations in biological and measurement noise. This is sometimes referred to as “fuzzy binning” [59]. For 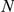 genes, this calculation results in an
genes, this calculation results in an 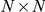 symmetric matrix of mutual information values. Here, to calculate the probability distributions for E. coli we use 10 discrete bins and a third-order B-spline function. The results do vary slightly if the number of bins used or the order of the B-spline function is changed. However, the results vary slowly with these parameters and do not change any of our principle conclusions.
symmetric matrix of mutual information values. Here, to calculate the probability distributions for E. coli we use 10 discrete bins and a third-order B-spline function. The results do vary slightly if the number of bins used or the order of the B-spline function is changed. However, the results vary slowly with these parameters and do not change any of our principle conclusions.
Mutual information between a gene pair can be due to random background effects, or a regulatory relationship. To distinguish the relevant mutual information from its background, the CLR algorithm compares each mutual information value 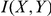 , to the distribution of the mutual information values between gene
, to the distribution of the mutual information values between gene 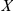 and all other genes
and all other genes 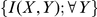 , and separately, to the distribution of the mutual information values between gene
, and separately, to the distribution of the mutual information values between gene 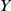 and all other genes
and all other genes 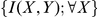 . The distributions are assumed to be normal and a Z-score value,
. The distributions are assumed to be normal and a Z-score value, 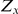 and
and 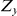 , is assigned to
, is assigned to 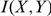 for distribution
for distribution 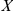 and
and  , respectively. The Z-score value of
, respectively. The Z-score value of 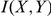 compared to a normal distribution
compared to a normal distribution  , with a mean
, with a mean  and standard deviation
and standard deviation 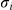 , is given by
, is given by
| (2) |
Any value of 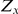 or
or 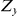 less than zero is set to zero. Finally, the relatedness value between gene
less than zero is set to zero. Finally, the relatedness value between gene 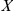 and gene
and gene 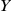 is defined as
is defined as
| (3) |
For 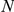 genes, this calculation results in an
genes, this calculation results in an 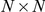 symmetric matrix of relatedness values.
symmetric matrix of relatedness values.
Once this matrix of relatedness values is calculated, we infer a network of regulatory interactions by placing links between every pair of genes whose relatedness value exceeds some threshold, 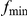 . For a given
. For a given 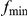 value, this procedure results in a defined interaction network. A list of the links in the network
value, this procedure results in a defined interaction network. A list of the links in the network 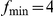 and
and 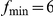 is given in Dataset S1.
is given in Dataset S1.
Network community detection methods
There are a number of different methods that can be used to determine the community structure of a given complex network [19]–[21], [29]–[31]. Here we use a method that aims to find a partitioning of nodes of the network into disjoint sets that maximizes the modularity of the network. Modularity is defined as the fraction of links that connect nodes in the same community minus the fraction expected if the partitioning and the degree sequence of the network remains fixed, but the links are randomly distributed [36]. Formally, for a network partitioning that assigns each node  to one member of a set of communities, the modularity
to one member of a set of communities, the modularity 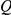 is
is
| (4) |
where 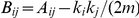 are the elements of the “modularity matrix” and
are the elements of the “modularity matrix” and 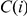 (
(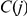 ) is the community to which node
) is the community to which node  (
(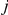 ) belongs. Here
) belongs. Here  is the total number of links in the network,
is the total number of links in the network, 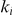 (
(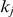 ) is the degree of node
) is the degree of node  (
(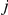 ),
), 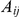 are the elements of the adjacency matrix, and
are the elements of the adjacency matrix, and 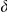 is the Kronecker delta function. The larger
is the Kronecker delta function. The larger 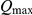 , the maximum value of
, the maximum value of 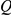 for all network partitionings, is for a network the more modular the network is. The largest possible value of
for all network partitionings, is for a network the more modular the network is. The largest possible value of 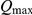 is one.
is one.
Unfortunately, finding the network partitioning that maximizes  is known to be an NP-hard problem and, thus, is computationally challenging [60]. In order to solve this problem, we use the leading eigenvalue method combined with final tuning [40]. Final tuning improves the approximate solution given by the leading eigenvalue method by removing constraints that bias the results. For widely studied example networks with up to a few thousand nodes, the size of the genetic network of E. coli used in our analysis, combining final tuning with the leading eigenvalue method has been demonstrated to produce network partitionings with the largest
is known to be an NP-hard problem and, thus, is computationally challenging [60]. In order to solve this problem, we use the leading eigenvalue method combined with final tuning [40]. Final tuning improves the approximate solution given by the leading eigenvalue method by removing constraints that bias the results. For widely studied example networks with up to a few thousand nodes, the size of the genetic network of E. coli used in our analysis, combining final tuning with the leading eigenvalue method has been demonstrated to produce network partitionings with the largest 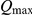 of any known method [40].
of any known method [40].
Creating artificial noisy datasets
To explore the effects of experimental noise we found the community structure in artificial datasets created to mimic the actual data with various levels of experimental noise. To generate these datasets, we first considered a restricted set of the actual data consisting of the 152 experiments that were repeated at least three times in the 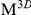 database. For each of the 152 experiments we calculated the mean
database. For each of the 152 experiments we calculated the mean 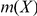 and standard error
and standard error 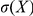 of the expression level of each gene
of the expression level of each gene 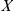 . Assuming a normal distribution of error, we then generated artificial data for an artificial experiment by randomly choosing a value for the expression of each gene
. Assuming a normal distribution of error, we then generated artificial data for an artificial experiment by randomly choosing a value for the expression of each gene 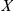 from a Gaussian distribution with mean
from a Gaussian distribution with mean 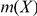 and standard deviation
and standard deviation 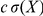 , where
, where  is a positive constant. The amount of noise in the artificial data can be adjusted by varying
is a positive constant. The amount of noise in the artificial data can be adjusted by varying  with
with 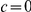 recreating the original data set. Artificial data sets were generated at values of
recreating the original data set. Artificial data sets were generated at values of  ranging from 0 to 4. For each value of
ranging from 0 to 4. For each value of  , ensembles of 20 different artificial data sets were constructed and then analyzed.
, ensembles of 20 different artificial data sets were constructed and then analyzed.
Statistical analysis of ensembles of network partitionings
As noted above, many community detection algorithms, including the one we use, are stochastic in nature and can give diverse partitionings that maximize Q between different runs. We account for this by studying statistical properties of the ensemble of partitionings that result from repeated application of the community detection algorithm. In particular, we study the correlations of the partitionings in the ensemble and produced matrix correlation plots that indicate the fraction of the pairs of partitionings for which pairs of genes are found to be in the same community. This ensemble analysis provides an understanding of the robustness of the community structure found. At the same time, it also provides information about the strength of the modular relationship between pairs of genes. Note that this ensemble analysis method, unlike usual modularity maximizing methods of community detection, allows for individual genes to be associated with more than one community. This is similar to information that can be obtained in, for example, clique [24] and core-periphery [26] community detection methods.
The gray scale plots of Figure 3 are the matrix correlation plots for the statistical ensemble analysis of the 200 partitionings constructed from the artificial noisy data for each noise value c. The grey scale of each matrix element in the plots corresponds to the fraction of pairs of partitionings in which the corresponding pairs of genes are found to be in the same community. Note that the order of genes used in a matrix correlation plot is arbitrary. However, by judiciously choosing an ordering, modular relationships become more apparent. The order of genes in Figure 3A is such that all of the genes in the largest core community are arbitrarily listed first, followed by a similar list of the genes in the second, third, fourth, and fifth largest core communities. Note that when 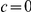 all genes are in one of the five core communities and therefore this list contains all genes. In Figure 3:B, C, D, and E, the genes in each of the 5 core communities at
all genes are in one of the five core communities and therefore this list contains all genes. In Figure 3:B, C, D, and E, the genes in each of the 5 core communities at 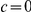 have been reordered, but the order of the genes with respect to these core communities has been preserved. That is, in each of these subfigures, all genes that are in the
have been reordered, but the order of the genes with respect to these core communities has been preserved. That is, in each of these subfigures, all genes that are in the 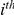 largest core community at
largest core community at 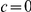 are always listed before any genes in the
are always listed before any genes in the 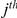 largest core community at
largest core community at 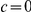 if
if 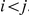 In each subfigure, the genes within a
In each subfigure, the genes within a 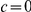 core community have been reordered such that the subset of those genes that comprise the largest core community at the
core community have been reordered such that the subset of those genes that comprise the largest core community at the  value corresponding to the subgraph are listed first, followed by those in the next largest such core community, etc. Until all genes within the
value corresponding to the subgraph are listed first, followed by those in the next largest such core community, etc. Until all genes within the 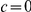 core community has been listed. Note that, some genes may be isolated in their own core community with this method. The list of the order of genes, for each subfigure, is given in Dataset S5.
core community has been listed. Note that, some genes may be isolated in their own core community with this method. The list of the order of genes, for each subfigure, is given in Dataset S5.
The multicolor matrix correlation plot of Figure 2 simultaneously shows the statistical correlations in the modular relationships between pairs of genes, in the full dataset, at supercritical, critical, and subcritical threshold values. First, single color, blue red and green, matrix correlation plots corresponding to 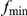 values of 2, 4, and 6, respectively, are created. The genes in each of these single color correlation plots are then simultaneously reordered as follows. First, the genes were ordered so that all of the genes in the same community at
values of 2, 4, and 6, respectively, are created. The genes in each of these single color correlation plots are then simultaneously reordered as follows. First, the genes were ordered so that all of the genes in the same community at 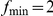 are listed together, according to the size of the community, beginning with the largest and ending with the smallest. Next, the genes in each of those communities are reordered such that the subset of those genes that comprise the largest community at
are listed together, according to the size of the community, beginning with the largest and ending with the smallest. Next, the genes in each of those communities are reordered such that the subset of those genes that comprise the largest community at 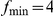 are listed first, followed by those in the next largest such community, etc. Until all genes within the
are listed first, followed by those in the next largest such community, etc. Until all genes within the  community have been listed. Then each of the genes within a
community have been listed. Then each of the genes within a 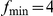 core community that are within an
core community that are within an 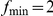 community are again reordered. The genes in each of those communities are reordered such that the subset of those genes that comprise the largest core community at
community are again reordered. The genes in each of those communities are reordered such that the subset of those genes that comprise the largest core community at 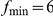 are listed first, followed by those in the next largest such community, etc. Until all genes within the
are listed first, followed by those in the next largest such community, etc. Until all genes within the  core community that are within an
core community that are within an 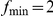 community have been listed. The resulting ordering of genes is given in the supplemental material. Finally, the three single color correlation plots are combined into the multicolor plot shown in Figure 2, where each matrix element of the resulting plot has an RGB color that simultaneously indicates its correlations in the modular structure at each of the three
community have been listed. The resulting ordering of genes is given in the supplemental material. Finally, the three single color correlation plots are combined into the multicolor plot shown in Figure 2, where each matrix element of the resulting plot has an RGB color that simultaneously indicates its correlations in the modular structure at each of the three 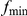 values. The list of the order of genes is given in Dataset S2.
values. The list of the order of genes is given in Dataset S2.
Hypergeometric tests
In order to establish the biological relevance of the functional communities found with our methods, we compare those functional communities to terms in the gene ontology, using a hypergeometric test with Benjamini-Hochberg correction. The hypergeometric test calculates the probability that a community of size  has
has 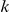 genes in common with a GO term of size
genes in common with a GO term of size  in a network with
in a network with 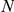 total genes. For random groupings this probability is
total genes. For random groupings this probability is
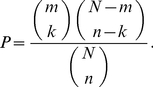 |
(5) |
If a community and a GO term are found to have an overlap that is unlikely to occur by chance (a low P value) then their relationship is likely to be relevant. Note that a low P value can occur if the number of genes in common, k, is either greater than or less than expected by chance. For a hypergeometric distribution the expected number of matches is given by 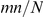 . We have reported only the “positive” enrichments for which
. We have reported only the “positive” enrichments for which 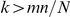 as relevant.
as relevant.
To control for false discoveries due to multiple comparisons, we correct the 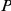 values obtained using Eq. 5 with the Benjamini-Hochberg (BH) procedure [61]. We implement the BH procedure as follows. For a given core community, the
values obtained using Eq. 5 with the Benjamini-Hochberg (BH) procedure [61]. We implement the BH procedure as follows. For a given core community, the 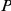 values obtained by comparing it to the
values obtained by comparing it to the 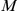 GO terms are ordered in a list such that they are increasing,
GO terms are ordered in a list such that they are increasing, 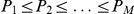 . The corrected
. The corrected 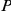 values are then taken to be
values are then taken to be 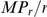 , where
, where  is the rank, or position on the ordered list, of the
is the rank, or position on the ordered list, of the  value. Then, as is commonly accepted, we judge the relationship between a community and a GO term to be relevant if their corrected
value. Then, as is commonly accepted, we judge the relationship between a community and a GO term to be relevant if their corrected  value is less than 0.05.
value is less than 0.05.
To account for the resolution limit of modularity optimization [51], only core communities of size 10 or larger are tested for biological relevance. The members of a GO term are restricted to the genes included in our data set.
Supporting Information
List of links in the
E. coli
CLR network at
 . The CLR algorithm is used to infer direct and indirect regulatory interactions between E. coli genes on the basis of the similarity of their expression response in 466 experiments. A matrix of relatedness values is calculated and a network of regulatory interactions is inferred by placing links between every pair of genes whose relatedness value exceeds some threshold,
. The CLR algorithm is used to infer direct and indirect regulatory interactions between E. coli genes on the basis of the similarity of their expression response in 466 experiments. A matrix of relatedness values is calculated and a network of regulatory interactions is inferred by placing links between every pair of genes whose relatedness value exceeds some threshold, 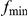 . A list of the links for the network at
. A list of the links for the network at 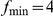 and
and 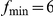 is provided. Each link is given by listing a gene name, the gene's Blattner number, followed by the target gene name and Blattner number.
is provided. Each link is given by listing a gene name, the gene's Blattner number, followed by the target gene name and Blattner number.
(XLS)
List of the order of genes in the correlation matrix plot. The multicolor matrix correlation plot simultaneously shows the statistical correlations in the modular relationships between pairs of genes, in the full dataset, at supercritical, critical, and subcritical threshold values. Each matrix element of the resulting plot has an RGB color that simultaneously indicates its correlations in the modular structure at each of the three 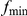 values. A list of the order of genes is given, by listing each gene name and Blattner number.
values. A list of the order of genes is given, by listing each gene name and Blattner number.
(XLS)
List of core community membership. At a particular 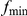 value, which defines a unique network, the community detection algorithm was run 10 times, generating a correlation matrix where each element represents the proportion of times gene
value, which defines a unique network, the community detection algorithm was run 10 times, generating a correlation matrix where each element represents the proportion of times gene 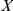 and gene
and gene 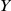 are found in the same community. Sets of genes that are always found in the same community is defined as a “core community”. For each
are found in the same community. Sets of genes that are always found in the same community is defined as a “core community”. For each 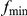 value, 2, 4 and 6, the gene name, Blattner number and core community number is given.
value, 2, 4 and 6, the gene name, Blattner number and core community number is given.
(XLS)
The hierarchical organization of the
E. coli
network. The relationship between communities at different 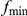 values indicates that the structure of the E. coli network is largely hierarchical. A hierarchical structure is revealed when a community breaks up into subcommunities as
values indicates that the structure of the E. coli network is largely hierarchical. A hierarchical structure is revealed when a community breaks up into subcommunities as 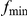 increases. Thus, if the E. coli regulatory network was completely hierarchical, one would see only block diagonal elements consisting of large blue blocks that break up into purple then white sub-blocks as
increases. Thus, if the E. coli regulatory network was completely hierarchical, one would see only block diagonal elements consisting of large blue blocks that break up into purple then white sub-blocks as 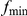 is increased. The hierarchical organization of genes is given, where the blue, purple, and white module membership of each gene is listed. The blue membership is listed first, numbered 1 through 6. The purple membership is listed next with the format x.y, where x is the blue membership and y is the purple membership. The purple membership is listed in the order a,b,c,d,….,z, aa, ab, …. Finally, the white membership is listed with format x.y.z, where x is the blue membership, y is the purple membership, and z is the white membership. The white membership is listed in numerical order.
is increased. The hierarchical organization of genes is given, where the blue, purple, and white module membership of each gene is listed. The blue membership is listed first, numbered 1 through 6. The purple membership is listed next with the format x.y, where x is the blue membership and y is the purple membership. The purple membership is listed in the order a,b,c,d,….,z, aa, ab, …. Finally, the white membership is listed with format x.y.z, where x is the blue membership, y is the purple membership, and z is the white membership. The white membership is listed in numerical order.
(XLS)
List of the order of genes in each noise correlation matrix plot. The gray scale plots of Figure 3 are the matrix correlation plots for the statistical ensemble analysis of the 200 partitionings constructed from the artificial noisy data for each noise value c. The grey scale of each matrix element in the plots corresponds to the fraction of pairs of partitionings in which the corresponding pairs of genes are found to be in the same community. For each noise value 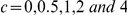 , each ordered gene name and Blattner number is listed.
, each ordered gene name and Blattner number is listed.
(XLS)
List of noise core community membership. For each noisy data set, the CLR algorithm is used to infer a regulation network at an 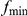 value of 2, and the community structure is determined with the methods described above. For each dataset, 10 different community partitionings are obtained, giving a total of 200 partititonings for each value of
value of 2, and the community structure is determined with the methods described above. For each dataset, 10 different community partitionings are obtained, giving a total of 200 partititonings for each value of  . Sets of genes that are always founds in the same community are defined as “core communities”. For each noise value
. Sets of genes that are always founds in the same community are defined as “core communities”. For each noise value 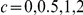 and
and 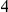 , a gene name and Blattner number, followed by its core community number is listed.
, a gene name and Blattner number, followed by its core community number is listed.
(XLS)
List of GO term enrichments. To determine whether the inferred community structure groups genes with similar biological functions, a test to determine whether the identified communities significantly enrich for any of the gene ontology (GO) terms identified in E. coli is performed. At each 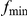 value, each significant enrichment is listed by giving it's corresponding p-value, GO term number, core community number, community size, GO term size, the number of genes in common, and the biological description of the GO term.
value, each significant enrichment is listed by giving it's corresponding p-value, GO term number, core community number, community size, GO term size, the number of genes in common, and the biological description of the GO term.
(XLS)
List of GO terms. To determine whether the inferred community structure groups genes with similar biological functions, a test to determine whether the identified communities significantly enrich for any of the gene ontology (GO) terms identified in E. coli is performed. To test for enrichment, genes were removed from each GO term that were not included in our dataset. For each resulting GO term, the gene name and Blattner number, followed by its GO term number is listed.
(XLS)
List of GO term enrichments at each noise value. To determine the effect of noise on GO term enrichment, at each noise value  , a test to determine whether the identified communities significantly enrich for any of the gene ontology (GO) terms identified in E. coli is performed. At each
, a test to determine whether the identified communities significantly enrich for any of the gene ontology (GO) terms identified in E. coli is performed. At each  value, each significant enrichment is listed by giving it's corresponding p-value, GO term number, core community number, community size, GO term size, the number of genes in common, and the biological description of the GO term.
value, each significant enrichment is listed by giving it's corresponding p-value, GO term number, core community number, community size, GO term size, the number of genes in common, and the biological description of the GO term.
(XLS)
Correlation matrix. Correlation matrix showing community structure found in the E. coli network with relatedness threshold values 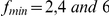 . Genes are ordered in the same sequence along the x and y axes beginning in the upper left corner, and this ordering is the same for all three relatedness values (gene order is given in SI). The matrix element in the position
. Genes are ordered in the same sequence along the x and y axes beginning in the upper left corner, and this ordering is the same for all three relatedness values (gene order is given in SI). The matrix element in the position 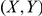 is colored blue, red, or green if genes
is colored blue, red, or green if genes 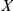 and
and 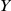 are in the same community at threshold values 2, 4 or 6, respectively. The density of the color indicates the strength of the correlation in the partitionings of the pair of genes. For example, considering the correlation between a pair of genes in the 10 replicate partitionings performed on the
are in the same community at threshold values 2, 4 or 6, respectively. The density of the color indicates the strength of the correlation in the partitionings of the pair of genes. For example, considering the correlation between a pair of genes in the 10 replicate partitionings performed on the 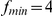 network, dark and light red indicates that the pair of genes are always and rarely found to be in the same community, respectively. The red, green and blue colors corresponding to
network, dark and light red indicates that the pair of genes are always and rarely found to be in the same community, respectively. The red, green and blue colors corresponding to 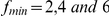 thresholds, respectively, are combined to indicate the correlations of each pair of genes at all three threshold values. Thus, the color of the matrix element in the position
thresholds, respectively, are combined to indicate the correlations of each pair of genes at all three threshold values. Thus, the color of the matrix element in the position 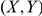 is white if genes
is white if genes 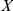 and
and 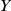 are in the same community at all three threshold values. It is purple (yellow) if the two genes are in the same community at thresholds 2 and 4 (4 and 6), but not at threshold 6 (2) and it is black if the two genes are not in the same community at any of the three threshold values. A list of the order of genes is given in Dataset S2.
are in the same community at all three threshold values. It is purple (yellow) if the two genes are in the same community at thresholds 2 and 4 (4 and 6), but not at threshold 6 (2) and it is black if the two genes are not in the same community at any of the three threshold values. A list of the order of genes is given in Dataset S2.
(TIF)
Core community hierarchy. An alternative view of the core community hierarchy where each core community is represented by a node. The node label x.y indicates the 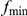 level, x, and core community number, y. The size of each node represents the number of genes in the community relative to communities at the same
level, x, and core community number, y. The size of each node represents the number of genes in the community relative to communities at the same 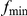 level. The edge width and color value indicate the proportion of the “daughter” community deriving from the connected “parent” community. For example, If all of the genes in a “daughter” community are from one “parent” community then there is one edge that is dark blue and thick. The nodes have been arranged to display the hierarchy of the network.
level. The edge width and color value indicate the proportion of the “daughter” community deriving from the connected “parent” community. For example, If all of the genes in a “daughter” community are from one “parent” community then there is one edge that is dark blue and thick. The nodes have been arranged to display the hierarchy of the network.
(EPS)
Noise correlation matrices. Change in core community structure as noise is increased from 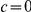 to
to 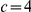 . The grey scale value of each element indicates the fraction of times the two genes occurred in the same community over replicate community partitionings. If the element is white (black) the two genes were always (never) found in the same community. At each noise value there are clearly white diagonal blocks indicating sets of genes that are always found in the same community, which we refer to as core communities. Note that, the five core communities at
. The grey scale value of each element indicates the fraction of times the two genes occurred in the same community over replicate community partitionings. If the element is white (black) the two genes were always (never) found in the same community. At each noise value there are clearly white diagonal blocks indicating sets of genes that are always found in the same community, which we refer to as core communities. Note that, the five core communities at 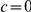 (Figure 3A) are in the same order in Figure 3:B, C, D, and E. Within each of the five core communities of Figure 3A, the node order is allowed to change in Figure 3:B, C, D, and E in order to display the largest subcommunity first. For each panel, he list of of the order of genes and the core community they belong to is given in Dataset S5 and Dataset S6, respectively.
(Figure 3A) are in the same order in Figure 3:B, C, D, and E. Within each of the five core communities of Figure 3A, the node order is allowed to change in Figure 3:B, C, D, and E in order to display the largest subcommunity first. For each panel, he list of of the order of genes and the core community they belong to is given in Dataset S5 and Dataset S6, respectively.
(TIF)
Operon by community. Fraction of E. coli operons that are retained whole in a single community. The fraction of 544 operons (comprising 2172 genes) identified in the E. coli genome where all genes in the operon were assigned to the same final tuning community was determined at  (indicated by arrows). These actual values were compared to 1000 random distributions of the same set of genes to empty community sets of the same size and number as were present in the final tuning partitionings (histograms). In all cases, actual operon retention proportions were much greater than in any of the 1000 randomly distributed sets, indicating that they were very unlikely to occur by chance and therefore that the final tuning community partitionings effectively group genes in the same operon to the same community.
(indicated by arrows). These actual values were compared to 1000 random distributions of the same set of genes to empty community sets of the same size and number as were present in the final tuning partitionings (histograms). In all cases, actual operon retention proportions were much greater than in any of the 1000 randomly distributed sets, indicating that they were very unlikely to occur by chance and therefore that the final tuning community partitionings effectively group genes in the same operon to the same community.
(EPS)
Regulatory links from
flhDC
and
fliA
in the
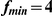 community that significantly enriches for flagellum associated genes. Genes are organized into operons as annotated by RegulonDB. Black, blue and red lines indicate regulatory interactions that are annotated in RegulonDB, inferred in the CLR network or both, respectively. For simplicity, only links from FlhDC and to targets of these links from fliA are shown. Many of the interactions that are found in the CLR network are not present in RegulonDB (blue lines). These interactions are candidates for indicating unrecognized regulatory interactions between FlhDC and the target genes. However, in most cases these interactions can be explained through the action of FlhDC on the sigma factor encoded by fliA (thick red line), which does directly affect all but one of the target genes. This point underlines the difference between the CLR network, which includes direct and indirect regulatory interactions, and the direct transcriptional network as annotated in RegulonDB. Note the CLR connection between FlhDC and the target gene ymdA cannot be explained through any known indirect interaction and is, therefore, a candidate for representing a new direct interaction.
community that significantly enriches for flagellum associated genes. Genes are organized into operons as annotated by RegulonDB. Black, blue and red lines indicate regulatory interactions that are annotated in RegulonDB, inferred in the CLR network or both, respectively. For simplicity, only links from FlhDC and to targets of these links from fliA are shown. Many of the interactions that are found in the CLR network are not present in RegulonDB (blue lines). These interactions are candidates for indicating unrecognized regulatory interactions between FlhDC and the target genes. However, in most cases these interactions can be explained through the action of FlhDC on the sigma factor encoded by fliA (thick red line), which does directly affect all but one of the target genes. This point underlines the difference between the CLR network, which includes direct and indirect regulatory interactions, and the direct transcriptional network as annotated in RegulonDB. Note the CLR connection between FlhDC and the target gene ymdA cannot be explained through any known indirect interaction and is, therefore, a candidate for representing a new direct interaction.
(EPS)
The community with the most significant GO term enrichment at
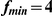 . The community with the most significant GO term enrichment at
. The community with the most significant GO term enrichment at 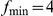 contains 72 genes, including all 24 genes in the GO term for bacterial-type flagellum. The remaining 48 genes in this community are implicated as having some relevance for the development, function or control of the E. coli flagellum.
contains 72 genes, including all 24 genes in the GO term for bacterial-type flagellum. The remaining 48 genes in this community are implicated as having some relevance for the development, function or control of the E. coli flagellum.
(XLS)
Acknowledgments
We are grateful to Gábor Balázsi, Bogdan Danila, Dan Graur, and Krešimir Josić for helpful discussions throughout this project.
Footnotes
The authors have declared that no competing interests exist.
The work of ST, YS, and KEB was supported by NSF grant number DMR-0908286. TFC was supported by NSF grant number IOS-1022373 and the Defense Advanced Research Projects Agency “Fun Bio” Program (HR0011-09-1-0055). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Balázsi G, Heath AP, Shi L, Gennaro ML. The temporal response of the Mycobacterium tuberculosis gene regulatory network during growth arrest. Mol Sys Biol. 2008;4:225. doi: 10.1038/msb.2008.63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Davidson EH, Rast JP, Oliveri P, Ransick A, Calestani C, et al. A genomic regulatory network for development. Science. 2002;295:1669–1678. doi: 10.1126/science.1069883. [DOI] [PubMed] [Google Scholar]
- 3.Faith JJ, Hayete B, Thaden JT, Mogno I, Wierzbowski J, et al. Large-scale mapping and validation of Escherichia coli transcriptional regulation from a compendium of expression profiles. PLoS Biol. 2007;5:e8. doi: 10.1371/journal.pbio.0050008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ma HW, Buer J, Zeng AP. Hierarchical structure and modules in the Escherichia coli transcriptional regulatory network revealed by a new top-down approach. BMC Bioinformatics. 2004;5:199. doi: 10.1186/1471-2105-5-199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cooper TF, Remold SK, Lenski RE, Schneider D. Expression profiles reveal parallel evolution of epistatic interactions involving the CRP regulon in Escherichia coli. PLoS Genetics. 2008;4:e35. doi: 10.1371/journal.pgen.0040035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Shi Z, Derrow C, Zhang B. Co-expression module analysis reveals biological processes, genomic gain, and regulatory mechanisms associated with breast cancer progression. BMC Sys Biol. 2010;4:74. doi: 10.1186/1752-0509-4-74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Segal E, Shapira M, Regev A, Pe'er D, Botstein D, et al. Module networks: identifying regulatory modules and their condition-specific regulators from gene expression data. Nat Genet. 2003;34:166–176. doi: 10.1038/ng1165. [DOI] [PubMed] [Google Scholar]
- 8.Bonnet E, Tatari M, Michoel A, Marchal K, Berx G, et al. Module network inference from a cancer gene expression data set identifies microRNA regulated modules. PLoS One. 2010;5:e10162. doi: 10.1371/journal.pone.0010162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Beyer A, Workman C, Hollunder J, Radke D, Moller U, et al. Integrated assessment and predication of transcription factor binding. PLoS Comp Biol. 2006;2:e70. doi: 10.1371/journal.pcbi.0020070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ravasz E, Somera AL, Mongru DA, Oltvai ZN, Barabási AL. Hierarchical organization of modularity in metabolic networks. Science. 2002;297:1551–1555. doi: 10.1126/science.1073374. [DOI] [PubMed] [Google Scholar]
- 11.Barabási AL, Oltvai ZN. Network biology: understanding the cell's functional organization. Nat Rev Genet. 2004;5:101. doi: 10.1038/nrg1272. [DOI] [PubMed] [Google Scholar]
- 12.Friedman N, Linial M, Pe'er D, Nachman I. Using bayesian networks to analyze expression data. J Comp Biol. 2000;7:601. doi: 10.1089/106652700750050961. [DOI] [PubMed] [Google Scholar]
- 13.Friedman N. Inferring cellular networks using probabilistic graphical models. Science. 2004;303:799–805. doi: 10.1126/science.1094068. [DOI] [PubMed] [Google Scholar]
- 14.Gardner TS, Bernardo D, Lorenz D, Mendes P. Inferring genetic networks and identifying compound mode of action via expression profiling. Science. 2003;301:102–105. doi: 10.1126/science.1081900. [DOI] [PubMed] [Google Scholar]
- 15.Veiga DFT, Dutta B, Balázsi G. Network inference and network response identification: moving genome-scale data to the next level of biological discovery. Mol BioSys. 2010;6:469–480. doi: 10.1039/b916989j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Getz G, Levine E, Domany E. Coupled two-way clustering analysis of gene microarray data. Proc Natl Acad Sci U S A. 2000;97:12079–12084. doi: 10.1073/pnas.210134797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Marbach D, Prill RJ, Schaffter T, Mattiussi C, Floreano D, et al. Revealing strengths and weaknesses of methods for gene network inference. Proc Natl Acad Sci U S A. 2010;107:6286–6291. doi: 10.1073/pnas.0913357107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Fortunato S. Community detection in graphs. Phys Rep. 2010;486:75–174. [Google Scholar]
- 19.Wen X, Fuhrman S, Michaels GS, Carr DB, Smith S, et al. Large-scale temporal gene expression mapping of central nervous system development. Proc Natl Acad Sci U S A. 1998;95:334. doi: 10.1073/pnas.95.1.334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Eisen MB, Spellman PT, Brown PO, Botstein D. Cluster analysis and display of genome-wide expression patterns. Proc Natl Acad Sci U S A. 1998;95:14863. doi: 10.1073/pnas.95.25.14863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Weinstein JN, Myers TG, O'Connor PM, Friend SH, Fornace AJ, et al. An information-intensive approach to the molecular pharmacology of cancer. Science. 1997;275:343. doi: 10.1126/science.275.5298.343. [DOI] [PubMed] [Google Scholar]
- 22.Seidman SB. Network structure and minimum degree. Soc Networks. 1983;5:269–287. [Google Scholar]
- 23.Seidman SB, Foster BL. A graph theoretic generalization of the clique concept. J Math Sociol. 1978;6:139–154. [Google Scholar]
- 24.Palla G, Derényi I, Farkas I, Vicsek T. Uncovering the overlapping community structure of complex networks in nature and society. Nature. 2005;435:814–818. doi: 10.1038/nature03607. [DOI] [PubMed] [Google Scholar]
- 25.Palla G, Barabási AL, Vicsek T. Quantifying social group evolution. Nature. 2007;446:664–667. doi: 10.1038/nature05670. [DOI] [PubMed] [Google Scholar]
- 26.Luo F, Li B, Wan XF, Scheuermann R. Core and periphery structures in protein interaction networks. BMC Bioinformatics. 2009;10:S8. doi: 10.1186/1471-2105-10-S4-S8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Borgatii SP, Everett MG. Models of core/periphery structures. Soc Networks. 1999;21:375–395. [Google Scholar]
- 28.Borgatii SP, Everett MG. Peripheries of cohesive subsets. Soc Networks. 1999;21:397–407. [Google Scholar]
- 29.Tavazoie S, Hughes JD, Campbell MJ, Cho RJ, Church GM. Systematic determination of genetic network architecture. Nat Genet. 1999;22:281. doi: 10.1038/10343. [DOI] [PubMed] [Google Scholar]
- 30.Raychaudhuri S, Stuart JM, Altman RB. Principal components analysis to summarize microarray experiments: application to sporulation time series. Pac Symp Biocomput. 2000;2000:455–456. doi: 10.1142/9789814447331_0043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Alter O, Brown P, Botstein D. Singular value decomposition for genome-wide expression data processing and modeling. Proc Natl Acad Sci U S A. 2000;97:10101. doi: 10.1073/pnas.97.18.10101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Raghavan UN, Albert R, Kumara S. Near linear time algorithm to detect community structures in large-scale networks. Phys Rev E. 2007;76:036106. doi: 10.1103/PhysRevE.76.036106. [DOI] [PubMed] [Google Scholar]
- 33.Lu Q, Korniss G, Szymanski B. The naming game in social networks: community formation and consensus engineering. Journal of Economic Interaction and Coordination. 2009;4:221–235. [Google Scholar]
- 34.Blatt M, Wiseman S, Domany E. Superparamagnetic clustering of data. Phys Rev Lett. 1996;76:3251–3254. doi: 10.1103/PhysRevLett.76.3251. [DOI] [PubMed] [Google Scholar]
- 35.Reichardt J, Bornholdt S. Detecting fuzzy community structures in complex networks with a potts model. Phys Rev Lett. 2004;93:218701. doi: 10.1103/PhysRevLett.93.218701. [DOI] [PubMed] [Google Scholar]
- 36.Newman MEJ, Girvan M. Finding and evaluating community structure in networks. Phys Rev E. 2004;69:026113. doi: 10.1103/PhysRevE.69.026113. [DOI] [PubMed] [Google Scholar]
- 37.Newman MEJ. Modularity and community structure in networks. Proc Natl Acad Sci U S A. 2006;103:8577–8582. doi: 10.1073/pnas.0601602103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Guimerà R, Sales-Pardo M, Amaral LAN. Modularity from fluctuations in random graphs and complex networks. Phys Rev E. 2004;70:025101. doi: 10.1103/PhysRevE.70.025101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Duch J, Arenas A. Community detection in complex networks using extremal optimization. Phys Rev E. 2005;72:027104. doi: 10.1103/PhysRevE.72.027104. [DOI] [PubMed] [Google Scholar]
- 40.Sun Y, Danila B, Josić K, Bassler KE. Improved community structure detection using a modified fine-tuning strategy. EPL (Europhysics Letters) 2009;86:28004. [Google Scholar]
- 41.Good BH, de Montijoyve YA, Clauset A. Performance of modularity maximization in practical contexts. Phys Rev E. 2010;81:046106. doi: 10.1103/PhysRevE.81.046106. [DOI] [PubMed] [Google Scholar]
- 42.Chen J, Hsueh HM, Delongchamp R, Lin CJ, Tsa CA. Reproducibility of microarray data: a further analysis of microarray quality control (MAQC) data. BMC Bioinformatics. 2007;8:412. doi: 10.1186/1471-2105-8-412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Baggerly K, Coombes K, Neeley E. Run batch effects potentially compromise the usefulness of genomic signatures for ovarian cancer. J Clin Oncology. 2008;26:1186–1187. doi: 10.1200/JCO.2007.15.1951. [DOI] [PubMed] [Google Scholar]
- 44.Duewer D, Jones W, Reid L, Salit M. Learning from microarray interlaboratory studies: measures of precision for gene expression. BMC Genet. 2009;10:153. doi: 10.1186/1471-2164-10-153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Faith JJ, Driscoll ME, Fusaro VA, Cosgrove EJ, Hayete B, et al. Many microbe microarrays database: uniformly normalized affymetrix compendia with structured experimental metadata. Nucleic Acids Res. 2008;36:D866. doi: 10.1093/nar/gkm815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Gama-Castro S, Salgado H, Peralta-Gil M, Santos-Zavaleta A, Muiz-Rascado L, et al. RegulonDB version 7.0: transcriptional regulation of Escherichia coli K-12 integrated within genetic sensory response units (gensor units). Nucleic Acids Res. 2010;39:D98–105. doi: 10.1093/nar/gkq1110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kernighan BW, Lin S. An efficient heuristic procedure for partitioning graphs. Bell Systems Technical Journal. 1970;49:291. [Google Scholar]
- 48.GO-Consortium. Gene Ontology: tool for the unification of biology. Nat Genet. 2000;25:25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Karp PD, Riley M, Saier M, Paulsen IT, Collado-Vides J, et al. The EcoCyc database. Nucleic Acids Res. 2002;28:56–58. doi: 10.1093/nar/30.1.56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Hubble J, Demeter J, Jin H, Mao M, Nitzberg M, et al. Implementation of genepattern within the stanford microarray database. Nucleic Acids Res. 2009;37(Database Issue):D898–901. doi: 10.1093/nar/gkn786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Fortunato S, Barthélemy M. Resolution limit in community detection. Proc Natl Acad Sci U S A. 2007;104:36–41. doi: 10.1073/pnas.0605965104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Riley M, Abe T, Arnaud MB, Berlyn MK, Blattner FR, et al. Escherichia coli k-12: a cooperatively developed annotation snapshot2005. Nucleic Acids Res. 2006;34:1–9. doi: 10.1093/nar/gkj405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Barker MM, Gaal T, Josaitis CA, Gourse RL. Mechanism of regulation of transcription initiation by ppGpp. i. effects of ppGpp on transcription initiation in vivo and in vitro. J Mol Biol. 2001;305:673–688. doi: 10.1006/jmbi.2000.4327. [DOI] [PubMed] [Google Scholar]
- 54.Lemke J, Sanchez-Vazquez P, Burgos H, Hedberg G, Ross W, et al. Direct regulation of Escherichia coli ribosomal protein promoters by the transcription factors ppGpp and DskA. Proc Natl Acad Sci U S A. 2011;108:5712–5717. doi: 10.1073/pnas.1019383108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Traxler MF, Summers SM, Nguyen HT, Zacharia VM, Hightower GA, et al. The global, ppGpp-mediated stringent response to amino acid starvation in Escherichia coli. Mol Microbiol. 2008;68:1128–1148. doi: 10.1111/j.1365-2958.2008.06229.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Irizarry RA, Warren D, Spencer F, Kim IF, Biswal S, et al. Multiple-laboratory comparison of microarray platforms. Nat Meth. 2005;2:345–349. doi: 10.1038/nmeth756. [DOI] [PubMed] [Google Scholar]
- 57.Zare H, Sangurdekar D, Srivastava P, Kaveh M, Khodursky A. Reconstruction of Escherichia coli transcriptional regulatory networks via regulon-based associations. Science. 2009;297:39. doi: 10.1186/1752-0509-3-39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Yeung KY, Dombek KM, Lo K, Mittler JE, Zhu J, et al. Construction of regulatory networks using expression time-series data of a genotyped population. Proc Natl Acad Sci U S A. 2011;108:19436–19441. doi: 10.1073/pnas.1116442108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Daub CO, Steuer R, Selbig J, Kloska S. Estimating mutual information using B-spline functions - an improved similarity measure for analyzing gene expression data. BMC Bioinformatics. 2004;5:118. doi: 10.1186/1471-2105-5-118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Brandes U, Delling D, Gaertler M, Goerke R, Hoefer M, et al. On modularity clustering. IEEE Trans Knowl Data Eng. 2008;20:172. [Google Scholar]
- 61.Benjamini Y, Hochberg Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J R Stat Soc B (Methodological) 1995;57:289–300. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
List of links in the
E. coli
CLR network at
 . The CLR algorithm is used to infer direct and indirect regulatory interactions between E. coli genes on the basis of the similarity of their expression response in 466 experiments. A matrix of relatedness values is calculated and a network of regulatory interactions is inferred by placing links between every pair of genes whose relatedness value exceeds some threshold,
. The CLR algorithm is used to infer direct and indirect regulatory interactions between E. coli genes on the basis of the similarity of their expression response in 466 experiments. A matrix of relatedness values is calculated and a network of regulatory interactions is inferred by placing links between every pair of genes whose relatedness value exceeds some threshold, 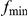 . A list of the links for the network at
. A list of the links for the network at 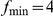 and
and 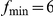 is provided. Each link is given by listing a gene name, the gene's Blattner number, followed by the target gene name and Blattner number.
is provided. Each link is given by listing a gene name, the gene's Blattner number, followed by the target gene name and Blattner number.
(XLS)
List of the order of genes in the correlation matrix plot. The multicolor matrix correlation plot simultaneously shows the statistical correlations in the modular relationships between pairs of genes, in the full dataset, at supercritical, critical, and subcritical threshold values. Each matrix element of the resulting plot has an RGB color that simultaneously indicates its correlations in the modular structure at each of the three  values. A list of the order of genes is given, by listing each gene name and Blattner number.
values. A list of the order of genes is given, by listing each gene name and Blattner number.
(XLS)
List of core community membership. At a particular  value, which defines a unique network, the community detection algorithm was run 10 times, generating a correlation matrix where each element represents the proportion of times gene
value, which defines a unique network, the community detection algorithm was run 10 times, generating a correlation matrix where each element represents the proportion of times gene  and gene
and gene 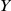 are found in the same community. Sets of genes that are always found in the same community is defined as a “core community”. For each
are found in the same community. Sets of genes that are always found in the same community is defined as a “core community”. For each 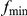 value, 2, 4 and 6, the gene name, Blattner number and core community number is given.
value, 2, 4 and 6, the gene name, Blattner number and core community number is given.
(XLS)
The hierarchical organization of the
E. coli
network. The relationship between communities at different 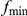 values indicates that the structure of the E. coli network is largely hierarchical. A hierarchical structure is revealed when a community breaks up into subcommunities as
values indicates that the structure of the E. coli network is largely hierarchical. A hierarchical structure is revealed when a community breaks up into subcommunities as 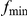 increases. Thus, if the E. coli regulatory network was completely hierarchical, one would see only block diagonal elements consisting of large blue blocks that break up into purple then white sub-blocks as
increases. Thus, if the E. coli regulatory network was completely hierarchical, one would see only block diagonal elements consisting of large blue blocks that break up into purple then white sub-blocks as 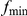 is increased. The hierarchical organization of genes is given, where the blue, purple, and white module membership of each gene is listed. The blue membership is listed first, numbered 1 through 6. The purple membership is listed next with the format x.y, where x is the blue membership and y is the purple membership. The purple membership is listed in the order a,b,c,d,….,z, aa, ab, …. Finally, the white membership is listed with format x.y.z, where x is the blue membership, y is the purple membership, and z is the white membership. The white membership is listed in numerical order.
is increased. The hierarchical organization of genes is given, where the blue, purple, and white module membership of each gene is listed. The blue membership is listed first, numbered 1 through 6. The purple membership is listed next with the format x.y, where x is the blue membership and y is the purple membership. The purple membership is listed in the order a,b,c,d,….,z, aa, ab, …. Finally, the white membership is listed with format x.y.z, where x is the blue membership, y is the purple membership, and z is the white membership. The white membership is listed in numerical order.
(XLS)
List of the order of genes in each noise correlation matrix plot. The gray scale plots of Figure 3 are the matrix correlation plots for the statistical ensemble analysis of the 200 partitionings constructed from the artificial noisy data for each noise value c. The grey scale of each matrix element in the plots corresponds to the fraction of pairs of partitionings in which the corresponding pairs of genes are found to be in the same community. For each noise value 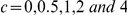 , each ordered gene name and Blattner number is listed.
, each ordered gene name and Blattner number is listed.
(XLS)
List of noise core community membership. For each noisy data set, the CLR algorithm is used to infer a regulation network at an 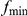 value of 2, and the community structure is determined with the methods described above. For each dataset, 10 different community partitionings are obtained, giving a total of 200 partititonings for each value of
value of 2, and the community structure is determined with the methods described above. For each dataset, 10 different community partitionings are obtained, giving a total of 200 partititonings for each value of  . Sets of genes that are always founds in the same community are defined as “core communities”. For each noise value
. Sets of genes that are always founds in the same community are defined as “core communities”. For each noise value 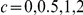 and
and 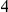 , a gene name and Blattner number, followed by its core community number is listed.
, a gene name and Blattner number, followed by its core community number is listed.
(XLS)
List of GO term enrichments. To determine whether the inferred community structure groups genes with similar biological functions, a test to determine whether the identified communities significantly enrich for any of the gene ontology (GO) terms identified in E. coli is performed. At each 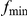 value, each significant enrichment is listed by giving it's corresponding p-value, GO term number, core community number, community size, GO term size, the number of genes in common, and the biological description of the GO term.
value, each significant enrichment is listed by giving it's corresponding p-value, GO term number, core community number, community size, GO term size, the number of genes in common, and the biological description of the GO term.
(XLS)
List of GO terms. To determine whether the inferred community structure groups genes with similar biological functions, a test to determine whether the identified communities significantly enrich for any of the gene ontology (GO) terms identified in E. coli is performed. To test for enrichment, genes were removed from each GO term that were not included in our dataset. For each resulting GO term, the gene name and Blattner number, followed by its GO term number is listed.
(XLS)
List of GO term enrichments at each noise value. To determine the effect of noise on GO term enrichment, at each noise value  , a test to determine whether the identified communities significantly enrich for any of the gene ontology (GO) terms identified in E. coli is performed. At each
, a test to determine whether the identified communities significantly enrich for any of the gene ontology (GO) terms identified in E. coli is performed. At each  value, each significant enrichment is listed by giving it's corresponding p-value, GO term number, core community number, community size, GO term size, the number of genes in common, and the biological description of the GO term.
value, each significant enrichment is listed by giving it's corresponding p-value, GO term number, core community number, community size, GO term size, the number of genes in common, and the biological description of the GO term.
(XLS)
Correlation matrix. Correlation matrix showing community structure found in the E. coli network with relatedness threshold values 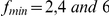 . Genes are ordered in the same sequence along the x and y axes beginning in the upper left corner, and this ordering is the same for all three relatedness values (gene order is given in SI). The matrix element in the position
. Genes are ordered in the same sequence along the x and y axes beginning in the upper left corner, and this ordering is the same for all three relatedness values (gene order is given in SI). The matrix element in the position 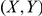 is colored blue, red, or green if genes
is colored blue, red, or green if genes 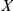 and
and 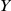 are in the same community at threshold values 2, 4 or 6, respectively. The density of the color indicates the strength of the correlation in the partitionings of the pair of genes. For example, considering the correlation between a pair of genes in the 10 replicate partitionings performed on the
are in the same community at threshold values 2, 4 or 6, respectively. The density of the color indicates the strength of the correlation in the partitionings of the pair of genes. For example, considering the correlation between a pair of genes in the 10 replicate partitionings performed on the 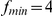 network, dark and light red indicates that the pair of genes are always and rarely found to be in the same community, respectively. The red, green and blue colors corresponding to
network, dark and light red indicates that the pair of genes are always and rarely found to be in the same community, respectively. The red, green and blue colors corresponding to 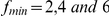 thresholds, respectively, are combined to indicate the correlations of each pair of genes at all three threshold values. Thus, the color of the matrix element in the position
thresholds, respectively, are combined to indicate the correlations of each pair of genes at all three threshold values. Thus, the color of the matrix element in the position 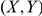 is white if genes
is white if genes  and
and  are in the same community at all three threshold values. It is purple (yellow) if the two genes are in the same community at thresholds 2 and 4 (4 and 6), but not at threshold 6 (2) and it is black if the two genes are not in the same community at any of the three threshold values. A list of the order of genes is given in Dataset S2.
are in the same community at all three threshold values. It is purple (yellow) if the two genes are in the same community at thresholds 2 and 4 (4 and 6), but not at threshold 6 (2) and it is black if the two genes are not in the same community at any of the three threshold values. A list of the order of genes is given in Dataset S2.
(TIF)
Core community hierarchy. An alternative view of the core community hierarchy where each core community is represented by a node. The node label x.y indicates the 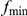 level, x, and core community number, y. The size of each node represents the number of genes in the community relative to communities at the same
level, x, and core community number, y. The size of each node represents the number of genes in the community relative to communities at the same 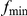 level. The edge width and color value indicate the proportion of the “daughter” community deriving from the connected “parent” community. For example, If all of the genes in a “daughter” community are from one “parent” community then there is one edge that is dark blue and thick. The nodes have been arranged to display the hierarchy of the network.
level. The edge width and color value indicate the proportion of the “daughter” community deriving from the connected “parent” community. For example, If all of the genes in a “daughter” community are from one “parent” community then there is one edge that is dark blue and thick. The nodes have been arranged to display the hierarchy of the network.
(EPS)
Noise correlation matrices. Change in core community structure as noise is increased from 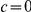 to
to 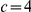 . The grey scale value of each element indicates the fraction of times the two genes occurred in the same community over replicate community partitionings. If the element is white (black) the two genes were always (never) found in the same community. At each noise value there are clearly white diagonal blocks indicating sets of genes that are always found in the same community, which we refer to as core communities. Note that, the five core communities at
. The grey scale value of each element indicates the fraction of times the two genes occurred in the same community over replicate community partitionings. If the element is white (black) the two genes were always (never) found in the same community. At each noise value there are clearly white diagonal blocks indicating sets of genes that are always found in the same community, which we refer to as core communities. Note that, the five core communities at 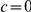 (Figure 3A) are in the same order in Figure 3:B, C, D, and E. Within each of the five core communities of Figure 3A, the node order is allowed to change in Figure 3:B, C, D, and E in order to display the largest subcommunity first. For each panel, he list of of the order of genes and the core community they belong to is given in Dataset S5 and Dataset S6, respectively.
(Figure 3A) are in the same order in Figure 3:B, C, D, and E. Within each of the five core communities of Figure 3A, the node order is allowed to change in Figure 3:B, C, D, and E in order to display the largest subcommunity first. For each panel, he list of of the order of genes and the core community they belong to is given in Dataset S5 and Dataset S6, respectively.
(TIF)
Operon by community. Fraction of E. coli operons that are retained whole in a single community. The fraction of 544 operons (comprising 2172 genes) identified in the E. coli genome where all genes in the operon were assigned to the same final tuning community was determined at  (indicated by arrows). These actual values were compared to 1000 random distributions of the same set of genes to empty community sets of the same size and number as were present in the final tuning partitionings (histograms). In all cases, actual operon retention proportions were much greater than in any of the 1000 randomly distributed sets, indicating that they were very unlikely to occur by chance and therefore that the final tuning community partitionings effectively group genes in the same operon to the same community.
(indicated by arrows). These actual values were compared to 1000 random distributions of the same set of genes to empty community sets of the same size and number as were present in the final tuning partitionings (histograms). In all cases, actual operon retention proportions were much greater than in any of the 1000 randomly distributed sets, indicating that they were very unlikely to occur by chance and therefore that the final tuning community partitionings effectively group genes in the same operon to the same community.
(EPS)
Regulatory links from
flhDC
and
fliA
in the
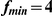 community that significantly enriches for flagellum associated genes. Genes are organized into operons as annotated by RegulonDB. Black, blue and red lines indicate regulatory interactions that are annotated in RegulonDB, inferred in the CLR network or both, respectively. For simplicity, only links from FlhDC and to targets of these links from fliA are shown. Many of the interactions that are found in the CLR network are not present in RegulonDB (blue lines). These interactions are candidates for indicating unrecognized regulatory interactions between FlhDC and the target genes. However, in most cases these interactions can be explained through the action of FlhDC on the sigma factor encoded by fliA (thick red line), which does directly affect all but one of the target genes. This point underlines the difference between the CLR network, which includes direct and indirect regulatory interactions, and the direct transcriptional network as annotated in RegulonDB. Note the CLR connection between FlhDC and the target gene ymdA cannot be explained through any known indirect interaction and is, therefore, a candidate for representing a new direct interaction.
community that significantly enriches for flagellum associated genes. Genes are organized into operons as annotated by RegulonDB. Black, blue and red lines indicate regulatory interactions that are annotated in RegulonDB, inferred in the CLR network or both, respectively. For simplicity, only links from FlhDC and to targets of these links from fliA are shown. Many of the interactions that are found in the CLR network are not present in RegulonDB (blue lines). These interactions are candidates for indicating unrecognized regulatory interactions between FlhDC and the target genes. However, in most cases these interactions can be explained through the action of FlhDC on the sigma factor encoded by fliA (thick red line), which does directly affect all but one of the target genes. This point underlines the difference between the CLR network, which includes direct and indirect regulatory interactions, and the direct transcriptional network as annotated in RegulonDB. Note the CLR connection between FlhDC and the target gene ymdA cannot be explained through any known indirect interaction and is, therefore, a candidate for representing a new direct interaction.
(EPS)
The community with the most significant GO term enrichment at
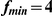 . The community with the most significant GO term enrichment at
. The community with the most significant GO term enrichment at 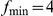 contains 72 genes, including all 24 genes in the GO term for bacterial-type flagellum. The remaining 48 genes in this community are implicated as having some relevance for the development, function or control of the E. coli flagellum.
contains 72 genes, including all 24 genes in the GO term for bacterial-type flagellum. The remaining 48 genes in this community are implicated as having some relevance for the development, function or control of the E. coli flagellum.
(XLS)