Understanding the role of hydrogen bonds in water dynamics and protein stability

Abstract

The mechanisms of cold and pressure denaturation of proteins are a matter of debate, but it is commonly accepted that water plays a fundamental role in the process. It has been proposed that the denaturation process is related to an increase of hydrogen bonds among hydration water molecules. Other theories suggest that the causes of denaturation are the density fluctuations of surface water, or the destabilization of hydrophobic contacts as a consequence of water molecule inclusions inside the protein, especially at high pressures. We review some theories that have been proposed to give insight into this problem, and we describe a coarse-grained model of water that compares well with experiments for proteins’ hydration water. We introduce its extension for a homopolymer in contact with the water monolayer and study it by Monte Carlo simulations in an attempt to understand how the interplay of water cooperativity and interfacial hydrogen bonds affects protein stability.

Introduction

One of the most intriguing challenges in biological physics is the nature of protein folding–unfolding processes. The temperature range of stability of a folded protein is, in general, small. For example, staphylococcal nuclease (Snase—a small protein containing 149 amino acids) folds at low pressure approximately between 260 and 320 K [1].

Heat destabilizes proteins. By increasing the bath temperature T, thermal fluctuations increase and disrupt the folded configurations of proteins. By decreasing T, proteins can crystallize, but surprisingly some proteins unfold at sufficiently low temperature instead of crystallizing [1-7]. Cold denaturation seems to be a general phenomenon for proteins, generally occurring well below 0°C, the freezing point of water. In some cases, for example for Snase [1], cold denaturation cannot be directly observed, but experimental data can be extrapolated to predicted the lowest temperature of protein stability. In general, destabilizing agents can be used to make the cold denaturation observable. Interestingly, Pastore et al. [7] observed that yeast frataxin under physiological conditions undergoes cold denaturation below 7°C and remains folded up to 30°C. Hence, yeast frataxin is an excellent prototype for studying the folding transition under accessible conditions for both hot and cold unfolding. The study of this protein could help in understanding the mechanism of cold unfolding that, as we will discuss in the next sections, is still a matter of debate.

Proteins can unfold also by pressurization. It has been observed that the increase of pressure induces the unfolding of proteins [8, 9]. The pressure-unfolding process can be rationalized by considering that the folded structure usually includes cavities. High pressure can induce an elastic response of the protein, deforming its structure, and pushing water molecules inside the cavities. The water molecules from inside would swell the protein, with consequent loss of protein functionality [9]. Because it is difficult to separate the protein response to high hydrostatic pressure from the response of the aqueous environment, the understanding of the pressure unfolding is still under debate.

Thermodynamics of proteins unfolding

By increasing the thermal energy k_BT (k_B is the Boltzmann constant), the protein residues vibrate faster, accessing new possible configurations, i.e., increasing the entropy S of the system. This increase leads to hot denaturation, in the same way an increase of k_BT leads to the melting of a crystal, at the expense of the energy of the system, compensated by an increase of entropy.

Cold denaturation, in contrast cannot be explained as the effect of an increase of entropy. By decreasing T, the entropy of the system decreases. Hence, in the case of proteins there must be a complex mechanism that induces cold denaturation.

General principles of thermodynamics tell us that at any value of T and P the system minimizes its Gibbs free energy, G ≡ H − TS, where H ≡ U + PV is the enthalpy of the system, U the internal energy of the system, V the volume and P the pressure. In our case, the system is the solution of proteins and water. Hence, the free-energy balance must take into account both water molecules and protein residues. The experimental fact that solvated proteins unfold by decreasing T means that at lower T the difference

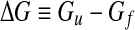1

between the unfolded (u) and folded (f ) states is

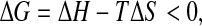2

where ΔH ≡ H_u − H_f and ΔS ≡ S_u − S_f.

The total variation of the entropy of the system is given by ΔS = ΔS_p + ΔS_w where ΔS_p and ΔS_w are the entropy variation of protein residues and water molecules, respectively. By unfolding, the protein entropy increases, ΔS_p > 0. On the other hand, the protein contribution to ΔH is positive, ΔH_p > 0, because the enthalpy of the protein increases when the protein unfolds (H_p decreases when the number of contact points of the protein increases). Therefore, the protein contribution to ΔG does not guarantee that (2) is satisfied, because ΔH_p − TΔS_p, could be negative or positive depending on the relative variations at the given T. Hence, water contribution to the total balance of (2) could be relevant. A commonly proposed idea is that the native-folded state is stabilized by the quasi-ordered network of water molecules hydrating the non-polar monomers [10–13].

Protein phase diagram

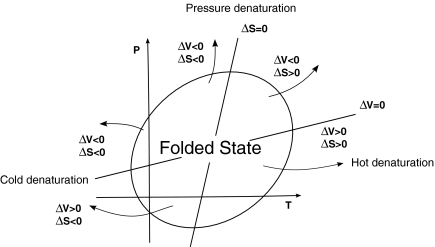
In this section, we summarize the main theoretical calculations given by Hawley [14] and reviewed by Smeller et al. [15] and Meersman et al. [16], predicting a close stability region in the P − T plane for proteins, consistent with experiments (Fig. 1) [1, 2, 4, 5, 7, 17]. Outside the elliptic region the protein unfolds, losing its biological function.

Fig. 1.

Schematic representation of the phase diagram of a protein. Within the elliptic region, the protein is folded, while it unfolds by increasing temperature T (hot denaturation), by decreasing T (cold denaturation), and by increasing or decreasing pressure P (pressure denaturation). Each folding–unfolding process is characterized by different variation of entropy ΔS and variation of volume ΔV as indicated in the figure. The axes of the ellipse are loci where ΔS = 0 and ΔV = 0 (see text for discussion). Adapted from [9]

Following Hawley [14, 15], we can calculate ΔG of the whole system (protein and water) assuming that a protein can stay in only two distinct states, folded and unfolded as in (1). Differentiating G, we get

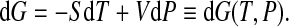3

Hence, we have

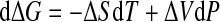4

with ΔV ≡ V_u − V_f. By expanding ΔS and ΔV to the first order around ΔS₀ and ΔV₀, we get

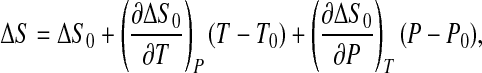5

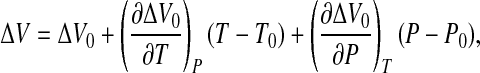6

and from (4) to (6), by integration,

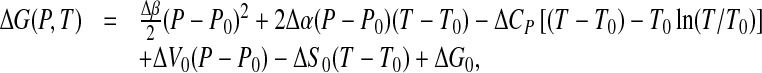7

where 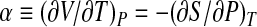is the thermal expansivity factor, related to the isobaric thermal expansion coefficient α_P by α_P = α/V; 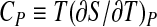is the isobaric heat capacity and 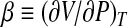is the isothermal compressibility factor related to the isothermal compressibility K_T by the relation K_T = − (β/V). All the quantities with the subscript equal to zero are usually referred to as ambient conditions. By developing the logarithm to the second order around (T₀,P₀)

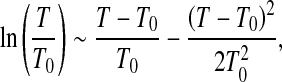8

we get

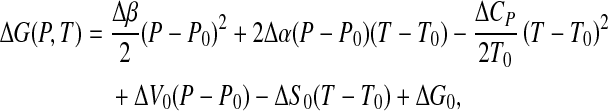9

which is the equation of en ellipse, as in Fig. 1, given the constraint

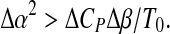10

This condition is guaranteed by the different signs of ΔC_P and Δβ, as can be observed for some proteins, as reported by Hawley [14].

Equation (9) is the Taylor expansion of ΔG(P,T) truncated at the second order, holding for Δα, Δβ and ΔC_P independent of T and P. These assumptions are generally valid and adding third order terms in the expansion has minimal effect on the elliptic shape of the stability region.

At maximum pressure P_max of stability for the protein, 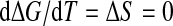, while at the maximum temperature T_max of stability, 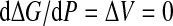. Therefore, based on Hawley’s theory, it is possible to make general predictions about the changes of ΔV and ΔS as schematically summarized in Fig. 1. This phenomenological theory does not take into account explicit information about the protein structure, and makes strong assumptions, such as, for example, that the protein only has two states, or that equilibrium thermodynamics holds during the denaturation. The last assumption, in particular, implies that the whole process would be reversible. Nevertheless, consistency with Hawley’s theory is a good test for models of protein unfolding. More details about the arguments summarized here can be found in [16].

In the next section, we review some of these models. The review does not pretend to be exhaustive, but it has the aim of mentioning a number of positive results of the theories formulated to understand protein folding.

Models for protein unfolding

Hydrophobic effect

To date the idea that hydrophobic interactions play an important role in protein folding is widely shared. A solute is considered hydrophobic if it binds to water more weakly than water itself.

A model for protein folding taking into account implicitly the hydrophobic effect was proposed in 1989 by Lau and Dill, known as the HP model [18]. By assuming that the exposed surface of hydrophobic residues is energetically unfavorable at low T, the model reproduces the folding of the protein (hydrophobic collapse). The protein is represented as a self-avoiding chain on a lattice. The chain is composed of two different categories of amino acids: H (hydrophobic non-polar) and P (polar). The presence of the aqueous environment is taken into account, introducing an attractive contact interaction between H monomers. This interaction captures the hydrophobic effect between water molecules and non-polar amino acids. No other interactions are present in the system.

Under these hypotheses, the authors show that the features of the folding process depend on the HH energy interaction, the length of the chain, and the specific sequence of H and P monomers. Moreover, for long chains one folded state dominates.

The model has the virtue of reducing the complexity of the folding process to a manageable level. All the electrostatic and chemical properties of each amino acid are simplified by allowing only two possible states. The degrees of freedom of the solvent are not explicitly included. Nevertheless, the HP model cannot describe cold denaturation. Therefore, the experimental evidence of cold denatured proteins calls for a reconsideration of the hydrophobic interaction and its dependence on temperature and on the structure of hydration water [4–6-3].

Back in 1945, Frank and Evans [10] discussed the tendency of water to form ordered structures around non-polar solutes to minimize the free-energy cost of solvation. As a consequence, hydrophobic solutes are “structure makers” for water, facilitating the formation of cages around the solute. The effect of these structures around hydrophobic solutes is to reduce the entropy with respect to the bulk and to compensate, approximately, the enthalpy cost for the creation of a cavity which can be occupied by the solute.

As discussed by Muller in 1990 [12], the compensation of the enthalpy implies that water–water hydrogen bonds (HBs) at the interface with the hydrophobic solute are stronger than those in the bulk. This is consistent with the experimental observation that the excess molar heat capacity for a non-polar solute at infinite dilution in water is positive. This quantity, defined as the difference of the partial molar heat capacity in solution with respect to the heat capacity of the pure liquid solute, is far larger at 25°C when the solvent is water than for any other solvent [12, 19].

The statement that HBs are stronger at the hydrophobic interface has led to the misconception that water around a hydrophobic solute has an iceberg-like structure. Computer simulations [20, 21], theoretical analysis [22–25], and neutron scattering studies [26] are inconsistent with iceberg-like structures. Hence, the restructuring of water around a solvent seems not to play a relevant role in the hydrophobic effect. Nevertheless, Muller [12] showed that if hydration HBs are enthalpically stronger, but fewer than in bulk, a model with two-state HBs can reproduce the sign reversal of the proton NMR chemical shift with T and the heat capacity change upon hydration.

On the other hand, a common opinion [27, 28] is that the large free-energy change associated with the hydrophobic effect is due to the small size of the water molecules with respect to the solutes, and that the free-energy change associated with the network reorganization around hydrophobic particles is negligible due to compensation of enthalpy and entropy, although it may account for the large heat capacity change upon hydration. This observation apparently ruled out the Muller model, where the enthalpy-entropy compensation upon hydration was not present.

Nevertheless, Lee and Graziano in 1996 [29] showed that the Muller model can be slightly modified to recover also the enthalpy-entropy compensation upon hydration. The Muller–Lee–Graziano model was further simplified by De los Rios and Caldarelli in 2000 [30–32] in order to reduce the number of parameters. Simplifying the description of bulk water, they recovered hot and cold denaturation for a protein represented as a hydrophobic homopolymer. A development of this model was used in 2005 to study the effective interaction between chaotropic agents and proteins [33].

The model by De los Rios and Caldarelli has been generalized by Bruscolini and Casetti [34, 35] in 2001 by allowing each monomer of a non-polar homopolymer to be in contact with a cluster of water molecules. Each cluster has an infinite number of possible states and only one state minimizes the free-energy cost of the interaction with the hydrophobic monomers. The model reproduces the trends of thermodynamic averages in accordance with experiments [36] and simulations [13], and predicts hot and cold denaturation. These results are qualitatively similar to those of the Muller–Lee–Graziano model, further supporting the relevant role of the solvent in the folding–unfolding process.

Cold denaturation and T-dependence of the hydrophobic effect were also observed by Dias et al. in 2008, analyzing a non-polar homopolymer in the Mercedes-Benz (MB) model for water [37]. The MB model, originally introduced by Ben-Naim [38] 1971, represents water molecules as disks in two dimensions with three possible HBs (arms) as in a Mercedes-Benz logo. Water molecules interact via van der Waals potential and HB interactions. HB interaction is modeled with a Gaussian potential, favoring a fixed value for the water–water distance and aligned arms for facing molecules. Simulations show that the average HB energy it is higher for shell water than for bulk water at high T, while it is lower at lower T. Therefore, by cooling the solution, it is energetically more convenient to increase the protein surface exposed to water, inducing protein unfolding. In this model, the water molecules forming a cage around the protein monomers are strongly H-bonded to each other. The highly ordered structure of the solvent around the monomers decreases the entropy of water, compensating for the increase of entropy associated with protein unfolding.

This model has been criticized [39] because it assumes, without proof, that the enthalpy gain dominates at low T, giving rise to free-energy gain upon unfolding of the protein. In particular, Yoshidome and Kinoshita in 2009 [39] analyzed by integral equation theory the behavior of a non-polar homopolymer composed by fused hard spheres of different diameters immersed in smaller hard spheres, with permanent electrostatic multiple moments, representing the solvent [40]. The protein–water interaction is represented by a hard sphere potential and water–water interaction by a hard sphere potential and an electrostatic contribution given by the electrostatic multipole expansion. The authors found that denaturation is characterized by large entropy loss and large enthalpy gain. However, these two contributions to the free energy almost completely cancel out and make no significant contribution to the free-energy change. They found that the driving mechanism for cold denaturation is the translational entropic loss of water due to the large excluded volume of the hydrophobic particles. They observed that at low T water diffuses less, therefore the hydrophobic effect is weaker and the protein unfolds.

A different approach to the role of hydrophobic interaction in polymer collapse and nanoparticle self-assembly is represented by the theory proposed by Lum et al. in 1999 [41], further developed by ten Wolde and Chandler in 2002 [42] and recently by Varilly et al. in 2011 [43]. They start from the observation that, at ambient conditions, the solvation free energy of hard sphere solutes increases: (a) with the solute volume for solutes of small radius and (b) with the solute surface for solutes of large radius.

Hence, the solvation free energy exhibits a crossover between two regimes: for small solutes the entropy leads to the dispersion of hydrophobic particles, while for large solutes the enthalpy drives the particles to hydrophobic collapse. The authors associate the enthalpy change responsible for the hydrophobic collapse to a dewetting transition, i.e., to a microscopic liquid-gas phase separation of water molecules at the interface with the solute. Therefore, the average number of water molecules in a probe volume close to the solute decreases with respect to bulk and a liquid-gas interface is formed near the hydrophobic particles, i.e., the solute is surrounded by a vapor bubble. In order to reduce the free-energy cost to form a liquid-gas interface, the solutes collapse. To take into account the crossover at different length scales, the authors propose a mean-field model for the water solvent. Water density is modeled as a sum of two scalar fields, representing the large and the small length-scale contributions to the water density. This decomposition is valid in thermodynamic conditions far away from critical regions of water, where density fluctuations are expected to be strong. The Hamiltonian for the water system is a bilinear form, coupling the two components of the density field. The solute–water coupling is represented by an excluded volume term or by an external tuning potential. The hydrophobic collapse of a polymer [42] and the dewetting transition of confined water [43] are studied under ambient conditions with interesting predictions. In particular, the tendency of vapor formation at the solute interface decreases as the system is moved away from liquid-vapor equilibrium, i.e., by lowering the temperature or increasing the pressure. Therefore, the authors offer a rationale for protein unfolding at low T and high P, as a consequence of destabilization of the hydrophobic collapse.

Nevertheless, the starting hypothesis of this theory, i.e., that an extended hydrophobic surface favors the formation of a liquid-gas interface, is at variance with classical MD simulations [44, 45] and first principles studies [46] of atomistic models showing that water density in the first shell near a hydrophobic surface is higher than in bulk.

Pressure effects

Pressure effects have been also considered in microscopic theoretical models for protein denaturation. For example, in 2003 Marqués and coworkers [47] considered a model in two dimensions with a hydrophobic homopolymer, represented as a self-avoiding random walk, embedded in water at constant P. They adopted the Sastry et al. water model [48] for water–water interactions. They considered that the polymer–water interaction is repulsive, hypothesizing that it is proportional to the density number of HBs and to the number of missed native contact points among monomers of the protein. The model displays hot denaturation, cold denaturation and denaturation at high pressure, in agreement with the stability diagram of some proteins [49]. A peculiarity of this model is that the effective repulsion between protein and solvent is mean field because it depends on the average number of HBs of bulk water, that is, an average property of the bulk.

To remove this coupling, in 2007 Patel and coworkers [50] proposed a model where water at the interface with a protein has a restricted number of accessible orientations for the HBs compared with the bulk. Along with this entropic reduction, the interfacial HBs also have an additional enthalpic bonus with respect to bulk water, following the ideas discussed by Muller et al. The model displays a stability phase diagram with hot, cold and pressure denaturation. However, it does not reproduce all the expected features of the schematic phase diagram of Fig. 1. In particular, the model does not reproduce the elliptic shape of the phase diagram and the low-P region with ΔV > 0 for hot denaturation. These results were confirmed by extending the model to the case with heteropolymers.

In an attempt to reproduce the elliptic phase diagram for protein stability in Fig. 1, we propose here a model starting from the assumption that HBs at the interface of a large hydrophobic object are stronger compared with HBs in bulk water [51]. The plan of this paper is as follows: in Section 3, we describe the model for hydration water, and in Section 4 we summarize the model properties, to clarify its water-like behavior. In Section 5, we present a geometrical description of correlated regions of molecules of hydration water. In Section 6, we calculate the free-energy landscape of hydration water. In Section 7, we introduce the model for protein folding with explicit water. In Section 8, we present preliminary results of this model and discuss the perspectives in Section 9.

Water monolayer between hydrophobic plates

We consider a monolayer of water nano-confined between two infinite flat hydrophobic plates parallel to each other and with separation of 0.6 nm ≤ H ≤ 0.9 nm. The interaction between water molecules and the plates is represented by a hard-core repulsion. The confinement is such to inhibit the formation of bulk water structures. For example, bulk water is known to preferentially form four HBs with four nearest neighbor molecules in an approximate tetrahedral structure at low temperature and pressure [52]. Hard confinement inhibits the formation of such bulk structure. Kumar et al. [53], by molecular dynamics simulations of TIP5P-water confined between flat hydrophobic plates separated by 0.7 nm, find an almost-flat monolayer of water molecules. They observe that each molecule has four neighbors forming an orientationally disordered square lattice.

To define a tractable model of water, we coarse grain this structure of confined water [54–57, 101]. We divide the volume accessible to water into N cells. Each cell contains one water molecule and has a volume V/N = r²h, where h is the separation between the flat plates, and r ≥ r₀ is the average distance between water molecules, with r₀ equal to the van der Waals diameter of a water molecule. The van der Waals attraction (due to dispersion forces) and the repulsive interactions (due to the Pauli exclusion principle) between water molecules are described by a Lennard–Jones interaction

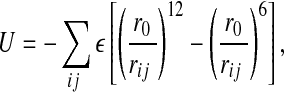11

where r_ij is the distance between molecules i and j and the sum is performed over all the molecules.

To each cell, we associate a variable n_i = 0,1. If the cell i is occupied by a water molecule and has a density ρ_i > ρ₀/2, where 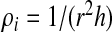and 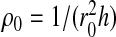with ρ_i/ρ₀ ≤ 1, then the cell is liquid-like and n_i = 1. If ρ_i ≤ ρ₀/2, then the cell is gas-like and n_i = 0.

To take into account the decrease of orientational entropy due to the formation of HBs, we introduce for each water molecule i four bonding indices σ_ij, one for each possible HB formed with nearest neighbor water molecule j. Each variable σ_ij can assume q different values, σ_ij = 1 ... q. We choose the parameter q by selecting 30° as the maximum deviation from linear bond (i.e., q = 180°/30° = 6). Hence, every molecule has q⁴ = 1,296 possible configurations. A HB is formed between two nearest neighbor molecules i and j only if both are in liquid-like cells (n_in_j = 1) and their variables σ_ij and σ_ji are in the same state (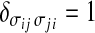, with δ_ab = 1 if a = b, 0 otherwise). The first condition corresponds to requiring that 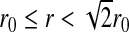, and the second corresponds to requiring that both molecules have the right relative orientation to form a HB. The conditions are expressed by the Hamiltonian term

12

representing the covalent (directional) HB component, where J > 0 represents the covalent energy gained per HB, and the sum is over nearest neighbor cells.

The experiments show that the formation of a HB leads to an open structure that induces an increase of volume per molecule [52, 58]. This effect is incorporated in the model by considering that the total volume of the system is

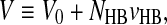13

where V₀ is the volume of the system without HBs, and v_HB is the increment due to the HB.

The term 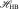quantifies the two-body component for HB interaction. On the other hand, the distribution of O-O-O angles shows a strong T dependence [59] that suggests the presence of many-body components for HB interactions due to long-range change interactions. We quantify this component by the Hamiltonian term

14

where J_σ > 0 is the characteristic energy of the cooperative interaction leading to the many-body term. The sum is performed over the six different pairs (k,l)_i of bonding indices of the molecule i, each facing another molecule and inducing a many-body interaction through the direction term in (12). Therefore, the total enthalpy for water is

15

where

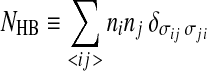16

is the total number of HBs and

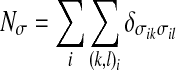17

is the total number of pairs of indices optimizing the cooperative interaction.

Dynamics and thermodynamics of a water monolayer

We study our model by Monte Carlo (MC) simulations [51, 56, 60–66] and mean-field calculations with the cavity method approach [54–57, 61, 62]. MC simulations are performed in the constant N, constant P and constant T (NPT) ensemble where the volume of the system is a stochastic variable. We consider periodic boundary conditions in the directions parallel to the confining surfaces.

Liquid-gas phase transition and anomalies

Previous calculations have shown that the system displays a liquid-gas first-order phase transition ending in a critical point C at approximately k_BT_C/ε = 1.9±0.1 and P_Cv₀/ε = 0.80±0.05 [54–56, 60–62, 66], in qualitative agreement with mean-field results [56, 57, 61, 62].

The model reproduces several anomalies of water. For example, the system presents a density anomaly, i.e., the isobaric increase of density upon cooling, up to a temperature of maximum density (TMD). The system also displays diffusion anomalies [67], maxima of isothermal compressibility K_T, isobaric heat capacity C_P and the isobaric thermal expansion coefficient α_P [56, 57, 61, 63–65] related to the anomalous behavior of water in the supercooled region.

Dynamical slowing down of water in supercooled region

The dynamical behavior of the model at low T has interesting features [60, 63, 64]. The dynamics of the HBs at constant P displays an increase of the correlation time when T is decreased. The increase is faster at higher T than at lower T and shows a crossover at the temperature at which C_P has a maximum [63, 64]. Results clarify that the crossover is due to a structural change in the HB network [63, 64]. The qualitative features of this crossover were successfully compared to experimental results for confined water at increasing P [68, 69]. In particular, Franzese and de los Santos [60] have shown that at high pressure (P ≃ 2,000 bar) the effect of HBs is negligible due to the high enthalpic cost of forming a HB and the correlation function decays as an exponential. At low P (P ≃ 1 bar), the correlation is large also at long times and the system becomes stuck in a glassy state. The structural analysis shows that under these conditions the HB network develops gradually by decreasing T and traps the system in metastable configurations. For intermediate values of pressure, the correlation function C(t) is well described by a stretched exponential function

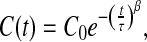18

where C₀, τ and β ≤ 1 are fitting constants (β = 1 correspond to exponential decay). As we approach a characteristic value of pressure P_C′, β reaches its minimum value (β ≃ 0.4). This is consistent with the experimental value of β ≃ 0.35, observed for an intermediate scattering correlation function of water hydrating myoglobin at low hydration level (h = 0.35 g H₂O/g protein) [70, 71]. Considering that, the quantity 1 − β is a measure of the heterogeneity in the system, and the decrease of β when P_C is approached found by Franzese and de los Santos indicates that the system exhibits the largest amount of heterogeneity at P_C′. As we will discuss in the next section, this heterogeneity is the consequence of a large increase of cooperativity in the vicinity of P_C′.

Thermodynamics of supercooled water

Four scenarios have been proposed to explain the thermodynamics of supercooled water. The stability limit scenario [72] hypothesizes that the limit of stability of superheated liquid water merges with the limit of stretched and supercooled water, giving rise to a single locus in the P − T plane, with positive slope at high T and negative slope at low T. The reentrant behavior of this locus would be consistent with the anomalies of water observed at higher T. As discussed by Debenedetti, thermodynamic inconsistency challenges this scenario [73].

The liquid-liquid critical point (LLCP) scenario [74] supposes a first-order phase transition in the supercooled region between two metastable liquids at different densities: the low-density liquid (LDL) at low P and T, and the high-density liquid (HDL) at high P and T. The phase transition line has a negative slope in the P − T plane and ends in a critical point. Numerical simulations for several models are consistent with this scenario [74–80].

The singularity-free scenario [48] focuses on the anticorrelation between entropy and volume as the cause of the large increase of response functions at low T and hypothesizes no HB cooperativity. The scenario predicts lines of maxima in the P − T plane for the response functions, similar to those observed in the LLCP scenario, but shows no singularity for T > 0.

The critical-point-free scenario [81] hypothesizes an order-disorder transition, with a possible weak discontinuity of density, that extends to P < 0 and reaches the supercooled limit of stability of liquid water. This scenario would effectively predict no critical point, and a behavior for the limit of stability of liquid water as in the stability limit scenario.

As showed by Stokely et al. [62], all these scenarios may be mapped into the space of parameters J and J_σ, of the model presented in the previous section, i.e., the coupling constants of the covalent component of the HBs and the coupling constants of the cooperative component of the HB interaction, respectively. In particular, Stokely et al. showed by mean-field calculations and numerical simulations that the absence of the cooperative component leads to the singularity-free scenario, while a large value of the many-body component with respect to the covalent component gives rise to the critical-point-free scenario, and that in this case the critical-point-free scenario coincides with the stability limit scenario [62].

By using estimates of these parameters from experimental results, the authors predict a liquid-liquid phase transition at low temperature and high pressure ending in a second critical point C′ for water [62]. Therefore, following this prediction, the increasing fluctuations related to C_P, K_T and α_P of water under cooling are a consequence of the liquid-liquid critical point C′ in the supercooled region of water. By approaching C′, the correlation length ξ of the HBs increases. In particular, for any P < P_C′, the critical pressure, there is a temperature T_W where the correlation length ξ(P) is maximum. The locus T_W(P), called the Widom line, converges toward C′ with a negative slope in the P − T plane [57, 82]. By increasing P along the Widom line, ξ increases and diverges at P = P_C′. Therefore, the regions of cooperativity of the HBs increase in size, leading to large cooperativity and, as a consequence, to large heterogeneity in the dynamics as observed by Franzese and de los Santos [60] and described in the previous section.

Before discussing in more details the features of these cooperative regions, it is worth mentioning that recent theoretical and experimental results about water hydrating lysozyme proteins at very low hydration level (h = 0.3 g H₂O/g protein) allow us to explain the phase diagram of a water monolayer at T ≃ 150 K and ambient pressure [83]. This investigation reveals that at low P two structural changes take place in the HB network of the hydration shell. One, at about 250 K, is due to the building up of the HB network [64], and another, at about 180 K, is a consequence of the cooperative reorganization of the HBs. These two structural changes give rise to two dynamical crossovers in the HB correlation time and the corresponding experimental quantity, the proton relaxation time [83]. By increasing P, approaching P_C′, the two structural changes merge and at P_C′ lead to diverging fluctuations associated with the liquid-liquid critical point, as discussed in a recent work by Mazza et al. [84]. Furthermore, the comparison of experiments and theory allows us to convert the simulations results into real units [83], estimating the occurrence of the critical point C′ at P_C′ ≃ 0.13 GPa, T_C′ ≃ 174 K [66].

Geometrical description of clusters of correlated HBs

As discussed in the previous section, a water monolayer between hydrophobic plates separated by less than 1 nm has a complex phase behavior at T below the limit of stability of bulk liquid water. The same phase diagram compares well with experiments with water monolayers hydrating a complex substrate formed by proteins at low hydration level [70, 71]. This can be understood if we admit that the main effect of the protein substrate at low hydration is to induce, in the first layers of hydrating water, a structure that is inconsistent with any possible crystal. Therefore, the substrate inhibits the crystallization, but does not inhibit the water–water HB formation. It is, therefore, interesting to understand how the region of correlated HBs builds up and gives rise to the cooperative rearrangement and the liquid-liquid phase transition.

To this goal we follow an approach that has been validated during the last three decades to describe critical phase transitions. It consists in a percolation approach elaborated in 1980 by Coniglio and Klein [85] for ferromagnetic systems and related to a mathematical mapping introduced by Fortuin and Kasteleyn [86]. The approach is also related to Swendsen-Wang [87] and Wolff [88] techniques for cluster MC methods. The Coniglio–Klein approach, called random-site-correlated-bond percolation, was extended to ferromagnetic systems with many states [89] and spin-glass-like systems [90–96]. In particular, in [85] it was proved that clusters, defined following the rules of this specific type of percolation, statistically coincide with the region of thermodynamically correlated variables. Moreover, in [91] it was proved that this result holds as long as the system has no competing interactions that give rise to frustration. Since in the case considered here there is no frustration, we can follow the percolation approach to define clusters of water molecules with statistically correlated HBs.

As described in [51], we adopt the Wolff cluster MC algorithm [61] to study the cooperative regions and their length scale. Thanks to the fact that a cluster represents a region of water molecules with statistically correlated HBs, the algorithm allows equilibration of the system at any T [61].

By definition, at given temperature T and pressure P, two bonding indices σ_ij and σ_ji of two nearest neighbor water molecules belong to the same cluster with probability

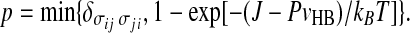19

On the other hand, by definition two bonding indices σ_il and σ_ik of the same water molecule i belong to some cluster of correlated degrees of freedom with probability

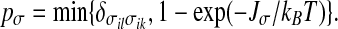20

Therefore, p depends on P and T, while p_σ depends only on T. This difference is a consequence of the local volume increase due to the formation of HBs. The size of a cluster is given by the total number of σ_ij variables belonging to the cluster. For each four σ_ij in a cluster we have, on average, one water molecule in the cluster. The average linear size of finite (non-percolating) clusters is, for the mapping discussed above, statistically equivalent to the correlation length of the HBs. Moreover, it is possible to prove [89] that each thermodynamic quantity, such as the compressibility, can be described in terms of an appropriate moment of the finite cluster distribution.

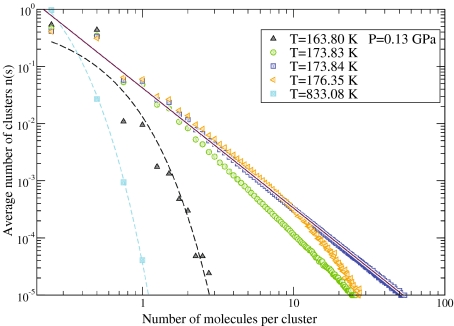
By approaching the critical point C′, we observe that the largest cluster percolates and its linear size becomes comparable to the system size. Under these conditions, the correlation length ξ diverges. The distribution n(s) of clusters of linear size s decays as an exponential away from C′, and n(s) has a power law decay near C′. This is indeed consistent with our results for P ≃1.93 GPa and different temperatures (Fig. 2). From this analysis, we estimate P_C′ ≃1.93 GPa and T_C′ ≃ 173 K, consistent with the estimate of the critical parameters for C′ based on the study of fluctuations [66].

Fig. 2.

Distribution n(s) of clusters with finite size s formed by correlated hydrogen bonds in a non-crystallizing water monolayer. Calculations are for P = 0.13 GPa ≃ P_C′, the liquid-liquid critical pressure, and different values of temperature for a system with N = 4×10⁴ water molecules. For T = 173.84 K ≃ T_C′, the liquid-liquid critical temperature, calculations (blue square points) decays as a power law n(s)~s^− τ (continuous line). We find τ = 2.1±0.1, as expected from theory near a critical point [91]. Consistent with the theory, we find that n(s) cannot be described by a power law decay away from the critical point. This is the case, for example, at T = 173.83 K (green circles) and T = 176.35 K (orange triangles). We find that at temperatures far from the critical temperature, n(s) has an exponential decay. For example, we find an exponential decay (dashed lines) at T = 833.08 K (light blue square) and T = 163.80 K (black triangles)

From general considerations it is possible to show that at the critical point n(s)~s^− τ with τ = 1 + d/D_F, where D_F is the fractal dimension of the cluster at the critical point and d = 2 is the embedding (Euclidean) dimension. A preliminary estimate τ ≃ 2 suggests that the clusters of correlated HBs at the percolation point are compact with D_F~2 (Bianco and Franzese, in preparation). Therefore, the mapping of the thermodynamic systems into a percolation problem allows us to give a geometrical description of the regions of correlated HBs.

It is worth mentioning that the percolation approach was already used with interesting results for the HB network of supercritical bulk water [97], and for the spanning HB network of water hydrating biomolecules [98]. In both cases, the authors use a pure geometrical definition of a cluster of molecules: two neighbor water molecules belong to the same cluster if they participate to the same HB. This cluster definition does not take into account the thermodynamic correlation among the HBs, hence, as can be demostrated, does not describe the region of correlated HBs. In general the clusters defined in [97, 98] percolate at higher T than the clusters defined in our work. We stress here that the statistical equality of the HB correlation length with the average linear cluster size holds only for the correlated percolation, adopted in our work.

Free-energy landscape analysis

The percolation approach allows us to adopt a cluster MC dynamics that is very efficient at low T [61]. Therefore, we can equilibrate the system at low P around the T_W(P), the temperature of maximum correlation length ξ, and around the temperature T_LL of liquid-liquid coexistence at high P, and calculate the free-energy landscape for the system.

By definition, the Gibbs free energy is

21

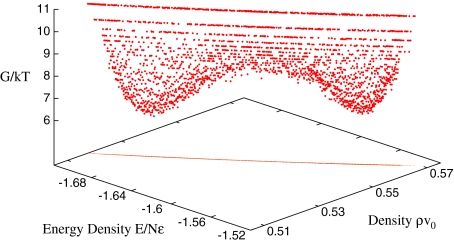
where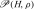 is the density of states with enthalpy H ∈ [H,H + δH] and density ρ ∈ [ρ,ρ + δρ], where δH and δρ are infinitesimal increments. In Fig. 3, we show G as a function of energy per particle E/N and density ρ. The free energy displays two equivalent minima straddling the line of phase transition. The two minima, equivalent within the numerical precision, are consistent with the coexistence of two phases with different density and energy. The one at higher density and higher energy represents the HDL phase. The other, at lower density and lower energy, represents the LDL phase. Approaching C′, the two minima get closer and the density separation disappears, as expected at a critical point. These results are consistent with the mean-field free-energy analysis of [61, 69], where the Gibbs free energy is calculated as a function of the HB order parameters relevant at the structural transition at high P and low T. In the mean-field analysis the minima of G are separated at high P, but merge for P approaching P_C′. All these results are consistent with the behavior of C_P, K_T and α_P, whose maxima move to lower T as P is increased [56, 63–65]. The loci of the maxima of C_P, K_T and α_P merge in the vicinity of C′ and the amplitude of their maxima increases approaching C′.

Fig. 3.

Gibbs free energy for a water monolayer with N = 4×10⁴ water molecules at P = 1.98 GPa and T = 158 K. The two minima, one at high energy and high density, and the other at low energy and low density, respectively the LDL and HDL phases of the system. The projection of G on the E/N − ρ plane shows that there is a linear relation between the accessible energies and densities for the coexisting states at the chosen P and T. The two minima have approximately the same G value, consistent with the coexistence of two phases

Therefore, with the coarse-grained model of confined water presented here, we can, on the one hand, calculate the free energy G landscape in the mean-field approximation; on the other hand, we can calculate G by simulations, even at very low T where detailed water models cannot be easily equilibrated. In both calculations we find a free-energy landscape typical of a first-order phase transition ending in a critical point.

A model for protein in water

In the previous section we define a coarse-grained model for a water monolayer. We show that the model compares well with experiments probing protein hydration water and that it predicts a complex phase diagram at low T, below the limit of stability of bulk liquid water, and high P. As described in the introduction, under these conditions folded proteins are destabilized. Following our discussion about how it could be relevant to take into account the HB free energy to explain the lost of stability of folded proteins, it is intriguing to test if the proposed water model could give insight into the mechanism of unfolding.

To this goal, we modify the water model to introduce the effect of the protein–water interface. For the sake of simplicity, we will limit our discussion to the case of a single protein embedded into a water monolayer. Although this case is far from the complex studies of a protein embedded into bulk water, the model gives instructive results.

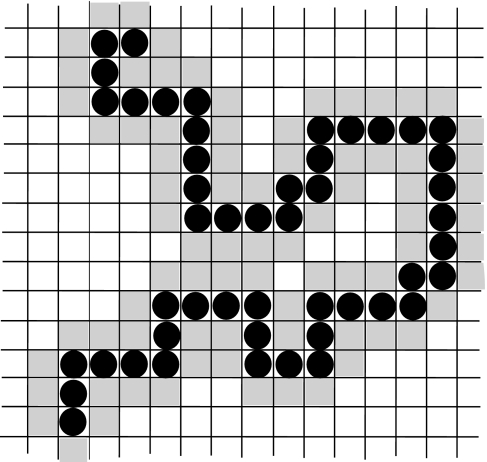
The simplest protein that we can consider is a hydrophobic homopolymer, schematized as a self avoiding chain (Fig. 4). Following the discussion of Muller [12], we require that, consistent with experiment, water molecules in contact with a hydrophobic monomer have a larger decrease of enthalpy upon HB formation than bulk water. Also consistent with Muller–Lee–Graziano’s discussion [29], the fraction of broken HBs at the hydrophobic interface is larger than the fraction of broken HBs in the bulk.

Fig. 4.

Example of configuration of a homopolymer in the coarse-grained model of a protein suspended in water. Each cell is occupied either by a water molecule (white and gray cells) or a hydrophobic homopolymer monomer (cells with a filled black circle). The gray cells represent the sites occupied by shell water. The enthalpy gain for HB formation between shell water molecules is larger than that between bulk water molecules, according to (22). Shell water molecules cannot form hydrogen bonds with nearest neighbor hydrophobic monomers

The first requirement is achieved by adding a term to the water Hamiltonian equation (15)

22

where the sum is taken over the nearest neighbor water molecules in the protein hydration shell (Fig. 4), and λ > 0 is an adjustable parameter accounting for the larger enthalpy decrease for HBs in the hydration shell. Hence, for a HB formed between water molecules in the shell, the enthalpy variation is − J(1 + λ) + Pv_HB, and the total enthalpy for protein into water is

23

where H is given by (15).

The second requirement of Muller–Lee–Graziano approach, i.e., a larger number of broken HBs at the interface, is achieved by volume exclusion. Once a cell of our system is occupied by a protein monomer, it cannot be occupied by a water molecule. Therefore, a water molecule in the hydration shell cannot form a HB in the direction of the monomer and loses at least one HB (and can lose more if it has more monomers as nearest neighbors, as shown in Fig. 4).

In the following section, we will define the algorithm adopted to generate protein equilibrium configurations. To this purpose, we follow a MC procedure that mimics the dynamics at large time scales.

Monte Carlo algorithm

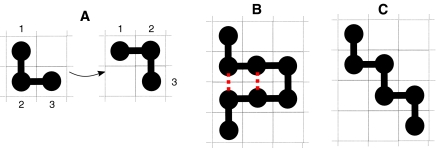
We perform MC simulations in the constant NPT ensemble. In every MC step, we choose a cell at random. If it is occupied by a water molecule, we change randomly one of its σ variables. If it is occupied by a monomer and if the monomer is in a corner configuration (Fig. 5a) then we swap its position with the position of the water molecules in the cell in the opposite corner. By doing this, we keep the inter-monomer distances constant.

Fig. 5.

a Monomer 2 is in a corner configuration and can be displaced from the configuration on the left to the configuration on the right and vice versa. b Homopolymer configuration with two contact points, indicated with dotted lines. c Homopolymer configuration without contact points

If the cell, picked at random, is occupied by a monomer not in a corner configuration, no displacement is performed because it would change the inter-monomer distance. This limitation is introduced in order to avoid in the enthalpy expression (23) any term accounting for the elastic energy of the homopolymer. The effects of this elastic contribution are for the moment outside of the scope of the present work.

Finally, as in the cases discussed in the previous section, to keep the pressure of the system constant, every N random changes of the cell variables (where N is the total number of cells in the system), we attempt to rescale all the system volume by a factor that is tuned in a way to guarantee a 50% acceptance ratio. All the MC moves described above are accepted or rejected according to the Boltzmann factor associated with the enthalpy change caused by the move.

In order to study the folding–unfolding process of the proteins, we calculate the number of contact points N_cpts as illustrated in Fig. 5. In this calculation, we do not count the monomers that are adjacent along the homopolymer.

Preliminary results for hydrated homopolymers

We study a system with N water molecules and a hydrophobic homopolymer chain with N_m monomers. In our preliminary simulations we used N = 650 or N = 1,000 and N_m = 12 or N_m = 50. The parameters are chosen, for consistency, as in previous analysis [66]: ε = 5.8 kJ/mol, J = 2.9 kJ/mol, J_σ = 0.29 kJ/mol, 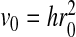, h = 7 Å, v_HB/v₀ = 0.5 and q = 6. We choose λ = 0.7 for the larger decrease of enthalpy at the hydrophobic interface.

Our results display a non-monotonic behavior of N_cpts as a function of T at low P. At high pressure we observe a region in the P − T plane where the number of contact points is at least 51% of the maximum possible number. By definition, we consider these configurations as belonging to the set of folded states. We observe that the region of folded states is included within a larger region in the P − T plane where the number of contact points is at least 49% of the maximum possible number. By definition, we consider those configurations as belonging to a molten globule (we thank M. Vendruscolo for discussing this point).

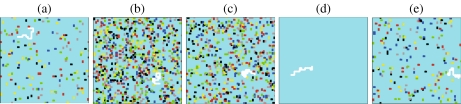
We find that the region of folded states has an elliptic shape that resembles the theoretical prediction (Fig. 1). In particular, we observe that a folded protein unfolds upon cooling, giving rise to the cold denaturation process. It also unfolds by increasing the pressure as expected by pressure denaturation (Fig. 6). Since our stability region is at high P, we are also able to observe the unfolding by decreasing pressure, a phenomena that is predicted by general theoretical considerations, as discussed in the Introduction. We also find that the axes of the elliptical stability region are tilted as expected (Fig. 1).

Fig. 6.

Typical configurations of folding–unfolding of a coarse-grained protein suspended in water at different temperatures T and high pressures P. The protein is represented as a fully hydrophobic chain (in white), surrounded by water molecules (turquoise background). We use different color sticks for HBs in different bonding states. a At high P and high T, the protein unfolds and the number of HBs of the surrounding water is small. b At the same pressure but lower T, the protein collapses into a molten globule state. c At lower T the protein folds, while the surrounding water has a large number of HBs. d At much lower T we observe cold denaturation of the protein when the number of HBs is largely reduced (zero in the configuration represented here). e At higher P the denaturation occurs at higher T, and the mechanism of unfolding seems to be dominated by the reduction of HBs under these conditions

Summary and discussion

Behavior of water supercooled at very low temperature is still an object of debate. The presence of a second critical point C′ could be relevant to understanding how the structure of liquid water changes around proteins and how affects protein properties. Experiments on water confined in nano-structures offer the possibility to access a range of temperatures where bulk liquid water would not be stable and would form ice. These conditions are common in crowded environments, such as inside biological cells. Moreover, at these temperatures a number of proteins unfold. Hence, confinement allows the study of water under conditions that are relevant to biological systems.

Despite the growing interest of the scientific community in water at hydrophobic and hydrophilic interfaces, it is still unclear how interaction with confining surfaces affects the thermodynamics of water. For example, recently Strekalova et al. [66] observed that the fluctuations of supercooled water confined into a hydrophobic porous material are drastically smaller than those of water in weaker confinement. They found that the response functions C_P, α_P and K_T are largely reduced as a consequence of the interaction with the porous medium. An extreme consequence of this change is the disappearance of the liquid-liquid phase transition at high pressures [66]. Therefore, further work is necessary to clarify the many issues related to the dynamics and thermodynamics of water at these interfaces.

Here, we presented a coarse-grained model for a monolayer of water and its extension to the case of solvated proteins. The model takes into account the cooperativity between HBs and has been studied by simulations and mean-field calculations. Previous results about the phase diagram, the diffusivity properties, the response functions C_P, α_P and K_T of the model and the connection of these quantities with HB dynamics are in agreement with experimental results and validate the model.

We adopted this model in the context of protein folding. For the sake of simplicity, we consider the case of a protein schematized as a self-avoiding hydrophobic homopolymer. Following Muller’s analysis [12], we assume that the network of HBs is perturbed by the presence of hydrophobic solute with large size leading to interaction among the water molecules at the interface that are stronger than in the bulk, and to a larger number of broken HBs with respect to the bulk.

Our preliminary results reproduce hot, cold and pressure denaturation as well as the existence of intermediate states (molten globule). We find that the stability region for the folded protein has the theoretically expected elliptic shape in the P − T plane. Further work is in progress to elucidate the relevant mechanism governing protein stability in this coarse-grained model.