Skip to main content
PMC home page
Annals of Botany logoLink to Annals of Botany
. 2011 Dec 30;109(4):681–692. doi: 10.1093/aob/mcr302

Maximum likelihood inference implies a high, not a low, ancestral haploid chromosome number in Araceae, with a critique of the bias introduced by ‘x’

Natalie Cusimano 1,*, Aretuza Sousa 1, Susanne S Renner 1
PMCID: PMC3286273  PMID: 22210850

Abstract

Background and Aims

For 84 years, botanists have relied on calculating the highest common factor for series of haploid chromosome numbers to arrive at a so-called basic number, x. This was done without consistent (reproducible) reference to species relationships and frequencies of different numbers in a clade. Likelihood models that treat polyploidy, chromosome fusion and fission as events with particular probabilities now allow reconstruction of ancestral chromosome numbers in an explicit framework. We have used a modelling approach to reconstruct chromosome number change in the large monocot family Araceae and to test earlier hypotheses about basic numbers in the family.

Methods

Using a maximum likelihood approach and chromosome counts for 26 % of the 3300 species of Araceae and representative numbers for each of the other 13 families of Alismatales, polyploidization events and single chromosome changes were inferred on a genus-level phylogenetic tree for 113 of the 117 genera of Araceae.

Key Results

The previously inferred basic numbers x = 14 and x = 7 are rejected. Instead, maximum likelihood optimization revealed an ancestral haploid chromosome number of n = 16, Bayesian inference of n = 18. Chromosome fusion (loss) is the predominant inferred event, whereas polyploidization events occurred less frequently and mainly towards the tips of the tree.

Conclusions

The bias towards low basic numbers (x) introduced by the algebraic approach to inferring chromosome number changes, prevalent among botanists, may have contributed to an unrealistic picture of ancestral chromosome numbers in many plant clades. The availability of robust quantitative methods for reconstructing ancestral chromosome numbers on molecular phylogenetic trees (with or without branch length information), with confidence statistics, makes the calculation of x an obsolete approach, at least when applied to large clades.

Keywords: Araceae, Bayesian inference, chromosome evolution, haploid chromosome number, dysploidy, maximum likelihood inference, polyploidy

INTRODUCTION

Chromosome numbers in angiosperms vary from n = 2 (Tsvelev and Zhukova, 1974; Singh and Harvey, 1975; Sokolovskaya and Probatova, 1977; Erben, 1996) over n = 250 (Oginuma et al., 2006) and n = 298 (Johnson et al., 1989) to n = 320 (Uhl, 1978). The range in animals is similar (Crosland and Crozier, 1986; Imai et al., 2002). Such drastic differences in chromosome number, sometimes even within small groups, raise questions about the evolutionary direction and frequency of the implied drastic genome rearrangements. Cytogenetic studies have shown that chromosome numbers can change due to fission, fusion or genome doubling (Guerra, 2008), and there is ample evidence that such changes can contribute to speciation. It has also been inferred that a large fraction of all plant species may have polyploid genomes (Stebbins, 1971; Goldblatt, 1980; Otto and Whitton, 2000; Ramsey and Schemske, 2002; Cui et al., 2006; Soltis et al., 2009; Wood et al., 2009; Jiao et al., 2011). Chromosome counts, however, exist only for 60 000 of the 300 000–352 000 species of flowering plants (Bennett, 1998; http://www.theplantlist.org/browse/A/). Most published numbers are listed in an electronic database for chromosome numbers, the ‘Index of Plant Chromosome numbers’ (http://mobot.mobot.org/W3T/Search/ipcn.html).

Given the incomplete knowledge of angiosperm chromosome numbers, evolutionary changes in chromosome numbers in most clades can only be estimated. Botanists do this by calculating a so-called basic, or monoploid, chromosome number, denoted x, to differentiate it from the haploid (usually the gametophytic) number n and the diploid (sporophytic or somatic) number 2n. The concept of x goes back to Langlet (1927) who explained it using Aconitum as an example; if different Aconitum species have n = 8, n = 12, n = 16 and n = approx. 32, their inferred monoploid number x is 4 (Langlet, 1927: 7). Langlet's idea took off, at least in botany, where thousands of basic chromosome numbers have been inferred, even for poorly counted groups. Thus, for flowering plants, Raven (1975, p. 760) suggested x = 7 as ‘characteristic of all major groups of both dicots and monocots except Caryophyllidae.’ Similarly, base chromosome numbers of x = 12 or x = 5 and 6 have been suggested for Poaceae (reviewed in Hilu, 2004) and x = 7 or x = 12 for Triticeae (Heslop-Harrison, 1992; Luo et al., 2009). Many further examples of divergent base numbers having been calculated for a clade could be cited (Soltis et al., 2005; Blöch et al., 2009). Part of the reason why different researchers arrived at different base numbers (x) has to do with the unclear definition of x, with some treating it in Langlet's original sense as an algebraically discoverable highest common factor, others as ‘the lowest detectable haploid number within a group of related taxa’ (Stuessy, 2009: 264; italics ours), and yet others as ‘the haploid number present in the initial population of a monophyletic clade’ (Guerra, 2008: 340), i.e. an inferred number, since the ‘initial population’ will not usually have its chromosomes counted. How to make the inference is up to the investigator. Zoologists, in contrast, never became enamoured of the concept of an inferred base number x.

Criteria for inferring ancestral (perhaps no longer present) chromosome numbers from empirical counts could come from phylogenetic analyses, the relative frequencies of different haploid numbers in various species groups, cytogenetic work on closely related species or, best, a combination of all such information. Data from genomics and molecular–cytogenetic methods, such as fluorescence in situ hybridization (FISH)-marking chromosomes, are probably the best way to search for evidence of past chromosome number changes because they can identify synteny, fusion sites or unusual locations of centromeres, in turn providing evidence for duplications, fusions or losses (Bowers et al., 2003; Lysak et al., 2006; Peruzzi et al., 2009). Such methods, however, may not be feasible in large clades or those with few species in cultivation.

In 2010, an approach was developed that moves the inference of chromosome number evolution to maximum likelihood (ML) character state reconstruction (Mayrose et al., 2010). Mayrose et al. (2010) formulated probabilistic models describing the evolution of chromosome number across a phylogenetic tree. Their approach makes use of branch lengths as a proxy for time and of the frequencies of different numbers at the tips and in outgroups to infer transition rates between the different states. Ancestral chromosome numbers have previously sometimes been reconstructed using maximum parsimony (e.g. Soltis et al., 2005: 178, 298–302). Parsimony, however, assigns all state transitions the same weight and disregards information contained in phylogenetic branch length, which tends to result in an underestimate of the number of transition events.

In this study we use the approach of Mayrose et al. (2010) to reconstruct ancestral haploid chromosome numbers in Araceae, a large and old family of monocotyledons. For a mainly tropical family, Araceae have a high number of chromosomes counts, with 862 (26 %) of their approx. 3300 species counted, including at least one species for most of the 117 genera (Petersen, 1989; Bogner and Petersen, 2007; Appendix; Supplementary Data Table S1 lists all species with their n and/or 2n counts and the respective references). Two basic chromosome numbers have been suggested for Araceae. Larsen (1969) and Marchant (1973) argued for x = 7, with higher numbers derived through ancient polyploidization events or ascending dysploid series. In contrast, Petersen (1993) hypothesized a base number of x = 14 because 2n = 28 is especially common in the family. The former hypothesis was put forward without the benefit of a phylogenetic framework, but Petersen (and also Bogner and Petersen, 2007) took into account morphological phylogenetic analyses (Grayum, 1990; Mayo et al., 1997).

Molecular phylogenetic work over the past few years has resulted in aroid relationships at the generic level becoming relatively clear (French et al., 1995; Cabrera et al., 2008; Cusimano et al., 2011). We here use the most recent phylogenetic analysis of Araceae to infer chromosome evolution in the family, using the model-based approach of Mayrose et al. (2010), in both its ML and Bayesian implementations, the latter having the advantage that uncertainty in ancestral state probabilities is readily quantified. To test the power of their method, Mayrose et al. (2010) first used simulated data and then four exemplar plant clades (Aristolochia, Carex, Passiflora and Helianthus) with relatively densely sampled phylogenetic trees and chromosome counts. Sampling in these clades ranged from 11 to 100 % of the species in the genera. The Araceae data set analysed here represents an entire family that is larger and older by at least an order of magnitude. This poses challenges that we tried to address by experimentally modifying character codings to take into account uncertainties in the larger genera and the 13 outgroup families.

METHODS

Family and order phylogeny

The phylogenetic tree for Araceae on which ancestral chromosome numbers were inferred in this study is based on the six-plastid marker matrix of Cusimano et al. (2011). Clades are named as proposed in that study. We used the ML tree from that study or an ultrametric Bayesian tree newly obtained using BEAST v. 1·6·1 (Drummond and Rambaut, 2007). In BEAST, we used the GTR + G model with four rate categories, a mean substitution rate estimated from the data, and a pure-birth Yule model as the tree prior. The GTR + G model fit the data best, as assessed with Modeltest (Posada and Crandall, 1998). The analysis was run for 37 million generations, sampling every 1000th step. The burn-in fraction, i.e. the number of trees to be discarded before runs reached stationarity, was assessed using the Tracer v. 1·4·1 program (part of the BEAST package) and AWTY (Nylander et al., 2008). For one set of analyses (below), we included only Araceae. For another, we included one exemplar each of the other families of Alismatales (Stevens, 2001 onwards), using branch lengths of 0·01 except for Tofieldiaceae (Tofieldia), which was the outgroup used by Cusimano et al. (2011) and had an empirical branch length.

Chromosome number coding

Total numbers of genera and species of Araceae were taken from the website Creating a Taxonomic eScience (CATE; http://www.cate-araceae.org/) and then updated by the Araceae specialist Josef Bogner (see Acknowledgements). Of the 117 currently recognized genera of Araceae, 29 are monospecific (and hence can be coded unambiguously for chromosome number), 19 have just two species, 31 have 3–10 species, 25 have 11–50 species and 13 have >50 species. Araceae chromosome counts were compiled from original literature (Supplementary Data Table S1, available online), checking the generic assignment of each species against the current classification and for synonymy. Chromosome numbers for four monotypic genera were contributed by J. Bogner and E. Vosyka (see Acknowledgements) and are newly reported here: Filarum manserichense Nicolson (M. Sizemore s.n., voucher in the herbarium M), Hestia longifolia (Ridl.) S. Y. Wong & P. C. Boyce (J. Bogner 3003, M), Philonotion americanum (A. M. E. Jonker & Jonker) S. Y. Wong & P. C. Boyce (J. Bogner 2911, M) and Pichinia disticha S. Y. Wong & P. C. Boyce (P. C. Boyce s.n., M; Supplementary Data Table S1). One genus was coded as unknown (X), namely the monotypic Schottariella, the chromosomes of which have not been counted. The presence of B chromosomes was not coded. Overall, our phylogenetic analysis includes 113 of the 117 accepted genera of Araceae, with 112 of them coded for haploid chromosome number (Appendix).

Chromosome numbers were coded in three ways to address the problem of genera with more than one chromosome number. First, we coded all reported numbers for each genus, regardless of frequency in different species, but excluding odd numbers (Appendix, column 5; Supplementary Data Table S1). This resulted in 55 genera coded as polymorphic. Our second coding scheme (‘reduced polymorphism’ coding) took into account the frequency of different numbers and treated the most common as the ancestral state (Appendix, column 7; Supplementary Data Table S1). For example, Lemnoideae have many different chromosome numbers, but n = 20 is especially common (Landolt, 1986; Appendix, Supplementary Data Table S1). For genera with numbers suggesting different ploidy levels, we used the lowest haploid chromosome number (e.g. Arum). Polymorphisms could thus be reduced to two states (chromosome numbers) per genus or even a single haploid number, leaving 34 instead of 55 genera with polymorphic numbers. In a third coding scheme (‘informed’ coding), we took into account molecular phylogenetic analyses for the genera Philodendron (Gauthier et al., 2008), Biarum and Typhonium (Cusimano et al., 2010), and assigned the state (chromosome number) found in the early-branching species to the entire genus. The numbers thus inferred were compared with those inferred by Bogner and Petersen (2007). This third approach left just ten genera coded as polymorphic with maximally two states (Appendix, column 8; Supplementary Data Table S1, Supplementary Data Figs S1 and S2). In this third scheme, Lazarum, a genus of 23 species with a few chromosome counts and insufficient phylogenetic information (Matthew Barrett, Botanic Gardens & Parks Authority, West Perth; personal communication, 2011) was coded as ‘unknown’ (X) because no ancestral haploid number could be inferred. In all cases, changes among character states (i.e. chromosome numbers) were assigned equal probability.

The remaining families of Alismatales were coded as follows: Alismataceae n = 7, 8; Aponogetonaceae n = 12, 16, 19; Butomaceae n = 7, 8, 10, 11, 12; Cymodoceaceae n = 7, 8, 10, 14, 15; Hydrocharitaceae n = notably variable; Juncaginaceae n = 6, 8, 15; Maundiaceae only Maundia triglochinoides, no chromosome count reported; Posidoniaceae n = 10; Ruppiaceae n = 8–12, 15; Potamogetonaceae n = 7, 12, 14–18; Scheuchzeriaceae n = 11; Tofieldiaceae n = 15; Zosteraceae n = 6, 9, 10 (numbers from Stevens, 2001 onwards). Those of these families with more than one number listed by Stevens were coded as polymorphic in all analyses. The above-described three coding schemes were first run on the phylogenetic tree that included only Araceae and then on the tree that included the 13 outgroups, resulting in six analyses (labelled A1–A6 in Table 1).

Table 1.

Results from the six analyses (A1–A6) carried out to infer chromosome number changes in Araceae under Bayesian and maximum likelihood optimization

Coding scheme
 Rate parameters
 Events inferred with PP >0·5
 Chromosome no. at Araceae root node
 Chromosome no. ranges at Araceae root node
Analysis Tree: outgroups All poly. Red. poly. Inf. Best model LogLik AIC δ λ ρ μ Losses Gains Dupl. Demi. Bayes: Best n; PP Bayes: 2nd best n; PP ML n Sum PP n Sum PP
A1 + + Mc2 –219·5 445 45·9 3·9 6·9 – 98·1 8·4 14·3 14·3 18; 0·18 16; 0·16 16 16–18 0·5 8–18 0·9
A2 + + Mc2 –236·4 478·9 56·4 0 6·3 – 112·2 0 11·5 13 18; 0·26 17; 0·13 16 17–19 0·51 10–20 0·85
A3 + + Mc2 –245·7 497·3 58·2 0 5·7 – 120·1 0 11·9 13·9 18; 0·26 19; 0·12 17 17–19 0·52 10–20 0·9
A4 – + Mc2 –196·6 399·1 50·4 1·8 6·6 – 86·6 3·2 10·5 9·3 18; 0·38 17; 0·3 17 17–19 0·86
A5 – + Mc2 –213·2 432·4 53·6 0 5·6 – 87·2 0 9·8 9·4 18; 0·42 17; 0·23 17 17–19 0·9
A6 – + Mc2 –222·4 450·7 58·1 0 5·4 – 94·4 0 9·7 10·5 18; 0·37 19; 0·34 18 17–19 0·85
Open in a new tab

Only the best-fitting models are shown. Tree (column 2) refers to whether outgroups were included or not; coding scheme refers to how genera with polymorphic haploid chromosome numbers were coded. All poly., all chromosome number polymorphism coded (scheme 1); Red. poly., reduced polymorphism coding (scheme 2); Inf., phylogenetically informed coding (scheme 3). Best model, Mc2 (constant rate model with duplication rate ρ and demi-duplication rate μ; compare Table 2); Logarithmic likelihood (LogLik) and AIC scores; rate parameters (δ = chromosome loss rate, λ = chromosome gain rate, ρ = duplication rate, μ = demi-duplication rate); frequency of the four possible event types with a posterior probability (PP) > 0·5; haploid chromosome number inferred at the root node under Bayesian optimization with the respective PP, and under maximum likelihood (ML). The last column shows the chromosome number range inferred for the root node, each with its PP.

Inference of chromosome number change

For ML and Bayesian phylogenetic inferences of ancestral haploid chromosome numbers, we relied on the chromEvol program v. 1·2 of Mayrose et al. (2010; http://www.zoology.ubc.ca/prog/ chromEvol.html). This implements eight models of chromosome number change (Table 2), two more than described in the original paper. The models include the following six parameters: polyploidization (chromosome number duplication with rate ρ, ‘demi-duplication’ or triploidization with rate μ) and dysploidization (ascending, chromosome gain rate λ; descending, chromosome loss rate δ) and two linear rate parameters, λ1 and δ1, for the dysploidization rates λ and δ, allowing them to depend on the current number of chromosomes. Four of the models have a constant rate, whereas the other four include the two linear rate parameters. Both model sets also have a null model that assumes no polyploidization events. We fitted all models to the data, each with 10 000 simulations to compute the expected number of changes of the four transition types along each branch. The maximum number of chromosomes was set to 10× higher then the highest number found in the empirical data, and the minimum number was set to 1. The null hypothesis (no polyploidy) was tested with likelihood ratio tests using the Akaike information criterion (AIC).

Table 2.

The eight models of chromosome number evolution implemented in the software of Mayrose et al. (2010), indicating the considered parameter estimates (δ, λ, ρ, μ, δ1, λ1), the number of parameters included, and, in the case of μ, with which condition

Model δ λ ρ μ δ1 λ1 No. of parameters
Mc1 + + + – – – 3
Mc2 + + + ρ = μ – – 3
Mc3 + + + ρ ≠ μ – – 4
Mc0 + + ρ = 0 μ = 0 – – 2
Ml1 + + + – + + 5
Ml2 + + + ρ = μ + + 5
Ml3 + + + ρ ≠ μ + + 6
Ml0 + + ρ = 0 μ = 0 + + 4
Open in a new tab

Mc indicates models with constant rates, and Ml models that include linear rate parameters (δ1, λ1). Zero indicates the respective null model.

We also ran an analysis, using the informed polymorphism-coding scheme, but excluding Calla because of its unclear relationships in Araceae (Cusimano et al., 2011). For a final sensitivity test, we again used the informed coding scheme but the non-ultrametric ML phylogenetic tree from Cusimano et al. (2011) instead of the ultrametric tree used in the remaining analyses.

RESULTS

The results obtained in the six analyses (A1–A6) are summarized in Table 1. The three-parameter constant-rate model (Mc2), with the chromosome duplication rate equal to the demi-duplication rate, was the best explanation of the empirical data in all analyses. All analyses rejected the null model of no polyploidy with high significance (P < 0·999). The inferred rates of change, chromosome numbers at nodes (and their probability) and numbers of events were similar regardless of which of the three schemes for polymorphism coding was applied. We therefore show the results obtained from Bayesian and ML analyses with the most conservative coding scheme, namely the one including all polymorphisms and all outgroups (Table 1, A1; Figs 1 and 2). For comparison, the results from analysis A6, without outgroups and the phylogenetically informed coding (Appendix, column 8), can be found in Supplementary Data Figs S1 and S2.

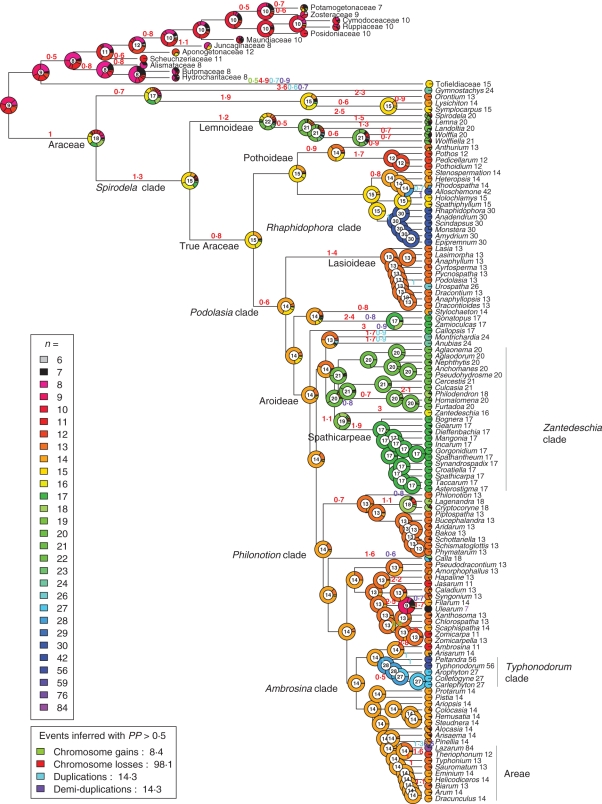
Fig. 1.

Fig. 1.

Open in a new tab

Chromosome number evolution in Araceae inferred under Bayesian optimization, with outgroups included and all polymorphic chromosome states coded (analysis A1 in Table 1). Pie charts at nodes and tips represent the probabilities of the inferred chromosome number(s); numbers inside charts have the highest probability. Numbers at the tips are chromosome numbers inferred with the highest probability, i.e. the inferred ancestral haploid chromosome number for each genus. Numbers above branches represent the inferred frequency of those of the four possible events (gains, losses, duplications and demi-duplications) that had a probability >0·5. The colour coding of chromosome numbers and event types is explained in the insets.

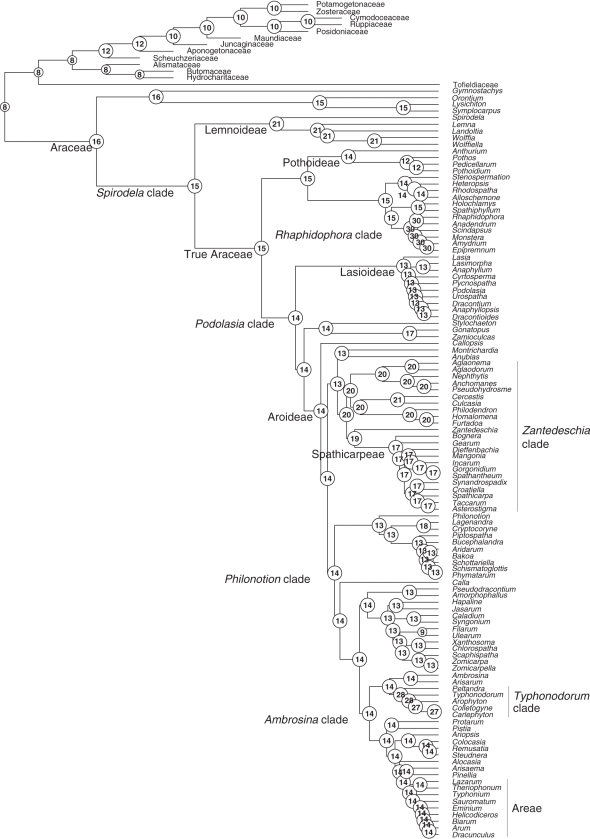
Fig. 2.

Fig. 2.

Open in a new tab

Chromosome number evolution in Araceae inferred under maximum likelihood optimization, with outgroups included and all polymorphic chromosome states coded (analysis A1 in Table 1).

The loss rate δ ranges from 45·9 (Table 1, A1) to 58·2 (A3), and the polyploidization rate ρ = μ from 5·4 (A6) to 6·9 (A1). A gain rate λ is inferred only for models A1 (3·9) and A4 (1·8, analyses with all polymorphisms coded). The number of events inferred with a probability of >0·5 is higher in the analyses using the tree with outgroups than in that without outgroups, simply because it has more branches. Inferred chromosome loss events range from 98·1 (A1) to 120·1 (A3), duplications from 11·5 (A2) to 14·3 (A1) and demi-duplications from 13 (A2) to 14·3 (A3) ); in A1, 8·4 chromosome gain events were inferred, whereas, in the tree without outgroups, the number of losses ranges from 86·6 (A4) to 94·4 (A6), that of duplications from 9·7 (A6) to 10·5 (A4) and that of demi-duplications from 9·3 (A4) to 10·5 (A6); finally in A4, 3·2 chromosome gain events were inferred (Table 1, Fig. 1 and Supplementary Data Fig. S1, Bayesian inference). In the Bayesian analyses, the haploid chromosome number at the root with the highest posterior probability (PP) was n = 18, and support for this number was higher in analyses without outgroups (0·37–0·42) than in those with outgroups (0·18–0·26, Table 1). Similarly, a range of n = 17–19 at the root node had a PP of ≥0·85 without outgroups, but only ≤0·52 when outgroups were included (Table 1). A broader range of ancestral numbers [n = 8–18 (A1); n = 10–20 (A2, A3)] could be inferred with higher PP (>0·85, Table 1, Fig. 1 and Supplementary Data Fig. S1). In the ML analyses with outgroups (Fig. 2), the most likely haploid number at the root was n = 16/17, and without outgroups it was 17/18 (Table 1; Supplementary Data Fig. S2).

To describe inferred chromosome evolution in Araceae, we focus on the Bayesian inference of the most conservative analysis scheme A1 depicted in Fig. 1. Starting from the root node, chromosome numbers decreased, becoming n =15 along the branch leading to the Spirodela clade (PP = 0·32; n = 16: PP = 0·29), n = 15 in Araceae (PP = 0·55; n = 14: PP = 0·21), and n = 14 in the Podolasia clade (PP = 0. 62; n = 15: PP = 0·24). The number n = 14 is inferred with increasing probability as one moves up the phylogenetic tree towards the present. It has 0·77 PP in Aroideae and 0·99 PP in the Ambrosina clade.

Increases in chromosome number are inferred as deriving from (demi-) duplication events, never via single chromosome gains (centric fission), whereas decreases in chromosome number are inferred as resulting from chromosome loss (fusion). The most likely events (PP >0·5) predicted by the best-fitting model are descending dysploidy (98·1 events), and these are inferred both on branches leading to major clades (e.g. Pothoideae, Lasioideae and Spathicarpeae) and on terminal branches. The only chromosome gain event in Araceae inferred with high probability occurred on the branch leading to Scaphispatha (n = 14). Polyploidization events (29 in total, Fig. 1) occur mainly towards the tips of the tree (Gymnostachys, Alloschemone, Urospatha, Anubias, Montrichardia, Cryptocoryneae, Calla, Filarum and Peltandra). Only three polyploidization events are inferred deeper in the tree: a genome duplication on the branch leading to the Rhaphidophora (Fig. 1) clade (from n = 15 to n = 30), a demi-duplication on the branch leading to the Zantedeschia clade (from n =14 to n = 21) and one duplication event on the branch leading to the Typhondorum clade (from n = 14 to n = 28).

Results of the two additional analyses (inclusion/exclusion of Calla; ultrametric or non-ultrametric trees) did not yield results substantially different from those obtained in analysis A6 and shown in Supplementary Data Fig. S1. Model Mc2 remained the best-fitting model, and chromosome number reconstructions at nodes and change rates were similar.

DISCUSSION

The results presented here provide an example of the power of ML-based or Bayesian inference of chromosome number changes. The new approach, which distinguishes (and separately infers) chromosome gains, losses, polyploidization and demi-ploidization, not only reconstructs numbers at particular phylogenetic nodes, but also infers rates of change throughout the phylogenetic tree. Equally importantly, Bayesian PPs yield a statistically well-understood measure of confidence in the results. Most previous ancestral chromosome numbers, in contrast, have been inferred without confidence assessment (examples and critical discussion in Soltis et al., 2005). The experiments we carried out with the different coding schemes for genera polymorphic for chromosome number revealed surprising robustness of the states inferred at interior nodes, although as expected the inclusion or exclusion of outgroups (in our case 13 families) affected the number inferred for the basal-most node, albeit only slightly (Table 1). The results of the present study further confirm that model-based chromosome inference works well even with large data matrices; the largest of the four matrices analysed by Mayrose et al. (2010) had 107 terminals, and the present tree had 126.

Chromosome fusion (loss) appears to be the predominant pattern in the evolution of chromosome number in Araceae; polyploidization events are much less frequent and apparently occurred mainly towards the tips of the tree. However, ancient polyploidization events may be harder to detect than recent ones, because of the genomic restructuring that follows polyploidization. Only detailed studies, perhaps involving chromosome painting techniques, will reveal how rapid intergenomic rearrangements have occurred after genome doubling, perhaps especially following hybridization (Hayasaki et al., 2000; Lim et al., 2008; Peruzzi et al., 2009; Tu et al., 2009).

In general, basic chromosome numbers inferred according to Langlet's (1927) approach, as the lowest detectable or somehow calculated haploid number within a group of related taxa, will be low, simply because of the way they are arrived at (see Introduction for Langlet's original example). For Araceae, the hypothesized ancestral numbers were x = 14 or x = 7 (Larsen, 1969; Marchant, 1973; Petersen, 1993). The present study instead inferred an ancestral haploid number of n = 16 (under ML) or n = 18 (with Bayesian inference) and, moreover, an evolutionary trend from higher to lower numbers, rather than the other way around. One needs to keep in mind that none of the earlier studies (Larsen, 1969; Marchant, 1973; Petersen, 1993) included Lemnoideae in Araceae, a taxonomic difference that greatly affects the range of chromosome numbers found in early-diverging clades (Figs 1 and 2). It is also likely that the high frequency of 2n = 28 in the well-counted unisexual Aroideae unduly influenced the hypotheses about x being 7 or 14. Finally, the earlier hypotheses were developed without the relatively complete and solid phylogenetic information that is available today.

Nevertheless, any inferences about character evolution from a taxon sampling of just 112 representatives, however well coded their states may be, must be regarded with caution. Every genus with more than one species must have its own, perhaps complex, history of cytogenetic change. It is also conceivable that dysploidy rates might change in different parts of the tree (e.g. in clades of taxa living in different environments) and that relatively derived and rapidly radiating clades, perhaps with frequent hybridization, might have different rates of polyploidization than older, genetically isolated groups. The phylogenetically informed coding scheme (our scheme three) may be the best way of coding ancestral haploid chromosome numbers in larger clades (here genera), an idea that could be tested by cytological work in small genera with solid phylogenetic hypotheses, such as Arum (e.g. Espíndola et al., 2010).

Given the inferred high ancestral haploid numbers, chromosome fusions (neutrally termed ‘losses’ in the models of Mayrose et al., 2010) must have been common during evolution of Araceae. This hypothesis now needs to be tested. Large chromosomes in Araceae, with distally positioned centromeres, may be the result of fusion between smaller metacentric chromosomes (Petersen, 1993). If so, one expects to find interstitial telomeric sites. With probes, using primer pairs homologous to the basic plant telomeric repeats, one can visualize these regions (Ijdo et al., 1991; Weiss-Schneeweiss et al., 2004). Such chromosome preparations are now being carried out in our laboratory on Typhonium species with suspected chromosome fusion (predicted from high or low chromosome numbers in species of known phylogenetic relationships).

The results of the present study suggest that quantitative methods for inferring ancestral haploid numbers should replace inferences that rely on algebraically finding the greatest common factor for a series of numbers or on interpreting the lowest available haploid count as the ancestral condition. The new approaches also yield a measure of statistical confidence or estimates of the rates of polyploidization, fusion or fission, We suggest that the concept ‘x’, which sets botanists apart from zoologists, be retained only in the context of small species groups in which the history of polyploidy is known in detail (Vanzela et al. 2003).

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and consist of the following. Table S1: chromosome counts for species of Araceae with references. Figure S1: chromosome number evolution in Araceae inferred under Bayesian optimization, with phylogenetically informed coding and outgroups excluded. Figure S2: chromosome number evolution in Araceae inferred under maximum likelihood optimization, with phylogenetically informed coding and outgroups excluded.

Supplementary Data
supp_109_4_681__index.html (1.2KB, html)

ACKNOWLEDGEMENTS

We are grateful to Michael Fay and two anonymous reviewers for the constructive suggestions, J. Bogner and L. Nauheimer for tirelessly discussing Araceae evolution with us and for checking Supplementary Table S1 for synonymous or transferred species names, and E. Vosyka for help with chromosome counts. This work was supported by the Deutsche Forschungsgemeinschaft, RE 693/7-1.

APPENDIX

The 117 genera of Araceae with number of species, number and percentage of species with chromosome counts, diploid chromosome numbers and coded ancestral haploid chromosome numbers in the three coding schemes used in this study (see Methods). X = unknown.

Genera Spp. number Spp. counted % Counted diploid chromosome numbers 2n = All polymorphic n = Reduced polymorphic n = Informed n =
1 Aglaodorum 1 1 100 40 20 20 20
2 Aglaonema 23 6 26 14, 40, 100 7, 20, 50 7, 20, 50 20
3 Alloschemone 2 1 50 84 42 42 42
4 Alocasia 107 17 16 24, 26. 28, 40,42, 56, 68, 70, 84 12, 13, 14, 20, 21, 28, 34, 35, 42 12, 13, 14, 20, 21, 28, 34, 35, 42 14
5 Ambrosina 1 1 100 22 11 11 11
6 Amorphophallus 196 47 24 26, 28, 39 13, 14 13, 14 13
7 Amydrium 5 2 40 60 30 30 30
8 Anadendrum 11 3 27 60 30 30 30
9 Anaphyllopsis 3 1 33 26 13 13 13
10 Anaphyllum 2 2 100 26 13 13 13
11 Anchomanes 6 3 50 40 20 20 20
12 Anthurium 903 171 19 14, 20, 24, 26, 28, 29, 30 + Bs, 34, 36, 40, 48, 49, 56, 60, 84, approx. 90, approx. 124 7, 13, 15, 17, 18, 30 7, 13, 15, 17, 18, 30 15
13 Anubias 8 8 100 48 24 24 24
14 Apoballis 12 6 50 26, 39, 56 13, 28 13 13
15 Aridarum 10 4 40 24, 26 12, 13 12, 13 12, 13
16 Ariopsis 2 1 50 28, 84, 86 14, 42, 43 14 14
17 Arisaema 150 97 65 20, 24, 26, 28, 32,42, 48, 52, 56, 64, 70, 72, 84, 112, 140, 168 10, 12, 13, 14, 16, 21, 24, 26, 28, 32, 42, 56, 70, 84 10, 12, 13, 14, 16, 21, 24, 26, 28, 32, 42, 56, 70, 84 14
18 Arisarum 4 2 50 14, 28, 42, 52, 56 7, 14, 21, 26, 28 7, 14, 21, 26, 28 14
19 Arophyton 7 6 86 38, 40, 54, approx. 76 19, 20, 27 19, 20, 27 19
20 Arum 29 26 90 28, 29, 30, 42, 56, 63, 70, 84 14, 15, 21, 28, 35, 42 14 14
21 Asterostigma 8 2 25 34 17 17 17
22 Bakoa 2 2 100 26 13 13 13
23 Biarum 21 12 57 16, 18, 22, 24, 26, 32, 36, 40, 74, approx. 96, 98, 108 8, 9, 11, 12, 13, 16, 18, 20, 37, 49, 54 8, 9, 11, 12, 13, 16, 18, 20, 37, 49, 54 13
24 Bognera 1 1 100 34 17 17 17
25 Bucephalandra 3 3 100 26 13 13 13
26 Caladium 12 6 50 19, 22, 26, 28, 30 11, 13, 14, 15 11, 13, 14, 15 13, 14
27 Calla 1 1 100 36, 54, 60, 72 18, 27, 30, 36 18 18
28 Callopsis 1 1 100 36 17 17 17
29 Carlephyton 3 3 100 54, 108 27, 54 27 27
30 Cercestis 10 6 60 approx. 36, 42 21 21 21
31 Chlorospatha 28 2 7 26 13 13 13
32 Colletogyne 1 1 100 44, 46, 54 22, 23, 27 27 27
33 Colocasia 16 5 31 26, 28, 30, 36, 38, 42, 44, 46, 48, 52, 58, 84, 116 13, 14, 15, 18, 19, 21, 22, 23, 24, 26, 42, 58 13, 14, 15, 18, 19, 21, 22, 23, 24, 26, 42, 58 14
34 Croatiella 1 1 100 34 17 17 17
35 Cryptocoryne 60 64 107 20, 22, 28, 30, 33, 34, 36, 42, 54, 56, 66, 68, 70, 72, 85, 88, 90, 102, 112, approx. 132 10, 11, 14, 15, 17, 18, 21, 27, 28, 33, 34, 35, 36, 44, 45, 51, 56 10, 11, 14, 15, 17, 18, 21, 27, 28, 33, 34, 35, 36, 44, 45, 51, 56 17, 18
36 Culcasia 24 9 38 approx. 40, 42 21 21 21
37 Cyrtosperma 12 4 33 24, 26 12, 13 12, 13 13
38 Dieffenbachia 57 14 25 34, 36, 40, 44, 68 17, 18, 20, 22, 34 17 17
39 Dracontioides 2 1 50 26 13 13 13
40 Dracontium 24 5 21 26 13 13 13
41 Dracunculus 2 2 100 28, 32 14, 16 14 14
42 Eminium 9 3 33 28 14 14 14
43 Epipremnum 15 3 20 60, 70, 84 30, 35, 42 30, 35, 42 30
44 Filarum 1 1 100 28 14 14 14
45 Furtadoa 2 1 50 40 20 20 20
46 Gearum 1 1 100 34, 68 17, 34 17 17
47 Gonatopus 5 4 80 34, approx. 68 17 17 17
48 Gorgonidium 8 3 38 34 17 17 17
49 Gymnostachys 1 1 100 48 24 24 24
50 Hapaline 8 2 25 26, 28 13, 14 13, 14 13, 14
51 Helicodiceros 1 1 100 56 14 14 14
52 Hestia 1 1 100 26 13 13 13
53 Heteropsis 17 1 6 26–28 13, 14 13, 14 14
54 Holochlamys 1 1 100 30, 60 15 15 15
55 Homalomena 117 24 21 38, 40, 42, 56 19, 20, 21, 28 19, 20, 21, 28 20
56 Incarum 1 1 100 34 17 17 17
57 Jasarum 1 1 100 22 11 11 11
58 Lagenandra 15 14 93 32, 36, approx. 72 16, 18 16, 18 18
59 Landoltia 1 1 100 40,46, 50 20, 23, 25 20 20
60 Lasia 2 1 50 26 13 13 13
61 Lasimorpha 1 1 100 26 13 13 13
62 Lazarum 23 2 9 approx. 118, 130, 152, approx. 160,168 59, 65, 76, 84 59, 65, 76, 84 X
63 Lemna 13 11 85 20, 30, 36, 40, 42, 44, 50, 60, 63, 64, 70, 80, 84, 126 10, 15, 18, 20, 21, 22, 25, 30, 32, 35, 40, 42, 63 20 20
64 Lysichiton 2 2 100 28 14 14 14
65 Mangonia 2 1 50 34 17 17 17
66 Monstera 39 5 13 24, 56, 58, 60 12, 28, 29, 30 30 30
67 Montrichardia 2 1 50 48 24 24 24
68 Nephthytis 6 5 83 36, 40, 60 18, 20, 30 18, 20 18, 20
69 Ooia 2 1 50 26 13 13 13
70 Orontium 1 1 100 26 13 13 13
71 Pedicellarum 1 1 100 24 12 12 12
72 Peltandra 2 1 50 112 56 56 56
73 Philodendron 483 31 6 26, 30, 32, 34, 36, 48, 54 13, 15, 16, 17, 18, 24, 27 13, 15, 16, 17, 18, 24, 27 17, 18
74 Philonotion 3 1 33 26 13 13 13
75 Phymatarum 1 1 100 26, 28 13 13 13
76 Pichinia 1 1 100 26 13, 14 13, 14 13
77 Pinellia 9 9 100 20, 26, 28, 39, 42, 52, 54, 72, 78, 90, 91, 99, 104, 108, 115, 116, 117, 128, 129 10, 13, 14, 21, 26, 27, 36, 39, 45, 52, 54, 58, 64 10, 13, 14, 21, 26, 27, 36, 39, 45, 52, 54, 58, 64 13
78 Piptospatha 10 6 60 26, 39 13 13 13
79 Pistia 1 1 100 14, 28 7, 14 7, 14 14
80 Podolasia 1 1 100 26 13 13 13
81 Pothoidium 1 1 100 24 12 12 12
82 Pothos 57 3 5 24, 36, 60 12, 18, 30 12 12
83 Protarum 1 1 100 28 14 14 14
84 Pseudodracontium 7 2 29 26 13 13 13
85 Pseudohydrosme 2 1 50 approx. 40 20 20 20
86 Pycnospatha 2 2 100 26 13 13 13
87 Remusatia 4 4 100 20, 28, 30, 42, 56 10, 14, 15, 21, 28 10, 14, 15, 21, 28 14
88 Rhaphidophora 98 8 8 26, 42, 54, 56, 60, approx. 120 13, 21, 27, 28, 30 28, 30 28, 30
89 Rhodospatha 29 3 10 28, 56, 60 14, 28, 30 14, 28 14
90 Sauromatum 9 7 78 26, 52, 54, 104 13, 26, 27, 52 13 13
91 Scaphispatha 2 1 50 28 14 14 14
92 Schismatoglottis 100 15 15 26, 30, 39, 52 13, 15, 26 13 13
93 Schottariella 1 0 0 – X X X
94 Scindapsus 35 8 23 48, 60 (42, 56, 58, 64, 70, 112), approx. 110 28, 30 28, 30 28, 30
95 Spathantheum 2 2 100 34 17 17 17
96 Spathicarpa 4 1 25 34 17 17 17
97 Spathiphyllum 49 9 18 30, 60 15, 30 15 15
98 Spirodela 3 2 67 20, 30, 32, 36, 38, 40, 50, 80 10, 15, 16, 18, 19, 20, 25, 40 15, 20 15, 20
99 Stenospermation 50 4 8 28 14 14 14
100 Steudnera 9 4 44 28, 36,56 14, 18, 28 14 14
101 Stylochaeton 18 4 22 28, 56 14, 28 14, 28 14
102 Symplocarpus 5 2 40 30, 60 15, 30 15, 30 15
103 Synandrospadix 1 1 100 34 17 17 17
104 Syngonium 35 9 26 22, 24, 26, 28 11, 12, 13, 14 14 14
105 Taccarum 6 1 17 34 17 17 17
106 Theriophonum 5 5 100 16, 24, 32 (14, 18) 8, 12, 16 8 8
107 Typhonium 68 8 12 10, 16, 18, 20, 26, 36, 52,65 5, 8, 9, 10, 13, 18, 26 5, 6, 7, 8, 9, 10, 13, 18, 26 8, 13
108 Typhonodorum 1 1 100 112 56 56 56
109 Ulearum 2 2 100 14 7 7 7
110 Urospatha 12 1 8 52 26 26 26
111 Wolffia 11 8 73 16, 20, 22, 23, 30, 40, 42, 46, 50, 60, 62, 63, 70, 80 8, 10, 11, 15, 20, 21, 23, 25, 30, 31, 35, 40 20 20
112 Wolffiella 10 7 70 20, 40, 42, 50, 70 10, 20, 21, 25, 35 20 20
113 Xanthosoma 75 11 15 22, 26, 39, 52 11, 13, 26 11, 13, 26 13
114 Zamioculcas 1 1 100 34 17 17 17
115 Zantedeschia 8 7 88 32 16 16 16
116 Zomicarpa 3 2 67 20, 22 10, 11 10, 11 10
117 Zomicarpella 2 1 50 26 13 13 13
Total 3309 847
Mean 61
Open in a new tab

LITERATURE CITED

  1. Bennett MD. Plant genome values: how much do we know? Proceedings of the National Academy of Sciences, USA. 1998;95:2011–2016. doi: 10.1073/pnas.95.5.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Blöch C, Weiss-Schneeweiss H, Schneeweiss GM, et al. Molecular phylogenetic analyses of nuclear and plastid DNA sequences support dysploid and polyploid chromosome number changes and reticulate evolution in the diversification of Melampodium (Millerieae, Asteraceae) Molecular Phylogenetics and Evolution. 2009;53:220–233. doi: 10.1016/j.ympev.2009.02.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bogner J, Petersen G. The chromosome numbers of the aroid genera. Aroideana. 2007;30:82–90. [Google Scholar]
  4. Bowers JE, Chapman BA, Rong J, Paterson AH. Unravelling angiosperm genome evolution by phylogenetic analysis of chromosomal duplication events. Nature. 2003;422:433–438. doi: 10.1038/nature01521. [DOI] [PubMed] [Google Scholar]
  5. Cabrera LI, Salazar GA, Chase MW, Mayo SJ, Bogner F, Davila P. Phylogenetic relationships of aroids and duckweeds (Araceae) inferred from coding and noncoding plastid DNA. American Journal of Botany. 2008;95:1153–1165. doi: 10.3732/ajb.0800073. [DOI] [PubMed] [Google Scholar]
  6. Crosland MWJ, Crozier RH. Myrmecia pilosula, an ant with only one pair of chromosomes. Science. 1986;231:1278–1281. doi: 10.1126/science.231.4743.1278. [DOI] [PubMed] [Google Scholar]
  7. Cui L, Wall PK, Leebens-Mack JH, et al. Widespread genome duplications throughout the history of flowering plants. Genome Research. 2006;16:738–749. doi: 10.1101/gr.4825606. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Cusimano N, Barrett M, Hetterscheid WLA, Renner SS. A phylogeny of the Areae (Araceae) implies that Typhonium, Sauromatum and the Australian species of Typhonium are distinct clades. Taxon. 2010;59:439–447. [Google Scholar]
  9. Cusimano N, Bogner J, Mayo SJ, et al. Relationships within the Araceae: comparisons of morphological patterns with molecular phylogenies. American Journal of Botany. 2011;98:654–668. doi: 10.3732/ajb.1000158. [DOI] [PubMed] [Google Scholar]
  10. Drummond AJ, Rambaut A. BEAST: Bayesian evolutionary analysis by sampling trees. BMC Evolutionary Biology. 2007;7:214. doi: 10.1186/1471-2148-7-214. http://dx.doi.org/10.1186/1471-2148-7-214 . [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Erben M. The significance of hybridization on the forming of species in the genus Viola. Bocconea. 1996;5:113–118. [Google Scholar]
  12. Espíndola A, Buerki S, Bedalov M, Küpfer P, Alvarez N. New insights into the phylogenetics and biogeography of Arum (Araceae): unravelling its evolutionary history. Botanical Journal of the Linnean Society. 2010;163:14–32. [Google Scholar]
  13. French JC, Chung MG, Hur YK. Chloroplast DNA phylogeny of the Ariflorae. In: Rudall PJ, Cribb P, Cutler DF, Humphries CJ, editors. Monocotyledons: systematics and evolution. Vol. 1. Kew, UK: Royal Botanic Gardens; 1995. pp. 255–275. [Google Scholar]
  14. Gauthier MPL, Barabe D, Bruneau A. Molecular phylogeny of the genus Philodendron (Araceae): delimitation and infrageneric classification. Botanical Journal of the Linnean Society. 2008;156:13–27. [Google Scholar]
  15. Goldblatt P. Polyploidy in angiosperms: monocotyledons. In: Lewis WH, editor. Polyploidy: biological relevance. New York: Plenum Press; 1980. pp. 219–239. [Google Scholar]
  16. Grayum MH. Evolution and phylogeny of the Araceae. Annals of the Missouri Botanical Garden. 1990;77:628–697. [Google Scholar]
  17. Guerra M. Chromosome numbers in plant cytotaxonomy: concepts and implications. Cytogenetic and Genome Research. 2008;120:339–350. doi: 10.1159/000121083. [DOI] [PubMed] [Google Scholar]
  18. Hayasaki M, Morikawa T, Tarumoto I. Intergenomic translocations of polyploid oats (genus Avena) revealed by genomic in situ hybridization. Genes and Genetic Systems. 2000;75:167–171. doi: 10.1266/ggs.75.167. [DOI] [PubMed] [Google Scholar]
  19. Heslop-Harrison JS. Molecular cytogenetics, cytology and genomic comparisons. Hereditas. 1992;116:93–99. [Google Scholar]
  20. Hilu KW. Phylogenetics and chromosomal evolution in the Poaceae (grasses) Australian Journal of Botany. 2004;52:13–22. [Google Scholar]
  21. Ijdo JW, Wells RA, Baldini A, Reeders ST. Improved telomere detection using a telomere repeat probe (TTAGGG)n generated by PCR. Nucleic Acids Research. 1991;19:4780. doi: 10.1093/nar/19.17.4780. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Imai HT, Sattaz Y, Waday M, Takahataz N. Estimation of the highest chromosome mumber of eukaryotes based on the minimum interaction theory. Journal of Theoretical Biology. 2002;217:61–74. doi: 10.1006/jtbi.2002.3016. [DOI] [PubMed] [Google Scholar]
  23. Jiao Y, Wickett NJ, Ayyampalayam S, et al. Ancestral polyploidy in seed plants and angiosperms. Nature. 2011;473:97–100. doi: 10.1038/nature09916. [DOI] [PubMed] [Google Scholar]
  24. Johnson MAT, Kenton AY, Bennett MD, Brandham PE. Voanioala gerardii has the highest known chromosome number in the monocotyledons. Genome. 1989;32:328–333. [Google Scholar]
  25. Landolt E. The family of Lemnaceae – a monographic study. Vol. 1. Zürich: Veröffentlichungen des Geobototanischen Instituts der ETH, Stiftung Rübel, Heft 71; 1986. Biosystematic investigations in the family of duckweeds (Lemnaceae) (vol. 2) [Google Scholar]
  26. Langlet O. Beiträge zur Zytologie der Ranunculaceen. Svensk Botanisk Tidskrift. 1927;21:1–17. [Google Scholar]
  27. Larsen K. Cytology of vascular plants: III. A study of aroids. Dansk Botanisk Arkiv. 1969;27:39–59. [Google Scholar]
  28. Lim KY, Soltis DE, Soltis PS, et al. Rapid chromosome evolution in recently formed polyploids in Tragopogon (Asteraceae) PLoS One. 2008;3:e3353. doi: 10.1371/journal.pone.0003353. http://dx.doi.org/10.1371/journal.pone.0003353 . [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Luo MC, Deala KR, Akhunova ED, Akhunova AR, et al. Genome comparisons reveal a dominant mechanism of chromosome number reduction in grasses and accelerated genome evolution in Triticeae. Proceedings of the National Academy of Sciences, USA. 2009;106:15780–15785. doi: 10.1073/pnas.0908195106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Lysak MA, Berr A, Pecinka A, Schmidt R, McBreen K, Schubert I. Mechanisms of chromosome number reduction in Arabidopsis thaliana and related Brassicaceae species. Proceedings of the National Academy of Sciences, USA. 2006;103:5224–5229. doi: 10.1073/pnas.0510791103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Marchant CJ. Chromosome variation in Araceae IV: from Acoreae to Lasieae. Kew Bulletin. 1973;28:199–210. [Google Scholar]
  32. Mayo SJ, Bogner J, Boyce PC. The genera of Araceae. Kew, UK: Royal Botanic Gardens; 1997. [Google Scholar]
  33. Mayrose I, Barker MS, Otto SP. Probabilistic models of chromosome number evolution and the inference of polyploidy. Systematic Biology. 2010;59:132–144. doi: 10.1093/sysbio/syp083. [DOI] [PubMed] [Google Scholar]
  34. Nylander JAA, Wilgenbusch JC, Warren DL, Swofford DL. AWTY (are we there yet?): a system for graphical exploration of MCMC convergence in Bayesian phylogenetics. Bioinformatics. 2008;24:581–583. doi: 10.1093/bioinformatics/btm388. [DOI] [PubMed] [Google Scholar]
  35. Oginuma K, Munzinger J, Tobe H. Exceedingly high chromosome number in Strasburgeriaceae, a monotypic family endemic to New Caledonia. Plant Systematics and Evolution. 2006;262:97–101. [Google Scholar]
  36. Otto SP, Whitton J. Polyploidy incidence and evolution. Annual Review of Genetics. 2000;34:401–437. doi: 10.1146/annurev.genet.34.1.401. [DOI] [PubMed] [Google Scholar]
  37. Peruzzi L, Leitch IJ, Caparelli KF. Chromosome diversity and evolution in Liliaceae. Annals of Botany. 2009;103:459–475. doi: 10.1093/aob/mcn230. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Petersen G. Cytology and systematics of Araceae. Nordic Journal of Botany. 1989;9:119–166. [Google Scholar]
  39. Petersen G. Chromosome numbers of the genera of Araceae. Aroideana. 1993;16:37–46. [Google Scholar]
  40. Posada D, Crandall KA. MODELTEST: testing the model of DNA substitution. Bioinformatics. 1998;14:817–818. doi: 10.1093/bioinformatics/14.9.817. [DOI] [PubMed] [Google Scholar]
  41. Ramsey J, Schemske DW. Neopolyploidy in flowering plants. Annual Review of Ecology and Systematics. 2002;33:589–639. [Google Scholar]
  42. Raven PH. The bases of angiosperm phylogeny: cytology. Annals of the Missouri Botanical Garden. 1975;67:724–764. [Google Scholar]
  43. Singh BD, Harvey BL. Selection for diploid cells in suspension cultures of Happlopappus gracilis. Nature. 1975;253:453. [Google Scholar]
  44. Sokolovskaya AP, Probatova NS. On the least main number of chromosomes (2n = 4) in Colpodium versicolor (Stev.) Woronow. Botanicheskij Zhurnal. 1977;62:241–245. (in Russian) [Google Scholar]
  45. Soltis DE, Soltis PS, Endress PK, Chase MW. Phylogeny and evolution of angiosperms. Sunderland, MA: Sinauer; 2005. [Google Scholar]
  46. Soltis DE, Albert VA, Leebens-Mack J, et al. Polyploidy and angiosperm diversification. American Journal of Botany. 2009;96:336–348. doi: 10.3732/ajb.0800079. [DOI] [PubMed] [Google Scholar]
  47. Stebbins GL. Chromosomal evolution in higher plants. London: Arnold; 1971. [Google Scholar]
  48. Stevens PF. 2001 onwards Angiosperm Phylogeny Website. Version 9, June 2008 [and more or less continuously updated since] [Google Scholar]
  49. Stuessy TF. Plant taxonomy: the systematic evaluation of comparative data. 2nd edn. New York: Columbia University Press; 2009. [Google Scholar]
  50. Tu Y, Sun J, Ge X, Li Z. Chromosome elimination, addition and introgression in intertribal partial hybrids between Brassica rapa and Isatis indigotica. Annals of Botany. 2009;103:1039–1048. doi: 10.1093/aob/mcp045. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Tzvelev NN, Zhukova PG. On the least main number of chromosomes in family Poaceae. Botanicheskij Zhurnal. 1974;59:265–269. (in Russian) [Google Scholar]
  52. Uhl CH. Chromosomes of Mexican Sedum II. Section Pachysedum. Rhodora. 1978;80:491–512. [Google Scholar]
  53. Vanzela ALL, Cuadrado A, Guerra M. Localization of 45S rDNA and telomeric sites in holocentric chromosomes of Rhynchospora tenuis Link (Cyperaceae) Genetics and Molecular Biology. 2003;26:199–201. [Google Scholar]
  54. Weiss-Schneeweiss H, Riha K, Jang CG, Puizina J, Scherthan H, Schweizer D. Chromosome termini of the monocot plant Othocallis siberica are maintained by telomerase, which specifically synthesises vertebrate-type telomere sequences. The Plant Journal. 2004;37:484–493. doi: 10.1046/j.1365-313x.2003.01974.x. [DOI] [PubMed] [Google Scholar]
  55. Wood TE, Takebayashi N, Barker MS, Mayrose I, Greenspoon PB, Rieseberg LH. The frequency of polyploid speciation in vascular plants. Proceedings of the National Academy of Sciences, USA. 2009;106:13875–13879. doi: 10.1073/pnas.0811575106. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_109_4_681__index.html (1.2KB, html)
supp_mcr302_mcr302supp_figs.pdf (864.7KB, pdf)
supp_mcr302_mcr302supp_table.pdf (561.6KB, pdf)

Articles from Annals of Botany are provided here courtesy of Oxford University Press

RESOURCES