BAYESIAN PHASE I/II ADAPTIVELY RANDOMIZED ONCOLOGY TRIALS WITH COMBINED DRUGS

Abstract

We propose a new integrated phase I/II trial design to identify the most efficacious dose combination that also satisfies certain safety requirements for drug-combination trials. We first take a Bayesian copula-type model for dose finding in phase I. After identifying a set of admissible doses, we immediately move the entire set forward to phase II. We propose a novel adaptive randomization scheme to favor assigning patients to more efficacious dose-combination arms. Our adaptive randomization scheme takes into account both the point estimate and variability of efficacy. By using a moving reference to compare the relative efficacy among treatment arms, our method achieves a high resolution to distinguish different arms. We also consider groupwise adaptive randomization when efficacy is late-onset. We conduct extensive simulation studies to examine the operating characteristics of the proposed design, and illustrate our method using a phase I/II melanoma clinical trial.

1. Introduction

Phase I trials usually aim to find the maximum tolerated dose (MTD) for an investigational drug, and phase II trials examine the efficacy of the drug at the identified MTD. Traditionally, phase I and phase II trials are conducted separately. There is a growing trend to integrate phase I and phase II trials in order to expedite the process of drug development and reduce the associated cost [Gooley et al. (1994); Thall and Russell (1998); O’Quigley, Hughes and Fenton (2001); Thall and Cook (2004); and Yin, Li and Ji (2006); among others]. The majority of these designs focus on single-agent clinical trials.

Treating patients with a combination of agents is becoming common in cancer clinical trials. Advantages of such drug-combination treatments include the potential to induce a synergistic treatment effect, target tumor cells with differing drug susceptibilities, or achieve a higher dose intensity with nonoverlapping toxicities. Trial designs for drug-combination studies involve several distinct features that are beyond the scope of methods for single-agent studies. In single-agent trials, we typically assume that toxicity mono-tonically increases with respect to the dose. However, in a drug-combination dose space, it is difficult to establish such ordering for dose combinations. Consequently, decision making for dose escalation or de-escalation is difficult in drug-combination trials due to the unknown toxicity order. Another important feature that distinguishes drug-combination trials from single-agent trials is the toxicity equivalent contour in the two-dimensional dose-toxicity space. As a result, multiple dose combinations with similar toxicity may be found in phase I drug-combination trials. For these reasons, single-agent phase I/II designs cannot be directly applied to drug-combination trials.

In spite of a rich body of literature on phase I dose-finding designs for drug-combination trials [Simon and Korn (1990); Korn and Simon (1993); Kramar, Lebecq and Candalh (1999); Thall et al. (2003); Conaway, Dunbar and Peddada (2004); Wang and Ivanova (2005); and Yin and Yuan (2009); among others], research on phase I/II designs has been very limited. Recently, Huang et al. (2007) proposed a parallel phase I/II clinical trial design for combination therapies, which, however, only targets MTDs with a toxicity probability of 33% because the “3+3” dose-finding design [Storer (1989)] is used in the phase I component.

Our research is motivated by a cancer clinical trial at M. D. Anderson Cancer Center for patients diagnosed with malignant melanoma. The experimental agents to be combined are decitabine (a DNA methyltransferase in-hibitor, which has shown clinical activity in patients diagnosed with leukemia or myelodysplastic syndrome) and a derivative of recombinant interferon which has been used to treat cancer patients with advanced solid tumors. The primary objective of the trial is to find the most effective, safe doses of both drugs when used in combination to treat melanoma. For this trial, an integrated phase I/II design is more plausible to speed up the drug discovery and reduce the total cost.

Toward this goal, we propose a new seamless phase I/II design to identify the most efficacious dose combination that also satisfies certain safety requirements for oncology drug-combination trials. In the phase I part of the trial, we employ a systematic dose-finding approach by using copula-type regression to model the toxicity of the drug combinations. Once phase I is finished, we take a set of admissible doses to phase II, in which patients are adaptively randomized to multiple treatment arms corresponding to those admissible doses. We propose a novel adaptive randomization (AR) procedure based on a moving reference to compare the relative efficacy among the treatments in comparison. Our AR has a high resolution to distinguish treatments with different levels of efficacy and thus can efficiently allocate more patients to more efficacious arms. The proposed design allows us to target any prespecified toxicity rate and fully utilize the available information to make dose-assignment decisions.

The rest of the paper is organized as follows. In Section 2 we adopt a copula-type probability model for toxicity and develop a new AR procedure for seamless implementation of the phase I/II drug-combination trial design. In Section 3 we apply our design to a melanoma clinical trial, and assess its operating characteristics through extensive simulation studies. In Section 4 we extend the proposed design to accommodate trials with late-onset efficacy using group sequential AR. We conclude with a brief discussion in Section 5.

2. Phase I/II drug-combination design

2.1. Dose finding in phase I

For ease of exposition, consider a trial with a combination of two agents, A and B; let a_i be the prespecified toxicity probability corresponding to A_i, the ith dose of drug A, with a₁ < a₂ < … < a_I; and let b_j be that of B_j, the jth dose of drug B, with b₁ < b₂ < … < b_J. Before the two drugs are combined, each drug should have been thoroughly investigated when administered alone. Given the relatively large dose-searching space and the limited sample size in a drug-combination trial, it is critical to utilize the rich prior information on a_i and b_j for dose finding. Typically, the maximum dose for each drug in the combination is either the individual MTD determined in the single-agent trials or a dose below the MTD. Therefore, the specification of a_i and b_j is quite accurate because the upper bounds a_I and b_J are known.

We employ the copula-type regression in Yin and Yuan (2009) to model the joint toxicity probability π_ij at the dose combination (A_i, B_j),

$${\pi }_{ij}=1-{\{{(1-a_i^{\alpha })}^{-\gamma }+{(1-b_j^{\beta })}^{-\gamma }-1\}}^{-1{∕}_{\gamma }},$$ (2.1)

where α, β, γ > 0 are unknown model parameters. This model satisfies the natural constraints for drug-combination trials. For example, if the toxicity probabilities of both drugs are zero, the joint toxicity probability is zero; and if the toxicity probability of either drug is one, the joint toxicity probability is one. Another attractive feature of model (2.1) is that if only one drug is tested, it reduces to the well-known continual reassessment method (CRM) for a single-agent dose-finding design [O’Quigley, Pepe and Fisher (1990)].

Although model (2.1) takes a similar functional form as the Clayton copula [Clayton (1978)], there are several fundamental differences [Yin and Yuan (2010)]. Copula models are widely used to model a bivariate distribution by expressing the joint probability distribution through the marginal distributions linked with a dependence parameter [for example, see Clayton (1978); Hougaard (1986); Genest and Rivest (1993); and Nelsen (2006)]. In a drug-combination trial, we in fact only observe a univariate dose-limiting toxicity (DLT) outcome for combined agents. For a patient treated by combined agents (A_i, B_j), a single binary variable X indicates whether this patient has experienced DLT: that is, X = 1 with probability π_ij, and X = 0 with probability 1−π_ij. Therefore, model (2.1) is actually not a copula; we simply borrow the structure of the Clayton copula to model the joint toxicity probability when the two drugs are administered together. Moreover, model (2.1) is indexed by three unknown parameters (α, β, γ), in which γ is similar to the dependence parameter in standard copula models and the two extra parameters α and β render model (2.1) more flexibility to accommodate the complex two-dimensional dose-toxicity surface for the purpose of dose finding. Analogous to the CRM, the parameters α and β also account for the uncertainty of the prespecification of the single-agent toxicity probabilities a_i and b_j, thereby enhancing the robustness of our design to the misspecification of these prior toxicity probabilities.

Suppose that at a certain stage of the trial, among n_ij patients treated at the paired doses (A_i, B_j), x_ij subjects have experienced DLT. The likelihood given the observed data D is

$$L(\alpha ,\beta ,\gamma \mid D)\propto \prod _{i=1}^I\prod _{j=1}^J{\pi }_{ij}^{xij}{(1-{\pi }_{ij})}^{n_{ij}-x_{ij}}.$$

In the Bayesian framework, the joint posterior distribution is given by

$$f(\alpha ,\beta ,\gamma \mid D)\propto L(\alpha ,\beta ,\gamma \mid D)f\left(\alpha \right)f\left(\beta \right)f\left(\gamma \right),$$

where f(α), f(β) and f(γ) denote vague gamma prior distributions with mean one and large variances for α, β and γ, respectively. We derive the full conditional distributions of these three parameters and obtain their posterior samples using the adaptive rejection Metropolis sampling algorithm [Gilks, Best and Tan (1995)].

2.2. Adaptive randomization in phase II

Once the phase I dose finding is complete, the trial seamlessly moves on to phase II for further efficacy evaluation. Although the main purpose of phase I is to identify a set of admissible doses satisfying the safety requirements, efficacy data are also collected. Based on the efficacy data collected in both phase I and phase II, each new cohort of patients enrolled in phase II are immediately randomized to a more efficacious treatment arm with a higher probability. Similar to most of the phase I/II trial designs, patients in phase I and phase II need to be homogeneous by meeting certain eligibility criteria, such that the efficacy data in phase I can be also used to guide adaptive randomization in phase II.

For ease of exposition, we assume that K admissible doses have been found in phase I and will be subsequently assessed for efficacy using K parallel treatment arms in phase II. Let (p₁, …, p_K) denote the response rates corresponding to the K admissible doses, and assume that among n_k patients treated in arm k, y_k subjects have experienced efficacy. We model efficacy using the Bayesian hierarchical model to borrow information across multiple treatment arms:

$$\begin{array}{cc}\hfill y_k\mid p_k& \sim B_i(n_k,p_k),\hfill \\ \hfill p_k& \sim B_e(\zeta ,\xi ),\hfill \\ \hfill \zeta & \sim G_a(0.01,0.01),\hfill \\ \hfill \xi & \sim G_a(0.01,0.01),\hfill \end{array}$$ (2.2)

where Bi(n_k, p_k) denotes a binomial distribution, and Be(ζ, ξ) denotes a beta distribution with a shape parameter ζ and a scale parameter ξ. We take vague gamma prior distributions Ga(0.01, 0.01) with mean one, for both ζ and ξ, to ensure that the data dominate the posterior distribution. The posterior full conditional distribution of p_k follows Be(ζ + y_k, ξ + n_k − y_k), but those of ζ and ξ do not have closed forms. As the trial proceeds, we continuously update the posterior estimates of the p_k’s under model (2.2) based on the cumulating data.

The goal of response-AR is to assign patients to more efficacious treatment arms with higher probabilities, such that more patients would benefit from better treatments [Rosenberger and Lachin (2002)]. A common practice is to take the assignment probability proportional to the estimated response rate of each arm, for example, using the posterior mean of p_k (k = 1, …, K). However, such an AR scheme does not take into account the variability of the estimated response rates. At the early stage of a trial, there is only a small amount of data observed, which would lead to widely spread and largely overlapping posterior distributions of the p_k’s. In this situation, the estimated response rates of arms 1 and 2, say, p̂₁ = 0.5 and p̂₂ = 0.6, should not play a dominant role for patient assignment, because more data are needed to confirm that arm 2 is truly superior to arm 1. Nevertheless, at a later stage, after more patients have been treated and a substantial amount of data has become available, if we observe p̂₁ = 0.5 and p̂₂ = 0.6, we would have more confidence in assigning more patients to arm 2, because its superiority would then be much more strongly supported. Thus, in addition to the point estimates of the p_k’s, their variance estimates are also critical when determining the randomization probabilities.

To account for the uncertainty associated with the point estimates, one can compare the p_k’s with a fixed target, say, p₀, and take the assignment probability proportional to the posterior probability pr(p_k > p₀|D). However, in the case where two or more p_k’s are much larger or much smaller than p₀, their corresponding posterior probabilities pr(p_k > p₀|D) are either very close to 1 or 0, and, therefore, this AR scheme would not be able to distinguish them.

Recognizing these limitations of the currently available AR methods, Huang et al. (2007) arbitrarily took one study treatment as the reference, say, the first treatment arm, and then randomized patients based on R_k = pr(p_k > p₁|D) for k > 1 while setting R₁ = 0.5. For convenience, we refer to this method as fixed-reference adaptive randomization (FAR), since each arm is compared with the same fixed reference to determine the randomization probabilities. By using one of the treatment arms as the reference, FAR performs better than that using an arbitrarily chosen target as the reference. Unfortunately, FAR cannot fully resolve the problem. For example, in a three-arm trial if p₁ is low but p₂ and p₃ are high, say, p₁ = 0.1, p₂ = 0.4 and p₃ = 0.6, FAR may have difficulty distinguishing arm 2 and arm 3, because both R₂ and R₃ would be very close to 1. Even with a su cient amount of data to support the finding that arm 3 is the best treatment, the probabilities of assigning a patient to arm 2 and arm 3 are still close. This reveals one limitation of FAR that is due to the use of a fixed reference: the reference (arm 1) is adequate to distinguish arm 1 from arms 2 and 3, but may not be helpful to compare arm 2 and arm 3. In addition, because R₁ = 0.5, no matter how ine cacious arm 1 is, it has an assignment probability of at least 1/5, if we use R₁/(R₁ + R₂ + R₃) as the randomization probability to arm 1. Even worse, in the case of a two-arm trial with p₁ = 0.1, and p₂ = 0.6, arm 1 has a lower bound of the assignment probability 1/3, which is true even if p₁ = 0 and p₂ = 1. This illustrates another limitation of FAR that is due to the direct use of one of the arms as the reference for comparison. Moreover, the performance of FAR depends on the chosen reference, with different reference arms leading to different randomization probabilities.

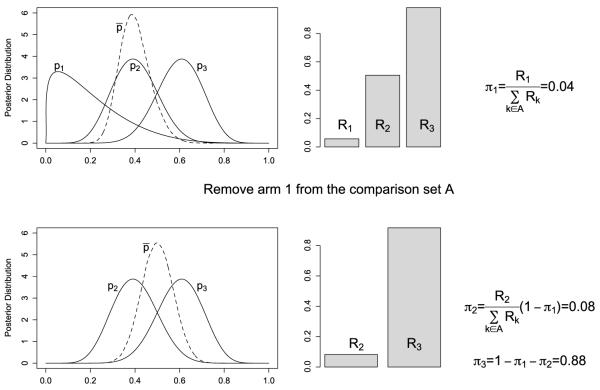
To fully address the issues with available AR schemes, we propose a new Bayesian moving-reference adaptive randomization (MAR) method that accounts for both the magnitude and uncertainty of the estimates of the p_k’s. Unlike FAR, the reference in MAR is adaptive and varies according to the set of treatment arms under consideration. One important feature of MAR is that the set of treatments in comparison is continuously reduced, because once an arm has been assigned a randomization probability, it will be removed from the comparison set. By assigning randomization probabilities to treatment arms on a one-by-one basis, we can achieve a high resolution to distinguish different treatments through such a zoomed-in comparison. Based on the posterior samples of the p_k’s, we diagram the Bayesian MAR in Figure 1 and describe it as follows:

1. Let Ā and A denote the set of indices of the treatment arms that have and have not been assigned randomization probabilities, respectively. We start with Ā = {·} an empty set, and A = {1, 2, …, K}.

2. Compute the mean response rate for the arms belonging to the set A, $\stackrel{‒}{p}={\sum }_{k\in \mathcal{A}}{p}_k∕{\sum }_{k\in \mathcal{A}}1$, and use p̄ as the reference to determine R_k = pr(p_k > p̄|D), for k ∈ A. Identify the arm that has the smallest value of R_k, R_l = min_k∈A R_k.

3. Assign arm l a randomization probability of π_l,

   $${\pi }_{\ell }=\frac{R_{\ell }}{{\Sigma }_{k\in \mathcal{A}}{R}_k}\left(1-\sum _{k^{\prime }\in \stackrel{‒}{\mathcal{A}}}{\pi }_{k^{\prime }}\right),$$

   and update A and Ā by removing arm l from A into Ā. Note that π_l is a fraction of the remaining probability $1-{\sum }_{k^{\prime }\in \stackrel{‒}{\mathcal{A}}}{\pi }_{k^{\prime }}$ because the assignment probability of ${\sum }_{k^{\prime }\in \stackrel{‒}{\mathcal{A}}}{\pi }_{k^{\prime }}$ has already been “spent” in the previous steps.

4. Repeat steps 2 and 3 and keep spending the rest of the randomization probability until all of the arms are assigned randomization probabilities, (π₁, …, π_K), and then randomize the next cohort of patients to the kth arm with a probability of π_k.

The proposed MAR scheme has a desirable limiting property as given below.

Fig. 1.

Diagram of the proposed moving-reference adaptive randomization for a three-arm trial. The top panels, from left to right, show that we first obtain posterior distributions of p₁, p₂, p₃ and p̄; then calculate R_k = pr(p_k > p̄|D) for k = 1, 2, 3; and assign the arm with the smallest value of R_k (i.e., arm 1) a randomization probability π₁. After spending π₁, we remove arm 1 from the comparison set and distribute the remaining randomization probability to the remaining arms (i.e, arms 1 and 2) in a similar manner, as demonstrated in the bottom panels.

Theorem 2.1. In a randomized trial with K treatments, asymptotically, MAR assigns patients to the most efficacious arm with a limiting probability of 1.

The proof is briefly outlined in the Appendix. In contrast, using FAR, the probability of allocating patients to the most efficacious arm may not converge to 1.

2.3. Phase I/II trial design

The proposed phase I/II drug-combination design seamlessly integrates each trial component discussed previously. Let ϕ_T and ϕ_E be the target toxicity upper limit and efficacy lower limit, and let n₁ and n₂ be the maximum sample sizes for the phase I and phase II parts of the trial, respectively. Let c_e, c_d, c_a and c_f be the fixed probability cuto s for dose escalation, de-escalation, dose admissibility and trial futility, the values of which are usually calibrated through simulation studies such that the trial has desirable operating characteristics. Our phase I/II design is displayed in Figure 2 and described as follows:

1. In phase I, the first cohort of patients is treated at the lowest dose combination (A₁, B₁).

2. During the course of the trial, at the current dose combination (A_i, B_j):

   1. If pr(π_ij < ϕ_T |D) > c_e, the doses move to an adjacent dose combination chosen from {(A_i+1, B_j), (A_i+1, B_j−1), (A_i−1, B_j+1), (A_i, B_j+1)}, which has a toxicity probability higher than the current doses and closest to ϕ_T. If the current dose combination is (A_I, B_J), the doses stay at the same levels.
   2. If pr(π_ij < ϕ_T|D) < c_d, the doses move to an adjacent dose combination chosen from {(A_i−1, B_j), (A_i−1, B_j+1), (A_i+1, B_j−1), (A_i, B_j−1)}, which has a toxicity probability lower than the current doses and closest to ϕ_T. If the current dose combination is (A₁, B₁), the trial is terminated.
   3. Otherwise, the next cohort of patients continues to be treated at the current dose combination.

3. Once the maximum sample size in phase I, n₁, is reached, suppose that there are K dose combinations with toxicity probabilities π_ij satisfying pr(π_ij < ϕ_T |D) > c_a, then they are selected as admissible doses and carried forward to phase II in parallel.

4. In phase II, MAR is invoked to randomize patients among the K treatment arms. Meanwhile, the toxicity and futility stopping rules apply to monitoring each arm: if pr(π_k < ϕ_T |D) < c_a (over-toxic), or pr(p_k > ϕ_E|D) < c_f (futility), arm k is closed, k = 1, …, K.

5. Once the maximum sample size in phase II, n₂, is reached, the dose combination that has the highest posterior mean of efficacy is selected as the best dose.

Fig. 2.

Diagram of the proposed phase I/II trial design for drug-combination trials.

In the proposed design, the response is assumed to be observable quickly so that each incoming patient can be immediately randomized based on the efficacy outcomes of previously treated patients. This assumption can be relaxed by using a group sequential AR approach, when the response is delayed. The group sequential AR updates the randomization probabilities after each group of patients’ outcomes become available rather than after each individual outcome [Jennison and Turnbull (2000)]. Our design is suitable for trials with a small number of dose combinations, because all the dose combinations satisfying the safety threshold would be taken into phase II. If a trial starts with a large number of dose combinations, many more doses could make it into phase II, possibly some with toxicity much lower than the upper bound. From a practical point of view, we could tighten the admissibility criteria by choosing only those with posterior toxicity probabilities closest to ϕ_T.

The proposed phase I/II drug-combination trial design has been implemented using C++. The executable file is available for free downloading at http://odin.mdacc.tmc.edu/~yyuan/, and the source code is available upon request.

3. Application

3.1. Motivating trial

We use a melanoma clinical trial to illustrate our phase I/II drug-combination design. The trial examined three doses of decitabine (drug A) and two doses of the derivative of recombinant interferon (drug B). The toxicity upper limit was ϕ_T = 0.33, and the efficacy lower limit was ϕ_E = 0.2. A maximum of 80 patients were to be recruited, with n₁ = 20 for phase I, and n₂ = 60 for phase II. In the copula-type toxicity model, we specified the prior toxicity probabilities of drug A as a_i = (0.05, 0.1, 0.2), and those of drug B as b_j = (0.1, 0.2). We elicited prior distributions Ga(0.5, 0.5) for α and β, and Ga(0.1, 0.1) for γ. The dose-limiting toxicity was defined as any grade 3 or 4 nonhematologic toxicity, grade 4 thrombocytopenia, or grade 4 neutropenia lasting more than two weeks or associated with infection. The clinical responses of interest included partial and complete response. In this trial, it took up to two weeks to assess both toxicity and efficacy, rendering the response-adaptive randomization practically feasible. The accrual rate was two patients per month, and thus no accrual suspension was needed to wait for patients’ responses in order to assign doses to new patients. It took approximately 10 months to conduct the phase I part and two and a half years to complete the phase II part of the trial. We used c_e = 0.8 and c_d = 0.45 to direct dose escalation and de-escalation, and c_a = 0.45 to define the set of admissible doses in phase I. We applied the toxicity stopping rule of pr(π_k < ϕ_T|D) < c_a and the futility stopping rule of pr(p_k > ϕ_E|D) < c_f with c_f = 0.1 in phase II. The decisions on dose assignment and adaptive randomization were made after observing the outcomes of every individual patient.

After 20 patients had been treated in the phase I part of the melanoma trial, three dose combinations (A₁, B₁), (A₁, B₂) and (A₂, B₁) were identified as admissible doses and carried forward to phase II for further evaluation of efficacy. During phase II, the MAR procedure was used to allocate the remaining 60 patients to the three dose combinations. Figure 3 displays the adaptively changing randomization probabilities for the three treatment arms as the trial proceeded. In particular, the randomization probability of (A₂, B₁) decreased first, and then increased; that of (A₁, B₂) increased first and then decreased; and that of (A₁, B₁) kept decreasing as the trial progressed. At the end of the trial, the dose combination (A₂, B₁) was selected as the most desirable dose with the highest estimated efficacy rate of 0.36.

Fig. 3.

Adaptive randomization probabilities for the three admissible dose combinations in the melanoma clinical trial.

3.2. Operating characteristics

We assessed the operating characteristics of the proposed design via simulation studies. Under each of the 12 scenarios given in Table 1, we simulated 1000 trials. In the Monte Carlo Markov chain (MCMC) procedure, we recorded 2000 posterior samples for the model parameters after 100 burn-in iterations.

Table 1. Selection probability and number of patients treated at each dose combination using the proposed phase I/II design, with the target dose combinations in boldface.

		Drug A						Simulation results
Sc.	Drug B	True pr(toxicity)			True pr(efficacy)			Selection percentage			Number of patients
		1	2	3	1	2	3
1	2	0.1	0.15	0.45	0.2	0.4	0.6	1.0	25.2	18.3	8.8	17.0	15.3
	1	0.05	0.15	0.2	0.1	0.3	0.5	0.0	10.7	42.8	8.5	11.3	18.0
2	2	0.1	0.2	0.5	0.2	0.4	0.55	4.0	44.5	2.8	11.3	21.2	8.1
	1	0.05	0.15	0.4	0.1	0.3	0.5	0.3	24.0	19.2	9.7	15.8	11.4
3	2	0.1	0.15	0.2	0.2	0.3	0.5	1.7	7.0	67.1	8.3	10.9	31.3
	1	0.05	0.1	0.15	0.1	0.2	0.4	0.0	1.9	19.8	8.2	7.9	11.9
4	2	0.1	0.4	0.6	0.3	0.5	0.6	16.3	25.4	0.2	16.1	15.1	3.7
	1	0.05	0.2	0.5	0.2	0.4	0.55	3.9	46.2	3.1	14.2	22.3	5.7
5	2	0.1	0.2	0.25	0.3	0.5	0.2	7.6	52.8	0.3	11.1	19.9	13.4
	1	0.05	0.15	0.2	0.2	0.4	0.4	0.8	20.5	15.4	10.2	12.5	11.2
6	2	0.05	0.05	0.05	0.2	0.3	0.5	0.3	5.2	77.8	7.5	9.6	37.9
	1	0.05	0.05	0.05	0.1	0.2	0.4	0.0	0.3	16.0	7.7	6.7	10.4
7	2	0.1	0.2	0.5	0.2	0.4	0.5	4.2	41.8	9.3	10.6	20.3	10.7
	1	0.05	0.15	0.2	0.1	0.3	0.4	0.5	10.7	29.8	9.5	12.1	15.0
8	2	0.5	0.55	0.6	0.5	0.5	0.5	0.0	0.0	0.0	0.4	0.3	0.1
	1	0.5	0.55	0.6	0.5	0.5	0.5	0.1	0.0	0.0	7.3	0.4	0.1
9	2	0.4	0.72	0.9	0.44	0.58	0.71	0.5	0.0	0.0	3.6	1.6	0.3
	1	0.23	0.4	0.59	0.36	0.49	0.62	23.9	3.7	0.0	20.9	6.0	0.8
10	2	0.24	0.56	0.83	0.4	0.6	0.78	10.8	2.5	0.0	11.6	6.0	1.2
	1	0.13	0.25	0.42	0.32	0.5	0.68	19.0	41.6	3.3	22.1	19.9	4.0
11	2	0.15	0.25	0.4	0.3	0.41	0.54	17.1	35.4	17.2	13.3	16.5	12.8
	1	0.11	0.15	0.2	0.15	0.22	0.31	1.6	7.3	11.3	10.8	10.3	9.8
12	2	0.15	0.19	0.23	0.17	0.33	0.55	1.6	10.1	54.1	7.7	11.3	25.6
	1	0.12	0.15	0.19	0.1	0.22	0.39	0.3	4.2	17.9	9.0	8.2	10.5

In each scenario, the target dose-combination is defined as the most e cacious one belonging to the admissible set. We present the selection percentages and the numbers of patients treated at all of the dose combinations. Scenarios 1–4 represent the most common cases in which both toxicity and efficacy increase with the dose levels, while the target doses are located differently in the two-dimensional space. The target dose is (A₃, B₁) in scenario 1, and (A₂, B₂) in scenario 2, which not only had the highest selection probability, but was also the arm to which most of the patients were randomized. In scenario 3 the target dose is the combination of the highest doses of drug A and drug B, for which the selection probability was close to 70%, and more than 30 patients were treated at the most efficacious dose. Scenario 4 also demonstrated a good performance of our design with a high selection probability of the target dose. In scenario 5 toxicity increases with the dose but efficacy first increases then decreases, and in scenario 6 toxicity maintains at a very low level, but efficacy gradually increases with the dose. Under these two scenarios, both the selection probabilities and the numbers of patients allocated to the target dose were plausible. Scenario 7 has two target doses due to the toxicity and efficacy equivalence contours. In that scenario, both the target doses were selected with much higher percentages and more patients were assigned to those two doses than others. Scenario 8 demonstrated the safety of our design by successfully terminating the trial early when toxicity is excessive even at the lowest dose. Scenarios 9–12 are constructed for a sensitivity analysis, which will be described in Section 3.3.

To better understand the performance of the phase I part of the proposed design, in Table 2 we display the percentage of each dose being selected into the admissible set, and the average number of admissible doses, K̄, at the end of phase I. In most of the cases, the selection percentages of the admissible doses were higher than 90%, and the average number of admissible doses determined by the proposed design was close to the true value. For example, in scenario 1, the true number of admissible doses is 5, and our design, on average, selected 5.4 admissible doses for further study in phase II.

Table 2. Selection percentage of each dose combination to the admissible set and the average size of the admissible set, K̄ , in phase I. The true admissible doses are in boldface.

% of admissible			K̄	% of admissible			K̄	% of admissible			K̄
Scenario 1				Scenario 2				Scenario 3
97.8	95.2	67.9	5.4	97.9	92.2	38.2	4.9	99.6	99.0	91.8	5.9
98.1	98.0	91.9		98.8	98.2	72.6		99.7	99.7	98.3
Scenario 4				Scenario 5				Scenario 6
93.3	75.9	14.6	4.2	98.0	95.9	81.6	5.6	99.5	99.5	99.0	6.0
96.5	94.9	52.1		98.6	98.5	93.7		99.5	99.5	99.5
Scenario 7				Scenario 8				Scenario 9
97.9	94.6	55.6	5.3	2.0	0.9	0.3	0.1	24.9	10.5	0.4	1.2
98.8	98.5	86.1		3.1	2.4	0.9		42.7	36.6	11.6
Scenario 10				Scenario 11				Scenario 12
69.6	42.7	4.9	3.1	88.4	82.5	53.5	4.8	91.9	89.3	73.4	5.3
82.4	78.3	36.4		91.1	90.1	77.7		92.5	92.4	87.6

As the number of admissible doses selected by phase I may vary from one trial to another, the final trial results shown in Table 1 are jointly a ected by both the phase I and phase II parts of the design. To disassemble their intertwining effects, we conducted a simulation study with a focus on the adaptive randomization only. In particular, we considered a phase II trial in which a total of 100 patients would be randomized to three treatment arms. Table 3 shows the results based on 1000 simulated trials under eight different scenarios. Scenarios 1–3 simulate cases in which the first arm has the lowest, intermediate and highest efficacy, respectively. Scenarios 4–6 are constructed in a similar setting, but the efficacy differences among the three arms are much larger. Scenarios 7 and 8 consider cases in which one or two arms are futile. In all of the scenarios, MAR allocated the majority of patients to the most efficacious arm in a more e cient way than FAR. For scenarios 1, 3 and 8, in Figure 4 we show the randomization probabilities averaged over 1000 simulations with respect to the cumulative number of patients using MAR and FAR, respectively. As more data are collected, MAR has a substantially higher resolution to distinguish and separate treatment arms than FAR in terms of efficacy. For example, in scenario 1 the curves are adequately separated using MAR after 20 patients are randomized, but are still not well spread even after enrolling 40 patients using FAR. Furthermore, considering scenarios 4, 5 and 6, we see that the number of patients assigned to the most efficacious arm (with a response rate of 0.6) using FAR changed substantially from 42.9 to 82.2, whereas that number stayed approximately the same as 81 when using MAR. This phenomenon indicates the invariance of MAR and the sensitivity of FAR to the reference arm.

Table 3. Number of patients randomized to each treatment arm using the fixed-reference adaptive randomization (FAR) compared to the moving-reference adaptive randomization (MAR). The most efficacious dose is in boldface.

	Response rate			FAR			MAR
Sc.	Arm 1	Arm 2	Arm 3	Arm 1	Arm 2	Arm 3	Arm 1	Arm 2	Arm 3
1	0.1	0.2	0.3	27.7	31.8	40.6	12.5	29.0	58.5
2	0.2	0.1	0.3	40.5	17.2	42.4	27.3	13.0	59.7
3	0.3	0.1	0.2	61.1	13.7	25.2	58.4	13.1	28.5
4	0.1	0.3	0.6	23.3	33.8	42.9	5.5	13.3	81.3
5	0.3	0.6	0.1	34.4	54.6	11.0	13.9	80.5	5.5
6	0.6	0.3	0.1	82.2	12.5	5.3	81.8	12.8	5.3
7	0.01	0.4	0.6	21.0	38.7	40.3	3.7	20.6	75.7
8	0.01	0.01	0.5	25.8	25.1	49.1	5.3	5.3	89.4

Fig. 4.

Randomization probabilities of the proposed moving-reference adaptive randomization (MAR) and the fixed-reference adaptive randomization (FAR) under scenarios 1, 3 and 8 listed in Table 3.

3.3. Sensitivity analysis

In the first sensitivity analysis, we examined the robustness of the proposed design to model misspecifications. We generated true toxicity and efficacy probabilities from the logistic regression model,

$${\pi }_{ij}=\frac{\exp ({\beta }_0+{\beta }_1{Z}_{Ai}+{\beta }_2{Z}_{Bj}+{\beta }_3{Z}_{Ai}{Z}_{Bj})}{1+\exp ({\beta }_0+{\beta }_1{Z}_{Ai}+{\beta }_2{Z}_{Bj}+{\beta }_3{Z}_{Ai}{Z}_{Bj})},$$ (3.1)

but applied models (2.1) and (2.2) for estimation. We took the standardized doses of drugs A and B in model (3.1) as Z_Ai = (0.05, 0.1, 0.2) and Z_Bj = (0.1, 0.2). These cases are listed as scenarios 9–12 in Table 1. When the models for toxicity and efficacy were misspecified, our design still performed very well: the target dose combination was selected with the highest probability and most of the patients were allocated to those efficacious dose combinations.

In the second sensitivity analysis, we evaluated the impact of the prior specifications using two more diffusive prior distributions for α and β under scenarios 1–4. The simulation results in Table 4 using the more diffusive priors are very close to those for scenarios 1–4 in Table 1. Therefore, the proposed design does not appear to be sensitive to the prior specification.

Table 4. Sensitivity analysis of the proposed Bayesian phase I/II drug-combination design under different prior specifications.

	Selection percentage						Number of treated patients
Sc.	α,β ~ Ga(0.1, 0.1)			α,β ~ Ga(0.05,0.05)			α,β ~ Ga(0.1, 0.1)			α,β ~ Ga(0.05,0.05)
1	2.0	21.0	25.4	2.0	19.9	27.1	7.8	15.7	20.2	7.7	15.7	20.8
	0.1	8.2	41.8	0	9.0	40.2	7.4	9.6	18.3	7.1	9.6	18.1
2	5.4	46.5	2.9	4.9	45.9	3.7	10.6	21.6	9.6	10.5	21.4	9.4
	0.4	21.0	20.3	0.2	22.9	17.9	8.8	14.4	13.0	8.8	14.9	12.5
3	2.0	6.3	69.6	0.9	6.1	70.2	7.2	10.1	36.3	6.8	9.8	36.4
	0.1	1.2	19.4	0	1.4	19.9	7.1	6.5	12.1	7.0	6.6	12.5
4	16.9	24.7	0.2	15.6	24.6	0.3	15.2	16.4	4.0	15.1	16.0	4.3
	4.8	44.2	2.8	4.1	45.1	3.0	13.1	20.6	6.8	13.2	20.4	6.2

4. Late-onset efficacy

In practice, toxicity and efficacy outcomes need to be ascertainable shortly after the initiation of the treatment in order to make a real-time decision on the treatment assignment for each incoming patient. Often, toxicity can be observed quickly; whereas efficacy is late-onset, for example, tumor shrinkage may take a relatively long time to assess. Such delayed efficacy outcomes pose new challenges to the use of AR in randomized trials. We propose using the group sequential AR procedure, which adapts randomization probabilities after a group of patients’ outcomes become available rather than after observing each individual’s outcome [Karrison, Huo and Chappell (2003)]. More specifically, for the n₂ patients to be randomized to K treatment arms in phase II, we update the AR probabilities after observing every m patients’ outcomes, 1 ≤ m ≤ n₂. Choosing an appropriate m is critical for the practical performance of the group sequential AR. With a larger value of m, the trial duration tends to be shortened because we suspend the accrual less frequently, but it may downgrade the AR performance. Using a smaller group size m, the group sequential AR procedure would better facilitate assigning more patients to more efficacious treatment arms, but it prolongs the trial duration. In addition to the group size, the performance of the design also depends on the accrual rate, the length of the follow-up required for efficacy assessment and the distribution of the time to efficacy.

To evaluate our design using the group sequential AR, we took efficacy to be late-onset, requiring three months for a complete evaluation. We considered six different group sizes: m = 1, 3, 6, 12, 20 and 30, corresponding to 1.7%, 5%, 10%, 20%, 33.3% and 50% of the total sample size, n₂ = 60, in phase II. We investigated two different accrual rates: two and eight patients per month, and simulated four different patterns of the hazard for the time to efficacy: increasing, constant, decreasing and hump-shaped over time. The first three hazards were generated from the Weibull distribution, and the hump-shaped hazard was generated from the log-logistic distribution. Other design parameters, such as ϕ_T, c_e, c_d and c_a, took the same values as those in Section 3.1.

Table 5 shows the number of patients allocated to the target dose combination and the duration of the trial under the first five scenarios listed in Table 1. In general, when the size of the sequential group m increases, the number of patients allocated to the target dose combination gradually decreases. This phenomenon was minor when m increased from 1 to 6, but more notable when m became larger. For example, in scenario 1 with an increasing hazard and an accrual rate of two patients per month, the numbers of patients allocated to the target dose combination were 18.4, 17.7 and 15.0, when m = 1, 6 and 30, respectively. The trial duration was more sensitive to the value of m, and changed dramatically when the size of the sequential group increased. When the accrual rate was two patients per month, we observed a substantial decrease in the trial duration when m increased from 1 to 6. For example, under scenario 2, the duration of the trial with m = 6 was approximately 1/4 of that with m = 1. However, when we further increased m from 6 to 30, the trial duration only changed slightly because in this circumstance the trial duration was essentially dominated by the accrual rate, which is typically a key factor a ecting the trial duration. With a higher accrual rate of eight patients per month, we observed additional reductions in the trial duration when m was larger than 6, but as a trade-off, slightly fewer patients were allocated to the target dose combination.

Table 5. Number of patients allocated to the target dose combination and the trial duration (shown as subscripts), with different group sizes m under scenarios 1–5.

	Hazard (accrual rate=2/month)				Hazard (accrual rate=8/month)
m	Increase	Constant	Decrease	Hump	Increase	Constant	Decrease	Hump
Scenario 1
1	18.4157.8	18.1150.3	17.7139.5	17.8159.9	18.2149.4	17.5143.0	17.8131.5	17.4152.2
3	18.069.8	18.069.2	17.568.7	17.969.4	17.261.6	17.760.9	17.960.7	17.561.5
6	17.742.4	17.442.4	16.942.4	17.342.2	17.633.0	17.132.8	17.332.8	16.732.9
12	16.542.2	16.842.2	16.142.1	16.542.0	16.618.8	16.618.7	16.918.8	16.918.7
20	15.842.1	16.042.1	15.842.1	15.742.1	15.613.8	16.313.8	16.113.8	15.413.7
30	15.042.1	15.442.1	15.042.0	15.242.0	15.012.8	15.112.8	15.312.8	14.312.8
Scenario 2
1	21.0160.2	20.7153.7	22.5145.3	21.9162.3	21.3151.9	21.7146.9	22.0135.8	21.2154.5
3	20.869.5	21.669.4	21.968.6	21.569.2	21.361.3	21.261.2	21.560.8	20.961.1
6	20.742.3	21.142.1	21.742.2	20.942.1	20.732.8	21.632.7	21.832.6	20.932.6
12	20.542.0	20.842.0	21.242.1	20.941.9	20.518.6	20.818.6	21.018.7	20.618.7
20	20.242.0	19.142.1	20.242.0	20.842.1	20.013.7	19.313.7	20.113.8	19.613.7
30	19.142.2	19.642.1	19.641.9	19.742.1	18.612.8	19.612.8	18.512.8	19.312.8
Scenario 3
1	32.2161.2	32.0154.6	31.7144.7	31.1163.6	31.9153.8	32.0147.1	32.1136.6	32.3156.5
3	31.570.1	31.869.7	31.469.2	31.569.9	31.061.8	31.361.7	32.061.2	31.561.9
6	32.442.4	31.042.4	32.242.3	30.942.4	31.233.0	31.033.0	32.432.9	31.532.9
12	30.842.2	31.042.2	30.342.1	30.342.3	30.418.8	30.618.8	31.418.8	31.918.8
20	29.542.3	30.442.1	29.642.2	30.142.1	28.713.8	28.213.8	28.213.8	29.013.8
30	29.442.2	29.142.2	28.942.2	29.142.2	26.412.8	26.712.8	26.412.8	26.512.8
Scenario 4
1	23.0158.4	23.7151.5	22.8139.4	22.4159.5	23.5150.4	22.7143.8	22.3131.3	22.6151.9
3	22.769.1	22.368.9	22.668.7	22.469.1	22.361.0	22.860.9	21.959.8	21.061.2
6	21.842.4	21.742.2	22.542.3	21.342.3	22.232.6	21.932.8	22.432.9	21.532.7
12	21.242.1	21.341.9	20.742.1	21.041.8	20.418.6	22.018.7	21.918.7	21.218.7
20	20.242.1	20.342.1	19.842.0	20.142.0	20.013.7	20.113.7	19.913.7	20.313.8
30	19.342.2	19.342.1	18.642.1	19.442.2	19.512.8	19.212.7	20.212.8	18.912.8
Scenario 5
1	20.4159.7	21.3152.1	19.8141.1	20.3161.6	20.5152.4	20.5144.7	21.1133.4	20.9154.1
3	20.070.1	20.669.9	20.469.1	20.169.9	20.461.8	20.061.5	20.361.1	19.661.9
6	19.942.5	19.642.5	19.942.5	20.042.5	19.533.0	19.632.9	20.033.0	20.533.0
12	19.242.2	19.342.3	19.742.2	20.042.3	19.118.8	19.218.8	18.718.8	19.618.8
20	19.542.3	19.542.3	18.842.2	18.842.3	18.313.8	18.813.8	18.613.8	18.813.8
30	18.542.3	18.142.2	19.142.2	18.442.3	17.212.8	17.612.8	17.712.8	17.712.8

In practice, trial duration is an important factor to be considered when designing clinical trials. We should choose an appropriate group size so as to achieve a reasonable balance between AR and the trial duration. It is worth noting that the group size is mainly used to determine when to update the randomization probabilities, not when to randomize patients. Patients are randomized on a one-by-one basis to the treatment arms no matter the size of the sequential group. In the extreme case that the group size equals the total sample size, we essentially apply an equal randomization scheme.

5. Concluding remarks

Drug-combination therapies are playing an increasingly important role in oncology research. Due to the toxicity equivalence contour in the two-dimensional dose-combination space, multiple dose combinations with similar toxicity may be identified in a phase I trial. Thus, a phase II trial with AR is natural and ethical to assign more patients to more efficacious doses. We have adopted a copula-type model to select the admissible doses and proposed a novel AR scheme when seamlessly connecting phase I and phase II trials. The attractive feature of this phase I/II design is that once the admissible doses are identified, AR immediately takes effect based on the efficacy data collected in the phase I study. The proposed design efficiently uses all of the available data resources and naturally bridges the phase I and phase II trials. In our design, AR is based only on efficacy comparison among admissible doses. It can be easily modified to take into account both toxicity and efficacy by using their odds ratio as a measure of the trade-off or desirability to adaptively randomize patients and select the best dose combination at the end of the trial [Yin, Li and Ji (2006)]. The proposed design assumes that both toxicity and efficacy endpoints are binary. In some cases, these endpoints can be ordinal or continuous, for example, it may be more direct to treat the toxicity endpoint as an ordinal outcome to account for multiple toxicity grades. To accommodate such an ordinal toxicity outcome, we can take the approach of Yuan, Chappell and Bailey (2007) by first converting the toxicity grades to numeric scores that reflect their impact on the dose allocation procedure, and then incorporating those scores into the copula-type model using the quasi-binomial likelihood. Another common scenario is that both toxicity and efficacy end-points take the form of time-to-event measurements. In this case, various survival models, such as the proportional hazards model, are available to model the times to toxicity and efficacy. Along this direction, Yuan and Yin (2009) discussed jointly modeling toxicity and efficacy as time-to-event outcomes in single-agent trials; similar approaches can be adopted here for phase I/II drug-combination trials.

APPENDIX: PROOF OF THEOREM 2.1

The proposed moving-reference adaptive randomization procedure is invariant to the labeling of the treatment arms. Without loss of generality, we assume that p₁ < p₂ < … < p_K, and determine the randomization probability for arm 1. Starting with A = {1, 2, …, K}, $\stackrel{‒}{p}={\sum }_{k=1}^K{p}_k∕K$. As the number of subjects goes to infinity, it follows that the rank of R_k = pr(p_k > p̄|D) is consistent with the order of the p_k’s, that is, R₁ < R₂ < … < R_K. Therefore, for the first treatment arm l = 1,

$$\begin{array}{cc}\hfill R_{\ell }& =\underset{k\in \mathcal{A}}{\min }{R}_k\hfill \\ \hfill & =\mathrm{pr}(p_1>\stackrel{‒}{p}\mid \mathcal{D})\hfill \\ \hfill & =\mathrm{pr}\{(p_1-p_2)+(p_1-p_3)+\cdots +(p_1-p_K)>0\mid \mathcal{D}\}\hfill \\ \hfill & \le \mathrm{pr}\{(k-1)(p_1-p_2)>0\mid \mathcal{D}\}\hfill \\ \hfill & =\mathrm{pr}(p_1>p_2\mid \mathcal{D}),\hfill \end{array}$$

which converges to 0 asymptotically. Thus, π₁ →0, that is, the probability of assigning patients to the least efficacious arm goes to zero. Following similar arguments, we can show that π_k →0 for k = 2, …, K − 1. Therefore, the probability of allocating patients to the most efficacious arm, ${\pi }_K=1-{\sum }_{k=1}^{K-1}{\pi }_k$, converges to 1.