Robust EM Continual Reassessment Method in Oncology Dose Finding

Abstract

The continual reassessment method (CRM) is a commonly used dose-finding design for phase I clinical trials. Practical applications of this method have been restricted by two limitations: (1) the requirement that the toxicity outcome needs to be observed shortly after the initiation of the treatment; and (2) the potential sensitivity to the prespecified toxicity probability at each dose. To overcome these limitations, we naturally treat the unobserved toxicity outcomes as missing data, and use the expectation-maximization (EM) algorithm to estimate the dose toxicity probabilities based on the incomplete data to direct dose assignment. To enhance the robustness of the design, we propose prespecifying multiple sets of toxicity probabilities, each set corresponding to an individual CRM model. We carry out these multiple CRMs in parallel, across which model selection and model averaging procedures are used to make more robust inference. We evaluate the operating characteristics of the proposed robust EM-CRM designs through simulation studies and show that the proposed methods satisfactorily resolve both limitations of the CRM. Besides improving the MTD selection percentage, the new designs dramatically shorten the duration of the trial, and are robust to the prespecification of the toxicity probabilities.

1. INTRODUCTION

The primary scientific goal of a phase I oncology trial is to identify the maximum tolerated dose (MTD) of a new drug, which is the highest dose with an acceptable risk of toxicity. Of many phase I dose-finding methods described by Chevret (2006), the continual reassessment method (CRM) proposed by O’Quigley, Pepe, and Fisher (1990) is a particularly popular design used to identify the MTD. The CRM continuously updates the estimates of the true toxicity probabilities of the considered doses based on a single-parameter model and the prespec-ified toxicity probabilities. Under some regularity conditions, the CRM is consistent in the sense that the MTD identified by the CRM generally converges to the true MTD, even when the working model is misspecified (Shen and O’Quigley 1996). Although the CRM was originally proposed in the Bayesian paradigm, O’Quigley and Shen (1996) showed that the CRM possesses similar theoretical properties and operating charac-teristics under the classical maximum likelihood theory.

The CRM has been modified to improve its practical imple-mentation and properties, in particular, by treating patients in cohorts and limiting each dose escalation by one dose level (Goodman, Zahurak, and Piantadosi 1995; Piantadosi, Fisher, and Grossman 1998). More refinements of the CRM include: using a preliminary up-and-down design in order to reach the neighborhood of the target dose (Møller 1995); terminating the trial early based on the width of the 95% posterior probability interval of the MTD (Heyd and Carlin 1999); weighing the like-lihood with the censoring time to accommodate late-onset toxi-cities (Cheung and Chappell 2000); monitoring a posterior den-sity function of toxicity to limit overdose (Ishizuka and Ohashi 2001); using decision theory to optimize certain objective function (Leung and Wang 2002); modeling bivariate competing outcomes (Braun 2002); and using a two-group CRM for ordered groups (O’Quigley and Paoletti 2003).

In spite of the success of the CRM, two major issues limit its applications in practice. First, the CRM requires that the toxi-city outcome must be observed quickly such that, by the time of the next dose assignment, the currently treated patients must have complete information on toxicity. However, late-onset tox-icities are common in phase I studies. For example, in radio-therapy trials, dose-limiting toxicities (DLTs) often occur long after the treatment is finished (Coia, Myerson, and Tepper 1995; Cooper et al. 1995). In the presence of such late-onset toxicities, a direct application of the CRM may underestimate the toxicity probabilities, which would cause an undesirably large number of patients to be treated at overly toxic doses. While a safer approach would be to suspend the accrual and wait for each pa-tient’s outcome to be observed, this strategy may result in an infeasibly long trial. In addition, frequently suspending the ac-crual is not practical, wastes resources, and also causes tremen-dous administrative inconvenience. Second, the CRM requires the prespecification of toxicity probabilities for the doses inves-tigated in the trial. These prior toxicity probabilities are known as the “skeleton” of the CRM. Because the true dose-toxicity profile of the agent under investigation is often largely unknown a priori, the specification of the skeleton can be quite subjective. Different skeletons may lead to rather different design proper-ties, and unfortunately there is little information to justify which skeleton is more appropriate in practice.

A phase I clinical trial was recently initiated to investi-ate a novel drug combination of a mitotic inhibitor and an immunomodulatory agent for treating prostate cancer. Fixing the dose of the immunomodulatory agent, the mitotic inhibitor was to be investigated at six dose levels. The goal of the study was to find the MTD of the mitotic inhibitor that can be givenwith the immunomodulatory agent to treat prostate cancer. The CRM was considered as a candidate design for the trial, however, the implementation of the CRM was complicated by the aforementioned two difficulties. Toxicities were not expected to be observed immediately following the treatment. Clinical investigators decided that three months would be a reasonable follow-up period to assess toxicities. Given the estimated ac-crual rate of three patients per month, when a new cohort of three patients was ready for treatment, some of the currently treated patients might still have not completed assessment and thus their toxicity outcomes would be missing. In addition, when we elicited the skeleton of the CRM, several investigators expressed quite different opinions on the prior toxicity proba-bilities at these six doses. As the true dose-toxicity curve of the drug was unknown a priori, it was not clear which set of prior toxicity probabilities should be used to carry out the CRM design.

Our goal is to address the two limitations of the CRM in order to further expand its application. To address the missing toxic-ity issue, we treat the unobserved toxicity outcomes as missing data (more strictly speaking, as censored observations due to incomplete follow up), and apply the missing data technique and theory to the CRM methodology. In particular, the expectation-maximization (EM) algorithm is used to handle the missing tox-icity outcomes when the toxicity outcomes cannot be observed quickly. To overcome the sensitivity of the CRM to the prespec-ification of the skeleton, we propose conducting the CRM design using multiple skeletons. We view the CRM model under each skeleton as a separate model, based on which the inference and dose escalation decisions are made through model selection and model averaging approaches. The proposed design includes the CRM as an important special case when there is no missing data and only a single skeleton is used.

The remainder of the article is organized as follows. In Section 2, we briefly review the original CRM methodology and propose a robust EM-CRM to address the issues of missing toxicity outcomes and the sensitivity associated with the skele-ton specification. In Section 3, we present simulation studies to compare the operating characteristics of the new designs with those of the original CRM. In Section 4, we describe the sensitivity analysis we conducted to further investigate the properties of the EM-CRM in terms of the accrual rates, event-time distributions, and multiple skeletons. We illustrate the proposed design using the prostate cancer trial in Section 5, and conclude with a brief discussion in Section 6.

2. METHODS

2.1 Continual Reassessment Method

In a phase I dose-finding trial, patients enter the study sequentially and are followed for a fixed period of time (0, T) to assess the toxicity of the drug. During this evaluation window (0, T), a binary variable Y = 1 if the patient has experienced the dose-limiting toxicity (DLT), and otherwise Y 0. Typi-cally, the length of the assessment period T is chosen = so that if a drug-related DLT occurs, it would occur within (0, T). Depending on the nature of the disease and the treatment agent, the assessment period T varies from days to months. Patients with Y = 0 can be regarded as “cured” or “insusceptible” in the sense that they will not experience the event of interest (i.e., DLT) even if we continue to follow them after T.

The CRM assumes a prior dose-toxicity curve, and then continuously updates this curve based on the observed toxicity outcomes in the trial. Using the updated dose-toxicity curve, a new cohort of patients is assigned to the dose with an estimated toxi-city probability closest to the prespecified target ϕ. Suppose that a set of J doses are under investigation for the new drug, and let (p₁, …, p_J) be the prespecified toxicity probabilities (skele-ton) at those doses, satisfying a monotonic dose-toxicity order p₁ < … < p_J. The CRM starts with treating the first cohort of patients at the lowest dose. To direct the dose escalation for an incoming cohort, the CRM links the dose level d with the associated toxicity probability π_d via a working dose-toxicity model, such as

$${\pi }_d\left(\alpha \right)=p_d^{\text{exp}\left(\alpha \right)},d=1,\cdots ,J,$$ (1)

where α is an unknown parameter.

Suppose that n patients have entered the trial, and let y_i and d_i denote the toxicity outcome and the received dose level for the ith subject, respectively. Then, the likelihood function for the observed toxicity outcomes y = {y_i, i = 1, …, n} is given by

$$L(\mathbf{y}\mid \alpha )=\prod _{i=1}^n{\left\{p_{di}^{\text{exp}\left(\alpha \right)}\right\}}^{yi}{\{1-p_{di}^{\text{exp}\left(\alpha \right)}\}}^{1-yi}.$$ (2)

The unknown parameter α can be estimated by Bayesian or frequentist methods. The original formulation of the CRM by O’Quigley, Pepe, and Fisher (1990) takes a Bayesian approach that assigns a prior distribution to α, and then estimates α and π_d(α) by their posterior means. Alternatively, the classical fre-quentist maximum likelihood method can be used to obtain α, the maximum likelihood estimator (MLE) of α. O’Quigley and Shen (1996) showed that these two inferential approaches yield fairly similar operating characteristics, especially in terms of the MTD selection.

After obtaining the MLEs of the toxicity probabilities at all of the doses considered, that is, ${\widehat{\pi }}_d={\pi }_d\left(\widehat{\alpha }\right)$, the recommended dose level for the next cohort of patientsis the one that has a toxicity probability closest to the target ϕ. That is, a new cohort of patients is assigned to dose level d* such that

$$d^{\ast }=\underset{d\in (1,\cdots ,J)}{\mathrm{argmin}}\mid {\widehat{\pi }}_d-\varphi \mid .$$

The trial continues until the exhaustion of the total sample size, and then the dose with an estimated toxicity probability closest to ϕ is selected as the MTD.

2.2 EM–CRM

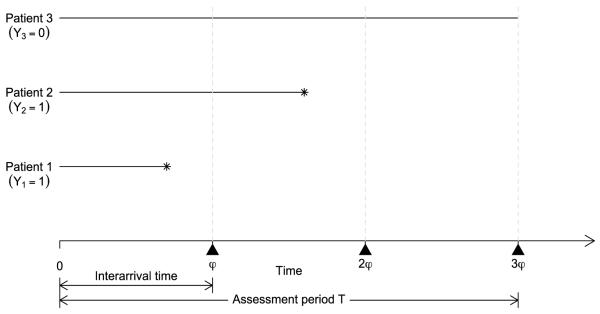
A practical limitation of the CRM is that the DLT needs to be ascertainable quickly after the initiation of the treatment. As illustrated by Figure 1, if the patient interarrival time, say φ, is shorter than the assessment period T, say T = 3φ, then by the time a dose is to be assigned to the newly accrued cohort of patients (at time φ), some of the patients who have entered the trial (i.e., patients 2 and 3) have been only partially followed and their toxicity outcomes have not yet been observed. More precisely, for subject i, let t_i denote the time to toxicity, and let u_i(u_i≤ T) denote the actual follow-up time at the moment of dose assignment for a newly arrived cohort. If subject i will not experience toxicity (i.e., Y_i= 0), we set t_i= ∞. It then follows that

$$Y_i=\{\begin{array}{cc}1\hfill & \text{if}{t}_i\le u_i\hfill \\ 0\hfill & \text{if}{t}_i>u_i\text{and}{u}_i=T\hfill \\ \text{missing}\hfill & \text{if}{t}_i>u_i\text{and}{u}_i<T.\hfill \end{array}\phantom{\}}$$ (3)

That is, the toxicity outcome is missing for patients who have not yet experienced toxicity (t_i> u_i) and have not been fully followed up to T (u_i< T). From the time-to-toxicity perspective, these missing outcomes can also be regarded as censored observations. In the trial conduct, the amount of missing data depends on the ratio of the assessment period T and the interarrival time φ, the A/I ratio. A larger value of the A/I ratio often leads to more missing data, as this indicates that a higher percentage of patients have not completed the toxicity assessment when a new cohort arrives. We assume that the arrival time of a new cohort does not depend on t_i, that is, censoring is noninformative.

Figure 1.

Illustration of missing toxicity outcomes. For each patient, the horizontal line segment represents the follow up, at the end of which toxicity is indicated by asterisk. At time φ, the toxicity outcomes of patients 2 and 3 are missing (i.e., Y₁ = 1, but Y₂ and Y₃ are missing); at time 2φ, the toxicity outcome of patient 3 is missing (i.e., Y₁ = Y₂ = 1, but Y₃ is missing); and at time 3φ, Y₁ = Y₂ = 1, and Y₃ = 0.

The missingness of toxicity outcomes poses difficulties when conducting a CRM trial design. One possibility is to simply discard the missing data and make the dose-escalation decision based only on the observed data. However, this approach is not efficient, and of greater consequence, often leads to overly aggressive dose escalation because patients who will not experience toxicity are more likely to have missing data. For example, in Figure 1, patient 3 does not experience toxicity during the assessment period and is more likely to have a missing toxicity outcome (i.e., at time φ and time 2φ) than patients 2 and 3 who have experienced toxicity. Because the probability of missingness for Y_i depends on the value of Y_i itself, such missing data are nonignorable and bring a new challenge to the trial design. Statistical analysis of nonignorable missing data is often plagued by the nonidentifiability problem due to the fact that the observed data contain no information about the nonignorable missing data mechanism. However, the missing data we consider here are a special case of nonignorable missing data with a known missing data mechanism as defined by (3). This feature eliminates the nonidentifiablity problem and renders statistical modeling using the EM algorithm (see Little and Rubin 2002, chap. 15.3).

In this article, we naturally treat the unobserved toxicity outcomes as missing data and address the problem using the EM algorithm (Dempster, Laird, and Rubin 1977). The EM alg rithm is a general iterative procedure for maximum likelihood estimation with incomplete data. Each iteration of the EM algorithm consists of an E (expectation) step and an M (maximization) step. The E step finds the conditional expectation of the missing data given the observed data and current parameter estimates, and then substitutes these expectations for the missing data. The M step maximizes the likelihood of the filled-in data to obtain the MLEs of the parameters. Let y = (y_obs, y_mis), where y_obs and y_mis denote the observed and missing data, respectively. For patients susceptible to the DLT (i.e., Y_i = 1), let τ₁ < τ₂ < … < τ_K represent distinct observed event times. Let m_k denote the number of DLTs occurred at τ_k, and c_k denote the number of censored observations in the interval τ_k, τ_k+1), for k = 1, …, K with τ_K+1≡ T. We denote the set of [m_k event times by M_k, the set of c_k censored observations by C_k, and use λ = (λ₁, …, λ_K) to denote the unknown discrete hazards C at the τ_k’s with λ_k = pr(t=τ_k|t ≥ τ_k). Under the CRM model, the log-likelihood of the complete data is a linear function of Y_i. Thus, at the rth iteration of the EM algorithm, given the current parameter estimates α^(r) and λ^(r), the E step at the (r+1)th iteration essentially substitutes the missing value of Y_i directly with its expectation in the form of

$$\begin{array}{cc}\hfill E& (Y_i\mid t_i>u_i,{\alpha }^{\left(r\right)},{\lambda }^{\left(r\right)})\hfill \\ \hfill & =\mathrm{pr}(Y_i=1\mid t_i>u_i,{\alpha }^{\left(r\right)},{\lambda }^{\left(r\right)})\hfill \\ \hfill & =\mathrm{pr}(Y_i=1\mid {\alpha }^{\left(r\right)})\mathrm{pr}(t_i>u_i\mid Y_i=1,{\lambda }^{\left(r\right)})\hfill \\ \hfill & ∕\{\mathrm{pr}(Y_i=0\mid {\alpha }^{\left(r\right)})\mathrm{pr}(t_i>u_i\mid Y_i=0,{\lambda }^{\left(r\right)})\hfill \\ \hfill & +\mathrm{pr}(Y_i=1\mid {\alpha }^{\left(r\right)})\mathrm{pr}(t_i>u_i\mid Y_i=1,{\lambda }^{\left(r\right)})\}\hfill \\ \hfill & =\frac{p_{di}^{\text{exp}}\left({\alpha }^{\left(r\right)}\right){\Pi }_{k:{\tau }_k<u_i}(1-{\lambda }_k^{\left(r\right)})}{1-p_{di}^{\text{exp}\left({\alpha }^{\left(r\right)}\right)}+p_{di}^{\text{exp}\left({\alpha }^{\left(r\right)}\right)}{\Pi }_{k:{\tau }_k<u_i}(1-{\lambda }_k^{\left(r\right)})}.\hfill \end{array}$$ (4)

In clinical practice, patients who do not experience toxicity during the assessment window (0, T) are typically considered “safe” or “insusceptible.” Thus, the patient population can be viewed as a mixture of subjects who would experience toxicity and those who would not, which is given in the denominator of (4) and characterized by the mixture cure rate model (Berkson and Gage 1952). After the E step, we obtain the filled-in complete data ŷ = {ŷ_i}, where ŷ_i = y_i if y_i is observed, and y_i=E(Y_i|t_i > u_i, α^(r), λ^(r)) if y_i is missing. Then in the M step, we calculate the MLE of α and λ as the updated estimate α^(r+1) and λ^(r+1). It can be shown that ${\lambda }_k^{(r+1)}=m_k∕{\sum }_{j=k}^K(m_j+{\sum }_{i\in C_j}{\widehat{y}}_i)$, k 1, …, K, an estimate analogous to Kaplan–Meier estimator (Kaplan and Meier 1958); and α^(r+1) is obtained maximizing the likelihood (2) with y_i replaced by ŷ_i.

The EM algorithm does not directly produce the variance estimate of $\widehat{\alpha }$, for which we take the approach of Louis (1982). We factorize the observed-data information $I(\widehat{\alpha }\mid {\text{y}}_{\text{obs}})$ as follows:

$$I(\widehat{\alpha }\mid y_{\text{obs}})=E[I(\alpha \mid \mathrm{y})\mid y_{\text{obs}},\widehat{\alpha }]-E[D^2(\alpha \mid y_{\text{mis}})\mid y_{\text{obs}},\widehat{\alpha }],$$ (5)

where I(α|y) = −∂² log L(y|α)/∂α² is the observed information based on the complete data y, and D(α y_mis) = ∂ log L(y_mis|α)/∂α denotes the score function from the missing data y_mis. As shown in the Appendix, the first term on the right-hand side of (5) is given by

$$E[I(\alpha \mid y)\mid y_{\text{obs}},\widehat{\alpha }]=-\sum _{i=1}^n\left\{{\widehat{y}}_i{e}^{\widehat{\alpha }}\log p_{d_i}+(1-{\widehat{y}}_i)\frac{p_{d_i}^{exp\left(\widehat{\alpha }\right)}{e}^{\widehat{\alpha }}\log p_{d_i}(p_{d_i}^{exp\left(\widehat{\alpha }\right)}-e^{\widehat{\alpha }}\log p_{d_i}-1)}{{(1-p_{d_i}^{exp\left(\widehat{\alpha }\right)})}^2}\right\},$$

and the second term is given by

$$E[D^2(\alpha \mid y_{\text{mis}})\mid y_{\text{obs}},\widehat{\alpha }]=\sum _{i:y_i\in y_{\text{mis}}}{e}^{2\widehat{\alpha }}{\left(\log p_{d_i}\right)}^2{p}_{d_i}^{exp\left(\widehat{\alpha }\right)}pr(t_i>u_i\mid Y_i=1)∕[(1-p_{d_i}^{exp\left(\widehat{\alpha }\right)})\times {\{1-p_{d_i}^{exp\left(\widehat{\alpha }\right)}+p_{d_i}^{exp\left(\widehat{\alpha }\right)}pr(t_i>u_i\mid Y_i=1)\}}^2].$$

Thus, an estimate of the variance of $\widehat{\alpha }$ is given by $\text{var}\left(\widehat{\alpha }\right)=I{(\widehat{\alpha }\mid {\text{y}}_{\text{obs}})}^{-1}$, and the 95% confidence interval of the toxicity probability π_d can be constructed as $(p_d^{\text{exp}(\widehat{\alpha }+1.96\text{se}\left(\widehat{\alpha }\right))},p_d^{\text{exp}(\widehat{\alpha }-1.96\text{se}\left(\widehat{\alpha }\right))})$. The variance estimate of $\widehat{\alpha }$ involves the unknown survival function pr(t_i > u_i|Y_i = 1), which can be replaced by its Kaplan–Meier type estimator obtained from the EM algorithm. The variance of $\widehat{\alpha }$ is used only when ˆ to stop the trial early all the considered doses are overly toxic, and the simulation study shows that this approximated variance provides very good operating characteristics.

2.3 Robust EM–CRM

Another issue associated with the CRM is the arbitrariness in the prespecification of the toxicity probabilities (p₁, …, p_J). Due to a lack of toxicity information on a new drug, the uncertainty associated with the specification of the toxicity probabilities is fairly large. Different physicians often have quite different opinions on the toxicity probabilities. Even with only one physician, typically a range of toxicity probabilities are given for each dose. For example, the toxicity probability at dose level one may range between 0.1 to 0.3, and that at dose level two between 0.25 to 0.4 and so on. If the p_d’s deviate far from the true dose-toxicity curve, this may lead to poor operating characteristics and a high probability of selecting the wrong dose as the MTD. To enhance the robustness of the trial design, we propose simultaneously prespecifying multiple, say S, sets of toxicity probabilities, that is, {p₁₁, …, p_1J}, …, {p_S1, …, p_S1}, each set leading to an independent CRM model of form (1). During the trial conduct, we fit each of the S CRM models to the observed data. In order to make inference across the multiple models and direct the dose escalation, two different approaches, model selection and model averaging, can be adopted. In the Bayesian paradigm, Yin and Yuan (2009) proposed using the Bayesian model averaging estimate to draw inference across multiple CRMs. To calculate the Bayesian model averaging estimate, the commonly used improper noninformative priors cannot be used (Raftery, Madigan, and Hoeting 1997), and proper priors need to be elicited for the unknown parameters of the CRM models, which could be a challenging task for practitioners. In addition, the resulting estimates may be sensitive to the priors, especially at the beginning of the trial with a very small sample size. We focus herein on the frequentist approach, which avoids specifying prior distributions.

Model selection is a process of identifying the best-fitting model among candidate models. Conditional on the observed data, different CRM models usually yield different estimates of the toxicity probabilities (${\widehat{\pi }}_1,\dots ,{\widehat{\pi }}_J$). Some of them may be to the true values, while others may not, depending on how well the models fit the cumulating data. In the model selection approach, at each time of decision making on dose assignment, we select the best model according to a suitable model selection criterion. Based on the estimates of the toxicity probabilities from the best-fitting model, we assign an appropriate dose to the new cohort of patients. A variety of model selection criteria have been proposed in the literature (see Burnham and Anderson 2002). Here we consider two commonly used information criteria: namley, the Akaike information criterion (AIC, Akaike 1973) and the Bayesian information criterion (BIC),

$$\text{AIC}=-2\log L+2r,$$

$$\text{BIC}=-2\log L+r\log n,$$

where L is the likelihood function, r is the number of model parameters and n is the number of observations. In our case, as all of the CRM models under consideration have the same r and n, the AIC and BIC are equivalent. Essentially, we select the model with the highest likelihood as the basis for inference and dose escalation. Dose finding is a sequential process. As the trial proceeds, more data are accumulated, and theselected model may vary from one decision-making time to an-other. Model selection provides an intuitive and straightforward way to make inference from several competing models. However, because the inference is solely based on the selected sin-gle model, the model selection approach ignores the uncertainty associated with the selection process, which often leads to narrow confidence intervals (Raftery, Madigan, and Hoeting 1997; Hjort and Claeskens 2003).

Model averaging has been proposed to account for the additional uncertainty introduced by different models. Unlike model selection, the model averaging approach explicitly acknowledges the uncertainty of models and makes inference based on all the competing models rather than a selected single model. Model averaging has been investigated from both Bayesian and frequentist perspectives. For a comprehensive review of Bayesian model averaging, see Hoeting et al. (1999). From the traditional frequentist perspective, Hjort and Claeskens (2003) laid down a unified likelihood-based framework for frequen-tist model averaging. Denoting S as the number of competing models under consideration, Hjort and Claeskens (2003) investigated a general class of model averaging estimators of the form

$$\stackrel{‒}{\alpha }=\sum _{s=1}^S{w}_s{\widehat{\alpha }}_s,$$ (6)

where the weight w_s is a measure of the relative influence of model s, and ${\widehat{\alpha }}_s$ is the estimate of parameter α under model s. We use a special case of (6), the so-called smoothed AIC estimator (Buckland, Burnham, and Augustin 1997; Hjort and Claeskens 2003), as an estimate of the toxicity probability across the multiple CRM models:

$${\stackrel{‒}{\pi }}_d=\sum _{s=1}^S{w}_s{\widehat{\pi }}_{sd},$$

where ${\widehat{\pi }}_{sd}$ is the MLE of the toxicity probability at dose level d obtained by the EM algorithm under the sth CRM model, and

$$w_s=\frac{exp(-{\text{AIC}}_s∕2)}{\sum _{s=1}^S\text{exp}(-{\text{AIC}}_s∕2)}$$

According to the goodness of fit, the smoothed AIC estimator assigns a larger weight to a better fitting model, and limits the influence of the poorly fitting model. In our case, the smoothed AIC estimator also has an intuitive Bayesian interpretation. Because all of the CRM models under consideration have the same number of parameters, w_s is exactly the ratio of the likelihood for model s versus the sum of likelihoods of all the candidate models. In addition, it easy to see that

$$w_s=\frac{exp(-{\text{BIC}}_s∕2)}{\sum _{s=1}^S\text{exp}(-{\text{BIC}}_s∕2)}$$

Therefore, w_s is also an approximation to the posterior probability of model s being correct (Schwarz 1978), and consequently ${\stackrel{‒}{\pi }}_d$ provides an approximation of the Bayesian model averaging estimator, in which the estimate from each model is weighted by the posterior model probability.

To estimate the variance of $\stackrel{‒}{\alpha }$, Buckland, Burnham, and Augustin (1997) suggested using the bootstrap method (Efron 1979), which, however, is problematic in our case due to a small sample size. At the early stage of a trial, only a small number of patients have been accrued. By the time the next dose assignment decision is to be made, most of the patients either have toxicity outcome Y missing or Y = 0, and very few patients have observed toxicities with Y = 1. Consequently, when bootstrapping such sparse data, many bootstrap samples have no observation with Y = 1, rendering estimation impossible. To circumvent this problem, we apply the resampling method by perturbing the objective function repeatedly with a nonnegative random variable (Jin, Ying, and Wei 2001) while keeping the data intact. Statistical inferences can then be made based on the empirical distribution of a large collection of perturbed estimators obtained from the perturbed objective functions. We incorporate the perturbation resampling method into the EM algorithm for incomplete data as follows:

1. Generate n random variates, (v₁, …, v_n), from the exponential distribution with mean one, Exp(1).

2. For each of the CRM models:

   1. At the E step, S calculate and substitute the missing value of Y with the expected value given by (4).
   2. At the M step, maximize the following perturbed log-likelihood function of α,

      $$\tilde{L}(\widehat{y}\mid \alpha )=\sum _{i=1}^n{v}_i\{{\widehat{y}}_i\log \left(p_{d_i}^{exp\left(\alpha \right)}\right)+(1-{\widehat{y}}_i)\log (1-p_{d_i}^{exp\left(\alpha \right)})\},$$

      and update the estimate of λ_k as ${\widehat{\lambda }}_k={\sum }_{i\in M_k}{v}_i∕{\sum }_{j=k}^K({\sum }_{i\in M_j}{v}_i+{\sum }_{i\in C_j}{v}_i{\widehat{y}}_i)$.
   3. Repeat the E and M steps until the algorithm converges to obtain the perturbed toxicity probability estimate ${\widehat{\pi }}_{sd}^{\ast }$.

3. Calculate the perturbed smoothed AIC estimator ${\stackrel{‒}{\pi }}_d^{\ast }={\sum }_{s=1}^S{w}_s^{\ast }{\widehat{\pi }}_{sd}^{\ast }$, where $w_s^{\ast }$ is calculated as ws based on the perturbed likelihood.

After repeating the perturbing procedure a large number of times, say 1000, the sampling distribution of ${\stackrel{‒}{\pi }}_d$ can be approximated by the empirical distribution of ${\stackrel{‒}{\pi }}_d^{\ast }$. In particular, the 90% confidence interval for ${\stackrel{‒}{\pi }}_d$ is given by the corresponding 5th and 95th sample quantiles of $\left\{{\stackrel{‒}{\pi }}_d^{\ast }\right\}$.

2.4 Dose-Finding Algorithm

Let ϕ denote the physician-specified toxicity target, and assume that patients are treated in cohorts, for example, with a cohort size of three. For safety, we restrict dose escalation or de-escalation by one dose level of change at a time. The dose-finding algorithm in the robust EM-CRM is described below:

1. Patients in the first cohort are treated at the lowest dose level.

2. At the current dose level d^curr, based on the cumulated data, we obtain the estimates for the toxicity probabilities, ${\stackrel{‒}{\pi }}_d$ (d = 1, …, J), using the EM-algorithm coupled with the model selection or model averaging procedure. We then find dose level d* that has a toxicity probability closest to ϕ, that is,

   $$d^{\ast }=\underset{d\in (1,\dots ,j)}{\text{argmin}}\mid {\stackrel{‒}{\pi }}_d-\varphi \mid$$

   If d^curr > d*, we de-escalate the dose level to d^curr − 1; if d^curr < d*, we escalate the dose level to d^curr + 1; otherwise, the dose stays at the same level, d^curr, for the next cohort of patients.

3. Once the maximum sample size is reached, the dose that has the toxicity probability closest to ϕ is selected as the MTD.

In the likelihood framework, we must have heterogeneity among the responses in order to estimate the parameter in the CRM (O’Quigley and Shen 1996). We begin the trial by treating the first cohort at the lowest dose. We fully follow each cohort of patients and continue escalating the dose until the first DLT occurs. Then, we switch to our EM-CRM dose-finding algorithm. We also impose a stopping rule for safety as follows. Let (l₁, u₁) denote the 90% confidence interval for the toxicity probability of the lowest dose; at any stage of the trial, if l₁ > ϕ, the trial is terminated.

3. SIMULATION STUDIES

We investigated the operating characteristics of the proposed robust EM-CRM design through simulation studies. We considered six dose levels and assumed that toxicity monotonically increased with respect to the dose. A maximum number of 36 patients were treated sequentially in a cohort size of 3, with the first cohort of patients treated at the lowest dose level. The assessment period was T = 3 months and the interarrival time be-tween patent cohorts was φ = 1 month. For patients who would experience toxicity in the assessment period [0, 3], we assumed the times to toxicity from a truncated Weibull distribution with the shape parameter of 2, the scale parameter of 0.51 and a supporting range of [0, 3], approximately that is, t ~ Weibull_{t∈[0, 3]} (2, 0.51). Under this distribution, 40% events were observed after one month of follow up. The target toxicity probability was ϕ = 30%. Under the robust EM-CRM, each cohort was treated immediately upon arrival. Three skeletons were elicited to represent three different prior opinions on the toxicity probabilities:

$$(p_1,p_2,p_3,p_4,p_5,p_6)=\{\begin{array}{cc}(0.05,0.14,0.18,0.22,0.26,0.30),\hfill & \text{skeleton}1\hfill \\ (0.08,0.12,0.20,0.30,0.40,0.50),\hfill & \text{skeleton}2\hfill \\ (0.20,0.30,0.40,0.50,0.60,0.70),\hfill & \text{skeleton}3\hfill \end{array}\phantom{\}}$$ (7)

As shown in Figure 2, the first skeleton stands for a conservative prior guess with the MTD located at the highest dose level; the second represents a typical prior with the MTD located at the middle of the dose levels; and the third is an aggressive prior with the MTD located at the low dose level. For convenience, we use EM-CRM_SEL and EM-CRM_AVG to denote the robust EM-CRM with model selection and model averaging, respectively. We compared the proposed designs with the standard CRM, in which we suspended patient accrual until all of the toxicity outcomes in the trial were completely observed prior to the next dose assignment. As such a CRM design is based on complete data, it represents the optimum case and provides a benchmark for comparison. We refer to the individual CRMs using each of these three skeletons as CRM 1, CRM 2, and CRM 3, respectively, and define EM-CRM 1, EM-CRM 2, and EM-CRM 3 similarly for the CRM coupled with the EM algorithm with a single skeleton. We considered eight toxicity scenarios as listed in Table 1, and carried out 10,000 simulated trials for each case.

Figure 2.

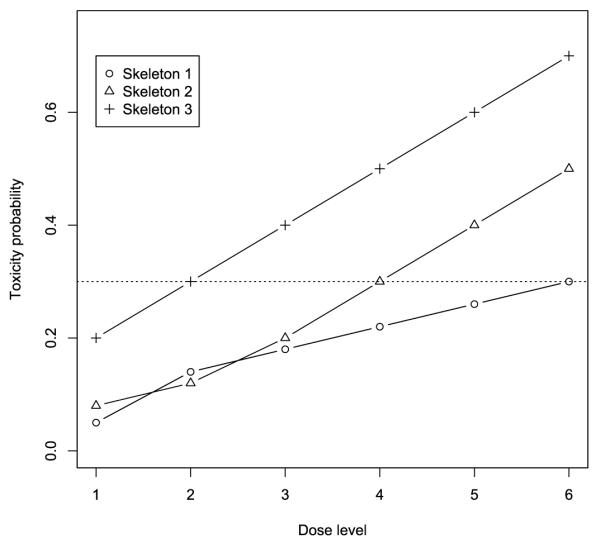
Profiles of three skeletons in the simulation study. The dotted line indicates the target toxicity probability of 30%.

Table 1.

Simulation study comparing the standard CRM, EM-CRM with a single skeleton, and EM-CRM with three skeletons coupled with model selection (EM-CRM_SEL), and model averaging (EM-CRM_AVG)

Design	Recommendation percentage at dose level							Average # toxicity	Average # patients	Average duration
	1	2	3	4	5	6	None
Scenario 1	0.08	0.10	0.12	0.30	0.50	0.60
CRM 1	0.1	2.9	24.4	49.2	20.5	2.9	0.1	10.3	36.0	37.0
# patients	4.1	4.2	6.8	10.2	7.0	3.7
EM-CRM 1	0.1	4.5	23.9	43.7	23.2	4.6	0.1	10.1	36.0	20.7
# patients	4.9	4.7	6.8	8.8	6.9	3.9
CRM 2	0.0	0.2	12.7	68.2	18.1	0.8	0.0	9.6	36.0	37.0
# patients	4.1	3.6	6.5	14.2	6.2	1.3
EM-CRM 2	0.0	0.3	12.7	66.3	19.9	0.7	0.1	9.4	36.0	20.8
# patients	4.6	3.7	7.4	12.7	6.1	1.5
CRM 3	0.0	0.6	13.4	67.0	18.4	0.6	0.1	9.4	36.0	37.0
# patients	4.2	3.7	6.7	14.0	6.4	0.9
EM-CRM 3	0.1	0.8	13.1	65.5	19.8	0.7	0.1	9.1	36.0	20.8
# patients	4.9	4.1	7.4	12.6	6.0	1.0
EM-CRMSEL	0.0	0.6	13.2	65.4	18.8	1.8	0.1	9.6	36.0	20.7
# patients	4.8	3.8	6.9	12.0	6.5	1.9
EM-CRMAVG	0.1	0.8	13.2	64.0	20.7	1.0	0.3	9.5	35.9	20.7
# patients	4.8	3.9	7.2	11.6	6.6	1.8
Scenario 2	0.06	0.08	0.10	0.15	0.30	0.45
CRM 1	0.0	0.3	3.1	18.3	39.9	38.4	0.0	9.3	36.0	37.0
# patients	3.8	3.5	3.7	5.5	8.1	11.4
EM-CRM 1	0.0	0.4	3.3	17.0	36.9	42.3	0.0	9.0	36.0	21.8
# patients	4.3	3.6	3.9	5.6	7.6	11.0
CRM 2	0.0	0.0	0.9	17.8	57.0	24.3	0.0	8.3	36.0	37.0
# patients	3.7	3.3	4.0	7.1	10.9	7.0
EM-CRM 2	0.0	0.1	1.4	17.0	57.2	24.4	0.0	7.9	36.0	21.7
# patients	4.1	3.4	4.6	7.5	10.3	6.1
CRM 3	0.0	0.1	1.6	18.8	59.6	19.9	0.0	8.1	36.0	37.0
# patients	3.8	3.4	4.1	7.4	11.6	5.7
EM-CRM 3	0.0	0.2	2.0	17.6	59.2	21.0	0.0	7.7	36.0	21.7
# patients	4.2	3.5	4.8	7.8	10.6	5.2
EM-CRMSEL	0.0	0.1	1.5	17.1	54.4	26.8	0.0	8.3	36.0	21.7
# patients	4.2	3.4	4.2	6.8	9.8	7.5
EM-CRMAVG	0.0	0.1	1.3	15.8	55.8	26.8	0.1	8.2	36.0	21.7
# patients	4.2	3.4	4.5	6.7	9.9	7.3
Scenario 3	0.05	0.14	0.18	0.22	0.26	0.30
CRM 1	0.0	1.6	6.0	11.9	18.1	62.5	0.0	7.9	36.0	37.0
# patients	3.8	4.4	4.9	5.0	5.6	12.2
EM-CRM 1	0.0	1.7	5.2	12.6	18.3	62.1	0.0	7.8	36.0	20.9
# patients	4.2	4.5	5.0	5.5	5.5	11.3
CRM 2	0.0	0.9	8.4	24.7	30.6	35.4	0.0	7.5	36.0	37.0
# patients	3.8	4.0	6.4	8.1	7.1	6.6
EM-CRM 2	0.0	1.0	9.5	25.6	31.8	32.1	0.0	7.3	36.0	20.9
# patients	4.1	4.1	7.0	8.3	6.9	5.5
CRM 3	0.0	1.3	8.7	26.1	34.5	29.4	0.0	7.4	36.0	37.0
# patients	3.8	4.2	6.3	8.5	7.8	5.5
EM-CRM 3	0.0	1.4	10.1	28.0	35.0	25.6	0.0	7.2	36.0	20.8
# patients	4.3	4.4	7.2	8.7	7.1	4.3
EM-CRMSEL	0.0	1.0	7.4	18.7	25.1	47.7	0.0	7.5	36.0	20.9
# patients	4.2	4.3	5.9	6.9	6.4	8.3
EM-CRMAVG	0.0	0.9	8.1	21.9	29.3	39.8	0.1	7.4	36.0	20.9
# patients	4.2	4.3	6.5	7.1	6.8	7.0
Scenario 4	0.20	0.30	0.40	0.50	0.60	0.70
CRM 1	25.4	50.8	17.7	4.0	0.4	0.0	1.7	10.8	35.5	36.6
# patients	13.4	12.5	6.0	2.6	0.8	0.2
EM-CRM 1	25.6	50.3	16.4	4.3	0.7	0.0	2.7	10.5	35.3	18.1
# patients	15.0	10.9	5.3	2.8	1.0	0.3
CRM 2	20.9	44.9	28.2	4.3	0.1	0.0	1.7	10.9	35.5	36.6
# patients	12.1	11.8	8.8	2.5	0.4	0.0
EM-CRM 2	21.1	43.8	27.8	4.1	0.2	0.0	3.0	10.6	35.2	18.1
# patients	13.6	10.7	8.0	2.3	0.5	0.1
CRM 3	22.1	48.2	24.2	3.7	0.2	0.0	1.6	10.7	35.5	36.6
# patients	12.8	12.3	7.8	2.2	0.3	0.0
EM-CRM 3	21.6	47.9	24.1	3.5	0.1	0.0	2.9	10.4	35.2	18.2
# patients	14.2	11.3	7.1	2.3	0.4	0.0
EM-CRMSEL	21.9	46.4	24.3	4.2	0.4	0.0	2.8	10.7	35.2	18.2
# patients	14.0	10.7	7.1	2.6	0.7	0.1
EM-CRMAVG	20.4	46.1	23.9	4.0	0.2	0.0	5.4	10.4	34.5	17.9
# patients	13.6	10.9	7.0	2.4	0.6	0.1
Scenario 5	0.08	0.12	0.20	0.30	0.40	0.50
CRM 1	0.1	5.3	22.5	35.5	25.6	11.0	0.1	10.0	36.0	37.0
# patients	4.2	4.9	6.9	8.1	6.7	5.0
EM-CRM 1	0.1	6.0	21.1	34.4	25.6	12.7	0.1	9.7	36.0	20.5
# patients	4.9	5.2	6.6	7.6	6.6	5.0
CRM 2	0.0	1.3	20.9	49.1	24.3	4.3	0.0	9.3	36.0	37.0
# patients	4.2	4.2	8.4	11.3	6.0	2.0
EM-CRM 2	0.0	1.7	21.8	47.6	24.5	4.3	0.1	9.0	36.0	20.4
# patients	4.7	4.4	9.0	10.3	5.7	1.9
CRM 3	0.1	1.9	22.0	49.3	23.9	2.9	0.0	9.1	36.0	37.0
# patients	4.2	4.4	8.5	11.2	6.2	1.4
EM-CRM 3	0.1	2.6	22.5	48.1	23.6	3.1	0.1	8.8	36.0	20.4
# patients	5.0	4.9	8.9	10.4	5.5	1.4
EM-CRMSEL	0.1	2.0	20.0	46.0	25.3	6.5	0.1	9.3	36.0	20.4
# patients	4.9	4.6	7.8	9.5	6.3	2.8
EM-CRMAVG	0.1	2.0	20.1	45.2	27.4	5.0	0.3	9.1	35.9	20.3
# patients	4.9	4.7	8.2	9.3	6.3	2.4
Scenario 6	0.05	0.10	0.30	0.50	0.60	0.70
CRM 1	0.1	23.7	54.9	19.6	1.7	0.0	0.0	10.9	36.0	37.0
# patients	3.8	8.4	12.5	7.8	2.7	0.8
EM-CRM 1	0.4	27.1	47.9	22.0	2.3	0.1	0.0	10.9	36.0	20.5
# patients	4.4	8.9	10.5	7.6	3.5	1.1
CRM 2	0.0	9.0	70.1	20.2	0.7	0.0	0.0	10.9	36.0	37.0
# patients	3.7	5.7	16.4	8.4	1.5	0.2
EM-CRM 2	0.1	8.4	69.6	21.1	0.8	0.0	0.0	10.8	36.0	20.4
# patients	4.2	6.4	15.0	8.2	1.9	0.3
CRM 3	0.0	9.8	69.8	19.7	0.7	0.0	0.0	10.8	36.0	37.0
# patients	3.7	6.1	16.4	8.2	1.5	0.1
EM-CRM 3	0.0	9.3	68.0	21.9	0.8	0.0	0.0	10.6	36.0	20.4
# patients	4.2	6.8	15.1	8.1	1.6	0.2
EM-CRMSEL	0.0	9.8	68.3	20.9	0.9	0.1	0.0	10.9	36.0	20.5
# patients	4.2	6.9	14.2	8.1	2.3	0.5
EM-CRMAVG	0.0	11.0	66.0	22.0	0.9	0.0	0.1	10.8	36.0	20.5
# patients	4.2	6.9	14.1	7.9	2.5	0.4
Scenario 7	0.02	0.03	0.04	0.05	0.30	0.50
CRM 1	0.0	0.0	1.4	15.9	46.2	36.5	0.0	9.8	36.0	37.0
# patients	3.2	3.0	3.1	4.7	8.1	13.8
EM-CRM 1	0.0	0.0	2.0	14.1	43.2	40.7	0.0	9.6	36.0	23.9
# patients	3.4	3.1	3.2	4.8	8.1	13.2
CRM 2	0.0	0.0	0.0	7.0	66.3	26.7	0.0	9.1	36.0	37.0
# patients	3.2	3.0	3.1	4.5	12.1	10.0
EM-CRM 2	0.0	0.0	0.0	6.1	65.3	28.5	0.0	8.8	36.0	23.9
# patients	3.3	3.0	3.3	5.0	11.9	9.4
CRM 3	0.0	0.0	0.0	5.9	70.0	24.1	0.0	8.9	36.0	37.0
# patients	3.2	3.0	3.1	4.5	13.3	8.9
EM-CRM 3	0.0	0.0	0.0	4.6	69.5	25.9	0.0	8.6	36.0	23.9
# patients	3.3	3.0	3.3	5.0	13.0	8.3
EM-CRMSEL	0.0	0.0	0.0	5.3	68.9	25.8	0.0	8.9	36.0	23.9
# patients	3.4	3.0	3.1	4.9	12.2	9.4
EM-CRMAVG	0.0	0.0	0.1	5.8	65.9	28.2	0.0	9.0	36.0	23.9
# patients	3.4	3.0	3.3	4.7	11.5	10.1
Scenario 8	0.50	0.60	0.70	0.80	0.85	0.90
CRM 1	18.5	0.1	0.0	0.0	0.0	0.0	81.4	9.5	18.7	21.8
# patients	17.5	1.0	0.2	0.0	0.0	0.0
EM-CRM 1	16.3	0.1	0.0	0.0	0.0	0.0	83.6	8.8	17.3	9.4
# patients	15.7	1.2	0.3	0.1	0.0	0.0
CRM 2	16.7	0.2	0.0	0.0	0.0	0.0	83.1	9.4	18.4	21.5
# patients	17.0	1.2	0.2	0.0	0.0	0.0
EM-CRM 2	14.0	0.2	0.0	0.0	0.0	0.0	85.8	8.6	16.7	9.1
# patients	15.0	1.4	0.3	0.0	0.0	0.0
CRM 3	18.7	0.1	0.0	0.0	0.0	0.0	81.2	9.4	18.6	21.7
# patients	17.4	1.1	0.2	0.0	0.0	0.0
EM-CRM 3	14.8	0.1	0.0	0.0	0.0	0.0	85.1	8.7	17.0	9.2
# patients	15.5	1.2	0.3	0.0	0.0	0.0
EM-CRMSEL	14.8	0.2	0.0	0.0	0.0	0.0	85.1	8.6	16.8	9.2
# patients	15.1	1.3	0.3	0.1	0.0	0.0
EM-CRMAVG	10.6	0.1	0.0	0.0	0.0	0.0	89.3	7.4	14.4	8.3
# patients	12.9	1.2	0.3	0.0	0.0	0.0

Under each scenario in Table 1, the first row represents the true toxicity probabilities; rows 2 through 5 show the dose selection probability and the average number of patients treated at each dose separately for CRM 1 and EM-CRM 1, followed by those of CRM 2, EM-CRM 2, CRM 3, and EM-CRM 3; and the last four rows correspond to the EM-CRM_SEL and EM-CRM_AVG. We also present the number of patients who experienced toxicity, the total number of patients treated, and the trial duration averaged across 10,000 simulated trials.

In scenario 1, the MTD is at dose level 4, and the three CRMs using different skeletons yielded quite different MTD selection percentages. CRM 2 and CRM 3 performed similarly with selection percentages of the target dose of 68.2% and 67.0%, respectively. CRM 1, however, performed substantially worse with a selection percentage of only 49.2%, demonstrating that the CRM is quite sensitive to the prespecified skeleton. If skeleton 1 had been recommended by physicians to carry out the CRM trial design, there is an almost 45% of chance that dose 3 or 5 would have been selected as the MTD. Compared to the CRMs, the performance of the EM-CRMs was very competitive. The selection probability and the number of toxicity under the EM-CRMs were only slightly lower than the CRMs. For example, using skeleton 2 or 3, the differences of the selection probabilities between the two designs were less than 2%. The major advantage of the EM-CRM over the CRM is that the trial duration is dramatically shortened: the average trial duration under the EM-CRM was less than 21 months in contrast to 37 months under the CRM. These results suggest that the EM algorithm satisfactorily addresses the problem of the late-onset toxicity without sacrificing the MTD selection probability and patient safety. Nevertheless, the EM-CRM also demonstrated a similar degree of sensitivity to the skeleton as the CRM. Forexample, under the EM-CRM, the selection probability of the MTD using skeleton 1 was 22.6% lower than that using skeleton 2. The robust EM-CRMs satisfactorily resolved the sensitivity of the EM-CRM. In particular, both the EM-CRM_SEL and EM-CRM_AVG correctly recommended the MTD more than 64% of the time. The average trial duration of the EM-CRM_SEL and EM-CRM_AVG was approximately 21 months, which was immensely shorter than those of the CRMs. The average numbers of toxicities under the EM-CRM_SEL and EM-CRM_AVG were quite close to those under other designs.

In scenario 2, with the MTD at the fifth dose level, CRM 1 behaved the worst, selecting the MTD less than 40%; CRM 3 performed the best, selecting the MTD close to 60%; EM-CRMs performed similarly to the CRMs in terms of the MTD selection, but yielded substantially shorter trial durations. The selection percentages of the MTD using the proposed EM-CRM_SEL and EM-CRM_AVG were approximately 55%, which were much better than CRM 1 and comparable to CRM 2 and CRM 3. Furthermore, the proposed designs shortened the duration of the trial from 37 to 22 months. In scenario 3, with the sixth dose as the MTD, CRM 3 had the lowest MTD selection percentage (less than 30%), whereas the proposed EM-CRM_SEL and EM-CRM_AVG recommended the MTD 47.7% and 39.8% of the time, respectively. In scenario 4, all of the selection percentages using different designs were close, but the trial durations of the proposed designs were only half of those using the CRMs. Scenario 5 is similar to scenario 1 with the fourth dose as the MTD, but represents a more difficult case because the toxicity probabilities are closer to each other and thus harder to distinguish. Under that scenario, the MTD selection percentages of the proposed designs were slightly lower than those of the best-performing CRMs 2 and 3, but substantially better than that of CRM 1. Similar results can also be observed in scenario 6, in which the MTD is at the third dose level. Scenario 7 is designed to simulate the case in which there is a sudden jump in the toxicity probabilities from the fourth to the fifth dose level. Under that scenario, CRM 3 performed the best with an MTD selection percentage of 70%, and CRM 1 performed the worst with an MTD selection percentage of 46.2%. Using model selection or model averaging, the proposed designs limited the influence of skeleton 1 and yielded an MTD selection percentage similar to those of CRMs 2 and 3. In scenario 8, even the first dose is overly toxic; all of the designs were able to terminate the trial early due to the safety rule we implemented. In conclusion, the simulation studies demonstrated that our proposed designs are robust, and can immensely shorten the trial duration without sacrificing trial performance.

4. SENSITIVITY ANALYSIS

In practice, the amount of missing data is controlled by two factors: the assessment and interarrival time ratio (A/I ratio = T/φ) and the distribution of the time to toxicity. When the A/I ratio is high, the new cohort arrives rapidly and the trial requires more frequent decision making on dose assignment. Consequently, at each moment of decision making, the cohorts that have already entered the trial are only followed for a short period of time, thus resulting in a high percentage of missing toxicity outcomes. On the other hand, given a fixed A/I ratio, if the distribution of the time to toxicity is skewed toward the end of the assessment period, we also tend to have more missing data because the toxicity outcome is less likely to be observed during the early stage of the follow up.

In our sensitivity analysis, we considered two A/I ratios (i.e., 3:1 and 5:1) and three different distributions for the time to toxicity: Weibull_[0,3] (0.9, 1.7), and two scaled beta distributions 3 × Beta(3.08, 2) and 3 × Beta(5.16, 2). The parameters in thethree distributions were chosen in such a way that by the middle of the assessment period, there were approximately 91%, 30%, and 10% of toxicity outcomes observed, respectively. Thus, the Weibull distribution represents a case that toxicity can be observed relatively quickly, that is, early-onset toxicity, while the two Beta distributions represent cases of more severely late-onset toxicity because it is more likely that toxicity would occur at the later stage of the follow up. As shown in Table 2, we simulated scenario 1 and presented the results by using EM-CRM 2 due to its superior performance. When the A/I ratio increased and the time-to-toxicity distribution was severely skewed to the right, the selection percentage of the MTD slightly deceased, and the increase in the number of observed toxicities was also minor. Therefore, the proposed designs are not particularly sensitive to the A/I ratio or the time-to-toxicity distribution.

Table 2.

Sensitivity analysis of the robust EM-CRM with different values of the ratio of the assessment period to the interarrival time (A/I) and different distributions of the time to toxicity under scenario 1

Design	Recommendation percentage at dose level							Average # toxicity	Average # patients	Average duration
	1	2	3	4	5	6	None
Scenario 1	0.08	0.10	0.12	0.30	0.50	0.60
A/I ratio = 3; t ~ Weibull[0,3](0.9, 1.7)
EM-CRM 2	0	0.3	12	67.6	19.2	0.8	0.1	9.3	36	20.8
# patients	4.3	3.6	7.2	13.8	5.9	1.1
EM-CRMSEL	0	0.6	12.2	66.2	19.3	1.6	0.1	9.4	36	20.8
# patients	4.4	3.8	7.1	13.2	6.2	1.3
EM-CRMAVG	0.1	0.7	12.5	65.0	20.6	0.9	0.2	9.4	35.9	20.7
# patients	4.5	3.9	7.1	13	6.2	1.3
A/I ratio = 3; t ~ 3×Beta(3.08, 2)
EM-CRM 2	0	0.4	15.3	64.6	18.8	0.8	0.1	9.6	36	20.7
# patients	5.1	3.8	7.3	11.2	6.6	2.1
EM-CRMSEL	0.1	0.8	18.3	62.7	16.5	1.7	0.1	10.4	36.0	20.8
# patients	5.0	3.7	6.2	10.0	7.2	3.8
EM-CRMAVG	0.0	0.9	18.1	60.6	19.2	0.9	0.3	10.1	35.9	20.7
# patients	5.1	3.9	6.7	9.5	7.4	3.4
A/I ratio = 3; t ~ 3×Beta(5.16, 2)
EM-CRM 2	0	0.4	16.1	64.2	18.6	0.7	0.1	9.6	36	20.8
# patients	5.4	3.8	7.2	10.6	6.5	2.6
EM-CRMSEL	0.0	0.9	18.6	61.6	17.2	1.7	0.1	10.5	36.0	20.8
# patients	5.4	3.7	6.1	9.4	7.0	4.3
EM-CRMAVG	0.0	1.0	18.5	60.2	19.0	0.9	0.3	10.2	35.9	20.7
# patients	5.4	3.8	6.9	8.8	7.4	3.7
A/I ratio = 5; t ~ Weibull[0,3](0.9, 1.7)
EM-CRM 2	0.0	0.3	12.5	66.0	20.3	0.8	0.1	9.3	36.0	17.1
# patients	4.5	3.8	7.4	13.1	5.9	1.2
EM-CRMSEL	0.0	0.4	12.6	65.9	19.2	1.8	0.1	9.5	36.0	17.1
# patients	4.5	3.8	7.1	12.7	6.2	1.5
EM-CRMAVG	0.0	0.6	12.3	64.9	20.9	0.9	0.3	9.4	35.9	17.0
# patients	4.7	3.9	7.2	12.4	6.3	1.4
A/I ratio = 5; t ~ 3×Beta(3.08, 2)
EM-CRM 2	0.0	0.9	17.8	60.1	20.1	1.0	0.1	9.6	36.0	17.1
# patients	6.1	3.8	7.5	8.9	6.5	3.1
EM-CRMSEL	0.0	1.5	21.9	57.8	16.8	2.1	0.0	10.9	36.0	17.1
# patients	6.0	3.7	5.5	8.2	6.7	6.0
EM-CRMAVG	0.0	1.6	21.3	56.6	19.0	1.2	0.3	10.5	35.9	17.1
# patients	5.8	3.8	6.6	7.3	7.4	4.9
A/I ratio = 5; t ~ 3×Beta(5.16, 2)
EM-CRM 2	0.1	0.9	19.2	59.7	19.1	1.0	0.1	9.7	36.0	17.1
# patients	6.5	3.8	7.5	8.2	6.4	3.5
EM-CRMSEL	0.0	1.5	22.4	56.6	17.3	2.2	0.0	10.9	36.0	17.1
# patients	6.3	3.6	5.3	8.0	6.2	6.6
EM-CRMAVG	0.1	1.8	21.8	54.7	20.1	1.2	0.3	10.5	35.9	17.1
# patients	6.4	3.8	6.7	6.4	7.1	5.4

Patient heterogeneity is another important factor influencing the practical performance of the trial design. We considered two types of heterogeneity in our sensitivity analysis. The first type concerns population heterogeneity. We assumed that the target patient population is an equal-proportion mixture of three sub-populations characterized by different time-to-toxicity distributions, namely, Weibull_[0,3](3, 0.17), Weibull_{[0, 3]}(1, 1.5], and Weibull_[0,3](0.75, 2). The second] type of heterogeneity we considered concerns the time-to-toxicity distribution. Specifically, we assumed that the time-to-toxicity profile varies across different dose levels with higher doses inducing toxicity sooner (see Figure 3). For convenience, we refer to these two types of heterogeneity as population and (time-to-toxicity) distribution heterogeneity, respectively. We simulated scenarios 1 and 2 under the two types of heterogeneity. The results in Table 3 show that our designs are not sensitive to heterogeneous patient populations. The MTD selection probabilities using the EM-CRM, EM-CRM_SEL, and EM-CRM_AVG are very similar to those in the absence of heterogeneity as listed in Table 1 (see scenarios 1 and 2), and the differences are typically less than 2%. The numbers of toxicities are also quite close and stable regardless of the presence of the heterogeneity.

Figure 3.

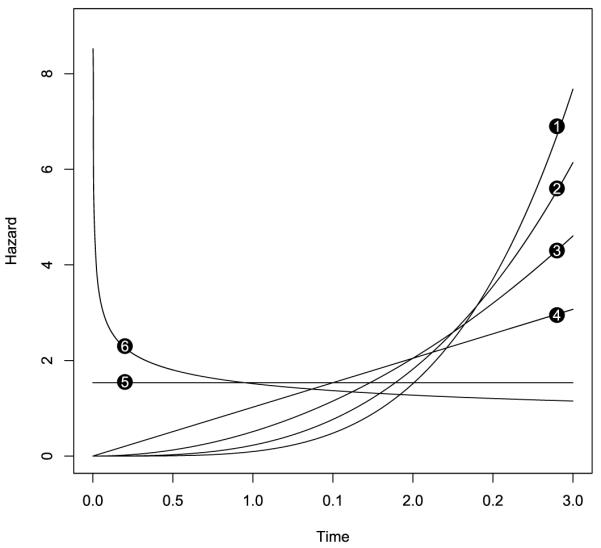
Hazards of the time to toxicity at different dose levels in the sensitivity analysis. The number attached to each hazard curve represents the corresponding dose level.

Table 3.

Sensitivity analysis of the EM-CRM and robust EM-CRMs with the population and (time-to-toxicity) distribution heterogeneity in scenarios 1 and 2

Design	Recommendation percentage at dose level							Average # toxicity	Average # patients	Average duration
	1	2	3	4	5	6	None
Scenario 1	0.08	0.10	0.12	0.30	0.50	0.60
Population heterogeneity
EM-CRM 2	0.0	0.4	12.6	66.0	20.3	0.7	0.1	9.3	36.0	20.7
# patients	4.5	3.7	7.2	13.1	6.1	1.3
EM-CRMSEL	0.0	0.5	12.8	65.7	19.4	1.5	0.1	9.6	36.0	20.8
# patients	4.6	3.8	7.0	12.3	6.5	1.8
EM-CRMAVG	0.0	0.7	13.1	63.7	21.2	1.0	0.3	9.5	35.9	20.8
# patients	4.6	3.9	7.0	12.1	6.6	1.6
Distribution heterogeneity
EM-CRM 2	0.0	0.4	12.1	65.7	21.0	0.8	0.0	9.0	36.0	20.8
# patients	5.3	3.7	7.5	12.7	5.8	1.0
EM-CRMSEL	0.0	0.6	12.1	64.7	20.4	2.1	0.1	9.1	36.0	20.7
# patients	5.4	3.9	7.0	12.7	6.1	1.1
EM-CRMAVG	0.1	0.7	12.6	62.5	22.9	1.0	0.3	9.1	35.9	20.7
# patients	5.3	3.9	7.2	12.0	6.4	1.1
Scenario 2	0.06	0.08	0.10	0.15	0.30	0.45
Population heterogeneity
EM-CRM 2	0.0	0.1	1.3	18.1	56.3	24.2	0.1	8.0	36.0	21.7
# patients	4.0	3.4	4.5	7.5	10.5	6.1
EM-CRMSEL	0.0	0.1	1.3	17.3	54.6	26.7	0.1	8.3	36.0	21.7
# patients	4.1	3.4	4.1	6.9	9.9	7.4
EM-CRMAVG	0.0	0.1	1.6	15.2	55.5	27.4	0.2	8.3	35.9	21.8
# patients	4.1	3.5	4.3	6.7	10.1	7.4
Distribution heterogeneity
EM-CRM 2	0.0	0.1	1.8	17.1	56.0	25.0	0.0	7.7	36.0	21.8
# patients	4.5	3.4	5.1	7.4	10.1	5.5
EM-CRMSEL	0.0	0.1	1.6	16.7	53.8	27.8	0.0	8.0	36.0	21.7
# patients	4.6	3.4	4.2	7.2	10.2	6.3
EM-CRMAVG	0.0	0.1	1.1	15.2	55.2	28.3	0.1	7.8	36.0	21.7
# patients	4.6	3.5	4.8	6.8	10.1	6.1

We also evaluated the performance of the proposed robust EM-CRM when using different numbers of skeletons. Under scenario 2, we increased the number of skeletons from one up to six, by successively adding one skeleton at a time in the original order. In addition to the three skeletons we previously considered, the fourth to sixth skeletons were (0.20, 0.30, 0.40, 0.50, 0.60, 0.70), (0.05, 0.14, 0.30, 0.40, 0.46, 0.55), and (0.08, 0.10, 0.15, 0.20, 0.30, 0.50), respectively. Table 4 shows the selection percentage and the number of patients treated at each dose when using two, four, five, and six skeletons. Recall that, using only the first skeleton in scenario 2, EM-CRM 1 yielded the lowest MTD selection percentage of 36.9%. By adding one more skeleton, the performance of the robust EM-CRM design was substantially improved, increasing the MTD selection percentage more than 10%. While adding more skeletons still improved the performance of the proposed designs, the improvement became less obvious after three skeletons, and started to diminish as the sixth skeleton was added. By employing the model selection and model averaging procedures, the robust EM-CRM automatically leans toward the best-performing CRM, and limits the influence of the poorly performing CRM. Thus, as long as the set of skeletons contains one good-performing skeleton, the proposed design should perform well. In practice, we recommend using three skeletons in the trial design, and these skeletons should be chosen in a way to cover a reasonable range of toxicity shapes. That is, when selecting three skeletons, as recommended, one should exercise care not to have equivalent profiles chosen. Given two skeletons {p_i1, …, p_iJ} and {p_k, …, p_kJ}, they have equivalent profiles if one skeleton can be expressed as a power transformation of the other, that is, $p_{ij}=p_{kj}^c$, j=1,…, J, where c is a constant, or equivalently,

$$\frac{\log p_{i1}}{\log p_{k1}}=\cdots =\frac{\log p_{ij}}{\log p_{kj}}=c.$$

Therefore, a natural measure of the “distance” or “dissimilarity” between skeletons i and k is the variability of the ratio of the log-probabilities var(logp_ij/logp_kj). A larger value of this variance indicates a higher level of dissimilarity between the two skeletons. When var(logp_ij/logp_kj) = 0, the two skeletons are equivalent. As an example, in our simulation study, the distance between skeletons 1 and 2 is 0.08, and the distance between skeletons 1 and 3 is 0.42.

Table 4.

Sensitivity analysis of the robust EM-CRMs with two, four, five, and six skeletons under scenario 2

Number of skeletons	Design	Recommendation percentage at dose level							Average # toxicity	Average # patients	Average duration
		1	2	3	4	5	6	None
	Scenario 2	0.06	0.08	0.10	0.15	0.30	0.45
2	EM-CRMSEL	0.0	0.1	1.2	18.4	50.9	29.4	0.0	8.4	36.0	21.8
	# patients	4.1	3.4	4.1	6.8	9.4	8.1
	EM-CRMAVG	0.0	0.1	1.4	15.5	52.5	30.5	0.1	8.5	36.0	21.7
	# patients	4.2	3.4	4.1	6.6	9.3	8.3
4	EM-CRMSEL	0.0	0.1	1.6	17.1	53.5	27.8	0.1	8.3	36.0	21.7
	# patients	4.2	3.4	4.4	7.0	9.5	7.5
	EM-CRMAVG	0.0	0.3	2.0	16.9	54.1	26.7	0.1	8.1	36.0	21.7
	# patients	4.2	3.6	4.7	6.8	9.6	7.1
5	EM-CRMSEL	0.0	0.1	1.0	13.5	58.2	27.2	0.0	8.4	36.0	21.7
	# patients	4.2	3.4	4.1	6.5	10.6	7.3
	EM-CRMAVG	0.0	0.2	1.3	14.7	58.2	25.5	0.1	8.1	36.0	21.7
	# patients	4.2	3.5	4.5	6.5	10.5	6.7
6	EM-CRMSEL	0.0	0.1	1.1	13.9	58.1	26.7	0.0	8.4	36.0	21.7
	# patients	4.2	3.4	4.1	6.3	10.7	7.3
	EM-CRMAVG	0.0	0.1	1.4	14.9	56.9	26.5	0.2	8.2	36.0	21.7
	# patients	4.2	3.5	4.5	6.4	10.2	7.2

The two proposed robust EM-CRMs have similar operating characteristics, but the EM-CRM_SEL is less computationally intensive than the EM-CRM_AVG as the latter involves a resampling procedure when calculating the variances of the estimated toxicity probabilities. For this reason, the EM-CRM_SEL design may be preferred for general practical use.

5. EXAMPLE

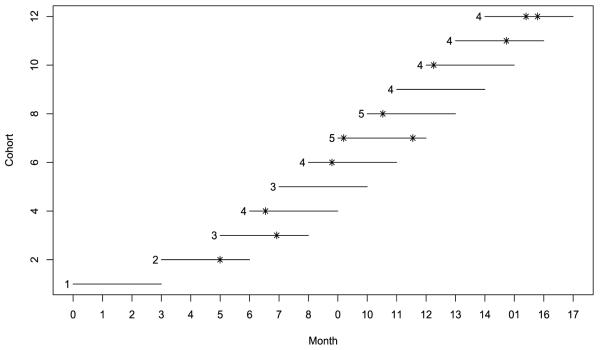
We illustrated the proposed EM-CRM_SEL design using the prostate cancer clinical trial. The target toxicity probability was 30%, and a total of 36 patients were treated sequentially in cohorts of size 3. We used the three skeletons given in (7). The dose assignment for each cohort is exhibited in Figure 4. The trial started by treating the first cohort at dose level 1. As no DLT was observed for the first cohort at the end of three months, we escalated the dose and treated the second cohort at dose level 2. After one DLT was observed around month 5, the EM-CRM_SEL was evoked to direct the dose assignment thereafter. Based on the observed data, the EM-CRM_SEL chose dose level 3 as the most appropriate dose to treat the third cohort. By month 6, no toxicity had been observed in the third cohort, and thus we escalated the dose and treated the fourth cohort at dose level 4. However, before assigning a dose to the fifth cohort at month 7, a total of two DLTs were observed in the third and fourth cohorts. These late-onset toxicities led us to de-escalate the dose and assign dose level 3 to the fifth cohort. Because no toxicity was observed in the fifth cohort, we escalated the dose back to level 4 for the sixth cohort, and then escalated the dose again to level 5 to treat the seventh and eighth cohorts. After two DLTs were observed at dose level 5 by month 11, we de-escalated the dose, and the last four remaining cohorts were treated at dose level 4. At the end of the trial, the dose at level 4 was selected as the MTD.

Figure 4.

Dose assignment with each horizontal line segment representing the follow up for a cohort. Toxicities are indicated by asterisk and numbers on the left side of the line segments are dose levels assigned to the cohorts.

Figure 5 shows the model selected after enrolling each cohort during the trial conduct. Before the ninth cohort entered the trial, model 2 (i.e., the CRM model with the second skeleton) mostly had the lowest AIC and was selected as the best model to determine the dose escalation. At the later stage of the trial, model 3 became the best-fitting model and directed the dose assignment. Throughout the trial, model 1 always had the highest AIC and thus was never selected, suggesting that the first skeleton may deviate far from the true toxicity profile of the drug. Had the investigators recommended the first skeleton to carry out the CRM trial design, the performance of the design could be compromised. By specifying multiple skeletons and coupling with the model selection procedure, our approach avoids such an undesirable case, and thus improves the robustness of the design.

Figure 5.

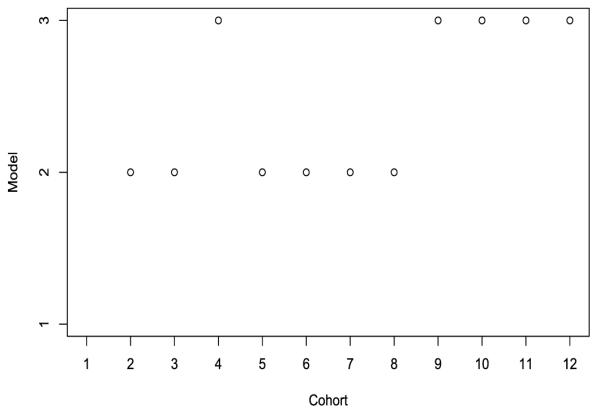
Model selection using the EM-CRM_SEL design.

6. CONCLUSION

We have proposed two versions of robust EM-CRM designs to meet the practical needs when toxicity outcomes cannot be observed quickly enough, and to improve the robustness of the CRM. Unlike the original CRM, the proposed designs do not require the toxicity outcome to be ascertainable shortly after the initiation of the treatment. In the new designs, unobserved toxicity outcomes are naturally treated as missing data, and the EM algorithm and missing data theory can be used to make inference and dose escalation decisions based on the incomplete data. By allowing a fast and continuous accrual, the proposed designs substantially shorten the duration of the trial if the toxicity is of late onset. To address the sensitivity of the CRM to the specification of prior toxicity probabilities, the new designs specify multiple sets of prior toxicity probabilities, and apply the model selection or averaging procedure to multiple CRM models. The selection of the MTD under the proposed designs is competitive with the best-performing CRM in the set of CRM models under consideration, and can be substantially superior to that of a CRM in which the skeleton happens to be very far off the true toxicity profile. In our designs, simultaneously specifying multiple skeletons reduces the chance that all of the sets of toxicity probabilities are misspecified. This dramatically improves the robustness of the CRM. In practice, the investigator often gives a range of toxicity probabilities for each dose, say, [p_d,min, p_d,max] for dose level d. We can naturally construct three skeletons by grouping the p_d,min’s, p_d,max’s and the averages (p_d,min + p_d,max)/2 across all the dose levels, respectively. The proposed robust EM-CRM design includes the standard CRM as a special case when the toxicity is ascertainable shortly after the treatment is administered and only one skeleton is specified.

The proposed methods focus on finding one single MTD in a homogenous patient population. However, the patient population may be heterogeneous and composed of several subgroups with differential MTDs. Our dose-finding approach may not be suitable or robust for heterogeneous populations. One way to accommodate such a heterogeneous case is to tighten the eligibility criteria for phase I trials to make patients more homo-geneous. Another way is to include patient characteristics as covariates in the CRM model and search for multiple MTDs. However, given small sample sizes of phase I trials with a relatively low percentage of toxicity events, the estimation under the expanded model may be rather challenging.

APPENDIX

Under the CRM model (1), the log-likelihood for the ith observation is

$$l_i=y_i{e}^{\alpha }\log p_{d_i}+(1-y_i)\log (1-p_{d_i}^{exp\left(\alpha \right)}).$$

The corresponding score function is given by

$$D(\alpha \mid y_i)=\frac{\partial l_i}{\partial \alpha }=y_i{e}^{\alpha }\log p_{d_i}-(1-y_i)\frac{p_{d_i}^{exp\left(\alpha \right)}{e}^{\alpha }\log p_{d_i}}{1-p_{d_i}^{exp\left(\alpha \right)}}$$

and the second derivative of the log-likelihood is,

$$\frac{{\partial }^2{l}_i}{\partial {\alpha }^2}=y_i{e}^{\alpha }\log p_{d_i}+(1-y_i)\frac{p_{d_i}^{exp\left(\alpha \right)}{e}^{\alpha }\log p_{d_i}(p_{d_i}^{exp\left(\alpha \right)}-e^{\alpha }\log p_{d_i}-1)}{{(1-p_{d_i}^{exp\left(\alpha \right)})}^2}$$

the first term on the right-hand Therefore, given y = {y_i, i 1, …, n} side of (5) is given by

$$\begin{array}{cc}\hfill E[I(\alpha \mid y)\mid y_{\text{obs}},\widehat{\alpha }]=& E\left[\sum _{i=1}^n-\frac{{\partial }^2{l}_i}{\partial {\alpha }^2}\mid y_{\text{obs}},\widehat{\alpha }\right]\hfill \\ \hfill =& -\sum _{i=1}^n\left\{{\widehat{y}}_i{e}^{\widehat{\alpha }}\log p_{d_i}+(1-{\widehat{y}}_i)\frac{p_{d_i}^{exp\left(\widehat{\alpha }\right)}{e}^{\widehat{\alpha }}\log p_{d_i}(p_{d_i}^{exp\left(\widehat{\alpha }\right)}-e^{\widehat{\alpha }}\log p_{d_i}-1)}{{(1-p_{d_i}^{exp\left(\widehat{\alpha }\right)})}^2}\right\}.\hfill \end{array}$$

Because E[D(α|y_i)]=0, hand it follows that the second term on the rightside of (5) is given by

$$\begin{array}{cc}\hfill E[D^2(\alpha \mid y_{\text{mis}})\mid y_{\text{obs}},\widehat{\alpha }]=& \text{var}[D(\alpha \mid y_{\text{mis}})\mid y_{\text{obs}},\widehat{\alpha }]\hfill \\ \hfill =& \sum _{i:y_i\in y_{\text{mis}}}{\left(e^{\widehat{\alpha }}\log p_{d_i}+\frac{p_{d_i}^{exp\left(\widehat{\alpha }\right)}{e}^{\widehat{\alpha }}\log p_{d_i}}{1-p_{d_i}^{exp\left(\widehat{\alpha }\right)}}\right)}^2\text{var}(y_i\mid y_{\text{obs}},\widehat{\alpha }).\hfill \end{array}$$

Note that y_i is a Bernoulli random variable; we have

$$\begin{array}{cc}\hfill \text{var}(y_i\mid y_{\text{obs}},\widehat{\alpha })& =E(y_i\mid t_i>u_i,\widehat{\alpha })(1-E(y_i\mid t_i>u_i,\widehat{\alpha }))\hfill \\ \hfill & =\frac{p_{d_i}^{exp\left(\widehat{\alpha }\right)}(1-p_{d_i}^{exp\left(\widehat{\alpha }\right)})pr(t_i>u_i\mid Y_i=1)}{{\{1-p_{d_i}^{exp\left(\widehat{\alpha }\right)}+p_{d_i}^{exp\left(\widehat{\alpha }\right)}pr(t_i>u_i\mid Y_i=1)\}}^2}\hfill \end{array}$$

Thus

$$E[D^2(\alpha \mid y_{\text{mis}})\mid y_{\text{obs}},\widehat{\alpha }]=\sum _{i:y_i\in y_{\text{mis}}}\frac{e_{2\widehat{\alpha }}{\left(\log p_{d_i}\right)}^2{p}_{d_i}^{\text{exp}\left(\widehat{\alpha }\right)}pr(t_i>u_i\mid Y_i=1)}{(1-p_{d_i}^{\text{exp}\left(\widehat{\alpha }\right)}){\{1-p_{d_i}^{\text{exp}\left(\widehat{\alpha }\right)}+p_{d_i}^{\text{exp}\left(\widehat{\alpha }\right)}pr(t_i>u_i\mid Y_i=1)\}}^2}.$$