A Weighted-Least-Squares Estimation Approach to Comparing Trends in Age-Adjusted Cancer Rates Across Overlapping Regions

Abstract

Li and Tiwari (2008) recently developed a corrected Z-test statistic for comparing the trends in cancer age-adjusted mortality and incidence rates across overlapping geographic regions, by properly adjusting for the correlation between the slopes of the fitted simple linear regression equations. One of their key assumptions is that the error variances have unknown but common variance. However, since the age-adjusted rates are linear combinations of mortality or incidence counts, arising naturally from an underlying Poisson process, this constant variance assumption may be violated. This paper develops a weighted-least-squares based test that incorporates heteroscedastic error variances, and thus significantly extends the work of Li and Tiwari. The proposed test generally outperforms the aforementioned test through simulations and through application to the age-adjusted mortality data from the Surveillance, Epidemiology, and End Results (SEER) Program of the National Cancer Institute.

1. Introduction

Cancer has been a major epidemic concern in the industralized nations, contributing, for example, 570,280 deaths each year in the United States (American Cancer Society 2005). Many public and private agencies dealing with cancer and related problems depend on the rates of cancer deaths or new cases as an estimate of cancer burden for planning and resource allocation. Among these agencies, the Surveillance, Epidemiology, and End Results (SEER) Program of the National Cancer Institute (NCI) is the most authoritative and comprehensive source of information on cancer incidence and deaths in the United States, which currently collects and publishes cancer incidence and survival data from population-based cancer registries covering approximately over a quarter of the entire US population.

One main task of the SEER program is to routinely monitor and compare trends in cancer mortality and incidence rates across geographic regions or over different time periods. The data are analyzed by SEER*STAT software, which is maintained by the NCI, with the results periodically published in SEER Cancer Statistics Review; see Ries et al. (2001). In this annual report (available at http://seer.cancer.gov/csr), the estimated annual percent change (APC) for over 80 cancer sites are presented across geographic regions (e.g. counties or states) for different specified periods. As the APC measures the trend in cancer mortality and incidence rates, its comparison across various regions has important social and economic ramifications, ranging from deciding which cancer programs get funded to deciding how the funds are allocated among various regions.

However, a fundamental statistical difficulty arises when such comparisons, largely for policy making purposes, have to be made for regions or time intervals that overlap, e.g. comparing the most recent changes in trends of cancer rates in a local area (e.g. the mortality rate of breast cancer in California) with a more global level (i.e. the national mortality rate) over two overlapping time periods, because of availability of the data. For example, as detailed in the data analysis section, it is of substantial interest to compare the changes in California cancer mortality rates with the national cancer mortality rates in the last 15 years. However, for a 15-year block, the California cancer rates were available for 1990–2004, while the national data were available for 1988–2002.

In the current SEER*STAT software, the two-sample pooled t-test (Kleinbaum et al., 1988) is available to compare two APC values from two non-overlapping regions or non-overlapping time intervals, based on two independent linear models with a common variance. But, when one wishes to compare APCs for two overlapping regions or time intervals, the samples are no longer independent, invalidating the two sample t-test. Recently, Li and Tiwari (2008) developed a corrected Z-test that properly accounts for the overlapping. However, their derivation relied on a common time-independent variance assumption. Indeed, as the age-adjusted rates are linear combinations of mortality or incidence counts, arising from an underlying Poisson process (Brillinger, 1986), such a constant variance assumption may be dubious. In this paper, we relax such an unrealistic assumption and derive a Z-test using weighted least squares (WLS) for comparing two APCs when the (transformed) cancer rates have heteroscedastic variances.

The rest of the paper is organized as follows. Section 2 gives the definition of the annual percent change (APC) and introduces the problem at hand of comparing two APCs. This section also briefly reviews the t-test of Kleinbaum et al. (1988) and the corrected Z-test of Li and Tiwari (2008). In Section 3, the new WLS Z-test is developed and, in Section 4, its performance with respect to the previous corrected Z-test is considered via a simulation study and application to SEER cancer mortality data. The conclusions are summarized in Section 5.

2. Annual Percent Change (APC) and Tests for Comparing Two APCs

Let n_kji and d_kji denote the mid-year population and counts for region k, age-group j and time t_i, and let w_j denote the standard for the age-group j standardized so that ${\sum }_{j=1}^J{w}_j=1$, i = 1, …, I_k, j = 1, …, J, k = 1, 2. The age-adjusted rate is defined as

$${\stackrel{\sim }{r}}_{ki}=\sum _{j=1}^J{w}_j\frac{d_{\mathit{kji}}}{n_{\mathit{kji}}},$$ (2.1)

where w_j > 0, j = 1, …, J, are the known standards for the age group j so that ${\sum }_{j=1}^J{w}_j=1$. For the SEER analysis, there are J = 19 standard age-groups consisting of 0–1, 1–4, 5–9, …, 85+, and w_j are chosen to be the year 2000 population standards (Fay et al. 2006).

To describe the change in cancer trend, we work with the logarithmic transformation of r̃_ki, and fit a linear regression of r̃_ki on calendar time t_i. However, since r̃_ki may be 0 for some rare cancer sites, we consider a discrete correction of r̃_ki as

$$r_{ki}=\sum _{j=1}^J{w}_j\frac{d_{\mathit{kji}}+\frac{1}{J}{Z}_{ji}}{n_{\mathit{kji}}}={\stackrel{\sim }{r}}_{ki}+{\overline{w}}_{ki}.$$ (2.2)

Here the random purtabation $Z_{ji}={\sum }_{l=1}^{J}I(X_{li}=j)$, where X_li, l = 1, …, J, i = 1, …, I_k are iid random variables, each of which takes values 1, …, J with equal probability 1/J. Note that Σ_j Z_ji = J with E(Z_ji) = 1. This amounts to distributing a count with mean 1 over all J age-groups at each time t_i, and hence avoids the singular situation. It is notable that this correction, specifically designed to accommodate the discrete nature of the counts, differs slightly from the continuous correction proposed in Tiwari et al. (2006), by introducing a correction factor, ${\overline{w}}_{ki}=\frac{1}{J}{\sum }_{j=1}^J\frac{w_j{Z}_{ji}}{n_{\mathit{kji}}}$.

Consider a simple linear regression of logarithm y_ki = log(r_ki) on calendar time t_i, given by

$$y_{ki}={\beta }_{k0}+{\beta }_{k1}{t}_i+e_{ki},i=1,\dots ,I_k;k=1,2,$$ (2.3)

where e_ki are independent random errors with E(e_ki) = 0. For the variance of e_ki, we note that (d_kji) behaves as independent realizations of Poisson random variables, with means equal to their variances. We further note that the random perturbation Z_ji follows Binomial(J, 1/J), cov(Z_ji, Z_j′i) = −1/J, cov(Z_ji, Z_j′i′) = 0 if i ≠ i′, and also Z_ji and d_kji are independent. Hence, using the delta method, we obtain the heterogeneous error variances of y_ki as

$${\nu }_{ki}^2\approx \frac{v_{ki}^2}{r_{ki}^2},$$ (2.4)

where

$$\begin{array}{l}{v}_{ki}^2=\sum _{j=1}^J{w}_j^2\frac{\mathit{Var}(d_{\mathit{kji}})}{n_{\mathit{kji}}^2}+\mathit{Var}(\sum _{j=1}^J{w}_j\frac{\frac{1}{J}{Z}_{ji}}{n_{\mathit{kji}}})\\ \doteq \sum _{j=1}^J{w}_j^2\frac{d_{\mathit{kji}}}{n_{\mathit{kji}}^2}+\frac{1}{J^2}\left[\sum _{j=1}^J\frac{w_j^2}{n_{\mathit{kji}}^2}-\frac{1}{J}{(\sum _{j=1}^J\frac{w_j}{n_{\mathit{kji}}})}^2\right]\end{array}$$

is the estimated variance of r_ki. Note that $v_{ki}^2$ is smaller than the Var(r_ki) given in Tiwari et al. (2006) by a term $\frac{1}{J}(1-\frac{1}{J}){\sum }_{j=1}^J\frac{w_j^2}{n_{\mathit{kji}}^2}+\frac{1}{J^3}{({\sum }_{j=1}^J\frac{w_j}{n_{\mathit{kji}}})}^2\ge 0$, a negligible constant.

With e_ki having a heteroscedastic variance structure, the weighted least squares estimates or the maximum likelihood estimates of (β_k0, β_k1) are given by (β̃_k0, β̃_k1), where

$$\begin{array}{l}{\stackrel{\sim }{\beta }}_{k0}={\stackrel{\sim }{y}}_k-{\stackrel{\sim }{\beta }}_{k1}{\stackrel{\sim }{t}}_k;\\ {\stackrel{\sim }{\beta }}_{k1}=\frac{{\sum }_{i=1}^{I_k}(y_{ki}-{\stackrel{\sim }{y}}_k)(t_i-{\stackrel{\sim }{t}}_k)/{\nu }_{ki}^2}{{\sum }_{i=1}^{I_k}{(t_i-{\stackrel{\sim }{t}}_k)}^2/{\nu }_{ki}^2},\end{array}$$

with

$${\stackrel{\sim }{t}}_k=\frac{{\sum }_{i=1}^{I_k}{t}_i/{\nu }_{ki}^2}{{\sum }_{i=1}^{I_k}1/{\nu }_{ki}^2},{\stackrel{\sim }{y}}_k=\frac{{\sum }_{i=1}^{I_k}{y}_{ki}/{\nu }_{ki}^2}{{\sum }_{i=1}^{I_k}1/{\nu }_{ki}^2}.$$ (2.5)

As a special case when $\mathit{Var}(e_{ki})={\sigma }_k^2$, k = 1, 2, which are invariant of i, the estimates of β_k1 its variance, and σ_k are given by

$$\begin{array}{l}{\stackrel{\sim }{\beta }}_{k1}=\frac{{\sum }_{i=1}^{I_k}(y_{ki}-{\overline{y}}_k)(t_i-{\overline{t}}_k)}{{\sum }_{i=1}^{I_k}{(t_i-{\overline{t}}_k)}^2};\\ {\widehat{\sigma }}_{{\widehat{\beta }}_{k1}}^2=\frac{{\widehat{\sigma }}_k^2}{{\sum }_{i=1}^{I_k}{(t_i-{\overline{t}}_k)}^2};\\ {\widehat{\sigma }}_k^2=\frac{{\sum }_{i=1}^{I_k}{(y_{ki}-{\widehat{y}}_{ki})}^2}{I_k-2},\end{array}$$

with ŷ_ki = β̂_k0 + β̂_k1t_i, ${\overline{y}}_k=\frac{1}{I_k}{\sum }_{i=1}^{I_k}{y}_{ki},{\overline{t}}_k=\frac{1}{I_k}{\sum }_{i=1}^{I_k}{t}_i$.

The annual percent change (APC), defined as APC_k = 100(e^β_k1 − 1) for each region, describes the change in trend of cancer mortality or incidence. When comparing the change trends of a cancer across two regions, it is often of interest to test the null hypothesis H₀: APC₁ = APC₂ versus the alternative hypothesis H₁ : APC₁ ≠ APC₂, or equivalently to test $H_0^{\prime }:{\beta }_{11}={\beta }_{21}$ versus $H_1^{\prime }:{\beta }_{11}\ne {\beta }_{21}$. Under a further assumption that ${\sigma }_1^2={\sigma }_2^2(={\sigma }^2)$, the two-sample pooled t-test is given by (Kleinbaum et al., 1988)

$$t=\frac{{\widehat{\beta }}_{11}-{\widehat{\beta }}_{21}}{{\left[{\widehat{\sigma }}^2\left(\frac{1}{{\sum }_{i=1}^{I_1}{(t_{1i}-{\overline{t}}_1)}^2}+\frac{1}{{\sum }_{i=1}^{I_2}{(t_{2i}-{\overline{t}}_2)}^2}\right)\right]}^{1/2}}\sim t_{(I_1+I_2-4)},$$ (2.6)

where the “pooled” estimate of σ² is given by

$${\widehat{\sigma }}^2=\frac{{\sum }_{i=1}^{I_1}{(y_{1i}-{\widehat{y}}_{1i})}^2+{\sum }_{i=1}^{I_2}{(y_{2i}-{\widehat{y}}_{2i})}^2}{I_1+I_2-4}.$$ (2.7)

This is the test that is implemented in SEER*STAT software. However, when there is an overlap between the two regions or in the two time intervals, the two samples are not independent, and there is a need to adjust for the covariance between β̂₁₁ and β̂₂₁. Li and Tiwari (2008) proposed a corrected Z-test procedure that includeds such an adjustment.

Specifically, they considered the following models

$$y_{1i}={\beta }_{10}+{\beta }_{11}{t}_i+e_{1i},i=1,\dots ,m,$$ (2.8)

$$y_{2i}={\beta }_{20}+{\beta }_{21}{t}_i+e_{2i},i=s+1,\dots ,s+I,$$ (2.9)

respectively for overlapping Regions 1 and 2. Region 1 was observed for the time points of {t₁, …, t_m}, while Region 2 was observed for the time points of {t_s+1, …, t_s+I}. When t₁ ≤ t_s+1 < t_m ≤ t_s+I (e.g. the two time periods are overlapping), these two regressions are not independent.

Further introduce $n_k={\sum }_{i=s+1}^m{\sum }_{j=1}^J{n}_{\mathit{kji}}$ for k = 1, 2, $n^{(O)}={\sum }_{i=s+1}^m{\sum }_{j=1}^J{n}_{ji}^{(O)}$, where the superscript ‘O’ is used to denote the intersection of Regions 1 and 2, and denoted by n_kji and $n_{ji}^{(O)}$ the numbers of underlying population at risk for age group j at time t_i in Region k(k = 1, 2), and in the overlapping subregion, respectively.

Li and Tiwari (2008) showed

$${\widehat{\beta }}_{11}-{\widehat{\beta }}_{21}\sim N\left({\beta }_{11}-{\beta }_{21},{\sigma }^2\left(\frac{1}{{\sigma }_{1t}^2}+\frac{1}{{\sigma }_{2t}^2}-\frac{2{\sigma }_{12t}}{{\sigma }_{1t}^2{\sigma }_{2t}^2}\frac{{(n^{(O)})}^2}{n_1{n}_2}\right)\right),$$ (2.10)

where ${\sigma }_{12t}={\sum }_{i=s+1}^m(t_i-{\overline{t}}_1)(t_i-{\overline{t}}_2)$, based on which, a corrected Z-test was proposed as

$$Z_{CT}=\frac{{\widehat{\beta }}_{11}-{\widehat{\beta }}_{21}}{\sqrt{{\widehat{\sigma }}^2\left(\frac{1}{{\sigma }_{1t}^2}+\frac{1}{{\sigma }_{2t}^2}-\frac{2{\sigma }_{12t}}{{\sigma }_{1t}^2{\sigma }_{2t}^2}\frac{{(n^{(O)})}^2}{n_1{n}_2}\right)}},$$

which reject the null hypothesis for large absolute values of Z_CT.

However, Li and Tiwari’s derivation hinged upon the common variance assumption of Var(e_1i) ≡ Var(e_2j) ≡ σ², which seems rather stringent. In the next section, we relax such an assumption and propose a weighted-least-squares (WLS) based Z-test, which accommodate Li and Tiwari’s test as a special case.

3. Proposed Test

Our proposed WLS Z-test stems from the assumption that the observed counts d_kji follow Poisson distributions, and from the transformed linear regression models (2.8) and (2.9) with the errors e_ki having heteroscedastic variances. The standard statistical theory reveals that the WLS estimators β̃₁₁, β̃₂₁ follow

$${\stackrel{\sim }{\beta }}_{11}-{\stackrel{\sim }{\beta }}_{21}\sim N\left({\beta }_{11}-{\beta }_{21},\frac{1}{{\stackrel{\sim }{\sigma }}_{1t}^2}+\frac{1}{{\stackrel{\sim }{\sigma }}_{2t}^2}-2\mathit{Cov}({\stackrel{\sim }{\beta }}_{11},{\stackrel{\sim }{\beta }}_{21})\right).$$

It turns out, however, that the derivation of Cov(β̃₁₁, β̃₂₁), when the two time intervals [t₁, t_m] and [t_s+1, t_s+I] under consideration are overlapping, is nontrivial as it requires a careful consideration of the overlapping of two regions. The detailed derivation is given in the Appendix, which shows

$$\mathit{Cov}({\stackrel{\sim }{\beta }}_{11},{\stackrel{\sim }{\beta }}_{21})\doteq \frac{{\stackrel{\sim }{\sigma }}_{12t}}{{\stackrel{\sim }{\sigma }}_{1t}^2{\stackrel{\sim }{\sigma }}_{2t}^2}\frac{{(n^{(O)})}^2}{n_1{n}_2},$$ (3.1)

where $n_k={\sum }_{i=s+1}^m{\sum }_{j=1}^J{n}_{\mathit{kji}}$ for k = 1, 2, $n^{(O)}={\sum }_{i=s+1}^m{\sum }_{j=1}^J{n}_{ji}^{(O)},{\stackrel{\sim }{\sigma }}_{1t}^2={\sum }_{i=1}^m{(t_i-{\stackrel{\sim }{t}}_1)}^2/{\nu }_{1i}^2,{\stackrel{\sim }{\sigma }}_{2t}^2={\sum }_{i=s+1}^{s+I}{(t_i-{\stackrel{\sim }{t}}_2)}^2/{\nu }_{2i}^2$ and

$${\stackrel{\sim }{\sigma }}_{12t}=\sum _{i+s+1}^m\frac{{\nu }_{12i}^{(O)}}{{\nu }_{1i}^2{\nu }_{2i}^2}(t_i-{\stackrel{\sim }{t}}_1)(t_i-{\stackrel{\sim }{t}}_2),$$

where t̃₁ and t̃₂ are defined in (2.5), ${\nu }_{1i}^2$ and ${\nu }_{2i}^2$ are as defined in (2.4), ${\nu }_{12i}^{(O)}=\frac{{(v_i^{(O)})}^2}{r_{1i}{r}_{2i}}$ with ${(v_i^{(O)})}^2={\sum }_{j=1}^J{w}_j^2\frac{d_{ji}^{(O)}}{{(n_{ji}^{(O)})}^2}+\frac{1}{J^2}\left[{\sum }_{j=1}^J\frac{w_j^2}{{(n_{ji}^{(O)})}^2}-\frac{1}{J}{({\sum }_{j=1}^J\frac{w_j}{n_{ji}^{(O)}})}^2\right]$.

Hence, we have that

$${\stackrel{\sim }{\beta }}_{11}-{\stackrel{\sim }{\beta }}_{21}\sim N\left({\beta }_{11}-{\beta }_{21},\frac{1}{{\stackrel{\sim }{\sigma }}_{1t}^2}+\frac{1}{{\stackrel{\sim }{\sigma }}_{2t}^2}-\frac{2{\stackrel{\sim }{\sigma }}_{12t}}{{\stackrel{\sim }{\sigma }}_{1t}^2{\stackrel{\sim }{\sigma }}_{2t}^2}\frac{{(n^{(O)})}^2}{n_1{n}_2}\right)$$ (3.2)

as the basis for the WLS Z-test statistic, defined as

$$Z_{\mathit{WLS}}=\frac{{\stackrel{\sim }{\beta }}_{11}-{\stackrel{\sim }{\beta }}_{21}}{\sqrt{\frac{1}{{\stackrel{\sim }{\sigma }}_{1t}^2}+\frac{1}{{\stackrel{\sim }{\sigma }}_{2t}^2}-\frac{2{\stackrel{\sim }{\sigma }}_{12t}}{{\stackrel{\sim }{\sigma }}_{1t}^2{\stackrel{\sim }{\sigma }}_{2t}^2}\frac{{(n^{(O)})}^2}{n_1{n}_2}}},$$

which would reject the null hypothesis for the large absolute value of Z_WLS.

To compare the efficiency of Z_WLS and Z_CT, we compute the ratio of the variances (RoV) in (2.10) and (3.2) as,

$$\mathit{RoV}=\frac{{\stackrel{\sim }{\sigma }}^2\left(\frac{1}{{\sigma }_{1t}^2}+\frac{1}{{\sigma }_{2t}^2}-\frac{2{\sigma }_{12t}}{{\sigma }_{1t}^2{\sigma }_{2t}^2}\frac{{(n^{(O)})}^2}{n_1{n}_2}\right)}{\frac{1}{{\stackrel{\sim }{\sigma }}_{1t}^2}+\frac{1}{{\stackrel{\sim }{\sigma }}_{2t}^2}-\frac{2{\stackrel{\sim }{\sigma }}_{12t}}{{\stackrel{\sim }{\sigma }}_{1t}^2{\stackrel{\sim }{\sigma }}_{2t}^2}\frac{{(n^{(O)})}^2}{n_1{n}_2}}.$$ (3.3)

Several points are worthy of noting. First, the RoV is essentially the Pitman asymptotic relative efficiency (ARE) under the assumption of common variance, when both tests are valid and maintain the nominal type I error. In particular, as a special case of ${\nu }_{ki}^2\equiv {\widehat{\sigma }}^2$ for all (k, i), ARE is 1 and further Z_CT ≡ Z_WLS, hence Z_CT is a special case of Z_WLS. In the violation of such common variance assumption, the RoV is no longer the ARE, but provides an approximate assessment of efficacies of these two tests. Secondly, the signs of σ_12t and σ̃_12t will determine, respectively, whether Cov(β̂₁₁, β̂₂₁) and Cov(β̃₁₁, β̃₂₁) are positive or negative, and their signs are often but not necessarily the same (as shown in simulations).

We will conduct simulation studies in the next section to evaluate (3.3), and to assess the performance of the proposed WLS Z-test.

4. Simulation and Application to SEER Data

To evaluate the finite sample performance of the proposed test under various scenarios, we conducted the following simulations to compare the APCs for two regions. We mimicked the comparision between, say, the Southern Region (Region 1) consisting of Georgia (GA), South Carolina (SC) and North Carolina (NC), and the Eastern Region (Region 2) consisting of NC, Virginia (VA) and Maryland (MD), with NC the overlapping state. The three different time periods, with varying degree of overlap in the intervals, are taken to be : (a) [1980,1989] for Region 1, and [1990,1999] for Region 2 so that there is no overlap between the two time intervals and σ_12t = 0, (b) [1980,1989] for Region 1, and [1983,1992] for Region 2 so that there a considerable overlap of six years between the two intervals and σ_12t = 12.25, and (c) [1980,1989] for Region 1, and [1987,1996] for Region 2 so that there is a little overlap of three years between the two intervals and σ_12t = −34.75.

For generating the counts, d_kji, we assume that $d_{\mathit{kji}}\stackrel{\mathit{ind}}{\sim }\mathit{Poisson}(n_{\mathit{kji}}{\lambda }_{\mathit{kji}})$, where log(λ_kji) = β_kj,0+β_k1t_i, with t_i taking values in the intervals corresponding to the two regions stated above. Note that this specification of for λ_kji leads to

$$\begin{array}{l}E(r_{ki})=exp({\beta }_{k1}{t}_i)\sum _{j=1}^J{w}_{j}exp({\beta }_{kj,0})\\ =exp({\beta }_{k1}{t}_i)B_{k,0}\end{array}$$

so that log(E(r_ki)) = log(B_k,0) + β_k1t_i where APC_k = 100(e^β_k1 − 1).

Now to specify the regression for λ_kji, we take β_k1 = log(100⁻¹ APC_k + 1), based on specified values of APC_k ranging from −0.3% to 3.0%, and assume that ${\beta }_{kj,0}=log(\frac{d_{kj,0}}{n_{kj,0}}-{\beta }_{k1}{t}_{k,0})$ where d_kj,0 and n_kj,0 are, respectively, the observed number of deaths and the number of person-years at risk at t_k,0, the beginning of the time interval considered for Region k. The age-specific counts for the overlapping state, NC, are generated from Poisson distributions with means $\frac{1}{3}min\{n_{1ji}{\lambda }_{1ji},n_{2ji}{\lambda }_{2ji}\}$.

The results of the simulation study for the three cases of overlapping time intervals, based on 1000 simulations per cancer site and (APC₁, APC₂) combination, are obtained. To save the space, we only report those for case (a) in Table 1, while the results for the other two cases are available upon request. Several points are worth mentioning.

Table 1.

No Overlap (σ_12t = 0): Simulation Results for GA,SC,NC [1980–1989] and NC,VA,MD [1990–1999]; Comparison of changes in age-adjusted cancer mortality rates in males; APC₁ and APC₂ are the annual percent changes specified for the respective regions

Cancer site	APC1	APC2	(a)	Average RoV	(b)	(c)
All Malignant Cancers	−0.3	−0.3	0.0	1.0193	0.0720	0.0490
	0.1	0.1	0.0	1.0258	0.0700	0.0590
	0.5	0.5	0.0	1.0266	0.0690	0.0600
	1.0	1.0	0.0	1.0187	0.0630	0.0480
	3.0	3.0	0.0	1.0327	0.0590	0.0470
	0.1	0.5	0.4	1.0261	0.8590	0.8770
	−0.3	0.3	0.6	1.0199	0.9930	0.9980
	1.0	2.0	1.0	1.0202	1.0000	1.0000
	1.0	3.0	2.0	1.0218	1.0000	1.0000
Esophagus	−0.3	−0.3	0.0	1.0058	0.0690	0.0510
	0.1	0.1	0.0	1.0034	0.0630	0.0490
	0.5	0.5	0.0	1.0065	0.0620	0.0520
	1.0	1.0	0.0	1.0075	0.0730	0.0580
	3.0	3.0	0.0	1.0173	0.0650	0.0410
	0.1	0.5	0.4	1.0062	0.1080	0.0870
	−0.3	0.3	0.6	1.0070	0.1420	0.1250
	1.0	2.0	1.0	1.0091	0.2930	0.2920
	1.0	3.0	2.0	1.0096	0.7900	0.7840
Lip	−0.3	−0.3	0.0	0.8318	0.0710	0.0160
	0.1	0.1	0.0	0.8324	0.0720	0.0160
	0.5	0.5	0.0	0.8383	0.0720	0.0160
	1.0	1.0	0.0	0.8465	0.0710	0.0130
	3.0	3.0	0.0	0.8692	0.0810	0.0160
	0.1	0.5	0.4	0.8394	0.0700	0.0160
	−0.3	0.3	0.6	0.8384	0.0670	0.0170
	1.0	2.0	1.0	0.8571	0.0660	0.0130
	1.0	3.0	2.0	0.8758	0.0720	0.0130
Prostate	−0.3	−0.3	0.0	1.0180	0.0660	0.0410
	0.1	0.1	0.0	1.0180	0.0660	0.0430
	0.5	0.5	0.0	0.9924	0.0580	0.0510
	1.0	1.0	0.0	1.0215	0.0650	0.0460
	3.0	3.0	0.0	1.0184	0.0700	0.0450
	0.1	0.5	0.4	1.0183	0.2120	0.1820
	−0.3	0.3	0.6	1.0185	0.3750	0.3570
	1.0	2.0	1.0	1.0222	0.7590	0.7730
	1.0	3.0	2.0	1.0232	1.0000	1.0000

Note: (a) = |APC₂ − APC₁|, (b) = P {Z_CT rejects H₀}, (c) = P {Z_WLS rejects H₀}.

• the table showa that, in general, Li and Tiwari’s corrected Z-test (referred to as Z_CT ) is aggressive in rejecting the null hypothesis, and has higher Type I error probabilities, whereas the proposed WLS Z-test (referred to as Z_WLS) is conservative and retains the Type I error probabilities, when the null hypothesis is true (or close to being true).

• for common cancer sites, as the absolute difference between the two APC values or the amount of the overlap between the comparison intervals increase, the power of the Z_WLS test gets better than that of the Z_CT test. The average RoV of the Z_WLS test is close to 1 and increases as we move from the case of σ_12t < 0, to σ_12t = 0, and to σ_12t > 0. When σ_12t > 0, the average RoV is greater than 1 for all the choices of APC values.

• for the rare cancer sites, such as the lip cancer, as there is higher variability in the observed counts, both tests show that there is not enough evidence to reject the null hypothesis. The Z_CT test, however, incurs higher-than-nominal Type I error probabilities, while the Z_WLS retains the nominal level.

• the simulation runs were used to reveal the relationship between σ̃_12t and σ_12t. We found that the sign of σ̃_12t followed that of σ_12t in most cases, though there were a few exceptions. Because of space, the results were omitted.

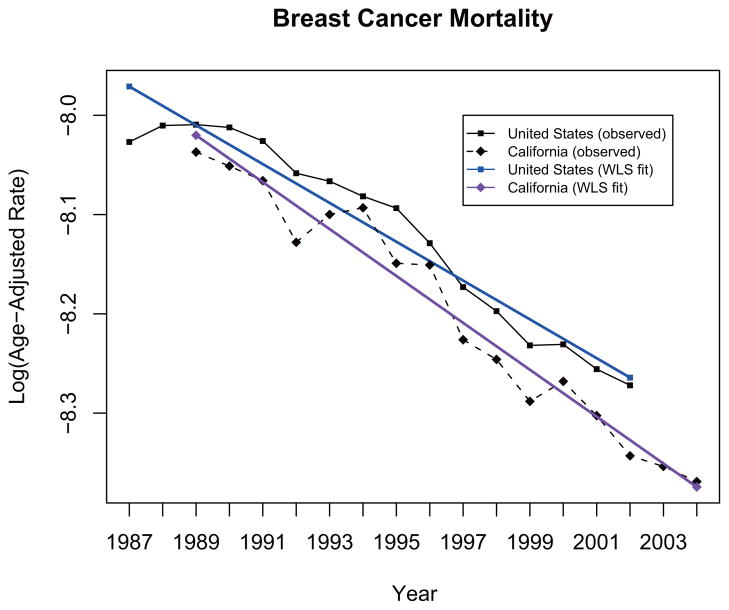
It is of substantial interest to compare the changes in cancer mortality rates in California with the national levels as a California law (Health and Safety Code, Section 103885) was passed in late 1980’s that mandated the reporting of malignancies diagnosed throughout the state. In particular, we applied the proposed methodology to compare the annual percent change (APC) in the age-adjusted mortality rate in Breast Cancer of California (CA) during the period from 1990 to 2004 to that of the United States (US) during the period from 1988 to 2002, for which the national mortality data were available. The mortality data for the United States are compiled by the National Center for Health Statistics (NCHS) of the Centers for Disease Control and Prevention (www.cdc.gov/nchs) and are available from the National Cancer Institute’s Surveillance, Epidemiology, and End Results (SEER) Program (http://www.seer.cancer.gov). The ratio of the total population for all age-groups combined for CA to that for the US for the overlapping years (i.e. n₁/n₂) was around 11% for females. The observed log-transformed annual age-adjusted rates and the fitted regression lines from the Z_WLS test procedure are shown in Figure 1, and the test results are summarized in Table 2. The calculated RoV is 4.42426. Both tests reject the null hypothesis of equal APCs, and suggest that the drop in the mortality rate of Breast cancer is greater in California than at the national level. But the Z_WLS test is much more powerful with a much smaller p-value, i.e., p_WLS = 0.000000757 while p_CT = 0.017372. Thus the Z_WLS test gives a much stronger evidence for the conclusion.

Figure 1.

Observed and fitted log-transformed age-adjusted breast cancer mortality rates in CA [1989–2004] and US [1987–2002]

Table 2.

Results of Comparison of CA [1989–2004] with the US [1987–2002] (σ_12t = 213.5) in annual percent changes (APC) of age-adjusted breast cancer mortality rates; ${\widehat{\mathit{APC}}}_k=100(e^{{\stackrel{\sim }{\beta }}_{k1}}-1)$ and ${\stackrel{\sim }{\mathit{APC}}}_k=100(e^{{\stackrel{\sim }{\beta }}_{k1}}-1)$.

	California	United States
$\widehat{\mathit{APC}}(\text{SE})$	−2.33 (0.127)	−1.93 (0.127)
$\stackrel{\sim }{\mathit{APC}}(\text{SE})$	−2.33 (0.084)	−1.94 (0.027)
ZWLS	−4.94	p-value=0.000000757
ZCT	−2.37	p-value= 0.017372

5. Conclusion

In this paper, we have considered an important problem where comparisons have to be made for two correlated linear regressions. Previous work, e.g., Li and Tiwari (2008), relied on constant residual variance assumption for the linear regressions, which is likely to be violated. Viewing the cancer rates as the linear combinations of mortality or incidence counts, which arise naturally from an underlying Poisson process, we have developed a weighted-least-squares based test that incorporates heteroscedastic error variances, and thus significantly extends the work of Li and Tiwari. The simulation results, along with the application to the SEER data, confirmed that our proposed method outperformed that proposed in Li and Tiwari.

One possible limitation of this study is the confinement of the local linearity for the cancer rates when the time periods of consideration is of short or moderate length. Indeed, linearity assumption for the cancer rates is debatable in cancer surveillance, which is likely to be violated over a longer period (e.g. ≥ 30 years). A detailed discussion on this issue has been made in Fay et al. (2006), which proposed a joinpoint linear regression for long-term cancer rate analysis. In a similar context, we plan to pursue APC comparisons for longer periods by considering joinpoint linear regressions, and will report the results in a subsequent communication.

Appendix: Derivation of (3.1)

For t₁ ≤ t_s+1 < t_m ≤ t_s+I,

$$\begin{array}{l}\mathit{Cov}({\stackrel{\sim }{\beta }}_{11},{\stackrel{\sim }{\beta }}_{21})=\frac{1}{{\stackrel{\sim }{\sigma }}_{1t}^2{\stackrel{\sim }{\sigma }}_{2t}^2}\mathit{Cov}\left(\sum _{i=1}^m\frac{1}{{\nu }_{1i}^2}(t_i-{\stackrel{\sim }{t}}_1)y_{1i},\sum _{i=s+1}^{s+I}\frac{1}{{\nu }_{2i}^2}(t_i-{\stackrel{\sim }{t}}_2)y_{2i}\right)\\ =\frac{1}{{\stackrel{\sim }{\sigma }}_{1t}^2{\stackrel{\sim }{\sigma }}_{2t}^2}\sum _{i=s+1}^m\frac{1}{{\nu }_{1i}^2{\nu }_{2i}^2}(t_i-{\stackrel{\sim }{t}}_1)(t_i-{\stackrel{\sim }{t}}_2)\mathit{Cov}(y_{1i},y_{2i}),\end{array}$$

with ${\stackrel{\sim }{\sigma }}_{1t}^2={\sum }_{i=1}^m{(t_i-{\stackrel{\sim }{t}}_1)}^2/{\nu }_{1i}^2,{\stackrel{\sim }{\sigma }}_{2t}^2={\sum }_{i=s+1}^{s+I}{(t_i-{\stackrel{\sim }{t}}_2)}^2/{\nu }_{2i}^2$.

Now, let d_kji, $d_{ji}^{(O)},d_{\mathit{kji}}^{(NO)}$ denote the number of events (e.g. deaths or cancer cases) and let n_kji, $n_{ji}^{(O)},n_{\mathit{kji}}^{(NO)}$ denote the population at risk for Region k, age-group j, and at time t_i, where the subscript “O” stands for the overlapping region and “NO” stands for the nonoverlapping region, and where we have dropped the subscript k in $d_{ji}^{(O)}$ and $n_{ji}^{(O)}$ as they are same for the two regions. Let $n_{ki}={\sum }_{j=1}^J{n}_{\mathit{kji}},n_i^{(O)}={\sum }_{j=1}^J{n}_{ji}^{(O)},n_{ki}^{(NO)}={\sum }_{j=1}^J{n}_{\mathit{kji}}^{(NO)}$, and similarly define d_ki, $d_i^{(O)},d_{ki}^{(NO)}$.

Assuming that in both the overlapping and nonoverlapping regions, the distribution of the population across different age-groups is same; that is (Pickle and White, 1995),

$$\frac{n_{1i}^{(O)}}{n_{k1i}}=\dots =\frac{n_{Ji}^{(O)}}{n_{\mathit{kJi}}}=p_{ki}^{(O)},\text{and}\frac{n_{k1i}^{(NO)}}{n_{k1i}}=\dots =\frac{n_{\mathit{kJi}}^{(NO)}}{n_{\mathit{kJi}}}=p_{ki}^{(NO)}.$$ (5.1)

We can express r_ki as

$$r_{ki}=p_{ki}^{(O)}{r}_i^{(O)}+p_{ki}^{(NO)}{\stackrel{\sim }{r}}_{ki}^{(NO)},$$ (5.2)

where

$$r_i^{(O)}=\sum _{j=1}^J{w}_j\frac{d_{ji}^{(O)}+\frac{1}{J}{Z}_{ji}}{n_{ji}^{(O)}},{\stackrel{\sim }{r}}_{ki}^{(NO)}=\sum _{j=1}^J{w}_j\frac{d_{\mathit{kji}}^{(NO)}}{n_{\mathit{kji}}^{(NO)}}.$$

Hence, using delta method,

$$\begin{array}{l}\mathit{Cov}(y_{1i},y_{2i})=\mathit{Cov}(log(r_{1i}),log(r_{2i}))\\ \approx \frac{1}{E(r_{1i})E(r_{2i})}\mathit{Cov}(r_{1i},r_{2i})\\ =\frac{1}{E(r_{1i})E(r_{2i})}{p}_{1i}^{(O)}{p}_{2i}^{(O)}\mathit{Var}(r_i^{(O)}).\end{array}$$

We can now estimate $p_{ki}^{(O)}$ by ${\widehat{p}}_{ki}^{(O)}=\frac{n_i^{(O)}}{n_{ki}}$. However, for the US population, we have noticed that ${\widehat{p}}_{ki}^{(O)}$ is approximately constant over years (i.e. over index i), and hence, we replace ${\widehat{p}}_{ki}^{(O)}$ by ${\widehat{p}}_k^{(O)}=\frac{n^{(O)}}{n_k}$, where $n_k={\sum }_{i=s+1}^m{\sum }_{j=1}^J{n}_{\mathit{kji}}$ and $n^{(O)}={\sum }_{i=s+1}^m{\sum }_{j=1}^J{n}_{ji}^{(O)}$. So that using the delta method,

$$\begin{array}{l}\widehat{\mathit{Cov}}(y_{1i},y_{2i})=\frac{1}{{\widehat{E}}_{(r_{1i})}\widehat{E}(r_{2i})}{\widehat{p}}_{1i}^{(O)}{\widehat{p}}_{2i}^{(O)}\widehat{\mathit{Var}}(r_i^{(O)})\\ =\frac{1}{r_{1i}{r}_{2i}}\frac{{(n^{(O)})}^2}{n_1{n}_2}{(v_i^{(O)})}^2\\ =\frac{{(n^{(O)})}^2}{n_1{n}_2}{\nu }_{12i}^{(O)},\end{array}$$

where ${\nu }_{1i}^2$ and ${\nu }_{2i}^2$ are as defined in (2.4), ${\nu }_{12i}^{(O)}={(v_i^{(O)})}^2/r_{1i}{r}_{2i}$ with

$${(v_i^{(O)})}^2=\sum _{j=1}^J{w}_j^2\frac{d_{ji}^{(O)}}{{(n_{ji}^{(O)})}^2}+\frac{1}{J^2}\left[\sum _{j=1}^J\frac{w_j^2}{{(n_{ji}^{(O)})}^2}-\frac{1}{J}{(\sum _{j=1}^J\frac{w_j}{n_{ji}^{(O)}})}^2\right].$$