Learning Algorithms for Human–Machine Interfaces

Abstract

The goal of this study is to create and examine machine learning algorithms that adapt in a controlled and cadenced way to foster a harmonious learning environment between the user and the controlled device. To evaluate these algorithms, we have developed a simple experimental framework. Subjects wear an instrumented data glove that records finger motions. The high-dimensional glove signals remotely control the joint angles of a simulated planar two-link arm on a computer screen, which is used to acquire targets. A machine learning algorithm was applied to adaptively change the transformation between finger motion and the simulated robot arm. This algorithm was either LMS gradient descent or the Moore–Penrose (MP) pseudoinverse transformation. Both algorithms modified the glove-to-joint angle map so as to reduce the endpoint errors measured in past performance. The MP group performed worse than the control group (subjects not exposed to any machine learning), while the LMS group outperformed the control subjects. However, the LMS subjects failed to achieve better generalization than the control subjects, and after extensive training converged to the same level of performance as the control subjects. These results highlight the limitations of coadaptive learning using only endpoint error reduction.

I. Introduction

An increasing amount of research is dedicated to the development of systems that provide severely disabled individuals with artificial means to control their mobility [1]–[4]. Electrical activities of the brain, eye or tongue movements, and joysticks or chin switches are just a few of the possible sources of control signals being investigated for this purpose [5]. Such signals offer a rich set of data that can be interpreted by computer algorithms to reveal the intent of the user. The user’s instructions can then be executed through the system in the form of wheelchair navigation, control of a prosthesis, control of a computer cursor, and more [3]. These types of systems are referred to here as human–machine interfaces (HMIs).

Many current HMIs do poorly at helping subjects because they are difficult to control [3], [7], [8]. Adding an algorithm that adapts the HMI based on the user’s performance of the task may address this problem [4]. Such an algorithm must update, or “learn,” the mapping from control signals to device output based on the user’s performance or strategy, while the user simultaneously forms a representation of that mapping. This creates a dual learning environment where the user and the adaptive algorithm are learning each other simultaneously. The system must adapt with the users by making noticeable adjustments to the mapping if it is to provide any benefit at all. Yet, if the system undergoes large and frequent changes the users will have to constantly learn novel environments, which may impair user performance.

We designed an experiment to test the effectiveness of two algorithms that adjust the HMI mapping by adapting to subjects’ performance. We asked subjects to control a simulated planar arm on a computer screen via finger movements that were captured by an instrumented data glove [9]. In each set of movements, the mapping between the hand joint angles and the arm’s free-moving tip (the “end-effector”) was updated so as to cancel the mean endpoint error in the previous set of movements. This was done in two ways as follows: 1) by a LMS gradient descent algorithm [10], which takes steps in the direction of the negative gradient of the endpoint error function or 2) by applying the Moore–Penrose (MP) pseudoinverse, which offers an analytical solution for error elimination while minimizing the norm of the mapping matrix as an additional constraint. The latter method corresponds to recalibrating the HMI anew after each set of movements, whereas the LMS method carries a memory of the previous map.

We hypothesized that updating the mapping between hand posture and simulated arm joint angles to cancel previous endpoint errors would improve subjects’ performance and ability to generalize across the entire workspace. Performance varied greatly depending on the algorithm used. Subjects exposed to LMS updates learned the task better than control subjects (who performed the task without any adaptive algorithms). However, subjects exposed to the pseudoinverse method failed to learn the task at all and performed much worse than control subjects. Finally, subjects training with LMS mapping updates did not show improved generalization. The ineffectiveness of the pseudoinverse method compared with LMS suggests that update rules must exploit the redundancy in the finger-to-endpoint mapping to do more than simply correct for endpoint error. The absence of improvement in generalization for the machine learning groups may also indicate that basing the update rules only on endpoint errors in training is an incomplete solution to the machine learning problem in HMIs.

II. Procedure for Paper Submission

A. Experimental Setup

Subjects wore a CyberGlove (Immersion Corporation) on their right hand. The CyberGlove captured the movements of each finger joint, palm arch, thumb rotation, and separation between fingers via 19 resistive sensors. Data from the glove were sampled in real time (xPC environment, Mathworks, MA) at a rate of 50 Hz.

The 19-D vector of sensor values was mapped to the position of a cursor presented on a computer monitor as follows: first, the glove signals were multiplied by a 2 × 19 transformation matrix to obtain a pair of angles [θ₁, θ₂]^T. These angles then served as inputs to a forward kinematics equation of a simulated two-link planar arm to determine the end-effector location (2). Fig. 1 graphically shows the equations for clarity

Fig. 1.

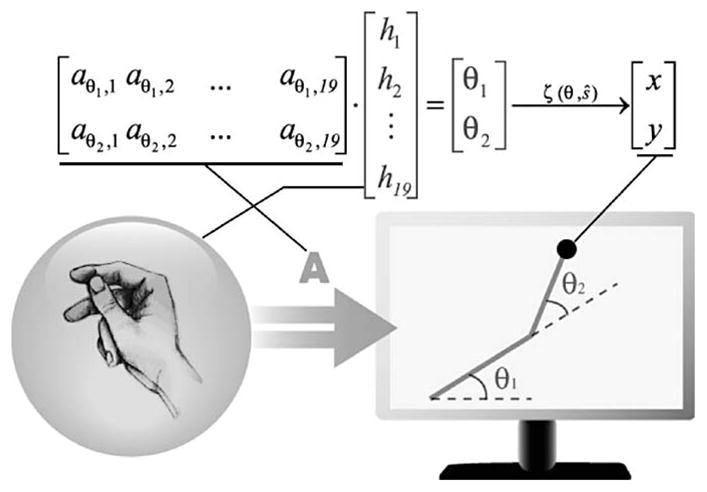
Hand-cursor mapping. Through finger manipulation subjects modulated the components of the h vector, thereby controlling the two joint angles of a planar two-link arm on the screen. The arm itself was not visible to the subjects, only the tip of the arm was revealed as a cursor. The tip location was calculated via standard forward kinematics ζ (θ, ŝ) in (2). The A matrix, established initially by a four-posture calibration, served as the mapping, between the hand posture and the configuration of the planar arm. During machine learning, the A matrix was adjusted so as to decrease errors in subject’s movements. The parameter vector ŝ was set with a y-value below all targets and an x-value equidistant from the training targets; the length of both links were set to 11.25 cm.

$$\theta =A·h\stackrel{\xi (\theta ,\widehat{s})}{\to }(x,y)$$ (1)

$$\left[\begin{array}{c}x\\ y\end{array}\right]=\zeta (\theta ,\widehat{s})=\left[\begin{array}{cccc}cos({\theta }_1)& cos({\theta }_1+{\theta }_2)& 1& 0\\ sin({\theta }_1)& sin({\theta }_1+{\theta }_2)& 0& 1\end{array}\right]·\widehat{s}$$ (2)

where ŝ = [l₁, l₂, x₀, y₀]^T is a constant parameter vector that includes the link lengths and the origin of the shoulder joint. The virtual arm was not displayed except for the arm’s endpoint, which was represented by a 0.5-cm-radius circle. Subjects were given no information about the underlying mapping of hand movement to cursor position and were not told that they controlled the joint angles of an arm. Equation (2) adds a nonlinear component to the transformation from glove to cursor coordinates.

The mapping matrix A was initially determined by having the subject generate four preset hand postures that were identical for all subjects. Each one of these postures was placed in correspondence with one of four “corners” inside the joint angle workspace. The corners of the computer screen were not used, because after the kinematic transformation not all portions of the workspace on the screen would necessarily be reachable. The A matrix was then calculated as A = Θ·H⁺, where Θ is a 2 × 4 matrix of angle pairs that represent the corners of the workspace, and H⁺ is the MP pseudoinverse of H, the 19 × 4 matrix whose columns are signal vectors corresponding to the calibration postures. Using the MP pseudoinverse corresponded to minimizing the norm of the A matrix in the Euclidean metric. As a result of this redundant geometry, each point of the workspace was reachable by many anatomically attainable postures. The initial calibration postures were chosen empirically such that all points in the convex workspace were reachable. During calibration, subjects did not see the cursor and thus had no information about the correspondence between hand postures and cursor locations.

A separate calibration procedure was carried out for the purpose of reconstructing the postures of the hand from the vector of glove signals. This was done by parameter estimation using data obtained as subjects moved their fingers and thumb together, keeping a fixed point of contact between them [11]. This procedure was repeated once for each finger to develop a complete model of the subject’s hand [12].

B. Protocol

Seventeen subjects each gave their informed, signed consent to participate in this experiment, which was approved by Northwestern University’s Institutional Review Board. Subjects were divided into three groups, the LMS group, the recalibration group (MP), and the control group. For two groups (LMS: six subjects; MP: six subjects), the hand-cursor map was changed adaptively after each training epoch via LMS and pseudoinverse, respectively. For the control group (five subjects), the map did not change throughout the experiment.

Subjects performed reaching movements to four different targets that appeared in random order on the screen. Once a new target appeared on the screen, the subject had unlimited planning time before starting the movement. Reaching error was calculated 800 ms after movement onset, and the subject was informed of this “deadline” by a color change in the target (Fig. 2). We characterized endpoint error in this way based on two considerations.

Fig. 2.

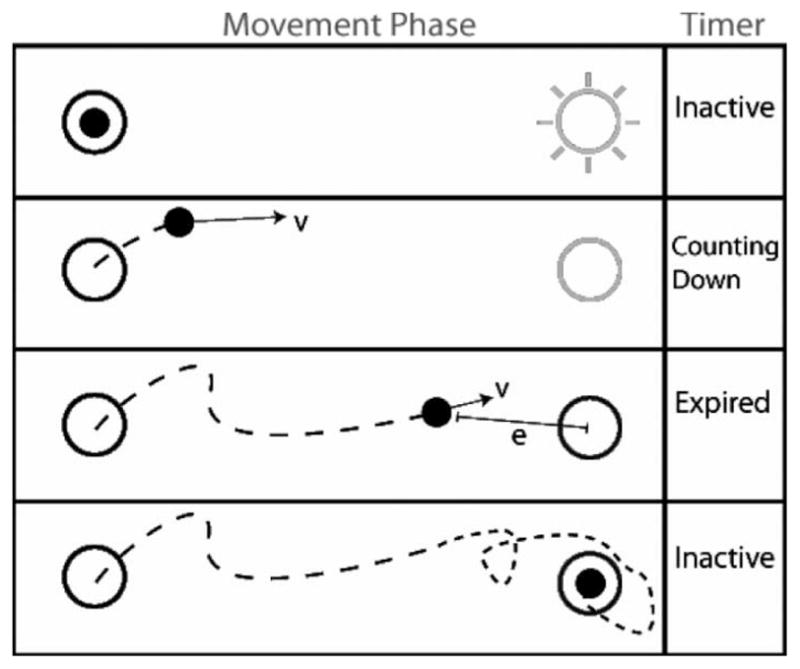
Movement protocol. Inactive: the target appears and the subject is allowed unlimited planning time prior to movement onset. Counting down: the subject initiates the rapid movement toward the target. Expired: 800 ms after movement onset endpoint error is calculated, after which point the subject makes corrective movements to acquire the target.

1. Monitoring reaching error when subjects are offered visual feedback of movement is not feasible in practice because subjects will only come to rest once they have reached the target, therefore achieving zero error. A possibility would have been to define the reaching error based on the first time the cursor reaches a stop. However, in practice, it is often impossible to establish with certainty where the first reaching attempt terminates and the corrective movement begins, because this transition need not take place at zero speed.

2. While identifying the first part of the movement in a reaching sequence is difficult and somewhat artificial, it is always possible to define (albeit arbitrarily) a goal for the subject to be reached. In this case, the goal is to get as close as possible within 800 ms—a time window that is comparable with a normal reaching movement of the arm.

This protocol allows us to chart an explicit learning curve of endpoint errors with constant visual feedback.

Subjects were instructed to minimize this error by getting as close as possible to the target before the target changed color. However, subjects had unlimited time to acquire the target, and the next trial was initiated only after the cursor remained within the target for 1 s. Subjects performed 24 movements per epoch with random target order comprised of exactly two reaches in each direction to each target in 11 daily epochs. To test generalization, a different set of four targets was used in three of the 11 daily epochs (Fig. 3).

Fig. 3.

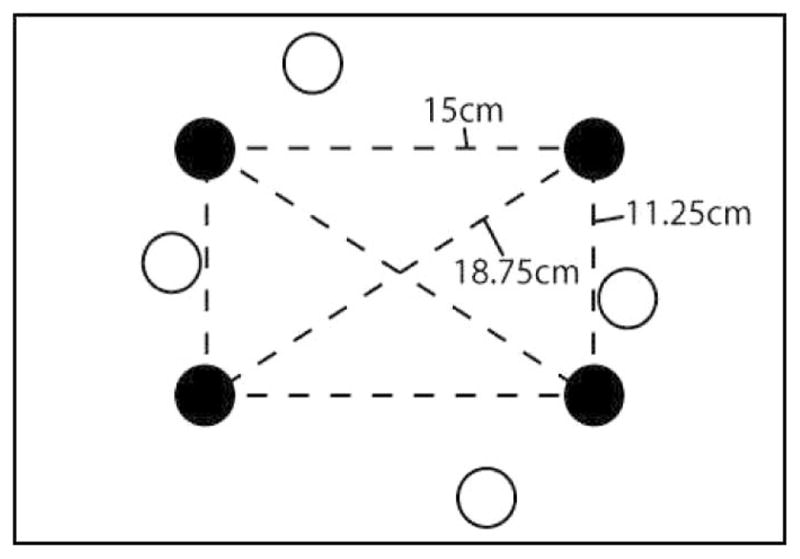
Target scheme: Black targets were training targets and white targets were generalization targets. The dashed lines connecting the training targets mark each one of the movements subjects were required to make. Connecting lines are not shown for the generalization targets. Generalization targets were a 40° rotation of the training target set.

Table I shows the breakdown and order of the experiment. Generalization epochs were preformed once before training to establish a benchmark of comparison, once during training to assess progress, and once after training.

TABLE I.

Mapping Update Schedule

	Gen	Tr	Tr	Tr	Tr	Gen	Tr	Tr	Tr	Tr	Gen
Ctrl.	A0	A0	A0	A0	A0	A0	A0	A0	A0	A0	A0
LMS	A0	A0	A1	A2	A3	A3	A4	A5	A6	A7	A7
MP	A0	A0	A1	A2	A3	A3	A4	A5	A6	A7	A7

The table indicates the order in which each epoch of targets was performed, left to right. Each row shows the progression of the A matrix for an experimental group. Each column shows the type of targets used, generalization or training. The subscript of the A indicates whether or not the A matrix mapping had been updated. This protocol was repeated for each day.

Between each training epoch, the A matrix was updated for the subjects in the LMS group using the LMS learning algorithm. The A matrix was updated for subjects in the MP group using the MP pseudoinverse in a recalibration operation. Control subjects began the experiment with the original matrix created during calibration A₀ and used only this matrix throughout the experiment. Subjects in the machine learning groups were not told that the mapping was updated between epochs. Data from generalization epochs were not used to update or influence the mapping in any way.

Subjects in the control and LMS groups performed the experiment for three days, such that the final day was no later than four days after the initial day. The MP group performed the experiment over only one day, unlike the other groups, due to prohibitive frustration and lack of effective learning.

C. Analysis/Statistics

Endpoint error was defined as the Euclidean distance between the cursor and the target 800 ms after movement onset (see protocol). Endpoint errors were averaged over all movements by epoch. This process resulted in 24 training values per subject (eight epochs/day * three days) and nine generalization values per subject. The values obtained for all epochs of each subject were then normalized by the first epoch and averaged together.

Trajectory linearity was measured as the maximum lateral excursion to the straight-line distance from the start to end of the entire movement divided by the distance between the start and end of the movement [9]. This measure is termed as the aspect ratio of the movement. A straight line has an aspect ratio of zero.

Hand postures were recorded when the subject placed the cursor in the target and held it still for 1 s. Postures were collected for each movement and separated into sets by the four training targets. Hand posture variance was then calculated for each of these four datasets as

$$\sigma =\sum _{i=1}^N\frac{\left|\right|h_i-E(h)\left|\right|}{N}$$ (3)

where N is the number of total movements in an epoch, and h_i is the ith hand posture in the set of postures h, and E(h) is the expected value of h. Each of these four variances was averaged by subject and by epoch.

As a metric for change in mapping, we used d = ||A_n − A_{n + 1}||, where A_n is the previous mapping, A_{n + 1} is the updated mapping, and || · ||is the norm operator, which yields the largest singular value of its argument.

A 95% confidence interval was calculated using the Student’s t-statistic for error bars shown in Figs. 4, 5, 7, 9, 10, and 11.

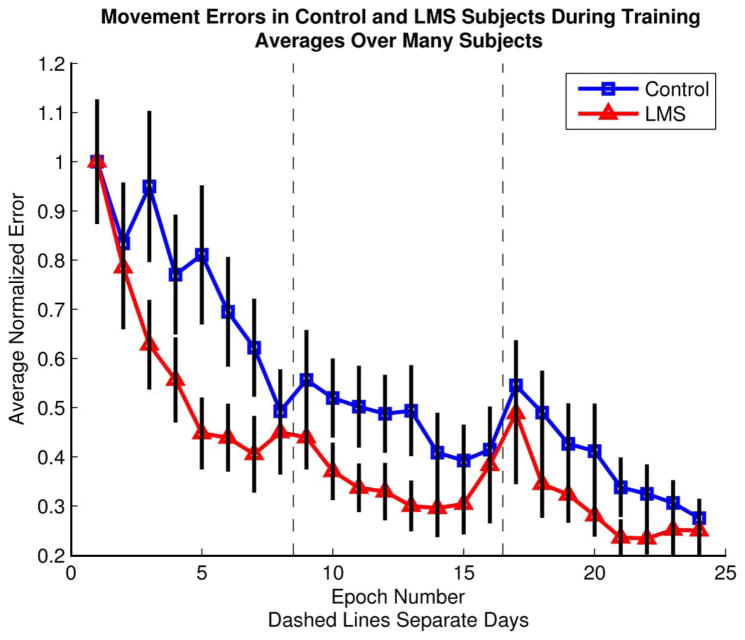
Fig. 4.

Average endpoint error approaches 30% of the initial error and the LMS group reaches this level of performance faster than the control group. Squares refer to control subjects and triangles to LMS subjects. Dashed vertical lines indicate daylong breaks from one epoch to the next. Black bars represent 95% confidence intervals.

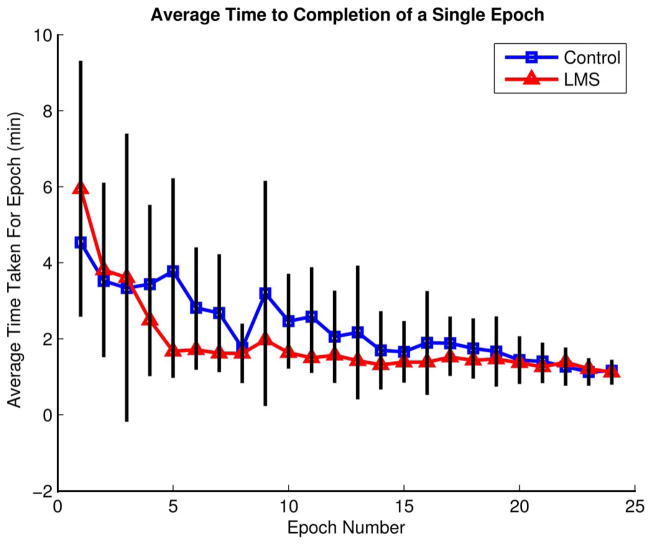
Fig. 5.

Average time to completion of an epoch (24 movements) drops faster for the LMS group (triangles) than the control group (squares). This trend, in combination with endpoint error reduction in Fig. 4, further supports the notion that the LMS machine learning algorithm facilitates subjects’ rapid learning of the system but does not improve performance after significant amounts training. Black bars represent 95% confidence intervals.

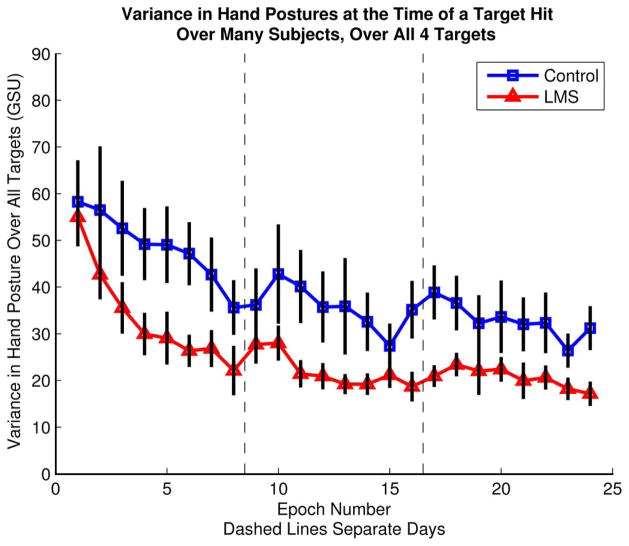
Fig. 7.

Variance of the vector of glove signals h for LMS (triangles) and control groups (squares). Variance is calculated in Glove Sensor Units and each of the 19-D ranges from 0 to 255 (see methods). Black bars are 95% confidence intervals.

Fig. 9.

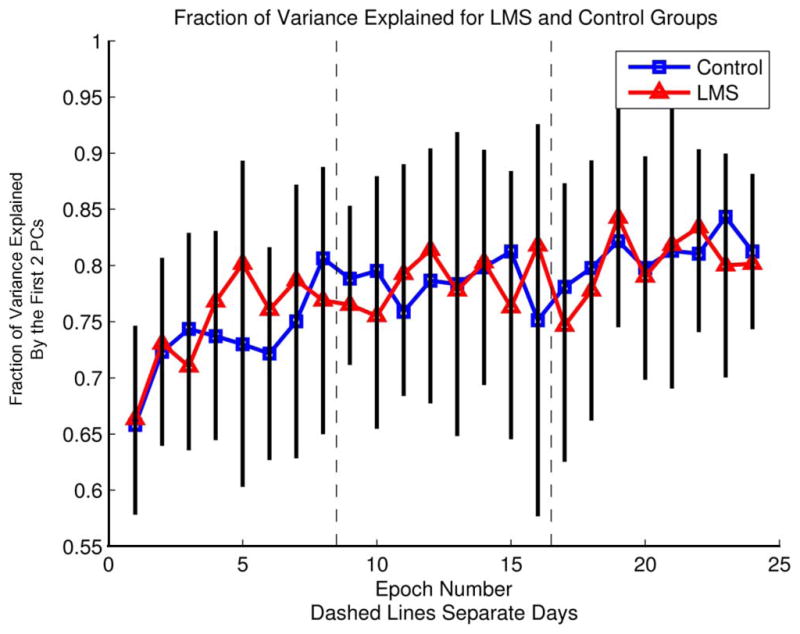
Contribution of the two highest principal components to the fraction of total variance in the data. Data were averaged across subjects in each group. The data set contains the variance of all of the subject’s hand postures once they reached their target. Squares are the control group and triangles are the LMS group. Black bars represent 95% confidence intervals.

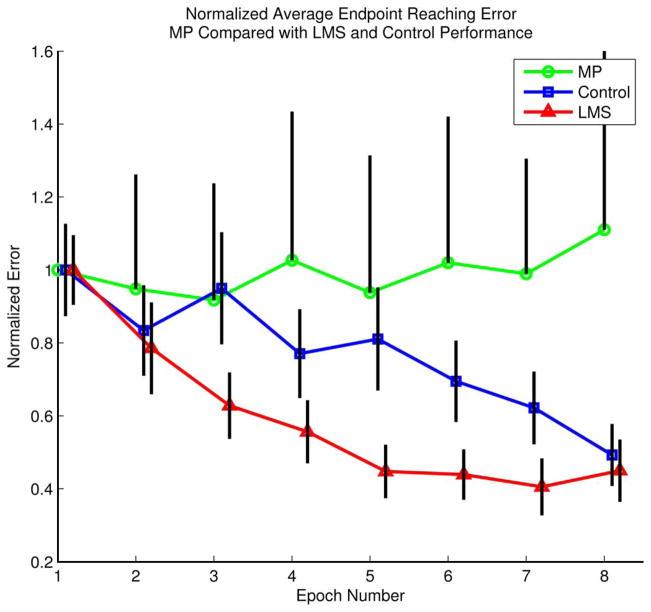
Fig. 10.

Endpoint error for MP subjects shows their lack of improvement. Black error bars are 95% confidence on the data. For clarity, only one side of the confidence interval is shown for the MP group. MP subjects are circles, control subjects are squares, and LMS subjects are triangles. Control and LMS data are reproduced from Fig. 3.

Fig. 11.

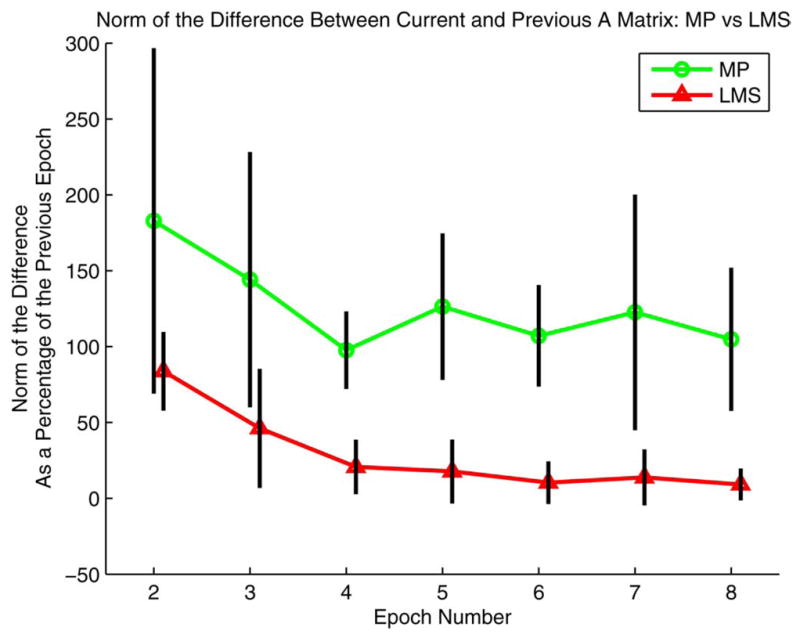
Beginning at the second epoch, each point represents the norm of the difference between the mapping in the current epoch and the previous epoch for two typical subjects, divided by the norm of the mapping in the previous epoch and converted into a percentage. The plot shows that LMS changes the mapping less on average than the pseudoinverse. Data for LMS are shown as triangles; data for MP are shown as circles.

D. Machine Learning

After each training epoch, the transformation matrix A was updated for the subjects in the LMS group using the gradient descent algorithm, LMS [10], [13]. LMS is an iterative procedure, which seeks to minimize the square of the performance error norm by iteratively modifying the elements, a_i,j, of the A matrix (4). The error was calculated as the average distance in joint space from the actual configuration to the target configuration of the virtual arm for each target. To take into account the nonlinear character of the joint-to-endpoint map, we considered for each target location, only the arm configurations that were included within a small neighborhood of each other. More precisely, for each epoch, we gathered together K movements to the same target. We then averaged the K joint angle pairs at the moment of endpoint error calculation. Thus, we derived a pair of average shoulder and elbow angles. This joint angle pair was put through the arm forward kinematics to yield a cursor location. However, because of the nonlinearity in arm kinematics, this location need not coincide with the average calculated directly from the cursor data. Using the notation introduced earlier, if θ¹, θ², …, θ^K indicate the K joint angle pairs and

$$x^1=\zeta ({\theta }^1),x^2=\zeta ({\theta }^2),\dots ,x^K=\zeta ({\theta }^K)$$

indicate the corresponding cursor locations, then

$$\frac{1}{K}\sum _{i=1}^K{x}^i\ne \frac{1}{K}\zeta \left(\sum _{i=1}^K{\theta }^i\right).$$

To reduce this nonlinear effect, we limited the LMS calculations to configurations that were close enough to each other to insure that

$$\Vert \frac{1}{K}\sum _{i=1}^K{x}^i-\frac{1}{K}\zeta \left(\sum _{i=1}^K{\theta }^i\right)\Vert \le 1.5\text{cm}.$$

Elements of the A matrix were then updated according to

$$a_{i,j}(m+1)=a_{i,j}(m)-\mu \sum _n{e}_i(n)·h_j(n)$$ (4)

where m is the iteration index, μ is the step size of a single iteration, e_i (n) is the error function evaluated in joint angle space at a particular dimension, i, and a particular movement n. Because the LMS algorithm was run offline, the otherwise important choice of the value of μ became much less critical. The algorithm was allowed to run after each training epoch until it converged to an acceptable joint-angle error. This was set empirically as ε = π/64.

The LMS algorithm was subject to an additional constraint. As the variance of the h vectors decreased over the course of training, the LMS algorithm would terminate if the difference between the old and new A matrices became too large. Specifically

$$\begin{array}{l}\text{if}:\sqrt{\sum {(A_N(:)-A_{N+1}(:))}^2}+\sqrt{\sum A_N{(:)}^2}>(1+\alpha )\\ \alpha =({var}_{N-1}-{var}_N)/{var}_{N-1}\\ \text{then}:\text{LMS}\text{stops}.\end{array}$$ (5)

Here A is the mapping, N is the index of the epoch number, and the equation for variance is given by (3). This mechanism aimed at improving learning stability by forcing the algorithm to make only small changes when a subject had settled into a particular strategy.

The MP group was exposed to the MP pseudoinverse in place of LMS

$$A·\overline{H}=\overline{\mathrm{\Theta }}\to A=\overline{\mathrm{\Theta }}·{\overline{H}}^{+}$$ (6)

where H is a matrix of average h vectors each taken 800 ms after movement onset and Θ is the matrix of targets in joint angle space. The MP pseudoinverse H⁺ gives the minimum norm solution for A. This process corresponds to carrying out the initial calibration procedure after each epoch, based on the average h vectors. To limit the amount of variation in the updated A matrix, the original four calibration postures were also included in the Θ and H matrices.

III. Results

A. Training

As subjects practiced controlling cursor movements through manipulation of their hand posture, their movements became less variable and more accurate, consistent with Mosier et al. [9]. The task in this study is different in that the subjects here were always provided with visual feedback of the controlled cursor. Furthermore, they controlled the nonlinear kinematics of a simulated two-joint arm, although only the cursor displaying the endpoint of the arm was visible to them. Subjects were able to demonstrate rapid and significant learning despite this added layer of complexity and nonlinearity. The pooled data indicates that final error, after three days of practice, was reduced to approximately 30% of the initial error in the control and LMS groups (Fig. 4). This final level of performance corresponds to 1.86 ± 0.7 cm for control and 2.10 ± 0.8 cm for the LMS group at 95% confidence.

The LMS group reduced error faster than the control group but ultimately seemed to converge to the same level of final performance. The substantially faster improvement demonstrated by the subjects training with LMS was the primary benefit seen by the group.

The time required for subjects to complete each movement was also recorded, and while the differences were not significant, the average time to completion of epochs 4–20 were all lower (by as much as 2 min) than the control group times. Both groups converged to roughly 70 s per epoch by epoch 21, shown in Fig. 5.

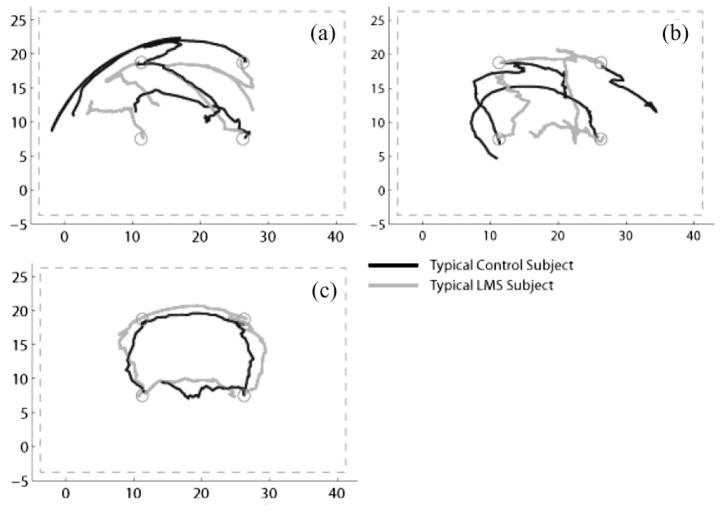
Fig. 6 qualitatively shows the general increase in task performance and movement linearity by displaying sample trajectories from two typical subjects, one in the control group and the other in the LMS group. Each panel illustrates performance at a particular stage of the experiment: 1) prior to any significant training; 2) at a stage in which LMS subjects outperformed control subjects; and 3) at the end of the third day of training. Prior to training, controlling the cursor was exceedingly difficult, as shown by high errors and erratic looking trajectories in panel a of Fig. 6. Panel b shows that by the sixth epoch, the LMS subject performs relatively straight movements with much improved endpoint error, while the control subject still displays large curvature and error. After training, in panel c, subjects from both groups exhibit well-established and quasi-linear movements of the cursor.

Fig. 6.

Representative trajectories across training. Each panel shows four cursor paths of a typical LMS subject (light) and four paths of a control subject (dark). In panel a, movements are taken from epoch 1, prior to training. In panel b, movements are taken from epoch 6, during training. In panel c, movements are taken from epoch 24, after training. Dashed lines represent the border of the visible workspace, and units are in centimeters.

B. Dimensionality Reduction and Behaviors

Experimental evidence has suggested that in movement tasks where there is visual feedback, moving straightly in the visual space with minimal jerk dominates the control strategy [6], [14], [15]. In our experiment, subjects were not instructed to move along rectilinear trajectories to reach targets but as they became proficient at the task the cursor trajectories became consistently more rectilinear.

Subjects in both groups began to make more rectilinear cursor movements almost immediately and continued this trend for approximately ten epochs before improvement leveled off. However, there was no significant difference in the trend toward trajectory linearity between subjects training with the LMS algorithm and the control group. Aspect ratio variability was quite high at the onset of the experiment but decreased sharply through training to approximately 0.35.

Subjects learned to position the cursor on various fixed-point targets in the 2-D screen space, implying that they were able to solve the underdetermined problem of mapping points in 2-D into the much larger dimensionality of the glove/hand-space. Next, we examine how subjects solved this highly redundant problem and compare strategies across experimental groups.

Fig. 7 shows the variability of hand postures once the subjects’ cursor remained stationary in the new target. The variance of postures of each subject was calculated during a single epoch, while the mapping remained constant for both experimental groups. Then it was averaged across subjects. The LMS group used a strategy that generated significantly lower variance of hand postures than the control group in reaching the training targets. The control subjects used a wider variety of postures to reach targets.

If all subjects gravitated towards the use of a particular set of hand postures to reach the training targets in the face of a highly redundant mapping, this might suggest that there is a very specific optimal control strategy being employed by the motor system to deal with the familiar kinematics of the hand in an unfamiliar high-dimensional task. To investigate this possibility, we wish to determine whether subjects solved the redundant mapping problem the same way, despite the existence of many possible solutions.

In each row in Fig. 8, a set of postures is shown for a single subject. The top two rows show results from LMS subjects and the bottom two show results from control subjects. Each column was obtained from a single epoch, and each hand image shows the posture of the hand after one movement, when the subject terminated all corrective actions and the cursor was stable in the target. Each hand image was taken at the same target. The dashed lines separate subjects that did not use the same mapping, except during epoch 1 where the mapping is the same for all subjects by design. LMS changes the mapping during the experiment, which strongly influences the hand postures used by the subjects, making it difficult to compare the evolution of their choice of postures. Intrasubject posture comparisons in Fig. 8 verify trends of reduced posture variability seen in Fig. 7. The subjects’ postures from both groups appear to be more consistent from epoch 12 to 24 than from epochs 1 to 6.

Fig. 8.

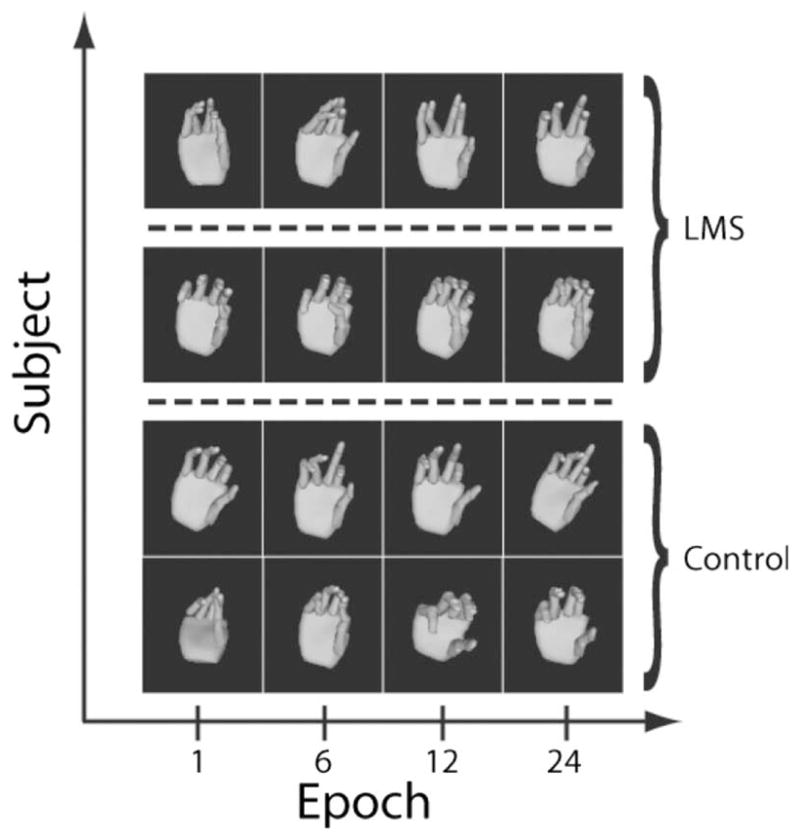
Hand images were reconstructed from the data using the kinematic model from [12]. These postures were collected from four subjects, when the cursor was at the same target. In each row, there are postures from one subject at each of the four epochs 1, 6, 12, and 24. The top two rows are from subjects who trained with LMS, the bottom two rows are postures from control subjects who did not train with LMS. Subjects separated by dashed lines indicate that they used different mappings.

Using a one-way multivariate analysis of variance (MANOVA) for repeated measures, with final 19-D h vectors as the dependent repeated measure and each of the five control subjects as groups of the independent factor, we tested the null-hypothesis that the mean of each subject’s h vectors were the same in the high-dimensional glove signal space [16]. The h vectors were drawn from the last epoch of training where posture variance reached a minimum (Fig. 7). This test was repeated once for each target and allows us to reject the null hypothesis for all targets at p < 0.0001. Interestingly, for target 1, the MANOVA fails to reject the hypothesis that the means reside in a 2-D manifold within the sensor space. This indicates that while the hand postures used for this target are indeed different across subjects, they may be contained in a lower variance space defined by the eigenvectors of the internal group sum of squares matrix.

It is evident that regardless of experimental group each subject used different sets of hand postures to reach the same targets. These differences highlight the redundancy involved in this experiment. Many solutions are attainable and equally feasible and not significantly limited by the kinematics of the hand.

We used principal component analysis (PCA) to examine the primary dimensions along which the final hand postures were most variable. Through training, subjects reduced the dimensionality of their hand postures. By the end of training, the first two principal components of the glove signals were sufficient to account for roughly 80% of the total variance (Fig. 9). This is consistent with other literature on the use of PCA for hand posture analysis during learned dexterous manipulation [17]. It does not appear that LMS enhanced or facilitated this reduction of dimensionality.

It has been proposed that the nervous system is primarily concerned with “correcting only those deviations that interfere with task goals,” and therefore, would confine variability of movement to nontask relevant dimensions [18]. However, experiments that lead to such conclusions were targeted at tasks in which subjects had the benefit of lifelong experience, such as standard reaching movements with path constraints. Here, in contrast, we were concerned with the development of novel reaching skills. Our results suggest that, regardless of the manifold to which variance is constrained during movement, reducing the dimensionality of the control signals is a direct expression of motor learning.

C. Generalization

The control and LMS groups’ endpoint error learning curves for the generalization targets were equivalent, and both groups steadily reduced their error throughout the experiment (not shown). This indicates that both groups developed a general representation of a mapping that they used to effectively reach targets for which they had not received any training. If subjects had instead simply memorized the hand postures required to reach the training targets, we would expect the errors in training to be much lower than in generalization, where subject received only three-eights the practice. However, in both the training and generalization, epochs’ error reduction in both groups reached approximately 30% of the initial performance error.

D. LMS versus Pseudoinverse

LMS is traditionally an algorithm used to track the minimum of a changing error function in real time. In this experiment, however, LMS is implemented between blocks of movements off line to search for the minimum. Why use LMS at all then? Why not simply solve the least squares underdetermined problem, (6), directly using the MP pseudoinverse? The recalibration (MP) group performed the experiment using mappings that were updated based on the pseudoinverse solution and met with little success.

Our results show that using the MP method resulted in unstable performance to a degree that prevented the subjects from even being able to complete the experiment due to frustration. Data are shown in Fig. 10 for six MP subjects who completed eight training epochs. The substantial intrasubject variability of the MP group prevents a detailed learning time-course comparison with the LMS group. However, there is a significant difference in performance between the first and eighth epochs of the LMS group while there is no significant difference in the performance of the MP group. This lack of evidence for learning and the massive variability in performance indicates a failure of the pseudoinverse method to facilitate an improvement in performance.

Fig. 11 illustrates the norm of the difference between A matrices as a percent of the norm of previous epoch for MP and LMS subjects. The LMS algorithm is changing the norm of the mappings significantly less than the pseudoinverse solution used with the MP group.

One possible explanation for the decline in performance is that the quantity ||A_MP − A_{N −1}|| is unconstrained, where A_MP is the mapping created by the recalibration method and A_N−1 is the previous mapping. This means that the solution of the pseudoinverse problem does not care about how far away, in the high-dimensional space of possible mappings, the new mapping is from the old one. Large changes in the map are likely responsible for unfamiliarity with the new mapping. In order to limit the amount of change induced by the pseudoinverse recalibration, the original calibration postures were concatenated with the subject’s data from each epoch, H in (6). Lack of increased overall performance persisted despite these added conditions to the linear system.

It is important to point out that both the MP and the LMS algorithms are capable of converging to an exact solution for the average reaching error Σ ||θ̂_i − Ah_i || = 0. This is a consequence of the abundance of free parameters in the A matrix. However, the LMS algorithm progresses iteratively towards zero reaching error starting from the original map. While this does not impose an explicit constraint on the norm of the difference between the original map and the updated mapping, the LMS algorithm, by design, will terminate as soon as the desired condition is met. This process, therefore, limits the amount of change from the initial map, unlike the MP method that minimizes the error signals without reference to a starting point.

IV. Conclusion

We investigated whether machine learning algorithms based on endpoint error reduction can help subjects learn to operate a nonlinear system using control commands from a higher dimensional signal space. In our experiment, finger joint angles served as a proxy for more typical HMI signals—such as EEG and electromyography—and were mapped linearly to joint angles of a planar arm, then by forward kinematics to the visible end-effector, in (1) and (2). The rationale for this approach in two steps was to separate the redundancy and the nonlinear features of the glove-to-endpoint map. The use of a linearly redundant map in (1) insured integrability of the local pseudoinverse [19]. The particular form of the nonlinear transformation in (2) matches the type of smooth nonlinearity that is typical of segmental kinematics.

Subjects in the LMS group achieved better performance with less training than the control group. However, both groups ultimately reached the same level of proficiency after extended training, and both groups performed equally well in generalization. Surprisingly, subjects in the MP group failed to improve their performance despite the MP pseudoinverse updating the mapping to account for previous endpoint errors.

A. Assessment of the Learning Algorithms

For an underconstrained set of linear equations, the MP pseudoinverse selects the minimum Euclidean norm solution out of the set of all possible solutions. In this case, the pseudoinverse finds the “smallest” transformation that maps the endpoints of a subject’s cursor movements from the most recent epoch directly onto the targets. The LMS algorithm finds a different solution that maps the endpoints from the previous epochs to the same targets. LMS iteratively reduces the error by walking down the error gradient of each element in the transformation, starting from the previous values. For both the LMS and MP methods, if the subjects were to produce the exact same set of hand postures as in the previous epoch, they would each obtain zero average error.

Subjects who trained with the MP method performed worse than a control group that practiced the task without the aid of any machine learning algorithm (Fig. 10). In fact, they were not able to learn the task at all. On the other hand, subjects who trained with the LMS machine learning reduced endpoint errors faster than control subjects who trained without adapting the map.

How can it be that two solutions, which equally compensate for error, result in such drastically different performances? Whenever there is online feedback, the path that the cursor takes to the target has a strong influence on how the subject learns the mapping [6], [14]. This control strategy is so central to motor learning that greatly altering the trajectory that the cursor takes to the target by changing the overall mapping seems to suppress the subject’s ability to form a representation of the mapping. Although neither the pseudoinverse nor the LMS algorithm explicitly place constraints on the resulting trajectory while updating the mapping, the LMS algorithm tends to preserve the general shape of trajectories while the pseudoinverse does not.

The LMS algorithm is able to preserve trajectories because it tends to implement small changes in the mapping while minimizing the error. This is because the initial condition of each coefficient in the A matrix is set to its value in the previous epoch. As a consequence, the LMS algorithm finds a solution that is similar to the solution found in the previous epoch without the need to incorporate calibration data. (Similarity of the A matrices can be measured as the norm of the element-wise difference of the two mappings.) The recalibration using the pseudoinverse, on the other hand, finds the solution to (1) without any regard to how similar the solution is to the previous mapping. When performing the pseudoinverse calculation there are, in fact, no initial conditions at all, which often causes trajectories from one epoch to the next to look very different.

The failure of the MP method and the limitations of the LMS methods (similar generalization and performance that plateaus at the same level as control group) indicate that machine learning based on endpoint errors alone may not be the best tool for acquiring an effective internal model of the map implemented by an HMI.

B. Kinematics and Variability

Our data show that the control subjects used many more hand postures than the LMS subjects to reach the same targets. This larger hand space variability may have contributed to the control group improving performance more slowly than the LMS group. However, learning a greater number of successful postures on the training set did not lead to better generalization, as both the LMS and control groups performed equivalently in generalizing.

The variable mapping causes LMS subjects to use different postures from one another (Fig. 8). However, the fact that control subjects also use different postures from each other indicates that hand kinematics and biomechanical constraints do not dominate their strategy. If these were the primary influence in determining the postures that subjects used to hit the targets, we would expect to see all control subjects using roughly the same postures, insofar as everyone has very similar hand kinematics and biomechanical constraints.

It is possible that the LMS algorithm actually corrals subjects into lower variance performance by rewarding posture consistency. After each epoch of movements, the algorithm changes the A matrix such that the postures subjects made most often in the previous epoch will now place the cursor near the target. When the mapping is updated it is likely that some subset of infrequently used or unused postures that previously resulted in hitting a particular target will now be unsuccessful. This may force LMS subjects to continue to use the familiar postures that the LMS optimized for on the previous epoch as opposed to learning a new subset of postures created by the updated mapping. Control subjects would have no such bias because the transformation does not change. They are able to train on a larger set of invariant postures that result in target hits and may be equally successful for any postures that work.

Notably, both the LMS and control groups exhibited strong preferences toward rectilinear movements despite operating in a nonlinear control space. This raises the possibility of using the tendency toward rectilinear movements by including deviation from linearity in a new formulation of the LMS cost function. Combining error history with path linearity may lead to improvements in the machine learning algorithm, such as a lowering of the learning floor or an increase in the rate at which users learn the mapping.

C. Implications for HMI Applications

Developments in brain–computer interface technology are beginning to supplement sophisticated neural decoding methods with performance-based algorithms that account for the cortical plasticity associated with learning. Notably, Taylor et al. have employed an effective coadaptive movement prediction algorithm in rhesus macaques to improve cortically controlled 3-D cursor movements [24]. Using an extensive set of empirically chosen parameters, they updated the system weights through a normalized balance between the subject’s most successful trials and their most recent errors, resulting in quick initial error reductions of about 7% daily. After significant training with exposure to the coadaptive algorithm, subjects performed a series of novel point-to-point reaching movements; neither subject’s performance was appreciably different from the training task, indicating that they were able to generalize successfully.

Preliminary studies have shown that for human subjects operating a computer cursor with a brain–machine interface (BMI) system via long-term implanted cortical electrodes in motor cortex [27], linear filters that correlate neural activity to desired movement trajectories perform comparably or better than correlates in monkeys [25], [26]. Studies with human subjects also indicate that training on one platform, such as a neural controlled cursor, can be easily generalized to the control of a simple robotic manipulator [27], which lends support to studies that test adaptive algorithms using cursor control.

Much of the research being done on neural decoding algorithms used to control a neural prosthesis focus on final efficiency or average tracking errors in completing discrete tasks, not on the learning rates of the users [28]. These performance measures make it difficult to quantitatively compare results achieved by these methods to our own. Some nonlinear approaches used to assist nuanced tracing tasks, such as Bayesian decoders [29] and nonlinear cascade system models [30], do well at facilitating consistent successful movements. However, linear filters, like the LMS considered here, have been shown to be sufficient for controlling robotic manipulators [28].

In this experiment, subjects carried out a task analogous, in three key ways, to controlling an actual robotic manipulator using multiple control signals from muscles or electroencephalographic activities. First, by employing many available degrees of freedom, subjects performed a task that is of an inherently lower dimensionality. In common HMI applications, the dimensionality of available control ranges from common 64 electrode arrays [3] to as low as 20 [1], for EEG devices, and these signals always control low-dimensional systems. Second, due to biomechanical coupling, many finger joint angles are not independent of one another. Many HMI signals have the same feature. For instance, noninvasive scalp electrodes capture local field potentials created by the activity of large populations of neurons in the brain, many of these channels are not independent of each other, perhaps making the user’s dimensionality reduction problem more complicated [20]. Third, many devices controlled through HMIs are nonlinear, such as wheelchair position or robotic manipulators [21]. This final issue is the primary motivation for introducing a nonlinear device into the system in our experiment.

In general, there are three levels of adaptation that must occur in an HMI to facilitate the user’s learning if the interface is to be successful. The first is feature extraction and filtering out the signal noise. The second is long-term adaptation to changing states and signal drift. The final level is an adaptation to the subject’s performance as it relates to learning the skills needed in the actual task [4].

This final level is perhaps the least well investigated, because feature extraction algorithms or signal drift filters that are normally crucial when dealing with complex brain or noisy muscle activity are at the center of nearly all current HMI studies [2], [8], [22], [24], [27]. In contrast, the CyberGlove captures finger kinematics robustly, without drift, and with high precision [23]. This allows the focus of the study to rest on algorithms that adapt to user performance of the task and not on elaborate input filtering techniques.

Adaptation by the interface to the subject’s actual performance is necessary to facilitate the motor learning required to effectively control a device through an HMI [4]. The experimental framework developed for this study is not limited to the two particular algorithms considered here and will allow the testing of a broader class of performance-based adaptation algorithms without contamination due to the use of other complex, nonstationary signals.

The next step in developing an HMI machine learning algorithm, therefore, can use this experimental paradigm to assess its effectiveness. These algorithms must include criteria that preserve trajectories and incorporate a cost function that is explicitly sensitive to movement smoothness and/or linearity. This will potentially allow subjects to generalize across all regions of the workspace more effectively and improve performance more quickly.

Biographies

Zachary Danziger was born in Chicago, IL, in 1983. He received the B.S. degree in biomedical engineering from the University of Michigan, Ann Arbor, and the M.S. degree in biomedical engineering in 2007 from Northwestern University, Evanston, IL, where he is currently working toward the Ph.D. degree.

He was at the University of Illinois, Chicago, where he was engaged in vancomycin-resistant Staphylococcus studies in microbiology and the effects of hydrocephalus on elastic brain tissue. His current research interests include the basic science of motor space remapping and its application to human–machine interfaces.

Alon Fishbach, photograph and biography not available at the time of publication.

Ferdinando A. Mussa-Ivaldi (M’02) was born in Torino, Italy, in 1953. He received the Laurea degree in physics from the University of Torino, Torino, Italy, in 1978, and the Ph.D. degree in biomedical engineering from the Politecnico of Milano, Milan, Italy, in 1987.

He is currently a Professor of physiology, physical medicine and rehabilitation, and biomedical engineering at Northwestern University, Evanston, IL. He is also a Senior Research Scientist at the Rehabilitation Institute of Chicago, Chicago, IL, where he founded and is the Director of the Robotics Laboratory. His current research interests include robotics, neurobiology of the sensory–motor system, and computational neuroscience. His achievements include the first measurement of human arm multijoint impedance, the development of a technique for investigating the mechanisms of motor learning through the application of deterministic force fields, the discovery of a family of integrable generalized inverses for redundant kinematic chains, the discovery of functional modules within the spinal cord that generate a discrete family of force fields, the development of a theoretical framework for the representation, generation and learning of limb movements, and the development of the first neurorobotic system in which the brainstem of a lamprey controls the behavior of a mobile robot through a closed-loop interaction. He is the author or coauthor of 110 full-length publications and 85 abstracts. He is a member of the Editorial Boards of the Journal of Neural Engineering and the Journal of Motor Behavior.

Prof. Mussa-Ivaldi is a member of the Society for Neuroscience and the Society for the Neural Control of Movement.