Temporally-independent functional modes of spontaneous brain activity

Abstract

Resting-state functional magnetic resonance imaging has become a powerful tool for the study of functional networks in the brain. Even “at rest,” the brain's different functional networks spontaneously fluctuate in their activity level; each network's spatial extent can therefore be mapped by finding temporal correlations between its different subregions. Current correlation-based approaches measure the average functional connectivity between regions, but this average is less meaningful for regions that are part of multiple networks; one ideally wants a network model that explicitly allows overlap, for example, allowing a region's activity pattern to reflect one network's activity some of the time, and another network's activity at other times. However, even those approaches that do allow overlap have often maximized mutual spatial independence, which may be suboptimal if distinct networks have significant overlap. In this work, we identify functionally distinct networks by virtue of their temporal independence, taking advantage of the additional temporal richness available via improvements in functional magnetic resonance imaging sampling rate. We identify multiple “temporal functional modes,” including several that subdivide the default-mode network (and the regions anticorrelated with it) into several functionally distinct, spatially overlapping, networks, each with its own pattern of correlations and anticorrelations. These functionally distinct modes of spontaneous brain activity are, in general, quite different from resting-state networks previously reported, and may have greater biological interpretability.

Functional connectivity in the brain can be observed using resting-state functional magnetic resonance imaging (FMRI), because the spontaneous temporal fluctuations from functionally related regions show temporal correlation with each other (1). However, brain function is mediated by many functionally distinct networks. These networks may overlap each other, either because a given region contains distinct functional units that cannot be separated with the limited spatial resolution of the data, or because a region truly is a part of more than one distinct functional network. If two regions participate in multiple functional networks, their apparent temporal correlation will reflect the combined contribution from all networks, obscuring the true underlying functional organization. The correlation will not necessarily be meaningful, being some unknown combination of correlations caused by various distinct processes. In this paper, we describe an approach that allows for overlap between functional networks, but differentiates the networks from each other on the basis of their temporal, rather than spatial, independence. The rationale is that in a resting FMRI dataset of sufficient duration, functionally distinct networks should be largely temporally distinct, even if spatially overlapping.

Two main modeling approaches have been used to estimate functional connectivity from resting FMRI data. The simplest (and most widely used) approach is seed-based correlation (1), in which temporal correlation is treated as a single fixed quantity to be estimated over the whole experiment's duration, although some recent work has examined how the correlation varies over time (2). A popular alternative approach is to carry out a low-dimensional spatial independent component analysis (ICA) (3) to define “resting-state networks” (RSNs). Spatial ICA decomposes the data into components that are maximally spatially independent of each other. With a low-dimensional ICA, each component contains (in general) several noncontiguous regions that all fluctuate together with similar spontaneous time courses; different components have different time courses. A further variant on these approaches is to parcellate the brain into a large number of functionally distinct regions (e.g., based on an anatomical atlas, or via a high-dimensional spatial ICA). The parcels (also referred to as network “nodes”) are then clustered into extended functional networks on the basis of the temporal correlations between their associated time courses.

Soon after spatial ICA was first proposed for task FMRI (3), temporal ICA (optimizing for temporal independence between components) was also applied to task FMRI (4). It was shown that both spatial and temporal ICA could identify a small number of strongly distinct task activation and artifact processes (5). However, it quickly became apparent that (for FMRI) ICA performs much more robustly in the spatial than the temporal domain, partly because ICA requires a large number of samples to function well, and in FMRI there are orders of magnitude more voxels than time points. Also, the underlying neural processes in the data may well be more non-Gaussian in space than in time (particularly for resting-state data), adding to the greater robustness of spatial ICA. With respect to the separation of activation from artifacts, and of spatially distinct activations from each other, spatial independence may be the most appropriate model, for example, where stimulus-induced head motion would be temporally correlated to the signal of interest (3). For these reasons, nearly all applications of ICA to FMRI (including resting-state FMRI) have to date used spatial ICA.

However, for finding functionally independent, potentially spatially overlapping, functional networks, temporal ICA may provide a better (or at least complementary and informative) approach. Indeed, a relevant point was made in a commentary on the original use of spatial ICA for FMRI: “On the negative side, the very nature of functional integration among brain areas means that [distinct] large scale neuronal dynamics can share a substantial anatomical infrastructure” (6). Here we propose to identify extended functional networks on the basis of their temporal independence. We show that these networks are in general different from the well-known RSNs identified by spatial ICA (7) and seed-based correlation; therefore we use a different terminology, referring to “temporal functional modes” (TFMs). We use the word “modes” rather than “networks” after observing many recurring spatial maps containing significant amounts of anticorrelated spontaneous activity; presumably, two functionally distinct networks may anticorrelate (e.g., if they represent alternative brain states that do not in general simultaneously coexist), and it would be inappropriate to consider the two networks as a single functional network—hence the more general term “modes.”

Although we aim to identify temporally independent modes, temporal ICA for FMRI data remains considerably less robust than spatial ICA. This means that to be able to identify TFMs robustly and reproducibly, we need to improve data quality and increase the temporal sampling rate, and also to develop an efficient analysis strategy to allow the estimation of temporal independence. We address the former by using improved FMRI pulse sequences, developed initially to address the challenges of high-resolution FMRI at ultra-high fields and subsequently developed further as part of the National Institutes of Health (NIH) Human Connectome Project. We used accelerated imaging to acquire multiple slices of data simultaneously, covering the entire brain in 0.8 s. A total of 36 10-min runs of resting FMRI data yielded 24,000 time points concatenated from five subjects. To maximize robustness of the final temporal ICA, we align multiple subjects’ datasets to each other with high accuracy and then perform an initial decomposition of the whole-group data with spatial ICA at high dimensionality. After removing artifact components, the remaining components are the desired functional parcels, whose time series are then fed into temporal ICA. This identifies TFMs—each temporal ICA component is a distinct TFM, comprising a time series (guaranteed to be independent of all other TFM time series) as well as a vector that describes the (positive or negative) strength of involvement of each of the many network nodes (functional parcels derived by the spatial ICA) in the given TFM.

We present results from a TFM analysis of a resting FMRI accelerated imaging dataset showing multiple functional networks that differ substantially from previously shown resting-state networks, and which are therefore of significant value in aiding our understanding of sensory, motor, and cognitive networks in the brain. We found both between-subject and between-study reproducibility.

Results

From 36 10-min sessions of resting FMRI data, concatenated temporally, we derived 200 spatial ICA components. We identified 58 of these as artifacts. The remaining 142 components have relatively compact spatial patterns, and we refer to these as “network nodes.” The 142 nodes’ time series were fed into 21-dimensional temporal ICA, identifying 21 TFMs. A TFM can be considered spatially as a pattern or set of weights over these spatial nodes. We now present the 21 TFMs and discuss their anatomical and functional relevance; the 21 spatial maps can be seen in greater detail in SI Appendix. Axial/coronal 2D slices are shown left–right reversed; color overlays denote significance of P < 0.05 (corrected for multiple comparisons; Methods).

Visual Areas.

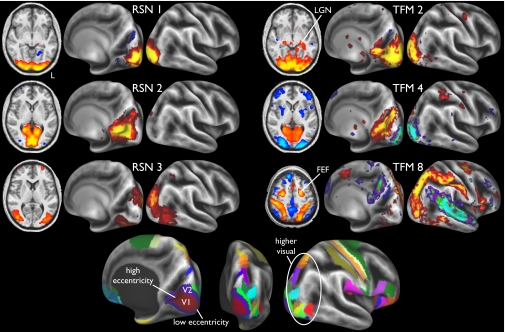
Fig. 1 compares the three major visual components derived from a standard low-dimensional spatial ICA decomposition of the group data (i.e., resting-state networks) with the three major visual components from the TFM analysis. Both analyses were carried out with a final ICA dimensionality of 21. These RSNs and TFMs were strongly symmetric between the left and right hemispheres. Comparison with an atlas-derived parcellation of visual areas shows that RSN 1 occupies the central-field representation of areas V1 and V2, RSN 2 mainly occupies peripheral V1 and V2, and RSN 3 occupies a broad neighboring swath of dorsal and ventral extrastriate visual cortex, including several “higher” retinotopic areas. The RSNs are spatially largely nonoverlapping, and their time courses were positively correlated with each other.

Fig. 1.

Three visual components from a 21-dimensional spatial ICA decomposition of the complete dataset, as well as three components from the 21-dimensional TFM analysis. To help localize the maps structurally, they are shown on the partially inflated cortical surface, with sulci indicated by darker background intensity. To help localize the maps functionally, the bottom row shows several cytoarchitecturally based (V1 and V2) and retinotopically based (higher visual) areas from the “FS_LR” atlas (11). LGN, lateral geniculate nucleus. FEF, frontal eye fields.

The three TFMs have distinctly different spatial patterns. TFM 2 includes all of V1 and V2, as well as lateral geniculate nucleus, with very little anticorrelation, indicating a functional mode in which activity is temporally coordinated throughout low-level visual areas and nuclei in both hemispheres. TFM 4 shows a spatially segregated pattern with anticorrelated activity between low and high eccentricity, indicating a different mode involving a push–pull relationship between the activity in regions corresponding approximately to RSNs 1 and 2. This is consistent with deactivation found in task studies (8), where foveal activation causes deactivation in the high eccentricity area and vice versa.

The spatial maps of TFMs 2 and 4 approximate the mean and difference of RSNs 1 and 2, respectively, as one might expect if one applied a principal component analysis, thus enforcing spatial and temporal orthogonality. However, there is no such constraint in the temporal ICA model to force this outcome. If, for example, one TFM covered all of V1 and the other only included the foveal part, the temporal ICA would be expected to report exactly that (7).

TFM 8 occupies much of the extrastriate swath found in RSN 3, but it also extends across the “dorsal visual stream” and into parietal somatosensory cortex, as well as the frontal eye fields. This has also been referred to as the “task-positive network” (9), and includes regions activated in attention tasks. The anticorrelated regions include several parts of the default mode network, including (somewhat weakly compared with some other TFMs) posterior cingulate cortex (PCC) and parts of primary and association auditory cortex. This TFM connects higher-level visual areas to the rest of the dorsal visual stream as a single integrated network more cleanly than is seen in any single RSN.

TFMs Relevant to the Default Mode Network.

The default mode network (DMN) is a well-characterized RSN that shows a consistent pattern of (temporally averaged) correlations and anticorrelations (9). The DMN deactivates (compared with baseline) under many attention tasks, and is often estimated in resting FMRI studies by seeding a correlation map from PCC. Several of the TFMs overlap spatially with the areas involved in the DMN.

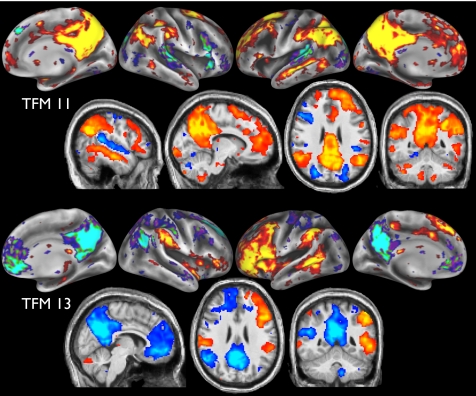
Consider, for example, TFMs 11 and 13 (Fig. 2). Both have strong overlap with parts of the DMN, but are different from one another in important respects. TFM 11 contains large portions of the DMN, including PCC/precuneus, anterior cingulate cortex (ACC), and widespread angular gyrus, along with Brodmann 22 and frontal areas 9/46. These regions are very similar to the “semantic network” found in a meta-analysis of 120 semantic system studies (10). Anticorrelated regions are less prominent, including early auditory (Brodmann 42) and higher-level visual regions. TFM 13 also includes large and asymmetric frontal areas (more lateral than in TFM 11), and is the only TFM to strongly cover Broca's area (Brodmann 44). This forms part of a strongly lateralized “language” network, including bilateral supramarginal gyrus, which anticorrelates with much of the known DMN (without including auditory), with the medial-frontal part of the DMN being strongly lateralized toward the right. TFM 13, which might be considered a “language versus default mode” system, is quite distinct from previously seen RSN spatial patterns, and is reproducible across studies (see below).

Fig. 2.

Spatial maps for TFMs 11 (semantic with default mode system) and 13 (language versus default mode system).

Even with the large reduction in dimensionality when modeling the entire dataset as 21 TFMs, we expect that the combined (averaged) behavior across all TFMs should reproduce any average correlation-based results obtained from the original dataset. We now compare these two analyses, with respect to PCC-seeded correlation, to demonstrate that this is indeed the case, before noting how the relevant TFMs are spatially overlapping but distinct from each other.

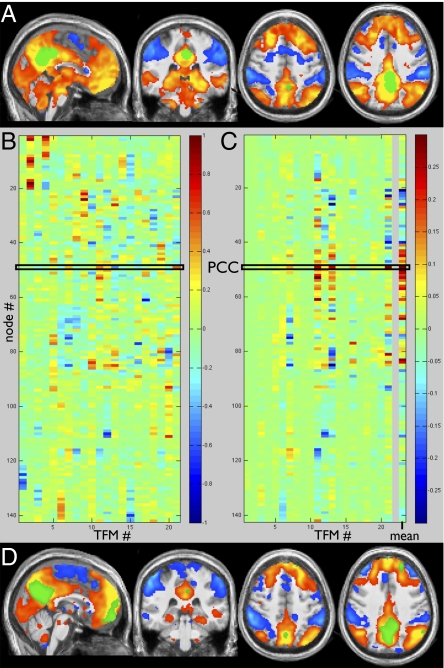
To carry out a standard seed-based correlation analysis (voxelwise) of the DMN with our dataset, we identified a PCC seed region using a combination of coordinates from three previous studies (2, 9, 12). Starting from a seed mask containing four voxels (in MNI152 space), we dilated about these points with a sphere of radius 6 mm, smoothed the result by a Gaussian of half-width 5 mm, and thresholded the result to give a PCC mask (Fig. 3A, green). From all subjects’ combined 4D datasets (in MNI152 space), we averaged the resting FMRI time series from all voxels in the PCC mask and regressed this into the 4D datasets, giving an average PCC-seeded correlation map (Fig. 3A). This corresponds well to published areas of DMN correlation and anticorrelation (e.g., in the studies from which we took the PCC seed coordinates).

Fig. 3.

Average correlations with PCC, estimated through seed-based correlation (A) and by averaging across all TFMs (B–D). (A) PCC seed region (green) is determined based on standard-space coordinates from the DMN literature: (−5.1, −52.5, 40.7), (−2, −39, 38.2), (0, −54.9, 26.5), (−6, −58, 28). The PCC's average time series is regressed against all voxels’ time series, resulting in the average map of correlation (red-yellow) and anticorrelation (blue). (B) The 21 TFM node-weight vectors; each column shows the node weights that make up the “spatial map” for a given TFM. (C) Each vector was multiplied by its entry for node 49 (PCC), and the results were then averaged across all TFMs, giving the right-most column. This average depicts the node weights corresponding to the average correlation with PCC, and is shown as a voxelwise map (D) by multiplying the value for each node by the corresponding node's spatial map. The PCC node is in green.

A similar average correlation map emerged from combining across all TFMs. The node-weight vectors for the 21 TFMs (the 142 × 21 temporal ICA mixing matrix) are shown in Fig. 3B. (Node ordering had previously been determined by clustering groups of nodes with similar time courses; SI Appendix, Fig. 1). The low node-number visual regions are prominent in TFMs 2 and 4 (Fig. 3B, Top Left); the anticorrelations within TFM 4 are apparent as red versus blue elements. Spatial correlation revealed that node 49 corresponded strongly to the PCC seed mask; this node can be seen in green in Fig. 3D. We then computed a spatial map (node-weight vector) that is the weighted average over all TFMs, with each TFM weighted according to the extent to which the PCC node (49) is involved in it (inverting the sign if the PCC's weight was negative). This is the average PCC correlation information, calculated via the TFM decomposition (Fig. 3C, Right). Multiplying this by the 142 nodes’ 3D voxelwise maps yields the average PCC correlation map (Fig. 3D).

Because the correlation with PCC, averaged across all TFMs, clearly shows the well-known DMN areas of correlation and anticorrelation, it is of interest to consider more carefully the message conveyed by the matrix in Fig. 3C. Several distinct TFMs contribute strongly to the average DMN appearance, in particular TFMs 7, 11, 12, 13, 16, and 21, and there is significant spatial overlap between these networks. Each of these TFMs has a distinct profile of node weights. For example, the areas showing anticorrelation with PCC (all blue elements in Fig. 3C) are quite different in the different TFMs. This indicates that separate temporal processes (that the time-averaged seed-based correlation does not separate from each other) give rise to the overall time-averaged pattern of correlations and anticorrelations traditionally associated with the DMN—it is not a single functional network. That distinct TFMs (e.g., 11, 13) relate to the DMN in quite different ways (positive correlation with semantics in TFM 11, and anticorrelation with language in TFM 13) provides insight into their functional significance.

Further Sensory-Motor and Cognitive TFMs.

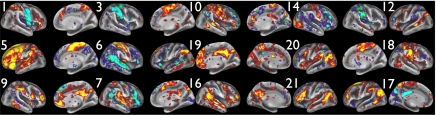
We now discuss the remaining “neuronal” TFMs, which can be seen in Fig. 4 (in addition to TFM 5; see below). TFM 1 contains much of the dorsal visual stream, similar to TFM 8. However, whereas in 8 the anticorrelated regions include the DMN and auditory areas, here anticorrelation is strongly found in primary motor-somatosensory (mouth or face), along with supplementary motor area (SMA) and posterior putamen/pallidum, premotor thalamus, and the cerebellar “face area.” TFM 3 is dominated by primary and secondary sensory-motor areas (particularly at the level of the upper extremity representation), along with superior temporal sulcus and cerebellum VI. The anticorrelated regions are weaker, including parts of superior parietal lobule and ACC. TFM 6 has strong anticorrelation between primary sensory-motor, SMA, premotor thalamus, SII, and cingulate motor, versus primary auditory, medial DMN, and Brodmann 45. TFM 10 contains widespread motor-somatosensory, posterior superior temporal sulcus, and areas 45 and 47l, anticorrelated with posterior intraparietal sulcus (IPS), angular gyrus, and dorso-lateral prefrontal cortex (DLPFC). TFM 14 sees extrastriate visual correlating with parts of somatosensory and retrosplenial cortex; anticorrelations include large parts of posterior right frontal cortex, striate visual cortex, and left cerebellum. TFM 18 is dominated by motor-somatosensory regions, with focal anticorrelation in areas 39/40. TFM 20 contains some higher-level visual, superior parietal-occipital sulcus, anterior insula, and posterior IPS, and anticorrelated regions in retrosplenial cortex (areas 29 and 30).

Fig. 4.

A further 15 TFMs from the set of 21. The most informative view(s) for each is chosen from the left/right, medial/lateral surfaces.

TFM 7 strongly involves medial parts of the DMN (PCC/precuneus and ACC), along with primary and early association auditory cortex, parts of the parietal-occipital fissure, and frontal area 10; anticorrelated regions include superior temporal sulcus and Broca (area 45 more than 44). TFM 9 includes dorso-lateral prefrontal cortex, inferior parietal lobule, and lateral occipital areas, anticorrelated with supramarginal/angular gyrus. TFM 12 contains parts of the semantic network on the left, anticorrelated with right somatosensory association areas. TFM 16 contains bilateral superior temporal sulcus correlated with parts of premotor bilaterally, retrosplenial cortex, DLPFC, and medial-parietal cortex; anticorrelated areas include pre-SMA and more anterior medial-frontal cortex. TFM 21 sees DMN areas (including PCC) anticorrelated with lateral-frontal regions often seen as part of the “executive control” RSN. TFM 17 is dominated by a distinctive posterior-medial pattern containing two close (but not connected) areas. Because of the position in/near PCC, this TFM has likely merged into many previous PCC-seeded DMN analyses; anticorrelated regions include area 39 and Brodmann 6 and 8. TFM 19 contains parts of the DMN and strong involvement of Crus I in the cerebellum; anticorrelation includes primary and association auditory cortex.

“Global” TFM Spatial Maps.

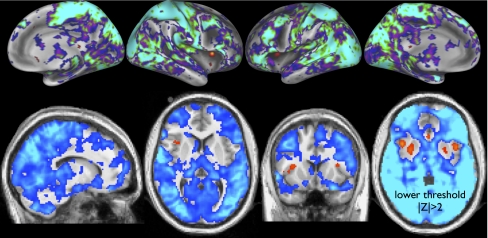
Finally, TFMs 15 (Fig. 5) and 5 (Fig. 4)are unlike the other TFMs in that they show widespread signal across much of the gray matter, with very small areas of anticorrelation. Their temporal power spectra (shown in SI Appendix) are largely similar to the other TFMs below 0.2 Hz, but have raised power above 0.2 Hz. There could well be some nonneural physiological contribution to these TFMs, although the temporal resolution is not quite high enough to avoid aliasing of cardiac pulsation, and hence it is not easy to differentiate (for example) cardiac and breathing effects in the spectra. TFM 15 includes anticorrelation in anterior insula (probably lateral agranular insula) and (more weakly) in the putamen. The insula is implicated in heart rate control and other autonomic functions (13–15); hence, the insular signal seen here might be neural in origin, and related to vascular (as distinct from neural) effects seen in gray matter in virtually all other regions.

Fig. 5.

TFM 15 (global versus insula mode).

TFM Reproducibility.

To gain further confidence in our results, we confirmed significant reproducibility in tests between separate groups of subjects. We also found encouraging results (several TFMs matching what we have shown above, including TFMs 8, 13, and 15) from a separate study utilizing a more traditional acquisition. See SI Appendix for details.

Discussion

We have demonstrated spontaneously varying modes of brain function, identified on the basis of their temporal independence. This approach presents technical challenges, as it is fundamentally less robust than the seed-based correlation and spatial ICA methods in common use. However, by using accelerated MRI acquisition that generates much more densely sampled time series, along with improved cross-subject alignment and two stages of artifact removal, we identified a set of temporal functional modes that are reproducible and robust. Several of these TFMs seem to be functionally interpretable, although much remains to be done on this front.

The well-known patterns of correlation and anticorrelation that make up the default mode network and the task-positive network appear to reflect the summation of multiple functionally (temporally) distinct processes, which overlap spatially, and hence become merged together in averaged seed-based correlation analyses. The notion that the DMN comprises multiple functional subnetworks has previously been suggested, based on changing patterns of correlation when a seed region is moved across distinct neighboring regions (e.g., 16). However, such analyses have generally been based on simple correlation, and so are fundamentally limited in their ability to differentiate spatially overlapping networks from each other.

Of relevance to this, an area of increasing interest is the study of temporal nonstationarities in resting-state patterns. The term “nonstationarity” implies that a statistic of interest is nonconstant, and it is used in a variety of ways; for example, nonstationarity might (i) refer to an apparent change over time in correlation between two regions (2); (ii) refer to changes in the mean and/or variance in the time course of a functional network (or TFM); or (iii) refer to the underlying network structure changing over time. If multiple functional networks are static over time in terms of each network's “internal” connection strengths, but each has its own fluctuating overall activity level (case ii), the network structure may be stationary, but apparent nonstationarity in correlation will occur (e.g., as measured via sliding-window correlation, or apparent as session variability). Indeed, many other factors (that may not be functionally interesting) can also cause apparent changes in correlation, including changing noise level or poor sampling of the correlation (e.g., allowing the signal to remain dominated by wavelengths longer than the scale of the window in sliding-window correlation). Given that the TFM model allows brain regions to be part of multiple networks, this model may account for some of the apparent nonstationarity seen in simple correlation (case i). By reconstructing the data from the TFM model (i.e., assuming each TFM's set of connections, and their strengths, is fixed), we can estimate the remaining apparent nonstationarity in correlation and hence estimate how much apparent correlation nonstationarity is due purely to the overlapping networks rather than other factors such as nonmodeled noise or “deeper” nonstationarities (case iii). Using sliding-window correlation (see SI Appendix for more details), we found that at least 25% of the apparent nonstationarity in raw data correlations is attributable to the fact that multiple (internally fixed) functional networks with time-varying amplitude are spatially overlapping.

Spatially, many (although not all) of the TFMs contain significant spatial areas of both strongly positive and negative values, meaning that, with respect to a given TFM's time course (and hence, we propose, function), there is considerable deactivation synchronized with activation. This is much less apparent in the spatial maps of resting-state networks identified from spatial ICA. Anticorrelations involving the DMN have been reported using seed-based correlation (9), and although there has been some debate over certain preprocessing enhancing (or even creating) this anticorrelation, it does now seem clear that there is indeed real underlying anticorrelation (12). The anticorrelations reported here support that conclusion, and are not subject to the same (preprocessing-related) methodological concerns. The most obvious interpretations of anticorrelations relate to mutual functional incompatibility (particularly in cognitive networks) and suppression (more likely in sensory areas). The former scenario might be most strongly argued for functional modes that require conscious involvement; if it is the case that conscious thought can only strongly be involved in one kind of cognitive task at any one moment (semantic, decision making, memory recall, etc.), this might lead to anticorrelation between the areas involved in those different tasks. If indeed there are multiple networks that are all mutually incompatible, this suggests that our focus on temporal independence, although being more appropriate than spatial independence, may still be suboptimal; one may need to relax constraints of total mutual independence (and orthogonality) in time (temporal ICA) and space (spatial ICA). One possible strategy would be to maximize non-Gaussianity in space and time, while not fully enforcing independence/orthogonality. Along these lines, although enforcing spatial sparsity may be a practical way to optimize non-Gaussianity, this is unlikely to be a sensible approach temporally (we see no evidence that the TFM time courses are sparse). Although the spatiotemporal approach of ref. 17 might be useful in this context, if it is the case that anticorrelation really does occur within a single biological component, it is unlikely to make sense to optimize for skew of the spatial maps. In the temporal domain, given that many object to the concept of deactivation as a meaningful biological concept (as opposed to nonactivation, including inhibition), it might make sense to constrain the component time courses to be only positive (or zero); this is achieved in a nonnegative matrix factorization (18). However, such methods assume that both domains (time and space) have to be fully nonnegative, so again this does not perfectly suit our needs. Instead, it would be valuable to develop methods for weakening the temporal independence constraint (and hence potentially improving interpretability of the components found), while also seeking to improve computational robustness.

We believe that the advances presented here make a contribution toward improved mapping of the brain's functional modes. Through FMRI data quality improvements such as the accelerated imaging used here, and with increased integration with other modalities such as magnetoencephalography, new modeling methods should be able to derive ever richer and more interpretable mapping of the brain's functions and networks.

Methods

For details, see SI Appendix Methods. We acquired 36 10-min resting FMRI datasets in seven sessions from five healthy adults (one subject being scanned on three separate occasions). The imaging was approved by the institutional review board at the University of Minnesota, and subjects provided informed consent. Data were acquired on a standard 3T Siemens Trio, with 40 mT⋅m⁻¹ maximum gradients and a slew rate of 200 mT⋅m⁻¹⋅s⁻¹. A 32-channel receive-only radio-frequency (RF) head-coil array was used, along with a body RF transmitter. The FMRI time-series data were acquired using multiband (MB) accelerated (19) echo-planar imaging with controlled aliasing. Three slices were simultaneously excited (MB = 3), giving a whole-brain temporal resolution of 0.8 s.

Data were analyzed primarily using tools from FSL (20) as well as FreeSurfer (21) for cortical surface modeling, and FastICA (22) for temporal ICA. For visualization, we used tools from FSL and Caret (http://brainvis.wustl.edu/wiki/index.php/Caret:About). Each 10-min FMRI dataset was corrected for head motion and high-pass–filtered to remove drifts before being fed into spatial ICA to find and remove the majority of artifacts. We then mapped each 4D dataset into a standard representation of gray matter (“grayordinates”) currently being developed for the NIH Human Connectome Project; this is a combination of cortical midgray surface vertices and 3D subcortical/cerebellar voxels (from a 3D nonlinear registration of the structural to the MNI152 standard template image). The set of grayordinates is arranged as a single long vector of vertices and voxels, and thus each FMRI time-series dataset can be represented in this standard system as a 2D matrix of grayordinates × time points.

We concatenated temporally all subjects’ datasets in this format to feed into the following groupwise ICA. We applied a high-dimensional spatial ICA to identify further artifactual components as well as achieve a high-dimensional functional parcellation of the group data. From a 200-dimensional spatial ICA, we manually identified 58 components as artifacts. These were then regressed out of the remaining 142 time series, leaving 142 functional nodes—node time series and associated spatial maps. The 142 node time series were then fed into temporal ICA (the TFM analysis) with an ICA dimensionality of 21, that is, to find the 21 strongest TFMs present in the group data as a whole. Thus, the overall model (see SI Appendix for details) is

X is the data matrix of size Voxels (or grayordinates) × Timepoints, represented as a product of three matrices: S_s are the spatial maps (network nodes) estimated by the initial K-dimensional spatial ICA (after regressing out the artifact components), S_t are the TFM time courses from the L-dimensional temporal ICA, and A_t is a central mixing matrix that describes the node membership for each TFM. The lth column in A_t contains the 142 node weights for TFM l; these weights can be positive or negative, and where we see significant positive and negative values in a single column, the analysis is telling us that different areas of the brain are anticorrelated with each other with respect to the particular behavior of that specific TFM. Fig. 3B is showing A_t. E combines noise and artifacts.

All TFM spatial maps shown were obtained by regressing the TFM time courses into the original datasets and averaging the resulting maps across all runs/subjects, with a within-run significance level of P < 0.05, corrected for multiple comparisons across space. The sign of the spatial maps (and associated time courses) is arbitrary; inverting the sign of one spatial map and its associated time course gives an equivalent model of the data. TFM spatial maps are shown both on the inflated cortical surface (what looks like the right hemisphere is the right hemisphere) and with axial/coronal/sagittal 2D slices (shown left–right reversed).

All analysis software used is either already publicly available or will be released in upcoming versions of FSL, Caret, and Human Connectome Project toolkits. The multiband FMRI pulse sequence and reconstruction code is available from the Center for Magnetic Resonance Research, University of Minnesota, for the Siemens VB17 platform with a 32-channel receive coil, and is expected shortly to be available as a Siemens “Works in Progress” package. Collection of the full Human Connectome Project datasets is due to begin in 2012, once the imaging protocols have been finalized; these datasets will be made publicly available. Our TFM and RSN maps are available from SumsDB (http://sumsdb.wustl.edu/sums/directory.do?id=8288032&dir_name=TFM_PNAS).